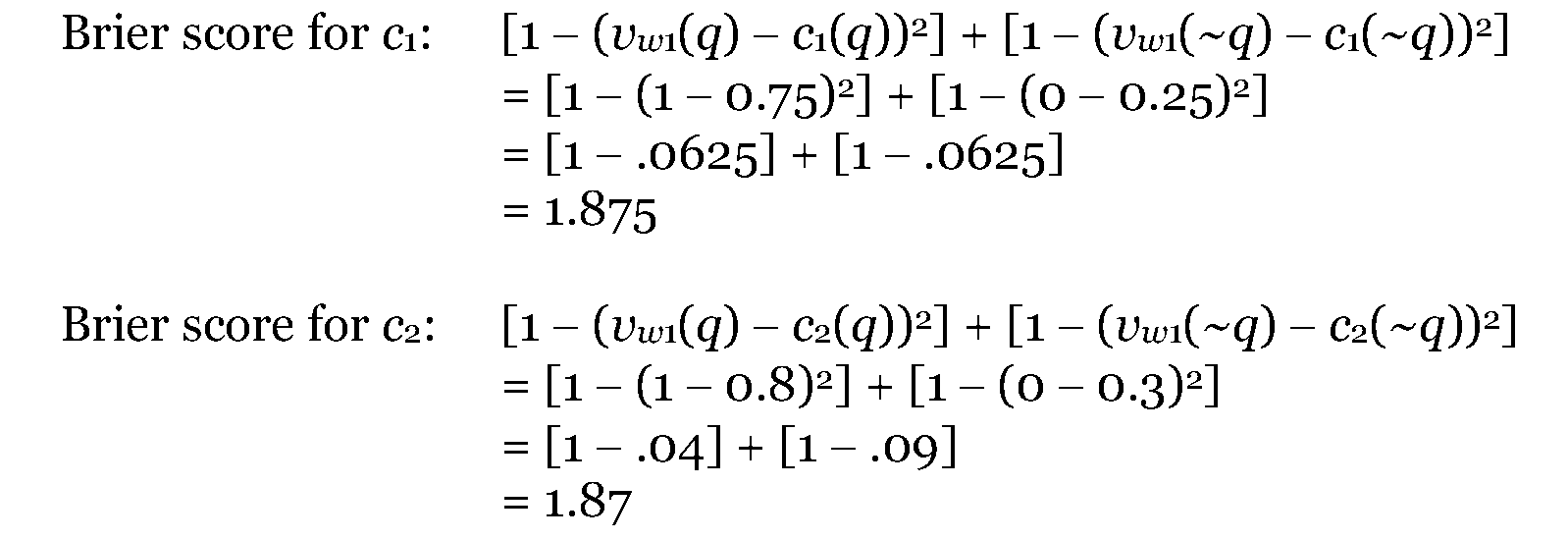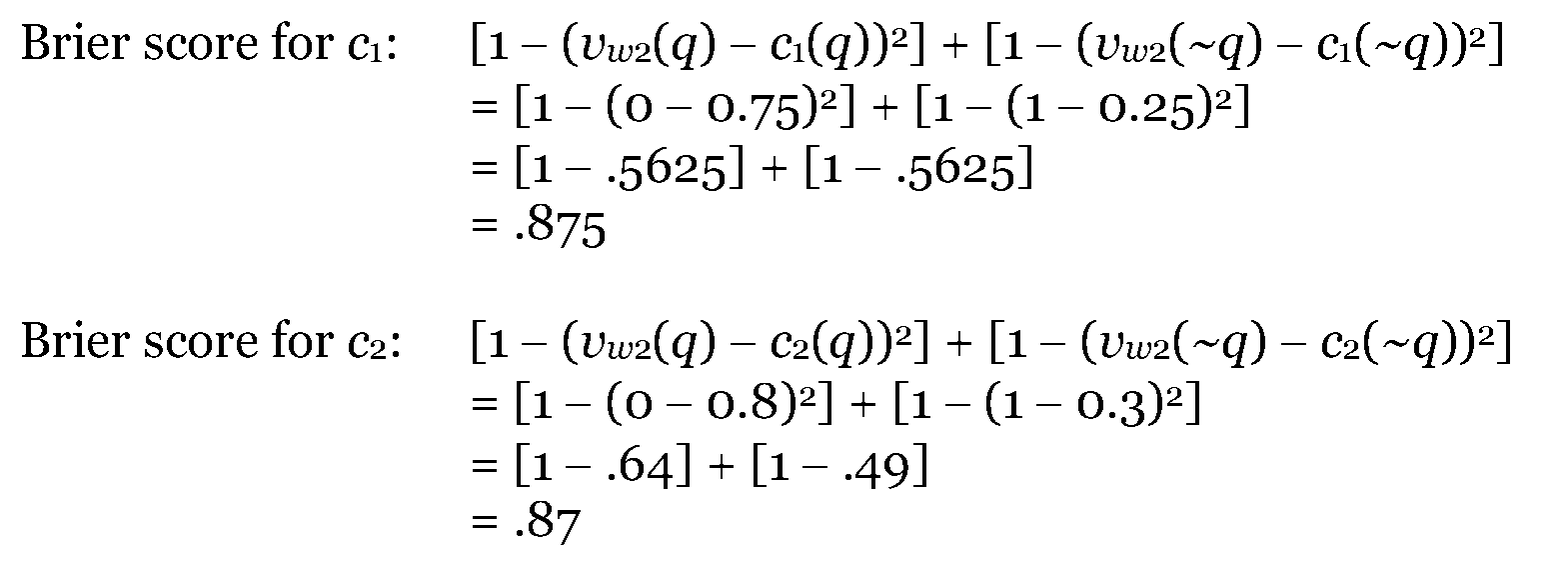Epistemic Consequentialism

Consequentialism is the view that, in some sense, rightness is to be understood in terms of conduciveness to goodness. Much of the philosophical discussion concerning consequentialism has focused on moral rightness or obligation or normativity. But there is plausibly also epistemic rightness, epistemic obligation, and epistemic normativity. Epistemic rightness is often denoted with talk of justification, rationality, or by merely indicating what should be believed. For example, my belief that I have hands is justified, while my belief that I will win the lottery is not; Alice’s total belief state is rational, while Lucy’s is not; we all should be at least as confident in p or q as we are in p. The epistemic consequentialist claims, roughly, that these kinds of facts about epistemic rightness depend solely on facts about the goodness of the consequences. In slogan form, such a view holds that the epistemic good is prior to the epistemic right.

Many epistemologists seem to have sympathy for the basic idea behind epistemic consequentialism, because many epistemologists have been attracted to the idea that epistemic norms that describe appropriate belief-forming behavior ultimately earn their keep by providing us with some means to garner what is often thought to be the epistemic good of accurate beliefs. Consequentialist thinking has also gained popularity among more formally minded epistemologists, who apply the tools of decision theory to argue in consequentialist fashion for various epistemic norms. And there is also a consequentialist strand in certain areas of philosophy of science, especially those areas that attempt to explain how it is that science as a whole might have considerable epistemic success even if individual scientists are acting irrationally. Thus, there is a kind of prima facie plausibility to epistemic consequentialism.

Consequentialism
Final Value and Veritism
Consequentialist Theories
Summing Up: Some Useful Distinctions
Objections to Epistemic Consequentialism
References and Further Reading

1. Consequentialism

There is unfortunately no consensus about what precisely makes a theory a consequentialist theory. Sometimes it is said that the consequentialist understand the right in terms of the good. Somewhat more generally, but still imprecisely, we could say that the consequentialist maintains that normative facts about Xs (for example, facts about the rightness of actions) depend solely on facts about the value of the consequences of Xs. In light of this, some see consequentialism as a reductive thesis: it purports to reduce normative facts (for instance, about what one ought to do) to evaluative facts of a certain sort (for instance, about what is good). Smith (2009) and others, however, mark what is distinctive about consequentialism differently. Some maintain that a consequentialist is committed to understanding what is right or obligatory in terms of what will maximize value (Smart and Williams 1973, Pettit 2000, Portmore 2007). Still others maintain that a consequentialist is one who is committed to only agent-neutral, rather than agent-relative prescriptions (where an example of an agent-relative prescription is one that instructs each person S to ensure that S not lie, whereas an agent-neutral prescription instructs each person S to minimize lying) (McNaughton and Rawling 1991). And finally, some maintain that what is distinctive about consequentialism is the lack of intrinsic constraints on action types (Nozick 1974, Nagel 1986, Kagan 1997).

Perhaps the best way to elucidate consequentialism, then, is to point to paradigm cases of consequentialist theories and attempt to generalize from them. On this score there is some agreement: classic hedonic utilitarianism (of the sort defended by Bentham and Mill) is thought to be a clear instance of a consequentialist theory. That theory maintains that an action is morally right if and only if the total sum of pleasure minus pain that results from that action exceeds the total sum of pleasure minus pain of any alternative to that action. The normative facts here are facts about the moral rightness of actions and the utilitarian claims that these facts depend solely on facts about the moral goodness of the consequences of actions, where moral goodness is measured by summing up total pleasure minus total pain.

Though it is not possible to give an uncontroversial set of necessary and sufficient conditions for a theory being a species of consequentialism, it is useful to see that there is some sort of unity to views, such as hedonic utilitarianism, normally classified as consequentialist. The following three-step “recipe” for a consequentialist theory evinces this unity, and will be useful to refer to later. (A similar recipe is given by Berker 2013a,b.)

Step 1. Final Value: identify what has final value, where something has final value iff it is valuable for its own sake (sometimes the term “intrinsic value” is used in the same way).

Example: For the classic hedonic utilitarian, pleasure is the sole thing of final value and pain is the sole thing of final disvalue; thus, final value is here generalizing the concept of moral goodness above.

Step 2. Ranking: explain how certain things relevant to the normative facts you care about are ranked in virtue of their conduciveness to things with final value.

Example: The normative facts of interest to the classic hedonic utilitarian are facts about the rightness and wrongness of actions, so actions are the relevant things to rank. The classic hedonic utilitarian says that actions can be ordered by calculating for each action the sum of the total final value in the consequences of that action.

Step 3. Normative Facts: explain how the normative facts are determined by facts about the rankings.

Example: The classic hedonic utilitarian says that an action a is right if and only if it is ranked at least as high as of any action that is an alternative to a.

2. Final Value and Veritism

Before looking at specific consequentialist epistemic theories, it is worth saying something about what epistemic consequentialists typically think about the first step in the recipe, which concerns final value. Many who are sympathetic to epistemic consequentialism also adhere to veritism (the term is due to Goldman 1999; Pritchard 2010 calls this view epistemic value t-monism). According to veritism, the only thing of final epistemic value is true belief and the only thing of final epistemic disvalue is false belief. Generalizing somewhat so that the view can capture approaches that think of belief as graded, we can say that according to veritism, the only thing of final epistemic value is accuracy and the only thing of final epistemic disvalue is inaccuracy. Not all epistemic consequentialists are veritists; others have thought that there is more to final epistemic value than mere accuracy, such as the informativeness or interestingness of the propositions believed, or whether the propositions believed are mutually explanatory or coherent. Others have thought that things such as wisdom (Whitcomb 2007), understanding (Kvanvig 2003), or a love of truth (Zagzebski 2003) have final epistemic value.

But even those consequentialists who think that accuracy does not exhaust what is epistemically valuable tend to think that accuracy is an important component of final epistemic value (for an alternative view, see Stich 1993). It is not hard to see why such a view is theoretically attractive. Although all explanations must come to an end somewhere, it seems that veritism, or at least something like it, is in a good position to give satisfying explanations of our epistemic norms. Veritism together with consequentialism can do so by showing how conforming to that norm conduces toward the goal of accuracy. If one could show, say, that by respecting one’s evidence one is likely to hold accurate beliefs, then one has a better explanation for an evidence-respecting norm than does the person who says such a norm is simply a brute epistemic fact.

Questions about final epistemic value are important for would-be epistemic consequentialists. This article notes the different views that epistemic consequentialists have held concerning final epistemic value, but there is little substantive discussion about the advantages and disadvantages of competing views about final epistemic value. That said, the debate concerning the nature of final epistemic value is an important debate for epistemic consequentialists to watch. In particular, the epistemic consequentialist will need a notion of final epistemic value according to which final epistemic value is the sort of thing that it makes sense to promote.

3. Consequentialist Theories

In light of the consequentialist recipe above, a specific epistemic consequentialist theory can be obtained by specifying the bearers of final epistemic value, the principle by which options are then ranked in terms of final epistemic value, and the normative facts that this ranking determines. Below, specific epistemic consequentialist theories are presented in this way.

a. A Simple Example

For illustrative purposes, consider a very simple consequentialist theory. According to this view, the only thing of final epistemic value is true belief. Then, say that a belief is justified to the extent that it garners epistemic value for the believer. This can be put in the consequentialist recipe as follows:

Step 1. Final Value: True beliefs have final epistemic value; false beliefs have final epistemic disvalue.

Step 2. Ranking: The normative facts at issue are facts about whether beliefs are justified, so beliefs are the natural thing to rank. According to this view, S’s belief that p is ranked above S’s belief that q iff the belief that p in itself and in its causal consequences garners more epistemic value for S than the belief that q.

Step 3. Normative Facts: The belief that p is justified iff it is ranked above every alternative to believing p.

One might think that this simple view has a relatively obvious flaw. It seems to imply that every true belief is justified and every false belief unjustified. This is what Maitzen (1995) argues:

If one seeks, above all else, to maximize the number of true (and minimize the number of false) beliefs in one’s (presumably large) stock of beliefs, then adding one more true belief surely counts as serving that goal, while adding a false belief surely counts as disserving it. (p. 870)

As clear as this seems, it is actually mistaken. For although the belief that p (when p is false) will not directly add value to S’s belief state, such a false belief may have an effect on other beliefs that S forms later and so, in total, be preferable to adopting the true belief that ~p. That said, no one has defended such a simple version of epistemic consequentialism. In actual practice, the relationship between final epistemic value and epistemic justifiedness is not proposed to be as direct as this simple view would have it. With that, we turn to examine such views.

b. Cognitive Decision Theory

Suppose that we think that rational agents have degrees of belief that can be represented by probability functions, but we think there are still important all-or-nothing epistemic options that these agents have regarding which propositions they accept as true. Patrick Maher (1993), for instance, argues that even if we think of scientists as having degrees of belief, we still need a theory of acceptance if we want to understand science. Why is this? Maher defines accepting that p as sincerely asserting that p (this is not the only definition of acceptance; van Fraassen (1980), though he is writing primarily about subjective probability, thinks of acceptance as a kind of cognitive commitment; Harman (1986, p. 47) sees acceptance as the same as belief and says that one accepts p when (1) one allows oneself to use p as part of one’s starting point for further reasoning and when (2) one takes the issue whether p to be closed in the sense that one is no longer investigating that issue). Further, Maher maintains that the scientific record tells us about which theories scientists asserted not about what credences scientists had. Thus, a theory of acceptance (in the sense of sincere assertion) is needed to understand science on Maher’s view.

If we think of things roughly in this way, then it is natural to turn to decision theory to determine what propositions agents should accept. Decision theory tells an agent which action it would be rational to perform based on a ranking of each action available to the agent in terms of the action’s expected value. To find the expected value of an action for an agent, one considers each set of consequences the agent thinks is possible given the performance of that action, and then sums up the value of those consequences, weighted by the agent’s degrees of belief that those consequences are realized conditional on that action. An action is then taken to be rational iff no other action is ranked higher than it in terms of expected value. When considering which proposition it would be rational for an agent to accept, it is natural to set things up similarly. Instead of evaluating the usual type of actions, one evaluates acts of acceptance of propositions that are available to the agent. These different acts of acceptance can be ranked in terms of the expected final epistemic value of each act of acceptance.

Such an approach to acceptance is briefly discussed by Hempel (1960). Isaac Levi (1967) presents a more complete theory of this kind. Levi imagines that a scientist has a set of mutually exclusive and jointly exhaustive hypotheses h₁, h₂,…,h_n and that the scientist’s options for acts of acceptance are to accept one of the h_i or to accept a disjunction of some of them. We suppose that scientists have subjective probability functions, which reflect the evidence that they have gathered with respect to the hypotheses in question. Levi’s basic proposal is that agents should accept some hypothesis (or disjunction of hypotheses) if so-doing maximizes expected final epistemic value where the weight for the expectation is provided by the subjective probability function (this is very similar to, though not identical to, the weighting in terms of degrees of belief mentioned above). What is final epistemic value for Levi (Levi uses the term “epistemic utility”)? According to Levi, final epistemic value has two dimensions that correspond to what the goals of any disinterested researcher ought to be. The first dimension is truth. True answers are valued more than false answers. The second dimension is “relief from agnosticism.” The idea here is that more-informative answers (for example, “X wins”) are valued more than less-informative answers (for example, “X or Y wins”). These values pull in opposite directions. One can easily accept a true proposition if informativeness is ignored as the disjunction “X wins or X does not win” is sure to be true. Similarly, one can easily accept an informative proposition if truth is ignored. Accordingly, Levi defines a family of functions that balance these two dimensions of value. He does not settle on one way of balancing, but instead considers as permissible the whole family functions that balance these two dimensions of value in different ways.

Several features of Levi’s approach are worth noting. First, note that on Levi’s view it can happen that the proposition a scientist should accept is not the one that the scientist sees as most probable, because final epistemic value is a function of both the truth/falsity of the proposition and its informativeness.

The second point worth noting brings us to an important distinction when considering epistemic consequentialism. Levi is interested in the expected final epistemic value of accepting some proposition h₁, but where the value of the consequences of accepting h₁ include only the value of accepting h₁ and not the causal consequences of this acceptance. That is, suppose an agent has the option of accepting h₁ or accepting h₂. Suppose that h₁ is both more likely to be true and more informative than h₂. So on any weighting, and on any final epistemic value function, accepting h₁ will rank higher than h₂ if we ignore the later causal consequences of these acts of acceptance. But suppose that accepting h₂ is known to open up opportunities for garnering much more final epistemic value later (perhaps by allowing one to work on a research project only open to those who accept h₂). Levi’s theory says that the agent should accept h₁, not h₂. Thus, it is a form of consequentialism that ignores the causal consequences of the options being evaluated. What matters are not the causal consequences of accepting h₁, but rather the expected final value of the acceptance of h₁ itself, ignoring its later causal consequences.

One might argue that this feature of Levi’s view is enough to make it thereby not a form of consequentialism, because it is not faithful to the idea that the total set of causal consequences of an option (for example, an action or a belief or an act of acceptance) is relevant to the normative verdict concerning that option. Be that as it may, there is still a teleological structure to Levi’s view: acts of acceptance inherit their normative properties in virtue of conducing to something with final epistemic value. It is just that “conducing” is construed noncausally, in this case as something more akin to instantiation (Berker (2013a,b) explicitly allows such views to count as instances of epistemic consequentialism or epistemic teleology—he uses both terms). For future reference, I will use the term “restricted consequentialism” to refer to views that are teleological in the sense of Levi’s view, but do not take the total set of causal consequences of an option to be relevant to its normative status. In section 5, this distinction is examined more carefully.

Cognitive decision theory fits into our consequentialist recipe as follows:

Step 1. Final Value: Accepting propositions that are true has final epistemic value, and accepting propositions that are informative has final epistemic value. The total final epistemic value of accepting a proposition is a function of both its truth and its informativeness, though the way that these values are balanced can permissibly differ from agent to agent.

Step 2. Ranking: The act of accepting some answer to a question is ranked according to its subjective expected final epistemic value.

Step 3. Normative Facts: One should accept answer a to question Q iff accepting a is ranked at least as high as every other alternative answer to Q.

For criticism of this approach, see Stalnaker (2002) and Percival (2002).

c. Accuracy First

Cognitive decision theory takes for granted that agents have a certain kind of doxastic state, represented by a probability function, and uses this to tell us about the norms for the different kind of doxastic state of acceptance. But suppose that one does not want to take for granted such an initial doxastic state. Does decision theory have anything to offer such an epistemic consequentialist?

James Joyce (1998) shows that the answer to this question is “yes” if we accept certain assumptions about final epistemic value that many find plausible. Joyce argues that degrees of belief—henceforth, credences—that are not probabilities are accuracy-dominated by credences that are probabilities. A credence function, c, is accuracy-dominated by another, c¢, when in all possible worlds, the accuracy of c¢ is at least as great as the accuracy of c, and in at least one world, the accuracy of c¢ is greater than the accuracy of c (for an introduction to possible worlds, see IEP article Modal Metaphysics). Joyce uses this, plus some assumptions about final epistemic value to establish probabilism, the thesis that rational credences are probabilities.

As Pettigrew (2013c) has noted, the basic Joycean framework requires one to do three things. First, one defines a final epistemic value function (often called an “epistemic utility function”). Second, one selects a decision rule from decision theory. Finally, one proves a mathematical theorem of the sort that says only doxastic states with certain features are permissible given the decision rule and final epistemic value function. Let us consider each of these steps in turn.

The final epistemic value functions that are typically used are different in kind than the functions used in cognitive decision theory. Whereas the final epistemic value functions in cognitive decision theory tend to value both accuracy—that is, truth and falsity—and informativeness, the final epistemic value functions in the Joycean tradition value only accuracy (this is why the moniker “accuracy first” is appropriate). Accuracy can be understood in different ways. There are two main issues here: (1) what counts as perfect accuracy? (2) how does one measure how far away a doxastic state is from perfect accuracy? With respect to (1), Joyce (1998) takes a credence function to be perfectly accurate at a world when the credence function matches the truth-values of propositions in that world (that is, assigns 1s to the truths and 0s to the falsehoods). Many have followed him in this, although there are alternatives (for example, one could think that a credence function is perfectly accurate at a world if it matches the chances at that world rather than the truth-values at that world). With respect to (2), things get more complicated. The appropriate mathematical tool to use to calculate the distance a credence function is from perfect accuracy is a scoring rule, that is, a function that specifies an accuracy score for credence x in a proposition relative to two possibilities: the possibility that the proposition is true and the possibility that it is false. There are many constraints that can be placed on scoring rules, but one popular constraint is that the scoring rule be proper. A scoring rule is proper if and only if the expected accuracy score of a credence of x in a proposition q, where the expectation is weighted by probability function P, is maximized at x = P(q). Putting together a notion of perfect accuracy and a notion of distance to perfect accuracy yields a final epistemic value function that is sensitive solely to accuracy. One proper scoring rule that is often used as a measure of accuracy is the Brier score. Let v_w(q) be a function that takes value 1 if proposition q is true at possible world w and that takes value 0 if proposition q is false at possible world w. Thus, v_w(q) merely tells us whether proposition q is true or false at possible world w. In addition, let c(q) be the credence assigned to proposition q, and let be the set of propositions to which our credence function assigns credences. Then the Brier score for that credence function at possible world w is:
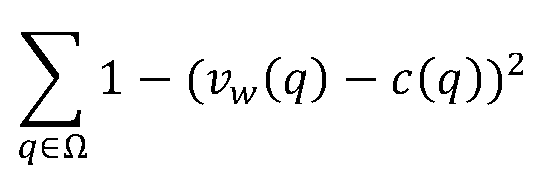This will give us an accuracy score for every credence function for any world we please. Suppose, for example, that we are considering two credence functions defined over only the proposition q and its negation:

c₁(q) = 0.75 c₂(q) = 0.8

c₁(~q) = 0.25 c₂(~q) = 0.3

There are two possible worlds to consider: the world where q is true and the world where it is false. In the world (call it “w1”) where q is true, the Brier score for each credence function is as follows:

As one can verify, c₁ scores better than c₂ in a world where q is true. Now, consider a world where q is false (call this world “w2”):

Again, as one can verify, c₁ scores better than c₂ in a world where q is false.

Once one has a final epistemic value function, such as the Brier score, one must pick a decision rule. Joyce (1998) uses the decision rule that dominated options are impermissible. In the example immediately above, c₁ is dominated by c₂ because c₁ scores better than or equal to c₂ in every possible world. Thus, c₂ is an impermissible credence function to have.

Our example considers only two very simple credence function. The final step in Joyce’s program is to prove a mathematical theorem that generalizes the specific thing we saw above. Joyce (1998) proves that for certain choices of accuracy measures, including the Brier score, every incoherent credence function is dominated by some coherent credence function, where a credence function is coherent iff it is a probability function. (Note that in our example, c₂ is incoherent while c₁ is coherent, thus illustrating an instance of this theorem.) Recall that probabilism is the thesis that rational credence functions are coherent. If we take permissible credence functions to be rational credence functions and if we can prove that no probabilistically coherent function is dominated by some probabilistically incoherent function—something that Joyce (1998) does not prove, but that is proven in Joyce (2009)—then we have a proof of probabilism from some assumptions about final epistemic value and about an appropriate decision rule.

Others have altered or extended this approach in various ways. One alteration of Joyce’s program is to use a different decision rule, for instance, the decision rule according to which permissible options maximize expected final epistemic value. Leitgeb and Pettigrew (2010a,b) use this decision rule to prove that no incoherent credence function maximizes expected utility.

The results can be extended to other norms, too. For instance, conditionalization is a rule about how to update one’s credence function in light of acquiring new information. Suppose that c is an agent’s credence function and c_e is the agent’s credence function after learning e and nothing else. Conditionalization maintains that the following should hold:

For all a, and all e, c(a|e) = c_e(a), so long as c(e) ≠ 0.

In this expression, c(a|e) is the conditional probability of a, given e. Greaves and Wallace (2006) prove that, with suitable choices for accuracy measures, the updating rule conditionalization maximizes expected utility in situations where the agent will get some new information from a partition (a simple case of this is where an agent will either learn p or learn ~p). Leitgeb and Pettigrew (2010a,b) give an alternative proof that conditionalization maximizes expected utility.

Joyce is concerned with proving norms for degrees of belief. The approach can be extended to prove norms where all-or-nothing belief states are taken as primitive. Easwaran and Fitelson (2015) extend the approach in this way. Interestingly, their approach yields the result that some logically inconsistent belief states are permissible (for instance, in lottery cases). The approach has also been extended to comparative confidence rankings (where a comparative confidence ranking represents only certain qualitative facts about how confident an agent is in propositions—for instance, that she is more confident in p than in q). Williams (2012) has extended the approach in a different direction by examining cases where the background logic is nonclassical.

Joyce’s (1998) approach fits nicely into the consequentialist recipe (and subsequent work can be made to fit into the recipe, too):

Step 1. Final Value: Credences have final epistemic value in proportion to how accurate they are.

Step 2. Ranking: Credence functions are put into two classes: dominated credence functions and non-dominated credence functions.

Step 3. Normative Facts: A credence function is permissible to hold if and only if it is non-dominated.

In this way, the accuracy-first approach appears to be an especially “pure” version of epistemic consequentialism. The project is to work out what the epistemic norms are for doxastic states given that you care only about the accuracy of those doxastic states.

However, one prominent objection to the accuracy-first approach questions this. To see this, note that the verdicts about which credence functions dominate (or maximize expected epistemic value) are not sensitive to the total causal consequences of adopting a credence function as they only look at the expected epistemic value of that state and not the causal effects of the adoption of that state. There are really two points here. This first point is the same point that was noted with respect to cognitive decision theory: the accuracy-first program seems to be an instance of restricted consequentialism. This can make the view seem to not genuinely be a consequentialist view. Greaves (2013) raises some objections to the program along these lines; the issue she raises is very similar to the kinds of issues that Berker (2013a,b) and Littlejohn (2012) have raised in objections to epistemic consequentialism in traditional epistemology. The general worry is discussed below in section 5a.

The second point concerns a distinction that can be drawn between evaluating a doxastic state and evaluating the adoption of a doxastic state. The accuracy-first program seems to be interested in the former rather than the latter, which can make it seem further still from traditional consequentialism. This issue can be brought out by an example due to Michael Caie (2013). Suppose we are considering what the permissible credence function is with respect to only the propositions q and ~q where q is a self-referential proposition that says “q is assigned less than 0.5 credence.” This is an odd proposition in that if q is assigned less than 0.5 credence, then it is true (and so it would be more accurate to increase one’s credence in q), but if one increases one’s credence in q to 0.5 or greater, then q is false (and so it would be more accurate to decrease one’s credence in q). In such a situation, an incoherent credence function appears to dominate the coherent ones. To see this, note that there are no worlds where c(q) = 1, c(~q) = 0, and where q is true (because if c(q) =1, then q is false) or where c(q) = 0, c(~q) = 1, and where q is false (because if c(q) = 0, then q is true). The best that a coherent credence function can do is to assign c(q) = c(~q) = 0.5. In that case, q is false, and so the Brier score is 1.5. But compare this with the credence function, c*, according to which c*(q) = 0.5 and c*(~q) = 1. In that case, q is again false, and so c*(~q) gets a better score than does c(~q). Overall, c* gets a Brier score of 1.75.

How can this be, if we have proofs that probabilistically coherent credence functions dominate incoherent credence functions? The answer to this is that the proofs by Joyce and others assume a very strong kind of independence between belief states and possible worlds. Even though there is no world where c(q) = 1, c(~q) = 0, and where q is true, Joyce and others still consider such worlds when working out which credence functions dominate or maximize expected epistemic value. With these possible worlds back in play, the incoherent c* is dominated. In particular, for the desired results (that probabilism is true, that conditionalization is the correct updating rule, and so forth) to go through, we must be able to assess how accurate a doxastic state is in a world where that doxastic state could not be held. Further, we must maintain that facts about the accuracy of doxastic states in worlds where they cannot be held are sometimes relevant to our evaluation of a doxastic state in some other world where it is actually held. This might lead one to question whether this accuracy-first approach really is a form of epistemic consequentialism (though that is of course complicated by the fact that there is no consensus about what it takes to be a consequentialist theory) and indeed whether the evaluative framework can be motivated.

d. Traditional Epistemology: Justification

i. Coherentism

According to coherentism about justification, a belief is justified if and only if it belongs to a coherent system of beliefs (note that the term “coherent” here refers to some informal notion of coherence, perhaps related to, but distinct from, the notion of coherent credences). This on its own does not commit coherentists to any sort of epistemic consequentialism. However, some of the debates and claims made within the coherentist literature suggest that some prominent coherentists are committed to some form of epistemic consequentialism. For instance, in The Structure of Empirical Knowledge, BonJour (1985) defends a version of coherentism about justification. In this work, BonJour devotes an entire chapter to giving an argument for the following thesis:

A system of beliefs which (a) remains coherent (and stable) over the long run and (b) continues to satisfy the Observation Requirement is likely, to a degree which is proportional to the degree of coherence (and stability) and the longness of the run, to correspond closely to independent reality. (p. 171)

BonJour is thus attempting to show that the degree of coherence of a set of beliefs is proportional to the likelihood that those beliefs are true. He calls this a metajustification for his coherence theory of justification. And why is such a metajustification required? He writes:

The basic role of justification is that of a means to truth, a more directly attainable mediating link between our subjective starting point and our objective goal. […] If epistemic justification were not conducive to truth in this way, if finding epistemically justified beliefs did not substantially increase the likelihood of finding true ones, then epistemic justification would be irrelevant to our main cognitive goal and of dubious worth. […] Epistemic justification is therefore in the final analysis only an instrumental value, not an intrinsic one. (pp. 7–8)

This strongly suggests that BonJour thinks of the epistemic right—justification—in consequentialist terms (Berker (2013a) claims that BonJour (1985) should be understood in this way). If justification understood as coherence is not conducive to truth, then justification understood as coherence is not valuable. This suggests the following picture:

Step 1. Final Value: True beliefs have final epistemic value; false beliefs have final epistemic disvalue.

Step 2. Ranking: Sets of beliefs are ranked in terms of their degree of coherence where this degree of coherence is proportional to the likelihood that the set of beliefs is true.

Step 3. Normative Facts: A belief is justified iff it belongs to a set of beliefs that is coherent above some threshold.

The claim in Step 2, that coherence is truth-conducive, has been addressed explicitly in the literature, starting with Klein and Warfield (1994). They argue that the fact that one set of propositions is more coherent than another set does not entail that the conjunction of the propositions in the first set is more likely to be true than the conjunction of propositions in the second set. The basic argument is that a set of propositions (say, the set including a and b) can sometimes be made more coherent by adding an additional proposition to it (to yield the set including a, b, and c). However, the conjunction (a and b and c) is never more probable than the conjunction (a and b). Bovens and Hartmann (2003) and Olsson (2005) add to this literature and each prove results to the effect that no matter one’s measure of coherence, there will be cases where one set is more coherent than another, but its propositions are less likely. (For one response to these arguments, see Huemer (2011); Angere (2007) considers whether these arguments undermine BonJour’s coherentism.)

In light of difficulties establishing that coherence is truth-conducive, it is open to coherence theorists to not go down the consequentialist route. Such a coherentist might maintain that beliefs that are members of coherent sets are epistemically right independent of whether such sets are likely to be true. This mimics the non-consequentialist Kantian who maintains that certain actions are right independent of the final value that taking these actions leads to.

ii. Reliabilism

Reliabilism about justification, as championed by Alvin Goldman (1979), maintains that beliefs are justified when they are produced by suitably reliable processes. Put another way, beliefs are justified when produced by the right kinds of processes, and the right kinds of processes are those that are truth-conducive. One helpful way to think about the consequentialist structure of reliabilism is to think of it as analogous to rule utilitarianism. According to the rule utilitarian, we evaluate moral rules for rightness directly in terms of the consequences of their widespread acceptance. Actions are then evaluated in terms of whether or not they conform to a right rule. Similarly, according to reliabilism, the things up for direct consequentialist evaluation are not acts of acceptance or particular beliefs that could be adopted. Rather, processes of belief formation are evaluated consequentially. Reliabilists tend to see true belief as the sole thing of final epistemic value. Processes are thus evaluated based on their truth-ratios, the ratio of true beliefs produced to total beliefs produced. However, unlike a maximizing theory, reliabilism maintains that a process is acceptable just in case it has a truth-ratio above some absolute threshold. It is thus different from maximizing theories in two ways. First, a process can be acceptable even if it is not the most reliable process and thus not the optimally truth-conducive process. Second, a process need not be acceptable even if it is the most reliable process, because the reliabilist requires that processes meet some minimum threshold to be acceptable.

We can put a simple version of reliabilism about justification into our consequentialist recipe:

Step 1. Final Value: True beliefs have final epistemic value; false beliefs have final epistemic disvalue.

Step 2. Ranking: Processes are put into two classes: acceptable and not acceptable. If the process has a reliability score at or above the threshold, the process is acceptable; otherwise, it is not acceptable. The reliability score of a process p at world w is given by the sum of the true beliefs that process p produces at w divided by the sum of the total beliefs that process p produces at w (that is, the truth-ratio of p at w).

Step 3. Normative Facts: A belief is justified for S at t at w iff S’s belief at t at w is produced by an appropriate belief-forming process at w.

There are subtle ways in which reliabilism can differ from what the recipe above suggests. One of the most notable differences concerns Goldman’s (1986) approach. Although Goldman (1979) gives a theory that looks very much like what is represented above, in Goldman (1986) it is not individual processes that are ranked at Step 2, but rather systems of rules about which processes may and may not be used. A system of rules is then acceptable if and only if a believer who follows those rules has an overall truth-ratio above a certain threshold. Thus, the analogy to rule utilitarianism is even stronger in Goldman (1986) than in Goldman (1979), something which he explicitly notes. There has also been some dispute among reliabilists about the exact way that processes should be scored for their reliability (and so the exact form of Step 2), but despite that, the view looks to be committed to some form of consequentialism.

iii. Evidentialism

One of the main rivals of reliabilism about justification is evidentialism, initially defended by Richard Feldman and Earl Conee (1985) (whether evidentialism is a rival of coherentism depends subtly on exactly how the views are spelled out). Evidentialism maintains that the belief that p is justified for an agent at time t iff p is supported by the agent’s total evidence at t. Conee (1992) motivates the total evidence requirement with reference to an overriding goal of true belief, in which case evidentialists agree with reliabilists and with BonJour-style coherentists that justification is a matter of truth conduciveness. Feldman (2000) motivates the total evidence requirement with reference to an overriding goal of reasonable belief (rather than true belief), in which case evidentialists disagree with reliabilists and BonJour-style consequentialists about the nature of final epistemic value, but agree that justification should be spelled out in consequentialist terms. More recently, Conee and Feldman (2008) have suggested that what has final epistemic value is coherence. Whether this view is committed to consequentialism depends on how the details are spelled out. If the idea is that a doxastic state is justified in proportion to how much it promotes the value of coherence, whether in itself or in its causal consequences, then such a view is plausibly committed to consequentialism, with the good of coherence substituted for the good of true belief. However, there may be other ways of interpreting their view according to which it looks less committed to consequentialism.

It should be noted that Feldman (1998) makes clear that the only thing relevant to whether one should believe p is one’s evidence now concerning p’s truth. The causal consequences of believing p are explicitly ruled out by Feldman as relevant to that belief’s justificatory status. So if Feldman is to count as a consequentialist, it is of a very restricted sort. Presumably, Feldman holds something similar in Conee and Feldman (2008). Conee (1992), on the other hand, has expressed more sympathy with the idea that we should sometimes sacrifice epistemic value now for more epistemic value later. Thus, there is perhaps a stronger case that Conee’s version of evidentialism is also some form of consequentialism.

e. Traditional Epistemology Not Concerned with Justification

Stephen Stich (1990) offers a method of epistemic evaluation not concerned with justification, but that is committed to consequentialism. According to Stich, there are no special epistemic values (such as true belief), there are just things that people happen to value. Reasoning processes and reasoning strategies are seen as one tool that we use to get what we value. Stich (1993, p. 24) writes: “One system of cognitive mechanism is preferable to another if, in using it, we are more likely to achieve those things that we intrinsically value.” Thus, we have cognitive mechanisms being ranked in terms of their consequences, but where the consequences that matter are not uniquely epistemic, but rather anything that we happen to intrinsically value.

Richard Foley’s (1987) The Theory of Epistemic Rationality is not directed at analyzing justification. Nevertheless, it provides another example of work in traditional epistemology that seems to be committed to some form of epistemic consequentialism. Foley identifies our epistemic goal as that of now believing those propositions that are true and not now believing those propositions that are false. It is then epistemically rational for a person to believe a proposition whenever on careful reflection that person has reason to believe that believing that proposition will promote his or her epistemic goals, provided that all else is equal. Foley is clear, however, that he does not intend his view to sanction as rational adopting a belief that one is now confident is false in order to garner more true beliefs later. Thus, like some of the other views canvassed here, Foley adopts something like a consequentialist framework for evaluating beliefs, but in a restricted way, where the causal consequences of beliefs are not relevant to the normative verdicts of those beliefs.

Though a large focus of Goldman (1986) is to give a reliabilist account of justification, he notes that there are other important ways that processes, and thus that beliefs produced by those processes, can be evaluated. In particular, Goldman considers evaluating processes for their speed and for their power. The speed of a process concerns how quickly a process issues true beliefs. The power of a process concerns how much information a process gives to you. A highly reliable process might have very little speed if it takes a very long time to issue a belief. And the same highly reliable process might have very little power if it produces only that one belief. Goldman suggests that we can use a consequentialist-style analysis to evaluate processes in these ways, too.

Bishop and Trout (2005) argue against the practice of so-called standard analytic epistemology, which includes many of the approaches to justification looked at above. Bishop and Trout propose a view according to which we evaluate reasoning strategies by drawing on empirical work in psychology, rather than by consulting our intuitions. According to Bishop and Trout, the three factors that affect the quality of a reasoning strategy are: (1) whether the strategy is reliable across a wide range of problems, (2) the ease with which the strategy is used, and (3) the significance of the problems toward which the reasoning strategy can be used. They emphasize that whether a set of reasoning strategies is an excellent one to use depends on a cost/benefit analysis. It is natural, then, to think of their normative verdicts about whether a reasoning strategy is excellent as depending on the consequences of using that strategy along dimensions (1)–(3).

In this section and in the one before, we have seen that some traditional epistemologists with otherwise diverse views about justification or epistemic evaluation more generally seem to be committed, at bottom, to a kind of epistemic consequentialism. The aforementioned theories do not merely identify some bearer of final epistemic value, but also define one designator of epistemic rightness (for example, justification, rationality, epistemic excellence) in terms of such value.

f. Social Epistemology

Social epistemology is concerned with the way that social institutions, practices, and interactions are related to our epistemic endeavors, such as knowledge generation. Several prominent approaches within social epistemology also seem to be committed to some form of epistemic consequentialism.

Alvin Goldman’s (1999) Knowledge in a Social World is a nice example of social epistemology done with explicit commitments to consequentialism. Goldman writes:

People have interest, both intrinsic and extrinsic, in acquiring knowledge (true belief) and avoiding error. It therefore makes sense to have a discipline that evaluates intellectual practices by their causal contributions to knowledge or error. This is how I conceive of epistemology: as a discipline that evaluates practices along truth-linked (veritistic) dimensions. Social epistemology evaluates specifically social practices along these dimensions. (p. 69)

Goldman’s general approach is to adopt a question-answering model. According to this approach, beliefs in propositions have value or disvalue when those propositions are answers to questions that interest the agent. This suggests that Goldman promotes a view according to which final epistemic value is accuracy with respect to questions of interest, and not mere accuracy alone. As Goldman conceives of it, the epistemic value of believing a true answer to a question of interest is 1, the epistemic value of withholding belief to a true answer is 0.5, and the epistemic value of rejecting a true answer is 0. Goldman extends this to degrees of belief in that natural way: the epistemic value of having a degree of belief x in a true proposition is x. (It is worth noting that this corresponds to a scoring rule that is improper, compare section 3c.) We can then evaluate social practices instrumentally, in terms of their causal contributions to belief states that have final epistemic value. Goldman does this by first specifying the appropriate range of applications for a practice. This will involve actual and possible applications (because some practices do not have an actual track record). Second, one takes the average performance of the practice across these applications. The average performance of a practice determines how it is ranked compared to its competitors. Thus, on this view, it is something like objective expected epistemic value that ranks the various practices.

Consider an example. Goldman argues that civil-law systems are better, from an epistemic perspective, than are common-law systems. The argument for this is complex, but the general structure follows the framework described above. Goldman considers various differences between the two systems, including the numerous exclusionary evidentiary rules in the common-law system as compared to the civil-law system, the large role that adversarial lawyers play in the common-law system as compared to the civil-law system, and the fact that the civil-law system employs trained judges as decision-makers rather than lay jurors. With respect to each of these differences, one can approximate the epistemic value for the relevant decision-makers under each system. For instance, one can estimate how many correct verdicts compared to incorrect verdicts jurors would reach if there were exclusionary evidentiary rules compared to if there were not. On balance, Goldman argues, the civil-law system performs better. For another evaluation of legal structures in consequentialist terms, see Laudan (2006).

Goldman (1999) directs this same style of consequentialist argument toward a variety of social practices, including testimony, argumentation, Internet communication, speech regulation, scientific conventions, law, voting, and education.

Note, however, an important shift in the consequentialist view Goldman defends here compared to earlier theories considered. Previously, the things being evaluated have been belief states or acts of acceptance. Here, Goldman is evaluating social practices and methodologies. We could call the approach in Goldman (1999) an instance of methodological epistemic consequentialism, whereas the former theories are instances of doxastic epistemic consequentialism (note that this terminology is not standard and is introduced simply for clarity within this article).

The basic view can be put into our recipe as follows:

Step 1. Final Value: Accurate beliefs of S in answer to questions that interest S have final epistemic value.

Step 2. Ranking: Social practices are ranked according to the average amount of final epistemic value that they produce across the range of situations they can be applied to.

Step 3. Normative Facts: Social practice A is epistemically better than social practice B just in case A and B are alternatives to each other and A is ranked higher than B in Step 2.

For criticism of Goldman’s social epistemology that focuses specifically on its consequentialist commitments, see DePaul (2004). See also Fallis (2000, 2006).

g. Philosophy of Science

Though Goldman’s work in social epistemology touches on aspects of science, more generally his focus is on social practices. Others are interested in similar questions about social practices, structures, and conventions, but specifically with respect to science. In some of this work, there is a clear foundation of something like epistemic consequentialism.

i. Group versus Individual Rationality

Philip Kitcher (1990) is one of the first to apply formal models to social structures in science to determine the optimal structure for a group of researchers to achieve their scientific goals. The guiding idea behind his work is that if everyone were rational, then they would each make decisions about which projects to explore based on what the evidence supports and there would be a uniformity of practices among scientists. This uniformity would be bad, however, because it would prevent people from pursuing research on new up-and-coming theories (for example, continental drift in the 1920s) as well as on older outgoing theories (for example, phlogiston theory in the 1780s). Kitcher defines two notions: X’s personal epistemic intentions are what X wishes to achieve himself and X’s impersonal epistemic intentions are what X wishes his community to achieve. The question at hand can then be put: how would scientists rationally decide to coordinate their efforts if their decisions were dominated by their impersonal epistemic intentions?

Kitcher formalizes this situation by supposing that there are N researchers working on a particular research question, and each has to determine which research program she will pursue. Define a return function, P_i(n), which represents the chance that program i will be successful given that n researchers are pursuing it. Suppose that each researcher’s personal epistemic intention is to successfully answer the research question. In that case, each researcher will adopt whichever program i has the largest value for P_i(n_i), where n_i is the number of researchers currently pursuing i. However, if we suppose that each researcher’s impersonal epistemic intention is that someone in the community of researchers successfully answers the question, then this way of choosing research programs may not be the way to realize the impersonal epistemic intention. Consider a simple example where there are two research programs, 1 and 2, and N researchers. The best way to achieve the group goal is to maximize P₁(n) + P₂(N–n). But this could be a different distribution than the one that would result were each researcher to be guided by her personal epistemic intention. To see this suppose that there are j researchers in program 1 and k researchers in program 2. It could be that P₁(j+1) > P₂(k+1) and so a new researcher would choose program 1. But for all that, it could be that P₁(j+1) – P₁(j) < P₂(k+1) – P₂(k). That is, the boost in probability of success that program 2 gets from the addition of one more researcher is greater than that of program 1. In that case, it is better for the group for a new researcher to join program 2. Kitcher goes on to argue that certain intuitively unscientific goals such as the goal of fame or popularity could help motivate researchers into a division of labor that helps to reach the impersonal goals rather than the personal goals of each researcher.

Kitcher does not claim that there is one objective answer to what the appropriate epistemic intentions or values are. Nevertheless, there is a consequentialist structure to his argument. Groups of scientists are seen as rational when they choose among options in such a way that they maximize their chance of attaining their epistemic goals. One could question whether this is enough to make the view count as a version of epistemic consequentialism. After all, the options that the agents in Kitcher’s model are choosing between are not beliefs or belief states, but instead decisions about which research program to pursue or about which experiment to run. In this way, Kitcher’s view looks to be an instance of methodological epistemic consequentialism as opposed to doxastic epistemic consequentialism: it is aimed at evaluating actions that are in some way closely related to epistemic ends, rather than at evaluating belief states themselves. Some have argued that approaches such as these do not actually address properly epistemic questions at all. For some thoughts on this, see Christensen (2004, 2007).

Others have followed the general argumentative structure of Kitcher (1990). Zollman (2007, 2010) and Mayo-Wilson, Zollman, and Danks (2011) have focused on the communication networks that might exist between scientists working on the same project. This work reveals some surprising conclusions, in particular, that it might sometimes be epistemically beneficial for the community of scientists to have less than full communication among the members. The basic reason for this is that limiting communication is one way to encourage diversity in research programs, which for Kitcher-like reasons can help the community do better than it otherwise would. Muldoon and Weisberg (2009) and Muldoon (2013) have focused on the kinds of research strategies that individual scientists might have, modeling scientific research as a hill-climbing problem in the computer science literature. They show how it can sometimes be beneficial for the group of scientists to have individuals who are more radical in their exploration strategies.

So far we have surveyed formal models in the philosophy of science literature that seem to take a consequentialist approach to epistemic evaluation. One of the main results of this work is to show how strategies that would be irrational if followed in isolation might yield rational group behavior. Others have emphasized something like this point, but without formal models. Miriam Solomon (1992), for instance, argues for a similar conclusion by drawing on work in psychology and considering the historical data about the shift in geology to accept continental drift. She argues that certain seeming psychological foibles of individual geologists, including cognitive bias and belief preservation, played an important role in the discovery of plate tectonics. Paradoxically, she argues, these attributes that are normally seen as rational failings were in fact conducive to scientific success because they made possible the distribution of research effort. That her work employs a kind of consequentialist picture is evidenced by the fact that she views the central normative question in the philosophy of science to be: “whether or not, and where and where not, our methods are conducive to scientific success…Scientific rationality is thus viewed instrumentally.” (p. 443)

Larry Laudan is another philosopher of science who adopts a generally consequentialist outlook. For Laudan (1984), the things we are ultimately evaluating are methodological rules. Writes Laudan:

… a little reflection makes clear that methodological rules possess what force they have because they are believed to be instruments or means for achieving the aims of science. More generally, both in science and elsewhere, we adopt the procedural and evaluative rules we do because we hold them to be optimal techniques for realizing our cognitive goals or utilities. (1984, p. 26)

There is, on Laudan’s view, not one set of acceptable cognitive goals, although there are ways to rationally challenge the cognitive goals that someone holds. This can be done by either showing that the goals are unrealizable or showing that the goals do not reflect the communal practices that we endorse. On Laudan’s view, then, what has final epistemic value is the realizing of the cognitive goals that we have, so long as these goals are not ruled out in one of the ways above. We can then rank methodological rules, or groups of methodological rules, in virtue of how well they reach those cognitive goals that we have. We then evaluate those rules as rational or not in virtue of this ranking. Laudan does not say that the methodological rules must be optimal, but does suggest, as the quote above notes, that we must think that they are.

ii. Why Gather Evidence?

Another area of philosophy of science that seems committed to epistemic consequentialism concerns the initially odd-sounding question: why should a scientist gather more evidence? On its face, the answer to this question is obvious. But if we idealize scientists as perfectly rational agents, some models of rationality make the question more pressing. For instance, consider an austere version of the Bayesian account of epistemic rationality according to which one is epistemically rational if and only if one’s degrees of belief are probabilistically coherent and one updates one’s beliefs via conditionalization upon receipt of any evidence. An agent can do this perfectly well without ever gathering new evidence. In addition, notice that there is a risk associated with gathering new evidence. Although in the best-case scenario, one acquires information that moves one closer to the truth, it is of course possible that one gets misleading evidence and so is pushed further from the truth. Is there anything that can be said in defense of the intuitive verdict that despite this, it is still rational to gather evidence?

An early answer to this question is provided by I. J. Good (1967). Suppose that you are going to have to make a decision and you can perform an experiment first and then make the decision or you can simply make the decision. Good shows that if you choose by maximizing subjective expected value, if there is no cost of performing the experiment, and if several other constraints are imposed, then the subjective expected value of your choice is always at least as great after performing the experiment as before. Here then we have an argument in favor of a certain sort of epistemic behavior—gathering evidence—that is consequentialist at heart. It says that if you do this sort of thing, you can expect to make better choices. However, it is not clear that this is an epistemic consequentialist argument. At best, it suggests that experimenting is pragmatically rational. To drive this point home, note that it seems there are experiments that are epistemically rational to perform even if there is no reason to expect that any decision we will make depends on the outcome.

Others, however, have attempted to extend the basic Good result to scenarios where only final epistemic value is at issue. Oddie (1997), for instance, shows that if one uses a proper scoring rule to measure accuracy and if one updates via conditionalization, then the expected final epistemic value of learning information from a partition is always at least as great as refusing to learn the information. Myrvold (2012) generalizes this basic result and shows that something similar holds even if we do not require that one updates via conditionalization. Instead, so long as one satisfies Bas van Fraassen’s (1984) reflection principle, then something similar to Oddie’s result holds. For commentary on van Fraassen’s reflection principle, see Maher (1992). For other work on the issue of gathering evidence, see Maher (1990) and Fallis (2007).

Work in this area seems clearly committed to an especially veritistic form of epistemic consequentialism. Here we have an argument in favor of acquiring new evidence (if it is available) that appeals solely to the increase in accuracy one can expect to get from such evidence. As Oddie (1997, p. 537) writes: “The idea that a cognitive state has a value which is completely independent of where the truth lies is just bizarre. Truth is the aim of inquiry.”

4. Summing Up: Some Useful Distinctions

Now that we have surveyed a variety of theories that seem to have some commitment to epistemic consequentialism, it is useful to remind ourselves of two important distinctions relevant to categorizing different species of epistemic consequentialism.

First, some of the theories discussed above are committed to restricted consequentialism. According to these views, the normative facts about Xs are determined by some restricted set of the consequences of the Xs. More precisely, consider a theory that will issue normative verdicts about some belief b. A restricted consequentialist view maintains that something has final epistemic value, but that the normative facts about b are not determined by the amount of final epistemic value contained in the entire set of b’s causal consequences. In the limit, none of the causal consequences of b are relevant; only the final epistemic value contained in b itself is relevant. For instance, Feldman’s view about justification, Foley’s view about rationality, the approach of cognitive decision theory, and some versions of the accuracy-first program appear to be restricted consequentialist views in this limiting sense. Feldman, recall, explicitly states that the causal consequences of adopting a belief are irrelevant to its justificatory status; Foley focuses on the goal of now believing the truth and not now believing falsely, so excludes causal consequences; and Joyce’s accuracy-first program looks at whether some doxastic state dominates another doxastic state when the states are looked at for their accuracy now. Reliabilism is arguably also a form of restricted consequentialism, because the causal consequences of the belief itself are not relevant to its normative status; rather, it is the status of the particular process of belief formation that led to the belief that is relevant to the belief’s normative status. A process of belief formation earns its status, in turn, in terms of the proportion of true beliefs that it directly produces, so not even the total consequences of a belief-forming process are relevant according to the reliabilist.

Unrestricted consequentialist views, on the other hand, are those according to which the normative facts about whatever is being evaluated are determined by the amount of final epistemic value in the entire set of that thing’s causal consequences. It is unclear whether we have seen any wholly unrestricted consequentialist views in this sense, although Goldman’s approach to social epistemology and Kitcher’s approach to the distribution of cognitive labor may come close.

It is something of an open question whether a restricted consequentialism is genuinely a form of consequentialism. Some discussions of consequentialism in ethics suggest that restricted versions of consequentialism are not genuinely instances of consequentialism (see, for instance, Pettit (1988), Portmore (2007), Smith (2009), and Brown (2011)). Klausen (2009) argues that restricted versions of consequentialism are not genuinely instances of consequentialism, specifically with respect to epistemology.

The second important distinction to keep in mind when categorizing species of epistemic consequentialism is a distinction between those theories that seek to evaluate belief states and those that seek to evaluate some sort of action of some epistemic relevance. An example will make this distinction clearer. The accuracy-first program seeks to evaluate belief states based solely on their accuracy. Kitcher’s approach to the distribution of cognitive labor seeks to evaluate the decisions of scientists to engage in certain lines of research based on the ultimate payoff in terms of true belief for the scientific community. As noted above, we could call the first approach an instance of doxastic epistemic consequentialism and the second sort of approach an instance of methodological epistemic consequentialism (again, note that these terms are not established in the literature). With this distinction in hand, we can sort some of the theories above along this dimension. Attempts to explain why it is rational to gather evidence, much of social epistemology, and the work on communication structures and exploration strategies among scientists are instances of methodological epistemic consequentialism. Consequentialist analyses of justification, cognitive decision theory, and the accuracy-first program are instances of doxastic epistemic consequentialism.

5. Objections to Epistemic Consequentialism

Theories committed to some form of epistemic consequentialism will have specific objections that can be lodged against them. Here we will focus on general objections to the fundamental idea behind epistemic consequentialism.

a. Epistemic Trade-Offs

Epistemic consequentialists maintain that, in some way, the right option is one that is conducive to whatever has final epistemic value. Say that you accept a trade-off if you sacrifice something of value for even more of what is valuable. Thus, if true belief has final epistemic value (and if each true belief has equal final epistemic value), you accept a trade-off when you sacrifice a true belief concerning p for two true beliefs about q and r. It is hard to see how one can hold a consequentialist view and not think that it is at least sometimes permissible to accept trade-offs. For then it would seem that rightness is no longer being understood in terms of conduciveness to what has value (though, as we will see, restricted consequentialists of a certain sort may be able to deny this).

The permissibility of accepting trade-offs, however, constitutes a problem for epistemic consequentialism. If one thinks about consequentialist theories in ethics, this is not so surprising. Some of the strongest intuitive objections to consequentialist moral theories are those that focus on trade-offs. Consider, for instance, the organ harvest counterexample to utilitarianism (Thomson 1985). In that scenario, a doctor has five patients all in dire need of a different organ transplant. The doctor also has a healthy patient who is a potential donor for each of the five patients. Because it is a consequentialist moral theory and endorses trade-offs, it seems that utilitarianism says the doctor is required to sacrifice the one to save the five. But, it is alleged, this flies in the face of common sense, and so we have a challenge for utilitarianism.

Trade-off objections to epistemic consequentialism (structurally similar to the organ harvest) have been made explicitly by Firth (1981), Jenkins (2007), Littlejohn (2012), Berker(2013a,b), and Greaves (2013). And one can see hints of such an objection in Fitelson and Easwaran (2012) and Caie (2013).

The basic objection starts with the observation that a belief can be justified or rational or epistemically appropriate (or whatever other term for epistemic rightness one prefers) even if adopting that belief causes some epistemic catastrophe. Similarly, it seems that a belief can be unjustified or irrational or epistemically inappropriate even if adopting that belief results causally in some epistemic reward. For an example of the first sort, S might have significant evidence that he is an excellent judge of character and so S believing this about himself might be justified for S. But it could be that this belief serves to make S overconfident in other areas of his life and so S ends up misreading evidence quite badly in the long run. For an example of the second sort, S might have no evidence that God exists, but believe it anyway to make it more likely that S receives a large grant from a religiously affiliated (and unscrupulous) funding agency. The grant will allow S to believe many more true and interesting propositions than otherwise (the example is due to Fumerton (1995), p. 12). These kinds of examples seem to show that epistemic rightness cannot be understood in terms of conduciveness to what has epistemic final value.

There are two main responses that the epistemic consequentialist can make to the trade-off objection, and each comes with a challenge. The first response is to maintain that, appearances to the contrary, there are versions of epistemic consequentialism that do not sanction unintuitive trade-offs. For a response in this vein, see Ahlstrom-Vij and Dunn (2014). In ethics, some who think of themselves as consequentialists respond to analogous objections by introducing agent-relative values (see, for instance, Sen (1982) and Broome (1995)). The basic idea is that we can have agent-relative values in the outcomes of states, which allows, for example, for agent S to value the state where S breaks no promises more than someone else values that same state. This allows for one to give a consequentialist-based evaluation of rightness that does not always require one to say that it is right for S to break a promise in order to ensure that two others do not break their promises. It is not clear how such a modification of consequentialism would best carry over to epistemic consequentialism, but it could represent a way of making this first response. The challenge for any response in this vein is to explain how such views are genuinely an instance of epistemic consequentialism.

The second response to trade-off objections is to maintain that while epistemic consequentialism does sanction trade-offs, we can explain away the felt unintuitiveness of such verdicts. The challenge for this second response is to actually give such an explanation.

b. Positive Epistemic Duties

When it comes to moral obligation, it seems plausible that we sometimes have obligations to take certain actions and sometimes have obligations to refrain from certain actions. It is then natural to distinguish between positive duties—say, the obligation to take care of my children—and negative duties—say, the obligation to not steal from others. Consider how a similar distinction would be drawn in epistemology. Obligations to believe certain propositions would correspond to positive epistemic duties, while obligations to refrain from believing certain propositions would correspond to negative epistemic duties.

Littlejohn (2012) has argued that certain forms of epistemic consequentialism look as though they will naturally lead to positive epistemic duties. Suppose, as certain doxastic epistemic consequentialists will maintain, that whether we are obligated to believe or refrain from believing a proposition is a function of the final epistemic value of believing or refraining from believing that proposition. And suppose that the consequentialist also maintains that we have some negative epistemic duties; that is, there are situations where one is epistemically obligated to refrain from believing a proposition. The consequences of refraining in such a situation will have some level of epistemic value. But it seems that we can surely find a situation where believing a proposition has consequences with equal epistemic value. Thus, it looks as though the consequentialist is committed to saying that there are positive epistemic duties: sometimes we are obligated to believe propositions.

However, some epistemologists hold that we have no positive epistemic duties. We may be obligated to refrain from believing certain things, but we have no duties to believe. Nelson (2010) provides one argument for this claim. He argues that if we had positive epistemic duties, we would have to believe each proposition that our evidence supported. But this means we would be epistemically obligated to believe infinitely many propositions, as Nelson argues that any bit of evidence supports infinitely many propositions. As we cannot believe infinitely many propositions, Nelson holds that we have no positive epistemic duties.

The thesis that there are no positive epistemic duties is controversial, as is Nelson’s argument for that claim. Nevertheless, this presents a potential worry for certain versions of epistemic consequentialism. It is perhaps worth noting that this sort of objection to epistemic consequentialism is in some ways analogous to objections that maintain that consequentialist views in ethics are overly demanding. For more on the issue of positive epistemic duties, see Stapleford (2013) and the discussion in Littlejohn (2012, ch. 2).

c. Lottery Beliefs

Suppose that you know there is a lottery with 10,000 tickets, each with an equal chance of winning, but where only one ticket will win. Consider the proposition that ticket 1437 will lose. It is incredibly likely that this proposition is true, and the same is true for each of the n propositions that say that ticket n will lose. Nevertheless, a number of epistemologists maintain that one is not justified in believing such lottery propositions (for instance, BonJour (1980), Pollock (1995), Evnine (1999), Nelkin (2000), Adler (2005), Douven (2006), Kvanvig (2009), Nagel (2011), Littlejohn (2012), Smithies (2012), McKinnon (2013), and Locke (2014)).

Some consequentialist approaches to justification, however, look as though they will say that one is justified in believing such lottery propositions. For instance, suppose that there is a process of belief formation that issues beliefs of the form ticket n is a loser. This process is highly reliable and so beliefs produced by it are justified according to one version of reliabilism about justification. Some process reliabilists about justification might maintain that there is no such process in an attempt to avoid this implication of their view. However, as Selim Berker (2013b) has noted, the very structure of consequentialist views in epistemology looks as though there will be some case that can be brought against the consequentialist where some set of beliefs are justified purely in virtue of statistical information about the relative lack of falsehoods in a set of propositions.

Again, not all maintain that there is no justification to be had in such cases; some maintain that while such lottery propositions cannot be known, they nevertheless can be justified. But there are a number of epistemologists who maintain such a view and so we again have a potential worry here for the consequentialist. For a response to this worry, see Ahlstrom-Vij and Dunn (2014).

6. References and Further Reading

Adler, J. (2005) ‘Reliabilist Justification (or Knowledge) as a Good Truth-Ratio’ Pacific Philosophical Quarterly 86: 445–458.
Ahlstrom-Vij, K. and Dunn, J. (2014) ‘A Defence of Epistemic Consequentialism’ Philosophical Quarterly 64: 541–551.
Angere, S. (2007) ‘The Defeasible Nature of Coherentist Justification’ Synthese 157: 321–335.
Berker, S. (2013a) ‘Epistemic Teleology and the Separateness of Propositions’ The Philosophical Review 122: 337–393.
Berker, S. (2013b) ‘The Rejection of Epistemic Consequentialism’ Philosophical Issues 23: 363–387.
Bishop, M. and Trout, J. D. (2005) Epistemology and the Psychology of Human Judgment. Oxford: Oxford University Press.
BonJour, L. (1980) ‘Externalist Theories of Empirical Knowledge’ Midwest Studies in Philosophy 5: 53–74.
BonJour, L. (1985) The Structure of Empirical Knowledge. Cambridge, MA: Harvard University Press.
Bovens, L., and Hartmann, S. (2003) Bayesian Epistemology. Oxford: Oxford University Press.
Broome, J. (1991) Weighing Goods: Equality, Uncertainty and Time. Oxford: Wiley-Blackwell.
Brown, C. (2011) ‘Consequentialize This’ Ethics 121: 749–771.
Caie, M. (2013) ‘Rational Probabilistic Incoherence’ Philosophical Review 122: 527–575.
Christensen, D. (2004) Putting Logic in Its Place. Oxford: Oxford University Press.
Christensen, D. (2007) ‘Epistemology of Disagreement: The Good News’ Philosophical Review 116: 187–217.
Conee, E. (1992) ‘The Truth Connection’ Philosophy and Phenomenological Research 52: 657–669.
Conee, E. and Feldman, R. (2008) ‘Evidence’ In Q. Smith (Ed.), Epistemology: New Essays. Oxford: Oxford University Press: 83–104.
DePaul, M. (2004) ‘Truth Consequentialism, Withholding and Proportioning Belief to the Evidence’ Philosophical Issues 14: 91–112.
Douglas, H. (2000) ‘Inductive Risk and Values in Science’ Philosophy of Science 67: 559–579.
Douglas, H. (2009) Science, Policy, and the Value-Free Ideal. Pittsburgh, PA: University of Pittsburgh Press.
Douven, I. (2006) ‘Assertion, Knowledge, and Rational Credibility’ Philosophical Review 115: 449–485.
Easwaran, K. and Fitelson, B. (2012) ‘An “Evidentialist” Worry about Joyce’s Argument for Probabilism’ Dialectica 66: 425–433.
Easwaran, K. and Fitelson, B. (2015) ‘Accuracy, Coherence, and Evidence’ In T. Szabo Gendler and J. Hawthorne (Eds.), Oxford Studies in Epistemology, Volume 5. Oxford: Oxford University Press.
Evnine, S. (1999) ‘Believing Conjunctions’ Synthese 118: 201–227.
Fallis, D. (2000) ‘Veritistic Social Epistemology and Information Science’ Social Epistemology 14: 305–316.
Fallis, D. (2006) ‘Epistemic Value Theory and Social Epistemology’ Episteme 2: 177–188.
Fallis, D. (2007) ‘Attitudes Toward Epistemic Risk and the Value of Experiments’ Studia Logica 86: 215–246.
Feldman, R. (1998) ‘Epistemic Obligations’ Philosophy Perspectives 2: 236–256.
Feldman, R. (2000) ‘The Ethics of Belief’ Philosophy and Phenomenological Research 60: 667–695.
Feldman, R. and Conee, E. (1985) ‘Evidentialism’ Philosophical Studies 48: 15–34.
Firth, R. (1981) ‘Epistemic Merit, Intrinsic and Instrumental’ Proceedings and Addresses of the American Philosophical Association 55: 5–23.
Foley, R. (1987) The Theory of Epistemic Rationality. Cambridge, MA: Harvard University Press.
Fumerton, R. (1995) Metaepistemology and Skepticism. Lanham, MD: Rowman & Littlefield.
Goldman, A. (1979) ‘What Is Justified Belief?’ In G. Pappas (Ed.), Justification and Knowledge. Springer: 1–23.
Goldman, A. (1986) Epistemology and Cognition. Cambridge, MA: Harvard University Press.
Goldman, A. (1999) Knowledge in a Social World. Oxford: Oxford University Press.
Good, I. J. (1967) ‘On the Principle of Total Evidence’ British Journal for the Philosophy of Science 17: 319–321.
Greaves, H. (2013) ‘Epistemic Decision Theory’ Mind 122: 915–952.
Greaves, H. and Wallace, D. (2006) ‘Justifying Conditionalization: Conditionalization Maximizes Expected Epistemic Utility’ Mind 115: 607–632.
Haddock, A., Millar, A., and Pritchard, D. (2009) Epistemic Value (Eds) Oxford: Oxford University Press.
Harman, G. (1988) Change in View. Cambridge, MA: MIT Press.
Hempel, C. (1960) ‘Inductive Inconsistencies.’ Synthese 12: 439–469.
Huemer, M. (2011) ‘Does Probability Theory Refute Coherentism?’ Journal of Philosophy 108: 35–54.
Jenkins, C. S. (2007) ‘Entitlement and Rationality’ Synthese 157: 25–45.
Joyce, J. (1998) ‘A Nonpragmatic Vindication of Probabilism.’ Philosophy of Science 65: 575–603.
Joyce, J. (2009) ‘Accuracy and Coherence: Prospects for an Alethic Epistemology of Partial Belief’ In Huber and Schmidt-Petri (Eds.) Degrees of Belief. Springer: 263–300.
Kagan, S. (1997) Normative Ethics. Boulder, CO: Westview Press.
Klausen, S. H. (2009) ‘Two Notions of Epistemic Normativity’ Theoria 75: 161–178.
Klein, P. and Warfield, T. A. (1994) ‘What Price Coherence?’ Analysis 54: 129–132.
Kitcher, P. (1990) ‘The Division of Cognitive Labor’ The Journal of Philosophy 87: 5–22.
Kvanvig, J. (2003) The Value of Knowledge and the Pursuit of Understanding. Cambridge: Cambridge University Press.
Kvanvig, J. (2009) ‘Assertion, Knowledge and Lotteries’ In Greenough and Pritchard (Eds.), Williamson on Knowledge. Oxford: Oxford University Press: 140–160.
Laudan, L. (1984) Science and Values. Berkeley: University of California Press.
Laudan, L. (2006) Truth, Error, and Criminal Law. Cambridge: Cambridge University Press.
Leitgeb, H. and Pettigrew, R. (2010a) ‘An Objective Justification of Bayesianism I: Measuring Inaccuracy’ Philosophy of Science 77: 201–235.
Leitgeb, H. and Pettigrew, R. (2010b) ‘An Objective Justification of Bayesianism II: The Consequences of Minimizing Inaccuracy’ Philosophy of Science 77: 236–272.
Levi, I. (1967) Gambling with Truth. Cambridge, MA: MIT Press.
Littlejohn, C. (2012) Justification and the Truth Connection. Cambridge: Cambridge University Press.
Locke, D. T. (2014) ‘The Decision-Theoretic Lockean Thesis’ Inquiry 57: 28–54.
Maher, P. (1990) ‘Why Scientists Gather Evidence’ British Journal for the Philosophy of Science 41: 103–119.
Maher, P. (1992) ‘Diachronic Rationality’ Philosophy of Science 59: 120–141.
Maher, P. (1993) Betting on Theories. Cambridge: Cambridge University Press.
Maitzen, S. (1995) ‘Our Errant Epistemic Aim’ Philosophy and Phenomenological Research 55: 869–876.
Mayo-Wilson, C., Zollman, K. J., and Danks, D. (2011) ‘The Independence Thesis: When Individual and Social Epistemology Diverge’ Philosophy of Science 78: 653–677.
McKinnon, R. (2013) ‘Lotteries, Knowledge, and Irrelevant Alternatives’ Dialogue 52: 523–549.
McNaughton, D. and Rawling, P. (1991) ‘Agent-Relativity and the Doing-Happening Distinction’ Philosophical Studies 63: 163–185.
Muldoon, R. (2013) ‘Diversity and the Division of Cognitive Labor’ Philosophy Compass 8: 117–125.
Muldoon, R. and Weisberg, M. (2009) ‘Epistemic Landscapes and the Division of Cognitive Labor’ Philosophy of Science 76: 225–252.
Myrvold, W. (2012) ‘Epistemic Values and the Value of Learning’ Synthese 187: 547–568.
Nagel, J. (2011) ‘The Psychological Basis of the Harman-Vogel Paradox’ Philosophers’ Imprint 11: 1–28.
Nagel, T. (1986) The View from Nowhere. Oxford: Oxford University Press.
Nelkin, D. K. (2000) ‘The Lottery Paradox, Knowledge, and Rationality’ Philosophical Review 109: 373–409.
Nelson, M. (2010) ‘We Have No Positive Epistemic Duties’ Mind 119: 83–102.
Oddie, G. (1997) ‘Conditionalization, Cogency, and Cognitive Value’ British Journal for the Philosophy of Science 48: 533–541.
Nozick, R. (1974) Anarchy, State, and Utopia. New York: Basic Books.
Olsson, E. J. (2005) Against Coherence: Truth, Probability, and Justification. Oxford: Oxford University Press.
Percival, P. (2002) ‘Epistemic Consequentialism’ Proceedings of the Aristotelian Society Supplementary Volume 76: 121–151.
Pettigrew, R. (2012) ‘Accuracy, Chance, and the Principal Principle’ Philosophical Review 121: 241–275.
Pettigrew, R. (2013a) ‘A New Epistemic Utility Argument for the Principal Principle’ Episteme 10: 19–35.
Pettigrew, R. (2013b) ‘Accuracy and Evidence’ Dialectica 67: 579–596.
Pettigrew, R. (2013c) ‘Epistemic Utility and Norms for Credences.’ Philosophy Compass 8: 897–908.
Pettigrew, R. (2015) ‘Accuracy and the Belief-Credence Connection’ Philosophers’ Imprint. 15: 1–20.
Pettit, P. (2000) ‘Non-consequentialism and Universalizability’ The Philosophical Quarterly 50: 175–190.
Pettit, P. (1988) ‘The Consequentialist Can Recognise Rights’ The Philosophical Quarterly 38: 42–55.
Pollock, J. (1995) Cognitive Carpentry. Cambridge, MA: MIT Press.
Portmore, D. (2007) ‘Consequentializing Moral Theories’ Pacific Philosophical Quarterly 88: 39–73.
Pritchard, D., Millar, A., and Haddock, A. (2010) The Nature and Value of Knowledge: Three Investigations. Oxford: Oxford University Press.
Sen, A. (1982) ‘Rights and Agency’ Philosophy & Public Affairs 11: 3–39.
Smart, J. J. C. and Williams, B. (1973) Utilitarianism: For and Against. Cambridge: Cambridge University Press.
Smith, M. (2009) ‘Two Kinds of Consequentialism’ Philosophical Issues 19: 257–272.
Smithies, D. (2012) ‘The Normative Role of Knowledge’ Nous 46: 265–288.
Solomon, M. (1992) ‘Scientific Rationality and Human Reasoning’ Philosophy of Science 59: 439–455.
Stalnaker, R. (2002) ‘Epistemic Consequentialism’ Proceedings of the Aristotelian Society Supplementary Volume 76: 152–168.
Stapleford, S. (2013) ‘Imperfect Epistemic Duties and the Justificational Fecundity of Evidence’ Synthese 190: 4065–4075.
Stich, S. (1990) The Fragmentation of Reason. Cambridge, MA: MIT Press.
Thomson, J. J. (1985) ‘The Trolley Problem’ The Yale Law Journal 94: 1395–1415.
van Fraassen, B. (1984) ‘Belief and the Will’ The Journal of Philosophy 81: 235–256.
Whitcomb, D. (2007) An Epistemic Value Theory. (Doctoral dissertation) Retrieved from Rutgers University Community Repository at: http://dx.doi.org/doi:10.7282/T3ZP46HD
Williams, J. R. G. (2012) ‘Gradational Accuracy and Nonclassical Semantics’ The Review of Symbolic Logic 5: 513–537.
Zagzebski, L. (2003) ‘Intellectual Motivation and the Good of Truth’ In Zagzebski, L. and DePaul, M. (Eds.) Intellectual Virtue: Perspectives from Ethics and Epistemology. Oxford University Press: 135–154.
Zollman, K. J. (2007) ‘The Communication Structure of Epistemic Communities’ Philosophy of Science 74: 574–587.
Zollman, K. J. (2010) ‘The Epistemic Benefit of Transient Diversity’ Erkenntnis 72: 17–35.

Author Information

Jeffrey Dunn
Email: jeffreydunn@depauw.edu
DePauw University
U. S. A.

Internet Encyclopedia of Philosophy

Epistemic Consequentialism

Table of Contents

1. Consequentialism

2. Final Value and Veritism

3. Consequentialist Theories

a. A Simple Example

b. Cognitive Decision Theory

c. Accuracy First

d. Traditional Epistemology: Justification

i. Coherentism

ii. Reliabilism

iii. Evidentialism

e. Traditional Epistemology Not Concerned with Justification

f. Social Epistemology

g. Philosophy of Science

i. Group versus Individual Rationality

ii. Why Gather Evidence?

4. Summing Up: Some Useful Distinctions

5. Objections to Epistemic Consequentialism

a. Epistemic Trade-Offs

b. Positive Epistemic Duties

c. Lottery Beliefs

6. References and Further Reading

Author Information

An encyclopedia of philosophy articles written by professional philosophers.