Two-Dimensional Semantics
Two-dimensional (2D) semantic theories distinguish between two different aspects, or ‘dimensions’, of the meaning of linguistic expressions. Many other theories identify the meaning of an expression with a dependency of its extension on the state of the world. (The extension of a sentence is its truth-value, and the extension of a sub-sentential expression is the object or objects it applies to.) Consider the following, true sentence:
(1) Anand is a chess player.
If Anand had decided to spend his time very differently, sentence (1) would be false. Which extension this sentence has thus depends on whether a specific individual plays a particular game. One could hold, in line with a common view, that the meaning of (1) is captured by this dependency of its truth-value on Anand’s relation to chess. But notice that there is more than one way in which an expression’s extension depends on the state of the world. For example, in counterfactual circumstances in which the speakers in our linguistic community use the word ‘chess’ so that it exclusively applies to what we call ‘tennis’, (1) would be false. 2D semantic theories identify two kinds of dependencies of extension on the world, both of which are meant to represent important aspects of meaning.
2D semantics is a version of possible worlds semantics. Such theories standardly capture dependency of extension on the world by means of an intension, that is, a function from possible worlds to extensions. 2D semantic theories postulate at least two intensions that capture two kinds of dependencies of extension on the world. One intension, which is sometimes called the ‘2-intension’, corresponds to the first way of construing the dependency of the extension of (1) on the world just outlined. This intension returns ‘True’ for all and only those worlds in which Anand plays chess. In addition, all 2D semantic theories introduce another intension, sometimes called the ‘1-intension’.
Proponents of 2D semantic theories generally agree about how to construe 2-intensions. However, they differ in how they construe 1-intensions, and in what they take to be the theoretical purposes of 1-intensions. Concerning the latter issue, 1-intensions have generally been taken to capture either epistemic features associated with linguistic expressions—such as apriority or cognitive significance—or matters related to context-dependency. There is also disagreement about what kinds of items the theory should be applied to. It is widely accepted that a 2D semantics can be fruitfully applied to some kinds of expressions, such as indexicals. Accounts that apply a 2D semantics only to specific kinds of expressions are called ‘local accounts’ in what follows. Other researchers have argued, more controversially, that 2D semantics is a useful tool for characterizing the meanings of all kinds of expressions, or even the contents of mental states. Accounts that apply a 2D semantics to all kinds of expressions are called ‘global accounts’ in what follows.
The philosophical significance of 2D semantics extends far beyond the philosophy of language. Issues concerning 2D semantics and its interpretation have been at the heart of debates about the mind-body problem and philosophical methodology.
Table of Contents
1. Introduction to 2D Semantics
a. From Extensions to Intensions
Meaningful linguistic expressions have extensions. The extension of a sentence, such as (1), is its truth-value, in this case True. The extension of a general term, such as ‘chess player’, is the class of individuals to which the term applies, in this case the class of people who play chess. The extension of a singular term, such as ‘Anand’, is the individual denoted by the term, in this case Anand. Extension is not the same as meaning. ‘Anand’ is not synonymous with ‘the 15th world chess champion’, even though the expressions denote the same individual. Even more obviously, (1) is not synonymous with ‘Serena Williams is a tennis player’, even though the expressions have the same truth-value.
A popular idea is to characterize meanings as truth- or application-conditions, that is, the conditions under which a sentence is true or the conditions under which an expression is correctly applied. For instance, (1) is true if and only if Anand is a chess player. Given a particular state of the world, these truth-conditions then determine the truth-value of the sentence. Truth- and application-conditions capture the (or a) dependency of an expression’s extension on the state of the world. In possible world theories of meaning, they are modeled as intensions. An intension is a function that assigns extensions with respect to possible worlds. For example, the intension of (1) assigns True with respect to all and only those worlds in which Anand is a chess player; and the intension of ‘chess player’ with respect to a particular world assigns all and only those individuals that play chess in that world. According to such possible worlds accounts, the meaning of an expression is thus its intension.
One way to motivate this idea is by arguing that the primary use of language is to exchange information, which suggests that the meaning of an expression (or at least a crucial aspect of its meaning) is its information content. Furthermore, information can be defined as the exclusion of possibilities, and possibilities are commonly characterized by means of possible worlds: Something is possible if and only if there is a possible world in which it is the case. Accordingly, the information conveyed by sentence (1) excludes all possible worlds in which it is not the case that Anand is a chess player. The remaining worlds are precisely those to which the intension of (1) assigns True. Hence, the intension of an expression is well suited for capturing its information content.
Another virtue of possible worlds theories of meaning is that they allow us to assign different meanings to expressions that share the same extension, thus respecting intuitive judgments about synonymy. For example, there is a possible world in which Anand never plays chess but in which Serena Williams is a tennis player. With respect to this world, (1) and ‘Serena Williams is a tennis player’ are assigned different truth-values, which implies that their intensions differ. Likewise, there is a possible world in which Gelfand wins the 2007 world chess championship tournament, thereby becoming the 15th world champion. With respect to this world, ‘Anand’ and ‘the 15th world chess champion’ have different extensions, which implies that their intensions differ as well.
b. Rigid Designators and Externalism
Saul Kripke (1980) forcefully argued that some types of expressions, among them proper names and indexicals, are rigid designators, that is, they refer to the same individual with respect to every possible world. Suppose, for instance, that Gelfand claims ‘Anand could have become a professional tennis player’. It seems obvious that this statement is about the same individual that (1) is about, that is, Anand. The statement could not be made true by someone else doing something in some possible world. Hence, when one uses the name ‘Anand’ to talk about counterfactual circumstances, one still talks about the same person. Likewise, Anand can use the indexical ‘I’ to talk about what he himself would have done in counterfactual situations. This suggests that proper names such as ‘Anand’, and indexicals such as ‘I’, ‘here’, and ‘now’, are rigid designators.
Most philosophers have accepted Kripke’s claim that names and indexicals are rigid designators. In fact, the claim made above that (1) is true in all and only those worlds in which Anand is a chess player already presupposed that the name ‘Anand’ is a rigid designator. This illustrates that in a possible worlds account of meaning, the existence of rigid designators has immediate consequences for the meanings of expressions containing them.
A less obvious consequence that many have drawn from the existence of rigid designators, following Kripke (1980) and Hilary Putnam (1975), is that the meaning of linguistic expressions is not determined by a subject’s intrinsic properties, that is, that meaning externalism is true. Take the name ‘Anand’, as used by Gelfand. A person who is intrinsically identical to Gelfand might refer to a different person by saying ‘Anand’—this might be because his ‘Anand’-utterances are causally related to this other person. Hence, the utterances of Gelfand and his twin have different extensions. Assuming that names are rigid designators, they have different intensions as well—one utterance picks out Anand with respect to every possible world, the other picks out some other person with respect to every possible world. If intensions are meanings, the two subjects’ utterances also have different meanings.
Probably the most famous argument for externalism is provided by Putnam’s ‘Twin Earth’ thought experiment (1975, 139–144). Suppose that on Twin Earth, which is a planet in a remote part of our galaxy (or in another possible world), there is a substance that is called ‘water’ by the inhabitants of this planet and that shares all of its superficial properties with our water: It is colorless, odorless and drinkable, it falls out of grey clouds and is the dominant substance in rivers and lakes, and so forth. However, this substance has a different molecular structure than water, viz. XYZ. According to Putnam, XYZ is not water, and the term ‘water’ has a different meaning on Earth than it does on Twin Earth. One way to support these claims is by appealing to the fact that ‘water’ and other terms for natural kinds, such as ‘tiger’, ‘electron’, and ‘gold’, rigidly denote the kind they pick out in the actual world. Given this, ‘water’ as used by Oscar on Earth picks out H2O with respect to all possible worlds and thus has a different intension from ‘water’ as used by Twoscar, who lives on Twin Earth. At the same time, as Putnam notes, Oscar and Twoscar might be intrinsically identical. Hence, the intension of ‘water’ is not determined by the intrinsic properties of a speaker, and so, it seems that neither is the expression’s meaning.
All the major proponents of 2D semantics accept that proper names, indexicals, and natural kind terms are rigid designators. They also accept that at least one aspect of meaning is not determined by a speaker’s intrinsic properties.
c. From 1D to 2D
The possible worlds account just sketched in effect yields a one-dimensional (1D) semantic theory, in which the meaning of an expression is modeled by means of a single intension. Proponents of 2D semantics, by contrast, hold that at least for some kinds of expressions, a single intension is not enough to capture their meaning. A natural way to motivate this claim is by considering indexical expressions. Take the following sentence:
(2) I am a chess player.
Assuming that (2) is uttered by Anand, and given that ‘I’ is a rigid designator, the intension of (2) is true with respect to all and only those worlds in which Anand is a chess player. It is thus identical to the intension of (1). However, it seems clear that Anand’s utterance is not synonymous with an utterance of (1). Furthermore, assume that Serena Williams utters (2). The intension of this utterance is true in all and only those worlds in which Williams is a chess player. It thus differs from the intension of Anand’s utterance. So, the intension of (2) varies between different tokens of (2)’s type. In a way, this seems adequate—there is a sense in which Williams and Anand express something different by uttering (2). But it seems that there is also a sense in which what they express is the same. More generally, it is natural to think that indexicals such as ‘I’, ‘here’, and ‘now’, have a stable meaning, even if they are uttered by different people, at different places, and at different times. Accordingly, the sentence (2), that is, the sentence type, and other indexical expressions should also have stable meanings that do not vary with its producer.
The intension of an utterance involving an indexical and, consequently, its extension systematically depends on the circumstances in which the utterance is produced. For example, the intension of (2) is true with respect to a world w if and only if the individual who in fact (but not necessarily in w) utters this sentence is a chess player in w. According to proponents of 2D semantics, this kind of dependency must be captured when giving an account of the meaning of indexical expressions. Here is one way to systematize this dependency. The circumstances in which an expression is uttered are often called ‘context of use’. The worlds with respect to which (according to 1D accounts) an expression’s intension outputs an extension are often called ‘circumstances of evaluation’.
Now assume, first, that one wants to capture how the truth-value of indexical expressions varies depending on the expressions’ context of use. In 2D semantics, this is done by means of a 1-intension:
(1-Intension) A 1-intension is a function from contexts of use to extensions.
For example, relative to a context in which Serena Williams is not a chess player and utters (2), the 1-intension of her utterance is false. In 1-intensions, the context of use also serves as the circumstances of evaluation. In 1D accounts, in which expressions only have one intension, these intensions are construed differently. There, it is assumed that the context of use is fixed, that is, an expression is uttered by a specific individual, at a particular place, and at a particular time. Then, the expression is assigned an extension relative to different circumstances of evaluation. Within a 2D account, this kind of intension is a 2-intension:
(2-Intension) A 2-intension is a function from circumstances of evaluation to extensions.
For example, if Serena Williams utters (2), then her utterance is true with respect to counterfactual circumstances of evaluation in which Serena Williams is a chess player. The 2-intensions of indexical expression types vary between different contexts of use. This is precisely why one needs to appeal to 1-intensions to characterize the meanings of indexical expressions. However, every expression token, that is, every utterance, has a context of use and therefore also has a 2-intension. How 2-intensions of expressions vary between different contexts of use, that is, how they depend on contexts of use, can itself be captured by another, 2D-intension. It is a function from contexts of use to 2-intensions. Equivalently, it can be defined as a function that takes pairs of a context of use and circumstances of evaluation as input and delivers an extension as output:
(2D-Intension) A 2D-intension is a function from pairs of contexts of use and circumstances of evaluation to extensions.
A note concerning the construal of contexts of use and circumstances of evaluation: Circumstances of evaluation can simply be understood as possible worlds. It is natural to understand contexts of use as possible worlds as well. However, there is a catch. In many possible worlds, a great number of utterances are made. Consider, for instance, a world in which both Anand and Williams utter (2). If contexts of use are just possible worlds, then it is impossible to identify the utterance that is to be assigned an extension. A common way to solve this problem is to construe contexts of use as centered worlds (compare Lewis 1979). A centered world is a triple of a possible world, an individual, and a time. A centered world can thus serve to pick out the relevant utterance by specifying, or ‘marking’, the producer of the utterance and the time at which it is uttered.
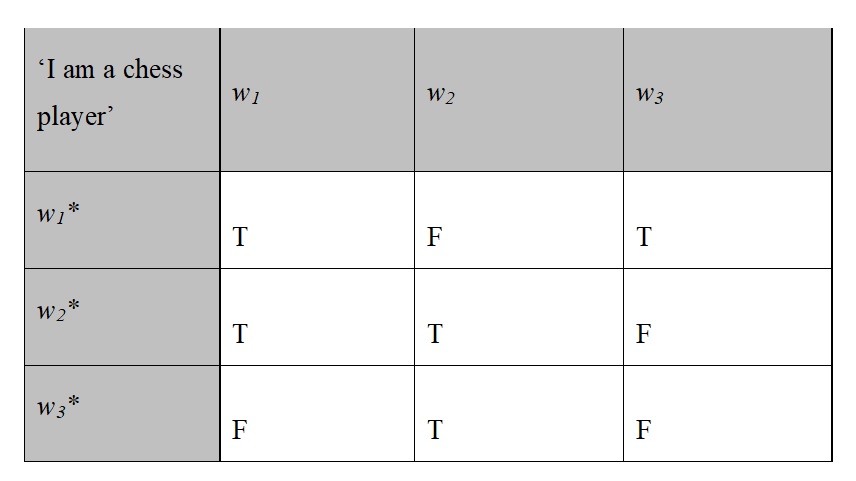
All of the intensions just defined can be represented in a 2D matrix. Figure 1 below depicts a snippet of the 2D matrix of sentence (2). In each centered world, the individual at the center utters (2) at the marked time. The worlds involved have the following character—notice that centered worlds are flagged by a ‘*’, and that any wn* differs from any wn only in that the former involves a center.
w1* is centered on Anand. In w1, Anand and Gelfand are chess players, and Williams is not.
w2* is centered on Gelfand. In w2, Gelfand and Williams are chess players, and Anand is not.
w3* is centered on Williams. In w3, Anand is a chess player, and Gelfand and Williams are not.
The worlds on the left side, marked with an ‘*’, are contexts of use, understood as centered possible worlds. The worlds on the top are circumstances of evaluation, understood as possible worlds. Notice that the class of contexts of use and the class of circumstances of evaluation are identical, the only difference being the presence or absence of centering. For the purposes of illustration, here is how the second row of the matrix is evaluated. In this row, w2* is assumed to be the context of use, in which Gelfand utters (2). Now this utterance is evaluated with respect to different circumstances of evaluation. Since Gelfand is a chess player in w1 and in w2, but not in w3, the first two cells in this row get assigned a ‘T’ (for True), while the third one gets assigned an ‘F’ (for False). Now assume that w1* is the actual world. That is to say, the utterance of (2) that we consider is in fact produced by Anand, who is a chess player. Then the three kinds of intensions identified above are represented in the matrix as follows. The top row of the matrix, with respect to which the actual world, centered on Anand, is the context of use, represents the 2-intension of (2). The other rows represent 2-intensions that (2) could have had, if it had been uttered in different contexts. The 1-intension is represented by the diagonal that runs from the top left to the bottom right of the matrix. The matrix itself represents the utterance’s 2D-intension.
According to the 2D account just sketched, indexical expressions are associated with three intensions. This raises the question: Which of these intensions represents the meaning of these expressions? The 1-intensions and 2D-intensions of indexical expressions do not vary with their context of use. This distinguishes them from 2-intensions and makes them more suitable for representing the meaning of such expressions. Relatedly, it is plausible that subjects who know the meaning of an indexical expression are able to evaluate 1-intensions and 2D-intensions. For example, a speaker is able to say that if, in the context of use, a is the speaker, and if, in the circumstances of evaluation, a is a chess player, (2) is true. An expression’s 2-intension, however, cannot be evaluated on the basis of mere semantic competence, because semantic competence does not provide knowledge of the context of an utterance. These considerations suggest that both the 1-intension and the 2D-intension of an indexical expression are better candidates for representing its meaning. But 2D accounts are not committed to the claim that one of these intensions represents the meaning of such an expression. Rather, proponents of 2D semantics could say that all three intensions represent important aspects of meaning. For instance, as was mentioned above, when Williams and Anand utter (2), one would like to say that in one sense, they expressed the same thing, and in another sense, they expressed something different. The sense in which what is expressed differs is reflected in the differences between the 2-intensions of the respective utterances. 2D semantics thus provides the resources to capture all these aspects of meaning.
All 2D semantic theories share the basic structure represented by a 2D matrix. This structure is 2D because the worlds involved play two different roles. Above, these roles were introduced as the contexts of use on the one hand, and the circumstances of evaluation on the other. However, notice that, while this is a natural and popular understanding of the two roles of possible worlds in 2D semantics, some 2D accounts understand these two roles in slightly different ways. In particular, the construal of the worlds involved in the ‘first dimension’, that is, the centered worlds listed on the left of each row in the 2D matrix, is contested. As a consequence, the construal of 1-intensions is contested as well. 2D accounts also differ in other respects. There is widespread agreement that a 2D account is well suited to describe the meanings of indexicals, and of indexical expressions. However, whether or not a 2D account should also be applied to other kinds of expressions, and if so, to what kinds of expressions, is controversial.
2. Local Accounts
a. Content and Character (Kaplan)
We just saw that indexicals provide a natural motivation for adopting a 2D theory. It is therefore unsurprising that the first 2D theories were introduced as accounts of indexical expressions (compare for example, Kamp 1971). One such account that has been particularly influential is David Kaplan’s general semantic theory of indexicals (compare Kaplan 1989). According to Kaplan, expressions have contents. These contents are supposed to correspond to ‘what is said’ by the relevant expression. Furthermore, the content of a sentence token is a proposition. Kaplan’s way of construing propositions, and contents in general, requires some elaboration. On his view, propositions are structured entities. The content of Anand’s utterance of (2), for instance, is a singular proposition that consists of Anand himself and the property of being a chess player. (A proposition is singular if it has an individual as its constituent.) According to Kaplan, the content of a singular expression, such as ‘Anand’, is an individual—in this case, Anand. The content of a general expression, such as ‘chess player’, is a property—in this case, the property of being a chess player. The contents of composite expressions then systematically depend on the contents of their parts.
This account of content seems very different from a possible words account. However, the contents postulated by Kaplan can be taken to determine intensions. And in fact, Kaplan often appeals to intensions to characterize contents. For Kaplan, an intension is a function from circumstances of evaluation to extensions. Kaplan’s intensions are basically the 2-intensions introduced above, except that Kaplan favors a different characterization of circumstances of evaluation. For Kaplan, circumstances of evaluation are not just possible worlds. They also include a designated time and potentially other features. Now consider again Anand’s utterance of (2), which expresses a singular proposition containing Anand and the property of being a chess player. This proposition determines an intension that is true with respect to all circumstances of evaluation in which Anand is a chess player.
According to Kaplan, indexicals are directly referential, which is to say that the only contribution they make to the contents of the expressions they figure in is their referent. He takes this to imply that indexicals pick out the same individual with respect to all circumstances of evaluation. Kaplan thus seconds Kripke’s claim that indexicals are rigid designators.
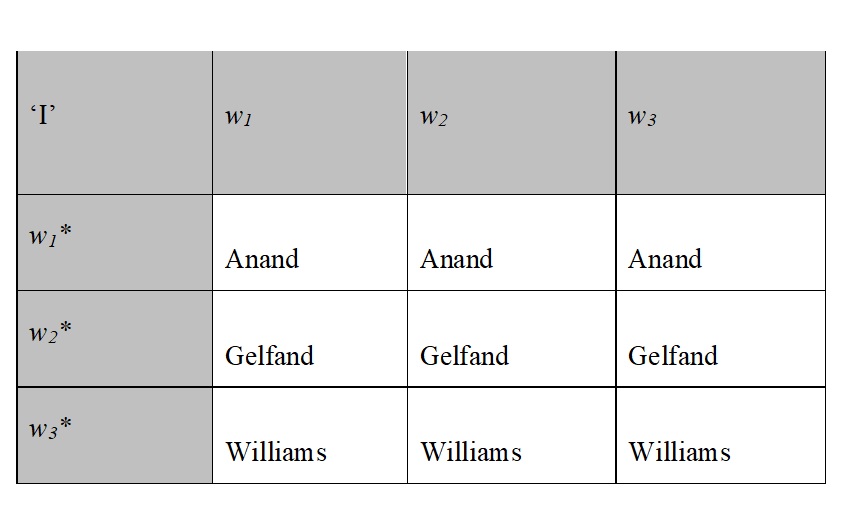
Up to this point, the account described is just a standard 1D account. However, Kaplan argues that content is not all there is to meaning. He therefore introduces another aspect of meaning, character. The character of an expression can be understood as a rule that specifies how the content of the expression depends on the context. For example, for the indexical ‘I’, the rule would be something like this: ‘If x is the producer of the utterance in the relevant context, then x is the content of ‘I’’. Similar rules apply to other indexicals. More formally, characters can be defined as functions from contexts to contents. Hence, on the possible worlds understanding of content, characters are 2D-intensions. The inclusion of characters thus makes Kaplan’s account a type of 2D semantics. Now consider three contexts, in all of which someone utters ‘I’. In w1*, it is Anand; in w2*, it is Gelfand; in w3*, Williams. Given these contexts, Kaplan’s account entails the following snippet of the matrix for the indexical ‘I’:
This matrix illustrates Kaplan’s claim that ‘I’ is a rigid designator: First, the reference of ‘I’ is determined by the context, and then the expression picks out the same individual with respect to all circumstances of evaluation.
For ease of exposition, it has so far been assumed that contents are assigned to utterances in Kaplan’s account, and that Kaplan’s contexts are just the contexts of use introduced in § 1. However, both assumptions are not entirely correct. According to Kaplan, contents are assigned to expressions with respect to contexts. (Characters, on the other hand, are assigned to expressions without relativization to anything.) The subject that is the content of, for instance, ‘I’, need not in fact have produced an utterance in a Kaplanian context. On his account, the context does not have to involve an utterance at all. Kaplan states that every context has an agent, a time, and a location within a possible world. (Contexts can thus be understood as centered worlds.) The content of the expression ‘I’ with respect to a context is the agent of the context, where this agent may or may not produce an utterance in the relevant context. This feature of Kaplan’s account has implications for the evaluation of some expressions. For instance, the sentence ‘I utter nothing’ is true with respect to some Kaplanian contexts, while it comes out as false with respect to all contexts of use as they were construed in § 1.
The character of an indexical expression corresponds to what a competent speaker can know in virtue of understanding the expression. The same does not hold for contents, since they vary between contexts. Should one therefore say that the character of an indexical is its meaning? While Kaplan affirms this in several places, he stresses elsewhere that content is also an important aspect of meaning. Again, it does not seem too important to settle the question of what the meaning of indexicals is. What is clear is that both characters and contents play crucial roles in Kaplan’s account of the semantics of indexicals.
On Kaplan’s account, all meaningful expressions can be assigned a character and a content. However, he believes that the characters of many expressions are not very interesting, since they assign the same content with respect to every context. Expressions of this type thus have a constant content. According to Kaplan, proper names fall into this category. In Kaplan’s view, we can say with respect to such expressions that their meaning is just their content. In any case, it would not be theoretically very fruitful to apply Kaplan’s 2D account to expressions with a constant content.
b. Superficial and Deep Modality (Evans, Davies & Humberstone)
Gareth Evans (1979), and Martin Davies & Lloyd Humberstone (1980) applied ideas from 2D semantics to give accounts of both contingent truths that can be known a priori, and of necessary truths that can only be known a posteriori. The existence of both kinds of truths seems to follow straightforwardly from the fact that some expressions are rigid designators. For instance, take the names ‘Hesperus’ and ‘Phosphorus’, both of which refer to the same object, the planet Venus. Since both names are rigid designators, they refer to Venus with respect to every possible world. And this implies that ‘Hesperus = Phosphorus’ is necessarily true. At the same time, it took substantial astronomical research to establish that Hesperus = Phosphorus, and it seems clear that no amount of a priori reasoning could have sufficed to come to know it. Hence, ‘Hesperus = Phosphorus’ is an example of a necessary a posteriori truth (or at least it is a necessary truth that if Hesperus exists, then Hesperus = Phosphorus.) A simple way of formulating contingent a priori truths is by drawing on sentences that contain the expression ‘actual’. This expression is standardly taken to be a device that turns non-rigid expressions into rigid designators. For instance, take the definite description ‘the 15th world chess champion’. This expression picks out Anand; but with respect to a world in which Gelfand wins the 2007 world championship tournament, it picks out Gelfand. The description at issue is therefore not rigid. However, if one adds the word ‘actual’ to it, changing the description to ‘the actual 15th world chess champion’, the new description will pick out the person who in our—the actual—world is the 15th world chess champion (that is, Anand) with respect to every possible world. With this in mind, consider the sentence ‘The actual 15th world chess champion is the 15th world chess champion’. This sentence is contingent—for instance, it is false with respect to the world just mentioned, in which Gelfand, and thus someone other than the actual 15th world chess champion, is the 15th world chess champion. At the same time, the sentence can be known a priori. Hence, ‘The actual 15th world chess champion is the 15th world chess champion’ is a contingent a priori truth.
Many people have found it puzzling that there could be contingent a priori truths and necessary a posteriori truths. If a sentence is contingent, then it seems that its truth depends on features that are not shared by all worlds. It is thus natural to think that to find out whether our world has these features, one needs to do empirical research. On the other hand, if a sentence is necessary, then it seems that its truth does not depend on specific features of our world. It is thus natural to think that to find out whether such a sentence is true, purely a priori reasoning is sufficient.
Evans tries to explain how there can be contingent a priori truths, focusing on examples that arise from what he calls “descriptive names”. To introduce such a name, he stipulates that the name ‘Julius’ is to refer to whoever invented the zipper (Evans 1979, 163). A descriptive name is thus a name whose reference is fixed by a description—in this case, the description ‘the inventor of the zipper’. Evans argues that since descriptive names are names, they are rigid designators. The descriptive name ‘Julius’ thus refers to the same person with respect to every possible world, unlike the definite description ‘the inventor of the zipper’. With this in mind, consider the following sentence:
(3) Julius invented the zipper.
With respect to a possible world in which someone other than the actual inventor of the zipper (Whitcomb Judson) invented the zipper, (3) is false. Hence, (3) is contingent. At the same time, according to Evans, someone who understands the expression ‘Julius’ knows its associated description and is thus in a position to know a priori that (3) is true. Therefore, (3) is a contingent a priori truth. To account for such sentences, Evans introduces a distinction between superficial and deep contingency. Superficial contingency corresponds to the ordinary understanding of contingency—as Evans puts it, whether a sentence is superficially contingent depends on how it “embeds in the scope of modal operators” (1979, 161). Deep contingency, on the other hand, depends on what makes a sentence true: A sentence is deeply contingent only if the world needs to satisfy some condition for this sentence to be true, that is, only if there is some feature that the world needs to have to make it true. What makes a sentence true, according to Evans, is in turn related to the sentence’s content. Accordingly, a deeply necessary sentence is one whose content guarantees its truth. Superficial and deep contingency can come apart because the notion of content is not tied to metaphysical modality. Evans’s notion of content thus differs from the one invoked, for instance, by Kaplan. Following Gottlob Frege (1892/1952), Evans holds that there are epistemic constraints on content: If two sentences have the same content, then a subject who understands both of them cannot believe what one of the sentences says without also believing what the other one says. Evans calls such sentences “epistemically equivalent”.
According to Evans’s distinction, (3) is superficially contingent. Evans also holds that ‘Julius’ and ‘the inventor of the zipper’ have the same content; therefore, (3) is deeply necessary. In his view, there can be no a priori sentences that are deeply contingent. Accordingly, contingent a priori truths are those sentences that are superficially contingent but deeply necessary, that is, those whose truth is guaranteed by their content, even though they are not true in all possible worlds. One might have doubts that such a separation of content and modality is sensible. Take the two sentences ‘Julius is male’ and ‘The inventor of the zipper is male’. These sentences place different demands on a possible world with respect to which they are to be true: ‘Julius is male’ is true with respect to some world if and only if the individual who invented the zipper in the actual world is male, while ‘The inventor of the zipper is male’ is true with respect to some world if and only if the individual who invented the zipper in that world is male. So how could these sentences have the same content, as Evans’s account has it? In response to this kind of worry, Evans points out that the sentences nevertheless place the exact same demands on the actual world: They are both true with respect to the actual world if and only if the individual who invented the zipper in that world is male. Since believing something means believing that it is actually the case, the two sentences are epistemically equivalent. And this, in turn, implies that they have the same content.
By distinguishing between two kinds of modality, Evans draws on a central idea of 2D semantics. Accordingly, deep and superficial modality could, in principle, be used to define 1- and 2-intensions, respectively. The connection to 2D semantics becomes even clearer once one considers the account of Davies & Humberstone (1980), who try to characterize Evans’s distinction between superficial and deep necessity in formal terms. They start from a standard modal logic, with ‘□’ as the sentential operator expressing necessity. Then they introduce the sentential operator ‘A’, which stands for ‘it is actually the case that’. In line with what was said above about ‘actually’-involving expressions, a sentence AS is true with respect to a world if and only if S is true with respect to the actual world. Accordingly, if S is true, then AS is necessarily true, that is, true with respect to every world. But as Davies & Humberstone note, there is an intuitive sense in which some other world might have been actual, and thus, we can consider different worlds as actual. Based on this idea, they introduce another sentential operator, F (for ‘fixedly’), such that FS is true with respect to a world w if and only S is true with respect to w irrespective of which world is considered as actual. Combining these two operators, one can derive another operator, FA, such that FAS is true if and only if S is true with respect to any world that is considered as actual. As Davies & Humberstone point out, the resulting logic can also be characterized in 2D terms. Accordingly, one can evaluate a sentence S with respect to pairs of a world considered as actual and a possible world—this way of evaluating expressions thus yields a kind of 2D-intension.
Davies & Humberstone argue that the distinction between □-truth and FA-truth captures Evans’s distinction between superficial and deep necessity. Accordingly, FAS is true if and only if S is deeply necessary. On Evans’s account, this implies that if S is a priori, then FAS is true. Davies & Humberstone hypothesize that all contingent a priori truths are A-involving. For instance, assume that it is part of the meaning of Evans’s descriptive name ‘Julius’ that it rigidly refers to the inventor of the zipper. Then we can take ‘Julius’ to abbreviate ‘the actual inventor of the zipper’. Given this, (3) is clearly FA-true: No matter which world w is considered as actual, the person who invented the zipper in w actually invented the zipper in w. Other examples of sentences that are FA-true and contingent a priori are easy to come by. These include all sentences of the form S ↔ AS, such as ‘Grass is green if and only if grass is actually green’. Davies & Humberstone also hold that there are many A-involving necessary a posteriori truths. For instance, if S is an ordinary (superficially and deeply) contingent truth, such as ‘Grass is green’, then AS is necessary and a posteriori.
As was noted above, Davies & Humberstone follow Evans in holding that all a priori truths are deeply necessary, which in their framework means that they are FA-true. According to Davies & Humberstone, contingent a priori truths involve a divergence between □-truth and FA-truth—such sentences are FA-true but not □-true—that is due to the involvement of an (implicit) A-operator. If this indeed applies to all contingent a priori truths, then these can be given a unified explanation in their framework. But it is not obvious that all contingent a priori truths are A-involving. Take, for instance, ‘The local theater is a theater’. Given that the expression ‘local’, like other indexicals, is a rigid designator, this sentence is contingent. It is also clearly a priori. But it is less clear that ‘local’, or any other expression in the sentence at hand, is even implicitly A-involving. It is therefore disputable both that Davies & Humberstone can explain all contingent a priori truths and that they can preserve Evans’s claim that all a priori truths are deeply necessary. Nevertheless, there is some plausibility to the claim that ‘The local theater is a theater’, and indeed all contingent a priori truths, involve some kind of implicit or explicit reference to actuality.
Davies & Humberstone tentatively suggest that many other expressions are also A-involving, among them natural kind terms, such as ‘water’. Recall that, since water is composed of H2O molecules, ‘water’ rigidly refers to H2O. This implies that ‘Water = H2O’ is necessarily true. Since this sentence cannot be known a priori, it represents another example of a necessary a posteriori truth. Davies & Humberstone’s suggestion is that ‘water’ and other natural kind terms can be understood analogously to descriptive names. For instance, the description associated with ‘water’ could be something like ‘the actual chemical kind exemplified by the liquid that falls from clouds, flows in rivers, is colorless and odorless, …’, (compare Davies & Humberstone 1980, 18) which rigidly refers to H2O. If this is correct, then sentences containing the term ‘water’ are A-involving, and the fact that ‘Water = H2O’ is a necessary a posteriori truth can be explained by Davies & Humberstone’s account. However, Davies & Humberstone believe that ordinary proper names are not even implicitly A-involving, and thus that true identity statements involving names, such as ‘Hesperus = Phosphorus’, are both □-true and FA-true. This is in line with Evans’s view, according to which such sentences are both superficially and deeply necessary. Hence, not all necessary a posteriori sentences are given a unified treatment in the account of Evans and Davies & Humberstone.
3. Global Accounts
a. Metasemantic 2D Semantics (Stalnaker)
Robert Stalnaker (1978) introduces his 2D account as a part of a theory of assertions and their role in communication. According to Stalnaker, the contents of assertions are propositions, which he construes as intensions, that is, functions from possible worlds to extensions. Every proposition thus corresponds to a set of possible worlds, viz. those worlds with respect to which the extension is True. In a conversation, each of the participants makes certain assumptions. These speaker presuppositions are those propositions that the participants in the conversation believe to be true, or at least accept for the purposes of the conversation, and that they believe to be accepted by all the other participants in the conversation. Those speaker presuppositions that are indeed shared, and known to be shared, by all participants in a conversation constitute their common knowledge. This common knowledge is characterized by the context set—the set of those possible worlds that are not ruled out by the common knowledge of the participants in the conversation. Now if a speaker in a conversation asserts a proposition that is accepted by the hearers, then this proposition is added to their common knowledge, which means that those possible worlds not compatible with it are eliminated from the context set. On this account, the goal of communication is to reduce the context set by means of making assertions.
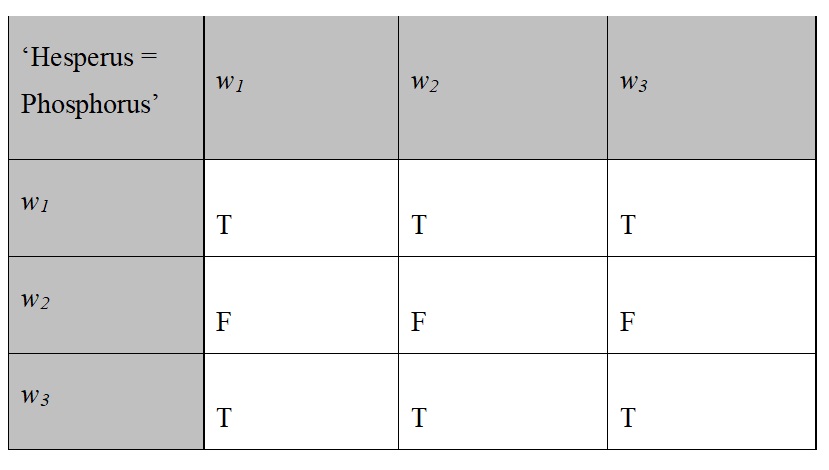
One problem about this very natural account of assertion and communication is that it seems unable to explain the use of certain perfectly sensible assertions. For example, there are many conceivable circumstances in which a speaker successfully communicates something by asserting ‘Hesperus = Phosphorus’. However, the proposition expressed by this utterance has a necessary intension (an intension that is constantly True in all possible worlds). Therefore, no matter what the common knowledge of the participants in such a conversation consists in, the utterance cannot eliminate any possibilities from the context set. Stalnaker thus needs to explain how an utterance of ‘Hesperus = Phosphorus’ and other utterances of this type can be informative. His explanation relies on the fact that which proposition a specific sentence expresses depends on features of the world. Suppose, for instance, as seems plausible, that if some celestial body other than Venus had been the brightest object in the evening sky (BOE), then that object would have been called ‘Hesperus’, and likewise that if some celestial body other than Venus had been the brightest object in the morning sky (BOM), then that object would have been called ‘Phosphorus’. Given this, if Mars had been the BOE and Venus the BOM, ‘Hesperus = Phosphorus’ would have expressed a different proposition that is necessarily false. In Stalnaker’s account, this dependency of the proposition expressed by an utterance on the state of the world is captured by a propositional concept. A propositional concept is a function from possible worlds to propositions or, equivalently, from pairs of possible worlds to truth-values. A propositional concept is thus a 2D-intension; it corresponds to a 2D matrix. Below is a snippet of the 2D matrix of ‘Hesperus = Phosphorus’, involving the following worlds:
w1: BOE = Venus; BOM = Venus
w2: BOE = Mars; BOM = Venus
w3: BOE = Mars; BOM = Mars
As was just noted, the whole matrix represents a propositional concept and thus a 2D-intension. Given that w1 is the actual world, the upper row of the matrix represents the intension actually expressed by ‘Hesperus = Phosphorus’. In 2D terminology, this horizontal intension is a 2-intension. The diagonal of the matrix running from the upper left to the bottom right is what Stalnaker calls a ‘diagonal proposition’. The diagonal proposition of ‘Hesperus = Phosphorus’, which in 2D terms is its 1-intension, is true with respect to a world if and only if the sentence expresses a true proposition in this world.
While the 2-intension, or horizontal proposition, of ‘Hesperus = Phosphorus’ is necessary, its 1-intension, or diagonal proposition, is contingent, which reflects the fact that (for all that is presupposed in a certain context) the sentence could have expressed a different, false proposition. This is crucial for Stalnaker’s explanation of the informativeness of assertions such as ‘Hesperus = Phosphorus’, because he argues that in uttering one of them, a speaker communicates the expression’s diagonal proposition. Assume, for instance, that w1, w2, and w3 are in the context set in a conversation, when the speaker utters ‘Hesperus = Phosphorus’. Interpreted according to its 2-intension—which for Stalnaker corresponds to literal interpretation—this utterance is uninformative and thus violates an important conversational rule. Moreover, a hearer who trusts this utterance knows that it is uninformative. According to Stalnaker, the utterance should thus be reinterpreted. What it really communicates is that the sentence ‘Hesperus = Phosphorus’ expresses something true. Assuming that it is common knowledge in the conversation that Hesperus is the BOE and Phosphorus the BOM, the utterance also conveys that the BOE is identical to the BOM. This content is captured by the utterance’s diagonal proposition. Hence, if the hearer accepts the speaker’s utterance, then w2, with respect to which the diagonal proposition is false, is eliminated from the context set.
There are some important differences between Stalnaker’s 2D account and the accounts considered in § 2. For a start, the accounts discussed previously were introduced to explain the behavior of specific kinds of expressions, such as indexicals (Kaplan), descriptive names (Evans; Davies & Humberstone), ‘actually’ (Evans; Davies & Humberstone), and natural kind terms (Davies & Humberstone). But since the proposition expressed by any sentence depends on the state of the world, Stalnaker’s 2D account can be sensibly applied to all kinds of sentences. Furthermore, Stalnaker (1987, 182f) stresses that his account concerns expression tokens, not types. The reason for this is that Stalnaker’s 2D account is not semantic, but metasemantic: Its 1-intension and its 2D-intension are not aspects of the meaning of expressions, but capture how their meanings depend on features of the world. And as Stalnaker notes, the latter dependency can vary between tokens of an expression type.
Stalnaker’s diagonal propositions have several further uses, for example in capturing the contents of mental states. For example, Stalnaker (1981) argues that diagonal propositions can serve to resolve puzzles raised by so-called ‘indexical’ or ‘egocentric’ beliefs, for example, ‘I am sleepy’ or ‘It is dark here’, that are essentially about the believer and her relation to the world. The following story, loosely based on a case devised by John Perry (1977, 492), illustrates one such puzzle. Suppose that Anand has lost his memory and does not remember who he is. From a book about the history of chess, he learns that Anand is the 15th world chess champion. But Anand is quite sure that he himself never even played in a world championship. Hence, Anand both believes I am not the 15th world chess champion and Anand is the 15th world chess champion. On the possible worlds account of content endorsed by Stalnaker, the former of these beliefs is true in all and only those worlds in which Anand is not the 15th world chess champion. Accordingly, the two beliefs are contradictory. But this does not seem right since, from Anand’s perspective, there is a clear sense in which his beliefs could both be true. Stalnaker’s solution is to ascribe to the subject the diagonal proposition of one of the beliefs in such cases. In the case at hand, one option is to reinterpret the belief of Anand’s that he would express by saying ‘I am not the 15th world chess champion’, such that he in fact believes not the horizontal proposition, that is, the 2-intension associated with this utterance, but rather the 1-intension associated with it, that is, the diagonal proposition. This belief is compatible with Anand being the 15th world chess champion because there are, for instance, worlds in which the amnesiac reading a book about chess history is not Anand, or has simply never played a match for the world championship. By ascribing the diagonal proposition to Anand, one can thus escape the undesirable conclusion that his belief state is inconsistent.
We saw above that Stalnaker’s 2D account can be applied to a posteriori necessities, such as ‘Hesperus = Phosphorus’. Stalnaker (2001, 155) suggests that his account can provide a general explanation for this phenomenon. This is a surprising claim, since the explanation he offers for the informativeness of ‘Hesperus = Phosphorus’ and other necessary a posteriori truths can be applied just as well to necessary a priori sentences, such as the following sentence that states Fermat’s last theorem: ‘No three positive integers a, b, and c satisfy an + bn = cn for any n greater than 2’. It is very plausible that mathematical truths, such as Fermat’s last theorem, are necessary. At the same time, it is intuitively obvious that the above sentence can be informative for a subject. On Stalnaker’s account, this is explained in the same way that the informativeness of necessary a posteriori truths is explained, by the fact that the diagonal proposition expressed by the above sentence is contingent. Intuitively, one might think that the informativeness of necessary a priori truths and that of necessary a posteriori truths are different kinds of phenomena that demand different explanations. However, whether one should consider this as a problem for Stalnaker’s account depends on one’s theoretical commitments. Stalnaker himself is skeptical about the existence of a priori truths. From his perspective, there is thus no deeper theoretical reason to provide structurally different explanations for the informativeness of, say, a statement of Fermat’s last theorem on the one hand and of ‘Hesperus = Phosphorus’ on the other.
One may have doubts that it is always adequate to ascribe diagonal propositions in cases that concern seemingly informative necessary (or necessarily false) statements or contents. For instance, is Anand’s belief, expressed by ‘I am not the 15th world chess champion’, really about the truth-value of this particular expression? Similarly, is the information a subject acquires upon hearing an utterance of ‘Hesperus = Phosphorus’ really metalinguistic? Notice, however, that the information conveyed in cases that involve the ascription of diagonal propositions need not be—at least not purely—metalinguistic. For instance, in the case discussed above, the speaker managed to convey to the hearer that the BOE is identical to the BOM by uttering ‘Hesperus = Phosphorus’. This is enabled by their common knowledge, in particular by the fact that in all the worlds in the context set, the BOE and the BOM are called ‘Hesperus’ and ‘Phosphorus’, respectively. This illustrates how diagonal contents can capture ordinary object-level information. Nevertheless, diagonal propositions do involve metalinguistic information, and their transmission in communication reflects a kind of ignorance of meaning or content on the side of the hearer. To motivate the view that such ignorance is quite common, it is useful to consider it in the context of Stalnaker’s general approach to linguistic meaning and mental content, which is externalist. The accounts of Kaplan, Evans, and Davies & Humberstone (and even more so the accounts discussed in the following section) can be interpreted as attempts to at least partially retain an internalist type of meaning or content (in the form of a 1-intension or a 2D-intension). Stalnaker rejects this interpretation of 2D semantics (2004). In his view, there is no viable internalist component of meaning or content, inter alia because he believes that one needs to appeal to features of the external world to obtain determinate content. From a purely externalist perspective, it is to be expected that even competent speakers often lack knowledge of the meaning of the expressions they use. It therefore makes sense to characterize the information they gain from utterances that express necessary propositions as (partly) metalinguistic, that is, as information about the meanings of certain expressions. But of course, this externalist viewpoint is contested. In the next section, we will consider a very different account of meaning and content, and accordingly, a very different interpretation of 2D semantics.
b. Epistemic 2D Semantics (Chalmers, Jackson)
Epistemic 2D semantics is a particularly ambitious, and also particularly controversial, theory that relies on an epistemic understanding of 1-intensions. These 1-intensions are supposed to capture the role of linguistic expressions for a subject’s reasoning and in a subject’s cognition more generally, and thus serve as the basis for a general internalist semantics. Epistemic 2D semantics also provides general explanations for the occurrence of contingent a priori truths and necessary a posteriori truths, in a way that promises to retain systematic a priori access to modality. The two main proponents of epistemic 2D semantics are David Chalmers and Frank Jackson, who have defended the account in a great number of writings (for example, Chalmers 2004; Jackson 2004).
Epistemic 2D semantics is based on the idea that there are two ways of considering a possible world: One can consider it as actual or as counterfactual. Putnam’s Twin Earth scenario serves to illustrate this distinction. Assume first that the scenario does not represent the state of our world and the planet we live on. In the actual world, the odorless, drinkable substance in our rivers and lakes is H2O, and hence the Twin Earth scenario represents a way the world is not, but could have been. Considering the Twin Earth world as counterfactual in this way lends plausibility to the view that the substance on Twin Earth is not water, because its molecular structure differs from that of the substance in our rivers and lakes. However, one can also consider Putnam’s scenario in a different way. To do this, suppose that the scenario describes the actual world. That is to say, suppose that what you have been told about the molecular structure of the odorless, drinkable substance in our rivers and lakes is wrong. The stuff that we drink every day, that comes out of our faucets, that we call ‘water’, and so forth, is really XYZ. It seems natural to say that under this assumption, one should conclude that water is XYZ. As Chalmers often puts it: If it turns out that the watery stuff (that is, the odorless, drinkable, substance in our rivers and lakes) is XYZ, then water is XYZ. In epistemic 2D semantics, these two ways of considering possible worlds are used to define two intensions:
A primary intension is a function from possible worlds considered as actual to extensions.
A secondary intension is a function from possible worlds considered as counterfactual to extensions.
The distinctive claim of epistemic 2D semantics is that every linguistic expression that is eligible for having an extension has both a primary intension and a secondary intension. Note that one can also define the epistemic version of a 2D-intension, as follows:
An epistemic 2D-intension is a function from pairs of possible worlds considered as actual and possible worlds considered as counterfactual to extensions.
Secondary intensions are closely related to the standard notion of modality—to what Evans called ‘superficial modality’ and what, following Kripke (1980), is today usually called ‘metaphysical modality’: A sentence is metaphysically necessary if and only if it has a necessary secondary intension, that is if and only if its secondary intension outputs True with respect to every world. Primary intensions, on the other hand, are closely connected to apriority: One of the key theses of epistemic 2D semantics is that a sentence is a priori if and only if it has a necessary primary intension. The worlds involved in primary intensions thus represent epistemic possibilities, that is, ways the world could be like for all one can know a priori. This thesis is based on the idea that primary intensions are a priori accessible, which can be motivated as follows. To consider a possible world as actual, one may need to bracket one’s empirical knowledge, such as one’s knowledge that the substance in our rivers and lakes is H2O. But, most importantly for epistemic 2D semantics, one does not need empirical knowledge to determine the extensions of one’s expressions with respect to worlds considered as actual. This is because any lack of empirical knowledge is ignorance of features of the actual world, and such ignorance is irrelevant if one assumes that the world one is considering is the actual world: In considering a possible world as actual, only information that is hypothetically assumed is brought to bear. The question of how the information about these possible worlds is presented to a subject, such that it is sufficient to determine the extensions of the expressions she uses, is discussed in more detail below.
Epistemic 2D semantics assigns intensions to linguistic tokens. One obvious reason for this is that, as with other kinds of 2-intensions, secondary intensions can vary between different linguistic tokens of the same type, for instance, when indexical expressions are involved. A less obvious reason is that, as we will see, primary intensions can also vary between tokens of the same type. The worlds involved in primary intensions are centered worlds. Again, this can be motivated by their usefulness in dealing with indexical expressions, in the way described in §§ 1.c and 2.a.
In what follows, the most important philosophical implications of epistemic 2D semantics will be discussed. Epistemic 2D semantics has been used to defend modal rationalism, that is, the view that we have a priori access to what is possible or necessary (compare § 3.b.i.). Another important claim made by proponents of epistemic 2D semantics is the thesis of scrutability, according to which all truths can be derived a priori from a narrowly constrained description of the world (compare § 3.b.ii.). Based on these epistemic theses, proponents of epistemic 2D semantics have argued that philosophical practice involves (or even has to involve) a central a priori element (compare § 3.b.iii.).
i. Modal Rationalism
According to epistemic 2D semantics, all expressions that are eligible for having an extension have both a primary and a secondary intension. Given the connections between primary intensions and apriority on the one hand, and between secondary intensions and metaphysical modality on the other, this implies that the 2D structures of all contingent a priori truths and of all necessary a posteriori truths can be described as follows:
(Contingent a priori) A sentence S is contingent a priori if and only if S has a necessary primary intension and a contingent secondary intension.
(Necessary a posteriori) A sentence S is necessary a posteriori if and only if S has a contingent primary intension and a necessary secondary intension.
On the standard construal, the worlds involved in primary and secondary intensions are the same, the only difference being that the worlds involved in primary intensions are centered. Any kind of divergence between epistemic and metaphysical modality can thus occur only when expressions are involved whose primary and secondary intensions yield different extensions with respect to some worlds, and this difference in extensions, in turn, must be due to the fact that it makes a difference whether the world in question is considered as actual or as counterfactual. The example of ‘water’, discussed above, suggests that this can indeed make a difference: If one considers the Twin Earth scenario as actual, the substance in its rivers and lakes falls under the extension of ‘water’, but if one considers it as counterfactual, it does not. But one might still wonder why an expression’s extension with respect to some possible world should depend on the way one considers this world. To explain this, it is helpful to reconsider ‘actually’-involving expressions, such as the following:
(4) The actual inventor of the zipper is male.
Let our world, in which Whitcomb Judson invented the zipper, be w@, and let w1 be a world in which his wife Annie invented the zipper. If one considers w@ as actual, then (4) is true with respect to it. If, however, one assumes that w@ is the actual world and thus considers w1 as a counterfactual world, then (4) is false with respect to w1, because the occurrence of the term ‘actual’ makes the truth-value of (4) depend on features of the actual world, that is, w@. Inter alia, its truth-value depends on features of Whitcomb Judson, since he invented the zipper in w@. Davies & Humberstone already suggested that the occurrence of expressions that either explicitly or implicitly refer to features of the actual world can give rise to both contingent a priori truths and necessary a posteriori truths. Epistemic 2D semantics generalizes this idea. Accordingly, all cases in which primary and secondary intensions diverge involve expressions that depend in some way on the actual world.
Since primary intensions involve the same worlds as secondary intensions, every epistemic possibility corresponds to a metaphysical possibility. Chalmers puts this as follows:
Metaphysical Plenitude: For all S, if S is epistemically possible, there is a centered metaphysically possible world that verifies S. (Chalmers 2006, 82)
(Roughly speaking, that a world w verifies an epistemic possibility S means that w makes S true provided that w is considered as actual.) Metaphysical plenitude may still seem like a surprising claim, since the existence of a posteriori necessities implies that there are epistemic possibilities that are metaphysically impossible. So how can a metaphysical impossibility, such as ‘water = XYZ’, be verified by a metaphysically possible world? The world that verifies ‘water = XYZ’ can be described as follows: It is a world in which the odorless, drinkable substance in rivers and lakes, that is, the watery stuff, is XYZ. Such a world is clearly metaphysically possible. However, if one describes it as a world in which water = XYZ, this misleadingly suggests that the world described is one in which the substance that is the watery stuff in the actual world (that is, H2O) is XYZ, due to the actuality-dependence of the term ‘water’. The latter scenario is indeed metaphysically impossible. To avoid any confusion, one should thus describe the possibility in question by using expressions that do not involve any actuality-dependence, that is, expressions whose primary and secondary intensions cannot come apart.
To sum up, epistemic 2D semantics provides the following account of our epistemic access to metaphysical modality. Both contingent a priori truths and necessary a posteriori truths are explained by the occurrence of expressions whose extension with respect to some worlds depends on whether these worlds are considered as actual or as counterfactual. Such expressions must involve some kind of explicit or implicit reference to the actual world, such that their 2-intensions vary depending on the actual world’s characteristics. This explanation of necessary a posteriori truths allows that whenever some hypothesis cannot be ruled out a priori, that is, whenever it is epistemically possible, there is a metaphysical possibility that corresponds to it. To correctly identify this metaphysical possibility, one just needs to make sure to describe it by using only expressions whose primary and secondary intensions cannot come apart. Because it postulates that we have a priori access to metaphysical modality, this account is often called ‘modal rationalism’.
Since philosophical inquiry is traditionally thought to proceed a priori, and since philosophy very often deals with sentences that are necessarily true (or necessarily false), it would be of great philosophical importance if modal rationalism could be established. However, the epistemic 2D account of modal knowledge is highly controversial. Objections to the account can be divided into two categories. Objections of the first category state that epistemic 2D semantics does not successfully explain the standard examples of a posteriori necessities, such as ‘Water = H2O’ and ‘Hesperus = Phosphorus’—or at least not all of them. It seems hard to deny that if epistemic 2D semantics accurately captures the semantics of the expressions involved, then its explanation of a posteriori necessities is compelling. The crucial question is thus whether the relevant semantic account is indeed accurate. The most pressing issue here is whether all the relevant expressions—including, for instance, proper names—really have primary intensions. This issue is discussed in the next section.
According to objections of the second category, there are other kinds of necessary truths that are different from the cases that have usually been discussed and that cannot be explained in the same way. One example sentence that has been brought up in this context is ‘God exists’. It has been argued that God exists necessarily. However, it is plausibly not a priori that God exists, and it is also plausible that the sentence does not exhibit any actuality-dependence. If all of this is correct, then ‘God does not exist’ is epistemically possible, but it is not verified by any metaphysically possible world. The example is of course highly controversial—the vast majority of philosophers do not believe that there is a necessarily existing God. But it illustrates what general form a counterexample of the type at issue would need to have. Modal rationalists have argued that there are general reasons to deny that such epistemic possibilities that do not correspond to metaphysical possibilities exist (for example, Chalmers 2009).
ii. The Scrutability of Truth
Primary and secondary intensions are defined in terms of how one considers a possible world—as actual or as counterfactual. But it is not obvious what it means to consider a possible world. Since one cannot perceive merely possible worlds, it is natural to assume that they are given to us via a description. Chalmers has explained in detail what such descriptions, which he calls “canonical descriptions”, should involve (for example, Chalmers 2006, 86–93). To begin with, a canonical description has to be complete, in the sense that it must not leave out any facts that might be relevant to the extension of some expression. However, completeness should not be achieved at the cost of triviality. Suppose, for instance, that one wonders whether a sentence S is true with respect to world w considered as actual. If S is part of the canonical description of w, then it is trivial that one can derive the extension of S a priori. According to Chalmers, the canonical description of a world should thus involve only a limited vocabulary. Furthermore, there are constraints on the kinds of expressions that may be used in a canonical description. For instance, ‘There is water in rivers and lakes’ should come out as true with respect to a world in which the only watery stuff is XYZ if that world is considered as actual, and it should come out as false with respect to such a world if that world is considered as counterfactual. However, if the canonical description of this world involves the word ‘water’, then this difference between the sentence’s primary and its secondary intension cannot be maintained, on pain of contradiction (compare Chalmers 2006, 86). Therefore, the limited vocabulary in which canonical descriptions are phrased should involve only expressions that are semantically neutral, that is, expressions whose primary and secondary intensions cannot come apart.
According to epistemic 2D semantics, primary intensions—that is, the extensions of our expressions with respect to worlds considered as actual—are a priori. Given this, the understanding of what it is to consider a world as actual in terms of canonical descriptions just explained leads to another central thesis of epistemic 2D semantics, the scrutability of truth. Here is one formulation of this thesis that concerns the actual world. (Notice that with respect to the actual world, primary and secondary intensions always yield the same extensions.)
(Scrutability of Truth) There is a description of the world in a limited and semantically neutral vocabulary from which every truth can be derived a priori.
Chalmers & Jackson (2001) make a specific proposal as to what such a description could look like. They argue that all truths follow a priori from a description they call ‘PQTI’—for Physics, Qualia, That’s all, and Indexicals. P stands for a complete microphysical description of the world, in the language of a completed future physics. Q is a complete description of the phenomenal states of all subjects, that is, of their subjective experiences. The word I adds indexical information, which picks out a subject and a time, in order to determine the truth-values of sentences such as ‘I am a chess player’ or ‘Today is Tuesday’. Finally, T is a totality clause, which states that this is all there is in the world. This clause is necessary to rule out things not entailed by PQI. Suppose, for instance, that there are no ghosts, and thus, ‘There are no ghosts’ is true. PQI does not entail the truth of this sentence, because it does not state that PQI provides a complete description of the world. The inclusion of T adds this information. Notice that, plausibly, ghosts could have existed. This illustrates that microphysical, phenomenal, indexical information plus a totality clause are insufficient to derive canonical descriptions of many other possible worlds. To describe these, one may thus need to expand one’s vocabulary.
The scrutability thesis brings out an important commitment of epistemic 2D semantics. According to this account, all of our expressions have a priori associations that are extensive enough to determine the expressions’ extensions. In fact, epistemic 2D semantics even entails that these a priori associations determine the extensions of our expressions with respect to every world considered as actual. However, there are highly influential arguments, originating in Kripke (1980), that seem to show that some kinds of expressions—most notably proper names—have no such a priori associations. The epistemic arguments suggest that everything a speaker associates with a name could turn out to be false in the light of additional empirical information—one might thus call these arguments ‘arguments from empirical defeasibility’. For instance, even our most central beliefs about Kurt Gödel—for instance, that he discovered the incompleteness of arithmetic—could be empirically defeated if, say, we got compelling evidence that the incompleteness proofs were developed by a man named ‘Schmidt’ and then later stolen and published by Gödel (Kripke 1980, 83f.). Thus, not even ‘discoverer of the incompleteness of arithmetic’ is a priori associated with the name ‘Kurt Gödel’, and it is hard to see what else could be. The epistemic arguments are compatible with the view that speaker associations determine the extension of our expressions—after all, Gödel is the unique discoverer of the incompleteness of arithmetic, even though it is not a priori that he is. However, the semantic arguments, also called ‘arguments from ignorance and error’, suggest that speaker associations need not suffice to determine the (correct) extension of an expression. Speaker associations might fail to do so in a given case either because they are insufficiently specific (in a case of ignorance), or because the speaker associations attribute features the referent does not have (in a case of error). The following examples due to Kripke exemplify these cases. First, a case of ignorance: Many people know that Feynman and Gell-Mann are physicists. But they know nothing to distinguish Gell-Mann from Feynman. Nevertheless, when these people say ‘Feynman’, they refer to Feynman, and when they say ‘Gell-Mann’, they refer to Gell-Mann. Second, a case of error: The only thing many people believe about Einstein is that he invented the atomic bomb. Nevertheless, when these people use the name ‘Einstein’, they refer not to Oppenheimer or Szilard, but to Einstein (Kripke 1980, 81). The example illustrates that the semantic arguments go one step further than the epistemic arguments: While cases like that of Gödel and Schmidt aim only to show that what speakers associate with a name could be erroneous, for all the speaker knows a priori, the case of Einstein is supposed to show that these associations are sometimes erroneous.
Similar kinds of arguments have been given concerning other kinds of expressions, such as natural kind terms (for example, Putnam 1975, 226). In order to defuse them, proponents of epistemic 2D semantics have to make a case that there are nevertheless speaker associations that are sufficient to determine an expression’s extension (including the extension with respect to other possible worlds considered as actual), and that these associations are also a priori. To do this, they have pointed out that the associations that determine primary intensions need not correspond to what first comes to a speaker’s mind. For example, in the case of a proper name such as ‘Gödel’, it is indeed plausible that ‘discoverer of the incompleteness of arithmetic’ is not part of the primary intension ordinary speakers associate with the name. Both Chalmers (2002, 617; 2003, 62–64; 2006, 91) and Jackson (1998b, 209–212; 2004, 270–271) suggest that speaker associations often concern other people’s usage of an expression. Accordingly, the primary intension of ‘Gödel’ could be approximately equivalent to the definite description ‘the individual called ‘Gödel’ by those from whom I acquired the name’. Other expressions can be treated in the same kind of way. If a speaker knows, for instance, that Gödel is called ‘Gödel’ by those from whom they acquired the name, then this proposal suffices to repudiate the arguments from ignorance and error. If the associations at issue are also a priori, then the proposal suffices to repudiate the arguments from empirical defeasibility. The claim that such associations are a priori is especially controversial, however, and will require further investigation.
Even if one accepts that linguistic expressions have primary intensions, and thus speaker associations that determine their extensions with respect to the actual world and with respect to other worlds considered as actual, one may still have doubts about the scrutability of truth. For instance, it seems extremely bold to claim that microphysical, qualitative, and indexical information, in conjunction with a ‘that’s all’ clause, is sufficient to derive a priori that Anand is a chess player—in any case, it is far beyond anyone’s cognitive capacities to perform such a derivation. Chalmers and Jackson try to explain in broad outline how certain kinds of truths, such as ordinary macroscopic truths like ‘Water covers most of the Earth’, are in principle a priori derivable from PQTI (Chalmers & Jackson 2001; Chalmers 2012). Another way of arguing for the scrutability thesis is by appealing to modal rationalism. It is plausible that the information in PQTI metaphysically determines all truths, in the sense that there is no other metaphysically possible world described by PQTI with respect to which some sentence has a different truth-value. More generally, the majority of philosophers believe that all facts are metaphysically determined by the facts in a small number of domains—most prominently, physical facts (according to physicalists), combined with some irreducible mental facts (according to dualists), and possibly some few other kinds of facts (perhaps including normative facts). Given this, if one adds to these facts indexical information and a ‘that’s all’ clause—for reasons explained above—a complete description stating these facts will metaphysically determine all truths. Now assume that some world w is considered as actual and described in terms of a semantically neutral vocabulary. If the explanation of necessary a posteriori truths provided by epistemic 2D semantics is correct and complete, then everything that is metaphysically determined by the features given the description of w is also epistemically determined, that is, a priori entailed. If one adds to this the assumption that our world has relatively few fundamental ingredients, and that one thus needs only a limited vocabulary to describe it, the scrutability of truth follows: All truths are a priori entailed by a complete description of the world in a limited and semantically neutral vocabulary.
iii. Philosophical Methodology
Epistemic 2D semantics has sparked many debates that revolve around the question whether there is an essential a priori component to philosophical inquiry. One instance of this general issue that has received particularly close attention concerns the issue of physicalism in the debate about the mind-body problem. Physicalism involves the claim that all facts about our world are metaphysically determined by the collection of physical facts. Both Chalmers (2009) and Jackson (2005) have argued that the truth of physicalism would entail that mental facts follow a priori from physical facts. Their claim is motivated by modal rationalism, which entails that metaphysical determination amounts to epistemic determination, given that the world is considered as actual and described in semantically neutral vocabulary. But many have argued that phenomenal facts are not a priori entailed by physical facts. Hence, modal rationalism seems to raise a problem for physicalism. (Notice that while Chalmers uses the epistemic 2D account to argue against physicalism, Jackson endorses physicalism and hence believes that there is an a priori entailment between physical and phenomenal facts.) Many physicalists have resisted the idea that they are committed to the existence of an a priori entailment between the physical and the mental. In making their case, they have either appealed to some special features of phenomenal concepts, or they have resisted modal rationalism on more general terms. At this point, no consensus regarding this issue is in sight.
Proponents of conceptual analysis hold that we can gain philosophical knowledge in virtue of our grasp of philosophical concepts and our understanding of philosophical expressions. Semantic externalism presents a challenge for this view, since externalism seems to imply that linguistic understanding and concept possession need not involve any significant knowledge about meaning. Now, one of the key claims of epistemic 2D semantics is that, against standard externalist views, our expressions come with a priori associations that determine the expressions’ extensions—that is to say, expressions have primary intensions. It is natural to suggest that these a priori associations can underpin the method of conceptual analysis. And indeed, Chalmers and Jackson have used insights from 2D semantics to defend this traditional philosophical method (Jackson 1998a; Chalmers & Jackson 2001). As they point out, conceptual analysis often involves thought experiments. A famous example is Edmund Gettier’s contribution to the analysis of knowledge. To undermine the claim that knowledge is justified true belief, Gettier (1963) describes two hypothetical cases in which a subject has a justified true belief, but no knowledge. If the central claims of epistemic 2D semantics are tenable, they can serve as a theoretical underpinning for this practice of doing conceptual analysis via thought experiments. If modal rationalism is correct, any hypothetical scenario that is epistemically possible corresponds to a metaphysical possibility. Furthermore, if the scrutability thesis is correct, this can explain our ability to determine the extension of expressions, such as ‘knowledge’, with respect to a hypothetical scenario.
For conceptual analysis to be fruitful as a philosophical method, the speaker associations that constitute primary intensions need to be shared with regard to at least some of those expressions that are subject to philosophical scrutiny. Otherwise, a philosopher engaged in conceptual analysis may acquire knowledge, but this knowledge will be based only on the primary intensions that this particular individual associates with the relevant expressions, and thus not be readily shareable with the philosophical community. Jackson (1998b; 2004) has argued that primary intensions are indeed usually shared among competent speakers in a linguistic community, along the following lines. Language is primarily used to convey information to others, that is, to communicate. This is possible only if linguistic expressions can be used to represent the state of the world, which requires there to be associations between words and properties. Furthermore, for speakers to be able to make use of this information, these associations between words and properties must be known to them. Jackson holds that the known associations between words and properties are primary intensions. On this view, it would be of little use if different speakers within a linguistic community ‘knew’ different associations between words and properties. Hence, primary intensions must be shared.
It seems plausible that it would be a serious hindrance for communication if the associations between words and properties differed greatly between subjects. But it is doubtful that successful communication requires perfect alignment of these associations. And indeed, Jackson concedes that often, communication can succeed if a speaker’s and a hearer’s primary intensions are sufficiently close to identical (Jackson 1998b, 214f.). However, this concession raises a worry regarding conceptual analysis. The cases discussed in conceptual analysis are often highly contrived and not very relevant to ordinary communication. Their evaluation is, however, often crucial for the evaluation of the underlying philosophical issues. Jackson’s argument thus leaves it open that there are often, or even always, divergences in the primary intensions associated by different speakers that, while irrelevant to ordinary communication, become apparent in the evaluation of philosophical thought experiments. During the early 21st century, experimental philosophers have collected a wealth of empirical data about subjects’ intuitions concerning philosophically relevant hypothetical cases. The results of these wide-ranging studies are varied and not easily summarized. In some cases, they have confirmed the philosophical consensus; in others, they have not.
4. References and Further Reading
a. Primary Sources
- Chalmers, David. 2002. The Components of Content. In D. Chalmers (ed.), Philosophy of Mind: Classical and Contemporary Readings. Oxford: Oxford University Press, 608–633.
- Motivates a 2D account of mental content.
- Chalmers, David. 2003. The Nature of Narrow Content. Philosophical Issues 13(1), 46–66.
- Argues that primary intensions can serve as a type of mental content that is determined by a subject’s intrinsic state.
- Chalmers, David. 2004. Epistemic Two-Dimensional Semantics. Philosophical Studies 118(1–2), 153–226.
- An extensive elaboration and defense of epistemic 2D semantics.
- Chalmers, David. 2006. The Foundations of Two-Dimensional Semantics. In M. Garcia-Carpintero & J. Macia (eds.), Two-Dimensional Semantics: Foundations and Applications. Oxford: Oxford University Press, 55–140.
- A survey of 2D theories, but with a focus on whether they yield a connection between 1-intensions and apriority.
- Chalmers, David. 2009. The Two-Dimensional Argument Against Materialism. In B. McLaughlin & S. Walter (eds.), Oxford Handbook to the Philosophy of Mind. Oxford: Oxford University Press.
- Articulates the 2D argument against physicalism in detail and gives an overview of the debate.
- Chalmers, David. 2012. Constructing the World. Oxford: Oxford University Press.
- A defense of various scrutability theses.
- Chalmers, David & Frank Jackson. 2001. Conceptual Analysis and Reductive Explanation. The Philosophical Review 110(3), 315–361.
- Argues that all truths are a priori implied by PQTI, and that physicalists should hold that phenomenal truths are a priori implied by physical truths.
- Davies, Martin & Humberstone, Lloyd. 1981. Two Notions of Necessity. Philosophical Studies 58, 1–30.
- Proposes to capture Evans’s distinction between deep and superficial contingency by means of the sentential operators ‘□’, ‘fixedly’, and ‘actually’.
- Evans, Gareth. 1979. Reference and Contingency. The Monist 62, 161–189.
- Explains the occurrence of contingent a priori truths on the basis of the distinction between deep and superficial contingency.
- Frege, Gottlob. 1892/1952. Über Sinn und Bedeutung. Translated in P. Geach & M. Black (eds.), Translations from the Philosophical Writings of Gottlob Frege. Oxford: Blackwell, 1952.
- Introduces the distinction between sense and reference, the former of which yields a type of content that is intimately connected to epistemic notions.
- Gettier, Edmund. 1963. Is Justified True Belief Knowledge? Analysis 23(6), 121–123.
- Presents two counterexamples against the traditional view that knowledge is justified true belief.
- Jackson, Frank. 1998a. From Metaphysics to Ethics: A Defence of Conceptual Analysis. Oxford: Clarendon Press.
- Uses 2D semantics to argue that conceptual analysis plays a vital role in answering philosophical questions.
- Jackson, Frank. 1998b. Reference and Description Revisited. Philosophical Perspectives 12, Language, Mind, and Ontology, 201–218.
- A defense of the view that speaker associations determine reference and meaning.
- Jackson, Frank. 2004. Why We Need A-Intensions. Philosophical Studies 118(1–2), 257–277.
- Argues that primary intensions capture the representational content of what is communicated from speaker to hearer.
- Jackson, Frank. 2005. The Case for A Priori Physicalism. In C. Nimtz & A. Beckermann (eds.), Philosophy–Science–Scientific Philosophy. Main Lectures and Colloquia of Gap 5, Fifth International Congress of the Society for Analytical Philosophy. Paderborn: Mentis.
- Argues that physicalists should hold that mental facts follow a priori from physical facts.
- Kamp, Hans. 1971. Formal Properties of ‘Now’. Theoria 37(3), 227–274.
- An early 2D account of the indexical ‘now’.
- Kaplan, David. 1989. Demonstratives. In J. Almog, J. Perry & H. Wettstein (eds.), Themes from Kaplan. Oxford: Oxford University Press, 481–563.
- Develops an account of indexicals on the basis of the distinction between character and content.
- Kripke, Saul. 1980. Naming and Necessity. Cambridge, MA: Harvard University Press.
- Argues that proper names, indexicals, and natural kind terms are rigid designators and spells out the consequences for the epistemology of modality.
- Lewis, David. 1979. Attitudes De Dicto and De Se. Philosophical Review 88(4), 513–543.
- Introduces a theory of mental content that can account for the phenomenon of egocentric belief.
- Perry, John. 1977. Frege on Demonstratives. Philosophical Review 86(4), 474–497.
- Argues that demonstrative expressions present a problem for Frege’s philosophy of language, and suggests an alternative account.
- Putnam, Hilary. 1975. The Meaning of ‘Meaning’. Minnesota Studies in the Philosophy of Science 7, 131–193.
- Argues for an externalist account of meaning.
- Stalnaker, Robert. 1978. Assertion, in P. Cole (ed.), Syntax and Semantics 9: Pragmatics. New York, NY: Academic Press, 315–332.
- Develops an account of communication that introduces 1-intensions as a way of reinterpreting certain kinds of utterances.
- Stalnaker, Robert. 1987. Semantics for Belief. Philosophical Topics 15, 177–190.
- Defends a possible world account of mental content, drawing on 2D semantics.
- Stalnaker, Robert. 2001. On Considering a Possible World as Actual. Aristotelian Society Supplementary Volume 75, 141–156.
- Defends a metasemantic account of 2D semantics and argues that this account suggests skepticism about apriority.
- Stalnaker, Robert. 2004. Assertion Revisited: On the Interpretation of Two-Dimensional Modal Semantics. Philosophical Studies 118 (1–2), 299–322.
- Suggests that epistemic 2D semantics is based on an internalist view of intentionality, in contrast with metasemantic 2D semantics, and argues that internalism is untenable.
b. Secondary Sources
- Chalmers, David. 2002b. Does Conceivability Entail Possibility? In T. Gendler & J. Hawthorne (eds.), Conceivability and Possibility. Oxford: Oxford University Press, 145–200.
- Offers a comprehensive statement and defense of modal rationalism.
- Chalmers, David. 2002c. On Sense and Intension. Philosophical Perspectives 16, 135–182.
- Argues that epistemic 2D semantics represents a viable account of meaning in the tradition of Frege.
- Garcia-Carpintero, Manuel & Josep Macia (eds.). 2006. Two-Dimensional Semantics: Foundations and Applications. Oxford: Oxford University Press.
- A collection of articles on 2D semantics.
- Jackson, Frank. 2010. Language, Names, and Information. Oxford: Wiley-Blackwell.
- Argues that the role of proper names in transmitting information is best explained by an account on which their meaning is given by speaker associations.
- Kipper, Jens. 2012. A Two-Dimensionalist Guide to Conceptual Analysis. Frankfurt a.M.: Ontos.
- Defends epistemic 2D semantics and discusses the role that conceptual analysis can play on the basis of this account.
- Nimtz, Christian. 2017. Two-Dimensional Semantics. In B. Hale, C. Wright & A. Miller (eds.), The Blackwell Companion to the Philosophy of Language, 2nd Edition. Oxford: Blackwell, 948–969.
- A survey of 2D semantic theories, with an emphasis on how they relate to Kripke’s semantic and metasemantic views.
- Schroeter, Laura. 2017. Two-Dimensional Semantics. In The Stanford Encyclopedia of Philosophy (Summer 2017 Edition), Edward N. Zalta (ed.).
- A survey of 2D semantic theories that includes an extensive elucidation of Chalmers’s 2D argument against physicalism.
Author Information
Jens Kipper
Email: jkipper@ur.rochester.edu
University of Rochester
U. S. A.