Abelard: Logic
 This article describes and reconstructs Peter Abelard’s logic of the twelfth century. Much of what he regarded as logic is now classified as ontology or philosophical semantics. The article concentrates on his treatment of the relation of consequence. Abelard’s most important logical innovations consist of two points:
This article describes and reconstructs Peter Abelard’s logic of the twelfth century. Much of what he regarded as logic is now classified as ontology or philosophical semantics. The article concentrates on his treatment of the relation of consequence. Abelard’s most important logical innovations consist of two points:
The distinction between two kinds of negation. This is used to extend the traditional Square of Opposition to an octagon.
The introduction of a relevant implication. The aim is to avoid the paradoxes of strict implication and to safeguard the basic principles of connexive logic.
For the latter goal, Abelard rejected the traditional “locus ab oppositis” which says that if one of two opposite concepts is predicated of a certain subject, the other concept has to be denied of the same subject. We now know this approach failed. Alberic of Paris developed an “embarrassing argument” which showed that—in contradiction to Aristotle’s connexive theses—there exist propositions which logically imply their own negation. The conclusiveness of Alberic’s counterexample does not presuppose the validity of the “locus ab oppositis.” Other aspects of Abelard’s philosophy are treated in the main Abelard article.
Table of Contents
- Abelard’s Logical Works
- Outlines of the Theory of the Syllogism
- Abelard’s Theory of Negation
- Abelard’s Quantification of the Predicate
- Inferences and Implications
- Abelard’s Defence of the Principles of Connexive Logic
- References and Further Reading
1. Abelard’s Logical Works
Abelard’s philosophical works were first edited in 1836 by Victor Cousin. Besides the rather theological essay “Sic et non,” the Ouvrages inédits d’Abélard contain various logical works, namely, commentaries on Aristotle, Porphyry, and Boethius, and a preliminary version of the Dialectica. The next important edition of Abelard’s logical writings was achieved by Bernhard Geyer who, in the period from 1919 to 1933, published Peter Abaelards Philosophische Schriften. This collection contains in particular a Logica ‘Ingredientibus’ and a Logica ‘Nostrorum petitioni.’ The strange titles do not have any specific meaning; Geyer simply chose them according to the words with which the texts begin. In 1954, Mario Dal Pra edited Pietro Abelardo Scritti filosofici, which contain, in particular, Abelard’s so-called “children’s logic” (“logica parvulorum”). A complete version of Abelard’s most important logical work, the Dialectica, based on a manuscript in Paris, was edited in 1959 by Lambert Marie de Rijk. This volume forms the basis for the reception of Abelard’s logic which started in the last third of the 20th century.
In 1964, Maria Teresa Beonio-Brocchieri Fumagalli published the small volume La Logica de Abelardo, which in 1969 appeared in English as The Logic of Abelard. The title, however, is sort of a misnomer because the book does not really deal with Abelard’s logic. The genuine innovations of Abelard’s logical theories were first uncovered by Christopher Martin in the 1980s, especially in his dissertation on Theories of Inference and Entailment in the Middle Ages, and in the papers Martin (1986), (1987), and (2006). Abelard’s theory of the modal operators is extensively discussed in Binini (2022).
King & Arlig (2018) maintain that:
Abelard […] devised a purely truth-functional logic […], and worked out a complete theory of entailment. […] An entailment is complete (perfecta) when it holds in virtue of the logical form (complexio) of the propositions involved. By this […] he means that the entailment holds under any uniform substitution in its terms […]. The traditional moods of the categorical syllogism […] are all instances of complete entailments, or as we should say, valid inference.
Abelard spends a great deal of effort to explore the complexities of the theory of topical inference […]. One of the surprising results of his investigation is that he denies that a correlate of the Deduction Theorem holds, maintaining that a valid argument need not correspond to an acceptable conditional […].
In the end, it seems that Abelard’s principles of topical inferences do not work, a fact that became evident with regard to the topic “from opposites.” Abelard’s principles lead to inconsistent results.
These claims have to be modified, corrected, and supplemented in several respects. First, for Abelard both entailment and disjunction are intensional or modal, but not extensional, that is, merely truth-functional. Second, his theory of entailment distinguishes not only between perfect and imperfect inferences, but also between what is nowadays called strict implication and the even stronger conception of “relevant” implication. Third, in connection with traditional logic it doesn’t make much sense to speak of the Deduction theorem which says that if, in a logic calculus with certain axioms and rules of deduction, one may deduce a conclusion C from a set (or conjunction) of premises P1, … Pn, then the implication (P1 ∧ … ∧ Pn → C) is provable (in that calculus). However, medieval logic has never been developed in the form of an axiomatic calculus! Fourth, as regards Abelard’s principles of “topical inference”, it is not quite correct to maintain that they lead to “inconsistent results.” Rather, Abelard rejected the traditional topic from opposites in order to save “Aristotle’s Theses” from refutation, but his attempt turned out to be unsuccessful since Alberic of Paris presented a genius counter-example to the connexive principles which does not make use of the topic from opposites.
2. Outlines of the Theory of the Syllogism
Abelard was well acquainted with the theory of the syllogism as it had been invented by Aristotle (ca. 384-322 BC) and elaborated by Boethius (ca. 480-525). This theory deals with the categorical forms, in which a subject term S is related to a predicate term P:
Universal affirmative proposition (UA) Every S is P
Universal negative proposition (UN) No S is P
Particular affirmative proposition (PA) Some S is P
Particular negative proposition (PN) Some S isn’t P.
Later medieval logicians referred to these forms by means of the vowels ‘a’, ‘e’, ‘i’, and ‘o.’ Although Abelard did not use such abbreviations, the forms are here symbolized as SaP, SeP, SiP, and SoP, respectively. The traditional doctrine of subalternation saying that the universal propositions entail their particular counterparts is then formalized as follows (where ‘⇒’ symbolizes a logical implication):
Sub 1 SaP ⇒ SiP
Sub 2 SeP ⇒ SoP.
According to the modern analysis of the categorical forms in terms of first order logic, these laws are not unrestrictedly valid but hold only under the assumption that the subject term S is not empty.
The theory of opposition says that the contradictory opposite, or negation, of the UA is the PN, and that the negation of the UN is the PA. If the negation operator is symbolized by ‘¬’, these laws take the form:
Opp 1 ¬SaP ⇔ SoP
Opp 2 ¬SeP ⇔ SiP.
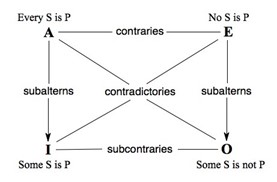
Hence, it is not the case that every S is P is equivalent to ‘Some S is not P’; and it is not the case that no S is P means as much as ‘Some S is P’. From this it follows that there is a contrary opposition between the two universal propositions, which means that SaP and SeP can never be together true while it is possible that none of them is true. Furthermore, the two particular forms are subcontrary, which means that SiP and SoP can never be together false while it is possible that both are true. The laws of subalternation and opposition are often summarized in the well-known “Square of Opposition”:
The traditional theory of conversion says that a PA and a UN may be converted “simpliciter,” that is, one may simply exchange the predicate and the subject:
Conv 1 SiP ⇒ PiS
Conv 2 SeP ⇒ PeS.
Clearly, if some S is P, then conversely some P is S; and if no S is P, then also no P is S. In contrast, the UA can only be converted “per accidens,” that is, the “quantity” of the proposition must be diminished from ‘universal’ to ‘particular’:
Conv 3 SaP ⇒ PiS.
The validity of Conv 3 follows from the law of subalternation, Sub 1, in conjunction with Conv 2: if every S is P, then a fortiori, some S is P so that, conversely, some P is S. Similarly, one might state another law of conversion according to which the UN can also be converted “accidentally”:
Conv 4 SeP ⇒ PoS.
This follows from Conv 2 by means of Sub 2.
Finally, most medieval logicians accepted the principle of “conversion by contraposition,” according to which the subject and the predicate of a UA may be exchanged when the terms ‘S’ and ‘P’ are replaced by their negations. That is, if every S is P, then every Not-P is not-S. If the negation of a term is symbolized by ‘~’ (thus distinguishing it from the negation operator for propositions, ‘¬’), the law of contraposition takes the form:
Contra SaP ⇒ ~Pa~S.
According to the principle of “obversion”, the negative propositions UN and PN can equivalently be transformed into affirmative propositions (with a negated predicate):
Obv 1 SeP ⇔ Sa~P
Obv 2 SoP ⇔ Si~P.
Hence, that no S is P is equivalent to ‘Every S is not-P’, and ‘Some S isn’t P’ is equivalent to ‘Some S is not-P.’ As a corollary, it follows that conversely the affirmative propositions UA and PA can equivalently be expressed as negative propositions (with a negated predicate):
Obv 3 SaP ⇔ Se~P
Obv 4 SiP ⇔ So~P.
The mutual derivability of these principles presupposes the law of double negation:
Neg 1 ~~T = T.
A proper syllogism is an inference from two premises P1, P2 to a conclusion C where (normally) all these propositions are categorical forms and the premises must have one term in common. The best-known examples are the four “perfect” syllogisms:
Barbara CaD, BaC ⇒ BaD
Celarent CeD, BaC ⇒ BeD
Darii CaD, BiC ⇒ BiD
Ferio CeD, BiC ⇒ BoD.
In Abelard’s logic these inferences are not presented in such an abstract form, however, but mainly by way of examples. For instance, Abelard illustrates the “sillogismi perfecti” as follows:
Every just is good; Every virtuous is just; therefore, Every virtuous is good
No good is bad; Every just is good; therefore, No just is bad
Every good is virtuous; Some just is good; therefore, Some just is virtuous
No good is bad; Some just is good; therefore, Some just is not bad. (Compare Dialectica, p. 236)
In some places, however, Abelard also mentions corresponding generalized rules such as, in the case of Barbara:
If something is predicated universally of something else, and another is subjected universally to the subject, then the same is also subjected in the same way, i.e., universally, to the predicate (Compare Dialectica, p. 237),
or, in the case of Ferio:
If something is removed universally from something else, and another is subjected particularly to the subject, then the first predicate is removed particularly from the second subject (ibid.)
Abelard largely endorsed the traditional theory of the syllogism including the laws of subalternation, opposition, conversion, and obversion. In particular, in Logica ‘Ingredientibus’ he painted a standard square of opposition in which the logical relation between the ‘a’ and the ‘o’ proposition as well as the relation between the ‘e’ and the ‘i’ proposition are characterized as “contradictorie,” while the ‘a’ and the ‘e’ proposition are opposed “contrarie” and the ‘i’ and the ‘o’ proposition “subcontrarie.” Finally, a “subalterne” relation is drawn between the ‘a’ and the ‘i’ and between the ‘e’ and the ‘o’ proposition. The only difference between Abelard’s square (p. 412) and the usual square consists in the fact that his example deals with the special case where the universe of discourse has only two elements. Thus, instead of ‘Every man is white,’ ‘No man is white.’ and ‘Some man is white’ Abelard has ‘Both men are white’ (“Uterque istorum est albus”), ‘Neither is white’ (“Neuter, i. e. nullus ipsorum est albus”) and ‘At least one of them is white’ (“Alter est albus”).
The next section shows, however, that in Dialectica Abelard eventually rejected the traditional laws of opposition. His distinction between so-called “destructive negation” and “separating negation” entails the consideration of each two variants of the categorical forms, and the ensemble of eight propositions, which Abelard arranged into two squares of opposition, can be united into an octagon.
3. Abelard’s Theory of Negation
As was mentioned already in the introduction, one of Abelard’s major logical innovations consists in the introduction of two kinds of negation by means of which the traditional Square of Opposition is extended to an octagon.
a. “Extinctive” vs. “Separating” Negation
In Logica ‘Ingredientibus,’ Abelard explains:
Not only with respect to categorical propositions, but also with respect to hypothetical propositions one has to distinguish between separating negation and extinctive negation. A separating negation [“negatio separativa”] obtains when by the position of the negative particle the terms are separated from each other […]. But an extinctive negation [“negatio exstinctiva” or “negatio destructiva”] obtains when by the position of the negative particle in front of the entire proposition this proposition is destroyed (Geyer, p. 406).
The extinctive negation of a proposition α is just the ordinary negation, ¬α. It can always be formed by putting ‘not’ in front of α. Thus, with respect to the categorical forms, one obtains:
Not every S is P
Not no S is P
Not some S is P
Not some S isn’t P.
With respect to “hypothetical” propositions, one similarly gets:
Not: If α then β ¬(α → β).
The extinctive negation satisfies the law of double negation,
Neg 2 ¬¬α ⇔ α,
but for some rather obscure reason Abelard hesitated to accept this law.
A separating negation obtains whenever the expression ‘not’ is placed somewhere “within” a proposition α so that it separates the predicate of a categorical proposition from its subject:
Every S is not P
No S is not P
Some S is not P
Some S isn’t not P.
With respect to hypothetical propositions, a separating ‘not’ separates the antecedent from the consequent:
If α, then not β.
Propositions with an extinctive negation differ from their separating counterparts in so far as, for example, the extinctively negated UA, ‘Not every S is P’, doesn’t have the same meaning (or the same truth-condition) as the separating negation ‘Every S is not P’. In view of the laws of obversion, the latter proposition rather expresses the same as a UN! Similarly, ‘Not no S is P’ means as much as ‘Some S is P’ while, according to the principle of obversion, ‘No S is not P’ amounts to ‘Every S is P’. Similar remarks apply to the extinctive vs. separating negations of the PA and the PN. Yet this doesn’t mean that there exists a general logical or semantical difference between the two kinds of negation. Let us have a closer look at Abelard’s theory of negation as applied, firstly, to singular propositions and then, secondly to categorical propositions.
b. Negating Singular Propositions
Starting from a singular proposition such as:
S1 Socrates is just (Socrates est iustus),
one can consider besides the extinctive negation:
S2 Not: Socrates is just (Non Socrates est iustus),
two variants of a separating negation:
S3a Socrates is-not just (Socrates non est iustus).
S3b Socrates is not-just (Socrates est non iustus).
According to Abelard, the variants S3a and S3b are equivalent. Therefore, in what follows, they shall simply be referred to as ‘S3’. Furthermore, S3 can itself be negated as:
S4 Not: Socrates is not just (Non Socrates est non iustus).
According to Abelard, the separating negation ‘Socrates is not just’, is the contrary opposite of the affirmation ‘Socrates is just,’ because both propositions become false when the subject ‘Socrates’ doesn’t exist! More generally, Abelard accepts the following principle:
Exist For any singular term s and any predicate P: the proposition ‘s is P’ implies (or presupposes) that ‘s is’, that is, that ‘s exists’.
Hence, if s doesn’t exist, both ‘s is P’ and ‘s is not-P’ are false. Therefore, the two (affirmative) propositions ‘s is P’ and ‘s is not-P’ together with their extinctive negations form the following square of opposition:
| S1 | s is P | contrary | s is ~P | S3 |
| ⇓ | ⇓ | |||
| S4 | ¬(s is ~P) | subcontrary | ¬(s is P) | S2 |
c. Negating Quantified Propositions
Starting from a PA such as:
C1 Some man is white (Quidam homo est albus),
one can consider besides the extinctive negation:
C2 Not: Some man is white (Non quidam homo est albus)
two variants of a separative negation:
C3a Some man is-not white (Quidam homo non est albus)
C3b Some man is not-white (Quidam homo est non albus).
While C3a is a particular negative proposition, C3b is usually considered as a particular affirmative proposition with a negative predicate. Since, in accordance with the theory of obversion, Abelard considered these propositions as equivalent, C3a and C3b may simply be referred to as ‘C3’.
Similarly, starting from a UA such as:
C4 Every man is white (Omnis homo est albus)
one can consider besides the extinctive negation:
C5 Not: Every man is white (Non omnis homo est albus)
two variants of a separative negation:
C6a Every man is-not white (Omnis homo non est albus)
C6b Every man is not-white (Omnis homo est non albus).
In view of the flexible grammar of the Latin language, C6a might be understood as synonymous with C5. Abelard, however, apparently understands C6a as equivalent to C6b, and both variants express the same state of affairs as the UN ‘No man is white.’ Therefore, both variants may simply be referred to as ‘C6’.
On p. 407 of Logica ‘Ingredientibus,’ Abelard draws the following diagram:
| Omnis homo est albus | [contrary] | Omnis homo non est albus |
| [⇓] | [⇓] | |
| Quidam homo est albus | [subcontrary] | Quidam homo non est albus |
This appears to be a normal Square of Opposition formed by the propositions C4, C6, C1, and C3. Next, Abelard draws another diagram consisting of the “extinctive” negations of the previous propositions:
| Non omnis homo est albus | Non omnis homo non est albus | |
| [⇑] | [⇑] | |
| Non quidam homo est albus | Non quidam homo non est albus |
This appears to be a mirrored version of a normal Square of Opposition formed by the propositions C5, C2, +:
C7 Not every man isn’t white (Non omnis homo non est albus)
C8 Not some man isn’t white (Non quidam homo non est albus).
A few pages later, Abelard presents variants of these diagrams. The first diagram is entitled ‘exstinctiva’ because all negations are “extinctive”:
| Omnis homo est albus | contrarie | Non quidam homo est albus |
| subalterne | subalterne | |
| Quidam homo est albus | subcontrarie | Non omnis homo est albus |
Abelard’s annotations ‘contrarie’, ‘contradictorie’, ‘subcontrarie’ and ‘subalterne’ suggest that the figure represents an ordinary square of opposition. This also appears to hold true for the next diagram which is entitled ‘separativa’ since each proposition is now paraphrased by means of a separating negation.
| Omnis homo non est albus | […] | Non quidam homo [non] est albus |
| […] | […] | |
| Quidam homo non est albus | […] | Non omnis homo non est albus |
Note that here again the structure of the ordinary square is mirrored: The UN stands at the place of the UA and vice versa.
d. Abelard’s Octagon of Opposition
However, both in Logica ‘Ingredientibus’ and in Dialectica Abelard insists that the traditional view of a contradictory opposition between the UA and the PN is mistaken. The contradictory opposite of SaP is ‘Not: Every S is P,’ but this proposition is not equivalent to SoP. Rather, ‘Some S is not P’ is contrary to ‘Every S is P’ because it is possible that both propositions are false. Thus, Abelard explains:
Also with respect to categorical propositions the only correct negation of an affirmation, sharing the truth-values with it, appears to be that proposition which destroys the sense of the sentence by placing the negation in front of it; thus the negation of ‘Every man is a man’ is ‘Not every man is a man’, but not ‘Some man is not a man’; the latter might be false together with the affirmation. For if it were the case that there are no men at all, then neither ‘Every man is a man’ nor ‘Some man is not a man’ would be true. (Compare Dialectica, p. 176)
Hence, according to Abelard, if the subject-term S is “empty,” then both ‘Some S is not S’ and ‘Every S is S’ become false. More generally, if S is “empty”, then, for every P, the UA ‘Every S is P’ is false, that is, this proposition has “existential import”, it entails that ∃xS(x). This consideration leads to the assumption of altogether eight propositions. On the one hand, we have the four “normal” categorical forms which can be formalized by means of the quantifiers ‘∃x’ (‘there exists at least one x’) and ‘∀x’ (‘for every x’) plus the symbols ‘∧’, ‘∨’ and ‘⊃’ for the propositional operators of conjunction, disjunction and (material) implication:
| C8 | UA | Not some S is not P | ¬∃x(S(x) ∧ ¬P(x)) |
| C2 | UN | Not some S is P | ¬∃x(S(x) ∧ P(x)) |
| C1 | PA | Some S is P | ∃x(S(x) ∧ P(x)) |
| C3 | PN | Some S is not P | ∃x(S(x) ∧ ¬P(x)) |
On the other hand, one obtains two “strong” versions of universal propositions with existential import:
| C4 | UA+ | Every S is P | ∃xS(x) ∧ ∀x(S(x) ⊃P(x)) |
| C6 | UN+ | Every S is not P | ∃xS(x) ∧ ∀x(S(x) ⊃ ¬P(x)) |
Furthermore, the negations of these “strong” universal propositions yield “weak” interpretations of corresponding particular propositions:
| C7 | PA- | Not every S is not P | ¬∃xS(x) ∨ ∃x(S(x) ∧ P(x)) |
| C5 | PN- | Not every S is P | ¬∃xS(x) ∨ ∃x(S(x) ∧ ¬P(x)) |
The logical relations between these propositions are displayed in the subsequent “Octagon of Opposition” where horizontal dotted lines indicate contradictory oppositions, or negations, bold arrows stand for (unrestrictedly valid) logical implications, while thin arrows symbolize the traditional inferences of subalternation which hold only for “non-empty” subject terms:
4. Abelard’s Quantification of the Predicate
According to the standard historiography of logic (for example, Kneale 1962), the theory of the “quantification of the predicate” was developed only in the 19th century by William Hamilton and by Augustus de Morgan. However, preliminary versions of such a theory may have already been apparent in the 17th-century work of Leibniz (Compare Lenzen 2010), in the 16th-century work of Caramuel (Compare Lenzen 2017), and in the 14th-century work of Buridan (Compare Read 2012). Interestingly, Abelard had already dealt with this issue both in Logica ‘Ingredientibus’ and in Dialectica. He developed the theory in two steps, first, for propositions with a singular subject, second, for categorical forms with a quantified subject.
a. Singular Propositions with Quantified Predicate
On pp. 189-190 of Dialectica, Abelard considers the following propositions:
| SQ1 | Socrates est omnis homo |
| SQ2 | Socrates non est aliquis homo |
| SQ3 | Socrates est aliquis homo |
| SQ4 | Socrates non est omnis homo |
According to Abelard, SQ1 and SQ2 are contrary to each other. Furthermore, SQ3 follows SQ1 with subalternation, and similarly SQ2 entails SQ4. Hence SQ3 and SQ4 are “opposed” as subcontraries, and one obtains the following Square of Opposition:
| SQ1 | Socr. is every man | Socr. is no man | SQ2 |
| ⇓ | ⇓ | ||
| SQ3 | Socr. is some man | Socr. is not every man | SQ4 |
Next, Abelard considers the following propositions:
| SQ5 | Omnis homo est Socrates |
| SQ6 | Nullus homo est Socrates |
| SQ7 | Aliquis homo est Socrates |
| SQ8 | Non omnis homo est Socrates |
According to Abelard, SQ5 is equivalent to SQ1, and SQ6 is equivalent to SQ2. Furthermore, although Abelard himself doesn’t explicitly say this, SQ7 is equivalent to SQ3, and SQ8 is equivalent to SQ4.
Within the framework of first-order logic, SQ5, ‘Every man is Socrates,’ is most naturally interpreted as: ‘For every x: If x is a man, then x is identical with Socrates,’ symbolically ∀x(M(x) ⊃ (x = s)). Similarly, SQ6, ‘No man is Socrates’ can be formalized as ¬∃x(M(x) ∧ (x = s)). By way of subalternation, SQ5 entails ∃x(M(x) ∧ (x = s)), and SQ6, or its equivalent ∀x(M(x) ⊃ (x ≠ s)), similarly entails ∃x(M(x) ∧ (x ≠ s)). All these relations can be represented by another Square of Opposition:
| SQ1/SQ5 | ∀x(M(x) ⊃ (x = s)) | ∀x(M(x) ⊃ (x ≠ s)) | SQ2/SQ6 |
| ⇓ | ⇓ | ||
| SQ3/SQ7 | ∃x(M(x) ∧ (x = s)) | ∃x(M(x) ∧ (x ≠ s)) | SQ4/SQ8 |
This reconstruction largely accords with two squares which Abelard himself presented in Logica Ingredientibus, p. 411 (for more details compare Lenzen (2021), ch. 10).
b. Categorical Forms with Quantified Predicate
In a very condensed passage of Dialectica (p. 190), Abelard sketches how the theory of the quantification of the predicate can be transferred from singular propositions to categorical propositions. He starts with a generalisation of ‘Socrates est omne animal’ and ‘Socrates non est omne animal’:
CQ1 Every man is every animal (Omnis homo est omne animal).
CQ2 No man is every animal (Nullus homo est omne animal).
According to Abelard, these two propositions are doubly contrary (“dupliciter contrarie”) to each other. Next Abelard considers the subcontrary propositions:
CQ3 Some man is some animal (Quidam homo est aliquod animal).
CQ4 Some man is not every animal (Quidam homo non est omne animal).
He maintains that CQ3 follows from CQ1 by subalternation. Similarly, CQ4 follows from CQ2 by subalternation. Furthermore, Abelard maintains that another subalternation exists between:
CQ5 No man is some animal (Nullus homo est aliquod animal).
CQ6 Some man is every animal (Quidam homo est omne animal).
These propositions can be formalized as follows:
| CQ1 | Every man is every animal | ∀x(Mx ⊃ ∀y(Ay ⊃ (x = y))) |
| CQ2 | No man is every animal | ¬∃x(Mx ∧ ∀y(Ay ⊃ (x = y))) |
| CQ3 | Some man is some animal | ∃x(Mx ∧ ∃y(Ay ∧ (x = y))) |
| CQ4 | Some man is not every animal | ∃x(Mx ∧ ¬∀y(Ay ⊃ (x = y))) |
| CQ5 | No man is some animal | ¬∃x(Mx ∧ ∃y(Ay ∧ (x = y))) |
| CQ6 | Some man is every animal | ∃x(Mx ∧ ∀y(Ay ⊃ (x = y))) |
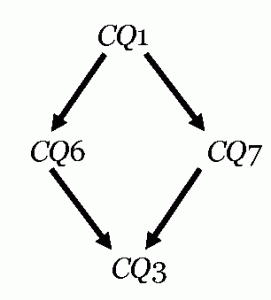
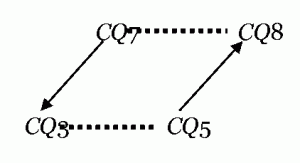
It is easy to see that Abelard’s theses concerning the contradictory opposition between CQ3 and CQ5 and between CQ4 and CQ1 are correct. Also, CQ1 and CQ2 are contrary to each other. Furthermore, as Abelard explains, CQ3 logically follows from CQ1 by way of subalternation. However, he failed to see that CQ3 follows from CQ1 so to speak by a double subalternation: CQ1 first entails:
| CQ7 | Every man is some animal | ∀x(Mx ⊃ ∃y(Ay ∧ (x = y))) |
And CQ7 in turn entails CQ3. Altogether the logical relations between the affirmative propositions CQ1, CQ3, CQ6, and CQ7 can be displayed as follows:
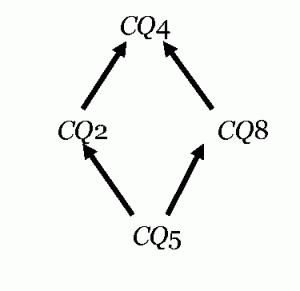
The logical relations of this diagram are reversed when one considers the negations of the four propositions. We know already that the negation of CQ1 is CQ4, that of CQ6 is CQ2, and that of CQ3 is CQ5. So, we only have to add the negation of CQ7 (‘Every man is some animal’) which amounts to:
| CQ8 | Some man is not some animal | ∃x(Mx ∧ ¬∃y(Ay ∧ (x = y))) |
Hence one obtains the following diagram for negative categorical propositions with quantified predicate:
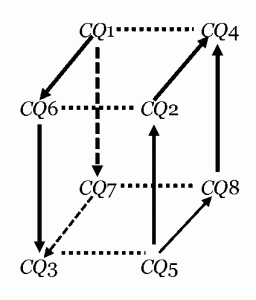
On p. 411 of Logica Ingredientibus, Abelard presents two squares of opposition, one entitled “exstinctiva”, the other “separativa.” After correcting a minor mistake, these squares accord with our diagrams, and both squares can easily be combined into the following octagon:
Here again dotted lines indicate a contradictory opposition while the arrows symbolize logical implications.
Most likely Abelard understood propositions CQ3 (‘Some S is some P’) and CQ5 (‘No S is some P’) as alternative formulations of the ordinary PA and UN. Similarly, propositions CQ7 (‘Every S is some P’) and CQ8 (‘Some S is not some P’), which were “overlooked” by Abelard, may be interpreted as alternative formulations of the ordinary UA and PN. Therefore, the above octagon contains as a substructure the usual square of opposition:
The thin arrows again signalize that these inferences of subalternation only hold for non-empty terms.
5. Inferences and Implications
Like many other medieval logicians, Abelard fails to make a systematic distinction between inferences and implications. He refers to them equally as “inferentia”, “consequentia”, or “consecutio.” If the inference is a genuine syllogism consisting of two categorical propositions as premisses and another categorical proposition as conclusion, Abelard typically separates them by means of “ergo,”, for instance:
Omnis homo est animal
Omne animal est animatum […]
Ergo omnis homo est animatus. (Dialectica, p. 254)
However, he has no qualms to express this inference equivalently by the conditional:
Si omnis homo est animal et omne animal est animatum, omnis homo est animatus (ibid.).
Also, he has no qualms to refer to the premise(s) of an inference as “antecedens,” to the conclusion as “consequens”, and to the entire inference as “argumentum.”
a. Perfect vs. Imperfect Inferences
Abelard defines an inference as perfect:
[…] when it holds in virtue of the logical form (complexio) of the propositions involved. By this […] he means that the entailment holds under any uniform substitution in its terms […]. The traditional moods of the categorical syllogism […] are all instances of complete entailments, or as we should say, valid inference. (King & Arlig 2018)
Somewhat surprisingly, Abelard was not willing to grant the attribute ‘perfect’ also to a tautology such as ‘si est animatum, est animatum’ (for a closer discussion compare Lenzen (2021), ch. 11).
Typical examples of imperfect inferences are enthymemes, which is to say, inferences which are not (yet) formally valid, but that can be turned into such by the addition of another premise. Thus, Abelard mentions the example ‘si omnis homo est animal, omnis homo est animatus,’ which may be transformed into a perfect syllogism by the addition of ‘omne animal est animatum’. The latter proposition, which Abelard also paraphrases without quantifier as ‘si est animal, est animatum’, is necessarily true because of the “nature of things.” Nowadays we would call such propositions analytically true.
b. Strict vs. Relevant Implication
As was already mentioned above, some modern commentators express their amazement that, allegedly, “Abelard denied the deduction theorem” (Guilfoy (2008)) or that he at least denied “that a correlate of the Deduction Theorem holds” (King & Arlig (2017)). This point had first been raised by Martin who pointed out:
The deduction theorem has often been regarded as central in logic, and it has been felt that one hardly has a logic for entailment if validity of argument and so derivability are not connected in an appropriate way to the truth of a conditional. There is some connection for Abelard since, if a conditional is true, it satisfies condition C, and so the corresponding argument will certainly be valid in the sense of satisfying condition I. In general, however, entailment [as] expressed in true conditionals is not the converse of derivability or logical consequence as expressed in valid arguments. (Martin 1986, p. 569)
In a later essay, he similarly maintained that:
[…] one cannot conditionalize a valid argument to obtain a true conditional and so the Deduction Theorem does not hold for Abelard’s logic, a feature which shocked his student John of Salisbury. (Martin 2006, p. 182)
Actually, John of Salisbury expressed his “shock” as follows:
I am amazed that the Peripatetic of Pallet so narrowly laid down the law for hypotheticals that he judged only those to be accepted the consequent of which is included in the antecedent […] indeed while he freely accepted argumenta, he rejected hypotheticals unless forced by the most manifest necessity. (Translation from Martin 2006, p. 196)
Now, ever since Aristotle, an inference has been regarded as logically valid if and only if it is impossible that the premise(s) are all true and yet the conclusion be false. A large majority of medieval logicians similarly considered a conditional A → C as true if and only if it can’t be the case that the antecedent A is true while the consequent C is false. This is the common definition of a strict implication (in distinction from a merely material implication) as it was re-invented in the 20th century by C. I. Lewis. Abelard thought it necessary to further distinguish between two kinds of the strictness or necessity of the consequence relation:
There seem to be two necessities of consequences, one in a larger sense, if namely that what is maintained in the antecedent cannot be the case without that what is maintained in the consequent; the other in a narrower sense, if namely not only the antecedent cannot be true without the consequent, but if also the antecedent by itself requires the consequent. (Cf. Dialectica, p. 283-4)
Abelard clearly saw that the former definition gives rise to what are nowadays called the “paradoxes” of strict implication, in particular the principle which later medieval logicians came to call “Ex impossibili quodlibet”:
EIQ If A is impossible, then the inference A ⇒ B (or the implication A → B) is valid (or true) for every proposition B.
Thus, Abelard considered the proposition ‘If Socrates is a stone, he is an ass’ which according to the first, liberal criterion counts as true because “it is impossible that Socrates should be a stone, and so impossible that he should be a stone without being an ass” (Kneale 1962, p. 217). For reasons discussed in section 6, Abelard did not want to accept this inference (or conditional) as sound. Therefore he suggested the stronger condition which Martin (2006: 181) explained as follows:
The antecedent is required to be relevant to the consequent in that its truth is genuinely sufficient for that of the consequent and this is guaranteed by the consequent being in some way contained in the antecedent.
As a standard example for a correct “relevant” implication Abelard mentions:
(i) If he is a man, he is an animal (“Si est homo, est animal”).
Here, the antecedent requires the consequent by itself (“ex se ipso”) since the notion of man contains the notion of animal. In contrast,
(ii) If he is a man, he is not a stone (“Si est homo, non est lapis”)
is not accepted by Abelard as a correct relevant implication, although, of course, it satisfies the weaker criterion of a strict implication. Abelard argues (Dialectica, p. 284) that the truth of (ii) only rests on our experience which shows that the properties ‘man’ and ‘stone’ are disparate, that is to say, they do not simultaneously subsist in one and the same thing. Yet, as the Kneales explained “the sense of the consequent […] is not contained in the sense of the antecedent” (Kneale 1962: p. 218).
In the wake of Abelard, many attempts have been made to elaborate the idea of a “relevant” implication and to develop a full-fledged logic of “containment.” Until today, no real agreement has been reached. Abelard contributed to this enterprise mainly by suggesting that, in generalization of example (i), a “relevant” implication obtains whenever the antecedent refers to a certain species while the consequent refers to the corresponding kind. The correctness of such conditionals does not depend on whether the antecedent is true or false. Even impossible antecedents can support correct conditionals, that is:
If Socrates is a pearl, Socrates is a stone (cf. Logica ‘Ingredientibus’, 329)
If Socrates is an ass, Socrates is an animal (cf. Dialectica, 346).
6. Abelard’s Defence of the Principles of Connexive Logic
In the 1960s, Storrs McCall introduced the idea of a connexive implication which can be characterized by the requirement that the operator ‘→’ satisfies “Aristotle’s Thesis” and “Boethius’ Thesis.” The crucial passage from Prior Analytics 57b3-14 was interpreted by McCall as follows:
What Aristotle is trying to show here is that two implications of the form ‘If p then q’ and ‘If not-p then q’ cannot both be true. The first yields, by contraposition, ‘If not-q then not-p’, and this together with the second gives ‘If not-q then q’ by transitivity. But this, Aristotle says, is impossible: a proposition cannot be implied by its own negation. […] We shall henceforth refer to the principle that no proposition can be implied by its own negation, in symbols ‘~(~p → p)’, as Aristotle’s [first] thesis […] The [other] connexive principle ~[(p → q) & (~p → q)] will be referred to as Aristotle’s second thesis. (McCall 2012, p. 415)
If one replaces McCall’s symbols ‘~’ and ‘&’ for negation and conjunction by our symbols ‘¬’ and ‘∧’, one obtains:
Arist 1 ¬(¬p → p)
Arist 2 ¬((p → q) ∧ (¬p → q)).
The second principle can be paraphrased by saying that no proposition is implied by both of two contradictory propositions. Abelard similarly maintained that “one and the same consequent cannot follow from the affirmation and from the negation of the same proposition” (cf. Dialectica, p. 290). Like Aristotle, Abelard also argued that if Arist 2 would not hold, then Arist 1 wouldn’t hold either, and this would be absurd since “the truth of one of two contradictory propositions not only does not require the truth of the other, but instead it expels and extinguishes it” (ibid.)
Moreover, Abelard pointed out that Aristotle’s Thesis (“regula aristotelica”) not only holds in the version where it is denied “that one and the same follows from the affirmation and from the negation of the same”, but also in the variant that “the affirmation and the negation of the same cannot be implied by one and the same proposition”, that is:
Abel 2 ¬((p → q) ∧ (p → ¬q)).
For example, the propositions ‘If x is a man, x is an animal’ and ‘If x is a man, x is not an animal’ cannot both be true, because otherwise one might derive the “inconveniency” ‘If x is a man, x is not a man,’ The corresponding generalization:
Abel 1 ¬(p → ¬p),
however, in Abelard’s opinion is “impossible.”
Principle Abel 2 is usually referred to as ‘Boethius’ Thesis’. Thus, McCall picked up a passage from De Syllogismo hypothetico where Boethius (ca. 480-524) maintained: “Si est A, cum sit B, est C; […] atqui cum sit B, non est C; non est igitur A’.” McCall then “transliterated” this as the inference:
If p, then if q then r,
If q then not-r
Therefore, not-p.
The reasoning that led Boethius to assert the validity of this schema was presumably this. Since the two implications ‘If q then r’ and ‘If q then not-r’ are incompatible, the second premise contradicts the consequent of the first premise. Hence, by modus tollens, we get the negation of the antecedent of the first premise, namely ‘not-p’. […] The corresponding conditional, If q → r then ~(q → ~r) will be denoted Boethius’ thesis, and serves with the thesis ~(p → ~p) as the distinguishing mark of connexive logic (McCall 2012, p. 416).
As was argued in Lenzen (2020), Boethius’ term-logical principle primarily expresses the idea that if a UA of type ‘If x is A, then x is B’ is true, then the UN ‘If x is A, then x is not-B’ can’t be true as well, which is to say, the two universal propositions are contrary to each other. Yet it is probably correct to assume that Boethius would also have endorsed the propositional principle called ‘Boethius’ Thesis’, that is, Abel 2. On the other hand, Boethius nowhere put forward a term-logical counterpart of Abel 1. Therefore, it seems preferable to refer to these principles as Abelard’s Theses.
a. The First “Embarrassing Argument”
Logicians from the 12th-century school of the “Montanae” developed an argument to show that the connexive principles do not hold without restriction. Martin (1986: 569-70) reconstructed their “embarrassing argument” as follows:
1. If Socrates is a man and a stone, Socrates is a man.
2. If Socrates is a man, Socrates is not a stone.
So 3. If Socrates is a man and a stone, Socrates is not a stone.
But 4. If Socrates is not a stone, Socrates is not a man and a stone.
So 5. If Socrates is a man and a stone, Socrates is not a man and a stone.
Conclusion (5) has the logical structure (p ∧ q) → ¬(p ∧ q), hence it contradicts Abel 1. However, Abelard wasn’t too much worried by this counterexample because he considered step (2) as not valid. This step consists of an application of the traditional “Locus ab oppositis.” In the invaluable collection Logica Modernorum edited by Lambert M. De Rijk, the rule is formulated as “si aliquid oppositorum predicatur de aliquo, aliud abnegatur ab illo” (De Rijk 1967, II/2, p. 62). This means:
Opp 3 If one of two opposite predicates is affirmed of a certain subject, then the other predicate must be denied (of the same subject).
The notion of opposite predicates here has to be understood as not only applying to contradictory concepts like ‘man’ and ‘not-man,’ but also to contrary concepts like ‘man’ and ‘horse’. Somewhat more exactly:
Opp 4 Two predicates (or concepts) P1, P2 are opposite to each other if and only if there can’t exist any x such that P1(x) and P2(x).
In particular, ‘man’ and ‘stone’ are opposite concepts; for any x, it is impossible that x is a man, M(x), and x is a stone, S(x)). Hence, according to the definition given above, M(x) strictly implies ¬S(x). Yet, for Abelard, this is not a relevant or “natural” implication because:
Not being a stone does not follow in the appropriate way from being a man, even though it is inseparable from being a man. It does not follow in the appropriate way since it is no part of the nature of a man that he not be a stone. (Martin 1987, p. 392)
The plausibility of this view need not be discussed here because it soon turned out that there are other counter-examples to the connexive principles Abel 1, 2 which do not rely on the “locus ab oppositis.”
b. Alberic’s Argument
As was first reported in Martin (1986), Alberic of Paris put forward the subsequent “embarrassing argument”:
1. If Socrates is a man and is not an animal, Socrates is not an animal.
2. If Socrates is not an animal, Socrates is not a man.
3. If Socrates is not a man it is not the case that Socrates is a man and an animal.
C*. If Socrates is a man and not an animal, it is not the case that Socrates is a man and not an animal. (Martin 1987, pp. 394-5)
Since conclusion C* has the structure (p ∧ ¬q) → ¬(p ∧ ¬q), it constitutes another counterexample to Abel 1. Furthermore, the argument does not depend on the “locus ab oppositis” because Line 2 is obtained by applying the principle of contraposition to the unproblematic conditional ‘If Socrates is a man, Socrates is an animal.’ Since the proof makes use only of logical laws which Abelard regarded as indispensable, “[…] confronted with this argument Master Peter essentially threw up his hands and granted its necessity” (Martin 1987, p. 395).
In the decades after Abelard, logicians from the schools of the Nominales, the Melidunenses and the Porretani tried to cope with the problems created by Alberic’s argument. As was argued in Lenzen (2023), however, their sophisticated arguments turned out to be inconclusive. As several brilliant logicians from the 13th to 15th century recognized, Aristotle’s and Abelard’s connexive theses have to be restricted to self-consistent antecedents and/or to non-necessary consequents. For example, Robert Kilwardby (1222-1277) who in his Notule libri Priorum desperately tried to defend Aristotle’s theses against counter-examples, eventually came to admit: “So it should be granted that from the impossible its opposite follows, and that the necessary follows from its opposite” (Thom & Scott 2015, p. 1145). Furthermore, in On the Purity of the Art of Logic, Walter Burley (ca. 1275-1345) proved that “every conditional is true in which an antecedent that includes opposites implies its contradictory. For example, it follows: ‘You know you are a stone; therefore, you do not know you are a stone’” (Spade 2000, p. 156). Burley concluded that Aristotle’s thesis is only restrictedly valid: “I say that the same consequent does not follow from the same antecedent affirmed and denied, unless the opposite of that consequent includes contradictories. And this is how Aristotle’s statement has to be understood” (Spade 2000, p. 160). In a similar way, John Buridan (ca. 1300-1360) rather incidentally noted that “a “possible [!] proposition never entails its own contradictory” (Hughes 1982, p. 38). The editor of Buridan’s Sophismata remarked: “Note that the principle appealed to is not that no proposition whatsoever can entail its own contradictory, but only that no possible proposition can do so. This is a standard principle of modal logic” (Hughes 1982, p. 86).
In view of these interesting and important discoveries, the history of connexive logic, as it was sketched in McCall (2012), needs to be fundamentally corrected. This has been achieved in Lenzen (2022).
7. References and Further Reading
a. Editions of Abelard’s Logical Works
- Victor Cousin (Ed.), Ouvrages inédits d’Abélard, Paris (Imprimerie Royale) 1836.
- Mario Dal Pra (Ed.), Pietro Abelardo Scritti Filosofici: Editio super Porphyrium; Glossae in Categorias; Super Aristotelem De Interpretatione; De divisionibus; Super Topica Glossae, Roma (Bocca) 1954.
- Lambert Marie De Rijk (Ed.), Petrus Abaelardus Dialectica – First Complete Edition of the Parisian Manuscript, Assen (van Gorcum) 1959. (The manuscript itself can be downloaded from the Bibliothèque Nationale de France under: https://gallica.bnf.fr/ark:/12148/btv1b6000788f?rk=321890;0
- Bernhard Geyer (Ed.), Peter Abaelards Philosophische Schriften. In: Beiträge zur Geschichte der Philosophie und Theologie des Mittelalters, vol. 21, issues 1-4, Münster (Aschendorf) 1919-1933.
b. Secondary Literature
- Maria Teresa Beonio-Brocchieri Fumagalli (1964): La Logica di Abelardo, Firenze (Pubblicazione della Università degli Studi di Milano); engl. translation: The Logic of Abelard, Dordrecht (Reidel) 1969.
- Irene Binini (2022): Possibility and Necessity in the Time of Peter Abelard, Leiden (Brill).
- Lambert Marie De Rijk (Ed.) (1967), Logica Modernorum – A Contribution to the History of Early Terminist Logic. Assen (Van Gorcum).
- Kevin Guilfoy (2008): “Peter Abelard”, in J. Fieser & B. Dowden (Ed.), Internet Encyclopedia of Philosophy: https://iep.utm.edu/abelard/
- George E. Hughes (1982): John Buridan on Self-Reference, Cambridge (Cambridge University Press).
- Peter King & Andrew Arlig (2018): “Peter Abelard”, in E. N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy, Fall 2018 edition: https://plato.stanford.edu/entries/abelard/
- William and Martha Kneale (1962): The Development of Logic, Oxford (Clarendon).
- Wolfgang Lenzen (2010): “The Quantification of the Predicate – Leibniz, Ploucquet and the (Double) Square of Opposition.” In J. A. Nicolás (Ed.), Leibniz und die Entstehung der Modernität, Stuttgart (Steiner), 179-191.
- Wolfgang Lenzen (2017): “Caramuel’s Theory of Opposition.” In South American Journal of Logic 3, 361-384.
- Wolfgang Lenzen (2020): “A Critical Examination of the Historical Origins of Connexive Logic.” In History and Philosophy of Logic 41, 16-35.
- Wolfgang Lenzen (2021): Abaelards Logik, Paderborn (mentis/Brill).
- Wolfgang Lenzen (2022): “Rewriting the History of Connexive Logic.” In Journal of Philosophical Logic 51, 523-553.
- Wolfgang Lenzen (2023): “Abelard and the Development of Connexive Logic.” In: M. Blicha & I. Sedlár (eds.), Logica 2022 Yearbook, London (College Publications), 55-78.
- Christopher Martin (1986): “William’s Machine.” In The Journal of Philosophy 83, 564-572.
- Christopher Martin (1987): “Embarrassing Arguments and Surprising Conclusions in the Development of Theories of the Conditional in the Twelfth Century.” In J. Jolivet & A. de Libera (Ed.), Gilbert de Poitiers et ses contemporains: aux origines de la Logica Modernorum, Napoli (Bibliopolis), 377-400.
- Christopher Martin (2006): “Logic.” In J. Brower & K. Guilfoy (Eds.), The Cambridge Companion to Abelard, Cambridge (Cambridge University Press), 158-199.
- Storrs McCall (2012): “A History of Connexivity.” In D. M. Gabbay, F. J. Pelletier & J. Woods (Ed.), Handbook of the History of Logic, Vol. 11, Logic: A History of its Central Concepts, Elsevier, 415-449.
- Jacques Paul Migne (Ed.) (1860): Anicii Manlii Severini Boethii Opera omnia, Paris.
- Stephan Read (2012): “John Buridan’s Theory of Consequence and His Octagons of Opposition.” In J.-Y. Béziau & D. Jacquette (Ed.), Around and Beyond the Square of Opposition, Basel (Birkhäuser), 93-110.
- Paul V. Spade (Ed.) (2000): Walter Burley – On the Purity of the Art of Logic – The Shorter and the Longer Treatise. New Haven & London (Yale University Press).
- Paul Thom & John Scott (Eds.) (2015): Robert Kilwardby, Notule libri Priorum. Oxford (Oxford University Press).
Author Information
Wolfgang Lenzen
Email: lenzen@uos.de
University of Osnabrück
Germany