The Cognitive Foundations and Epistemology of Arithmetic and Geometry

How is knowledge of arithmetic and geometry developed and acquired? In the tradition established by Plato and often associated with Kant, the epistemology of mathematics has been focused on a priori approaches, which take mathematical knowledge and its study to be essentially independent of sensory experience. Within this tradition, there are two a priori approaches. In the epistemological a priori approach, mathematical knowledge is seen as being a priori in character. In the methodological a priori approach, the study of the nature of mathematical knowledge is seen primarily as an a priori philosophical pursuit. Historically, there have been philosophers, most notably Mill in 1843, who have challenged the epistemological a priori approach. By contrast, until the 21^st century, the methodological a priori approach has remained unchallenged by philosophers.

In the first two decades of the 21^st century, the methodological a priori approach has received serious challenges concerning both arithmetic and geometry, which are generally considered to be among the most fundamental areas of mathematics. Empirical results have emerged that suggest that human infants and many non-human animals have something akin to arithmetical and geometrical capacities. There has been a great deal of disagreement over the philosophical significance of such results. Some philosophers believe that these results are directly relevant to philosophical questions concerning mathematical knowledge, while others remain sceptical.

This article presents some key empirical findings from the cognitive sciences and how they have been applied to the epistemology of arithmetic and geometry. It is divided into two parts. The first part is focused on arithmetic. Results on early quantitative cognition are reviewed, and important conceptual terminological distinctions are made, after which the importance of these empirical data for the epistemology of arithmetic is discussed. Two separate but connected problems are distinguished: the development of arithmetical knowledge on the level of individual ontogeny, and on the level of phylogeny and cultural history. The role of culture in the development of arithmetical knowledge is discussed, after which general epistemological considerations are provided. While at present the empirical data relevant to the development of arithmetic are stronger and more plentiful, there is also a growing body of data relevant to the development of geometry. In the second part, these data are used to provide geometrical knowledge with a similar treatment to that provided to arithmetical knowledge.

Table of Contents

1. Arithmetic
   1. The A Posteriori and Mathematics
      1. Empiricism in the Philosophy of Mathematics
   2. Empirical Research and the Philosophy of Mathematics
2. Numerical and Arithmetical Cognition
   1. Arithmetic and Proto-Arithmetic
   2. Acquisition of Number Concepts and Arithmetical Knowledge
   3. Embodied Mind and Enculturation
   4. From Ontogeny to Phylogeny and Cultural History
   5. Ordinal or Cardinal
   6. Empirically-Informed Epistemology of Arithmetic
3. Geometry
   1. The Cognitive Foundations of Geometry
      1. Proto-Geometrical Cognition
      2. Shape Recognition
      3. Orientation
   2. The Development of Geometric Cognition
4. References and Further Reading

1. Arithmetic

a. The A Posteriori and Mathematics

i. Empiricism in the Philosophy of Mathematics

Traditional pre-19^th-century Western philosophy of mathematics is often associated with two specific views. The first is Plato’s (The Republic) notion that mathematics concerns mind-independent abstract objects. The second is Immanuel Kant’s (1787) view of mathematical knowledge as synthetic a priori. These views, while not necessarily connected, are compatible. By combining them, readers obtain a standard Platonist view of mathematics: mathematical knowledge is acquired and justified through reason and recollection, and it concerns mind-independent abstract objects.

This standard view can be challenged from different directions. Conventionalists, for example, deny that mathematical knowledge concerns mind-independent objects. Hence, mathematics does not give us genuinely new knowledge about the world (in a broad sense), and should be considered analytically a priori (see, for example, Carnap, 1937). A less popular challenge claims that mathematical knowledge is not essentially independent of sensory experience, but a posteriori in character. The most famous such empiricist view was presented by John Stuart Mill (1843). By the late 20^th century, empiricist epistemologies of mathematics had been supported by Philip Kitcher (1983) and Penelope Maddy (1990). Maddy connects empiricism to mathematical realism, while, according to Kitcher, mathematical knowledge concerns generalisations of operations that we undertake in our environment. A similar view is supported by George Lakoff and Rafael Núñez (2000), who focus on the use of conceptual metaphors in cognitive development.

While there are many similarities in the approaches of Kitcher and Lakoff and Núñez, there are also notable differences. Importantly, Lakoff and Núñez make more connections to the empirical literature on the development of mathematical cognition. From the 1990s on, authors began taking this approach even more seriously, making important use of empirical studies on early numerical and geometrical cognition in the epistemology of mathematics. Significantly, such authors are not necessarily empiricists concerning mathematical knowledge. Accordingly, it is important to distinguish between empiricist and empirically-informed epistemological theories of mathematics. While the former are likely to include the latter, the opposite is not necessarily the case. Since the late 20^th century, many philosophers have proposed epistemological accounts of arithmetic and geometry that are based in a significant way on empirical research, but which do not support the view that mathematical knowledge is essentially empirical in character.

b. Empirical Research and the Philosophy of Mathematics

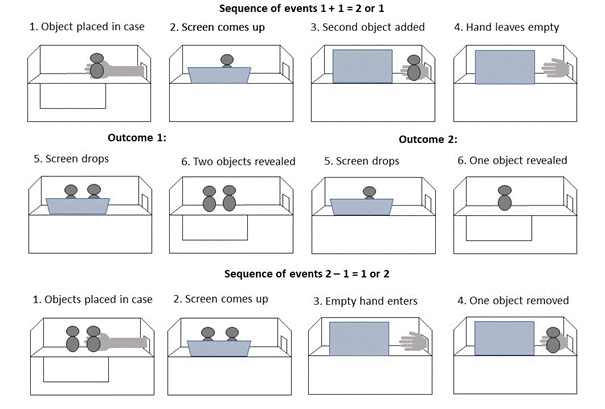
An important reason for the emergence of empirically-informed accounts is the extensive development of empirical research on numerical cognition in the 1990s. This empirical work was presented in two popular books: The Number Sense by Stanislas Dehaene (Dehaene 1997) and What Counts: How Every Brain is Hardwired for Math (Butterworth 1999), published in the United Kingdom as The Mathematical Brain. Within this research corpus, one of the most famous items is Karen Wynn’s paper “Addition and subtraction by human infants” (Wynn 1992). In it, Wynn presents her research on five-month-old infants, whom she interprets as possessing genuine number concepts and arithmetical abilities. Wynn’s experiment is widely discussed in the subsequent literature, and since it illuminates the different kinds of interpretations that can be made of empirical research, it is worth presenting in detail.

In the experiment, infants were shown dolls, and their reactions were observed to determine whether they had numerical abilities. In the first variation of the experiment, infants were shown two dolls placed, one by one, behind an opaque screen. In some trials, one of the dolls was removed without the infant seeing its removal, revealing only one doll when the screen was lifted. In others, both dolls were left behind the screen, revealing two dolls. In the second variation of the experiment, the infants were first shown two dolls and, after one was visibly removed, either one or two dolls were revealed.

Wynn’s experiment showed that infants reacted with surprise (measured through longer looking times) to the trials where the revealed quantity of dolls was unnatural (namely, when only one doll was revealed in the first variation, and when two dolls were revealed in the second variation). Wynn argued that this showed that “infants can calculate the results of simple arithmetical operations on small numbers of items. This indicates that infants possess true numerical concepts, and suggests that humans are innately endowed with arithmetical abilities.” (Wynn 1992, 749). Others were equally excited by the results. Dehaene, for example, motivated his book by asking: “How can a five-month-old baby know that 1 plus 1 equals 2?” (Dehaene 2011, xvii). Yet, a lot is assumed in these claims. Do infants really possess true numerical concepts? Are they innately endowed with arithmetical abilities? Their behaviour in the experiment notwithstanding, do they know that one plus one equals two? These questions warrant a detailed analysis before we say more about the arithmetical capacities of infants. But, clearly, empirical research of this type is highly philosophically relevant; after all, if Wynn’s and Dehaene’s interpretations are correct, some mathematical knowledge is already possessed by infants. This would pose a serious challenge to epistemological theories according to which mathematical knowledge is acquired solely through reason and recollection.

2. Numerical and Arithmetical Cognition

a. Arithmetic and Proto-Arithmetic

Neither Wynn nor Dehaene propose that infants possess arithmetical knowledge in the same sense in which arithmetically-educated adults do. Yet, as they interpret the empirical results, adult arithmetical knowledge is a later stage of a developmental trajectory that builds on innate arithmetical abilities. Standardly, two innate abilities are identified (see, for example, Dehaene, 2011; Feigenson et al., 2004; Hyde, 2011; Spelke, 2011). First is the ability to subitize, which was first reported in (Kaufman et al. 1949). Subitizing is the ability to determine the quantity of objects in the field of vision without counting. The subitizing ability allows for the precise determination of quantities but standardly stops being applied for collections larger than four items. In one of the earliest results supporting the existence of an infant ability to discriminate quantities, Starkey and Cooper (1980) reported that 22-week-old infants subitize. Since then, it has been established that many non-human animals have the ability to subitize (see, for example, Dehaene, 2011 for an overview). The second ability is estimating the size of an observed collection of objects. Unlike subitizing, the estimating ability is not limited to small quantities. Yet, it becomes increasingly inaccurate as the estimated collections become larger. Indeed, the accuracy of the estimations decreases in a logarithmic manner, following the so-called Weber-Fechner law (also called Weber’s law in the literature): it is more difficult to distinguish between, say, 17 and 18 objects than it is between 7 and 8 (Dehaene 2011; Fechner 1948). Since the performance signatures of these abilities (for both human children and non-human animals) are different for small and large collections of objects, subitizing (being precise but limited) and estimating (being approximate but essentially unlimited) are standardly thought to be distinct abilities (Feigenson, Dehaene, and Spelke 2004).

In addition to infants, the subitizing and estimating abilities have been detected in many non-human animals. Among them are animals that are generally considered to be intelligent, like primates and birds in the corvid family (for review, see Dehaene 2011; Knops 2020; Nieder 2019). More surprising have been empirical results showing that goldfish (DeLong et al. 2017), newborn chicks (Rugani et al. 2009) and honeybees (Howard et al. 2019) also seem to possess similar quantitative abilities. These data suggest that the abilities have early evolutionary origins, or evolved several times. In either case, their existence has been an important reason to reconsider the origins of numerical abilities.

Given that subitizing and estimating are innate abilities, it is commonplace among empirical researchers to attribute them to so-called core cognitive systems (Carey 2009; Spelke 2000). According to Susan Carey, core cognition refers to how human cognition begins with “highly structured innate mechanisms designed to build representations with specific content” (Carey 2009, 67). The core system responsible for the subitizing ability allows for the tracking of persisting objects in the field of vision, and it is usually called the object tracking system (OTS) (Knops 2020), but sometimes also the parallel individuation system (Carey 2009; Hyde 2011). Unlike the OTS, which has functions besides determining the quantity of objects, the core system responsible for the estimating ability is standardly thought to be quantity specific. It is usually called the approximate number system (ANS) (Spelke 2000), and it is what Dehaene called the number sense (Dehaene 1997), even though some research suggests that instead of being number-specific, the estimation system is common to space, time, and number (Walsh 2003).

As mentioned above, it is commonplace to think of the OTS and the ANS as two distinct core cognitive systems (see, for example, Hyde, 2011; Nieder, 2019). Recently, though, a mathematical model has been proposed according to which, under limited informational capacity, only one innate system is responsible for different performance signatures for small and large collections (Cheyette and Piantadosi 2020). From a philosophical standpoint, more important than the exact division between systems is how the core cognitive systems should be understood in terms of the development of arithmetical cognition. Based on Wynn’s (1992) report of her experiment, it is likely that infants are subitizing when determining the quantity of the dolls. She believes that they also practice arithmetic and possess true numerical concepts. This prompts the question: could the infants’ behaviour be understood in another way, one that does not assign genuine arithmetical ability or numerical concepts to them? Many researchers believe that subitizing, based on the OTS, works by means of the observed objects occupying mental object files (Carey 2009; Noles, Scholl, and Mitroff 2005). When two objects are observed, two object files are occupied. Under this explanation, the infants’ surprise during Wynn’s experiment is explained by their observations not matching the occupied object files. Importantly, the infants are not thought to observe “twoness”, representing the number of dolls in terms of numerical concepts.

Based on such considerations, it is commonplace to distinguish between genuinely arithmetical ability and the innate quantitative abilities of subitizing (that is, quickly recognizing and naming the number in a group without counting) and estimating. For this reason, Markus Pantsar (2014; 2019) has called the latter abilities proto-arithmetical, whereas Núñez (2017) calls them quantical. Arithmetic, under these distinctions, refers exclusively to the culturally developed human system of natural numbers and their operations. Arithmetic does not necessarily mean modern sophisticated formal systems, like the Dedekind-Peano axiomatization (Peano 1889). Instead, under the characterization of Pantsar (2018, 287), arithmetic refers to a “sufficiently rich discrete system of explicit number words or symbols with specified rules of operations.” What counts as “sufficiently rich” is left purposefully undefined; more important is the idea that arithmetic, in contrast to proto-arithmetic, needs to consistently and specifically discriminate between different cardinalities (unlike with the ANS), without there being a pre-set limit in size (unlike with the OTS). Put more precisely in mathematical terms, the system must “sufficiently follow the structure of the omega progression, that is, the standard ordering of the set of natural numbers” (ibid.).

A similar distinction has also been proposed when it comes to the subject matter of proto-arithmetical/quantical abilities. While some argue that they concern numbers (see, for example, Carey, 2009; Clarke & Beck, 2021), others insist that we need to distinguish them from numbers as objects of arithmetic. Hence it has been proposed that instead of numbers, proto-arithmetical abilities should be discussed as detecting numerosities (De Cruz and De Smedt 2010; Pantsar 2014). Under this distinction, numerosities refer to the quantity-specific content that can be processed using proto-arithmetical abilities. In what follows, we employ the double distinction between arithmetic and proto-arithmetic and between numbers and numerosities.

b. Acquisition of Number Concepts and Arithmetical Knowledge

Recall that Wynn interpreted the results of her experiment to imply that “infants possess true numerical concepts” (Wynn 1992, 749). With the distinction between numbers and numerosities in place, this conclusion seems dubious. The infants do appear to be able to process numerosities, but this ability is entirely proto-arithmetical, not arithmetical. Hence there is no reason to believe that number concepts are innate to humans (or non-human animals). This is supported by evidence from anumeric cultures such as the Pirahã and the Munduruku of the Amazon. These cultures have not developed arithmetic and their languages do not have numeral words, with the possible exceptions of words for one and two; their members show no arithmetical abilities (Gordon 2004; Pica et al. 2004). Yet experiments show that members of these cultures do possess proto-arithmetical abilities (Dehaene et al. 2008; Everett and Madora 2012; Frank et al. 2008). Therefore, it is likely that, while proto-arithmetical abilities are innate and universal to neurotypical humans, number concepts develop only in particular cultural contexts, in close connection with the development of numeral words (or symbols).

There are, however, disagreeing voices in the literature. Aside from Wynn, Rochel Gelman and C. Randy Gallistel are proponents of a nativist view according to which number concepts are innate and pre-verbal (Gallistel 2017; Gelman and Gallistel 2004). In addition, Dehaene and Brian Butterworth have both presented influential accounts which could be interpreted as forms of nativism. Butterworth (1999) has argued for the existence of an innate “number module”, while Dehaene (2011) has argued for an innate “mental number line.” Yet, it seems that nativist interpretations of these accounts result from misleading terminology. While both authors support innate numerical capacities, given our terminological distinctions, this amounts to the innateness of proto-arithmetical abilities.

If number concepts are not innate, they must be acquired during individual ontogeny. The first influential account along these lines was presented by Jean Piaget (1965). At the time, it was not known that children possess pre-verbal proto-arithmetical abilities, so Piaget endorsed a view according to which all numerical abilities arise from logical capacities and only typically emerge at around the age of five. Over the years after Piaget, researchers have contended that he was wrong about numerical abilities, but he seems to have been right about number concepts not being innate. Moreover, Piaget got the age of this development wrong, as the first number concepts seem to emerge at the age of two.

Parents of young children may want to object at this point, since children can count already before the age of two. Yet it is important to distinguish between different types of counting. Paul Benacerraf (1965) distinguishes between intransitive and transitive counting. The former consists merely of repeating the numeral word sequence in order, as in the beginning of a game of hide and seek. In the latter, the numeral words are used to enumerate items in a collection, like when counting grapes on a plate. In the empirical literature, these two types of counting are often referred to by different terms. Transitive counting is often called enumeration, and the word “counting” is simply used for intransitive counting (for example, Rips et al., 2008).

When exploring number concept acquisition, it is imperative that we distinguish both types of counting from counting with number concepts, which is a further stage in cognitive development. It is known that intransitive counting precedes transitive counting, but also that transitive counting is not sufficient for possession of number concepts (see, for example, Davidson et al., 2012). The way this is usually established is through the “give-n” test developed by Wynn (1990). In the test, children are presented with a collection of objects and asked to give n of them. If they consistently give n objects, they are thought to possess the number concept of n. Yet, as pointed out by Davidson and colleagues, there is a stage at which children can transitively count objects but do not pass the give-n test.

At about two years of age, children start passing the test for n = 1, at which point they are called one-knowers. After that, they acquire the next three number concepts in ascending order, in stages that typically take 4-5 months (Knops 2020). Subsequently, a qualitative change occurs in children’s cognitive processing. After becoming four-knowers, instead of following this trajectory, in the next stage, children grasp something more general about numbers: in addition to the give-5 test, they start passing the give-n test for six, seven and so on (Lee and Sarnecka 2010). At this point, when they have acquired a general understanding that the last uttered word in the counting list refers to the cardinality of the objects, they are called cardinality-principle-knowers (Lee and Sarnecka 2011).

What happens in children’s cognitive development when they become cardinality-principle-knowers? The theory of number concept acquisition that is currently most thoroughly developed in the literature is called bootstrapping. Originally presented by Susan Carey (2004), this theory has since been further developed and clarified by Carey and others (Beck 2017; Carey 2009; Pantsar 2021a). In a nutshell, the bootstrapping account ascribes a central role to the object tracking system in the process. After acquiring the counting list (that is, being able to intransitively count), children are thought to form mental models of different sizes of collections, based on computational constraints set by the object files of the OTS (Beck 2017, 116). When observing two objects, for example, two mental object files are occupied. Such instances are thought to form a representation of two objects in the long-term memory (Carey 2009, 477). Then, through counting games in which the counting list is repeated while pointing to objects, this representation is connected to a particular number word, like “two” (Beck 2017, 119). This explanation can only hold for up to four, though, which is the limit of the OTS. After this, in the last stage of the bootstrapping process, children are thought to grasp, through inductive and analogous reasoning, that the way in which the first four number concepts are in an ascending, regular, order can be extrapolated to the rest of the counting list (Beck 2017, 119). This is the stage at which children become cardinality-principle-knowers.

The bootstrapping theory has critics. Pantsar (2021a) has asked how children ever grasp that there are numerosities larger than four if the OTS is the sole proto-arithmetical system relevant to the bootstrapping process. Lance Rips and colleagues (2006) ask why children bootstrap a linear number system and not, say, a cyclical one? Why, after acquiring the number concept for twelve, for example, is thirteen the next step, instead of one? Rips and colleagues (2008) argue that there needs to be a mathematical schema concerning numbers already in place to prevent such cyclical systems or other “deviant interpretations”. For them, grasping the concept of natural number requires understanding general truths of the type “for all numbers, a + b = b + a”. This, however, is quite problematic as it implies that grasping natural numbers requires understanding something like the Dedekind-Peano axioms, which standardly only happens quite late in individual ontogeny (if at all). It is problematic to associate grasping number concepts with such sophisticated mathematical understanding given that children already possess considerable arithmetical knowledge and skills much earlier.

The conclusion of Rips and colleagues (2008, p. 640) is that the concept of natural number may be completely independent of proto-arithmetical abilities. While they believe that number concepts are learned in a “top-down” manner by grasping general principles, others have suggested different explanations for why we do not acquire deviant interpretations such as cyclical number systems. Margolis and Laurence (2008) have suggested that the deviant interpretation challenge supports a nativist view about number concepts. Yet others have looked for solutions to the challenge that do not entirely abandon the bootstrapping account. Paula Quinon (2021) has suggested that an innate sense for rhythm can explain the preference for linear, regular number systems. Pantsar (2021a) has argued that the approximate number system can influence the bootstrapping process so as to prevent cyclical number systems. Jacob Beck (2017), by contrast, rejects the overall importance of the problem, pointing out that it is just another instance of the general problem of inductive learning, as formulated by the likes of Kripke (1982) and Goodman (1955).

So far, we have been discussing number concepts, but acquiring them is only the first step in developing arithmetical knowledge and skills. While acquiring number concepts would seem to be a necessary condition for having arithmetical knowledge, possessing number concepts alone does not ensure possession of arithmetical knowledge. In accounts like that of Lakoff & Núñez (2000), detailed schemas of the acquisition of arithmetical knowledge are presented. They see the application of conceptual metaphors as the foundation of mathematical knowledge. Addition, for example, is seen as the metaphorical counterpart of the physical task of putting collections of objects together (Lakoff and Núñez 2000, 55).

In other accounts, addition is understood as a more direct continuation of counting procedures, which are mastered in the process of acquiring number concepts. The psychologists Fuson and Secada (1986), for example, presented an account of grasping the addition operation based on a novel understanding of counting. In counting a + b, children typically first use the “counting-all” strategy. When presented with a objects, the children count to a. When presented with b additional objects and asked to count all (that is, a + b) objects, they re-count to a and then continue the count to a + b. Yet, at some stage, children switch to the “counting-on” strategy, starting the count directly from where they finished with a. That is, instead of counting, say, 5 + 3 by counting 1, 2, 3, 4, 5, 6, 7, 8, when applying the “counting-on” strategy, children simply count 6, 7, 8 in the second stage. This strategy has been shown to be helpful in understanding addition (Fuson and Secada 1986, 130).

This example shows how arithmetical operations can be grasped by applying knowledge that children already possess (that is, about counting). Addition is thus understood as a direct descendant of counting. Similarly, multiplication can be understood as a descendant of addition, and so on. Therefore, acquiring arithmetical knowledge and skills can build directly on number concept acquisition and the knowledge and skills that children learn in that process. One should be careful, though, not to make too many assumptions about ontogenetic trajectory. For empirically-informed approaches, it is important to be faithful to the actual empirical details regarding the development of children during ontogeny. While schemas like that presented by Lakoff and Núñez (2000) can be instructive, we should not confuse them with empirical evidence. Understanding ontogenetic trajectories in learning arithmetic is an important challenge that, like that of number concept acquisition, needs further empirical research.

c. Embodied Mind and Enculturation

One consequence of the traditional a priori emphasis in philosophy of mathematics has been that the embodied aspects of mathematics have often been dismissed as philosophically inconsequential. This was famously the case for Frege (1879), who distinguished between the context of discovery (how truths are learned) and the context of justification (how truths are established). For arithmetic, Frege (1884) deemed the context of discovery philosophically irrelevant, ridiculing Mill’s empiricist account as “pebble arithmetic”. However, as we have seen, many researchers currently see the ontogenetic aspects of arithmetic as important to a philosophical understanding of arithmetical knowledge. So far, we have been focused on the role of the proto-arithmetical abilities of subitizing and estimating, and the cognitive core systems associated with them. But in individual ontogeny, embodied aspects and external resources also play important roles. Therefore, it is important to expand epistemological accounts of arithmetic beyond proto-arithmetical abilities.

This is the case already for number concepts. Recognizing the role of embodied aspects of cognition and external resources within cognitive development does not, by itself, imply a preference for one account of number concepts over another. In Beck’s (2017) formulation of the bootstrapping account, number concepts are acquired with the help of two types of external resources: the counting list and counting games. But it is not the presence of external resources that distinguishes between bootstrapping accounts and nativist accounts. Nativists concerning number concepts also acknowledge the importance of education in grasping number concepts. The difference lies in what kind of influence the external resources have. Within nativist accounts, external resources are seen as facilitators that help innate number concepts to emerge. Within bootstrapping accounts, number concepts are shaped by a combination of innate cognitive capacities and external cultural influences.

While non-nativist accounts acknowledge the importance of external factors for number concept acquisition and the development of arithmetical cognition in general, it is not always clear how such accounts view interactions between learning subjects and their environment. Helen De Cruz (2008) was one of the first to tackle this problem systematically by adopting the extended mind perspective within the philosophy of arithmetical cognition. According to the extended mind thesis, cognitive processes are extended into the environment in the sense that they are constituted by both internal cognitive capacities and external resources (Clark and Chalmers 1998). De Cruz argued that this holds for arithmetical cognition; external media such as numeral words, body parts, and numeral symbols are constitutive of number concepts and arithmetical operations on them.

The embodiment of mind is often associated with the extended mind thesis. Arithmetical cognition seems to provide good examples of how our bodies shape our cognitive processes. The use of fingers, in particular, has been widely established across cultures to be significant in the early grasp of counting processes (Barrocas et al. 2020; Bender and Beller 2012; Fuson 1987). Furthermore, finger gnosis, the ability to differentiate between one’s own fingers without visual feedback, is a predictor of numerical and arithmetical ability levels (Noël 2005; Penner-Wilger and Anderson 2013; Wasner et al. 2016). The use of body parts has also been identified by philosophers as an important factor in developing arithmetical cognition (Fabry 2020). In addition to finger (and other body part) counting, there are many other important embodied processes involved in learning arithmetic. Manipulating physical objects like building blocks has been established as important in early arithmetic education (Verdine et al. 2014). The use of cognitive tools, such as pen and paper or abacus, becomes important in later stages (Fabry and Pantsar 2021). It is important to note, though, that this kind of support for the embodiment of mind does not require subscribing to the stronger extended mind thesis. Under a weaker understanding of the embodiment of mind, embodied processes shape the concepts and cognitive processes involved in arithmetic. According to the extended mind thesis, embodied processes are constitutive of concepts and cognitive processes.

External resources are important for the development of arithmetical cognition in many ways. In addition to body part counting and the use of physical cognitive tools, numeral word and numeral symbol systems also play an important role. The Mandarin numeral word system, for example, has shorter words than the English system and follows the recursive base of ten more closely. This has been suggested as an explanation of why native Mandarin speakers typically learn to count faster than native English speakers (Miller et al. 1995). For numeral symbol systems, similar data is not available, largely due to the widespread use of Indo-Arabic numerals. Yet, philosophers have worked on different numeral symbol systems and the way they can shape arithmetical cognition (see, for example, Schlimm 2021).

The importance of external resources for the development of arithmetical cognition appears to raise an age-old question: what is the role of nature and what is the role of nurture in this process? How much of arithmetical cognition comes from evolutionarily developed and innate proto-arithmetical abilities, and how much comes from culturally developed practices? From the above considerations, it seems clear that both play important roles, yet it is difficult to determine their relative impact. These types of considerations have led some researchers to abandon the crude nature vs. nurture framework. Influentially, Richard Menary (2015) has argued that arithmetical cognition is the result of enculturation. Enculturation refers to the transformative process through which interactions with the surrounding culture determine the way cognitive practices are acquired and developed (Fabry 2018; Jones 2020; Menary 2015; Pantsar 2020; Pantsar and Dutilh Novaes 2020). In the enculturation account, we must consider the development of cognitive abilities through such interactions. Menary focuses mainly on the brain and its capacity to adapt learning in accordance with the surrounding culture. Regina Fabry (2020) has extended this focus to the rest of the body, emphasizing the importance of embodied processes for the development of arithmetical cognition. The enculturation account has also proven to be fruitful for studying the general role of material representations, like symbols and diagrams, in the development of arithmetical (and other mathematical) cognition (Johansen and Misfeldt 2020; Vold and Schlimm 2020).

The enculturation account helps us understand how the brain changes as a result of learning cognitive practices involving cognitive tools, such as numeral symbol systems or tools for writing, like pen and paper. These changes typically involve the same areas of the brain across individuals. Menary (2015) has explained such predictable changes in the brain through the notion of learning driven plasticity, which includes both structural and functional changes. At present, there are two competing accounts for explaining learning driven plasticity. Menary follows Dehaene’s (2009) notion of neuronal recycling, according to which evolutionarily developed neural circuits are recycled for new, culturally specific purposes. In the case of arithmetic, that means that evolutionary developed proto-arithmetical neural circuits are (partly) redeployed for culturally specific, arithmetical, purposes. There is empirical data in support of this, showing, for example, that the prefrontal and posterior parietal lobes, especially the intraparietal sulcus, activate when processing numerosities both symbolically and non-symbolically (Nieder and Dehaene 2009).

Michael Anderson (2010; 2015), by contrast, has argued that neural reuse is the basic organizational principle involved in enculturation. According to the neural reuse principle, neural circuits generally do not perform specific cognitive or behavioural functions. Instead, due to the flexibility of the brain, cognitive and behavioural functions can employ (and re-deploy) resources from many neural circuits across different brain areas. Brain regions do, though, have functional biases, which explain why, during enculturation, the brains of individuals typically go through similar structural and functional changes. Recently, both Fabry (2020) and Max Jones (2020) have argued for neural reuse as a better explanation of enculturation in the specific context of arithmetic (see Pantsar (2024a) for further discussion). In addition, due to the importance of the embodied aspects of arithmetical cognition, Fabry (2020) has emphasized the need for also explaining adaptability outside the brain, introducing the notion of learning driven bodily adaptability.

One further question that has emerged in the literature on the development of arithmetical cognition is that of representations. The standard accounts among empirical researchers imply that proto-arithmetical numerosities are represented in the mind either in object files (OTS) or a mental number line (ANS) (see, for example, Carey, 2009; Dehaene, 2011). However, this goes against radical enactivist views according to which basic, that is, unenculturated, minds do not have content or representations (Hutto and Myin 2013; 2017). Recently, radical enactivist accounts of mathematical cognition have been presented (Hutto 2019; Zahidi 2021; Zahidi and Myin 2018). These accounts try to explain the development of arithmetical cognition in ontogeny without evoking representational models of proto-arithmetical abilities. This topic can be expected to get more attention in the future, as our empirical understanding of proto-arithmetical abilities improves.

d. From Ontogeny to Phylogeny and Cultural History

The surrounding culture and its impact on learning play key roles in the enculturation account of arithmetical knowledge. This prompts the question: how can cultures develop arithmetical knowledge in the first place? The problem is already present at the level of number concepts. In the bootstrapping account, for example, counting lists and counting games are thought to be integral to the acquisition of number concepts. But how can such cultural practices develop if members of a culture do not already possess number concepts? In many cultures, this happened through cultural transmissions from other cultures (Everett 2017). But this cannot be the case for all cultures. Most fundamentally, as Jean-Charles Pelland, among others, observed, the question concerns the origin of numeral words. Is it possible that numeral words – and consequently counting lists – could have developed without there first being number concepts (Pelland 2018)?

In response to this question, the role of external representations of numbers has become an important topic in the literature (see, for example, Schlimm, 2018, 2021). To explain how external representations like numeral symbols and words can influence concept formation, many researchers have turned to the cultural evolution of practices and concepts. Particularly influential in this field is the theory of cumulative cultural evolution (Boyd and Richerson 1985; 2005; Henrich 2015; Heyes 2018; Tomasello 1999). The central idea of cumulative cultural evolution is that cultural developments frequently take place in small (trans-)generational increments. From this background, it has been argued that material engagement with our environment (Malafouris 2013) has been central to the cultural evolution of numeral words, numeral symbols, and number concepts (dos Santos 2021; Overmann 2023; Pantsar 2024a). The emergence of numeral symbols has been traced to around 8,000-4,500 B.C.E. in Elam and Mesopotamia, where clay tokens were used to represent quantities in accounting (Overmann 2018; Schmandt-Besserat 1996). At first, a proper array of different tokens was put in a clay case to represent the quantity, but later the outside of the case was marked with a symbol to signal the contents (Ifrah 1998, xx). In the next phase, people bypassed the case and simply used the symbol (Nissen, Damerow, and Englund 1994).

For numeral words, similar connections to material practices have been identified. Not all languages have a system of numeral words. Hence, we must ask: how can numeral words be introduced into a language? Recently, César dos Santos (2021) has brought philosophical attention to the interesting case of the Hup language spoken by cultures in the Amazonia, which seem to be in the process of developing a numeral word system. In the Hup language, the word for two means “eye quantity” and the word for three comes from a word for a three-chambered rubber plant seed (Epps 2006). Thus, in the Hup language, numeral words appear to be emerging from prototypic representations of quantities of natural phenomena. Lieven Decock (2008) has called such representations “canonical collections”. Canonical collections may also hold the key to understanding how number concepts have evolved. The linguist Heike Wiese (2007) has argued that numeral words and number concepts co-evolved. Within philosophy, this idea has been pursued by dos Santos (2021) and Pantsar (2024b). Canonical collections in natural phenomena, in addition to body parts like fingers, have provided references that proto-arithmetical numerosity representations can latch onto. The word for the rubber plant seed in the Hup language, for example, has gradually changed meaning to also concern a quantity. Such words can be connected to body part counting procedures, which make them part of the counting procedure, and together with other similarly evolved words, part of the counting list. Through this process of co-evolution, the concept of number develops into the kind of exact notion of natural number that we have in arithmetic. Thus, the co-evolution of numeral words and number concepts is a proposed solution to the question presented by Pelland; numeral words can develop without there being prior number concepts because the concepts themselves can emerge as part of the same (or parallel) development.

Unfortunately, the emergence of numeral words and number concepts is, in most cases, impossible to trace. Similarly, the evolution of arithmetical operations is difficult to study due to a dearth of surviving material from the early stages. There are, however, important works that help improve our understanding of the evolution of numbers and arithmetic, including those by the mathematician Georges Ifrah (1998), the cognitive archaeologist Karenleigh Overmann (2023), and the anthropologist Caleb Everett (2017). History of mathematics also provides important insights concerning the development of arithmetic into the modern discipline with which we are familiar (for example, Merzbach and Boyer 2011). This kind of interdisciplinary research is highly philosophically relevant; it provides important material for recent epistemological accounts of arithmetic, like that of Pantsar (2024a). There are good reasons to expect this development to continue in the future, with the cultural development of arithmetic receiving more philosophical attention.

For the epistemology and ontology of arithmetic, both the ontogenetic proto-arithmetical foundations and the cultural development of arithmetical knowledge and skills are highly relevant. According to one view, mathematical objects like numbers are social constructs (Cole 2013; 2015; Feferman 2009). If this is the case, then an important question arises: what kind of social constructs they are? According to conventionalist philosophy of mathematics, which has found popularity in different forms ever since the early 20^th century, mathematical truths are merely firmly entrenched conventions (Ayer 1970; Carnap 1937; Warren 2020; Wittgenstein 1978). Thus, one way of interpreting numbers as social constructs would be as parts of such conventions, which ultimately could be arbitrary. However, it has been argued that the proto-arithmetical origins of arithmetic (partly) determine its content, which means that arithmetical truths are (partly) based on evolutionarily developed cognitive architecture and not purely conventional (Pantsar 2021b).

e. Ordinal or Cardinal

Let us next consider whether knowledge of natural numbers is primarily ordinal or cardinal. In many languages, numeral symbols are connected to two numeral words, one cardinal (one, two, three, so on) and the other ordinal (first, second, third, so on). In the philosophy of mathematics, this is an old and much-discussed problem that traces back to Cantor (1883), who defined the cardinal numbers based on the ordinal numbers, which has been interpreted to imply the primariness of ordinals (Hallett 1988). Also, within set theory, ordinals are often seen as more fundamental, since the cardinal number of a set can be defined as the least ordinal number whose members can be put in a one-to-one correspondence with the members of the set (Assadian and Buijsman 2019, 565). Finally, in structuralist philosophy of mathematics, numbers are understood to be fundamentally places in the natural number structure. In Stewart Shapiro’s structuralist account, for example, natural numbers are explicitly defined in terms of their (ordinal) position in the natural number structure (Shapiro 1997, 72).

Are the cognitive foundations of arithmetic relevant to whether our knowledge of natural numbers is primarily ordinal or cardinal? If the OTS and the ANS are indeed integral cognitive systems relevant to acquiring number concepts, this is at least plausible. Both subitizing and estimating detect the cardinality of the observed collection of objects, and there is nothing to suggest that the order of the occupied object files in the OTS, for example, influences numerosity determination. Therefore, our first numerosity representations are likely cardinal in nature. This also receives direct empirical support. Studies show that children who do not possess numeral words cannot make ordinal judgments while they are able to make (some) cardinal judgments (Brannon and Van de Walle 2001). It could be that the ordinal understanding of numerosities is something that only emerges through numeral words and the ordered counting lists they comprise.

Stefan Buijsman (2019) has suggested that the acquisition of the first number concepts depends on understanding claims of the logical form “there exists exactly one F, which requires grasping the singular/plural distinction from syntactic clues. Since that distinction does not concern ordinality, this may likewise suggest that the first number concepts are cardinal in nature. Yet, Buijsman (2021) has also argued that acquisition of larger number concepts requires ordinal understanding, which fits well, for example, with the role of ordered counting lists in the bootstrapping process.

f. Empirically-Informed Epistemology of Arithmetic

To conclude our discussion of arithmetic, we evaluate the philosophical significance of the work presented above. This is important because there is a potential counterargument to it having any philosophical significance. Specifically, one can acknowledge that we conduct meaningful research on numerical cognition, yet insist, as Frege (1884) did, that such considerations are only about the context of discovery and not the philosophically important context of justification. From this perspective, arithmetical knowledge can be completely a priori and fit the rationalist paradigm; the empirical studies reviewed above merely concern developmental trajectories in acquiring the kind of conceptual and reasoning abilities required for arithmetical knowledge.

This potential counterargument should be taken seriously. After all, even within the kind of empirically-informed philosophy of arithmetic that this article presents, there are empirical dimensions that are not considered to be philosophically relevant. The fact that we need to have visual (or tactile) access to number symbols, for example, is generally not considered to make epistemology of arithmetic somehow empirical, even though it clearly connects arithmetical knowledge to sensory experience. The counterargument formulated above is essentially similar: what if most – perhaps even all – of the empirical data on numerical cognition is connected to arithmetical knowledge only within the context of discovery, and not relevant to the context of justification and the philosophically important characteristics of arithmetical knowledge?

This counterargument can be divided into two. First, one may agree that the empirical data on numerical cognition is epistemologically relevant but insist that there can be multiple routes to arithmetical knowledge; while people can acquire arithmetical knowledge based on proto-arithmetical abilities, this is not necessarily the case. According to this counterargument, there is no path-dependency or arithmetical knowledge that necessarily develops through proto-arithmetical abilities. Most advocates of empirically-informed philosophy of arithmetic accept this counterargument. They are not claiming that arithmetical knowledge could not be acquired, at least in principle, through an essentially different ontogenetic path. What they maintain is that arithmetical knowledge standardly develops based on (one or more) proto-arithmetical abilities. Given that proto-arithmetical abilities are universal, this ontogenetic path is available to anyone who has access to the kind of enculturation required to move from proto-arithmetical abilities to proper arithmetic. But it is not a necessary path: we cannot rule out that somebody learns arithmetic entirely based on principles of equinumerosity and logic, as described by Frege (see also (Linnebo 2018)).

The second form of the counterargument is more serious. According to it, the empirical data on numerical cognition is not epistemologically relevant at all. This is similar to the way Frege (1884) dismissed contemporary psychologist theories of arithmetic, though we should resist the temptation to speculate about what he would have thought of the kind of modern empirical research presented in this article. While this counterargument is rarely explicitly stated, it seems to be implicitly accepted by many philosophers of mathematics that the importance of empirical research is at least very limited, as demonstrated by the way the topic is ignored in most modern textbooks and encyclopaedia articles on the philosophy of mathematics (see, for example, Horsten 2023; Linnebo 2017).

While further work is needed to determine the epistemological consequences of empirical research on numerical cognition, some progress has already been made. Pantsar (2024a) has presented an epistemological account within which arithmetical knowledge is characterized as contextually a priori. According to this account, the experience of applying our proto-arithmetical abilities in ontogeny sets the context for developing arithmetical knowledge. While that context is thus constrained by our way of experiencing the world, within that context, arithmetical statements are thought to be knowable a priori. Therefore, arithmetical statements are neither refuted nor corroborated by observations. Distinguishing the account from that of Kitcher (1983), Pantsar does not claim that basic arithmetical truths (concerning finite natural numbers and their operations) are generalizations of operations in our environment. Instead, they are determined by our proto-arithmetical abilities. This also distinguishes the account from conventionalist views of mathematics. In his account, the reason for, say, 2 + 2 = 4 being an arithmetical truth is not that it is a firmly entrenched convention; instead, it is because our evolutionarily developed cognitive architecture—in this case the OTS—(partly) determines the domain of arithmetical truths.

3. Geometry

a. The Cognitive Foundations of Geometry

i. Proto-Geometrical Cognition

Historically, within the philosophy of mathematics, geometry has generally been seen in a similar light to arithmetic. In Ancient Greece, geometry was the paradigmatic field of mathematics and provided key content for Plato’s (The Republic) treatment of mathematics. Indeed, Euclid, who gathered the Ancient knowledge of arithmetic into his famous Elements (Euclid, 1956), treated arithmetic essentially as an extension of geometry, with numbers defined as lengths of line segments. Geometry and arithmetic are likewise treated similarly in the work of Kant (1787), for whom geometry is also a paradigmatic case of synthetic a priori knowledge. These philosophical views suggest the innateness of geometrical abilities. Recently, this suggestion has been supported by the psychologist Gallistel (1990), who takes both arithmetic and (Euclidean) geometry to be the result of innate cognitive mechanisms.

More recently still, though, nativist views concerning geometrical abilities have been contested. There have been philosophical accounts, like that of Ferreirós and García-Pérez (2020), that emphasize the cultural characteristics of Euclidean geometry. Yet philosophers have also pursued accounts, like the arithmetical ones discussed above, according to which geometry is based on proto-mathematical, evolutionarily developed, capacities. While the empirical research on proto-geometrical abilities has not been as extensive as that on proto-arithmetical abilities, there are important results that should be considered by philosophers. Potentially, these may provide at least a partial cognitive foundation for the ontogenetic, and perhaps also the phylogenetic and cultural development, of geometrical knowledge and skills. This kind of philosophical work has been discussed most extensively by Mateusz Hohol in his book Foundations of Geometric Cognition (Hohol 2019), but there are also articles focusing on similar approaches concerning the cognitive foundations of geometry (for example, Hohol & Miłkowski, 2019; Pantsar, 2022).

The state of the art in empirical research on proto-geometrical cognition is fundamentally similar to that on proto-arithmetical cognition: two proto-geometrical abilities have been identified in the literature. The first of these concerns shape recognition, the second concerns orientation. Similarly to the OTS and the ANS, it has been proposed that these two abilities are due to two different core cognitive systems (Spelke 2011). And just like in the case of arithmetic, both have been seen as forming (at least a partial) cognitive foundation for the development of geometry (Hohol 2019).

ii. Shape Recognition

Let us first focus on the ability to recognize geometric shapes, which Hohol (2019) calls object recognition (shape recognition is a more fitting term because it is not clear that all recognized shapes are treated cognitively as objects). For a long time, psychology was dominated by the views of Piaget (1960), according to which children are born with no conception of objects and consequently, no conception of shapes. This view started to be contested in the 1970s, as evidence of neonates recognizing geometrical shapes emerged (Schwartz, Day, and Cohen 1979). Since then, there have been various empirical reports of infants (Bomba and Siqueland 1983; Newcombe and Huttenlocher 2000), non-human animals (Spelke and Lee 2012), and members of isolated cultures (Dehaene et al. 2006) being sensitive to geometric shapes in their observations and behaviour. Importantly, these abilities are almost always reported in terms of Euclidean geometry. Véronique Izard and colleagues, for example, report that Munduruku adults and children show an “intuitive understanding [of] essential properties of Euclidean geometry” (p. 9782). This includes estimating the sum of internal angles to be roughly 180 degrees and there being one parallel line to any given line drawn through a given point. Izard and Elizabeth Spelke (2009) have also described the different developmental stages in children’s learning of shape recognition in Euclidean terms.

Is there an innate ability, or at least a tendency, toward recognising Euclidean geometric shapes? In addition to psychologists like Gallistel, some philosophers have supported strong nativist views of Euclidean representations (see, for example, Hatfield, 2003). However, as described by Izard and Spelke (2009), the shape recognition system does not have enough resources to fully represent Euclidean geometry. While preschool children can detect, for example, curved lines among straight lines, and right angles among different types of angles, there are many notions of Euclidean geometry that they are not sensitive to. These are typically higher-order properties, such as symmetry (Izard and Spelke 2009). Given the limitations of the preschoolers’ abilities, we need to ask whether it makes sense to call them geometrical in the first place. Mirroring the distinction between arithmetic and proto-arithmetic, it seems necessary to distinguish between proto-geometrical and properly geometrical abilities. This distinction takes proto-geometrical abilities to be evolutionarily developed and innate, while geometrical abilities are culturally developed. Unlike proto-geometrical abilities, proper geometrical abilities are not limited to specific characteristics of shapes.

This does not mean that geometrical ability requires knowledge of Euclidean geometry, or other axiomatic systems. Such a definition would classify most people as geometrically ignorant. While it is not possible to precisely define geometrical ability, we can characterize the difference between geometrical and proto-geometrical abilities. In terms of distinguishing between angles, for example, Izard and Spelke (2009) report preschool children as being able to distinguish a different angle regardless of whether it is presented among acute, straight, or obtuse angles. This kind of ability is far from geometrical knowledge that, for example, the angles of a triangle are equal to two right angles. This latter kind of systematic knowledge about shapes and ways to understand them through precise notions, such as the size of an angle, should be considered geometrical. Under this characterization, it does not make sense to talk about proto-geometrical cognition being “Euclidean”. Only properly geometrical abilities can be Euclidean or non-Euclidean, proto-geometrical abilities are too imprecise to be so classified.

The core cognitive system for shape recognition should therefore be understood as proto-geometrical, but what kind of system is it, and what is the evidence for it? One key experiment reported that infants react to changes in angle size rather than to changes in the orientation of an angle (Cohen and Younger 1984). In this experiment, which has since been replicated by others (Lindskog et al. 2019), 6-week-old and 14-week-old infants were habituated to simple two-dimensional forms consisting of two lines that formed an angle. In the test trials, the angle (which was either 45 or 135 degrees) remained the same, but its orientation was changed. The eye movements of the infants showed that six-week-olds dishabituated (indicated by longer looking times) to a change in orientation, suggesting that they were surprised by the changing orientation. However, the fourteen-week-olds dishabituated to the angle size and not the orientation. If the angle stayed the same, they were not surprised by the next form being presented, but as soon as the angle size changed, their looking times became longer.

Cohen and Younger (1984) concluded that there has to be a developmental shift between the ages of six and fourteen weeks during which the infants start to recognize the geometric property of two lines being at a certain angle. Similar tests have been run on older children and it has been established that, starting from at least four years of age, children can consistently pick out a deviant geometric form, such as a different angle, from a collection of forms (Izard and Spelke 2009). Such results strongly imply that that there is a core cognitive ability that enables shape recognition, and which develops with age without explicit understanding of geometry as a mathematical theory. This is also in line with data on members of the Amazonian Munduruku culture. Adults and children of at least four years of age have been reported to make similar shape discriminations as European and North American children (Izard et al. 2011). Hence there are good reasons to understand the core cognitive shape recognition ability as being proto-geometrical.

iii. Orientation

In addition to shape recognition, there are also extensive data on a proto-geometrical ability concerning orientation, which Hohol (2019) calls spatial navigation (orientation is a better term, given that spatial navigation also applies the shape recognition ability). In cognitive and comparative psychology, there is a long-standing idea that navigation in both humans and non-human animals is based on so-called “cognitive maps” (Tolman 1948). Cognitive maps are thought to be mental representations that animals form of new environments. In Tolman’s account, these representations are enduring, Euclidean, and independent of the location of the observer. Thus, the account can be seen as an early hypothesis suggesting a proto-geometrical orientation ability, even though under the present distinction between proto-geometrical and geometrical we should not call the representations Euclidean. Recently, these types of mental representations have been extensively criticized by the so-called radical enactivist philosophers (Hutto and Myin 2013), according to whom all representations are dependent on language. Among psychologists, though, the idea of cognitive maps has endured. Yet, according to the modern understanding, cognitive maps are not necessarily enduring, observer-free, or Euclidean (Spelke and Lee 2012). Instead, they can be momentary and tied to particular viewpoints, and contain “wormholes” that go against Euclidean characteristics (Rothman and Warren 2006; Wehner and Menzel 1990).

While the characteristics, and indeed the very existence, of cognitive maps is a topic of much debate, there is little doubt about the existence of the orientation ability with which they are connected in the literature. This ability is thought to represent distances and directions on large-scale surfaces and spaces. In one key early experiment reported by Ken Cheng (1986), rats were shown the location of buried food in a rectangular space. After being disoriented, they looked for the food almost equally at the right location and at the point rotated 180 degrees from it. This was remarkable, because the rectangular environment had distinct features in the corners, which the rat could have used to represent the space. It was only after training that rats started to use these features for navigation, suggesting that the orientation ability is the primary one used in spatial navigation. Similar behaviour has been reported for young children (Hermer and Spelke 1996; McGurk 1972), as well as  non-human animals like ants (Wystrach and Beugnon 2009).

Moreover, there is evidence that the proto-geometrical ability for orientation is based on abstract representations that animals can use in a multi-modal manner. In one experiment, it was reported that rats navigate according to the shape of a chamber even in the dark (Quirk, Muller, and Kubie 1990). In addition, the orientation ability appears to overrun other changes in the environment. It has been reported that rats’ navigation in a chamber remains unchanged even with radical changes in the texture, material, and colour of the chamber (Lever et al. 2002). In the brain, the orienting ability has been strongly associated with the hippocampus (O’Keefe and Burgess 1996). Interestingly, some studies suggest that the spatial structure is mirrored in the location of neurons firing in the hippocampus. Colin Lever and colleagues, for example, report an experiment in which rats repeatedly exposed to two differently shaped environments develop different hippocampal place-cell representations (Lever et al. 2002). This is explained by there being “grid cells” located in the entorhinal cortex, which is the interface between the hippocampus and the neocortex. The grid cells are thought to be “activated whenever the animal’s position coincides with any vertex of a regular grid of equilateral triangles spanning the surface of the environment” (Hafting et al. 2005, 801). Such studies should not be seen as suggesting that spatial representations are generally expected to be mirrored in neural coding, but they do raise interesting questions about the way proto-geometrical representations are implemented in the brain.  The connection between hippocampus and spatial representations could also explain interesting phenomena in humans, including data showing that London taxi drivers – who presumably need extensive cognitive maps for orientation – have significantly larger posterior hippocampal volume than control subjects (Maguire et al. 2000).

Spatial navigation in small children and non-human animals is not conducted exclusively with the orientation ability, though. In navigation, animals also use cues from so-called “landmark objects,” applying the proto-geometrical ability for shape recognition (Izard et al. 2011). Object representations based on shape recognition are thought to be different in three ways from spatial representations due to the orientation system (Spelke and Lee 2012, 2789). First, the shape representations fail to capture absolute lengths and distances between parts. Second, they are “sense-invariant,” that is, they do not capture the difference between a shape and its mirror image. Third, the shape representations capture relationships between lengths and angles that allow distinguishing between shapes. The cognitive map of grid cells is thought to be anchored also to landmarks, but it remains in their absence. This has been seen as evidence for the orientation ability being a distinct system from the shape recognition system (Hafting et al. 2005). Further support for this comes from there being distinct correlates both in neural (concerning brain areas) and cognitive (concerning learning strategies) terms for navigating based on landmarks (shape recognition) and extended surfaces (orientation), with data showing similar neural activity in rats and humans (Doeller, King, and Burgess 2008; Doeller and Burgess 2008; Spelke and Lee 2012).

b. The Development of Geometric Cognition

As in the case of arithmetic, the development of geometrical cognition needs to be divided into two questions, one concerning its ontogeny and the other its phylogeny and cultural history. Based on the kind of research summarized above, Hohol (2019) has argued that geometrical cognition has developed in a largely similar way to how arithmetical development was described in the enculturation account above. The two proto-geometrical core cognitive systems that we possess already in infancy and share with many non-human animals form a partial foundation of geometry, but the development of geometry would not be possible without human linguistic capacity, the ability to abstract, and the capacity to create and understand diagrams (Hohol 2019). Turning attention to these capacities—evidently exclusive to humans—it is apparent how they have shaped the development of geometry in phylogeny and cultural history, continuing to do so in ontogeny for every new generation.

It should be noted at this point that, just like in the case of arithmetic, the empirical literature on proto-geometrical cognition does not distinguish terminologically between proto-geometrical and geometrical abilities, or between proto-geometrical representations and geometrical abilities. Virtually all articles report the abilities of young children and non-human animals as concerning “geometry.” As in the case of the epistemology of arithmetic, the conflation of two very different types of abilities and representations can be damaging for developing a proper philosophical understanding of the nature of geometrical knowledge.

To understand just how important that difference is, we must consider both the ontogeny and the phylogeny and cultural history. In terms of ontogeny, it is clear that acquiring proper geometrical knowledge requires a considerable amount of education even in order to grasp general geometrical notions like line and angle. Furthermore, many additional years of education must typically be completed before one can reach an understanding of geometry in the formal mathematical sense of a system of axioms and proofs based on them. In terms of phylogeny and cultural history, the matter is likely to be no less complex. If we accept that geometrical knowledge is based (partly) on proto-geometrical abilities, we are faced with the enormous challenge of explaining how these simple abilities for shape recognition and orientation have developed into axiomatic systems of geometry. This has led philosophers to criticize the notion of Spelke and colleagues (2010) that Euclidean geometry is “natural geometry.” Ferreirós and García-Pérez (2020) have argued that the gap between proto-geometrical abilities and Euclidean geometry is so wide that the latter cannot be called “natural” in any relevant sense. Instead, it is the product of a long line of cultural development in which cognitive artifacts (such as the ruler and the compass) and external representations (such as pictures and diagrams) have played crucial roles.

Ferreirós and García-Pérez (2020, 194) formulate a three-level model of the emergence of geometrical knowledge. The first level is called visuo-spatial cognition, which includes what has here been called proto-geometrical cognition. The second level they call “proto-geometry” which, contrary to the use of this terminology in this article to refer to evolutionarily developed abilities, refers in their taxonomy to developing basic concepts like circles and squares. On this level, tools and external representations play a key role. Finally, on the third level we get actual geometry, which requires the systematic and specific development of the second level. While the conceptual distinctions made by Ferreirós and García-Pérez are partly different from the ones introduced in this article, their key content is compatible with the approach here. We should be careful not to confuse lower-level abilities with higher-level concepts. Terminology-wise, the most important consequence is that we cannot call the ability of ants and rats “geometry,” as is often done in the literature (for example, Wystrach and Beugnon 2009). But the philosophically more important point is that geometry is so far away from our evolutionarily developed cognitive abilities that any conception of Euclidean geometry as “natural” geometry is potentially problematic.

This is directly related to one key problem Ferreirós and García-Pérez see with the approach of Spelke and colleagues (2010), namely the way the latter describe Euclidean concepts as “extremely simple,” because “just five postulates, together with some axioms of logic, suffice to specify all the properties of points, lines, and forms” (Spelke, Lee, and Izard 2010, 2785). To challenge this idea, Ferreirós and García-Pérez (2020, 187) point out two ways in which Euclidean concepts are not as simple as they may seem. First, the logical foundation of a system of geometry must be much richer than that of Euclid’s five postulates (Manders 2008). Second, and more importantly for the present purposes, Euclidean geometry cannot be equated with modern formal Hilbert-type (Hilbert 1902) theories of geometry that focus on logical step-by-step proofs. Instead, Euclidean geometry is fundamentally based on proofs that use (lettered) diagrams (Manders 2008; Netz 1999). Hence, Ferreirós (2016) has argued that the Euclidean postulates cannot be considered similar to modern Hilbertian axioms. The upshot of this, Ferreirós and García-Pérez (2020, 188) argue, is that very different types of cognitive abilities are involved in the two ways of practicing geometry. While Hilbertian geometry can be seen as reasoning based on simple postulates, Euclidean geometry is possible only by means of artifacts (ruler and compass) that allow for the construction of lettered diagrams. Therefore, Euclidean concepts may not be so simple after all.

While this history of geometry is important to recognize, it does not imply that we cannot trace the development of Euclidean geometry from proto-geometrical abilities. Such an effort is made by Hohol (2019), who has identified embodiment, abstraction, and cognitive artifacts as key notions in explaining this development. Among others sources, he refers to the work of Lakoff and Núñez (2000) in explaining the process of abstraction. They describe the process of abstraction as creating metaphorical counterparts of embodied processes in our environment. In the case of arithmetic, for example, addition is seen as the metaphorical counterpart of putting collections of physical objects together (p. 55). Geometrical concepts can feasibly be seen as being based on this kind of abstraction: a line in geometry, for example, has no width so it corresponds to no physical object, but it can be seen as an abstract counterpart of physically drawn lines.

In his analysis of cognitive artifacts, Hohol (2019) focuses on diagrams and formulae. As argued by Netz (1999), the introduction of lettered diagrams was central to the development of Greek geometry and its deductive method. While agreeing with this, Hohol and Miłkowski emphasize also the general role of linguistic formulae as cognitive artifacts in the development of geometry (Hohol and Miłkowski 2019). It was only through these cognitive artifacts that ancient practitioners of geometry could communicate with each other and intersubjectively develop their knowledge.

Finally, the matter of non-Euclidean geometries should be discussed. While there are competing axiomatizations of arithmetic, their differences are not as fundamental as the difference between Euclidean and non-Euclidean geometries. In non-Euclidean geometries, the fifth postulate of Euclid (called the parallel postulate) is rejected. According to this postulate, for any line l and point a not on l, there is exactly one line through a that does not intersect l. In hyperbolic geometry, there are infinitely many such non-intersecting lines. In elliptic geometry, all lines through a intersect l.

From the perspective of cognitive foundations, how can we account for non-Euclidean geometries? This problem used to be mainly academic, but gained importance when Einstein used non-Euclidean Riemann geometry in his general theory of relativity. Currently, our best theory of macro-level physics applies a non-Euclidean geometry (even though the effects of general relativity tend to be detectable only in phenomena that are on a much larger scale than our everyday experiences). If, as argued by Spelke and others, our “natural” geometry is Euclidean, how is it possible that this natural geometry is not the geometry of the world, so to speak? Should this be seen as evidence against Euclidean geometry being natural in the sense of it being based on our basic cognitive architecture, that is, our proto-geometrical abilities? While such connections may be tempting to make, it is important to not read too much into proto-geometrical origins. First, we must remember that Euclidean geometry is a distant development from proto-geometrical origins, and, as such, it already contains a lot that is not present in our basic cognitive architecture. Non-Euclidean geometries may simply be a further step in culturally developing geometry. Second, it is possible that our basic proto-geometrical abilities are proto-Euclidean in the specific sense of agreeing with the intuitive content of the parallel axiom. The geometrical structure of the world, on the other hand, may be different from that intuitive content.

As in the case of arithmetic, it is important to note that this type of empirically-informed epistemology emerged over the last decades of the 20^th century. So far, quite little has been written explicitly about the connection between the foundations of geometrical cognition and the nature of geometrical knowledge. Indeed, even less has been written about geometrical knowledge than arithmetical knowledge. There are at least two reasons for this. First, the empirical data relevant to arithmetical cognition are currently stronger both in quantity and quality. Second, philosophers have been working for longer on the cognitive foundations of arithmetic. There is, however, no reason to believe that geometrical knowledge will not be given an empirically-informed epistemological treatment similar to that provided for arithmetical knowledge. In fact, many of the considerations relevant to arithmetic seem to be applicable, mutatis mutandis, to geometry. For example, the point made above about the path-dependency of arithmetical knowledge also applies to geometrical knowledge: while there is growing evidence that geometrical knowledge is at least partly based on evolutionarily developed proto-arithmetical abilities, that does not imply that this is the only ontogenetic or cultural historical trajectory leading to geometrical knowledge. It is at least in principle possible that geometrical knowledge can be acquired and developed independently of proto-geometrical abilities. Yet, there are good reasons to think that, standardly, children apply their proto-geometrical abilities in learning geometry. Exactly how this happens is a question that demands a lot more future work, and progress in this work will most likely make it increasingly philosophically relevant. It is to be expected that in coming years both fields will receive increasing attention from philosophers.

4. References and Further Reading

• Anderson, Michael. 2015. After Phrenology: Neural Reuse and the Interactive Brain. Cambridge, MA: MIT Press.
• Anderson, Michael. 2010. “Neural reuse: A fundamental organizational principle of the brain.” Behavioral and brain sciences 33 (4): 245–66.
• Assadian, Bahram, and Stefan Buijsman. 2019. “Are the Natural Numbers Fundamentally Ordinals?” Philosophy and Phenomenological Research 99 (3): 564–80. https://doi.org/10.1111/phpr.12499.
• Ayer, Alfred Jules. 1970. Language, Truth and Logic. Unabridged and Unaltered republ. of the 2. (1946) ed. New York, NY: Dover Publications.
• Barrocas, Roberta, Stephanie Roesch, Caterina Gawrilow, and Korbinian Moeller. 2020. “Putting a Finger on Numerical Development – Reviewing the Contributions of Kindergarten Finger Gnosis and Fine Motor Skills to Numerical Abilities.” Frontiers in Psychology 11:1012. https://doi.org/10.3389/fpsyg.2020.01012.
• Beck, Jacob. 2017. “Can Bootstrapping Explain Concept Learning?” Cognition 158: 110–21.
• Benacerraf, Paul. 1965. “What Numbers Could Not Be.” The Philosophical Review 74 (1): 47–73. https://doi.org/10.2307/2183530.
• Bender, Andrea, and Sieghard Beller. 2012. “Nature and Culture of Finger Counting: Diversity and Representational Effects of an Embodied Cognitive Tool.” Cognition 124 (2): 156–82. https://doi.org/10.1016/j.cognition.2012.05.005.
• Bomba, Paul C., and Einar R. Siqueland. 1983. “The Nature and Structure of Infant Form Categories.” Journal of Experimental Child Psychology 35 (2): 294–328. https://doi.org/10.1016/0022-0965(83)90085-1.
• Boyd, Robert and Peter J. Richerson. 1985. Culture and the Evolutionary Process. Chicago: University of Chicago Press.
• Boyd, Robert and Peter J. Richerson 2005. Not by Genes Alone. Chicago: University of Chicago Press.
• Brannon, Elizabeth M., and Gretchen A. Van de Walle. 2001. “The Development of Ordinal Numerical Competence in Young Children.” Cognitive Psychology 43 (1): 53–81. https://doi.org/10.1006/cogp.2001.0756.
• Buijsman, Stefan. 2019. “Learning the Natural Numbers as a Child.” Noûs 53 (1): 3–22.
• Buijsman, Stefan. 2021. “How Do We Semantically Individuate Natural Numbers?†.” Philosophia Mathematica 29 (2): 214–33. https://doi.org/10.1093/philmat/nkab001.
• Butterworth, Brian. 1999. What Counts: How Every Brain Is Hardwired for Math. New York: The Free Press.
• Cantor, Goerg. 1883. “Über unendliche, lineare Punktmannigfaltigkeiten, 5.” Mathematische Annalen 21: 545–86.
• Carey, Susan. 2004. “Bootstrapping & the Origin of Concepts.” Daedalus 133 (1): 59–68.
• Carey, Susan. 2009. The Origin of Concepts. Oxford: Oxford University Press.
• Carnap, Rudolf. 1937. The Logical Syntax of Language. Open Court Classics. Chicago, Ill: Open Court.
• Cheng, Ken. 1986. “A Purely Geometric Module in the Rat’s Spatial Representation.” Cognition 23 (2): 149–78. https://doi.org/10.1016/0010-0277(86)90041-7.
• Cheyette, Samuel J., and Steven T. Piantadosi. 2020. “A Unified Account of Numerosity Perception.” Nature Human Behaviour 4 (12): 1265–72. https://doi.org/10.1038/s41562-020-00946-0.
• Clark, Andy, and David Chalmers. 1998. “The Extended Mind.” Analysis 58 (1): 7–19.
• Clarke, Sam, and Jacob Beck. 2021. “The Number Sense Represents (Rational) Numbers.” Behavioral and Brain Sciences, April, 1–57. https://doi.org/10.1017/S0140525X21000571.
• Cohen, Leslie B., and Barbara A. Younger. 1984. “Infant Perception of Angular Relations.” Infant Behavior and Development 7: 37–47.
• Cole, Julian C. 2013. “Towards an Institutional Account of the Objectivity, Necessity, and Atemporality of Mathematics†.” Philosophia Mathematica 21 (1): 9–36. https://doi.org/10.1093/philmat/nks019.
• Cole, Julian C. 2015. “Social Construction, Mathematics, and the Collective Imposition of Function onto Reality.” Erkenntnis 80 (6): 1101–24. https://doi.org/10.1007/s10670-014-9708-8.
• Davidson, Kathryn, Kortney Eng, and David Barner. 2012. “Does Learning to Count Involve a Semantic Induction?” Cognition 123: 162–73.
• De Cruz, Helen and Johan De Smedt. 2010. “The Innateness Hypothesis and Mathematical Concepts.” Topoi 29 (1): 3–13.
• De Cruz, Helen. 2008. “An Extended Mind Perspective on Natural Number Representation.” Philosophical Psychology 21 (4): 475–90. https://doi.org/10.1080/09515080802285289.
• Decock, Lieven. 2008. “The Conceptual Basis of Numerical Abilities: One-to-One Correspondence Versus the Successor Relation.” Philosophical Psychology 21 (4): 459–73. https://doi.org/10.1080/09515080802285255.
• Dehaene, Stanislas. 1997. The Number Sense: How the Mind Creates Mathematics. 2nd ed. New York: Oxford University Press.
• Dehaene, Stanislas. 2009. Reading in the Brain: The New Science of How We Read. London: Penguin.
• Dehaene, Stanislas, Véronique Izard, Elizabeth Spelke, and Pierre Pica. 2008. “Log or Linear? Distinct Intuitions of the Number Scale in Western and Amazonian Indigene Cultures.” Science 320: 1217–20.
• Dehaene, Stanislas. 2011. The Number Sense: How the Mind Creates Mathematics, Revised and Updated Edition. Revised, Updated ed. edition. New York: Oxford University Press.
• Dehaene, Stanislas, Véronique Izard, Pierre Pica, and Elizabeth Spelke. 2006. “Core Knowledge of Geometry in an Amazonian Indigene Group.” Science 311 (5759): 381–84. https://doi.org/10.1126/science.1121739.
• DeLong, Caroline M., Stephanie Barbato, Taylor O’Leary, and K. Tyler Wilcox. 2017. “Small and Large Number Discrimination in Goldfish (Carassius Auratus) with Extensive Training.” Behavioural Processes, The Cognition of Fish, 141 (August):172–83. https://doi.org/10.1016/j.beproc.2016.11.011.
• Doeller, Christian F., and Neil Burgess. 2008. “Distinct Error-Correcting and Incidental Learning of Location Relative to Landmarks and Boundaries.” Proceedings of the National Academy of Sciences 105 (15): 5909–14. https://doi.org/10.1073/pnas.0711433105.
• Doeller, Christian F., John A. King, and Neil Burgess. 2008. “Parallel Striatal and Hippocampal Systems for Landmarks and Boundaries in Spatial Memory.” Proceedings of the National Academy of Sciences 105 (15): 5915–20. https://doi.org/10.1073/pnas.0801489105.
• Epps, Patience. 2006. “Growing a Numeral System: The Historical Development of Numerals in an Amazonian Language Family.” Diachronica 23 (2): 259–88. https://doi.org/10.1075/dia.23.2.03epp.
• Euclid. 1956. The Thirteen Books of Euclid’s Elements. Vol. 1: Introduction and Books I, II. Second edition revised with additions. Vol. 1. New York: Dover Publications.
• Everett, Caleb. 2017. Numbers and the Making of Us: Counting and the Course of Human Cultures. Harvard University Press.
• Everett, Caleb, and Keren Madora. 2012. “Quantity Recognition Among Speakers of an Anumeric Language.” Cognitive Science 36 (1): 130–41. https://doi.org/10.1111/j.1551-6709.2011.01209.x.
• Fabry, Regina E. 2018. “Betwixt and between: The Enculturated Predictive Processing Approach to Cognition.” Synthese 195 (6): 2483–2518.
• Fabry, Regina E. 2020. “The Cerebral, Extra-Cerebral Bodily, and Socio-Cultural Dimensions of Enculturated Arithmetical Cognition.” Synthese 197:3685–3720.
• Fabry, Regina E., and Markus Pantsar. 2021. “A Fresh Look at Research Strategies in Computational Cognitive Science: The Case of Enculturated Mathematical Problem Solving.” Synthese 198 (4): 3221–63. https://doi.org/10.1007/s11229-019-02276-9.
• Fechner, Gustav Theodor. 1948. “Elements of Psychophysics, 1860.” In Readings in the History of Psychology, 206–13. Century Psychology Series. East Norwalk, CT, US: Appleton-Century-Crofts. https://doi.org/10.1037/11304-026.
• Feferman, Solomon. 2009. “Conceptions of the Continuum.” Intellectica 51 (1): 169–89.
• Feigenson, Lisa, Stanislas Dehaene, and Elizabeth Spelke. 2004. “Core Systems of Number.” Trends in Cognitive Sciences 8 (7): 307–14.
• Ferreirós, José. 2016. Mathematical Knowledge and the Interplay of Practices. Princeton: Princeton.
• Ferreirós, José, and Manuel J. García-Pérez. 2020. “Beyond Natural Geometry: On the Nature of Proto-Geometry.” Philosophical Psychology 33 (2): 181–205.
• Frank, Michael C., Daniel L. Everett, Evelina Fedorenko, and Edward Gibson. 2008. “Number as a Cognitive Technology: Evidence from Pirahã Language and Cognition.” Cognition 108 (3): 819–24. https://doi.org/10.1016/j.cognition.2008.04.007.
• Frege, Gottlob. 1879. “Begriffsschift.” In From Frege to Gödel: A source book in mathematical logic, 1879-1931, edited by J. Heijenoort, 1–82. Harvard University Press.
• Frege, Gottlob. 1884. The Foundations of Arithmetic. Oxford: Basil Blackwell.
• Fuson, Karen C. 1987. Children’s Counting and Concepts of Number. New York: Springer.
• Fuson, Karen C., and Walter G. Secada. 1986. “Teaching Children to Add by Counting-On with One-Handed Finger Patterns.” Cognition and Instruction 3 (3): 229–60.
• Gallistel, Charles R. 1990. The Organization of Learning. Cambridge, Mass: Mit Pr.
• Gallistel, Charles R. 2017. “Numbers and Brains.” Learning & Behaviour 45 (4): 327–28.
• Gelman, Rochel and Charles R. Gallistel. 2004. “Language and the Origin of Numerical Concepts.” Science 306: 441–43.
• Goodman, Nelson. 1955. Fact, Fiction, and Forecast. Second. Harvard University Press.
• Gordon, Peter. 2004. “Numerical Cognition without Words: Evidence from Amazonia.” Science 306 (5695): 496–99.
• Hafting, Torkel, Marianne Fyhn, Sturla Molden, May-Britt Moser, and Edvard I. Moser. 2005. “Microstructure of a Spatial Map in the Entorhinal Cortex.” Nature 436 (7052): 801–6. https://doi.org/10.1038/nature03721.
• Hallett, Michael. 1988. Cantorian Set Theory and Limitation of Size. Oxford Logic Guides 10. Oxford [England] : New York: Clarendon Press ; Oxford University Press.
• Hatfield, Gary. 2003. The Natural and the Normative: Theories of Spatial Perception from Kant to Helmholtz. The MIT Press. https://doi.org/10.7551/mitpress/4852.001.0001.
• Henrich, Joseph. 2015. The Secret of Our Success: How Culture Is Driving Human Evolution, Domesticating Our Species, and Making Us Smarter. Princeton University Press.
• Hermer, Linda, and Elizabeth Spelke. 1996. “Modularity and Development: The Case of Spatial Reorientation.” Cognition 61 (3): 195–232. https://doi.org/10.1016/S0010-0277(96)00714-7.
• Heyes, Cecilia. 2018. Cognitive Gadgets: The Cultural Evolution of Thinking. Cambridge: Harvard University Press.
• Hilbert, David. 1902. The Foundations of Geometry. Open court publishing Company.
• Hohol, Mateusz. 2019. Foundations of Geometric Cognition. New York: Routledge.
• Hohol, Mateusz, and Marcin Miłkowski. 2019. “Cognitive Artifacts for Geometric Reasoning.” Foundations of Science 24 (4): 657–80. https://doi.org/10.1007/s10699-019-09603-w.
• Horsten, Leon. 2023. “Philosophy of Mathematics.” In The Stanford Encyclopedia of Philosophy, edited by Edward N. Zalta and Uri Nodelman, Winter 2023. Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/archives/win2023/entries/philosophy-mathematics/.
• Howard, Scarlett R., Aurore Avarguès-Weber, Jair E. Garcia, Andrew D. Greentree, and Adrian G. Dyer. 2019. “Numerical Cognition in Honeybees Enables Addition and Subtraction.” Science Advances 5 (2): eaav0961. https://doi.org/10.1126/sciadv.aav0961.
• Hutto, Daniel D. 2019. “Re-Doing the Math: Making Enactivism Add Up.” Philosophical Studies 176: 827–37.
• Hutto, Daniel D., and Erik Myin. 2013. Radicalizing Enactivism. Basic Minds without Content. Cambridge, MA: MIT Press.
• Hutto, Daniel D., and Erik Myin. 2017. Evolving enactivism. Basic minds meet content. Cambridge, MA: MIT Press.
• Hyde, Daniel C. 2011. “Two Systems of Non-Symbolic Numerical Cognition.” Frontiers in Human Neuroscience 5: 150.
• Ifrah, Georges. 1998. The Universal History of Numbers: From Prehistory to the Invention of the Computer. London: Harville Press.
• Izard, Véronique, Pierre Pica, Elizabeth S. Spelke, and Stanislas Dehaene. 2011. “Flexible Intuitions of Euclidean Geometry in an Amazonian Indigene Group.” Proceedings of the National Academy of Sciences 108 (24): 9782–87.
• Izard, Véronique, and Elizabeth S. Spelke. 2009. “Development of Sensitivity to Geometry in Visual Forms.” Human Evolution 23 (3): 213.
• Izard, Véronique, Pierre Pica, Stanislas Dehaene, Danielle Hinchey, and Elizabeth Spelke. 2011. “Geometry as a Universal Mental Construction.” In Space, Time and Number in the Brain, edited by Stanislas Dehaene and Elizabeth M. Brannon, 319–32. San Diego: Academic Press. https://doi.org/10.1016/B978-0-12-385948-8.00019-0.
• Johansen, Mikkel W., and Morten Misfeldt. 2020. “Material Representations in Mathematical Research Practice.” Synthese 197 (9): 3721–41. https://doi.org/10.1007/s11229-018-02033-4.
• Jones, Max. 2020. “Numerals and Neural Reuse.” Synthese 197: 3657–81.
• Kant, Immanuel. 1787. Critique of Pure Reason. Cambridge University Press.
• Kaufman, Edna L., Miles W. Lord, Thomas W. Reese, and John Volkmann. 1949. “The Discrimination of Visual Number.” The American Journal of Psychology 62: 498–525. https://doi.org/10.2307/1418556.
• Kitcher, Philip. 1983. The Nature of Mathematical Knowledge. New York: Oxford University Press.
• Knops, Andre. 2020. Numerical Cognition. The Basics. New York: Routledge.
• Kripke, Saul A. 1982. Wittgenstein on Rules and Private Language: An Elementary Exposition. Harvard University Press.
• Lakoff, George, and Rafael Núñez. 2000. Where Mathematics Comes From. New York: Basic Books.
• Lee, Michael D., and Barbara W. Sarnecka. 2010. “A Model of Knower‐level Behavior in Number Concept Development.” Cognitive Science 34 (1): 51–67.
• Lee, Michael D., and Barbara W. Sarnecka. 2011. “Number-Knower Levels in Young Children: Insights from Bayesian Modeling.” Cognition 120 (3): 391–402.
• Lever, Colin, Tom Wills, Francesca Cacucci, Neil Burgess, and John O’Keefe. 2002. “Long-Term Plasticity in Hippocampal Place-Cell Representation of Environmental Geometry.” Nature 416 (6876): 90.
• Lindskog, Marcus, Maria Rogell, Gustaf Gredebäck and Ben Kenward. 2019. “Discrimination of Small Forms in a Deviant-Detection Paradigm by 10-Month-Old Infants.” Frontiers in Psychology 10: 1032.
• Linnebo, Øystein. 2017. Philosophy of Mathematics. Princeton: Princeton Unviesrity Press.
• Linnebo, Øystein. 2018. Thin Objects. Oxford: Oxford University Press.
• Maddy, Penelope. 1990. Realism in Mathematics. Oxford: Oxford University Press.
• Maguire, Eleanor A., David G. Gadian, Ingrid S. Johnsrude, Catriona D. Good, John Ashburner, Richard S. J. Frackowiak, and Christopher D. Frith. 2000. “Navigation-Related Structural Change in the Hippocampi of Taxi Drivers.” Proceedings of the National Academy of Sciences 97 (8): 4398–4403. https://doi.org/10.1073/pnas.070039597.
• Malafouris, Lambros. 2013. How Things Shape the Mind: A Theory of Material Engagement. Cambridge, MA, USA: MIT Press.
• Manders, Kenneth. 2008. “The Euclidean Diagram.” In The Philosophy of Mathematical Practice, edited by P. Mancosu, 80–133. Oxford: Oxford University Press.
• Margolis, Eric and Stephen Laurence. 2008. “How to Learn the Natural Numbers: Inductive Inference and the Acquisition of Number Concepts.” Cognition 106: 924–39.
• McGurk, Harry. 1972. “Infant Discrimination of Orientation.” Journal of Experimental Child Psychology 14 (1): 151–64. https://doi.org/10.1016/0022-0965(72)90040-9.
• Menary, Richard. 2015. Mathematical Cognition: A Case of Enculturation. Frankfurt am Main: Open MIND, MIND Group.
• Merzbach, Uta C., and Carl B. Boyer. 2011. A History of Mathematics. 3rd ed. Hoboken, N.J: John Wiley.
• Mill, John Stuart. 1843. “A System of Logic.” In Collected Works of John Stuart Mill, edited by J.M. Robson. Vol. vols. 7 & 8. Toronto: University of Toronto Press.
• Miller, Kevin F., Catherine M. Smith, Jianjun Zhu, and Houcan Zhang. 1995. “Preschool Origins of Cross-National Differences in Mathematical Competence: The Role of Number-Naming Systems.” Psychological Science 6 (1): 56–60.
• Netz, Reviel. 1999. The Shaping of Deduction in Greek Mathematics. Cambridge, UK: Cambridge University Press.
• Newcombe, Nora S., and Janellen Huttenlocher. 2000. Making Space: The Development of Spatial Representation and Reasoning. 1st edition. Cambridge, Mass: Bradford Books.
• Nieder, A., and S. Dehaene. 2009. “Representation of Number in the Brain.” Annual Review of Neuroscience 32:185–208.
• Nieder, Andreas. 2019. A Brain for Numbers: The Biology of the Number Instinct. Illustrated edition. Cambridge, Massachusetts: The MIT Press.
• Nissen, Hans J., Peter Damerow, and Robert K. Englund. 1994. Archaic Bookkeeping: Early Writing and Techniques of Economic Administration in the Ancient Near East. Translated by Paul Larsen. 1st edition. Chicago, Ill: University of Chicago Press.
• Noël, Marie-Pascale. 2005. “Finger Gnosia: A Predictor of Numerical Abilities in Children?” Child Neuropsychology 11 (5): 413–30. https://doi.org/10.1080/09297040590951550.
• Noles, Nicholaus S., Brian J. Scholl, and Stephen R. Mitroff. 2005. “The Persistence of Object File Representations.” Perception & Psychophysics 67 (2): 324–34. https://doi.org/10.3758/BF03206495.
• Núñez, Rafael E. 2017. “Is There Really an Evolved Capacity for Number?” Trends in Cognitive Science 21:409–24.
• O’Keefe, John, and Neil Burgess. 1996. “Geometric Determinants of the Place Fields of Hippocampal Neurons.” Nature 381 (6581): 425–28. https://doi.org/10.1038/381425a0.
• Overmann, Karenleigh A. 2018. “Constructing a Concept of Number.” Journal of Numerical Cognition 4 (2).
• Overmann, Karenleigh A. 2023. The Materiality of Numbers: Emergence and Elaboration from Prehistory to Present. Cambridge ; New York, NY: Cambridge University Press.
• Pantsar, Markus and Catarina Dutilh Novaes. 2020. “Synthese Special Issue: Mathematical Cognition and Enculturation.” Synthese 197. https://doi.org/10.1007/s11229-019-02478-1.
• Pantsar, Markus. 2014. “An Empirically Feasible Approach to the Epistemology of Arithmetic.” Synthese 191 (17): 4201–29. https://doi.org/10.1007/s11229-014-0526-y.
• Pantsar, Markus. 2018. “Early Numerical Cognition and Mathematical Processes.” THEORIA. Revista de Teoría, Historia y Fundamentos de La Ciencia 33 (2): 285–304.
• Pantsar, Markus. 2019. “The Enculturated Move from Proto-Arithmetic to Arithmetic.” Frontiers in Psychology 10:1454.
• Pantsar, Markus. 2020. “Mathematical Cognition and Enculturation: Introduction to the Synthese Special Issue.” Synthese 197 (9): 3647–55. https://doi.org/10.1007/s11229-019-02478-1.
• Pantsar, Markus. 2021a. “Bootstrapping of Integer Concepts: The Stronger Deviant-Interpretation Challenge.” Synthese 199 (3–4): 5791–5814. https://doi.org/10.1007/s11229-021-03046-2.
• Pantsar, Markus. 2021b. “Objectivity in Mathematics, Without Mathematical Objects†.” Philosophia Mathematica 29 (3): 318–52. https://doi.org/10.1093/philmat/nkab010.
• Pantsar, Markus. 2022. “On the Development of Geometric Cognition: Beyond Nature vs. Nurture.” Philosophical Psychology 35 (4): 595–616. https://doi.org/10.1080/09515089.2021.2014441.
• Pantsar, Markus. 2024a. Numerical Cognition and the Epistemology of Arithmetic. Cambridge University Press.
• Pantsar, Markus. 2024b. “Why Do Numbers Exist? A Psychologist Constructivist Account.” Inquiry 0 (0): 1–33. https://doi.org/10.1080/0020174X.2024.2305386.
• Peano, Giuseppe. 1889. “The Principles of Arithmetic, Presented by a New Method.” In Selected Works of Giuseppe Peano, edited by H. Kennedy, 101–34. Toronto; Buffalo: University of Toronto Press.
• Pelland, Jean-Charles. 2018. “Which Came First, the Number or the Numeral?” In Naturalizing Logico-Mathematical Knowledge: Approaches from Philosophy, Psychology and Cognitive Science, edited by S. Bangu, 179–94. New York and London: Routledge.
• Penner-Wilger, Marcie, and Michael L. Anderson. 2013. “The Relation between Finger Gnosis and Mathematical Ability: Why Redeployment of Neural Circuits Best Explains the Finding.” Frontiers in Psychology 4 (December):877. https://doi.org/10.3389/fpsyg.2013.00877.
• Piaget, Jean. 1960. Childs Concept Of Geometry. Basic Books.
• Piaget, Jean. 1965. Child’s Conception Of Number. Copyright 1965 edition. Princeton, N.J.: W. W. Norton & Company.
• Pica, Pierre, Cathy Lemer, Véronique Izard, and Stanislas Dehaene. 2004. “Exact and Approximate Arithmetic in an Amazonian Indigene Group.” Science 306 (5695): 499–503.
• Plato. 1992. The Republic. Translated by G.M.A Grube. Second. Indianapolis: Hackett Publishing Company. Putnam.
• Quinon, Paula. 2021. “Cognitive Structuralism: Explaining the Regularity of the Natural Numbers Progression.” Review of Philosophy and Psychology. Springer. https://link.springer.com/article/10.1007/s13164-021-00524-x.
• Quirk, Gregory J., Robert U. Muller, and John L. Kubie. 1990. “The Firing of Hippocampal Place Cells in the Dark Depends on the Rat’s Recent Experience.” Journal of Neuroscience 10 (6): 2008–17.
• Rips, Lance J., Amber Bloomfield, and Jennifer Asmuth. 2008. “From Numerical Concepts to Concepts of Number.” Behavioral and Brain Sciences 31 (6): 623–42. https://doi.org/10.1017/S0140525X08005566.
• Rips, Lance J., Jennifer Asmuth, and Amber Bloomfield. 2006. “Giving the Boot to the Bootstrap: How Not to Learn the Natural Numbers.” Cognition 101 (3): 51–60.
• Rothman, Daniel B., and William H. Warren. 2006. “Wormholes in Virtual Reality and the Geometry of Cognitive Maps.” Journal of Vision 6 (6): 143. https://doi.org/10.1167/6.6.143.
• Rugani, Rosa, Laura Fontanari, Eleonora Simoni, Lucia Regolin, and Giorgio Vallortigara. 2009. “Arithmetic in Newborn Chicks.” Proceedings of the Royal Society B: Biological Sciences 276 (1666): 2451–60.
• dos Santos, César Frederico. 2021. “Enculturation and the Historical Origins of Number Words and Concepts.” Synthese, June. https://doi.org/10.1007/s11229-021-03202-8.
• Schlimm, Dirk. 2018. “Numbers Through Numerals: The Constitutive Role of External Representations.” In Naturalizing Logico-Mathematical Knowledge. Routledge.
• Schlimm, Dirk 2021. “How Can Numerals Be Iconic? More Varieties of Iconicity.” In Diagrammatic Representation and Inference, edited by Amrita Basu, Gem Stapleton, Sven Linker, Catherine Legg, Emmanuel Manalo, and Petrucio Viana, 520–28. Lecture Notes in Computer Science. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-030-86062-2_53.
• Schmandt-Besserat, Denise. 1996. How Writing Came About. University of Texas Press.
• Schwartz, Marcelle, R. H. Day, and Leslie B. Cohen. 1979. “Visual Shape Perception in Early Infancy.” Monographs of the Society for Research in Child Development 44 (7): 1–63. https://doi.org/10.2307/1165963.
• Shapiro, Stewart. 1997. Philosophy of Mathematics: Structure and Ontology. New York: Oxford University Press.
• Spelke, Elizabeth, Sang Ah Lee, and Véronique Izard. 2010. “Beyond Core Knowledge: Natural Geometry.” Cognitive Science 34 (5): 863–84. https://doi.org/10.1111/j.1551-6709.2010.01110.x.
• Spelke, Elizabeth S. 2000. “Core Knowledge.” American Psychologist 55 (11): 1233–43. https://doi.org/10.1037/0003-066X.55.11.1233.
• Spelke, Elizabeth S., and Sang Ah Lee. 2012. “Core Systems of Geometry in Animal Minds.” Philosophical Transactions of the Royal Society B: Biological Sciences 367 (1603): 2784–93. https://doi.org/10.1098/rstb.2012.0210.
• Spelke, Elizabeth S. 2011. “Natural Number and Natural Geometry.” In Space, Time and Number in the Brain, edited by S. Dehaene and E. Brannon, 287–317. London: Academic Press.
• Starkey, Prentice, and Robert G. Cooper. 1980. “Perception of Numbers by Human Infants.” Science 210 (4473): 1033–35.
• Tolman, Edward C. 1948. “Cognitive Maps in Rats and Men.” Psychological Review 55 (4): 189–208. https://doi.org/10.1037/h0061626.
• Tomasello, Michael. 1999. The Cultural Origins of Human Cognition. Cambridge, MA: Harvard University Press.
• Verdine, Brian N., Roberta Michnick Golinkoff, Kathryn Hirsh-Pasek, Nora S. Newcombe, Andrew T. Filipowicz, and Alicia Chang. 2014. “Deconstructing Building Blocks: Preschoolers’ Spatial Assembly Performance Relates to Early Mathematics Skills.” Child Development 85 (3): 1062–76. https://doi.org/10.1111/cdev.12165.
• Vold, Karina, and Dirk Schlimm. 2020. “Extended Mathematical Cognition: External Representations with Non-Derived Content.” Synthese 197 (9): 3757–77. https://doi.org/10.1007/s11229-019-02097-w.
• Walsh, Vincent. 2003. “A Theory of Magnitude: Common Cortical Metrics of Time, Space and Quantity.” Trends in Cognitive Sciences 7 (11): 483–88. https://doi.org/10.1016/j.tics.2003.09.002.
• Warren, Jared. 2020. Shadows of Syntax: Revitalizing Logical and Mathematical Conventionalism. New York, NY, United States of America: Oxford University Press.
• Wasner, Mirjam, Hans-Christoph Nuerk, Laura Martignon, Stephanie Roesch, and Korbinian Moeller. 2016. “Finger Gnosis Predicts a Unique but Small Part of Variance in Initial Arithmetic Performance.” Journal of Experimental Child Psychology 146:1–16.
• Wehner, Rüdiger, and Randolf Menzel. 1990. “Do Insects Have Cognitive Maps?” Annual Review of Neuroscience 13 (1): 403–14. https://doi.org/10.1146/annurev.ne.13.030190.002155.
• Wiese, Heike. 2007. “The Co-Evolution of Number Concepts and Counting Words.” Lingua 117: 758–72.
• Wittgenstein, Ludwig. 1978. Remarks on the Foundations of Mathematics. Translated by Georg Henrik von Wright. Rev. ed., 4. print. Cambridge, Mass.: MIT Press.
• Wynn, Karen. 1990. “Children’s Understanding of Counting.” Cognition 36 (2): 155–93.
• Wynn, Karen. 1992. “Addition and Subtraction by Human Infants.” Nature 358:749–51.
• Wystrach, Antoine and Guy Beugnon. 2009. “Ants Learn Geometry and Features.” Current Biology 19 (1): 61–66.
• Zahidi, Karim. 2021. “Radicalizing numerical cognition.” Synthese 198 (Suppl 1): 529–45.
• Zahidi, Karim and Erik Myin. 2018. “Making Sense of Numbers without a Number Sense.” In Naturalizing Logico Mathematical Knowledge : Approaches from Philosophy, Psychology and Cognitive Science, edited by S. Bangu, 218–33. London: Routledge.

 

Author Information

Markus Pantsar
Email: markus.pantsar@gmail.com
RWTH Aachen University
Germany