Propositional Logic
Propositional logic, also known as sentential logic and statement logic, is the branch of logic that studies ways of joining and/or modifying entire propositions, statements or sentences to form more complicated propositions, statements or sentences, as well as the logical relationships and properties that are derived from these methods of combining or altering statements. In propositional logic, the simplest statements are considered as indivisible units, and hence, propositional logic does not study those logical properties and relations that depend upon parts of statements that are not themselves statements on their own, such as the subject and predicate of a statement. The most thoroughly researched branch of propositional logic is classical truth-functional propositional logic, which studies logical operators and connectives that are used to produce complex statements whose truth-value depends entirely on the truth-values of the simpler statements making them up, and in which it is assumed that every statement is either true or false and not both. However, there are other forms of propositional logic in which other truth-values are considered, or in which there is consideration of connectives that are used to produce statements whose truth-values depend not simply on the truth-values of the parts, but additional things such as their necessity, possibility or relatedness to one another.
Table of Contents
- Introduction
- History
- The Language of Propositional Logic
- Syntax and Formation Rules of PL
- Truth Functions and Truth Tables
- Definability of the Operators and the Languages PL’ and PL”
- Tautologies, Logical Equivalence and Validity
- Deduction: Rules of Inference and Replacement
- Natural Deduction
- Rules of Inference
- Rules of Replacement
- Direct Deductions
- Conditional and Indirect Proofs
- Axiomatic Systems and the Propositional Calculus
- Meta-Theoretic Results for the Propositional Calculus
- Other Forms of Propositional Logic
- References and Further Reading
1. Introduction
A statement can be defined as a declarative sentence, or part of a sentence, that is capable of having a truth-value, such as being true or false. So, for example, the following are statements:
- George W. Bush is the 43rd President of the United States.
- Paris is the capital of France.
- Everyone born on Monday has purple hair.
Sometimes, a statement can contain one or more other statements as parts. Consider for example, the following statement:
- Either Ganymede is a moon of Jupiter or Ganymede is a moon of Saturn.
While the above compound sentence is itself a statement, because it is true, the two parts, “Ganymede is a moon of Jupiter” and “Ganymede is a moon of Saturn”, are themselves statements, because the first is true and the second is false.
The term proposition is sometimes used synonymously with statement. However, it is sometimes used to name something abstract that two different statements with the same meaning are both said to “express”. In this usage, the English sentence, “It is raining”, and the French sentence “Il pleut”, would be considered to express the same proposition; similarly, the two English sentences, “Callisto orbits Jupiter” and “Jupiter is orbited by Callisto” would also be considered to express the same proposition. However, the nature or existence of propositions as abstract meanings is still a matter of philosophical controversy, and for the purposes of this article, the phrases “statement” and “proposition” are used interchangeably.
Propositional logic, also known as sentential logic, is that branch of logic that studies ways of combining or altering statements or propositions to form more complicated statements or propositions. Joining two simpler propositions with the word “and” is one common way of combining statements. When two statements are joined together with “and”, the complex statement formed by them is true if and only if both the component statements are true. Because of this, an argument of the following form is logically valid:
Paris is the capital of France and Paris has a population of over two million.
Therefore, Paris has a population of over two million.
Propositional logic largely involves studying logical connectives such as the words “and” and “or” and the rules determining the truth-values of the propositions they are used to join, as well as what these rules mean for the validity of arguments, and such logical relationships between statements as being consistent or inconsistent with one another, as well as logical properties of propositions, such as being tautologically true, being contingent, and being self-contradictory. (These notions are defined below.)
Propositional logic also studies way of modifying statements, such as the addition of the word “not” that is used to change an affirmative statement into a negative statement. Here, the fundamental logical principle involved is that if a given affirmative statement is true, the negation of that statement is false, and if a given affirmative statement is false, the negation of that statement is true.
What is distinctive about propositional logic as opposed to other (typically more complicated) branches of logic is that propositional logic does not deal with logical relationships and properties that involve the parts of a statement smaller than the simple statements making it up. Therefore, propositional logic does not study those logical characteristics of the propositions below in virtue of which they constitute a valid argument:
- George W. Bush is a president of the United States.
- George W. Bush is a son of a president of the United States.
- Therefore, there is someone who is both a president of the United States and a son of a president of the United States.
The recognition that the above argument is valid requires one to recognize that the subject in the first premise is the same as the subject in the second premise. However, in propositional logic, simple statements are considered as indivisible wholes, and those logical relationships and properties that involve parts of statements such as their subjects and predicates are not taken into consideration.
Propositional logic can be thought of as primarily the study of logical operators. A logical operator is any word or phrase used either to modify one statement to make a different statement, or join multiple statements together to form a more complicated statement. In English, words such as “and”, “or”, “not”, “if … then…”, “because”, and “necessarily”, are all operators.
A logical operator is said to be truth-functional if the truth-values (the truth or falsity, etc.) of the statements it is used to construct always depend entirely on the truth or falsity of the statements from which they are constructed. The English words “and”, “or” and “not” are (at least arguably) truth-functional, because a compound statement joined together with the word “and” is true if both the statements so joined are true, and false if either or both are false, a compound statement joined together with the word “or” is true if at least one of the joined statements is true, and false if both joined statements are false, and the negation of a statement is true if and only if the statement negated is false.
Some logical operators are not truth-functional. One example of an operator in English that is not truth-functional is the word “necessarily”. Whether a statement formed using this operator is true or false does not depend entirely on the truth or falsity of the statement to which the operator is applied. For example, both of the following statements are true:
- 2 + 2 = 4.
- Someone is reading an article in a philosophy encyclopedia.
However, let us now consider the corresponding statements modified with the operator “necessarily”:
- Necessarily, 2 + 2 = 4.
- Necessarily, someone is reading an article in a philosophy encyclopedia.
Here, the first example is true but the second example is false. Hence, the truth or falsity of a statement using the operator “necessarily” does not depend entirely on the truth or falsity of the statement modified.
Truth-functional propositional logic is that branch of propositional logic that limits itself to the study of truth-functional operators. Classical (or “bivalent”) truth-functional propositional logic is that branch of truth-functional propositional logic that assumes that there are are only two possible truth-values a statement (whether simple or complex) can have: (1) truth, and (2) falsity, and that every statement is either true or false but not both.
Classical truth-functional propositional logic is by far the most widely studied branch of propositional logic, and for this reason, most of the remainder of this article focuses exclusively on this area of logic. In addition to classical truth-functional propositional logic, there are other branches of propositional logic that study logical operators, such as “necessarily”, that are not truth-functional. There are also “non-classical” propositional logics in which such possibilities as (i) a proposition’s having a truth-value other than truth or falsity, (ii) a proposition’s having an indeterminate truth-value or lacking a truth-value altogether, and sometimes even (iii) a proposition’s being both true and false, are considered. (For more information on these alternative forms of propositional logic, consult Section VIII below.)
2. History
The serious study of logic as an independent discipline began with the work of Aristotle (384-322 BCE). Generally, however, Aristotle’s sophisticated writings on logic dealt with the logic of categories and quantifiers such as “all”, and “some”, which are not treated in propositional logic. However, in his metaphysical writings, Aristotle espoused two principles of great importance in propositional logic, which have since come to be called the Law of Excluded Middle and the Law of Contradiction. Interpreted in propositional logic, the first is the principle that every statement is either true or false, the second is the principle that no statement is both true and false. These are, of course, cornerstones of classical propositional logic. There is some evidence that Aristotle, or at least his successor at the Lyceum, Theophrastus (d. 287 BCE), did recognize a need for the development of a doctrine of “complex” or “hypothetical” propositions, that is, those involving conjunctions (statements joined by “and”), disjunctions (statements joined by “or”) and conditionals (statements joined by “if… then…”), but their investigations into this branch of logic seem to have been very minor.
More serious attempts to study statement operators such as “and”, “or” and “if… then…” were conducted by the Stoic philosophers in the late 3rd century BCE. Since most of their original works—if indeed, these writings were even produced—are lost, we cannot make many definite claims about exactly who first made investigations into what areas of propositional logic, but we do know from the writings of Sextus Empiricus that Diodorus Cronus and his pupil Philo had engaged in a protracted debate about whether the truth of a conditional statement depends entirely on it not being the case that its antecedent (if-clause) is true while its consequent (then-clause) is false, or whether it requires some sort of stronger connection between the antecedent and consequent—a debate that continues to have relevance for modern discussion of conditionals. The Stoic philosopher Chrysippus (roughly 280-205 BCE) perhaps did the most in advancing Stoic propositional logic, by marking out a number of different ways of forming complex premises for arguments, and for each, listing valid inference schemata. Chrysippus suggested that the following inference schemata are to be considered the most basic:
- If the first, then the second; but the first; therefore the second.
- If the first, then the second; but not the second; therefore, not the first.
- Not both the first and the second; but the first; therefore, not the second.
- Either the first or the second [and not both]; but the first; therefore, not the second.
- Either the first or the second; but not the second; therefore the first.
Inference rules such as the above correspond very closely to the basic principles in a contemporary system of natural deduction for propositional logic. For example, the first two rules correspond to the rules of modus ponens and modus tollens, respectively. These basic inference schemata were expanded upon by less basic inference schemata by Chrysippus himself and other Stoics, and are preserved in the work of Diogenes Laertius, Sextus Empiricus and later, in the work of Cicero.
Advances on the work of the Stoics were undertaken in small steps in the centuries that followed. This work was done by, for example, the second century logician Galen (roughly 129-210 CE), the sixth century philosopher Boethius (roughly 480-525 CE) and later by medieval thinkers such as Peter Abelard (1079-1142) and William of Ockham (1288-1347), and others. Much of their work involved producing better formalizations of the principles of Aristotle or Chrysippus, introducing improved terminology and furthering the discussion of the relationships between operators. Abelard, for example, seems to have been the first to clearly differentiate exclusive disjunction from inclusive disjunction (discussed below), and to suggest that inclusive disjunction is the more important notion for the development of a relatively simple logic of disjunctions.
The next major step forward in the development of propositional logic came only much later with the advent of symbolic logic in the work of logicians such as Augustus DeMorgan (1806-1871) and, especially, George Boole (1815-1864) in the mid-19th century. Boole was primarily interested in developing a mathematical-style “algebra” to replace Aristotelian syllogistic logic, primarily by employing the numeral “1” for the universal class, the numeral “0” for the empty class, the multiplication notation “xy” for the intersection of classes x and y, the addition notation “x + y” for the union of classes x and y, etc., so that statements of syllogistic logic could be treated in quasi-mathematical fashion as equations; for example, “No x is y” could be written as “xy = 0”. However, Boole noticed that if an equation such as “x = 1” is read as “x is true”, and “x = 0” is read as “x is false”, the rules given for his logic of classes can be transformed into a logic for propositions, with “x + y = 1” reinterpreted as saying that either x or y is true, and “xy = 1” reinterpreted as meaning that x and y are both true. Boole’s work sparked rapid interest in logic among mathematicians. Later, “Boolean algebras” were used to form the basis of the truth-functional propositional logics utilized in computer design and programming.
In the late 19th century, Gottlob Frege (1848-1925) presented logic as a branch of systematic inquiry more fundamental than mathematics or algebra, and presented the first modern axiomatic calculus for logic in his 1879 work Begriffsschrift. While it covered more than propositional logic, from Frege’s axiomatization it is possible to distill the first complete axiomatization of classical truth-functional propositional logic. Frege was also the first to systematically argue that all truth-functional connectives could be defined in terms of negation and the material conditional.
In the early 20th century, Bertrand Russell gave a different complete axiomatization of propositional logic, considered on its own, in his 1906 paper “The Theory of Implication”, and later, along with A. N. Whitehead, produced another axiomatization using disjunction and negation as primitives in the 1910 work Principia Mathematica. Proof of the possibility of defining all truth functional operators in virtue of a single binary operator was first published by American logician H. M. Sheffer in 1913, though American logician C. S. Peirce (1839-1914) seems to have discovered this decades earlier. In 1917, French logician Jean Nicod discovered that it was possible to axiomatize propositional logic using the Sheffer stroke and only a single axiom schema and single inference rule.
The notion of a “truth table” is often utilized in the discussion of truth-functional connectives (discussed below). It seems to have been at least implicit in the work of Peirce, W. S. Jevons (1835-1882), Lewis Carroll (1832-1898), John Venn (1834-1923), and Allan Marquand (1853-1924). Truth tables appear explicitly in writings by Eugen Müller as early as 1909. Their use gained rapid popularity in the early 1920s, perhaps due to the combined influence of the work of Emil Post, whose 1921 work makes liberal use of them, and Ludwig Wittgenstein’s 1921 Tractatus Logico-Philosophicus, in which truth tables and truth-functionality are prominently featured.
Systematic inquiry into axiomatic systems for propositional logic and related metatheory was conducted in the 1920s, 1930s and 1940s by David Hilbert, Paul Bernays, Alfred Tarski, Jan Łukasiewicz, Kurt Gödel, Alonzo Church, and others. It is during this period, that most of the important metatheoretic results such as those discussed in Section VII were discovered.
Complete natural deduction systems for classical truth-functional propositional logic were developed and popularized in the work of Gerhard Gentzen in the mid-1930s, and subsequently introduced into influential textbooks such as that of F. B. Fitch (1952) and Irving Copi (1953).
Modal propositional logics are the most widely studied form of non-truth-functional propositional logic. While interest in modal logic dates back to Aristotle, by contemporary standards the first systematic inquiry into this modal propositional logic can be found in the work of C. I. Lewis in 1912 and 1913. Among other well-known forms of non-truth-functional propositional logic, deontic logic began with the work of Ernst Mally in 1926, and epistemic logic was first treated systematically by Jaakko Hintikka in the early 1960s. The modern study of three-valued propositional logic began in the work of Jan Łukasiewicz in 1917, and other forms of non-classical propositional logic soon followed suit. Relevance propositional logic is relatively more recent; dating from the mid-1970s in the work of A. R. Anderson and N. D. Belnap. Paraconsistent logic, while having its roots in the work of Łukasiewicz and others, has blossomed into an independent area of research only recently, mainly due to work undertaken by N. C. A. da Costa, Graham Priest and others in the 1970s and 1980s.
3. The Language of Propositional Logic
The basic rules and principles of classical truth-functional propositional logic are, among contemporary logicians, almost entirely agreed upon, and capable of being stated in a definitive way. This is most easily done if we utilize a simplified logical language that deals only with simple statements considered as indivisible units as well as complex statements joined together by means of truth-functional connectives. We first consider a language called PL for “Propositional Logic”. Later we shall consider two even simpler languages, PL’ and PL”.
a. Syntax and Formation Rules of PL
In any ordinary language, a statement would never consist of a single word, but would always at the very least consist of a noun or pronoun along with a verb. However, because propositional logic does not consider smaller parts of statements, and treats simple statements as indivisible wholes, the language PL uses uppercase letters ‘A‘, ‘B‘, ‘C‘, etc., in place of complete statements. The logical signs ‘\land‘, ‘\lor‘, ‘→’, ‘↔’, and ‘\neg‘ are used in place of the truth-functional operators, “and”, “or”, “if… then…”, “if and only if”, and “not”, respectively. So, consider again the following example argument, mentioned in Section I.
Paris is the capital of France and Paris has a population of over two million.
Therefore, Paris has a population of over two million.
If we use the letter ‘C‘ as our translation of the statement “Paris is the captial of France” in PL, and the letter ‘P‘ as our translation of the statement “Paris has a population of over two million”, and use a horizontal line to separate the premise(s) of an argument from the conclusion, the above argument could be symbolized in language PL as follows:
\(<br />
\begin{array}{l} C \land P\\<br />
\hline P<br />
\end{array}<br />
\)
In addition to statement letters like ‘C‘ and ‘P‘ and the operators, the only other signs that sometimes appear in the language PL are parentheses which are used in forming even more complex statements. Consider the English compound sentence, “Paris is the most important city in France if and only if Paris is the capital of France and Paris has a population of over two million.” If we use the letter ‘I‘ in language PL to mean that Paris is the most important city in France, this sentence would be translated into PL as follows:
I \leftrightarrow (C \land P)
The parentheses are used to group together the statements ‘C‘ and ‘P‘ and differentiate the above statement from the one that would be written as follows:
(I \leftrightarrow C) \land P
This latter statement asserts that Paris is the most important city in France if and only if it is the capital of France, and (separate from this), Paris has a population of over two million. The difference between the two is subtle, but important logically.
It is important to describe the syntax and make-up of statements in the language PL in a precise manner, and give some definitions that will be used later on. Before doing this, it is worthwhile to make a distinction between the language in which we will be discussing PL, namely, English, from PL itself. Whenever one language is used to discuss another, the language in which the discussion takes place is called the metalanguage, and language under discussion is called the object language. In this context, the object language is the language PL, and the metalanguage is English, or to be more precise, English supplemented with certain special devices that are used to talk about language PL. It is possible in English to talk about words and sentences in other languages, and when we do, we place the words or sentences we wish to talk about in quotation marks. Therefore, using ordinary English, I can say that “parler” is a French verb, and “I \land C” is a statement of PL. The following expression is part of PL, not English:
(I \leftrightarrow C) \land P
However, the following expression is a part of English; in particular, it is the English name of a PL sentence:
“(I \leftrightarrow C) \land P”
This point may seem rather trivial, but it is easy to become confused if one is not careful.
In our metalanguage, we shall also be using certain variables that are used to stand for arbitrary expressions built from the basic symbols of PL. In what follows, the Greek letters ‘\alpha‘, ‘\beta‘, and so on, are used for any object language (PL) expression of a certain designated form. For example, later on, we shall say that, if \alpha is a statement of PL, then so is \ulcorner \neg \alpha \urcorner. Notice that ‘\alpha‘ itself is not a symbol that appears in PL; it is a symbol used in English to speak about symbols of PL. We will also be making use of so-called “Quine corners”, written ‘\ulcorner‘ and ‘\urcorner‘, which are a special metalinguistic device used to speak about object language expressions constructed in a certain way. Suppose \alpha is the statement “(I \leftrightarrow C)” and \beta is the statement “(P \land C)“; then \ulcorner \alpha \lor \beta \urcorner is the complex statement “(I \leftrightarrow C) \lor (P \land C)“.
Let us now proceed to giving certain definitions used in the metalanguage when speaking of the language PL.
Definition: A statement letter of PL is defined as any uppercase letter written with or without a numerical subscript.
Note: According to this definition, ‘A‘, ‘B‘, ‘B_2‘, ‘C_3‘, and ‘P_{14}‘ are examples of statement letters. The numerical subscripts are used just in case we need to deal with more than 26 simple statements: in that case, we can use ‘P_1‘ to mean something different than ‘P_2‘, and so forth.
Definition: A connective or operator of PL is any of the signs ‘\neg‘, ‘\land‘, ‘\lor‘, ‘→’, and ‘↔’.
Definition: A well-formed formula (hereafter abbreviated as wff) of PL is defined recursively as follows:
- Any statement letter is a well-formed formula.
- If \alpha is a well-formed formula, then so is \ulcorner \neg \alpha \urcorner.
- If \alpha and \beta are well-formed formulas, then so is \ulcorner (\alpha \land \beta) \urcorner.
- If \alpha and \beta are well-formed formulas, then so is \ulcorner (\alpha \lor \beta) \urcorner.
- If \alpha and \beta are well-formed formulas, then so is \ulcorner (\alpha \rightarrow \beta) \urcorner.
- If \alpha and \beta are well-formed formulas, then so is \ulcorner (\alpha \leftrightarrow \beta) \urcorner.
- Nothing that cannot be constructed by successive steps of (1)-(6) is a well-formed formula.
Note: According to part (1) of this definition, the statement letters ‘C‘, ‘P‘ and ‘M‘ are wffs. Because ‘C‘ and ‘P‘ are wffs, by part (3), “(C \land P)” is a wff. Because it is a wff, and ‘M‘ is also a wff, by part (6), “(M \leftrightarrow (C \land P))” is a wff. It is conventional to regard the outermost parentheses on a wff as optional, so that “M \leftrightarrow (C \land P)” is treated as an abbreviated form of “(M \leftrightarrow (C \land P))“. However, whenever a shorter wff is used in constructing a more complicated wff, the parentheses on the shorter wff are necessary.
The notion of a well-formed formula should be understood as corresponding to the notion of a grammatically correct or properly constructed statement of language PL. This definition tells us, for example, that “\neg (Q \lor \neg R)” is grammatical for PL because it is a well-formed formula, whereas the string of symbols, “\neg Q \neg \lor ( \leftrightarrow P \land“, while consisting entirely of symbols used in PL, is not grammatical because it is not well-formed.
b. Truth Functions and Truth Tables
So far we have in effect described the grammar of language PL. When setting up a language fully, however, it is necessary not only to establish rules of grammar, but also describe the meanings of the symbols used in the language. We have already suggested that uppercase letters are used as complete simple statements. Because truth-functional propositional logic does not analyze the parts of simple statements, and only considers those ways of combining them to form more complicated statements that make the truth or falsity of the whole dependent entirely on the truth or falsity of the parts, in effect, it does not matter what meaning we assign to the individual statement letters like ‘P‘, ‘Q‘ and ‘R‘, etc., provided that each is taken as either true or false (and not both).
However, more must be said about the meaning or semantics, of the logical operators ‘\land‘, ‘\lor‘, ‘→’, ‘↔’, and ‘\neg‘. As mentioned above, these are used in place of the English words, ‘and’, ‘or’, ‘if… then…’, ‘if and only if’, and ‘not’, respectively. However, the correspondence is really only rough, because the operators of PL are considered to be entirely truth-functional, whereas their English counterparts are not always used truth-functionally. Consider, for example, the following statements:
- If Bob Dole is president of the United States in 2004, then the president of the United States in 2004 is a member of the Republican party.
- If Al Gore is president of the United States in 2004, then the president of the United States in 2004 is a member of the Republican party.
For those familiar with American politics, it is tempting to regard the English sentence (1) as true, but to regard (2) as false, since Dole is a Republican but Gore is not. But notice that in both cases, the simple statement in the “if” part of the “if… then…” statement is false, and the simple statement in the “then” part of the statement is true. This shows that the English operator “if… then…” is not fully truth-functional. However, all the operators of language PL are entirely truth-functional, so the sign ‘→’, though similar in many ways to the English “if… then…” is not in all ways the same. More is said about this operator below.
Since our study is limited to the ways in which the truth-values of complex statements depend on the truth-values of the parts, for each operator, the only aspect of its meaning relevant in this context is its associated truth-function. The truth-function for an operator can be represented as a table, each line of which expresses a possible combination of truth-values for the simpler statements to which the operator applies, along with the resulting truth-value for the complex statement formed using the operator.
The signs ‘\land‘, ‘\lor‘, ‘→’, ‘↔’, and ‘\neg‘, correspond, respectively, to the truth-functions of conjunction, disjunction, material implication, material equivalence, and negation. We shall consider these individually.
Conjunction: The conjunction of two statements \alpha and \beta, written in PL as \ulcorner (\alpha \land \beta) \urcorner, is true if both \alpha and \beta are true, and is false if either \alpha is false or \beta is false or both are false. In effect, the meaning of the operator ‘\land‘ can be displayed according to the following chart, which shows the truth-value of the conjunction depending on the four possibilities of the truth-values of the parts:
| \alpha |
\beta |
(\alpha \land \beta) |
|
T
T
F
F
|
T
F
T
F
|
T
F
F
F
|
Conjunction using the operator ‘\land‘ is language PL’s rough equivalent of joining statements together with ‘and’ in English. In a statement of the form \ulcorner (\alpha \land \beta) \urcorner, the two statements joined together, \alpha and \beta, are called the conjuncts, and the whole statement is called a conjunction.
Instead of the sign ‘\land‘, some other logical works use the signs ‘\&‘ or ‘\bullet‘ for conjunction.
Disjunction: The disjunction of two statements \alpha and \beta, written in PL as \ulcorner (\alpha \lor \beta) \urcorner, is true if either \alpha is true or \beta is true, or both \alpha and \beta are true, and is false only if both \alpha and \beta are false. A chart similar to that given above for conjunction, modified for to show the meaning of the disjunction sign ‘\lor‘ instead, would be drawn as follows:
| \alpha |
\beta |
(\alpha \lor \beta) |
|
T
T
F
F
|
T
F
T
F
|
T
T
T
F
|
This is language PL’s rough equivalent of joining statements together with the word ‘or’ in English. However, it should be noted that the sign ‘\lor‘ is used for disjunction in the inclusive sense. Sometimes when the word ‘or’ is used to join together two English statements, we only regard the whole as true if one side or the other is true, but not both, as when the statement “Either we can buy the toy robot, or we can buy the toy truck; you must choose!” is spoken by a parent to a child who wants both toys. This is called the exclusive sense of ‘or’. However, in PL, the sign ‘\lor‘ is used inclusively, and is more analogous to the English word ‘or’ as it appears in a statement such as (for example, said about someone who has just received a perfect score on the SAT), “either she studied hard, or she is extremely bright”, which does not mean to rule out the possibility that she both studied hard and is bright. In a statement of the form \ulcorner (\alpha \lor \beta) \urcorner, the two statements joined together, \alpha and \beta, are called the disjuncts, and the whole statement is called a disjunction.
Material Implication: This truth-function is represented in language PL with the sign ‘→’. A statement of the form \ulcorner (\alpha \rightarrow \beta) \urcorner, is false if \alpha is true and \beta is false, and is true if either \alpha is false or \beta is true (or both). This truth-function generates the following chart:
| \alpha |
\beta |
(\alpha \rightarrow \beta) |
|
T
T
F
F
|
T
F
T
F
|
T
F
T
T
|
Because the truth of a statement of the form \ulcorner (\alpha \rightarrow \beta) \urcorner rules out the possibility of \alpha being true and \beta being false, there is some similarity between the operator ‘→’ and the English phrase, “if… then…”, which is also used to rule out the possibility of one statement being true and another false; however, ‘→’ is used entirely truth-functionally, and so, for reasons discussed earlier, it is not entirely analogous with “if… then…” in English. If \alpha is false, then \ulcorner (\alpha \rightarrow \beta) \urcorner is regarded as true, whether or not there is any connection between the falsity of \alpha and the truth-value of \beta. In a statement of the form \ulcorner (\alpha \rightarrow \beta) \urcorner, we call \alpha the antecedent, and we call \beta the consequent, and the whole statement \ulcorner (\alpha \rightarrow \beta) \urcorner is sometimes also called a (material) conditional.
The sign ‘\supset‘ is sometimes used instead of ‘→’ for material implication.
Material Equivalence: This truth-function is represented in language PL with the sign ‘↔’. A statement of the form \ulcorner (\alpha \leftrightarrow \beta) \urcorner is regarded as true if \alpha and \beta are either both true or both false, and is regarded as false if they have different truth-values. Hence, we have the following chart:
| \alpha |
\beta |
(\alpha \leftrightarrow \beta) |
|
T
T
F
F
|
T
F
T
F
|
T
F
F
T
|
Since the truth of a statement of the form \ulcorner (\alpha \leftrightarrow \beta) \urcorner requires \alpha and \beta to have the same truth-value, this operator is often likened to the English phrase “…if and only if…”. Again, however, they are not in all ways alike, because ‘↔’ is used entirely truth-functionally. Regardless of what \alpha and \beta are, and what relation (if any) they have to one another, if both are false, \ulcorner (\alpha \leftrightarrow \beta) \urcorner is considered to be true. However, we would not normally regard the statement “Al Gore is the President of the United States in 2004 if and only if Bob Dole is the President of the United States in 2004” as true simply because both simpler statements happen to be false. A statement of the form \ulcorner (\alpha \leftrightarrow \beta) \urcorner is also sometimes referred to as a (material) biconditional.
The sign ‘\equiv‘ is sometimes used instead of ‘↔’ for material equivalence.
Negation: The negation of statement \alpha, simply written \ulcorner \neg \alpha \urcorner in language PL, is regarded as true if \alpha is false, and false if \alpha is true. Unlike the other operators we have considered, negation is applied to a single statement. The corresponding chart can therefore be drawn more simply as follows:
| \alpha |
\neg \alpha |
T
F |
F
T |
The negation sign ‘\neg‘ bears obvious similarities to the word ‘not’ used in English, as well as similar phrases used to change a statement from affirmative to negative or vice-versa. In logical languages, the signs ‘\sim‘ or ‘-‘ are sometimes used in place of ‘\neg‘.
The five charts together provide the rules needed to determine the truth-value of a given wff in language PL when given the truth-values of the independent statement letters making it up. These rules are very easy to apply in the case of a very simple wff such as “(P \land Q)“. Suppose that ‘P‘ is true, and ‘Q‘ is false; according to the second row of the chart given for the operator, ‘\land‘, we can see that this statement is false.
However, the charts also provide the rules necessary for determining the truth-value of more complicated statements. We have just seen that “(P \land Q)” is false if ‘P‘ is true and ‘Q‘ is false. Consider a more complicated statement that contains this statement as a part, for example, “((P \land Q) \rightarrow \neg R)“, and suppose once again that ‘P‘ is true, and ‘Q‘ is false, and further suppose that ‘R‘ is also false. To determine the truth-value of this complicated statement, we begin by determining the truth-value of the internal parts. The statement “(P \land Q)“, as we have seen, is false. The other substatement, “\neg R“, is true, because ‘R‘ is false, and ‘\neg‘ reverses the truth-value of that to which it is applied. Now we can determine the truth-value of the whole wff, “((P \land Q) \rightarrow \neg R)“, by consulting the chart given above for ‘→’. Here, the wff “(P \land Q)” is our \alpha, and “\neg R” is our \beta, and since their truth-values are F and T, respectively, we consult the third row of the chart, and we see that the complex statement “((P \land Q) \rightarrow \neg R)” is true.
We have so far been considering the case in which ‘P‘ is true and ‘Q‘ and ‘R‘ are both false. There are, however, a number of other possibilities with regard to the possible truth-values of the statement letters, ‘P‘, ‘Q‘ and ‘R‘. There are eight possibilities altogether, as shown by the following list:
|
P
|
Q
|
R
|
|
T
T
T
T
F
F
F
F
|
T
T
F
F
T
T
F
F
|
T
F
T
F
T
F
T
F
|
Strictly speaking, each of the eight possibilities above represents a different truth-value assignment, which can be defined as a possible assignment of truth-values T or F to the different statement letters making up a wff or series of wffs. If a wff has n distinct statement letters making up, the number of possible truth-value assignments is 2n. With the wff, “((P \land Q) \rightarrow \neg R)“, there are three statement letters, ‘P‘, ‘Q‘ and ‘R‘, and so there are 8 truth-value assignments.
It then becomes possible to draw a chart showing how the truth-value of a given wff would be resolved for each possible truth-value assignment. We begin with a chart showing all the possible truth-value assignments for the wff, such as the one given above. Next, we write out the wff itself on the top right of our chart, with spaces between the signs. Then, for each, truth-value assignment, we repeat the appropriate truth-value, ‘T’, or ‘F’, underneath the statement letters as they appear in the wff. Then, as the truth-values of those wffs that are parts of the complete wff are determined, we write their truth-values underneath the logical sign that is used to form them. The final column filled in shows the truth-value of the entire statement for each truth-value assignment. Given the importance of this column, we highlight it in some way. Here, we highlight it in yellow.
|
P
|
Q
|
R
|
| |
((P
|
\land
|
Q)
|
→
|
\neg
|
R)
|
|
T
T
T
T
F
F
F
F
|
T
T
F
F
T
T
F
F
|
T
F
T
F
T
F
T
F
|
|
T
T
T
T
F
F
F
F
|
T
T
F
F
F
F
F
F
|
T
T
F
F
T
T
F
F
|
F
T
T
T
T
T
T
T
|
F
T
F
T
F
T
F
T
|
T
F
T
F
T
F
T
F
|
Charts such as the one given above are called truth tables. In classical truth-functional propositional logic, a truth table constructed for a given wff in effects reveals everything logically important about that wff. The above chart tells us that the wff “((P \land Q) \rightarrow \neg R)” can only be false if ‘P‘, ‘Q‘ and ‘R‘ are all true, and is true otherwise.
c. Definability of the Operators and the Languages PL’ and PL”
The language PL, as we have seen, contains operators that are roughly analogous to the English operators ‘and’, ‘or’, ‘if… then…’, ‘if and only if’, and ‘not’. Each of these, as we have also seen, can be thought of as representing a certain truth-function. It might be objected however, that there are other methods of combining statements together in which the truth-value of the statement depends wholly on the truth-values of the parts, or in other words, that there are truth-functions besides conjunction, (inclusive) disjunction, material implication, material equivalence and negation. For example, we noted earlier that the sign ‘\lor‘ is used analogously to ‘or’ in the inclusive sense, which means that language PL has no simple sign for ‘or’ in the exclusive sense. It might be thought, however, that the langauge PL is incomplete without the addition of an additional symbol, say ‘\veebar‘, such that \ulcorner (\alpha \veebar \beta) \urcorner would be regarded as true if \alpha is true and \beta is false, or \alpha is false and \beta is true, but would be regarded as false if either both \alpha and \beta are true or both \alpha and \beta are false.
However, a possible response to this objection would be to make note that while language PL does not include a simple sign for this exclusive sense of disjunction, it is possible, using the symbols that are included in PL, to construct a statement that is true in exactly the same circumstances. Consider, for example, a statement of the form \ulcorner \neg (\alpha \leftrightarrow \beta) \urcorner. It is easily shown, using a truth table, that any wff of this form would have the same truth-value as a would-be statement using the operator ‘\veebar‘. See the following chart:
|
\alpha
|
\beta
|
| |
\neg
|
(\alpha
|
↔
|
\beta)
|
|
T
T
F
F
|
T
F
T
F
|
|
F
T
T
F
|
T
T
F
F
|
T
F
F
T
|
T
F
T
F
|
Here we see that a wff of the form \ulcorner \neg (\alpha \leftrightarrow \beta) \urcorner is true if either \alpha or \beta is true but not both. This shows that PL is not lacking in any way by not containing a sign ‘\veebar‘. All the work that one would wish to do with this sign can be done using the signs ‘↔’ and ‘\neg‘. Indeed, one might claim that the sign ‘\veebar‘ can be defined in terms of the signs ‘↔’, and ‘\neg‘, and then use the form \ulcorner (\alpha \veebar \beta) \urcorner as an abbreviation of a wff of the form \ulcorner \neg (\alpha \leftrightarrow \beta) \urcorner, without actually expanding the primitive vocabulary of language PL.
The signs ‘\land‘, ‘\lor‘, ‘→’, ‘↔’ and ‘\neg‘, were chosen as the operators to include in PL because they correspond (roughly) the sorts of truth-functional operators that are most often used in ordinary discourse and reasoning. However, given the preceding discussion, it is natural to ask whether or not some operators on this list can be defined in terms of the others. It turns out that they can. In fact, if for some reason we wished our logical language to have a more limited vocabulary, it is possible to get by using only the signs ‘\neg‘ and ‘→’, and define all other possible truth-functions in virtue of them. Consider, for example, the following truth table for statements of the form \ulcorner \neg (\alpha \rightarrow \neg \beta) \urcorner:
|
\alpha
|
\beta
|
| |
\neg
|
(\alpha
|
→
|
\neg
|
\beta)
|
|
T
T
F
F
|
T
F
T
F
|
|
T
F
F
F
|
T
T
F
F
|
F
T
T
T
|
F
T
F
T
|
T
F
T
F
|
We can see from the above that a wff of the form \ulcorner \neg (\alpha \rightarrow \neg \beta) \urcorner always has the same truth-value as the corresponding statement of the form \ulcorner (\alpha \land \beta) \urcorner. This shows that the sign ‘\land‘ can in effect be defined using the signs ‘\neg‘ and ‘→’.
Next, consider the truth table for statements of the form \ulcorner (\neg \alpha \rightarrow \beta) \urcorner:
|
\alpha
|
\beta
|
| |
(\neg
|
\alpha
|
→
|
\beta)
|
|
T
T
F
F
|
T
F
T
F
|
|
F
F
T
T
|
T
T
F
F
|
T
T
T
F
|
T
F
T
F
|
Here we can see that a statement of the form \ulcorner (\neg \alpha \rightarrow \beta) \urcorner always has the same truth-value as the corresponding statement of the form \ulcorner (\alpha \lor \beta) \urcorner. Again, this shows that the sign ‘\lor‘ could in effect be defined using the signs ‘→’ and ‘\neg‘.
Lastly, consider the truth table for a statement of the form \ulcorner \neg (( \alpha \rightarrow \beta) \rightarrow \neg (\beta \rightarrow \alpha)) \urcorner:
|
\alpha
|
\beta
|
| |
\neg
|
((\alpha
|
→
|
\beta)
|
→
|
\neg
|
(\beta
|
→
|
\alpha))
|
|
T
T
F
F
|
T
F
T
F
|
|
T
F
F
T
|
T
T
F
F
|
T
F
T
T
|
T
F
T
F
|
F
T
T
F
|
F
F
T
F
|
T
F
T
F
|
T
T
F
T
|
T
T
F
F
|
From the above, we see that a statement of the form \ulcorner \neg (( \alpha \rightarrow \beta) \rightarrow \neg (\beta \rightarrow \alpha)) \urcorner always has the same truth-value as the corresponding statement of the form \ulcorner (\alpha \leftrightarrow \beta) \urcorner. In effect, therefore, we have shown that the remaining operators of PL can all be defined in virtue of ‘→’, and ‘\neg‘, and that, if we wished, we could do away with the operators, ‘\land‘, ‘\lor‘ and ‘↔’, and simply make do with those equivalent expressions built up entirely from ‘→’ and ‘\neg‘.
Let us call the language that results from this simplication PL’. While the definition of a statement letter remains the same for PL’ as for PL, the definition of a well-formed formula (wff) for PL’ can be greatly simplified. In effect, it can be stated as follows:
Definition: A well-formed formula (or wff) of PL’ is defined recursively as follows:
- Any statement letter is a well-formed formula.
- If \alpha is a well-formed formula, then so is \ulcorner \neg \alpha \urcorner.
- If \alpha and \beta are well-formed formulas, then so is \ulcorner (\alpha \rightarrow \beta) \urcorner.
- Nothing that cannot be constructed by successive steps of (1)-(3) is a well-formed formula.
Strictly speaking, then, the langauge PL’ does not contain any statements using the operators ‘\lor‘, ‘\land‘, or ‘↔’. One could however, utilize conventions such that, in language PL’, an expression of the form \ulcorner (\alpha \land \beta) \urcorner is to be regarded as a mere abbreviation or short-hand for the corresponding statement of the form \ulcorner \neg (\alpha \rightarrow \neg \beta) \urcorner, and similarly that expressions of the forms \ulcorner (\alpha \lor \beta) \urcorner and \ulcorner (\alpha \leftrightarrow \beta) \urcorner are to be regarded as abbreviations of expressions of the forms \ulcorner (\neg \alpha \rightarrow \beta) \urcorner or \ulcorner \neg (( \alpha \rightarrow \beta) \rightarrow \neg (\beta \rightarrow \alpha)) \urcorner, respectively. In effect, this means that it is possible to translate any wff of language PL into an equivalent wff of language PL’.
In Section VII, it is proven that not only are the operators ‘\neg‘ and ‘→’ sufficient for defining every truth-functional operator included in language PL, but also that they are sufficient for defining any imaginable truth-functional operator in classical propositional logic.
Nevertheless, the choice of ‘\neg‘ and ‘→’ for the primitive signs used in language PL’ is to some extent arbitrary. It would also have been possible to define all other operators of PL (including ‘→’) using the signs ‘\neg‘ and ‘\lor‘. On this approach, \ulcorner (\alpha \land \beta) \urcorner would be defined as \ulcorner \neg (\neg \alpha \lor \neg \beta) \urcorner, \ulcorner (\alpha \rightarrow \beta) \urcorner would be defined as \ulcorner (\neg \alpha \lor \beta) \urcorner, and \ulcorner (\alpha \leftrightarrow \beta) \urcorner would be defined as \ulcorner \neg (\neg(\neg \alpha \lor \beta) \lor \neg (\neg \beta \lor \alpha)) \urcorner. Similarly, we could instead have begun with ‘\neg‘ and ‘\land‘ as our starting operators. On this way of proceeding, \ulcorner (\alpha \lor \beta) \urcorner would be defined as \ulcorner \neg (\neg \alpha \land \neg \beta) \urcorner, \ulcorner (\alpha \rightarrow \beta) \urcorner would be defined as \ulcorner \neg (\alpha \land \neg \beta) \urcorner, and \ulcorner (\alpha \leftrightarrow \beta) \urcorner would be defined as \ulcorner (\neg (\alpha \land \neg \beta) \land \neg (\beta \land \neg \alpha) \urcorner.
There are, as we have seen, multiple different ways of reducing all truth-functional operators down to two primitives. There are also two ways of reducing all truth-functional operators down to a single primitive operator, but they require using an operator that is not included in language PL as primitive. On one approach, we utilize an operator written ‘|’, and explain the truth-function corresponding to this sign by means of the following chart:
| \alpha |
\beta |
(\alpha | \beta) |
|
T
T
F
F
|
T
F
T
F
|
F
T
T
T
|
Here we can see that a statement of the form \ulcorner (\alpha | \beta) \urcorner is false if both \alpha and \beta are true, and true otherwise. For this reason one might read ‘|’ as akin to the English expression, “Not both … and …”. Indeed, it is possible to represent this truth-function in language PL using an expression of the form, \ulcorner \neg (\alpha \land \beta) \urcorner. However, since it is our intention to show that all other truth-functional operators, including ‘\neg‘ and ‘\land‘ can be derived from ‘|’, it is better not to regard the meanings of ‘\neg‘ and ‘\land‘ as playing a part of the meaning of ‘|’, and instead attempt (however counterintuitive it may seem) to regard ‘|’ as conceptually prior to ‘\neg‘ and ‘\land‘.
The sign ‘|’ is called the Sheffer stroke, and is named after H. M. Sheffer, who first publicized the result that all truth-functional connectives could be defined in virtue of a single operator in 1913.
We can then see that the connective ‘\land‘ can be defined in virtue of ‘|’, because an expression of the form \ulcorner ((\alpha | \beta) | (\alpha | \beta)) \urcorner generates the following truth table, and hence is equivalent to the corresponding expression of the form \ulcorner (\alpha \land \beta) \urcorner:
|
\alpha
|
\beta
|
| |
((\alpha
|
|
|
\beta)
|
|
|
(\alpha
|
|
|
\beta))
|
|
T
T
F
F
|
T
F
T
F
|
|
T
T
F
F
|
F
T
T
T
|
T
F
T
F
|
T
F
F
F
|
T
T
F
F
|
F
T
T
T
|
T
F
T
F
|
Similarly, we can define the operator ‘\lor‘ using ‘|’ by noting that an expression of the form \ulcorner ((\alpha | \alpha) | (\beta | \beta)) \urcorner always has the same truth-value as the corresponding statement of the form \ulcorner (\alpha \lor \beta) \urcorner:
|
\alpha
|
\beta
|
| |
((\alpha
|
|
|
\alpha)
|
|
|
(\beta
|
|
|
\beta))
|
|
T
T
F
F
|
T
F
T
F
|
|
T
T
F
F
|
F
F
T
T
|
T
T
F
F
|
T
T
T
F
|
T
F
T
F
|
F
T
F
T
|
T
F
T
F
|
The following truth table shows that a statement of the form \ulcorner (\alpha | (\beta | \beta)) \urcorner always has the same truth table as a statement of the form \ulcorner (\alpha \rightarrow \beta) \urcorner:
|
\alpha
|
\beta
|
| |
(\alpha
|
|
|
(\beta
|
|
|
\beta))
|
|
T
T
F
F
|
T
F
T
F
|
|
T
T
F
F
|
T
F
T
T
|
T
F
T
F
|
F
T
F
T
|
T
F
T
F
|
Although far from intuitively obvious, the following table shows that an expression of the form \ulcorner (((\alpha | \alpha) | (\beta | \beta)) | (\alpha | \beta)) \urcorner always has the same truth-value as the corresponding wff of the form \ulcorner (\alpha \leftrightarrow \beta) \urcorner:
|
\alpha
|
\beta
|
| |
(((\alpha
|
|
|
\alpha)
|
|
|
(\beta
|
|
|
\beta))
|
|
|
(\alpha
|
|
|
\beta))
|
|
|
T
F
T
F
|
|
T
T
F
F
|
F
F
T
T
|
T
T
F
F
|
T
T
T
F
|
T
F
T
F
|
F
T
F
T
|
T
F
T
F
|
T
F
F
T
|
T
T
F
F
|
F
T
T
T
|
T
F
T
F
|
This leaves only the sign ‘\neg‘, which is perhaps the easiest to define using ‘|’, as clearly \ulcorner (\alpha | \alpha) \urcorner, or, roughly, “not both \alpha and \alpha“, has the opposite truth-value from \alpha itself:
|
\alpha
|
| |
(\alpha
|
|
|
\alpha)
|
|
|
|
T
F
|
F
T
|
T
F
|
If, therefore, we desire a language for use in studying propositional logic that has as small a vocabulary as possible, we might suggest using a language that employs the sign ‘|’ as its sole primitive operator, and defines all other truth-functional operators in virtue of it. Let us call such a language PL”. PL” differs from PL and PL’ only in that its definition of a well-formed formula can be simplified even further:
Definition: A well-formed formula (or wff) of PL” is defined recursively as follows:
- Any statement letter is a well-formed formula.
- If \alpha and \beta are well-formed formulas, then so is \ulcorner (\alpha | \beta) \urcorner.
- Nothing that cannot be constructed by successive steps of (1)-(2) is a well-formed formula.
In language PL”, strictly speaking, ‘|’ is the only operator. However, for reasons that should be clear from the above, any expression from language PL that involves any of the operators ‘\neg‘, ‘\land‘, ‘\lor‘, ‘→’, or ‘↔’ could be translated into language PL” without the loss of any of its important logical properties. In effect, statements using these signs could be regarded as abbreviations or shorthand expressions for wffs of PL” that only use the operator ‘|’.
Even here, the choice of ‘|’ as the sole primitive is to some extent arbitrary. It would also be possible to reduce all truth-functional operators down to a single primitive by making use of a sign ‘\downarrow‘, treating it as roughly equivalent to the English expression, “neither … nor …”, so that the corresponding chart would be drawn as follows:
| \alpha |
\beta |
(\alpha \downarrow \beta) |
|
T
T
F
F
|
T
F
T
F
|
F
F
F
T
|
If we were to use ‘\downarrow‘ as our sole operator, we could again define all the others. \ulcorner \neg \alpha \urcorner would be defined as \ulcorner (\alpha \downarrow \alpha) \urcorner; \ulcorner (\alpha \lor \beta) \urcorner would be defined as \ulcorner ((\alpha \downarrow \beta) \downarrow (\alpha \downarrow \beta)) \urcorner; \ulcorner (\alpha \land \beta) \urcorner would be defined as \ulcorner ((\alpha \downarrow \alpha) \downarrow (\beta \downarrow \beta)) \urcorner; and similarly for the other operators. The sign ‘\downarrow‘ is sometimes also referred to as the Sheffer stroke, and is also called the Peirce/Sheffer dagger.
Depending on one’s purposes in studying propositional logic, sometimes it makes sense to use a rich language like PL with more primitive operators, and sometimes it makes sense to use a relatively sparse language such as PL’ or PL” with fewer primitive operators. The advantage of the former approach is that it conforms better with our ordinary reasoning and thinking habits; the advantage of the latter is that it simplifies the logical language, which makes certain interesting results regarding the deductive systems making use of the language easier to prove.
For the remainder of this article, we shall primarily be concerned with the logical properties of statements formed in the richer language PL. However, we shall consider a system making use of language PL’ in some detail in Section VI, and shall also make brief mention of a system making use of language PL”.
4. Tautologies, Logical Equivalence and Validity
Truth-functional propositional logic concerns itself only with those ways of combining statements to form more complicated statements in which the truth-values of the complicated statements depend entirely on the truth-values of the parts. Owing to this, all those features of a complex statement that are studied in propositional logic derive from the way in which their truth-values are derived from those of their parts. These features are therefore always represented in the truth table for a given statement.
Some complex statements have the interesting feature that they would be true regardless of the truth-values of the simple statements making them up. A simple example would be the wff “P \lor \neg P“; that is, “P or not P“. It is fairly easy to see that this statement is true regardless of whether ‘P‘ is true or ‘P‘ is false. This is also shown by its truth table:
|
P
|
| |
P
|
\lor
|
\neg
|
P
|
|
|
|
T
F
|
T
T
|
F
T
|
T
F
|
There are, however, statements for which this is true but it is not so obvious. Consider the wff, “R \rightarrow ((P \rightarrow Q) \lor \neg (R \rightarrow Q))“. This wff also comes out as true regardless of the truth-values of ‘P‘, ‘Q‘ and ‘R‘.
|
P
|
Q
|
R
|
| |
R
|
→
|
((P
|
→
|
Q)
|
\lor
|
\neg
|
(R
|
→
|
Q))
|
|
T
T
T
T
F
F
F
F
|
T
T
F
F
T
T
F
F
|
T
F
T
F
T
F
T
F
|
|
T
F
T
F
T
F
T
F
|
T
T
T
T
T
T
T
T
|
T
T
T
T
F
F
F
F
|
T
T
F
F
T
T
T
T
|
T
T
F
F
T
T
F
F
|
T
T
T
F
T
T
T
T
|
F
F
T
F
F
F
T
F
|
T
F
T
F
T
F
T
F
|
T
T
F
T
T
T
F
T
|
T
T
F
F
T
T
F
F
|
Statements that have this interesting feature are called tautologies. Let us define this notion precisely.
Definition: a wff is a tautology if and only if it is true for all possible truth-value assignments to the statement letters making it up.
Tautologies are also sometimes called logical truths or truths of logic because tautologies can be recognized as true solely in virtue of the principles of propositional logic, and without recourse to any additional information.
On the other side of the spectrum from tautologies are statements that come out as false regardless of the truth-values of the simple statements making them up. A simple example of such a statement would be the wff “P \land \neg P“; clearly such a statement cannot be true, as it contradicts itself. This is revealed by its truth table:
|
P
|
| |
P
|
\land
|
\neg
|
P
|
|
|
|
T
F
|
F
F
|
F
T
|
T
F
|
To state this precisely:
Definition: a wff is a self-contradiction if and only if it is false for all possible truth-value assignments to the statement letters making it up.
Another, more interesting, example of a self-contradiction is the statement “\neg (P \rightarrow Q) \land \neg (Q \rightarrow P)“; this is not as obviously self-contradictory. However, we can see that it is when we consider its truth table:
|
P
|
Q
|
| |
\neg
|
(P
|
→
|
Q)
|
\land
|
\neg
|
(Q
|
→
|
P)
|
|
|
T
F
T
F
|
|
F
T
F
F
|
T
T
F
F
|
T
F
T
T
|
T
F
T
F
|
F
F
F
F
|
F
F
T
F
|
T
F
T
F
|
T
T
F
T
|
T
T
F
F
|
A statement that is neither self-contradictory nor tautological is called a contingent statement. A contingent statement is true for some truth-value assignments to its statement letters and false for others. The truth table for a contingent statement reveals which truth-value assignments make it come out as true, and which make it come out as false. Consider the truth table for the statement “(P \rightarrow Q) \land (P \rightarrow \neg Q)“:
|
P
|
Q
|
| |
(P
|
→
|
Q)
|
\land
|
(P
|
→
|
\neg
|
Q)
|
|
|
T
F
T
F
|
|
T
T
F
F
|
T
F
T
T
|
T
F
T
F
|
F
F
T
T
|
T
T
F
F
|
F
T
T
T
|
F
T
F
T
|
T
F
T
F
|
We can see that of the four possible truth-value assignments for this statement, two make it come as true, and two make it come out as false. Specifically, the statement is true when ‘P‘ is false and ‘Q‘ is true, and when ‘P‘ is false and ‘Q‘ is false, and the statement is false when ‘P‘ is true and ‘Q‘ is true and when ‘P‘ is true and ‘Q‘ is false.
Truth tables are also useful in studying logical relationships that hold between two or more statements. For example, two statements are said to be consistent when it is possible for both to be true, and are said to be inconsistent when it is not possible for both to be true. In propositional logic, we can make this more precise as follows.
Definition: two wffs are consistent if and only if there is at least one possible truth-value assignment to the statement letters making them up that makes both wffs true.
Definition: two wffs are inconsistent if and only if there is no truth-value assignment to the statement letters making them up that makes them both true.
Whether or not two statements are consistent can be determined by means of a combined truth table for the two statements. For example, the two statements, “P \lor Q” and “\neg (P \leftrightarrow \neg Q)” are consistent:
|
P
|
Q
|
| |
P
|
\lor
|
Q
|
|
\neg
|
(P
|
↔
|
\neg
|
Q)
|
|
|
T
F
T
F
|
|
T
T
F
F
|
T
T
T
F
|
T
F
T
F
|
|
T
F
F
T
|
T
T
F
F
|
F
T
T
F
|
F
T
F
T
|
T
F
T
F
|
Here, we see that there is one truth-value assignment, that in which both ‘P‘ and ‘Q‘ are true, that makes both “P \lor Q” and “\neg (P \leftrightarrow \neg Q)” true. However, the statements “(P \rightarrow Q) \land P” and “\neg (Q \lor \neg P)” are inconsistent, because there is no truth-value assignment in which both come out as true.
|
P
|
Q
|
| |
(P
|
→
|
Q)
|
\land
|
P
|
|
\neg
|
(Q
|
\lor
|
\neg
|
P))
|
|
|
T
F
T
F
|
|
T
T
F
F
|
T
F
T
T
|
T
F
T
F
|
T
F
F
F
|
T
T
F
F
|
|
F
T
F
F
|
T
F
T
F
|
T
F
T
T
|
F
F
T
T
|
T
T
F
F
|
Another relationship that can hold between two statements is that of having the same truth-value regardless of the truth-values of the simple statements making them up. Consider a combined truth table for the wffs “\neg P \rightarrow \neg Q” and “\neg (Q \land \neg P)“:
|
P
|
Q
|
| |
\neg
|
P
|
→
|
\neg
|
Q
|
|
\neg
|
(Q
|
\land
|
\neg
|
P))
|
|
|
T
F
T
F
|
|
F
F
T
T
|
T
T
F
F
|
T
T
F
T
|
F
T
F
T
|
T
F
T
F
|
|
T
T
F
T
|
T
F
T
F
|
F
F
T
F
|
F
F
T
T
|
T
T
F
F
|
Here we see that these two statements necessarily have the same truth-value.
Definition: two statements are said to be logically equivalent if and only if all possible truth-value assignments to the statement letters making them up result in the same resulting truth-values for the whole statements.
The above statements are logically equivalent. However, the truth table given above for the statements “P \lor Q” and “\neg (P \leftrightarrow \neg Q)” show that they, on the other hand, are not logically equivalent, because they differ in truth-value for three of the four possible truth-value assignments.
Finally, and perhaps most importantly, truth tables can be utilized to determine whether or not an argument is logically valid. In general, an argument is said to be logically valid whenever it has a form that makes it impossible for the conclusion to be false if the premises are true. (See the encyclopedia article on “Validity and Soundness“.) In classical propositional logic, we can give this a more precise characterization.
Definition: a wff \beta is said to be a logical consequence of a set of wffs \alpha_1, \alpha_2, ..., \alpha_n, if and only if there is no truth-value assignment to the statement letters making up these wffs that makes all of \alpha_1, \alpha_2, ..., \alpha_n true but does not make \beta true.
An argument is logically valid if and only if its conclusion is a logical consequence of its premises. If an argument whose conclusion is \beta and whose only premise is \alpha is logically valid, then \alpha is said to logically imply \beta.
For example, consider the following argument:
\(<br />
\begin{array}{l} P \rightarrow Q\\<br />
\neg Q \rightarrow P\\<br />
\hline Q<br />
\end{array}<br />
\)
We can test the validity of this argument by constructing a combined truth table for all three statements.
|
P
|
Q
|
| |
P
|
→
|
Q
|
|
\neg
|
Q
|
→
|
P
|
|
Q
|
|
|
T
F
T
F
|
|
T
T
F
F
|
T
F
T
T
|
T
F
T
F
|
|
F
T
F
T
|
T
F
T
F
|
T
T
T
F
|
T
T
F
F
|
|
T
F
T
F
|
Here we see that both premises come out as true in the case in which both ‘P‘ and ‘Q‘ are true, and in which ‘P‘ is false but ‘Q‘ is true. However, in those cases, the conclusion is also true. It is possible for the conclusion to be false, but only if one of the premises is false as well. Hence, we can see that the inference represented by this argument is truth-preserving. Contrast this with the following example:
\(<br />
\begin{array}{l} P \rightarrow Q\\<br />
\hline \neg Q \lor \neg P<br />
\end{array}<br />
\)
Consider the truth-value assignment making both ‘P‘ and ‘Q‘ true. If we were to fill in that row of the truth-value for these statements, we would see that “P \rightarrow Q” comes out as true, but “\neg Q \lor \neg P” comes out as false. Even if ‘P‘ and ‘Q‘ are not actually both true, it is possible for them to both be true, and so this form of reasoning is not truth-preserving. In other words, the argument is not logically valid, and its premise does not logically imply its conclusion.
One of the most striking features of truth tables is that they provide an effective procedure for determining the logical truth, or tautologyhood of any single wff, and for determining the logical validity of any argument written in the language PL. The procedure for constructing such tables is purely rote, and while the size of the tables grows exponentially with the number of statement letters involved in the wff(s) under consideration, the number of rows is always finite and so it is in principle possible to finish the table and determine a definite answer. In sum, classical propositional logic is decidable.
5. Deduction: Rules of Inference and Replacement
a. Natural Deduction
Truth tables, as we have seen, can theoretically be used to solve any question in classical truth-functional propositional logic. However, this method has its drawbacks. The size of the tables grows exponentially with the number of distinct statement letters making up the statements involved. Moreover, truth tables are alien to our normal reasoning patterns. Another method for establishing the validity of an argument exists that does not have these drawbacks: the method of natural deduction. In natural deduction an attempt is made to reduce the reasoning behind a valid argument to a series of steps each of which is intuitively justified by the premises of the argument or previous steps in the series.
Consider the following argument stated in natural language:
Either cat fur or dog fur was found at the scene of the crime. If dog fur was found at the scene of the crime, officer Thompson had an allergy attack. If cat fur was found at the scene of the crime, then Macavity is responsible for the crime. But officer Thompson didn’t have an allergy attack, and so therefore Macavity must be responsible for the crime.
The validity of this argument can be made more obvious by representing the chain of reasoning leading from the premises to the conclusion:
- Either cat fur was found at the scene of the crime, or dog fur was found at the scene of the crime. (Premise)
- If dog fur was found at the scene of the crime, then officer Thompson had an allergy attack. (Premise)
- If cat fur was found at the scene of the crime, then Macavity is responsible for the crime. (Premise)
- Officer Thompson did not have an allergy attack. (Premise)
- Dog fur was not found at the scene of the crime. (Follows from 2 and 4.)
- Cat fur was found at the scene of the crime. (Follows from 1 and 5.)
- Macavity is responsible for the crime. (Conclusion. Follows from 3 and 6.)
Above, we do not jump directly from the premises to the conclusion, but show how intermediate inferences are used to ultimately justify the conclusion by a step-by-step chain. Each step in the chain represents a simple, obviously valid form of reasoning. In this example, the form of reasoning exemplified in line 5 is called modus tollens, which involves deducing the negation of the antecedent of a conditional from the conditional and the negation of its consequent. The form of reasoning exemplified in step 5 is called disjunctive syllogism, and involves deducing one disjunct of a disjunction on the basis of the disjunction and the negation of the other disjunct. Lastly, the form of reasoning found at line 7 is called modus ponens, which involves deducing the truth of the consequent of a conditional given truth of both the conditional and its antecedent. “Modus ponens” is Latin for affirming mode, and “modus tollens” is Latin for denying mode.
A system of natural deduction consists in the specification of a list of intuitively valid rules of inference for the construction of derivations or step-by-step deductions. Many equivalent systems of deduction have been given for classical truth-functional propositional logic. In what follows, we sketch one system, which is derived from the popular textbook by Irving Copi (1953). The system makes use of the language PL.
b. Rules of Inference
Here we give a list of intuitively valid rules of inference. The rules are stated in schematic form. Any inference in which any wff of language PL is substituted unformly for the schematic letters in the forms below constitutes an instance of the rule.
Modus ponens (MP):
\(<br />
\begin{array}{l} \alpha \rightarrow \beta, \alpha\\<br />
\hline \beta<br />
\end{array}<br />
\)
(Modus ponens is sometimes also called “modus ponendo ponens”, “detachment” or a form of “→-elimination”.)
Modus tollens (MT):
\(<br />
\begin{array}{l} \alpha \rightarrow \beta, \neg \beta\\<br />
\hline \neg \alpha<br />
\end{array}<br />
\)
(Modus tollens is sometimes also called “modus tollendo tollens” or a form of “→-elimination”.)
Disjunctive syllogism (DS): (two forms)
\(<br />
\begin{array}{l} \alpha \lor \beta, \neg \alpha\\<br />
\hline \beta<br />
\end{array}<br />
\)
\(<br />
\begin{array}{l} \alpha \lor \beta, \neg \beta\\<br />
\hline \alpha<br />
\end{array}<br />
\)
(Disjunctive syllogism is sometimes also called “modus tollendo ponens” or “\lor-elimination”.)
Addition (Add): (two forms)
\(<br />
\begin{array}{l} \alpha\\<br />
\hline \alpha \lor \beta<br />
\end{array}<br />
\)
\(<br />
\begin{array}{l} \beta\\<br />
\hline \alpha \lor \beta<br />
\end{array}<br />
\)
(Addition is sometimes also called “disjunction introduction” or “\lor–introduction”.)
Simplification (Simp): (two forms)
\(<br />
\begin{array}{l} \alpha \land \beta\\<br />
\hline \alpha<br />
\end{array}<br />
\)
\(<br />
\begin{array}{l} \alpha \land \beta\\<br />
\hline \beta<br />
\end{array}<br />
\)
(Simplification is sometimes also called “conjunction elimination” or “\land-elimination”.)
Conjunction (Conj):
\(<br />
\begin{array}{l} \alpha, \beta\\<br />
\hline \alpha \land \beta<br />
\end{array}<br />
\)
(Conjunction is sometimes also called “conjunction introduction”, “\land-introduction” or “logical multiplication”.)
Hypothetical syllogism (HS):
\(<br />
\begin{array}{l} \alpha \rightarrow \beta, \beta \rightarrow \gamma\\<br />
\hline \alpha \rightarrow \gamma<br />
\end{array}<br />
\)
(Hypothetical syllogism is sometimes also called “chain reasoning” or “chain deduction”.)
Constructive dilemma (CD):
\(<br />
\begin{array}{l} (\alpha \rightarrow \gamma) \land (\beta \rightarrow \delta), \alpha \lor \beta\\<br />
\hline \gamma \lor \delta<br />
\end{array}<br />
\)
Absorption (Abs):
\(<br />
\begin{array}{l} \alpha \rightarrow \beta\\<br />
\hline \alpha \rightarrow (\alpha \land \beta)<br />
\end{array}<br />
\)
c. Rules of Replacement
The nine rules of inference listed above represent ways of inferring something new from previous steps in a deduction. Many systems of natural deduction, including those initially designed by Gentzen, consist entirely of rules similar to the above. If the language of a system involves signs introduced by definition, it must also allow the substitution of a defined sign for the expression used to define it, or vice versa. Still other systems, while not making use of defined signs, allow one to make certain substitutions of expressions of one form for expressions of another form in certain cases in which the expressions in question are logically equivalent. These are called rules of replacement, and Copi’s natural deduction system invokes such rules. Strictly speaking, rules of replacement differ from inference rules, because, in a sense, when a rule of replacement is used, one is not inferring something new but merely stating what amounts to the same thing using a different combination of symbols. In some systems, rules for replacement can be derived from the inference rules, but in Copi’s system, they are taken as primitive.
Rules of replacement also differ from inference rules in other ways. Inference rules only apply when the main operators match the patterns given and only apply to entire statements. Inference rules are also strictly unidirectional: one must infer what is below the horizontal line from what is above and not vice-versa. However, replacement rules can be applied to portions of statements and not only to entire statements; moreover, they can be implemented in either direction.
The rules of replacement used by Copi are the following:
Double negation (DN):
\ulcorner \neg \neg \alpha \urcorner is interreplaceable with \alpha
(Double negation is also called “\neg-elimination”.)
Commutativity (Com): (two forms)
\ulcorner \alpha \land \beta \urcorner is interreplaceable with \ulcorner \beta \land \alpha \urcorner
\ulcorner \alpha \lor \beta \urcorner is interreplaceable with \ulcorner \beta \lor \alpha \urcorner
Associativity (Assoc): (two forms)
\ulcorner (\alpha \land \beta) \land \gamma \urcorner is interreplaceable with \ulcorner \alpha \land (\beta \land \gamma) \urcorner
\ulcorner (\alpha \lor \beta) \lor \gamma \urcorner is interreplaceable with \ulcorner \alpha \lor (\beta \lor \gamma) \urcorner
Tautology (Taut): (two forms)
\alpha is interreplaceable with \ulcorner \alpha \land \alpha \urcorner
\alpha is interreplaceable with \ulcorner \alpha \lor \alpha \urcorner
DeMorgan’s Laws (DM): (two forms)
\ulcorner \neg (\alpha \land \beta) \urcorner is interreplaceable with \ulcorner \neg \alpha \lor \neg \beta \urcorner
\ulcorner \neg (\alpha \lor \beta) \urcorner is interreplaceable with \ulcorner \neg \alpha \land \neg \beta \urcorner
Transposition (Trans):
\ulcorner \alpha \rightarrow \beta \urcorner is interreplaceable with \ulcorner \neg \beta \rightarrow \neg \alpha \urcorner
(Transposition is also sometimes called “contraposition”.)
Material Implication (Impl):
\ulcorner \alpha \rightarrow \beta \urcorner is interreplaceable with \ulcorner \neg \alpha \lor \beta \urcorner
Exportation (Exp):
\ulcorner \alpha \rightarrow (\beta \rightarrow \gamma) \urcorner is interreplaceable with \ulcorner (\alpha \land \beta) \rightarrow \gamma \urcorner
Distribution (Dist): (two forms)
\ulcorner \alpha \land (\beta \lor \gamma) \urcorner is interreplaceable with \ulcorner (\alpha \land \beta) \lor (\alpha \land \gamma) \urcorner
\ulcorner \alpha \lor (\beta \land \gamma) \urcorner is interreplaceable with \ulcorner (\alpha \lor \beta) \land (\alpha \lor \gamma) \urcorner
Material Equivalence (Equiv): (two forms)
\ulcorner \alpha \leftrightarrow \beta \urcorner is interreplaceable with \ulcorner (\alpha \rightarrow \beta) \land (\beta \rightarrow \alpha) \urcorner
\ulcorner \alpha \leftrightarrow \beta \urcorner is interreplaceable with \ulcorner (\alpha \land \beta) \lor (\neg \alpha \land \neg \beta) \urcorner
(Material equivalence is sometimes also called “biconditional introduction/elimination” or “↔-introduction/elimination”.)
d. Direct Deductions
A direct deduction of a conclusion from a set of premises consists of an ordered sequence of wffs such that each member of the sequence is either (1) a premise, (2) derived from previous members of the sequence by one of the inference rules, (3) derived from a previous member of the sequence by the replacement of a logically equivalent part according to the rules of replacement, and such that the conclusion is the final step of the sequence.
To be even more precise, a direct deduction is defined as an ordered sequence of wffs, \beta_1, \beta_2, ..., \beta_n, such that for each step \beta_i where i is between 1 and n inclusive, either (1) \beta_i is a premise, (2) \beta_i matches the form given below the horizontal line for one of the 9 inference rules, and there are wffs in the sequence prior to \beta_i matching the forms given above the horizontal line, (3) there is a previous step in the sequence \beta_j where j < i and \beta_j differs from \beta_i at most by matching or containing a part that matches one of the forms given for one of the 10 replacement rules in the same place in whcih \beta_i contains the wff of the corresponding form, and such that the conclusion of the argument is \beta_n.
Using line numbers and the abbreviations for the rules of the system to annotate, the chain of reasoning given above in English, when transcribed into language PL and organized as a direct deduction, would appear as follows:
| 1. C \lor D |
Premise |
| 2. C \rightarrow O |
Premise |
| 3. D \rightarrow M |
Premise |
| 4. \neg O |
Premise |
| 5. \neg C |
2,4 MT |
| 6. D |
1,5 DS |
| 7. M |
2,6 MP |
There is no unique derivation for a given conclusion from a given set of premises. Here is a distinct derivation for the same conclusion from the same premises:
| 1. C \lor D |
Premise |
| 2. C \rightarrow O |
Premise |
| 3. D \rightarrow M |
Premise |
| 4. \neg O |
Premise |
| 5. (C \rightarrow O) \land (D \rightarrow M) |
2,3 Conj |
| 6. O \lor M |
1,5 CD |
| 7. M |
4,6 DS |
Consider next the argument:
\(<br />
\begin{array}{l} P \leftrightarrow Q\\<br />
(S \lor T) \rightarrow Q\\<br />
\neg P \lor (\neg T \land R)\\<br />
\hline T \rightarrow U<br />
\end{array}<br />
\)
This argument has six distinct statement letters, and hence constructing a truth table for it would require 64 rows. The table would have 22 columns, thereby requiring 1,408 distinct T/F calculations. Happily, the derivation of the conclusion of the premises using our inference and replacement rules, while far from simple, is relatively less exhausting:
| 1. P \leftrightarrow Q |
Premise |
| 2. (S \lor T) \rightarrow Q |
Premise |
| 3. \neg P \lor (\neg T \land R) |
Premise |
| 4. (P \rightarrow Q) \land (Q \rightarrow P) |
1 Equiv |
| 5. Q \rightarrow P |
4 Simp |
| 6. (S \lor T) \rightarrow P |
2,5 HS |
| 7. P \rightarrow (\neg T \land R) |
3 Impl |
| 8. (S \lor T) \rightarrow (\neg T \land R) |
6,7 HS |
| 9. \neg (S \lor T) \lor (\neg T \land R) |
8 Impl |
| 10. (\neg S \land \neg T) \lor (\neg T \land R) |
9 DM |
| 11. ((\neg S \land \neg T) \lor \neg T) \land ((\neg S \land \neg T) \lor R) |
10 Dist |
| 12. (\neg S \land \neg T) \lor \neg T |
11 Simp |
| 13. \neg T \lor (\neg S \land \neg T) |
12 Com |
| 14. (\neg T \lor \neg S) \land (\neg T \lor \neg T) |
13 Dist |
| 15. \neg T \lor \neg T |
14 Simp |
| 16. \neg T |
15 Taut |
| 17. \neg T \lor U |
16 Add |
| 18. T \rightarrow U |
17 Impl |
e. Conditional and Indirect Proofs
Together the nine inference rules and ten rules of replacement are sufficient for creating a deduction for any logically valid argument, provided that the argument has at least one premise. However, to cover the limiting case of arguments with no premises, and simply to facillitate certain deductions that would be recondite otherwise, it is also customary to allow for certain methods of deduction other than direct derivation. Specifically, it is customary to allow the proof techniques known as conditional proof and indirect proof.
A conditional proof is a derivation technique used to establish a conditional wff, that is, a wff whose main operator is the sign ‘→’. This is done by constructing a sub-derivation within a derivation in which the antecedent of the conditional is assumed as a hypothesis. If, by using the inference rules and rules of replacement (and possibly additional sub-derivations), it is possible to arrive at the consequent, it is permissible to end the sub-derivation and conclude the truth of the conditional statement within the main derivation, citing the sub-derivation as a conditional proof, or ‘CP’ for short. This is much clearer by considering the following example argument:
\(<br />
\begin{array}{l} P \rightarrow (Q \lor R)\\<br />
P \rightarrow \neg S\\<br />
S \leftrightarrow Q\\<br />
\hline P \rightarrow R<br />
\end{array}<br />
\)
While a direct derivation establishing the validity of this argument is possible, it is easier to establish the validity of this argument using a conditional derivation.
| 1. P \rightarrow (Q \lor R) |
Premise |
| 2. P \rightarrow \neg S |
Premise |
| 3. S \leftrightarrow Q |
Premise |
| 4. P |
Assumption |
| 5. Q \lor R |
1,4 MP |
| 6. \neg S |
2,4 MP |
| 7. (S \rightarrow Q) \land (Q \rightarrow S) |
3 Equiv |
| 8. Q \rightarrow S |
7 Simp |
| 9. \neg Q |
6,8 MT |
| 10. R |
5,9 DS |
| 11. P \rightarrow R |
4-10 CP |
Here in order to establish the conditional statement “P \rightarrow R“, we constructed a sub-derivation, which is the portion found at lines 4-10. First, we assumed the truth of ‘P‘, and found that with it, we could derive ‘R‘. Given the premises, we therefore had shown that if ‘P‘ were also true, so would be ‘R‘. Therefore, on the basis of the sub-derivation we were justified in concluding “P \rightarrow R“. This is the usual methodology used in logic and mathematics for establishing the truth of a conditional statement.
Another common method is that of indirect proof, also known as proof by reductio ad absurdum. (For a fuller discussion, see the article on reductio ad absurdum in the encyclopedia.) In an indirect proof (‘IP’ for short), our goal is to demonstrate that a certain wff is false on the basis of the premises. Again, we make use of a sub-derivation; here, we begin by assuming the opposite of that which we’re trying to prove, that is, we assume that the wff is true. If on the basis of this assumption, we can demonstrate an obvious contradiction, that is, a statement of the form \ulcorner \alpha \land \neg \alpha \urcorner, we can conclude that the assumed statement must be false, because anything that leads to a contradiction must be false.
For example, consider the following argument:
\(<br />
\begin{array}{l} P \rightarrow Q\\<br />
P \rightarrow (Q \rightarrow \neg P)\\<br />
\hline \neg P<br />
\end{array}<br />
\)
While, again, a direct derivation of the conclusion for this argument from the premises is possible, it is somewhat easier to prove that “\neg P” is true by showing that, given the premises, it would be impossible for ‘P‘ to be true by assuming that it is and showing this to be absurd.
| 1. P \rightarrow Q |
Premise |
| 2. P \rightarrow (Q \rightarrow \neg P) |
Premise |
| 3. P |
Assumption |
| 4. Q |
1,3 MP |
| 5. Q \rightarrow \neg P |
2,3 MP |
| 6. \neg P |
4,5 MP |
| 7. P \land \neg P |
3,6 Conj |
| 8. \neg P |
3-7 IP |
Here we were attempting to show that “\neg P” was true given the premises. To do this we assumed instead that ‘P‘ was true. Since this assumption was impossible, we were justified in concluding that ‘P‘ is false, that is, that “\neg P” is true.
When making use of either conditional proof or indirect proof, once a sub-derivation is finished, the lines making it up cannot be used later on in the main derivation or any additional sub-derivations that may be constructed later on.
This completes our characterization of a system of natural deduction for the language PL.
The system of natural deduction just described is formally adequate in the following sense. Earlier, we defined a valid argument as one in which there is no possible truth-value assignment to the statement letters making up its premises and conclusion that makes the premises all true but the conclusion untrue. It is provable that an argument in the language of PL is formally valid in that sense if and only if it is possible to construct a derivation of the conclusion of that argument from the premises using the above rules of inference, rules of replacement and techniques of conditional and indirect proof. Space limitations preclude a full proof of this in the metalanguage, although the reasoning is very similar to that given for the axiomatic Propositional Calculus discussed in Sections VI and VII below.
Informally, it is fairly easy to see that no argument for which a deduction is possible in this system could be invalid according to truth tables. Firstly, the rules of inference are all truth-preserving. For example, in the case of modus ponens, it is fairly easy to see from the truth table for any set of statements of the appropriate form that no truth-value assignment could make both \ulcorner \alpha \rightarrow \beta \urcorner and \alpha true while making \beta false. A similar consideration applies for the others. Moreover, truth tables can easily be used to verify that statements of one of the forms mentioned in the rules of replacement are all logically equivalent with those the rule allows one to swap for them. Hence, the statements could never differ in truth-value for any truth-value assignment. In case of conditional proof, note that any truth-value assignment must make either the conditional true, or it must make the antecedent true and consequent false. The antecedent is what is assumed in a conditional proof. So, if the truth-value assignment makes both it and the premises of the argument true, because the other rules are all truth-preserving, it would be impossible to derive the consequent unless it were also true. A similar consideration justifies the use of indirect proof.
This system represents a useful method for establishing the validity of an argument that has the advantage of coinciding more closely with the way we normally reason. (As noted earlier, however, there are many equivalent systems of natural deduction, all coinciding relatively closely to ordinary reasoning patterns.) One disadvantage this method has, however, is that, unlike truth tables, it does not provide a means for recognizing that an argument is invalid. If an argument is invalid, there is no deduction for it in the system. However, the system itself does not provide a means for recognizing when a deduction is impossible.
Another objection that might be made to the system of deduction sketched above is that it contains more rules and more techniques than it needs to. This leads us directly into our next topic.
6. Axiomatic Systems and the Propositional Calculus
The system of deduction discussed in the previous section is an example of a natural deduction system, that is, a system of deduction for a formal language that attempts to coincide as closely as possible to the forms of reasoning most people actually employ. Natural systems of deduction are typically contrasted with axiomatic systems. Axiomatic systems are minimalist systems; rather than including rules corresponding to natural modes of reasoning, they utilize as few basic principles or rules as possible. Since so few kinds of steps are available in a deduction, relatively speaking, an axiomatic system usually requires more steps for the deduction of a conclusion from a given set of premises as compared to a natural deduction system.
Typically, an axiomatic system consists in the specification of certain wffs that are specified as “axioms”. An axiom is something that is taken as a fundamental truth of the system that does not itself require proof. To allow for the deduction of results from the axioms or the premises of an argument, the system typically also includes at least one (and often only one) rule of inference. Usually, an attempt is made to limit the number of axioms to as few as possible, or at least, limit the number of forms axioms can take.
Because axiomatic systems aim to be minimal, typically they employ languages with simplified vocabularies whenever possible. For classical truth-functional propositional logic, this might involve using a simpler language such as PL’ or PL” instead of the full language PL.
For most of the remainder of this section, we shall sketch an axiomatic system for classical truth-functional propositional logic, which we shall dub the Propositional Calculus (or PC for short). The Propositional Calculus makes use of language PL’, described above. That is, the only connectives it uses are ‘→’ and ‘\neg‘, and the other operators, if used at all, would be understood as shorthand abbreviations making use of the definitions discussion in Section III(c).
System PC consists of three axiom schemata, which are forms a wff fits if it is axiom, along with a single inference rule: modus ponens. We make this more precise by specifying certain definitions.
Definition: a wff of language PL’ is an axiom of PC if and only if it is an instance of one of the following three forms:
| \alpha \rightarrow (\beta \rightarrow \alpha) |
(Axiom Schema 1, or AS1) |
| (\alpha \rightarrow (\beta \rightarrow \gamma)) \rightarrow ((\alpha \rightarrow \beta) \rightarrow (\alpha \rightarrow \gamma)) |
(Axiom Schema 2, or AS2) |
| (\neg \alpha \rightarrow \neg \beta) \rightarrow ((\neg \alpha \rightarrow \beta) \rightarrow \alpha) |
(Axiom Schema 3, or AS3) |
Note that according to this definition, every wff of the form \ulcorner \alpha \rightarrow (\beta \rightarrow \alpha) \urcorner is an axiom. This includes an infinite number of different wffs, from simple cases such as “P \rightarrow (Q \rightarrow P)“, to much more complicated cases such as “(\neg R \rightarrow \neg \neg S) \rightarrow (\neg(\neg M \rightarrow N) \rightarrow (\neg R \rightarrow \neg \neg S))“.
An ordered step-by-step deduction constitutes a derivation in system PC if and only if each step in the deduction is either (1) a premise of the argument, (2) an axiom, or (3) derived from previous steps by modus ponens. Once again we can make this more precise with the following (more recondite) definition:
Definition: an ordered sequence of wffs \beta_1, \beta_2, ..., \beta_n is a derivation in system PC of the wff \beta_n from the premises \alpha_1, \alpha_2, ..., \alpha_m if and only if, for each wff \beta_i in the sequence \beta_1, \beta_2, ..., \beta_n, either (1) \beta_i is one of the premises \alpha_1, \alpha_2, ..., \alpha_m, (2) \beta_i is an axiom of PC, or (3) \beta_i follows from previous members of the series by the inference rule modus ponens (that is, there are previous members of the sequence, \beta_j and \beta_k, such that \beta_j takes the form \ulcorner \beta_k \rightarrow \beta_i \urcorner).
For example, consider the following argument written in the language PL’:
\(<br />
\begin{array}{l} P\\<br />
(R \rightarrow P) \rightarrow (R \rightarrow (P \rightarrow S))\\<br />
\hline R \rightarrow S<br />
\end{array}<br />
\)
The following constitutes a derivation in system PC of the conclusion from the premises:
| 1. P |
Premise |
| 2. (R \rightarrow P) \rightarrow (R \rightarrow (P \rightarrow S)) |
Premise |
| 3. P \rightarrow (R \rightarrow P) |
Instance of AS1 |
| 4. R \rightarrow P |
1,3 MP |
| 5. R \rightarrow (P \rightarrow S) |
2,4 MP |
| 6. (R \rightarrow (P \rightarrow S)) \rightarrow ((R \rightarrow P) \rightarrow (R \rightarrow S)) |
Instance of AS2 |
| 7. (R \rightarrow P) \rightarrow (R \rightarrow S) |
5,6 MP |
| 8. R \rightarrow S |
4,7 MP |
Historically, the original axiomatic systems for logic were designed to be akin to other axiomatic systems found in mathematics, such as Euclid’s axiomatization of geometry. The goal of developing an axiomatic system for logic was to create a system in which to derive truths of logic making use only of the axioms of the system and the inference rule(s). Those wffs that can be derived from the axioms and inference rule alone, that is, without making use of any additional premises, are called theorems or theses of the system. To make this more precise:
Definition: a wff \alpha is said to be a theorem of PC if and only if there is an ordered sequence of wffs, specifically, a derivation, \beta_1, \beta_2, ..., \beta_n such that, \alpha is \beta_n and each wff \beta_i in the sequence \beta_1, \beta_2, ..., \beta_n, is such that either (1) \beta_i is an axiom of PC, or (2) \beta_i follows from previous members of the series by modus ponens.
One very simple theorem of system PC is the wff “P \rightarrow P“. We can show that it is a theorem by constructing a derivation of “P \rightarrow P” that makes use only of axioms and MP and no additional premises.
| 1. P \rightarrow (P \rightarrow P) |
Instance of AS1 |
| 2. P \rightarrow ((P \rightarrow P) \rightarrow P) |
Instance of AS1 |
| 3. (P \rightarrow ((P \rightarrow P) \rightarrow P)) \rightarrow ((P \rightarrow (P \rightarrow P)) \rightarrow (P \rightarrow P)) |
Instance of AS2 |
| 4. (P \rightarrow (P \rightarrow P)) \rightarrow (P \rightarrow P) |
2,3 MP |
| 5. P \rightarrow P |
1,4 MP |
It is fairly easy to see that not only is “P \rightarrow P” a theorem of PC, but so is any wff of the form \ulcorner \alpha \rightarrow \alpha \urcorner. Whatever \alpha happens to be, there will be a derivation in PC of the same form:
| 1. \alpha \rightarrow (\alpha \rightarrow \alpha) |
Instance of AS1 |
| 2. \alpha \rightarrow ((\alpha \rightarrow \alpha) \rightarrow \alpha) |
Instance of AS1 |
| 3. (\alpha \rightarrow ((\alpha \rightarrow \alpha) \rightarrow \alpha)) \rightarrow ((\alpha \rightarrow (\alpha \rightarrow \alpha)) \rightarrow (\alpha \rightarrow \alpha)) |
Instance of AS2 |
| 4. (\alpha \rightarrow (\alpha \rightarrow \alpha)) \rightarrow (\alpha \rightarrow \alpha) |
2,3 MP |
| 5. \alpha \rightarrow \alpha |
1,4 MP |
So even if we make \alpha in the above the more complicated wff, for example, “\neg (\neg M \rightarrow N)“, a derivation with the same form shows that “\neg (\neg M \rightarrow N) \rightarrow \neg (\neg M \rightarrow N)” is also a theorem of PC. Hence, we call \ulcorner \alpha \rightarrow \alpha \urcorner a theorem schema of PC, because all of its instances are theorems of PC. From now on, let’s call it “Theorem Schema 1”, or “TS1” for short.
The following are also theorem schemata of PC:
| \alpha \rightarrow \neg \neg \alpha |
(Theorem Schema 2, or TS2) |
| \neg \alpha \rightarrow (\alpha \rightarrow \beta) |
(TS3) |
| \alpha \rightarrow (\neg \beta \rightarrow \neg (\alpha \rightarrow \beta)) |
(TS4) |
| (\alpha \rightarrow \beta) \rightarrow ((\neg \alpha \rightarrow \beta) \rightarrow \beta) |
(TS5) |
You may wish to verify this for yourself by attempting to construct the appropriate proofs for each. Be warned that some require quite lengthy derivations!
It is common to use the notation:
\vdash \beta
to mean that β is a theorem. Similarly, it is common to use the notation:
\alpha_1, \alpha_2, ..., \alpha_m \vdash \beta
to mean that it is possible to construct a derivation of \beta making use of \alpha_1, \alpha_2, ..., \alpha_m as premises.
Considered in terms of number of rules it employs, the axiomatic system PC is far less complex than the system of natural deduction sketched in the previous section. The natural deduction system made use of nine inference rules, ten rules of replacement and two additional proof techniques. The axiomatic system instead, makes use of three axiom schemata and a single inference rule and no additional proof techniques. Yet, the axiomatic system is not lacking in any way.
Indeed, for any argument using language PL’ that is logically valid according to truth tables it is possible to construct a derivation in system PC for that argument. Moreover, every wff of language PL’ that is a logical truth, that is, a tautology according to truth tables, is a theorem of PC. The reverse of these results is true as well; every theorem of PC is a tautology, and every argument for which a derivation in system PC exists is logically valid according to truth tables. These and other features of the Propositional Calculus are discussed, and some are even proven in the next section below.
While the Propositional Calculus is simpler in one way than the natural deduction system sketched in the previous section, in many ways it is actually more complicated to use. For any given argument, a deduction of the conclusion from the premises conducted in PC is likely to be far longer and less psychologically natural than one carried out in a natural deduction system. Such deductions are only simpler in the sense that fewer distinct rules are employed.
System PC is only one of many possible ways of axiomatizing propositional logic. Some systems differ from PC in only very minor ways. For example, we could alter our definition of “axiom” so that a wff is an axiom iff it is an instance of (A1), an instance of (A2), or an instance of the following:
(A3′) (\neg \alpha \rightarrow \neg \beta) \rightarrow (\beta \rightarrow \alpha)
Replacing axiom schema (A3) with (A3′), while altering the way certain deductions must be constructed (making the proofs of many important results longer), has little effect otherwise; the resulting system would have all the same theorems and every argument for which a deduction is possible in the system above would also have a deduction in the revised system, and vice versa.
We also noted above that, strictly speaking, there are an infinite number of axioms of system PC. Instead of utilizing an infinite number of axioms, we might alternatively have utilized only three axioms, namely, the specific wffs:
(A1*) P \rightarrow (Q \rightarrow P)
(A2*) (P \rightarrow (Q \rightarrow R)) \rightarrow ((P \rightarrow Q) \rightarrow (P \rightarrow R))
(A3*) (\neg P \rightarrow \neg Q) \rightarrow ((\neg P \rightarrow Q) \rightarrow P)
Note that (A1*) is just a unique wff; on this approach, the wff “(\neg R \rightarrow \neg \neg S) \rightarrow (\neg(\neg M \rightarrow N) \rightarrow (\neg R \rightarrow \neg \neg S))” would not count as an axiom, even though it shares a common form with (A1*). To such a system it would be necessary to add an additional inference rule, a rule of substitution or uniform replacement. This would allow one to infer, from a theorem of the system, the result of uniformly replacing any given statement letter (for example, ‘P‘ or ‘Q‘) that occurs within the theorem, with any wff, simple or complex, provided that the same wff replaces all occurrences of the same statement letter in the theorem. On this approach, “(\neg R \rightarrow \neg \neg S) \rightarrow (\neg(\neg M \rightarrow N) \rightarrow (\neg R \rightarrow \neg \neg S))“, while not an axiom, would still be a theorem because it could be derived from the rule of uniform replacement twice, that is, by first replacing ‘P‘ in (A1*) with “(\neg R \rightarrow \neg \neg S)“, and then replacing ‘Q‘ with “\neg(\neg M \rightarrow N)“. The resulting system differs in only subtle ways from our earlier system PC. System PC, strictly speaking, uses only one inference rule, but countenances an infinite number of axioms. This system uses only three axioms, but makes use of an additional rule. System PC, however, avoids this additional inference rule by allowing everything that one could get by substitution in (A1*) to be an axiom. For every theorem \alpha, therefore, if \beta is a wff obtained from \alpha by uniformly substituting wffs for statement letters in \alpha, then \beta is also a theorem of PC, because there would always be a proof of \beta analogous to the proof of \alpha only beginning from different axioms.
It is also possible to construct even more austere systems. Indeed, it is possible to utilize only a single axiom schema (or a single axiom plus a rule of replacement). One possibility, suggested by C. A. Meredith (1953), would be to define an axiom as any wff matching the following form:
((((\alpha \rightarrow \beta) \rightarrow (\neg \gamma \rightarrow \neg \delta)) \rightarrow \gamma) \rightarrow \epsilon) \rightarrow ((\epsilon \rightarrow \alpha) \rightarrow (\delta \rightarrow \alpha))
The resulting system is equally powerful as system PC and has exactly the same set of theorems. However, it is far less psychologically intuitive and straightforward, and deductions even for relatively simple results are often very long.
Historically, the first single axiom schema system made use, instead of language PL’, the even simpler language PL” in which the only connective is the Sheffer stroke, ‘|’, as discussed above. In that case, it is possible to make use only of the following axiom schema:
(\alpha | (\beta | \gamma)) | ((\delta | (\delta | \delta)) | ((\epsilon | \beta) | ((\alpha | \epsilon) | (\alpha | \epsilon))))
The inference rule of MP is replaced with the rule that from wffs of the form \ulcorner \alpha | (\beta | \gamma) \urcorner and \alpha, one can deduce the wff \gamma. This system was discovered by Jean Nicod (1917). Subsequently, a number of possible single axiom systems have been found, some faring better than others in terms of the complexity of the single axiom and in terms of how long deductions for the same results are required to be. (For research in this area, consult McCune et. al. 2002.) Generally, however the more the system allows, the shorter the deductions.
Besides axiomatic and natural deduction forms, deduction systems for propositional logic can also take the form of a sequent calculus; here, rather than specifying definitions of axioms and inference rules, the rules are stated directly in terms of derivability or entailment conditions; for example, one rule might state that if (either \alpha \vdash \beta or \alpha \vdash \gamma) then if \gamma, \alpha \vdash \beta then \alpha \vdash \beta. Sequent calculi, like modern natural deduction systems, were first developed by Gerhard Gentzen. Gentzen’s work also suggests the use of tree-like deduction systems rather than linear step-by-step deduction systems, and such tree systems have proven more useful in automated theorem-proving, that is, in the creation of algorithms for the mechanical construction of deductions (for example, by a computer). However, rather then exploring the details of these and other rival systems, in the next section, we focus on proving things about the system PC, the axiomatic system treated at length above.
7. Important Meta-Theoretic Results for the Propositional Calculus
Note: this section is relatively more technical, and is designed for audiences with some prior background in logic or mathematics. Beginners may wish to skip to the next section.
In this section, we sketch informally the proofs given for certain important features of the Propositional Calculus. Our first topic, however, concerns the language PL’ generally.
Metatheoretic result 1: Language PL’ is expressively adequate, that is, within the context of classical bivalent logic, there are no truth-functions that cannot be represented in it.
We noted in Section III(c) that the connectives ‘\land‘, ‘↔’ and ‘\lor‘ can be defined using the connectives of PL’ (‘→’ and ‘\neg‘). More generally, metatheoretic result 1 holds that any statement built using truth-functional connectives, regardless of what those connectives are, has an equivalent statement formed using only ‘→’ and ‘\neg‘. Here’s the proof.
1. Assume that \alpha is some wff built in some language containing any set of truth-functional connectives, including those not found in PL, PL’ or PL”. For example, \alpha might make use of some three or four-place truth-functional connectives, or connectives such as the exclusive or, or the sign ‘\downarrow‘, or any others you might imagine.
2. We need to show that there is a wff \beta formed only with the connectives ‘→’ and ‘\neg‘ that is logically equivalent with \alpha. Because we have already shown that forms equivalent to those built from ‘\land‘, ‘↔’, and ‘\lor‘ can be constructed from ‘→’ and ‘\neg‘, we are entitled to use them as well.
3. In order for it to be logically equivalent to \alpha, the wff \beta that we construct must have the same final truth-value for every possible truth-value assignment to the statement letters making up \alpha, or in other words, it must have the same final column in a truth table.
4. Let p_1, p_2, ..., p_n be the distinct statement letters making up \alpha. For some possible truth-value assignments to these letters, \alpha may be true, and for others \alpha may be false. The only hard case would be the one in which \alpha is contingent. If \alpha were not contingent, it must either be a tautology, or a self-contradiction. Since clearly tautologies and self-contradictions can be constructed in PL’, and all tautologies are logically equivalent to one another, and all self-contradictions are equivalent to one another, in those cases, our job is easy. Let us suppose instead that \alpha is contingent.
5. Let us construct a wff \beta in the following way.
(a) Consider in turn each truth-value assignment to the letters p_1, p_2, ..., p_n. For each truth-value assignment, construct a conjunction made up of those letters the truth-value assignment makes true, along with the negations of those letters the truth-value assignment makes false. For instance, if the letters involved are ‘A‘, ‘B‘ and ‘C‘, and the truth-value assignment makes ‘A‘ and ‘C‘ true but ‘B‘ false, consider the conjunction ‘((A \land \neg B) \land C)‘.
(b) From the resulting conjunctions, form a complex disjunction formed from those conjunctions formed in step (a) for which the corresponding truth-value assignment makes \alpha true. For example, if the truth-value assignment making ‘A‘ and ‘C‘ true but ‘B‘ false makes \alpha true, include it the disjunction. Suppose, for example, that this truth-value assignment does make \alpha true, as does that assignment in which ‘A‘ and ‘B‘ and ‘C‘ are all made false, but no other truth-value assignment makes \alpha true. In that case, the resulting disjunction would be ‘((A \land \neg B) \land C) \lor ((\neg A \land \neg B) \land \neg C)‘.
6. The wff \beta constructed in step 5 is logically equivalent to \alpha. Consider that for those truth-value assignments making \alpha true, one of the conjunctions making up the disjunction \beta is true, and hence the whole disjunction is true as well. For those truth-value assignments making \alpha false, none of the conjunctions making up \beta is true, because each conjunction will contain at least one conjunct that is false on that truth-value assignment.
7. Because \beta is constructed using only ‘\land‘, ‘\lor‘ and ‘\neg‘, and these can in turn be defined using only ‘\neg‘ and ‘→’, and because \beta is equivalent to \alpha, there is a wff built up only from ‘\neg‘ and ‘→’ that is equivalent to \alpha, regardless of the connectives making up \alpha.
8. Therefore, PL’ is expressively adequate.
Corollary 1.1: Language PL” is also expressively adequate.
The corollary follows at once from metatheoretic result 1, along with the fact, noted in Section III(c), that ‘→’, and ‘\neg‘ can be defined using only ‘|’.
Metatheoretic result 2 (a.k.a. “The Deduction Theorem”): In the Propositional Calculus, PC, whenever it holds that \alpha_1, ..., \alpha_n \vdash \beta, it also holds that \alpha_1, ..., \alpha_{n-1} \vdash \alpha_n \rightarrow \beta
What this means is that whenever we can prove a given result in PC using a certain number of premises, then it is possible, using all the same premises leaving out one exception, \alpha_n, to prove the conditional statement made up of the removed premise, \alpha_n, as antecedent and the conclusion of the original derivation, \beta, as consequent. The importance of this result is that, in effect, it shows that the technique of conditional proof, typically found in natural deduction (see Section V), is unnecessary in PC, because whenever it is possible to prove the consequent of a conditional by taking the antecedent as an additional premise, a derivation directly for the conditional can be found without taking the antecedent as a premise.
Here’s the proof:
1. Assume that \alpha_1, ..., \alpha_n \vdash \beta. This means that there is a derivation of \beta in the Propositional Calculus from the premises \alpha_1, ..., \alpha_n. This derivation takes the form of an ordered sequence \gamma_1, \gamma_2, ..., \gamma_m, where the last member of the sequence, \gamma_m, is \beta, and each member of the sequence is either (1) a premise, that is, it is one of \alpha_1, ..., \alpha_n, (2) an axiom of PC, (3) derived from previous members of the sequence by modus ponens.
2. We need to show that there is a derivation of \ulcorner \alpha_n \rightarrow \beta \urcorner, which, while possibly making use of the other premises of the argument, does not make use of \alpha_n. We’ll do this by showing that for each member, \gamma_i, of the sequence of the original derivation: \gamma_1, \gamma_2, ..., \gamma_m, one can derive \ulcorner \alpha_n \rightarrow \gamma_i \urcorner without making use of \alpha_n as a premise.
3. Each step \gamma_i in the sequence of the original derivation was gotten at in one of three ways, as mentioned in (1) above. Regardless of which case we are dealing with, we can get the result that \alpha_1, ..., \alpha_{n-1} \vdash \alpha_n \rightarrow \gamma_i. There are three cases to consider:
Case (a): Suppose \gamma_i is a premise of the original argument. Then \gamma_i is either one of \alpha_1, ..., \alpha_{n-1} or it is \alpha_n itself. In the latter subcase, what we desire to get is that \ulcorner \alpha_n \rightarrow \alpha_n \urcorner can be gotten at without using \alpha_n as a premise. Because \ulcorner \alpha_n \rightarrow \alpha_n \urcorner is an instance of TS1, we can get it without using any premises. In the latter case, notice that \gamma_i is one of the premises we’re allowed to use in the new derivation. We’re also allowed to introduce the instance of AS1, \ulcorner \gamma_i \rightarrow (\alpha_n \rightarrow \gamma_i) \urcorner. From these, we can get \ulcorner \alpha_n \rightarrow \gamma_i \urcorner by modus ponens.
Case (b): Suppose \gamma_i is an axiom. We need to show that we can get \ulcorner \alpha_n \rightarrow \gamma_i \urcorner without using \alpha_n as a premise. In fact, we can get it without using any premises. Because \gamma_i is an axiom, we can use it in the new derivation as well. As in the last case, we have \ulcorner \gamma_i \rightarrow (\alpha_n \rightarrow \gamma_i) \urcorner as another axiom (an instance of AS1). From these two axioms, we arrive at \ulcorner \alpha_n \rightarrow \gamma_i \urcorner by modus ponens.
Case (c): Suppose that \gamma_i was derived from previous members of the sequence by modus ponens. Specifically, there is some \gamma_j and \gamma_k such that both j and k are less than i, and \gamma_j takes the form \ulcorner \gamma_k \rightarrow \gamma_i \urcorner. We can assume that we have already been able to derive both \ulcorner \alpha_n \rightarrow \gamma_j \urcorner—that is, \ulcorner \alpha_n \rightarrow (\gamma_k \rightarrow \gamma_i) \urcorner—and \ulcorner \alpha_n \rightarrow \gamma_k \urcorner in the new derivation without making use of \alpha_n. (This may seem questionable in the case that either \gamma_j or \gamma_k was itself gotten at by modus ponens. But notice that this just pushes the assumption back, and eventually one will reach the beginning of the original derivation. The first two steps of the sequence, namely, \gamma_1 and \gamma_2, cannot have been derived by modus ponens, since this would require there to have been two previous members of the sequence, which is impossible.) So, in our new derivation, we already have both \ulcorner \alpha_n \rightarrow (\gamma_k \rightarrow \gamma_i) \urcorner and \ulcorner \alpha_n \rightarrow \gamma_k \urcorner.
Notice that \ulcorner (\alpha_n \rightarrow (\gamma_k \rightarrow \gamma_i)) \rightarrow ((\alpha_n \rightarrow \gamma_k) \rightarrow (\alpha_n \rightarrow \gamma_i)) \urcorner is an instance of AS2, and so it can be introduced in the new derivation. By two steps of modus ponens, we arrive at \ulcorner \alpha_n \rightarrow \gamma_i \urcorner, again without using \alpha_n as a premise.
4. If we continue through each step of the original derivation, showing for each such step \gamma_i, we can get \ulcorner \alpha_n \rightarrow \gamma_i \urcorner without using \alpha_n as a premise, eventually, we come to the last step of the original derivation, \gamma_m, which is \beta itself. Applying the procedure from step (3), we get that \ulcorner \alpha_n \rightarrow \beta \urcorner without making use of \alpha_n as a premise. Therefore, the new derivation formed in this way shows that \alpha_1, ..., \alpha_{n-1} \vdash \alpha_n \rightarrow \beta, which is what we were attempting to show.
What’s interesting about this proof for metatheoretic result 2 is that it provides a recipe, given a derivation for a certain result that makes use of one or more premises, for transforming that derivation into one of a conditional statement in which one of the premises of the original argument has become the antecedent. This may be much clearer with an example.
Consider the following derivation for the result that Q \rightarrow R \vdash (P \rightarrow Q) \rightarrow (P \rightarrow R):
| 1. Q \rightarrow R |
Premise |
| 2. (Q \rightarrow R) \rightarrow (P \rightarrow (Q \rightarrow R)) |
AS1 |
| 3. P \rightarrow (Q \rightarrow R) |
1,2 MP |
| 4. (P \rightarrow (Q \rightarrow R)) \rightarrow ((P \rightarrow Q) \rightarrow (P \rightarrow R)) |
AS2 |
| 5. (P \rightarrow Q) \rightarrow (P \rightarrow R) |
3,4 MP |
It is possible to transform the above derivation into one that uses no premises and that shows that \ulcorner (Q \rightarrow R) \rightarrow ((P \rightarrow Q) \rightarrow (P \rightarrow R)) \urcorner is a theorem of PC. The procedure for such a transformation involves looking at each step of the original derivation, and for each one, attempting to derive the same statement, only beginning with “(Q \rightarrow R) \rightarrow ...“, without making use of “(Q \rightarrow R)” as a premise. How this is done depends on whether the step is a premise, an axiom, or a result of modus ponens, and depending on which it is, applying one of the three procedures sketched in the proof above. The result is the following:
| 1. (Q \rightarrow R) \rightarrow (Q \rightarrow R) |
TS1 |
| 2. (Q \rightarrow R) \rightarrow (P \rightarrow (Q \rightarrow R)) |
AS1 |
| 3. ((Q \rightarrow R) \rightarrow (P \rightarrow (Q \rightarrow R))) \rightarrow ((Q \rightarrow R) \rightarrow ((Q \rightarrow R) \rightarrow (P \rightarrow (Q \rightarrow R)))) |
AS1 |
| 4. (Q \rightarrow R) \rightarrow ((Q \rightarrow R) \rightarrow (P \rightarrow (Q \rightarrow R))) |
2,3 MP |
| 5. ((Q \rightarrow R) \rightarrow ((Q \rightarrow R) \rightarrow (P \rightarrow (Q \rightarrow R)))) \rightarrow (((Q \rightarrow R) \rightarrow (Q \rightarrow R)) \rightarrow ((Q \rightarrow R) \rightarrow (P \rightarrow (Q \rightarrow R)))) |
AS2 |
| 6. ((Q \rightarrow R) \rightarrow (Q \rightarrow R)) \rightarrow ((Q \rightarrow R) \rightarrow (P \rightarrow (Q \rightarrow R)))) |
4,5 MP |
| 7. (Q \rightarrow R) \rightarrow (P \rightarrow (Q \rightarrow R)) |
1,6 MP |
| 8. (P \rightarrow (Q \rightarrow R)) \rightarrow ((P \rightarrow Q) \rightarrow (P \rightarrow R)) |
AS2 |
| 9. ((P \rightarrow (Q \rightarrow R)) \rightarrow ((P \rightarrow Q) \rightarrow (P \rightarrow R))) \rightarrow \big((Q \rightarrow R) \rightarrow ((P \rightarrow (Q \rightarrow R)) \rightarrow ((P \rightarrow Q) \rightarrow (P \rightarrow R)))\big) |
AS1 |
| 10. (Q \rightarrow R) \rightarrow ((P \rightarrow (Q \rightarrow R)) \rightarrow ((P \rightarrow Q) \rightarrow (P \rightarrow R))) |
8,9 MP |
| 11. \big((Q \rightarrow R) \rightarrow ((P \rightarrow (Q \rightarrow R)) \rightarrow ((P \rightarrow Q) \rightarrow (P \rightarrow R)))\big) \rightarrow (((Q \rightarrow R) \rightarrow (P \rightarrow (Q \rightarrow R))) \rightarrow ((Q \rightarrow R) \rightarrow ((P \rightarrow Q) \rightarrow (P \rightarrow R)))) |
AS2 |
| 12. ((Q \rightarrow R) \rightarrow (P \rightarrow (Q \rightarrow R))) \rightarrow ((Q \rightarrow R) \rightarrow ((P \rightarrow Q) \rightarrow (P \rightarrow R))) |
10,11 MP |
| 13. (Q \rightarrow R) \rightarrow ((P \rightarrow Q) \rightarrow (P \rightarrow R)) |
7,12 MP |
The procedure for transforming one sort of derivation into another is purely rote. Moreover, the result is quite often not the most elegant or easy way to show that which you were trying to show. Notice, for example, in the above that lines (2) and (7) are redudant, and more steps were taken than necessary. However, the purely rote procedure is effective.
This metatheoretic result is due to Jacques Herbrand (1930).
It is interesting on its own, especially when one reflects on it as a substitution or replacement for the conditional proof technique. However, it is also very useful for proving other metatheoretic results, as we shall see below.
Metatheoretic result 3: If \alpha is a wff of language PL’, and the statement letters making it up are p_1, p_2, ..., p_n, then if we consider any possible truth-value assignment to these letters, and consider the set of premises, \Delta, that contains p_1 if the truth-value assignment makes p_1 true, but contains \ulcorner \neg p_1 \urcorner if the truth-value assignment makes p_1 false, and similarly for p_2, ..., p_n, if the truth-value assignment makes \alpha true, then in PC, it holds that \Delta \vdash \alpha, and if it makes \alpha false, then \Delta \vdash \neg \alpha.
Here’s the proof.
1. By the definition of a wff, \alpha is either itself a statement letter, or ultimately built up from statement letters by the connectives ‘\neg‘ and ‘→’.
2. If \alpha is itself a statement letter, then obviously either it or its negation is a member of \Delta. It is a member of \Delta if the truth-value assignment makes it true. In that case, obviously, there is a derivation of \alpha from \Delta, since a premise maybe introduced at any time. If the truth-value assignment makes it false instead, then \ulcorner \neg \alpha \urcorner is a member of \Delta, and so we have a derivation of \ulcorner \neg \alpha \urcorner from \Delta, since again a premise may be introduced at any time. This covers the case in which our wff is simply a statement letter.
3. Suppose that \alpha is built up from some other wff \beta with the sign ‘\neg‘, that is, suppose that \alpha is \ulcorner \neg \beta \urcorner. We can assume that we have already gotten the desired result for \beta. (Either \beta is a statement letter, in which case the result holds by step (2), or is itself ultimately built up from statement letters, so even if verifying this assumption requires making a similar assumption, ultimately we will get back to statement letters.) That is, if the truth-value assignment makes \beta true, then we have a derivation of \beta from \Delta. If it makes it false, then we have a derivation of \ulcorner \neg \beta \urcorner from \Delta. Suppose that it makes \beta true. Since \alpha is the negation of \beta, the truth-value assignment must make \alpha false. Hence, we need to show that there is a derivation of \ulcorner \neg \alpha \urcorner from \Delta . Since \alpha is \ulcorner \neg \beta \urcorner, \ulcorner \neg \alpha \urcorneris \ulcorner \neg \neg \beta \urcorner. If we append to our derivation of \beta from \Delta the derivation of \ulcorner \beta \rightarrow \neg \neg \beta \urcorner, an instance of TS2, we can reach a derivation of \ulcorner \neg \neg \beta \urcorner by modus ponens, which is what was required. If we assume instead that the truth-value assignment makes \beta false, then by our assumption, there is a derivation of \ulcorner \neg \beta \urcorner from \Delta. Since \alpha is the negation of \beta, this truth-value assigment must make \alpha true. Now, \alpha simply is \ulcorner \neg \beta \urcorner, so we already have a derivation of it from \Delta.
4. Suppose instead that \alpha is built up from other wffs \beta and \gamma with the sign ‘→’, that is, suppose that \alpha is \ulcorner \beta \rightarrow \gamma \urcorner. Again, we can assume that we have already gotten the desired result for \beta and \gamma. (Again, either they themselves are statement letters or built up in like fashion from statement letters.) Suppose that the truth-value assignment we are considering makes \alpha true. Because \alpha is \ulcorner \beta \rightarrow \gamma \urcorner, by the semantics for the sign ‘→’, the truth-value assignment must make either \beta false or \gamma true. Take the first subcase. If it makes \beta false, then by our assumption, there is a derivation of \ulcorner \neg \beta \urcorner from \Delta. If we append to this the derivation of the instance of TS3, \ulcorner \neg \beta \rightarrow (\beta \rightarrow \gamma) \urcorner, by modus ponens we arrive at derivation of \ulcorner \beta \rightarrow \gamma \urcorner, that is, \alpha, from \Delta. If instead, the truth-value assignment makes \gamma true, then by our assumption there is a derivation of \gamma from \Delta. If we add to this derivation the instance of AS1, \ulcorner \gamma \rightarrow (\beta \rightarrow \gamma) \urcorner, by modus ponens, we then again arrive at a derivation of \ulcorner \beta \rightarrow \gamma \urcorner, that is, \alpha, from \Delta. If instead, the truth-value assignment makes \alpha false, then since \alpha is \ulcorner \beta \rightarrow \gamma \urcorner, the truth-value assignment in question must make \beta true and \gamma false. By our assumption, then it is possible to prove both \beta and \ulcorner \neg \gamma \urcorner from \Delta. If we concatenate these two derivations, and add to them the derivation of the instance of TS4, \ulcorner \beta \rightarrow (\neg \gamma \rightarrow \neg (\beta \rightarrow \gamma)) \urcorner, then by two applications of modus ponens, we can derive \ulcorner \neg (\beta \rightarrow \gamma) \urcorner, which is simply \ulcorner \neg \alpha \urcorner, which is what was desired.
From the above we see that the Propositional Calculus PC can be used to demonstrate the appropriate results for a complex wff if given as premises either the truth or falsity of all its simple parts. This is of course the foundation of truth-functional logic, that the truth or falsity of those complex statements one can make in it be determined entirely by the truth or falsity of the simple statements entering in to it. Metatheoretic result 3 is again interesting on its own, but it plays a crucial role in the proof of completeness, which we turn to next.
Metatheoretic result 4 (Completeness): If \alpha is a wff of language PL’ and a tautology, then \alpha is a theorem of the Propositional Calculus.
This feature of the Propositional Calculus is called completeness because it shows that the Propositional Calculus, as a deductive system aiming to capture all the truths of logic, is a success. Every wff true solely in virtue of the truth-functional nature of the connectives making it up is something that one can prove using only the axioms of PC along with modus ponens. Here’s the proof:
1. Suppose that \alpha is a tautology. This means that every possible truth-value assignment to its statement letters makes it true.
2. Let the statement letters making up \alpha be p_1, p_2, ..., p_n, arranged in some order (say alphabetically and by the numerical order of their subscripts). It follows from (1) and metatheoretic result 3, that there is a derivation in PC of \alpha using any possible set of premises that consists, for each statement letter, of either it or its negation.
3. By metatheoretic result 2, we can remove from each of these sets of premises either p_n or \ulcorner \neg p_n \urcorner, depending on which it contains, and make it an antecedent of a conditional in which \alpha is consequent, and the result will be provable without using p_n or \ulcorner \neg p_n \urcorner as a premise. This means that for every possible set of premises consisting of either p_1 or \ulcorner \neg p_1 \urcorner and so on, up until p_{n-1}, we can derive both \ulcorner p_n \rightarrow \alpha \urcorner and \ulcorner \neg p_n \rightarrow \alpha \urcorner.
4. The wff \ulcorner (p_n \rightarrow \alpha) \rightarrow ((\neg p_n \rightarrow \alpha) \rightarrow \alpha) \urcorner is an instance of TS5. Therefore, for any set of premises from which one can derive both \ulcorner p_n \rightarrow \alpha \urcorner and \ulcorner \neg p_n \rightarrow \alpha \urcorner, by two applications of modus ponens, one can also derive \alpha itself.
5. Putting (3) and (4) together, we have the result that \alpha can be derived from every possible set of premises consisting of either p_1 or \ulcorner \neg p_1 \urcorner and so on, up until p_{n-1}.
6. We can apply the same reasoning given in steps (3)-(5) to remove p_{n-1} or its negation from the premise sets by the deduction theorem, arriving at the result that for every set of premises consisting of either p_1 or \ulcorner \neg p_1 \urcorner and so on, up until p_{n-2}, it is possible to derive \alpha. If we continue to apply this reasoning, eventually, we’ll get the result that we can derive \alpha with either p_1 or its negation as our sole premise. Again, applying the deduction theorem, this means that both \ulcorner p_1 \rightarrow \alpha \urcorner and \ulcorner \neg p_1 \rightarrow \alpha \urcorner can be proven in PC without using any premises, that is, they are theorems. Concatenating the derivations of these theorems, along with the instance of TS5, \ulcorner (p_1 \rightarrow \alpha) \rightarrow ((\neg p_1 \rightarrow \alpha) \rightarrow \alpha) \urcorner, and by two applications of modus ponens, it follows that \alpha itself is a theorem, which is what we sought to demonstrate.
The above proof of the completeness of system PC is easier to appreciate when visualized. Suppose, just for the sake of illustration, that the tautology we wish to demonstrate in system PC has three statement letters, ‘P‘, ‘Q‘ and ‘R‘. There are eight possible truth-value assignments to these letters, and since \alpha is a tautology, all of them make \alpha true. We can sketch in at least this much of \alpha‘s truth table:
|
P
|
Q
|
R
|
| |
\alpha
|
|
T
T
T
T
F
F
F
F
|
T
T
F
F
T
T
F
F
|
T
F
T
F
T
F
T
F
|
|
T
T
T
T
T
T
T
T
|
Now, given this feature of \alpha, it follows from metatheoretic result 3, that for every possible combination of premises that consists of either ‘P‘ or “\neg P” (but not both), either ‘Q‘ or “\neg Q“, and ‘R‘ or “\neg R“, it is possible from those premises to construct a derivation showing \alpha. This can be visualized as follows:
| P, Q, R |
\vdash \alpha |
| P, Q, \neg R |
\vdash \alpha |
| P, \neg Q, R |
\vdash \alpha |
| P, \neg Q, \neg R |
\vdash \alpha |
| \neg P, Q, R |
\vdash \alpha |
| \neg P, Q, \neg R |
\vdash \alpha |
| \neg P, \neg Q, R |
\vdash \alpha |
| \neg P, \neg Q, \neg R |
\vdash \alpha |
By the deduction theorem, we can pull out the last premise from each list of premises and make it an antecedent. However, because from the same remaining list of premises we get both \ulcorner R \rightarrow \alpha \urcorner and \ulcorner \neg R \rightarrow \alpha \urcorner, we can get \alpha by itself from those premises according to TS5. Again, to visualize this:
| P, Q |
\vdash R \rightarrow \alpha |
… and so P, Q \vdash \alpha |
| P, Q |
\vdash \neg R \rightarrow \alpha |
| P, \neg Q |
\vdash R \rightarrow \alpha |
… and so P, \neg Q \vdash \alpha |
| P, \neg Q |
\vdash \neg R \rightarrow \alpha |
| \neg P, Q |
\vdash R \rightarrow \alpha |
… and so \neg P, Q \vdash \alpha |
| \neg P, Q |
\vdash \neg R \rightarrow \alpha |
| \neg P, \neg Q |
\vdash R \rightarrow \alpha |
… and so \neg P, \neg Q \vdash \alpha |
| \neg P, \neg Q |
\vdash \neg R \rightarrow \alpha |
We can continue this line of reasoning until all the premises are removed.
| P, Q \vdash \alpha |
P \vdash Q \rightarrow \alpha |
and so P \vdash \alpha |
and so \vdash P \rightarrow \alpha |
and so \vdash \alpha |
| P, \neg Q \vdash \alpha |
P \vdash \neg Q \rightarrow \alpha |
| \neg P, Q \vdash \alpha |
\neg P \vdash Q \rightarrow \alpha |
and so \neg P \vdash \alpha |
and so \vdash \neg P \rightarrow \alpha |
| \neg P, \neg Q \vdash \alpha |
\neg P \vdash \neg Q \rightarrow \alpha |
At the end of this process, we see that \alpha is a theorem. Despite only having three axiom schemata and a single inference rule, it is possible to prove any tautology in the simple Propositional Calculus, PC. It is complete in the requisite sense.
This method of proving the completeness of the Propositional Calculus is due to Kalmár (1935).
Corollary 4.1: If a given wff \beta of language PL’ is a logical consequence of a set of wffs \alpha_1, \alpha_2, ..., \alpha_n, according to their combined truth table, then there is a derivation of \beta with \alpha_1, \alpha_2, ..., \alpha_n as premises in the Propositional Calculus.
Without going into the details of the proof of this corollary, it follows from the fact that if \beta is a logical consequence of \alpha_1, \alpha_2, ..., \alpha_n, then the wff of the form \ulcorner (\alpha_1 \rightarrow (\alpha_2 \rightarrow ... (\alpha_n \rightarrow \beta)...)) \urcorner is a tautology. As a tautology, it is a theorem of PC, and so if one begins with its derivation in PC and appends a number of steps of modus ponens using \alpha_1, \alpha_2, ..., \alpha_n as premises, one can derive \beta.
Metatheoretic result 5 (Soundness): If a wff \alpha is a theorem of the Propositional Calculus (PC), then \alpha is a tautology.
Above, we saw that all tautologies are theorems of PC. The reverse is also true: all theorems of PC are tautologies. Here’s the proof:
1. Suppose that \alpha is a theorem of PC. This means that there is an ordered sequence of steps, each of which is either (1) an axiom of PC, or (2) derived from previous members of the sequence by modus ponens, and such that \alpha is the last member of the sequence.
2. We can show that not only is \alpha a tautology, but so are all the members of the sequence leading to it. The first thing to note is that every axiom of PC is a tautology. To be an axiom of PC, a wff must match one of the axiom schemata AS1, AS2 or AS3. All such wffs must be tautologous; this can easily be verified by constructing truth tables for AS1, AS2 and AS3. (This is left to the reader.)
3. The rule of modus ponens preserves tautologyhood. If \alpha is a tautology and \ulcorner \alpha \rightarrow \beta \urcorner is also a tautology, \beta must be a tautology as well. This is because if \beta were not a tautology, it would be false on some truth-value assignments. However, \alpha, as a tautology, is true for all truth-value assignments. Because a statement of the form \ulcorner \alpha \rightarrow \beta \urcorner is false for any truth-value assignment making \alpha true and \beta false, it would then follow that some truth-value assignment makes \ulcorner \alpha \rightarrow \beta \urcorner false, which is impossible if it too is a tautology.
4. Hence, we see that the axioms with which we begin the sequence, and every step derived from them using modus ponens, must all be tautologies, and consequently, the last step of the sequence, \alpha, must also be a tautology.
This result is called the soundness of the Propositional Calculus; it shows that in it, one cannot demonstrate something that is not logically true.
Corollary 5.1: A wff \alpha of language PL’ is a tautology if and only if \alpha is a theorem of system PC.
This follows immediately from metatheoretic results 4 and 5.
Corollary 5.2 (Consistency): There is no wff \alpha of language PL’ such that both \alpha and \ulcorner \neg \alpha \urcorner are theorems of the Propositional Calculus (PC).
Due to metatheoretic result 5, all theorems of PC are tautologies. It is therefore impossible for both \alpha and \ulcorner \neg \alpha \urcorner to be theorems, as this would require both to be tautologies. That would mean that both are true for all truth-value assignments, but obviously, they must have different truth-values for any given truth-value assignment, and cannot both be true for any, much less all, such assignments.
This result is called consistency because it guarantees that no theorem of system PC can be inconsistent with any other theorem.
Corollary 5.3: If there is a derivation of the wff \beta with \alpha_1, \alpha_2, ..., \alpha_n as premises in the Propositional Calculus, then \beta is a logical consequence of the set of wffs \alpha_1, \alpha_2, ..., \alpha_n, according to their combined truth table.
This is the converse of Corollary 4.1. It follows by the reverse reasoning involved in that corollary. If there is a derivation of \beta taking \alpha_1, \alpha_2, ..., \alpha_n as premises, then by multiple applications of the deduction theorem (Metatheoretic result 2), it follows that \ulcorner (\alpha_1 \rightarrow (\alpha_2 \rightarrow ... (\alpha_n \rightarrow \beta)...)) \urcorner is a theorem of PC. By metatheoretic result 5, \ulcorner (\alpha_1 \rightarrow (\alpha_2 \rightarrow ... (\alpha_n \rightarrow \beta)...)) \urcorner must be a tautology. If so, then there cannot be a truth-value assignment making all of \alpha_1, \alpha_2, ..., \alpha_n true while making \beta false, and so \beta is a logical consequence of \alpha_1, \alpha_2, ..., \alpha_n.
Corollary 5.4: There is a derivation of the wff \beta with \alpha_1, \alpha_2, ..., \alpha_n as premises in the Propositional Calculus if and only if \beta is a logical consequence of \alpha_1, \alpha_2, ..., \alpha_n, according to their combined truth table.
This follows at once from corollaries 4.1 and 5.3. In sum, then, the Propositional Calculus method of demonstrating something to follow from the axioms of logic is extensionally equivalent to the truth table method of determining whether or not something is a logical truth. Similarly, the truth-table method for testing the validity of an argument is equivalent to the test of being able to construct a derivation for it in the Propositional Calculus. In short, the Propositional Calculus is exactly what we wanted it to be.
Corollary 5.5 (Decidability): The Propositional Calculus (PC) is decidable, that is, there is a finite, effective, rote procedure for determining whether or not a given wff \alpha is a theorem of PC or not.
By Corollary 5.1, a wff \alpha is a theorem of PC if and only if it is a tautology. Truth tables provide a rote, effective, and finite procedure for determining whether or not a given wff is a tautology. They therefore also provide such a procedure for determining whether or not a given wff is a theorem of PC.
8. Forms of Propositional Logic
So far we have focused only on classical, truth-functional propositional logic. Its distinguishing features are (1) that all connectives it uses are truth-functional, that is, the truth-values of complex statements formed with those connectives depend entirely on the truth-values of the parts, and (2) that it assumes bivalence: all statements are taken to have exactly one of two truth-values—truth or falsity—with no statement assigned both truth-values or neither. Classical truth-functional propositional logic is the most widely studied and discussed form, but there are other forms of propositional logic.
Perhaps the most well known form of non-truth-functional propositional logic is modal propositional logic. Modal propositional logic involves introducing operators into the logic involving necessity and possibility, usually along with truth-functional operators such as ‘→’, ‘\land‘, ‘\neg‘, etc.. Typically, the sign ‘\Box‘ is used in place of the English operator, “it is necessary that…”, and the sign ‘\Diamond‘ is used in place of the English operator “it is possible that…”. Sometimes both these operators are taken as primitive, but quite often one is defined in terms of the other, since \ulcorner \neg \Box \neg \alpha \urcorner would appear to be logically equivalent with \ulcorner \Diamond \alpha \urcorner. (Roughly, it means the same to say that something is not necessarily not true as it does to say that it is possibly true.)
To see that modal propositional logic is not truth-functional, just consider the following pair of statements:
\Box P
\Box (P \lor \neg P)
The first states that it is necessary that P. Let us suppose in fact that ‘P‘ is true, but might have been false. Since P is not necessarily true, the statement “\Box P” is false. However, the statement “P \lor \neg P” is a tautology and so it could not be false. Hence, the statement “\Box (P \lor \neg P)” is true. Notice that both ‘P‘ and “P \lor \neg P” are true, but different truth-values result when the operator ‘\Box‘ is added. So, in modal propositional logic, the truth-value of a statement does not depend entirely on the truth-values of the parts.
The study of modal propositional logic involves identifying under what conditions statements involving the operators ‘\Box‘ and ‘\Diamond‘ should be regarded as true. Different notions or conceptions of necessity lead to different answers to that question. It also involves discovering what inference rules or systems of deduction would be appropriate given the addition of these operators. Here, there is more controversy than with classical truth-functional logic. For example, in the context of discussions of axiomatic systems for modal propositional logic, very different systems result depending on whether instances of the following schemata are regarded as axiomatic truths, or even truths at all:
\Box \alpha \rightarrow \Box \Box \alpha
\Diamond \alpha \rightarrow \Box \Diamond \alpha
If a statement is necessary, is it necessarily necessary? If a statement is possible, is it necessarily possible? A positive answer to the first question is a key assumption in a logical system known as S4 modal logic. Positive answers to both these questions are key assumptions in a logical system known as S5 modal logic. Other systems of modal logic that avoid such assumptions have also been developed. (For an excellent introduction survey, see Hughes and Cresswell 1996.)
Deontic propositional logic and epistemic propositional logic are two other forms of non-truth-functional propositional logic. The former involves introduction of operators similar to the English operators “it is morally obligatory that…” and “it is morally permissible that…”. Obviously, some things that are in fact true were not morally obligatory, whereas some things that are true were morally obligatory. Again, the truth-value of a statement in deontic logic does not depend wholly on the truth-value of the parts. Epistemic logic involves the addition of operators similar to the English operators “it is known that…” and “it is believed that …”. While everything that is known to be the case is in fact the case, not everything that is the case is known to be the case, so a statement built up with a “it is known that…” will not depend entirely on the truth of the proposition it modifies, even if it depends on it to some degree.
Yet another widely studied form of non-truth-functional propositional logic is relevance propositional logic, which involves the addition of an operator ‘Rel‘ used to connect two statements \alpha and \beta to form a statement \ulcorner Rel(\alpha, \beta) \urcorner, which is interpreted to mean that \alpha is related to \beta in theme or subject matter. For example, if ‘P‘ means that Ben loves Jennifer and ‘Q‘ means that Jennifer is a pop star, then the statement “Rel(P, Q)” is regarded as true; whereas if ‘S‘ means The sun is shining in Tokyo, then “Rel(P, S)” is false, and hence “\neg Rel(P, S)” is true. Obviously, whether or not a statement formed using the connective ‘Rel‘ is true does not depend solely on the truth-value of the propositions involved.
One of the motivations for introducing non-truth-functional propositional logics is to make up for certain oddities of truth-functional logic. Consider the truth table for the sign ‘→’ used in Language PL. A statement of the form \ulcorner \alpha \rightarrow \beta \urcorner is regarded as true whenever its antecedent is false or consequent is true. So if we were to translate the English sentence, “if the author of this article lives in France, then the moon is made of cheese” as “E \rightarrow M“, then strangely, it comes out as true given the semantics of the sign ‘→’ because the antecedent, ‘E‘, is false. In modal propositional logic it is possible to define a much stronger sort of operator to use to translate English conditionals as follows:
\ulcorner \alpha ⥽ \beta \urcorner is defined as \ulcorner \Box (\alpha \rightarrow \beta) \urcorner
If we transcribe the English “if the author of this article lives in France, then the moon is made of cheese” instead as “E ⥽ M“, then it does not come out as true, because presumably, it is possible for the author of this article to live in France without the moon being made of cheese. Similarly, in relevance logic, one could also define a stronger sort of connective as follows:
\ulcorner \alpha \Rightarrow \beta \urcorner is defined as \ulcorner Rel(\alpha, \beta) \land (\alpha \rightarrow \beta) \urcorner
Here too, if we were to transcribe the English “if the author of this article lives in France, then the moon is made of cheese” as “E \Rightarrow M” instead of simply “E \rightarrow M“, it comes out as false, because the author of this article living in France is not related to the composition of the moon.
Besides non-truth-functional logic, other logical systems differ from classical truth-functional logic by allowing statements to be assigned truth-values other than truth or falsity, or to be assigned neither truth nor falsity or both truth and falsity. These sorts of logical systems may still be truth-functional in the sense that the truth-value of a complex statement may depend entirely on the truth-values of the parts, but the rules governing such truth-functionality would be more complicated than for classical logic, because it must consider possibilities that classical logic rejects.
Many-valued or multivalent logics are those that consider more than two truth-values. They may admit anything from three to an infinite number of possible truth-values. The simplest sort of many-valued logic is one that admits three truth-values, for example, truth, falsity and indeterminancy. It might seem, for example, that certain statements such as statements about the future, or paradoxical statements such as “this sentence is not true” cannot easily be assigned either truth or falsity, and so, it might be concluded, must have an indeterminate truth-value. The admission of this third truth-value requires one to expand the truth tables given in Section III(a). There, we gave a truth table for statements formed using the operator ‘→’; in three-valued logic, we have to decide what the truth-value of a statement of the form \ulcorner \alpha \rightarrow \beta \urcorner is when either or both of \alpha and \beta has an indeterminate truth-value. Arguably, if any component of a statement is indeterminate in truth-value, then the whole statement is indeterminate as well. This would lead to the following expanded truth table:
| \alpha |
\beta |
(\alpha \rightarrow \beta) |
|
T
T
T
I
I
I
F
F
F
|
T
I
F
T
I
F
T
I
F
|
T
I
F
I
I
I
T
I
T
|
However, we might wish to retain the feature of classical logic that a statement of the form \ulcorner \alpha \rightarrow \beta \urcorner is always true when its antecedent is false or its consequent is true, and hold that it is indeterminate only when its antecedent is indeterminate and its consequent false or when its antecedent is true and its consequent indeterminate, so that its truth table appears:
| \alpha |
\beta |
(\alpha \rightarrow \beta) |
|
T
T
T
I
I
I
F
F
F
|
T
I
F
T
I
F
T
I
F
|
T
I
F
T
T
I
T
T
T
|
Such details will have an effect on the remainders of the logical systems. For example, if an axiomatic or natural deduction system is created, and a desirable feature is that something be provable from no premises if and only if it is a tautology in the sense of being true (and not just not false) for all possible truth-value assignments, if we make use of the first truth table for ‘→’, then “P \rightarrow P” should not be provable, because it is indeterminate when ‘P‘ is, whereas if we use the second truth table, then “P \rightarrow P” should be provable, since it is a tautology according to that truth table, that is, it is true regardless of which of the three truth-values is assigned to ‘P‘.
Here we get just a glimpse at the complications created by admitting more than two truth-values. If more than three are admitted, and possibly infinitely many, then the issues become even more complicated.
Intuitionistic propositional logic results from rejecting the assumption that every statement is true or false, and countenances statements that are neither. The result is a sort of logic very much akin to a three-valued logic, since “neither true nor false”, while strictly speaking the rejection of a truth-value, can be thought of as though it were a third truth-value. In intuitionistic logic, the so-called “law of excluded middle,” that is, the law that all statements of the form \ulcorner \alpha \lor \neg \alpha \urcorner are true is rejected. This is because intuitionistic logic takes truth to coincide with direct provability, and it may be that certain statements, such as Goldbach’s conjecture in mathematics, are neither provably the case nor provably not the case.
Paraconsistent propositional logic is even more radical, in countenancing statements that are both true and false. Again, depending on the nature of the system, semantic rules have to be given that determine what the truth-value or truth-values a complex statement has when its component parts are both true and false. Such decisions determine what sorts of new or restricted rules of inference would apply to the logical system. For example, paraconsistent logics, if not trivial, must restrict the rules of inference allowable in classical truth-functional logic, because in systems such as those sketched in Sections V and VI above, from a contradiction, that is, a statement of the form \ulcorner \alpha \land \neg \alpha \urcorner, it is possible to deduce any other statement. Consider, for example, the following deduction in the natural deduction system sketched in Section V.
| 1. P \land \neg P |
Premise |
| 2. P |
1 Simp |
| 3. \neg P |
1 Simp |
| 4. P \lor Q |
2 Add |
| 5. Q |
3,4 DS |
In order to avoid this result, paraconsistent logics must restrict the notion of a valid inference. In order for an inference to be considered valid, not only must it be truth-preserving, that is, that it be impossible to arrive at something untrue when starting with true premises, it must be falsity-avoiding, that is, it must be impossible, starting with true premises, to arrive at something that is false. In paraconsistent logic, where a statement can be both true and false, these two requirements do not coincide. The inference rule of disjunctive syllogism, while truth-preserving, is not falsity-avoiding. In cases in which its premises are true, its conclusion can still be false; more specifically, provided that at least one of its premises is both true and false, its conclusion can be false.
Other forms of non-classical propositional logic, and non-truth-functional propositional logic, continue to be discovered. Obviously any deviance from classical bivalent propositional logic raises complicated logical and philosophical issues that cannot be fully explored here. For more details both on non-classical logic, and on non-truth-functional logic, see the recommended reading section.
9. Suggestions for Further Reading
- Anderson, A. R. and N. D. Belnap [and J. M. Dunn]. 1975 and 1992. Entailment. 2 vols. Princeton, NJ: Princeton University Press.
- Bocheński, I. M. 1961. A History of Formal Logic. Notre Dame, Ind.: University of Notre Dame Press.
- Boole, George. 1847. The Mathematical Analysis of Logic. Cambridge: Macmillan.
- Boole, George. 1854. An Investigation into the Laws of Thought. Cambridge: Macmillan.
- Carroll, Lewis. 1958. Symbolic Logic and the Game of Logic. London: Dover.
- Church, Alonzo. 1956. Introduction to Mathematical Logic. Princeton, NJ: Princeton University Press.
- Copi, Irving. 1953. Introduction to Logic. New York: Macmillan.
- Copi, Irving. 1974. Symbolic Logic. 4th ed. New York: Macmillan.
- da Costa, N. C. A. 1974. “On the Theory of Inconsistent Formal Systems,” Notre Dame Journal of Formal Logic 25: 497-510.
- De Morgan, Augustus. 1847. Formal Logic. London: Walton and Maberly.
- Fitch, F. B. 1952. Symbolic Logic: An Introduction. New York: Ronald Press.
- Frege, Gottlob. 1879. Begriffsschrift, ene der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle: L. Nerbert. Published in English as Conceptual Notation, ed. and trans. by Terrell Bynum. Clarendon: Oxford, 1972.
- Frege, Gottlob. 1923. “Gedankengefüge,” Beträge zur Philosophie des deutchen Idealismus 3: 36-51. Published in English as “Compound Thoughts,” in The Frege Reader, edited by Michael Beaney. Oxford: Blackwell, 1997.
- Gentzen, Gerhard. 1934. “Untersuchungen über das logische Schließen” Mathematische Zeitschrift 39: 176-210, 405-31. Published in English as “Investigations into Logical Deduction,” in Gentzen 1969.
- Gentzen, Gerhard. 1969. Collected Papers. Edited by M. E. Szabo. Amsterdam: North-Holland Publishing.
- Haack, Susan. 1996. Deviant Logic, Fuzzy Logic. Chicago: University of Chicago Press.
- Herbrand, Jacques. 1930. “Recherches sur la théorie de la démonstration,” Travaux de la Société des Sciences et de la Lettres de Varsovie 33: 133-160.
- Hilbert, David and William Ackermann. 1950. Principles of Mathematical Logic. New York: Chelsea.
- Hintikka, Jaakko. 1962. Knowledge and Belief: An Introduction to the Logic of the Two Notions. Ithaca: Cornell University Press.
- Hughes, G. E. and M. J. Cresswell. 1996. A New Introduction to Modal Logic. London: Routledge.
- Jevons, W. S. 1880. Studies in Deductive Logic. London: Macmillan.
- Kalmár, L. 1935. “Über die Axiomatisierbarkeit des Aussagenkalküls,” Acta Scientiarum Mathematicarum 7: 222-43.
- Kleene, Stephen C. 1952. Introduction to Metamathematics. Princeton, NJ: Van Nostrand.
- Kneale, William and Martha Kneale. 1962. The Development of Logic. Clarendon: Oxford.
- Lewis, C. I. and C. H. Langford. 1932. Symbolic Logic. New York: Dover.
- Łukasiewicz, Jan. 1920. “O logice trojwartosciowej,” Ruch Filozoficny 5: 170-171. Published in English as “On Three-Valued Logic,” in Łukasiewicz 1970.
- Łukasiewicz, Jan. 1970. Selected Works. Amsterdam: North-Holland.
- Łukasiewicz, Jan and Alfred Tarski. 1930. “Untersuchungen über den Aussagenkalkül,” Comptes Rendus des séances de la Société des Sciences et de la Lettres de Varsovie 32: 30-50. Published in English as “Investigations into the Sentential Calculus,” in Tarski 1956.
- Mally, Ernst. 1926. Grundgesetze des Sollens: Elemente der Logik des Willens. Graz: Leuschner und Lubensky.
- McCune, William, Robert Veroff, Branden Fitelson, Kenneth Harris, Andrew Feist and Larry Wos. 2002. “Short Single Axioms for Boolean Algebra,” Journal of Automated Reasoning 29: 1-16.
- Mendelson, Elliot. 1997. Introduction to Mathematical Logic. 4th ed. London: Chapman and Hall.
- Meredith, C. A. 1953. “Single Axioms for the Systems (C, N), (C, O) and (A, N) of the Two-valued Propositional Calculus,” Journal of Computing Systems 3: 155-62.
- Müller, Eugen, ed. 1909. Abriss der Algebra der Logik, by E. Schröder. Leipzig: Teubner.
- Nicod, Jean. 1917. “A Reduction in the Number of the Primitive Propositions of Logic,” Proceedings of the Cambridge Philosophical Society 19: 32-41.
- Peirce, C. S. 1885. “On the Algebra of Logic,” American Journal of Mathematics 7: 180-202.
- Post, Emil. 1921. “Introduction to a General Theory of Propositions,” American Journal of Mathematics 43: 163-185.
- Priest, Graham, Richard Routley and Jean Norman, eds. 1990. Paraconsistent Logic. Munich: Verlag.
- Prior, Arthur. 1990. Formal Logic. 2nd. ed. Oxford: Oxford University Press.
- Read, Stephen, 1988. Relevant Logic. New York: Blackwell.
- Rescher, Nicholas. 1966. The Logic of Commands. London: Routledge and Kegan Paul.
- Rescher, Nicholas. 1969. Many-Valued Logic. New York: McGraw Hill.
- Rosser, J. B. 1953. Logic for Mathematicians. New York: McGraw Hill.
- Russell, Bertrand. 1906. “The Theory of Implication,” American Journal of Mathematics 28: 159-202.
- Schlesinger, G. N. 1985. The Range of Epistemic Logic. Aberdeen: Aberdeen University Press.
- Sheffer, H. M. 1913. “A Set of Five Postulates for Boolean Algebras with Application to Logical Constants,” Transactions of the American Mathematical Society 14: 481-88.
- Smullyan, Raymond. 1961. Theory of Formal Systems. Princeton: Princeton University Press.
- Tarski, Alfred. 1956. Logic, Semantics and Meta-Mathematics. Oxford: Oxford University Press.
- Urquhart, Alasdair. 1986. “Many-valued Logic,” In Handbook of Philosophical Logic, vol. 3, edited by D. Gabbay and F. Guenthner. Dordrecht: Reidel.
- Venn, John. 1881. Symbolic Logic. London: Macmillan.
- Whitehead, Alfred North and Bertrand Russell. 1910-1913. Principia Mathematica. 3 vols. Cambridge: Cambridge University Press.
- Wittgenstein, Ludwig. 1922. Tractatus Logico-Philosophicus. London: Routledge and Kegan Paul.
Author Information
Kevin C. Klement
Email: klement@philos.umass.edu
University of Massachusetts, Amherst
U. S. A.



 Known in antiquity as an accomplished orator, a companion of Socrates, and a philosopher, Antisthenes presently gains renown from his status as either a founder or a forerunner of
Known in antiquity as an accomplished orator, a companion of Socrates, and a philosopher, Antisthenes presently gains renown from his status as either a founder or a forerunner of 
 G. E. Moore was a highly influential British philosopher of the early twentieth century. His career was spent mainly at Cambridge University, where he taught alongside Bertrand Russell and, later, Ludwig Wittgenstein. The period of their overlap there has been called the “golden age” of Cambridge philosophy. Moore’s main contributions to philosophy were in the areas of metaphysics, epistemology, ethics, and philosophical methodology. In
G. E. Moore was a highly influential British philosopher of the early twentieth century. His career was spent mainly at Cambridge University, where he taught alongside Bertrand Russell and, later, Ludwig Wittgenstein. The period of their overlap there has been called the “golden age” of Cambridge philosophy. Moore’s main contributions to philosophy were in the areas of metaphysics, epistemology, ethics, and philosophical methodology. In  Johann Gottlieb Fichte is one of the major figures in German philosophy in the period between Kant and Hegel. Initially considered one of Kant’s most talented followers, Fichte developed his own system of transcendental philosophy, the so-called Wissenschaftslehre. Through technical philosophical works and popular writings Fichte exercised great influence over his contemporaries, especially during his years at the University of Jena. His influence waned towards the end of his life, and Hegel’s subsequent dominance relegated Fichte to the status of a transitional figure whose thought helped to explain the development of
Johann Gottlieb Fichte is one of the major figures in German philosophy in the period between Kant and Hegel. Initially considered one of Kant’s most talented followers, Fichte developed his own system of transcendental philosophy, the so-called Wissenschaftslehre. Through technical philosophical works and popular writings Fichte exercised great influence over his contemporaries, especially during his years at the University of Jena. His influence waned towards the end of his life, and Hegel’s subsequent dominance relegated Fichte to the status of a transitional figure whose thought helped to explain the development of 

 The subject matter of architectonic is the structure of all human knowledge. The purpose of providing an architectonic scheme is to classify different types of knowledge and explain the relationships that exist between these classifications. The architectonic system of
The subject matter of architectonic is the structure of all human knowledge. The purpose of providing an architectonic scheme is to classify different types of knowledge and explain the relationships that exist between these classifications. The architectonic system of  Jean-Jacques Rousseau was one of the most influential thinkers during the Enlightenment in eighteenth century Europe. His first major philosophical work, A Discourse on the Sciences and Arts, was the winning response to an essay contest conducted by the Academy of Dijon in 1750. In this work, Rousseau argues that the progression of the sciences and arts has caused the corruption of virtue and morality. This discourse won Rousseau fame and recognition, and it laid much of the philosophical groundwork for a second, longer work, The Discourse on the Origin of Inequality. The second discourse did not win the Academy’s prize, but like the first, it was widely read and further solidified Rousseau’s place as a significant intellectual figure. The central claim of the work is that human beings are basically good by nature, but were corrupted by the complex historical events that resulted in present day civil society.Rousseau’s praise of nature is a theme that continues throughout his later works as well, the most significant of which include his comprehensive work on the philosophy of education, the Emile, and his major work on political philosophy, The Social Contract: both published in 1762. These works caused great controversy in France and were immediately banned by Paris authorities. Rousseau fled France and settled in Switzerland, but he continued to find difficulties with authorities and quarrel with friends. The end of Rousseau’s life was marked in large part by his growing paranoia and his continued attempts to justify his life and his work. This is especially evident in his later books, The Confessions, The Reveries of the Solitary Walker, and Rousseau: Judge of Jean-Jacques.
Jean-Jacques Rousseau was one of the most influential thinkers during the Enlightenment in eighteenth century Europe. His first major philosophical work, A Discourse on the Sciences and Arts, was the winning response to an essay contest conducted by the Academy of Dijon in 1750. In this work, Rousseau argues that the progression of the sciences and arts has caused the corruption of virtue and morality. This discourse won Rousseau fame and recognition, and it laid much of the philosophical groundwork for a second, longer work, The Discourse on the Origin of Inequality. The second discourse did not win the Academy’s prize, but like the first, it was widely read and further solidified Rousseau’s place as a significant intellectual figure. The central claim of the work is that human beings are basically good by nature, but were corrupted by the complex historical events that resulted in present day civil society.Rousseau’s praise of nature is a theme that continues throughout his later works as well, the most significant of which include his comprehensive work on the philosophy of education, the Emile, and his major work on political philosophy, The Social Contract: both published in 1762. These works caused great controversy in France and were immediately banned by Paris authorities. Rousseau fled France and settled in Switzerland, but he continued to find difficulties with authorities and quarrel with friends. The end of Rousseau’s life was marked in large part by his growing paranoia and his continued attempts to justify his life and his work. This is especially evident in his later books, The Confessions, The Reveries of the Solitary Walker, and Rousseau: Judge of Jean-Jacques. Yang Xiong (
Yang Xiong (

 The English philosopher Thomas Hobbes (1588-1679) is best known for his political thought, and deservedly so. His vision of the world is strikingly original and still relevant to contemporary politics. His main concern is the problem of social and political order: how human beings can live together in peace and avoid the danger and fear of civil conflict. He poses stark alternatives: we should give our obedience to an unaccountable sovereign (a person or group empowered to decide every social and political issue). Otherwise what awaits us is a state of nature that closely resembles civil war – a situation of universal insecurity, where all have reason to fear violent death and where rewarding human cooperation is all but impossible.
The English philosopher Thomas Hobbes (1588-1679) is best known for his political thought, and deservedly so. His vision of the world is strikingly original and still relevant to contemporary politics. His main concern is the problem of social and political order: how human beings can live together in peace and avoid the danger and fear of civil conflict. He poses stark alternatives: we should give our obedience to an unaccountable sovereign (a person or group empowered to decide every social and political issue). Otherwise what awaits us is a state of nature that closely resembles civil war – a situation of universal insecurity, where all have reason to fear violent death and where rewarding human cooperation is all but impossible.
 A paradox is generally a puzzling conclusion we seem to be driven towards by our reasoning, but which is highly counterintuitive, nevertheless. There are, among these, a large variety of paradoxes of a logical nature which have teased even professional logicians, in some cases for several millennia. But what are now sometimes isolated as “the logical paradoxes” are a much less heterogeneous collection: they are a group of antinomies centered on the notion of self-reference, some of which were known in Classical times, but most of which became particularly prominent in the early decades of last century. Quine distinguished amongst paradoxes such antinomies. He did so by first isolating the “veridical” and “falsidical” paradoxes, which, although puzzling riddles, turned out to be plainly true, or plainly false, after some inspection. In addition, however, there were paradoxes which “produce a self-contradiction by accepted ways of reasoning,” and which, Quine thought, established “that some tacit and trusted pattern of reasoning must be made explicit, and henceforward be avoided or revised.” We will first look, more broadly, and historically, at several of the main conundrums of a logical nature which have proved difficult, some since antiquity, before concentrating later on the more recent troubles with paradoxes of self-reference. They will all be called “logical paradoxes.”
A paradox is generally a puzzling conclusion we seem to be driven towards by our reasoning, but which is highly counterintuitive, nevertheless. There are, among these, a large variety of paradoxes of a logical nature which have teased even professional logicians, in some cases for several millennia. But what are now sometimes isolated as “the logical paradoxes” are a much less heterogeneous collection: they are a group of antinomies centered on the notion of self-reference, some of which were known in Classical times, but most of which became particularly prominent in the early decades of last century. Quine distinguished amongst paradoxes such antinomies. He did so by first isolating the “veridical” and “falsidical” paradoxes, which, although puzzling riddles, turned out to be plainly true, or plainly false, after some inspection. In addition, however, there were paradoxes which “produce a self-contradiction by accepted ways of reasoning,” and which, Quine thought, established “that some tacit and trusted pattern of reasoning must be made explicit, and henceforward be avoided or revised.” We will first look, more broadly, and historically, at several of the main conundrums of a logical nature which have proved difficult, some since antiquity, before concentrating later on the more recent troubles with paradoxes of self-reference. They will all be called “logical paradoxes.”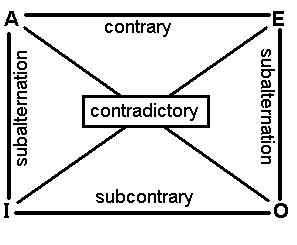
 Zhang Zai was one of the pioneers of the Song dynasty philosophical movement called “Study of the Way,” often known as
Zhang Zai was one of the pioneers of the Song dynasty philosophical movement called “Study of the Way,” often known as  Xuanzang, world-famous for his sixteen-year pilgrimage to India and career as a translator of Buddhist scriptures, is one of the most illustrious figures in the history of scholastic Chinese Buddhism. Born into a scholarly family at the outset of the Tang (T’ang) Dynasty, he enjoyed a classical Confucian education. Under the influence of his elder brother, a Buddhist monk, however, he developed a keen interest in Buddhist subjects and soon became a monk himself at the age of thirteen. Upon his return to Chang’an in 645, Xuanzang brought back with him a great number of Sanskrit texts, of which he was able to translate only a small portion during the remainder of his lifetime. In addition to his translations of the most essential Mahayana scriptures, Xuanzang authored the Da tang xi yu ji (Ta-T’ang Hsi-yu-chi or Records of the Western Regions of the Great T’ang Dynasty) with the aid of Bianji (Bian-chi). It is through Xuanzang and his chief disciple Kuiji (K’uei-chi) (632-682) that the Faxiang (Fa-hsiang or Yogacara/Consciousness-only) School was initiated in China. In order to honor the famous Buddhist scholar, the Tang Emperor Gaozong (Gao-tsung) cancelled all audiences for three days after Xuanzang’s death. (See
Xuanzang, world-famous for his sixteen-year pilgrimage to India and career as a translator of Buddhist scriptures, is one of the most illustrious figures in the history of scholastic Chinese Buddhism. Born into a scholarly family at the outset of the Tang (T’ang) Dynasty, he enjoyed a classical Confucian education. Under the influence of his elder brother, a Buddhist monk, however, he developed a keen interest in Buddhist subjects and soon became a monk himself at the age of thirteen. Upon his return to Chang’an in 645, Xuanzang brought back with him a great number of Sanskrit texts, of which he was able to translate only a small portion during the remainder of his lifetime. In addition to his translations of the most essential Mahayana scriptures, Xuanzang authored the Da tang xi yu ji (Ta-T’ang Hsi-yu-chi or Records of the Western Regions of the Great T’ang Dynasty) with the aid of Bianji (Bian-chi). It is through Xuanzang and his chief disciple Kuiji (K’uei-chi) (632-682) that the Faxiang (Fa-hsiang or Yogacara/Consciousness-only) School was initiated in China. In order to honor the famous Buddhist scholar, the Tang Emperor Gaozong (Gao-tsung) cancelled all audiences for three days after Xuanzang’s death. (See  Xunzi, along with
Xunzi, along with 


 and:
and: 
 is called γ, letting us write these equations more simply as:
is called γ, letting us write these equations more simply as:
 Rudolf Carnap, a German-born philosopher and naturalized U.S. citizen, was a leading exponent of
Rudolf Carnap, a German-born philosopher and naturalized U.S. citizen, was a leading exponent of