Logical Consequence
Logical consequence is arguably the central concept of logic. The primary aim of logic is to tell us what follows logically from what. In order to simplify matters we take the logical consequence relation to hold for sentences rather than for abstract propositions, facts, state of affairs, etc. Correspondingly, logical consequence is a relation between a given class of sentences and the sentences that logically follow. One sentence is said to be a logical consequence of a set of sentences, if and only if, in virtue of logic alone, it is impossible for the sentences in the set to be all true without the other sentence being true as well. If sentence X is a logical consequence of a set of sentences K, then we may say that K implies or entails X, or that one may correctly infer the truth of X from the truth of the sentences in K. For example, Kelly is not at work is a logical consequence of Kelly is not both at home and at work and Kelly is at home. However, the sentence Kelly is not a football fan does not follow from All West High School students are football fans and Kelly is not a West High School student. The central question to be investigated here is: What conditions must be met in order for a sentence to be a logical consequence of others?
One popular answer derives from the work of Alfred Tarski, one of the preeminent logicians of the twentieth century, in his famous 1936 paper, “The Concept of Logical Consequence.” Here Tarski uses his observations of the salient features of what he calls the common concept of logical consequence to guide his theoretical development of it. Accordingly, we begin by examining the common concept focusing on Tarski’s observations of the criteria by which we intuitively judge what follows from what and which Tarski thinks must be reflected in any theory of logical consequence. Then two theoretical definitions of logical consequence are introduced: the model theoretic and the deductive theoretic definitions. They represent two major approaches to making the common concept of logical consequence more precise. The article concludes by highlighting considerations relevant to evaluating model theoretic and deductive theoretic characterizations of logical consequence.
Table of Contents
- Introduction
- The Concept of Logical Consequence: Model-Theoretic and Deductive-Theoretic Conceptions of Logic
- Model-Theoretic and Deductive-Theoretic Conceptions of Logic
- Conclusion
- References and Further Reading
1. Introduction
For a given language, a sentence is said to be a logical consequence of a set of sentences, if and only if, in virtue of logic alone, the sentence must be true if every sentence in the set were to be true. This corresponds to the ordinary notion of a sentence “logically following” from others. Logicians have attempted to make the ordinary concept more precise relative to a given language L by sketching a deductive system for L, or by formalizing the intended semantics for L. Any adequate precise characterization of logical consequence must reflect its salient features such as those highlighted by Alfred Tarski: (1) that the logical consequence relation is formal, that is, depends on the forms of the sentences involved, (2) that the relation is a priori, that is, it is possible to determine whether or not it holds without appeal to sense-experience, and (3) that the relation has a modal element.
For more comprehensive presentations of the two definitions of logical consequence, as well as further critical discussion, see the entries Logical Consequence, Model-Theoretic Conceptions and Logical Consequence, Deductive-Theoretic Conceptions.
2. The Concept of Logical Consequence
a. Tarski’s Characterization of the Common Concept of Logical Consequence
Tarski begins his article, “On the Concept of Logical Consequence,” by noting a challenge confronting the project of making precise the common concept of logical consequence.
The concept of logical consequence is one of those whose introduction into a field of strict formal investigation was not a matter of arbitrary decision on the part of this or that investigator; in defining this concept efforts were made to adhere to the common usage of the language of everyday life. But these efforts have been confronted with the difficulties which usually present themselves in such cases. With respect to the clarity of its content the common concept of consequence is in no way superior to other concepts of everyday language. Its extension is not sharply bounded and its usage fluctuates. Any attempt to bring into harmony all possible vague, sometimes contradictory, tendencies which are connected with the use of this concept, is certainly doomed to failure. We must reconcile ourselves from the start to the fact that every precise definition of this concept will show arbitrary features to a greater or less degree. (Tarski 1936, p. 409)
Not every feature of the technical account will be reflected in the ordinary concept, and we should not expect any clarification of the concept to reflect each and every deployment of it in everyday language and life. Nevertheless, despite its vagueness, Tarski believes that there are identifiable, essential features of the common concept of logical consequence.
…consider any class K of sentences and a sentence X which follows from this class. From an intuitive standpoint, it can never happen that both the class K consists of only true sentences and the sentence X is false. Moreover, since we are concerned here with the concept of logical, that is, formal consequence, and thus with a relation which is to be uniquely determined by the form of the sentences between which it holds, this relation cannot be influenced in any way by empirical knowledge, and in particular by knowledge of the objects to which the sentence X or the sentences of class K refer. The consequence relation cannot be affected by replacing designations of the objects referred to in these sentences by the designations of any other objects. (Tarski 1936, pp. 414-415)
According to Tarski, the logical consequence relation as it is employed by typical reasoners is (1) necessary, (2) formal, and (3) not influenced by empirical knowledge. I now elaborate on (1)-(3) in order to shape two preliminary characterizations of logical consequence.
i. The Logical Consequence Relation Has a Modal Element
Tarski countenances an implicit modal notion in the common concept of logical consequence. If X is a logical consequence of K, then not only is it the case that not all of the elements of K are true and X is false, but also this is necessarily the case. That is, X follows from K only if it is not possible for all of the sentences in K to be true with X false. For example, the supposition that All West High School students are football fans and that Kelly is not a West High School student does not rule out the possibility that Kelly is a football fan. Hence, the sentences All West High School students are football fans and Kelly is not a West High School student do not entail Kelly is not a football fan, even if she, in fact, isn’t a football fan. Also, Most of Kelly’s male classmates are football fans does not entail Most of Kelly’s classmates are football fans. What if the majority of Kelly’s class is composed of females who are not fond of football?
We said above that Kelly is not both at home and at work and Kelly is at home jointly imply Kelly is not at work. Note that it doesn’t seem possible for the first two sentences to be true and Kelly is not at work false. But it is hard to see what this comes to without further clarification of the relevant notion of possibility. For example, consider the following pairs of sentences.
| Kelly kissed her sister at 2:00pm. 2:00pm is not a time during which Kelly and her sister were 100 miles apart. |
Kelly is a female. Kelly is not the US President. |
| There is a chimp in Paige’s house. There is a primate in Paige’s house. |
Ten is a prime number. Ten is greater than nine. |
For each pair of sentences, there is a sense in which it is not possible for the first to be true and the second false. At the very least an account of logical consequence must distinguish logical possibility from other types of possibility. Should truths about physical laws, US political history, zoology, and mathematics constrain what we take to be possible in determining whether or not the first sentence of each pair could logically be true with the second sentence false? If not, then this seems to mystify logical possibility (e.g., how could ten be a prime number?). To paraphrase questions asked by G.E. Moore (1959, pp. 231-238), given that I know that George W. Bush is US President and that he is not a female named Kelly, isn’t it inconsistent for me to grant the logical possibility of the truth of Kelly is a female and the falsity of Kelly is not the US President? Or should I ignore my present state of knowledge in considering what is logically possible? Tarski does not derive a clear notion of logical possibility from the common concept of logical consequence. Perhaps there is none to be had, and we should seek the help of a proper theoretical development in clarifying the notion of logical possibility. Towards this end, let’s turn to the other features of logical consequence highlighted by Tarski, starting with the formality criterion of logical consequence.
ii. The Logical Consequence Relation is Formal
Tarski observes that logical consequence is a formal consequence relation. And he tells us that a formal consequence relation is a consequence relation that is uniquely determined by the form of the sentences between which it holds. Consider the following pair of sentences
(1) Some children are both lawyers and peacemakers.
(2) Some children are peacemakers
Intuitively, (2) is a logical consequence of (1). It appears that this fact does not turn on the subject matter of the sentences. Replace ‘children’, ‘lawyers’, and ‘peacemakers’ in (1) and (2) with the variables S, M, and P to get the following.
(1′) Some S are both M and P
(2′) Some S are P
(1′) and (2′) are forms of (1) and (2), respectively. Note that there is no interpretation of S, M, and P according to which the sentence that results from (1′) is true and the resulting instance of (2′) is false. Hence, (2) is a formal consequence of (1) and on each interpretation of S, M, and P the resulting (2′) is a formal consequence of the sentence that results from (1′) (e.g., Some clowns are sad is a formal consequence of Some clowns are both lonely and sad). Tarski’s observation is that for any sentence X and set K of sentences, X is a logical consequence of K only if X is a formal consequence of K. The formality criterion of logical consequence can work in explaining why one sentence doesn’t entail another in cases where it seems impossible for the first to be true and the second false. For example, (3) is false and (4) is true.
(3) Ten is a prime number
(4) Ten is greater than nine
Does (4) follow from (3)? One might think that (4) does not follow from (3) because being a prime number does not necessitate being greater than nine. However, this does not require one to think that ten could be a prime number and less than or equal to nine, which is probably a good thing since it is hard to see how this is possible. Rather, we take
(3′) a is a P
(4′) a is R than b
to be the forms of (5) and (6) and note that there are interpretations of ‘a’, ‘b’, ‘P’, and ‘R’ according to which the first is true and the second false (e.g. let ‘a’ and ‘b’ name the numbers two and ten, respectively, and let ‘P’ mean prime number, and ‘R’ greater). Note that the claim here is not that formality is sufficient for a consequence relation to qualify as logical but only that it is a necessary condition. I now elaborate on this last point by saying a little more about forms of sentences (that is, sentential forms) and formal consequence.
Distinguishing between a term of a sentence replaced with a variable and one held constant determines a form of the sentence. In Some children are both lawyers and peacemakers we may replace ‘Some’ with a variable and treat all the other terms as constant. Then
(1”) D children are both lawyers and peacemakers
is a form of (1), and each sentence generated by assigning a meaning to D shares this form with (1). For example, the following three sentences are instances of (1”), produced by interpreting D as ‘No’, ‘Many’, and ‘Few’.
No children are both lawyers and peacemakers
Many children are both lawyers and peacemakers
Few children are both lawyers and peacemakers
Whether X is a formal consequence of K then turns on a prior selection of terms as constant and others replaced with variables. Relative to such a determination, X is a formal consequence of K if and only if (iff) there is no interpretation of the variables according to which each of the K are true and X is false. So, taking all the terms, except for ‘Some’, in (1) Some children are both philosophers and peacemakers and in (2) Some children are peacemakers as constants makes the following forms of (1) and (2).
(1”) D children are both lawyers and peacemakers
(2”) D children are peacemakers
Relative to this selection, (2) is not a formal consequence of (1) because replacing ‘D’ with ‘No’ yields a true instance of (1”) and a false instance of (2”).
Consider the following pair.
(5) Kelly is female
(6) Kelly is not US President
(6) is a formal consequence of (5) relative to replacing ‘Kelly’ with a variable. Given current U.S. political history, there is no individual whose name yields a true (5) and a false (6) when it replaces ‘Kelly’. This is not, however, sufficient reason for seeing (6) as a logical consequence of (5). There are two ways of thinking about why, a metaphysical consideration and an epistemological one. First the metaphysical consideration. It seems possible for (5) to be true and (6) false. The course of U.S. political history could have turned out differently. One might think that the current US President could–logically–have been a female named, say, ‘Sally’. Using ‘Sally’ as a replacement for ‘Kelly’ would yield in that situation a true (5) and a false (6). Also, it seems possible that in the future there will be a female US President. In order for a formal consequence relation from K to X to qualify as logical it has to be the case that it is necessary that there is no interpretation of the variables in K and X according to which the K-sentences are true and X is false.
The epistemological consideration is that one might think that knowledge that X follows logically from K should not essentially depend on being justified by experience of extra-linguistic states of affairs. Clearly, the determination that (6) follows formally from (5) essentially turns on empirical knowledge, specifically knowledge about the current political situation in the US. This leads to the final highlight of Tarski’s rendition of the intuitive concept of logical consequence: that logical consequence cannot be influenced by empirical knowledge.
iii. The Logical Consequence Relation is A Priori
Tarski says that by virtue of being formal, knowledge that X follows logically from K cannot be affected by knowledge of the objects that X and the sentences of K are about. Hence, our knowledge that X is a logical consequence of K cannot be influenced by empirical knowledge. However, as noted above, formality by itself does not insure that the extension of a consequence relation is not influenced by empirical knowledge. So, let’s view this alleged feature of logical consequence as independent of formality. We characterize empirical knowledge in two steps as follows. First, a priori knowledge is knowledge “whose truth, given an understanding of the terms involved, is ascertainable by a procedure which makes no reference to experience” (Hamlyn 1967, p. 141). Empirical, or a posteriori, knowledge is knowledge that is not a priori, that is, knowledge whose validation necessitates a procedure that does make reference to experience. We can safely read Tarski as saying that a consequence relation is logical only if knowledge that something falls in its extension is a priori, that is, only if the relation is a priori. Knowledge of physical laws, a determinant in people’s observed sizes, is not a priori and such knowledge is required to know that there is no interpretation of k, h, and t according to which (7) is true and (8) false.
(7) k kissed h at time t
(8) t is not a time during which k and h were 100 miles apart
So (8) cannot be a logical consequence of (7). However, my knowledge that Kelly is not Paige’s only friend follows from Kelly is taller than Paige’s only friend is a priori since I know a priori that nobody is taller than herself.
Let’s summarize and tie things together. We began by asking, for a given language L, what conditions must be met in order for a sentence X of L to be a logical consequence of a class K of L-sentences? Tarski thinks that an adequate response must reflect the common concept of logical consequence, that is, the concept as it is ordinarily employed. By the lights of this concept, an adequate account of logical consequence must reflect the formality and necessity of logical consequence, and must also reflect the fact that knowledge of what follows logically from what is a priori. Tying the criteria together, in order to fix what follows logically from what in a given language L, we must select a class of constants that determines a formal consequence relation that is both necessary and known, if at all, a priori. Such constants are called logical constants, and we say that the logical form of a sentence is a function of the logical constants that occur in the sentence and the pattern of the remaining expressions. As was illustrated above, the notion of formality does not presuppose a criterion of logical constancy. A consequence relation based on any division between constants and terms replaced with variables will automatically be formal with respect to the latter.
b. Logical and Non-Logical Terminology
Tarski’s basic move from his rendition of the common concept of logical consequence is to distinguish between logical terms and non-logical terms and then say that X is a logical consequence of K only if there is no possible interpretation of the non-logical terms of the language L that makes all of the sentences in K true and X false. The choice of the right terms as logical will reflect the modal element in the concept of logical consequence, that is, will insure that there is no ‘possible’ interpretation of the variable, non-logical terms of the language L that makes all of the K true and X false, and will insure that this is known a priori. Of course, we have yet to spell out the modal notion in the concept of logical consequence. Tarski pretty much left this underdeveloped in his (1936). Lacking such an explanation hampers our ability to clarify the rationale for a selection of terms to serve as the logical ones.
Traditionally, logicians have regarded sentential connectives such as and, not, or, if…then, the quantifiers all and some, and the identity predicate ‘=’ as logical terms. Remarking on the boundary between logical and non-terms, Tarski (1936, p. 419) writes the following.
Underlying this characterization of logical consequence is the division of all terms of the language discussed into logical and extra-logical. This division is not quite arbitrary. If, for example, we were to include among the extra-logical signs the implication sign, or the universal quantifier, then our definition of the concept of consequence would lead to results which obviously contradict ordinary usage. On the other hand, no objective grounds are known to me which permit us to draw a sharp boundary between the two groups of terms. It seems to be possible to include among logical terms some which are usually regarded by logicians as extra-logical without running into consequences which stands in sharp contrast to ordinary usage.
Tarski seems right to think that the logical consequence relation turns on the work that the logical terminology does in the relevant sentences. It seems odd to say that Kelly is happy does not logically follow from All are happy because the second is true and the first false when All is replaced with Few. However, by Tarski’s version of the ordinary concept of logical consequence there is no reason not to treat say taller than as a logical term along with not and, therefore, no reason not to take Kelly is not taller than Paige as following logically from Paige is taller than Kelly. Also, it seems plausible to say that I know a priori that there is no possible interpretation of Kelly and is mortal according to which it is necessary that Kelly is mortal is true and Kelly is mortal is false. This makes Kelly is mortal a logical consequence of it is necessary that Kelly is mortal. Given that taller than and it is necessary that, along with other terms, were not generally regarded as logical terms by logicians of Tarski’s day, the fact that they seem to be logical terms by the common concept of logical consequence, as observed by Tarski, highlights the question of what it takes to be a logical term. Tarski says that future research will either justify the traditional boundary between the logical and the non-logical or conclude that there is no such boundary and the concept of logical consequence is a relative concept whose extension is always relative to some selection of terms as logical (p. 420). For further discussion of Tarski’s views on logical terminology and contemporary views see Logical Consequence, Model-Theoretic Conceptions: Section 5.3.
How, exactly, does the terminology usually regarded by logicians as logical work in making it the case that one sentence follows from others? In the next two sections two distinct approaches to understanding the nature of logical terms are sketched. Each approach leads to a unique way of characterizing logical consequence and thus yields a unique response to the above question.
i. The Nature of Logical Constants Explained in Terms of Their Semantic Properties
Consider the following metaphor, borrowed from Bencivenga (1999).
The locked room metaphor
Suppose that you are locked in a dark windowless room and you know everything about your language but nothing about the world outside. A sentence X and a class K of sentences are presented to you. If you can determine that X is true if all the sentences in K are, X is a logical consequence of K.
Ignorant of US politics, I couldn’t determine the truth of Kelly is not US President solely on the basis of Kelly is a female. However, behind such a veil of ignorance I would be able to tell that Kelly is not US President is true if Kelly is female and Kelly is not US President is true. How? Short answer: based on my linguistic competence; longer answer: based on my understanding of the semantic contribution of and to the determination of the truth conditions of a sentence of the form P and Q. For any sentences P and Q, I know that P and Q is true just in case P is true and Q is true. So, I know, a priori, if P and Q is true, then Q is true. As noted by one philosopher, “This really is remarkable since, after all, it’s what they mean, together with the facts about the non-linguistic world, that decide whether P or Q are true” (Fodor 2000, p.12).
Taking not and and to be the only logical constants in (9) Kelly is not both at home and at work, (10) Kelly is at home, and (11) Kelly is not at work, we formalize the sentences as follows, letting k mean Kelly, H mean is at home, and W mean is at work.
(9′) not-(Hk and Wk)
(10′) Hk
(11′) not-Wk
There is no interpretation of k, H, and W according to which (9′) and (10′) are true and (11′) is false. The reason why turns on the semantic properties of and and not, which are knowable a priori. Suppose (9′) and (10′) are true on some interpretation of the variable terms. Then the meaning of not in (9′) makes it the case that Hk and Wk is false, which, by the meaning of and requires that Hk is false or Wk is false. Given (10′), it must be that Wk is false, that is, not-Wk is true. So, there can’t be an interpretation of the variable terms according to which (9′) and (10′) are true and (11′) is false, and, as the above reasoning illustrates, this is due exclusively to the semantic properties of not and and. So the reason that it is impossible that an interpretation of k, H, and W make (9′) and (10′) true and (11′) false is that the supposition otherwise is inconsistent with the semantic functioning of not and and. Compare: the supposition that there is an interpretation of k according to which k is a female is true and k is not US President is false does not seem to violate the semantic properties of the constant terms. If we identify the meanings of the predicates with their extensions in all possible worlds, then the supposition that there is a female U.S. President does not violate the meanings of female and US President for surely it is possible that there be a female US President. But, supposing that (9′) and (10′) could be true with (11′) false on some interpretation of k, H, and W, violates the semantic properties of either and or not.
In sum, our first-step characterization of logical consequence is the following. For a given language L,
X is a logical consequence of K if and only if there is no possible interpretation of the non-logical terminology of L according to which all the sentence in K are true and X is false.
A possible interpretation of the non-logical terminology of the language L according to which sentences are true or false is a reading of the non-logical terms according to which the sentences receive a truth-value (that is, is either true or false) in a situation that is not ruled out by the semantic properties of the logical constants. The philosophical locus of the technical development of ‘possible interpretation’ in terms of models is Tarski (1936). A model for a language L is the theoretical development of a possible interpretation of non-logical terminology of L according to which the sentences of L receive a truth-value. Models have become standard tools for characterizing the logical consequence relation, and the characterization of logical consequence in terms of models is called the Tarskian or model-theoretic characterization of logical consequence. We say that X is a model-theoretic consequence of K if and only if all models of K are models of X. This relation may be represented as K ⊨ X. If model-theoretic consequence is adequate as a representation of logical consequence, then it must reflect the salient features of the common concept, which, according to Tarski means that it must be necessary, formal and a priori.
For further discussion of this conception of logical consequence, see the article, Logical Consequence, Model-Theoretic Conceptions.
ii. The Nature of Logical Constants Explained in Terms of Their Inferential Properties
We now turn to a second approach to understanding logical constants. Instead of understanding the nature of logical constants in terms of their semantic properties as is done on the model-theoretic approach, on the second approach we appeal to their inferential properties conceived of in terms of principles of inference, that is, principles justifying steps in deductions. We begin with a remark made by Aristotle. In his study of logical consequence, Aristotle comments that
A syllogism is discourse in which, certain things being stated, something other than what is stated follows of necessity from their being so. I mean by the last phrase that they produce the consequence, and by this, that no further term is required from without in order to make the consequence necessary. (Prior Analytics, p. 24b)
Adapting this to our X and K, we may say that X is a logical consequence of K when the sentences of K are sufficient to produce X. How are we to think of a sentence being produced by others? One way of developing this is to appeal to a notion of an actual or possible deduction. X is a deductive consequence of K if and only if there is a deduction of X from K. In such a case, we say that X may be correctly inferred from K or that it would be correct to conclude X from K. A deduction is associated with a pair ; the set K of sentences is the basis of the deduction, and X is the conclusion. A deduction from K to X is a finite sequence S of sentences ending with X such that each sentence in S (that is, each intermediate conclusion) is derived from a sentence (or more) in K or from previous sentences in S in accordance with a correct principle of inference.
For example, intuitively, the following inference seems correct.
| Kelly is not both at home and at work | |
| Kelly is at home | |
| (therefore) | Kelly is not at work |
The set K of sentences above the line is the basis of the inference and the sentence X below is the conclusion. We represent their logical forms, again, as follows.
| (9′) not-(Hk and Wk) | |
| (10′) Hk | |
| (therefore) | (11′) not-Wk |
Consider the following deduction of (11′) from (10′) and (9′).
Deduction: Assume that (12′) Wk. Then from (10′) and (12′) we may deduce that (13′) Hk and Wk. (13′) contradicts (9′) and so (12′), our initial assumption, must be false. We have deduced not-Wk from not-(Hk and Wk) and Hk.
Since the deduction of not-Wk from not-(Hk and Wk) and Hk did not depend on the interpretation of k, W, and H, the deductive relation is formal. Furthermore, my knowledge of this is a priori because my knowledge of the underlying principles of inference in the above deduction is not empirical. For example, letting P and Q be any sentences, we know a priori that P and Q may be inferred from the set K={P, Q} of basis sentences. This principle grounds the move from (10′) and (12′) to (13′). Also, the deduction appeals to the principle that if we deduce a contradiction from an assumption, then we may infer that the assumption is false. The correctness of this principle seems to be an a priori matter. Let’s look at another example of a deduction.
| (1) Some children are both lawyers and peacemakers | |
| (therefore) | (2) Some children are peacemakers |
The logical forms are, again, the following.
| (1′) Some S are both M and P | |
| (therefore) | (2′) Some S are P |
Again, intuitively, (2′) is deducible from (1′).
Deduction: The basis tells us that at least one S–let’s call this S ‘a‘–is both an M and a P. Clearly, a is a P may be deduced from a is both an M and a P. Since we’ve assumed that a is an S, what we derive with respect to a we derive with respect to some S. So our derivation of a is a P is a derivation of Some S is a P, which is our desired conclusion.
Since the deduction is formal, we have shown not merely that (2) can be correctly inferred from (1), but we have shown that for any interpretation of S, M, and P it is correct to infer (2′) from (1′).
Typically, deductions leave out steps (perhaps because they are too obvious), and they usually do not justify each and every step made in moving towards the conclusion (again, obviousness begets brevity). The notion of a deduction is made precise by describing a mechanism for constructing deductions that are both transparent and rigorous (each step is explicitly justified and no steps are omitted). This mechanism is a deductive system (also known as a formal system or as a formal proof calculus). A deductive system D is a collection of rules that govern which sequences of sentences, associated with a given , are allowed and which are not. Such a sequence is called a proof in D (or, equivalently, a deduction in D) of X from K. The rules must be such that whether or not a given sequence associated with qualifies as a proof in D of X from K is decidable purely by inspection and calculation. That is, the rules provide a purely mechanical procedure for deciding whether a given object is a proof in D of X from K.
We say that a deductive system D is correct when for any K and X, proofs in D of X from K correspond to intuitively valid deductions. For example, intuitively, there are no correct principles of inference according to which it is correct to conclude
Some animals are both mammals and reptiles
on the basis of the following two sentences.
Some animals are mammals
Some animals are reptiles
Hence, a proof in a deductive system of the former sentence from the latter two is evidence that the deductive system is incorrect. The point here is that a proof in D may fail to represent a deduction if D is incorrect.
A rich variety of deductive systems have been developed for registering deductions. Each system has its advantages and disadvantages, which are assessed in the context of the more specific tasks the deductive system is designed to accomplish. Historically, the general purpose of the construction of deductive systems was to reduce reasoning to precise mechanical rules (Hodges 1983, p. 26). Some view a deductive system defined for a language L as a mathematical model of actual or possible chains of correct reasoning in L. Sundholm (1983) offers a thorough survey of three main types of deductive systems. For a shorter, excellent introduction to the concept of a deductive system see Henkin (1967). A deductive system is developed in detail in the accompanying article, Logical Consequence, Deductive-Theoretic Conceptions.
If there is a proof of X from K in deductive system D, then we may say that X is a deductive consequence in D of K, which is sometimes expressed as K ⊢D X. Relative to a correct deductive system D, we characterize logical consequence in terms of deductive consequence as follows.
X is a logical consequence of K if and only if X is a deductive consequence in D of K, that is, there is an actual or possible proof in D of X from K.
This is called the deductive-theoretic (or proof-theoretic) characterization of logical consequence.
3. Model-Theoretic and Deductive-Theoretic Conceptions of Logic
We began with Tarski’s observations of the common or ordinary concept of logical consequence that we employ in daily life. According to Tarski, if X is a logical consequence of a set of sentences, K, then, in virtue of the logical forms of the sentences involved, if all of the members of K are true, then X must be true, and furthermore, we know this a priori. The formality criterion makes the logical constants the essential determinant of the logical consequence relation. The logical consequence relation is fixed exclusively in terms of the nature of the logical terminology. We have highlighted two different approaches to the nature of a logical constant: (1) in terms of its semantic contribution to sentences in which it occurs and (2) in terms of its inferential properties. The two approaches yield distinct conceptions of the notion of necessity inherent in the common concept of logical consequence, and lead to the following characterizations of logical consequence.
(1) X is a logical consequence of K if and only if there is no possible interpretation of the non-logical terminology of the language according to which all the sentences in K are true and X is false.
(2) X is a logical consequence of K if and only if X is deducible from K.
We make the notions of possible interpretation in (1) and deducibility in (2) precise by appealing to the technical notions of model and deductive system. This leads to the following theoretical characterizations of logical consequence.
(1) The model-theoretic characterization of logical consequence: X is a logical consequence of K iff all models of K are models of X.
(2) The deductive- theoretic characterization of logical consequence: X is a logical consequence of K iff there is a deduction in a correct deductive system of X from K.
Following Shapiro (1991, p. 3) define a logic to be a language L plus either a model-theoretic or a deductive-theoretic account of logical consequence. A language with both characterizations is a full logic just in case both characterizations coincide. A soundness proof establishes K ⊢D X only if K ⊨ X, and a completeness proof establishes K ⊢D X if K ⊨ X. These proofs together establish that the two characterizations coincide, and in such a case the deductive system D is said to be complete and sound with respect to the model-theoretic consequence relation defined for the relevant language L.
We said that the primary aim of logic is to tell us what follows logically from what. These two characterizations of logical consequence lead to two different orientations or conceptions of logic (see Tharp 1975, p. 5).
Model-theoretic approach: Logic is a theory of possible interpretations. For a given language the class of situations that can–logically–be described by that language.
Deductive-theoretic approach: Logic is a theory of formal deductive inference.
The article now concludes by highlighting three considerations relevant to evaluating a particular deployment of the model-theoretic or deductive-theoretic definition in defining logical consequence. These considerations emerge from the above development of the two theoretic definitions from the common concept of logical consequence.
4. Conclusion
The two theoretical characterizations of logical consequence do not provide the means for drawing a boundary in a language L between logical and non-logical terms. Indeed, their use presupposes that a list of logical terms is in hand. Hence, in evaluating a model-theoretic or deductive-theoretic definition of logical consequence for a language L the issue arises whether or not the boundary in L between logical and non-logical terms has been correctly drawn. This requires a response to a central question in the philosophy of logic: what qualifies as a logical constant? Tarski gives a well-reasoned response in his (1986). (For more recent discussion see McCarthy 1981 and 1998, Hanson 1997, and Warbrod 1999.)
A second thing to consider in evaluating a theoretical account of logical consequence is whether or not its characterization of the logical terminology is accurate. For example, model-theoretic and deductive accounts of logical consequence are inadequate unless they reflect the semantic and inferential properties of the logical terms, respectively. So a model-theoretic account is inadequate unless it gets right the semantic contributions of the logical terms to the truth conditions of the sentences formed using them. For a particular deductive system D, the question arises whether or not D’s rules of inference reflect the inferential properties of the logical terms. (For further discussion of the semantic and inferential properties of logical terms see Haack 1978 and 1996, Read 1995, and Quine 1986.)
A third consideration in assessing the success of a theoretical definition of logical consequence is whether or not the definition, relative to a selection of terms as logical, reflects the salient features of the common concept of logical consequence. There are criticisms of the theoretical definitions that claim that they are incapable of reflecting the common concept of logical consequence. Typically, such criticisms are used to question the status of the model-theoretic and deductive-theoretic approaches to logic.
For example, there are critics who question the model-theoretic approach to logic by arguing that any model-theoretic account lacks the conceptual resources to reflect the notion of necessity inherent in the common concept of logical consequence because such an account does not rule out the possibility of there being logically possible situations in which sentences in K are true and X is false even though every model of K is a model of X. Kneale (1961) is an early critic, Etchemendy (1988, 1999) offers a sustained and multi-faceted attack. Also, it is argued that the model-theoretic approach to logic makes knowledge of what follows from what depend on knowledge of the existence of models, which is knowledge of worldly matters of fact. But logical knowledge should not depend on knowledge about the extra-linguistic world (recall the locked room metaphor in 2.2.1). This standard logical positivist line has been recently challenged by those who see logic penetrated and permeated by metaphysics (e.g., Putnam 1971, Almog 1989, Sher 1991, Williamson 1999).
The status of the deductive-theoretic approach to logic is not clear for, as Tarski argues in his (1936), deductive-theoretic accounts are unable to reflect the fact that, according to the common concept, logical consequence is not compact. Relative to any deductive system D, the ⊢D-consequence relation is compact if and only if for any sentence X and set K of sentences, if K ⊢D X, then K’ ⊢D X, where K’ is a finite subset of sentences from K. But there are intuitively correct principles of inference according to which one may infer a sentence X from a set K of sentences, even though it is incorrect to infer X from any finite subset of K. This suggests that the intuitive notion of deducibility is not completely captured by any compact consequence relation. We need to weaken
X is a logical consequence of K if and only if there is a proof in a correct deductive system of X from K,
given above, to
X is a logical consequence of K if there is a proof in a correct deductive system of X from K.
In sum, the issue of the nature of logical consequence, which intersects with other areas of philosophy, is still a matter of debate. Tarski’s analysis of the concept is not universally accepted; philosophers and logicians differ over what the features of the common concept are. For example, some offer accounts of the logical consequence relation according to which it is not a priori (e.g., see Koslow 1999, Sher 1991 and see Hanson 1997 for criticism of Sher) or deny that it even need be strongly necessary (Smiley 1995, 2000, section 6). The entry Logical Consequence, Model-Theoretic Conceptions gives a model-theoretic definition of logical consequence. For a detailed development of a deductive system see the entry Logical Consequence, Deductive-Theoretic Conceptions. The critical discussion in both articles deepens and extends points made in the conclusion of this article.
5. References and Further Reading
- Almog, J. (1989): “Logic and the World”, pp. 43-65 in Themes From Kaplan, ed. J. Almog, J. Perry, J., and H. Wettstein. New York: Oxford UP.
- Aristotle. (1941): Basic Works, ed. R. McKeon. New York: Random House.
- Bencivenga, E. (1999): “What is Logic About?”, pp. 5-19 in Varzi (1999).
- Etchemendy, J. (1983): “The Doctrine of Logic as Form”, Linguistics and Philosophy 6, pp. 319-334.
- Etchemendy, J. (1988): “Tarski on truth and logical consequence”, Journal of Symbolic Logic 53, pp. 51-79.
- Etchemendy, J. (1999): The Concept of Logical Consequence. Stanford: CSLI Publications.
- Fodor, J. (2000): The Mind Doesn’t Work That Way. Cambridge: The MIT Press.
- Gabbay, D. and F. Guenthner, eds. (1983): Handbook of Philosophical Logic, Vol 1. Dordrecht: D. Reidel Publishing Company.
- Haack, S. (1978): Philosophy of Logics . Cambridge: Cambridge University Press.
- Haack, S. (1996): Deviant Logic, Fuzzy Logic. Chicago: The University of Chicago Press.
- Hodges, W. (1983): “Elementary Predicate Logic”, in Gabbay, D. and F. Guenthner (1983).
- Hamlyn, D.W. (1967): “A Priori and A Posteriori”, pp.105-109 in The Encyclopedia of Philosophy, Vol. 1, ed. P. Edwards. New York: Macmillan & The Free Press.
- Hanson, W. (1997): “The Concept of Logical Consequence”, The Philosophical Review 106, pp. 365-409.
- Henkin, L. (1967): “Formal Systems and Models of Formal Systems”, pp. 61-74 in The Encyclopedia of Philosophy, Vol. 8, ed. P. Edwards. New York: Macmillan & The Free Press.
- Kneale, W. (1961): “Universality and Necessity”, British Journal for the Philosophy of Science 12, pp. 89-102.
- Koslow, A. (1999): “The Implicational Nature of Logic: A Structuralist Account”, pp. 111-155 in Varzi (1999).
- McCarthy, T. (1981): “The Idea of a Logical Constant”, Journal of Philosophy 78, pp. 499-523.
- McCarthy, T. (1998): “Logical Constants”, pp. 599-603 in Routledge Encyclopedia of Philosophy, Vol. 5, ed. E. Craig. London: Routledge.
- McGee, V. (1999): “Two Problems with Tarski’s Theory of Consequence”, Proceedings of the Aristotelean Society 92, pp. 273-292.
- Moore, G.E., (1959): “Certainty”, pp. 227-251 in Philosophical Papers. London: George Allen & Unwin.
- Priest. G. (1995): “Etchemendy and Logical Consequence”, Canadian Journal of Philosophy 25, pp. 283-292.
- Putnam, H. (1971): Philosophy of Logic. New York: Harper & Row.
- Quine, W.V. (1986): Philosophy of Logic, 2nd ed.. Cambridge: Harvard UP.
- Read, S. (1995): Thinking About Logic. Oxford: Oxford UP.
- Shapiro, S. (1991): Foundations without Foundationalism: A Case For Second-Order Logic. Oxford: Clarendon Press.
- Shapiro, S. (1993): ” Modality and Ontology”, Mind 102, pp. 455-481.
- Shapiro, S. (1998): “Logical Consequence: Models and Modality”, pp. 131-156 in The Philosophy of Mathematics Today, ed. Matthias Schirn. Oxford, Clarendon Press.
- Shapiro, S. (2000): Thinking About Mathematics , Oxford: Oxford University Press.
- Sher, G. (1989): “A Conception of Tarskian Logic”, Pacific Philosophical Quarterly 70, pp. 341-368.
- Sher, G. (1991): The Bounds of Logic: A Generalized Viewpoint, Cambridge, MA: The MIT Press.
- Sher, G. (1996): “Did Tarski commit ‘Tarski’s fallacy’?” Journal of Symbolic Logic 61, pp. 653-686.
- Sher, G. (1999): “Is Logic a Theory of the Obvious?”, pp. 207-238 in Varzi (1999).
- Smiley, T. (1995): “A Tale of Two Tortoises”, Mind 104, pp. 725-36.
- Smiley, T. (1998): “Consequence, Conceptions of”, pp. 599-603 in Routledge Encyclopedia of Philosophy, vol. 2, ed. E. Craig. London: Routledge.
- Sundholm, G. (1983): “Systems of Deduction”, in Gabbay and Guenthner (1983).
- Tarski, A. (1933): “Pojecie prawdy w jezykach nauk dedukeycyjnych”, translated as “On the Concept of Truth in Formalized Languages”, pp. 152-278 in Tarski (1983).
- Tarski, A. (1936): “On the Concept of Logical Consequence”, pp. 409-420 in Tarski (1983).
- Tarski, A. (1983): Logic, Semantics, Metamathematics, 2nd ed. Indianapolis: Hackett Publishing.
- Tarski, A. (1986): “What are logical notions?” History and Philosophy of Logic 7, pp. 143-154.
- Tharp, L. (1975): “Which Logic is the Right Logic?” Synthese 31, pp. 1-21.
- Warbrod, K., (1999): “Logical Constants” Mind 108, pp. 503-538.
- Williamson, T. (1999): “Existence and Contingency”, Proceedings of the Aristotelian Society Supplementary Vol. 73, pp. 181-203.
- Varzi, A., ed. (1999): European Review of Philosophy, Vol. 4: The Nature of Logic, Stanford: CSLI Publications.
Author Information
Matthew McKeon
Email: mckeonm@msu.edu
Michigan State University
U. S. A.

 The Russell-Myhill Antinomy, also known as the Principles of Mathematics Appendix B Paradox, is a contradiction that arises in the logical treatment of classes and “propositions”, where “propositions” are understood as mind-independent and language-independent logical objects. If propositions are treated as objectively existing objects, then they can be members of classes. But propositions can also be about classes, including classes of propositions. Indeed, for each class of propositions, there is a proposition stating that all propositions in that class are true. Propositions of this form are said to “assert the logical product” of their associated classes. Some such propositions are themselves in the class whose logical product they assert. For example, the proposition asserting that all-propositions-in-the-class-of-all-propositions-are-true is itself a proposition, and therefore it itself is in the class whose logical product it asserts. However, the proposition stating that all-propositions-in-the-null-class-are-true is not itself in the null class. Now consider the class w, consisting of all propositions that state the logical product of some class m in which they are not included. This w is itself a class of propositions, and so there is a proposition r, stating its logical product. The contradiction arises from asking the question of whether r is in the class w. It seems that r is in w just in case it is not.
The Russell-Myhill Antinomy, also known as the Principles of Mathematics Appendix B Paradox, is a contradiction that arises in the logical treatment of classes and “propositions”, where “propositions” are understood as mind-independent and language-independent logical objects. If propositions are treated as objectively existing objects, then they can be members of classes. But propositions can also be about classes, including classes of propositions. Indeed, for each class of propositions, there is a proposition stating that all propositions in that class are true. Propositions of this form are said to “assert the logical product” of their associated classes. Some such propositions are themselves in the class whose logical product they assert. For example, the proposition asserting that all-propositions-in-the-class-of-all-propositions-are-true is itself a proposition, and therefore it itself is in the class whose logical product it asserts. However, the proposition stating that all-propositions-in-the-null-class-are-true is not itself in the null class. Now consider the class w, consisting of all propositions that state the logical product of some class m in which they are not included. This w is itself a class of propositions, and so there is a proposition r, stating its logical product. The contradiction arises from asking the question of whether r is in the class w. It seems that r is in w just in case it is not. A paradox is generally a puzzling conclusion we seem to be driven towards by our reasoning, but which is highly counterintuitive, nevertheless. There are, among these, a large variety of paradoxes of a logical nature which have teased even professional logicians, in some cases for several millennia. But what are now sometimes isolated as “the logical paradoxes” are a much less heterogeneous collection: they are a group of antinomies centered on the notion of self-reference, some of which were known in Classical times, but most of which became particularly prominent in the early decades of last century. Quine distinguished amongst paradoxes such antinomies. He did so by first isolating the “veridical” and “falsidical” paradoxes, which, although puzzling riddles, turned out to be plainly true, or plainly false, after some inspection. In addition, however, there were paradoxes which “produce a self-contradiction by accepted ways of reasoning,” and which, Quine thought, established “that some tacit and trusted pattern of reasoning must be made explicit, and henceforward be avoided or revised.” We will first look, more broadly, and historically, at several of the main conundrums of a logical nature which have proved difficult, some since antiquity, before concentrating later on the more recent troubles with paradoxes of self-reference. They will all be called “logical paradoxes.”
A paradox is generally a puzzling conclusion we seem to be driven towards by our reasoning, but which is highly counterintuitive, nevertheless. There are, among these, a large variety of paradoxes of a logical nature which have teased even professional logicians, in some cases for several millennia. But what are now sometimes isolated as “the logical paradoxes” are a much less heterogeneous collection: they are a group of antinomies centered on the notion of self-reference, some of which were known in Classical times, but most of which became particularly prominent in the early decades of last century. Quine distinguished amongst paradoxes such antinomies. He did so by first isolating the “veridical” and “falsidical” paradoxes, which, although puzzling riddles, turned out to be plainly true, or plainly false, after some inspection. In addition, however, there were paradoxes which “produce a self-contradiction by accepted ways of reasoning,” and which, Quine thought, established “that some tacit and trusted pattern of reasoning must be made explicit, and henceforward be avoided or revised.” We will first look, more broadly, and historically, at several of the main conundrums of a logical nature which have proved difficult, some since antiquity, before concentrating later on the more recent troubles with paradoxes of self-reference. They will all be called “logical paradoxes.” Russell’s paradox represents either of two interrelated logical antinomies. The most commonly discussed form is a contradiction arising in the logic of sets or classes. Some classes (or sets) seem to be members of themselves, while some do not. The class of all classes is itself a class, and so it seems to be in itself. The null or empty class, however, must not be a member of itself. However, suppose that we can form a class of all classes (or sets) that, like the null class, are not included in themselves. The paradox arises from asking the question of whether this class is in itself. It is if and only if it is not. The other form is a contradiction involving properties. Some properties seem to apply to themselves, while others do not. The property of being a property is itself a property, while the property of being a cat is not itself a cat. Consider the property that something has just in case it is a property (like that of being a cat) that does not apply to itself. Does this property apply to itself? Once again, from either assumption, the opposite follows. The paradox was named after Bertrand Russell (1872-1970), who discovered it in 1901.
Russell’s paradox represents either of two interrelated logical antinomies. The most commonly discussed form is a contradiction arising in the logic of sets or classes. Some classes (or sets) seem to be members of themselves, while some do not. The class of all classes is itself a class, and so it seems to be in itself. The null or empty class, however, must not be a member of itself. However, suppose that we can form a class of all classes (or sets) that, like the null class, are not included in themselves. The paradox arises from asking the question of whether this class is in itself. It is if and only if it is not. The other form is a contradiction involving properties. Some properties seem to apply to themselves, while others do not. The property of being a property is itself a property, while the property of being a cat is not itself a cat. Consider the property that something has just in case it is a property (like that of being a cat) that does not apply to itself. Does this property apply to itself? Once again, from either assumption, the opposite follows. The paradox was named after Bertrand Russell (1872-1970), who discovered it in 1901.
 Zhang Zai was one of the pioneers of the Song dynasty philosophical movement called “Study of the Way,” often known as
Zhang Zai was one of the pioneers of the Song dynasty philosophical movement called “Study of the Way,” often known as  Xunzi, along with
Xunzi, along with  Xuanzang, world-famous for his sixteen-year pilgrimage to India and career as a translator of Buddhist scriptures, is one of the most illustrious figures in the history of scholastic Chinese Buddhism. Born into a scholarly family at the outset of the Tang (T’ang) Dynasty, he enjoyed a classical Confucian education. Under the influence of his elder brother, a Buddhist monk, however, he developed a keen interest in Buddhist subjects and soon became a monk himself at the age of thirteen. Upon his return to Chang’an in 645, Xuanzang brought back with him a great number of Sanskrit texts, of which he was able to translate only a small portion during the remainder of his lifetime. In addition to his translations of the most essential Mahayana scriptures, Xuanzang authored the Da tang xi yu ji (Ta-T’ang Hsi-yu-chi or Records of the Western Regions of the Great T’ang Dynasty) with the aid of Bianji (Bian-chi). It is through Xuanzang and his chief disciple Kuiji (K’uei-chi) (632-682) that the Faxiang (Fa-hsiang or Yogacara/Consciousness-only) School was initiated in China. In order to honor the famous Buddhist scholar, the Tang Emperor Gaozong (Gao-tsung) cancelled all audiences for three days after Xuanzang’s death. (See
Xuanzang, world-famous for his sixteen-year pilgrimage to India and career as a translator of Buddhist scriptures, is one of the most illustrious figures in the history of scholastic Chinese Buddhism. Born into a scholarly family at the outset of the Tang (T’ang) Dynasty, he enjoyed a classical Confucian education. Under the influence of his elder brother, a Buddhist monk, however, he developed a keen interest in Buddhist subjects and soon became a monk himself at the age of thirteen. Upon his return to Chang’an in 645, Xuanzang brought back with him a great number of Sanskrit texts, of which he was able to translate only a small portion during the remainder of his lifetime. In addition to his translations of the most essential Mahayana scriptures, Xuanzang authored the Da tang xi yu ji (Ta-T’ang Hsi-yu-chi or Records of the Western Regions of the Great T’ang Dynasty) with the aid of Bianji (Bian-chi). It is through Xuanzang and his chief disciple Kuiji (K’uei-chi) (632-682) that the Faxiang (Fa-hsiang or Yogacara/Consciousness-only) School was initiated in China. In order to honor the famous Buddhist scholar, the Tang Emperor Gaozong (Gao-tsung) cancelled all audiences for three days after Xuanzang’s death. (See 
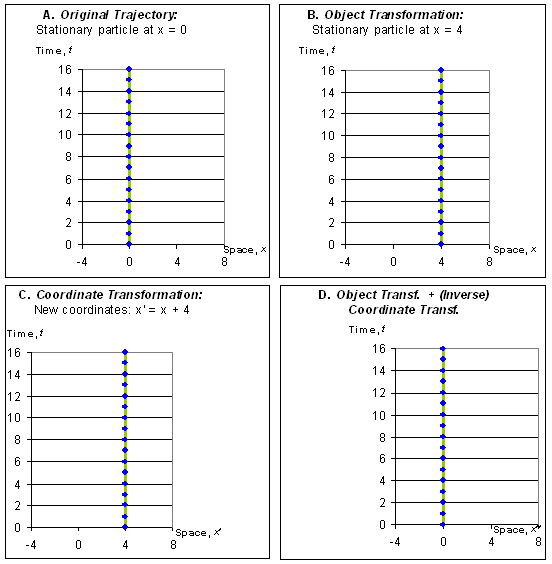


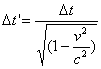 and:
and: 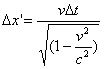
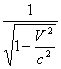 is called γ, letting us write these equations more simply as:
is called γ, letting us write these equations more simply as:
 Rudolf Carnap, a German-born philosopher and naturalized U.S. citizen, was a leading exponent of
Rudolf Carnap, a German-born philosopher and naturalized U.S. citizen, was a leading exponent of