The Compactness Theorem
The compactness theorem is a fundamental theorem for the model theory of classical propositional and first-order logic. As well as having importance in several areas of mathematics, such as algebra and combinatorics, it also helps to pinpoint the strength of these logics, which are the standard ones used in mathematics and arguably the most important ones in philosophy.
The main focus of this article is the many different proofs of the compactness theorem, applying different Choice-like principles before later calibrating the strength of these and the compactness theorems themselves over Zermelo-Fraenkel set theory ZF. Although the article’s focus is mathematical, much of the discussion keeps an eye on philosophical applications and implications.
We first introduce some standard logics, detailing whether the compactness theorem holds or fails for these. We also broach the neglected question of whether natural language is compact. Besides algebra and combinatorics, the compactness theorem also has implications for topology and foundations of mathematics, via its interaction with the Axiom of Choice. We detail these results as well as those of a philosophical nature, such as apparent ‘paradoxes’ and non-standard models of arithmetic and analysis. We then provide several different proofs of the compactness theorem based on different Choice-like principles.
In later sections, we discuss several variations of compactness in logics that allow for infinite conjunctions / disjunctions or generalised quantifiers, and in higher-order logics. The article concludes with a history of the compactness theorem and its many proofs, starting from those that use syntactic proofs before moving to the semantic proofs model theorists are more accustomed to today.
Contents
- Introduction
- Compactness: Common Logics and Natural Language
- Implications of Compactness
- Some Non-topological Proofs
- Connection to Topology
- Extensions and Generalisations
- Relative Strength
- History of the Compactness Theorem
- References and Further Reading
1. Introduction
A logic consists of a language, grammar, semantics, and consequence relation ![]() . If
. If ![]() is a set of sentences of this logic and
is a set of sentences of this logic and ![]() one of its sentences,
one of its sentences, ![]() means that any model of
means that any model of ![]() is a model of
is a model of ![]() . (A model of
. (A model of ![]() is a model of all sentences in
is a model of all sentences in ![]() .) Informally, a logic is called compact if it is determined by its behaviour on finite sets of sentences; there may be infinitely many sentences in the language, but we can always reduce our considerations to finitely many in any given situation.
.) Informally, a logic is called compact if it is determined by its behaviour on finite sets of sentences; there may be infinitely many sentences in the language, but we can always reduce our considerations to finitely many in any given situation.
More formally, a logic is compact just when:
- If every finite subset
 of
of  is satisfiable then
is satisfiable then  is also satisfiable.
is also satisfiable. - If
 is an unsatisfiable set of sentences then so is
is an unsatisfiable set of sentences then so is 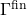 for some finite subset
for some finite subset 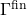 of
of 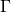 .
.
Some authors take the compactness of a logic to be its satisfaction of these statements’ biconditional versions. We have chosen to omit the reverse implication from the definition as it easily follows from the meaning of ![]() . These two characterisations of compactness are equivalent, since the second statement is effectively the contrapositive of the first. In a logic containing a classical negation connective (by which we mean for each sentence
. These two characterisations of compactness are equivalent, since the second statement is effectively the contrapositive of the first. In a logic containing a classical negation connective (by which we mean for each sentence ![]() there is a sentence
there is a sentence ![]() such that
such that ![]() if and only if
if and only if ![]() ), both statements are equivalent to:
), both statements are equivalent to:
- If
 then
then 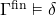 for some finite subset
for some finite subset 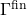 of
of 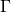 .
.
This equivalence follows from
![]()
The compactness theorem is said to hold for a logic precisely when the logic is compact.
Alongside its close cousin, the completeness theorem for first-order logic, the compactness theorem for first-order logic is one of the most important theorems in contemporary logic.
In this entry, we give a few examples of compact and incompact logics and briefly discuss whether natural languages such as English are compact (Section 2). We then mention some mathematical and philosophical implications of the compactness of first-order logic (Section 3). Following that, we give some non-topological proofs of the compactness of propositional and first-order logic (Section 4), followed by a topological proof of the propositional case, which gives the compactness theorem its name (Section 5). We continue with a sketch of some generalisations of the usual notion of compactness (Section 6), a calibration of the strength of the compactness theorems relative to the ![]() axioms (Section 7), and end with some notes on the history of the compactness theorems (Section 8). Our discussion concerns the logics philosophers are most familiar with.
axioms (Section 7), and end with some notes on the history of the compactness theorems (Section 8). Our discussion concerns the logics philosophers are most familiar with.
2. Compactness: Common Logics and Natural Language
a. Common Logics
Propositional logic is usually taken to consist of a set of sentential atoms ![]() ,
, ![]() and some truth-functionally complete set of Boolean connectives, for instance
and some truth-functionally complete set of Boolean connectives, for instance ![]() . If we denote by
. If we denote by ![]() a propositional logic with
a propositional logic with ![]() sentential atoms,
sentential atoms, ![]() is a propositional logic with a countable infinity of atoms. (
is a propositional logic with a countable infinity of atoms. (![]() will usually be taken to be an infinite cardinal in what follows.) Any propositional logic
will usually be taken to be an infinite cardinal in what follows.) Any propositional logic ![]() is compact, whatever its set of truth-functional connectives may be. Notice that when
is compact, whatever its set of truth-functional connectives may be. Notice that when ![]() is finite, the compactness of any
is finite, the compactness of any ![]() is a trivial consequence of the fact that any sentence is logically equivalent to a sentence drawn from a fixed set of size no greater than
is a trivial consequence of the fact that any sentence is logically equivalent to a sentence drawn from a fixed set of size no greater than ![]() . (This set is of size exactly
. (This set is of size exactly ![]() just when the set of connectives is truth-functionally complete.)
just when the set of connectives is truth-functionally complete.)
First-order logic with standard semantics is also compact. This fact is of tremendous importance for logic and its applications, since first-order logic remains the canonical logic to this day, the widespread interest in higher, supplementary and alternative logics notwithstanding. By `first-order logic’, we understand throughout first-order logic with identity. First-order logic without identity is of course also compact, since it is a sublogic of first-order logic with identity.
By second-order logic we mean second-order logic with standard or full semantics, in which second-order ![]() -place predicate variables range over all the
-place predicate variables range over all the ![]() -tuples from the domain of interpretation (and similarly for functional variables). In contrast to first-order logic, second-order logic is not compact. To see this, let
-tuples from the domain of interpretation (and similarly for functional variables). In contrast to first-order logic, second-order logic is not compact. To see this, let ![]() be a sentence of first-order logic satisfied in all and only models with domain of size
be a sentence of first-order logic satisfied in all and only models with domain of size ![]() may thus be taken as
may thus be taken as ![]() ,
, ![]() as
as ![]() , and so on. Since first-order logic is a sublogic of second-order logic,
, and so on. Since first-order logic is a sublogic of second-order logic, ![]() is a sentence of second-order logic too. Consider next the sentence
is a sentence of second-order logic too. Consider next the sentence
![]()
where ![]() is a binary predicate variable, `
is a binary predicate variable, `![]() is functional’ abbreviates
is functional’ abbreviates ![]() , `
, `![]() is injective’ abbreviates
is injective’ abbreviates ![]() and `
and `![]() is surjective’ abbreviates
is surjective’ abbreviates ![]() . Any interpretation of this sentence states that the domain is Dedekind-infinite. The following second-order argument is then valid:
. Any interpretation of this sentence states that the domain is Dedekind-infinite. The following second-order argument is then valid:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
However, no finite subset of the premisses entails the conclusion. For let the finite subset be ![]() and take
and take ![]() . Then there is a model of size
. Then there is a model of size ![]() in which the
in which the ![]() premisses
premisses ![]() are true but the argument’s conclusion is false. Hence second-order logic is not compact.
are true but the argument’s conclusion is false. Hence second-order logic is not compact.
The compactness theorem also typically, but not invariably, fails for infinitary logics. Any logic which allows infinite disjunctions, for example, is incompact, since the set of sentences ![]() is
is ![]() (every finite subset is satisfiable) but unsatisfiable. We return to infinitary logics and to generalisations of the notion of compactness in Section 6.
(every finite subset is satisfiable) but unsatisfiable. We return to infinitary logics and to generalisations of the notion of compactness in Section 6.
b. Natural Language
Natural languages are languages such as English, Mandarin, French, and Arabic. Formal languages in contrast are logical languages such as those of propositional, first-order and second-order logic. Although of great mathematical and philosophical importance, the latter are not `natural’ in the intended sense because they are not anyone’s native language and are only ever `spoken’, if at all, in limited contexts.
Is natural language, say English, compact? We must first clarify what the question means. Assume there is such a thing as the relation of logical consequence in natural language. For example, consider these two natural-language arguments:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The first argument is logically valid, whereas the second argument is invalid.
These two examples, of a logically valid English argument and a logically invalid one respectively, help us home in on the notion we are interested in, namely English’s logical validity, but they do not, of course, provide definitions of it. Next, let’s say that a natural language is compact just when, for any logically valid argument in this language, there is a logically valid argument whose conclusion remains the same, yet the premiss set is a finite subset of the original argument’s premiss set. This definition is the analogue of our last definition of compactness above for a formal language: if ![]() then
then ![]() for some finite subset
for some finite subset ![]() of
of ![]() . An equivalent definition could be given based on the other definition of compactness for a formal language.
. An equivalent definition could be given based on the other definition of compactness for a formal language.
The overwhelming majority of linguists, philosophers, and other theorists of language take natural language to consist of infinitely many sentences. The idea is that since such sentences are of finite, but arbitrary, length, there must be infinitely many of them. The set of these sentences may be specified by a set of recursive procedures, which generate sentences of arbitrary length. For example, all the following are sentences of English:
![]()
![]()
![]()
Now as a matter of empirical fact, there is some finite number ![]() such that I do not have a great
such that I do not have a great![]() -grandfather (which
-grandfather (which ![]() is the least such may be vague). That does not affect the point at issue, which is that these infinitely many sentences are bona fide sentences of English.
is the least such may be vague). That does not affect the point at issue, which is that these infinitely many sentences are bona fide sentences of English.
Consider now an English argument roughly analogous to the following English analogue of the second-order-logic argument presented earlier:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
This argument appears to be valid. Clearly, no finite subset of the premiss set entails the conclusion. If this is right, the English consequence relation is incompact. The moral carries over to any natural language into which the argument is translatable.
Resistance to the argument for the incompactness of English may take several forms. One line of resistance, for instance, would query whether any natural language has a single consequence relation. According to this objection, there are only various consequence relations that arise from looking at, say, English through a particular theoretical lens; none is the correct one. Logical pluralists would all take this view, as would some other philosophers of logic: Beall and Restall (2006) and Shapiro (2014) defend different versions of logical pluralism. The objection, then, is that the argument for the incompactness of English given above assumes that there is a determinate notion: the English consequence relation.
This objection, and others, must be addressed before we can conclude that English is incompact. Here we do not take sides but flag the issue as an important one. For more discussion, see Paseau and Griffiths (2021), and Griffiths and Paseau (2022, chap. 5).
3. Implications of Compactness
This section draws some implications of the compactness of first-order logic. The sample below is a small selection from a list that could fill volumes.Our choices are mostly guided by their philosophical implications, although there are a few examples of primarily mathematical interest. From this point on, we assume some knowledge of elementary model theory (Chang and Keisler 1990; Hodges 1997).
- Any compact logic extending first-order logic cannot express the notions of finitude or infinitude (of a model). Suppose towards a contradiction that
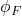 is satisfied by all and only finite models. Then
is satisfied by all and only finite models. Then 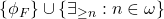 is unsatisfiable, and hence by compactness it must have an unsatisfiable finite subset, which must be a subset of
is unsatisfiable, and hence by compactness it must have an unsatisfiable finite subset, which must be a subset of 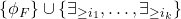 for some
for some  . But any finite model with domain of size
. But any finite model with domain of size 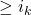 satisfies (any subset of)
satisfies (any subset of) 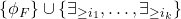 , thereby contradicting our hypothesis. And if there were a sentence
, thereby contradicting our hypothesis. And if there were a sentence 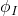 satisfied by all and only infinite models then
satisfied by all and only infinite models then 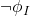 would be satisfied by all and only finite models, a hypothesis we have just refuted.This application of the compactness theorem is entirely typical. Schematically, one shows by contradiction that the class of models with some
would be satisfied by all and only finite models, a hypothesis we have just refuted.This application of the compactness theorem is entirely typical. Schematically, one shows by contradiction that the class of models with some  -property (expressible by the conjunction of an infinite set
-property (expressible by the conjunction of an infinite set 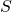 of first-order sentences) is not definable by a single sentence
of first-order sentences) is not definable by a single sentence 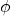 . In these arguments,
. In these arguments,  together with any finite subset of
together with any finite subset of 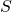 is satisfiable, but
is satisfiable, but 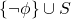 is not, contradicting compactness.
is not, contradicting compactness.
Informally speaking, in these applications the
 -property is the conjunction of the
-property is the conjunction of the 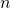 -properties ; in our example, the
-properties ; in our example, the 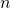 -property was having size at least
-property was having size at least 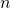 and the
and the  -property was having infinite size.However, it is possible that (depending on the language) there is a sentence which implies that any of these models must be infinite. As an example, take the first-order language with a single unary function symbol, and take the sentence
-property was having infinite size.However, it is possible that (depending on the language) there is a sentence which implies that any of these models must be infinite. As an example, take the first-order language with a single unary function symbol, and take the sentence![Rendered by QuickLaTeX.com \[\phi \df := \forall x \forall y (f(x) = f(y) \to x = y) \wedge \exists x \forall y \neg (f(y) = x).\]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-217314de1201e69873d35d0ed12ce42e_l3.png)
The models of this sentence are sets endowed with an injective, but non-surjective function. By the pigeonhole-principle, each such model must be infinite. Since this sentence cannot express infinitude, there must be an infinite model not satisfying
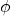 . An example is the domain of natural numbers, over which
. An example is the domain of natural numbers, over which 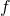 is interpreted as the identity function on the natural numbers.As a further illustration of this technique, compactness implies that the class of torsion-free abelian groups is not finitely-axiomatisable in first-order logic. (A group is torsion-free if the identity is the only element with finite order. The prototypical example of a torsion-free abelian group is (
is interpreted as the identity function on the natural numbers.As a further illustration of this technique, compactness implies that the class of torsion-free abelian groups is not finitely-axiomatisable in first-order logic. (A group is torsion-free if the identity is the only element with finite order. The prototypical example of a torsion-free abelian group is (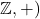 .) For if it were, by the single sentence
.) For if it were, by the single sentence 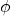 say, then the set
say, then the set![Rendered by QuickLaTeX.com \[\text{[abelian group axioms]} \cup \{\neg \phi\} \cup \{\forall x \ne 0 (\underbrace{x + \cdots + x}_{n \text{ times}} \ne 0) : n = 1, 2, \dots\}\]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-8f73b82d52580ce9b039296d51601525_l3.png)
would be finitely-satisfiable (for finite sets where the sums are bounded by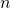 in the sentences from the rightmost set, take the integers under addition modulo
in the sentences from the rightmost set, take the integers under addition modulo 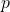 for some prime
for some prime 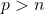 ). But the set itself is unsatisfiable, since
). But the set itself is unsatisfiable, since![Rendered by QuickLaTeX.com \[\set{\text{[abelian group axioms]}} \cup \{\forall x \ne 0 (\underbrace{x + \cdots + x}_{n \text{ times}} \ne 0) : n = 1, 2, \dots\}\]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-0482c882c82c3e6417e835ef763942dd_l3.png)
is satisfied by all and only torsion-free abelian groups. This contradicts compactness. Note that here the
 -property is that all non-identity elements of the model have infinite order, and the
-property is that all non-identity elements of the model have infinite order, and the 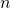 -property that all non-identity elements have order
-property that all non-identity elements have order  (all these properties incorporate the abelian group axioms too).As a still further illustration, the same type of argument shows that the class of algebraically-closed fields is also not finitely-axiomatisable. The relevant
(all these properties incorporate the abelian group axioms too).As a still further illustration, the same type of argument shows that the class of algebraically-closed fields is also not finitely-axiomatisable. The relevant  -property is that the field is algebraically-closed, and the relevant
-property is that the field is algebraically-closed, and the relevant 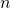 -property is
-property is![Rendered by QuickLaTeX.com \[\forall y_1 \forall y_2 \ldots \forall y_n \exists x(x^n + y_1 \cdot x^{n-1} + \cdots + y_{n-1} \cdot x + y_n = 0)\]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-0157a87defbdaa6eaab9e40d15666bba_l3.png)
This style of argument is easily applied to many other domains.
- Suppose
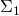 and
and  are two sets of sentences of a compact logic (in which conjunction and negation are definable) with the property that every model satisfies either
are two sets of sentences of a compact logic (in which conjunction and negation are definable) with the property that every model satisfies either 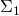 or
or  but not both. Then there is a sentence
but not both. Then there is a sentence 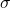 such that
such that 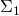 is logically equivalent to
is logically equivalent to 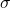 (meaning that
(meaning that  and
and 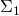 have the same models) and
have the same models) and  is logically equivalent to
is logically equivalent to 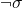 (Chang and Keisler 1990, p. 12, cor. 1.2.15).
(Chang and Keisler 1990, p. 12, cor. 1.2.15). - The compactness theorem may be used to show that any first-order theory of arithmetic
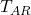 satisfied by the standard model has a non-standard model. (By the standard model of arithmetic, for the theory
satisfied by the standard model has a non-standard model. (By the standard model of arithmetic, for the theory 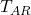 in question, we mean the structure of natural numbers with the standard interpretation of the non-logical symbols in the language of
in question, we mean the structure of natural numbers with the standard interpretation of the non-logical symbols in the language of 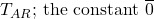 denotes 0, the two-place symbol + denotes addition,
denotes 0, the two-place symbol + denotes addition,  denotes multiplication, and so forth. A nonstandard model can have `infinite’ elements: objects greater than those denoted by the terms
denotes multiplication, and so forth. A nonstandard model can have `infinite’ elements: objects greater than those denoted by the terms 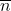 for all
for all 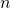 . As an ordered set, a nonstandard model looks like
. As an ordered set, a nonstandard model looks like  followed by blocks of
followed by blocks of  , which themselves form a dense linear order without endpoints.) Assuming that each numeral
, which themselves form a dense linear order without endpoints.) Assuming that each numeral 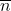 is definable in
is definable in 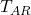 , consider
, consider
![Rendered by QuickLaTeX.com \[T_{AR}^+ = T_{AR} \cup \{c \neq \overline{n}:n \in \omega \}\]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-3ea60c7e10ead6dbf05d1f9df486d77b_l3.png)
where
 is any constant not in the language of
is any constant not in the language of 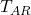 . Any finite subset of
. Any finite subset of  is satisfied by the standard model, because we may interpret
is satisfied by the standard model, because we may interpret  as a number distinct from those
as a number distinct from those 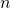 where
where 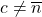 occurs in the given finite subset. Hence by compactness,
occurs in the given finite subset. Hence by compactness,  has a model
has a model 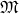 . The reduct of
. The reduct of 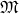 to the language of
to the language of 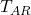 is non-standard since it contains an element
is non-standard since it contains an element 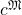 (the denotation of
(the denotation of  in
in 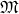 not identical to any natural number.Supplementing the argument just given with an appeal to the downward Löwenheim-Skolem Theorem (Chang and Keisler 1990, p. 66, cor. 2.1.4; Hodges 1997, p. 72, cor. 3.1.4) shows that any such first-order theory of arithmetic
not identical to any natural number.Supplementing the argument just given with an appeal to the downward Löwenheim-Skolem Theorem (Chang and Keisler 1990, p. 66, cor. 2.1.4; Hodges 1997, p. 72, cor. 3.1.4) shows that any such first-order theory of arithmetic 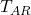 is not even
is not even  -categorical, since it has a countably infinite non-standard model. (For an infinite cardinal
-categorical, since it has a countably infinite non-standard model. (For an infinite cardinal 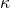 , a theory is
, a theory is 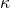 -categorical if it has exactly one model, up to isomorphism, of cardinality
-categorical if it has exactly one model, up to isomorphism, of cardinality 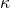 .) Observe that a theory may be complete even if it is not
.) Observe that a theory may be complete even if it is not  -categorical. To see this, run the previous argument supplemented by an application of the downward Löwenheim-Skolem Theorem for a complete theory of arithmetic
-categorical. To see this, run the previous argument supplemented by an application of the downward Löwenheim-Skolem Theorem for a complete theory of arithmetic 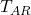 . More generally, a theory may fail to be
. More generally, a theory may fail to be 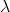 -categorical for every infinite cardinal
-categorical for every infinite cardinal 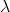 and still be complete—in other words the converse of the Łoś-Vaught test (Chang and Keisler 1990, p. 139, prop. 3.1.7) fails.The same general idea can be used to demonstrate the existence of non-standard models of real analysis. Let
and still be complete—in other words the converse of the Łoś-Vaught test (Chang and Keisler 1990, p. 139, prop. 3.1.7) fails.The same general idea can be used to demonstrate the existence of non-standard models of real analysis. Let 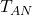 be a first-order theory of analysis satisfied by the standard model (the ordered field of real numbers). As above, consider
be a first-order theory of analysis satisfied by the standard model (the ordered field of real numbers). As above, consider 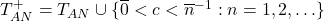 where
where  is any constant not in
is any constant not in 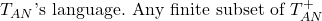 is satisfied by the standard model, because we may interpret
is satisfied by the standard model, because we may interpret  as a positive real number smaller than
as a positive real number smaller than 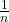 , where
, where 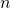 is the largest number for which the sentence
is the largest number for which the sentence 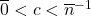 is in the given finite subset. Hence by compactness,
is in the given finite subset. Hence by compactness,  has a model
has a model 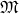 . The reduct of
. The reduct of 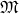 to the language of
to the language of 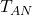 is non-standard since it contains an element
is non-standard since it contains an element 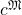 not identical to any real number. Indeed, this element must be a positive infinitesimal, meaning that it is a number greater than
not identical to any real number. Indeed, this element must be a positive infinitesimal, meaning that it is a number greater than 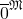 but smaller than every
but smaller than every  . As well as infinitesimals, our non-standard model also contains infinite elements, since the the model satisfies
. As well as infinitesimals, our non-standard model also contains infinite elements, since the the model satisfies 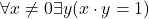 and thus any non-zero element has an inverse. From these foundations, a consistent theory of the calculus that revives to a degree the use of infinitesimals in early modern mathematics may be constructed, called non-standard analysis: see Goldblatt (1998) or the original Robinson (1966). Furthermore, since
and thus any non-zero element has an inverse. From these foundations, a consistent theory of the calculus that revives to a degree the use of infinitesimals in early modern mathematics may be constructed, called non-standard analysis: see Goldblatt (1998) or the original Robinson (1966). Furthermore, since 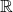 and
and 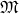 have the same theory, any sentence in the language of
have the same theory, any sentence in the language of 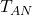 that can be proven from
that can be proven from  will hold in
will hold in 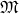 and thus automatically holds in
and thus automatically holds in 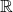 . This is the transfer principle of non-standard analysis.
. This is the transfer principle of non-standard analysis. Since second-order logic is incompact, the arguments just given fail for second-order theories of arithmetic and analysis. Indeed, there are categorical second-order axiomatisations of arithmetic (for example, Peano Arithmetic with second-order induction (Shapiro 1991, p. 82, thm. 4.8)) and real analysis (for example, the axioms for a complete ordered field (p. 84, thm. 4.10)). For more on second-order theories, consult (chap. 3–6).
- Assuming the downward Löwenheim-Skolem Theorem, another corollary of the compactness of first-order logic is the upward Löwenheim-Skolem Theorem (Chang and Keisler 1990, p. 67, cor. 2.1.6; Hodges 1997, p. 127,cor. 5.1.4). This upward version of the theorem states that if a first-order language
 has cardinality
has cardinality  and
and 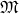 is an infinite model with domain of cardinality
is an infinite model with domain of cardinality  then
then 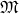 has an elementary extension of cardinality
has an elementary extension of cardinality 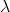 . For the proof, we consider the set of sentences consisting of the elementary diagram (the set
. For the proof, we consider the set of sentences consisting of the elementary diagram (the set 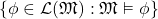 , where
, where 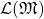 is the extension of
is the extension of  obtained by adding constant symbols
obtained by adding constant symbols 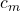 for each
for each 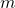 in the domain of
in the domain of 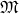 , and the interpretation of
, and the interpretation of 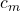 in
in 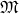 is simply
is simply 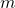 together with the sentences
together with the sentences 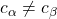 for all distinct
for all distinct 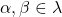 , where the
, where the 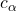 are new constants.This set is finitely-satisfiable (because the infinite model
are new constants.This set is finitely-satisfiable (because the infinite model 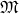 satisfies any finite subset), and hence by compactness it is satisfiable. Say that it is satisfied by a model
satisfies any finite subset), and hence by compactness it is satisfiable. Say that it is satisfied by a model 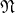 , which must be of size
, which must be of size 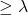 as it satisfies
as it satisfies 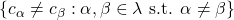 . Since
. Since 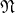 also satisfies the elementary diagram of
also satisfies the elementary diagram of 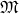 , an elementary embedding of
, an elementary embedding of 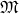 into
into 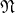 exists, and thus there is an elementary extension
exists, and thus there is an elementary extension 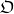 of
of 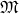 with domain of size
with domain of size 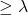 (
(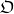 is an isomorph of
is an isomorph of 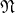 whose domain includes that of
whose domain includes that of 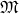 ). To find an elementary extension of
). To find an elementary extension of 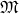 of size exactly
of size exactly 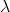 , now apply the downward Löwenheim-Skolem Theorem to
, now apply the downward Löwenheim-Skolem Theorem to 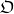 .The upward Löwenheim-Skolem Theorem may be applied to show not only that theories of arithmetic and analysis satisfied by their respective standard models have non-standard models, but also that they have non-standard models of every infinite cardinality. More generally, any first-order theory in a countable language satisfied by an infinite model has models of every cardinality. Applying this to
.The upward Löwenheim-Skolem Theorem may be applied to show not only that theories of arithmetic and analysis satisfied by their respective standard models have non-standard models, but also that they have non-standard models of every infinite cardinality. More generally, any first-order theory in a countable language satisfied by an infinite model has models of every cardinality. Applying this to 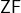 or
or  , we obtain Skolem’s paradox: if there exists a model of set theory, then there exists a countably-infinite model, which will nonetheless model the existence of uncountable sets (Skolem 1922, 295–96).The upward and downward Löwenheim-Skolem Theorems and the so-called Skolem paradox have generated much philosophical debate. The most famous philosophical use of these results is found in Putnam (1980). Wielding the theorems, Putnam argued that our mathematical-scientific theories do not admit a determinate intepretation. In particular, he claimed that set theory augmented with any theoretical principles from science and scientific data we care to add admits a countable model. This argument has given rise to an extensive literature. The responses to Putnam’s argument, and to other versions, include technical discussion of exactly what Putnam’s argument requires mathematically speaking, as well as philosophical commentary.
, we obtain Skolem’s paradox: if there exists a model of set theory, then there exists a countably-infinite model, which will nonetheless model the existence of uncountable sets (Skolem 1922, 295–96).The upward and downward Löwenheim-Skolem Theorems and the so-called Skolem paradox have generated much philosophical debate. The most famous philosophical use of these results is found in Putnam (1980). Wielding the theorems, Putnam argued that our mathematical-scientific theories do not admit a determinate intepretation. In particular, he claimed that set theory augmented with any theoretical principles from science and scientific data we care to add admits a countable model. This argument has given rise to an extensive literature. The responses to Putnam’s argument, and to other versions, include technical discussion of exactly what Putnam’s argument requires mathematically speaking, as well as philosophical commentary. - The compactness theorem may be used to prove the Order-Extension Principle (also known as Szpilrajn’s Extension Theorem): any partial order may be extended to a linear order. A partial order (
 ) consists of a domain
) consists of a domain 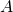 with an irreflexive and transitive relation
with an irreflexive and transitive relation 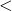 . A linear order is a partial order satisfying the additional linearity axiom
. A linear order is a partial order satisfying the additional linearity axiom 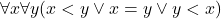 . A linear order (
. A linear order ( ) extends the partial order (
) extends the partial order ( ) just when for all
) just when for all  in
in 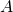 , if
, if 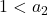 then
then  ; in other words, the identity map from (
; in other words, the identity map from ( ) into (
) into (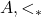 ) is a homomorphism. The notions of partial and linear order are first-order definable in the language consisting of a single two-place non-logical predicate, which is what permits the application of the compactness theorem.Unusually for applications of the compactness theorem, this result is of potential importance outside mathematics, logic, and philosophy. A standard assumption in economics is that a subject’s preferences over goods are linearly ordered. Empirically, however, we find that people’s preferences tend at best to be partially ordered: I may prefer going out for a Japanese meal rather than an Italian meal, but I may have no preference between going to the cinema and going out for a Japanese meal. In light of the Order-Extension Principle, one might try to argue that preferences being linearly ordered is a justifiable idealisation of the empirical data. See Szpilrajn (1930) for the first proof of this theorem and Richter (1966) for an early economic application, as well as Gonczarowski, Kominers, and Shorrer
) is a homomorphism. The notions of partial and linear order are first-order definable in the language consisting of a single two-place non-logical predicate, which is what permits the application of the compactness theorem.Unusually for applications of the compactness theorem, this result is of potential importance outside mathematics, logic, and philosophy. A standard assumption in economics is that a subject’s preferences over goods are linearly ordered. Empirically, however, we find that people’s preferences tend at best to be partially ordered: I may prefer going out for a Japanese meal rather than an Italian meal, but I may have no preference between going to the cinema and going out for a Japanese meal. In light of the Order-Extension Principle, one might try to argue that preferences being linearly ordered is a justifiable idealisation of the empirical data. See Szpilrajn (1930) for the first proof of this theorem and Richter (1966) for an early economic application, as well as Gonczarowski, Kominers, and Shorrer
(2019) for more applications of the compactness theorem in economics.How does one prove the Order-Extension Principle? A relatively straight-forward proof by induction on the size of the domain shows that every partial order with a finite domain can be extended to a linear order. We may then use the compactness theorem to prove that every partial order can be extended to a linear order, whatever the size of the domain, be it finite or infinite. Given a partial order ( ), let
), let 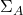 be a set of sentences consisting of the (Robinson) diagram of (
be a set of sentences consisting of the (Robinson) diagram of ( ) (the diagram of an
) (the diagram of an  -structure
-structure 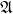 is the set of literals—atomic sentences or negations of atomic sentences—in the language
is the set of literals—atomic sentences or negations of atomic sentences—in the language  {
{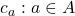 }, where
}, where 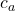 are new constant symbols, satisfied in the expansion
are new constant symbols, satisfied in the expansion 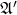 of
of 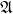 where we interpret
where we interpret 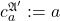 for each
for each 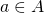 .), together with the axioms
.), together with the axioms  for all distinct
for all distinct  ,
, 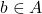 .
.
Since every partial order with a finite domain can be extended to a linear order, it follows that any finite subset of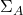 is satisfiable. By compactness,
is satisfiable. By compactness, 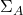 is therefore satisfiable. If
is therefore satisfiable. If 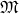 is a model of
is a model of 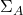 then (
then ( ) embeds into the
) embeds into the 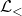 -reduct of
-reduct of 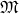 , which we call (
, which we call ( ), via
), via  to (
to ( ) say. The required linear order extending (
) say. The required linear order extending ( ) is the inverse under
) is the inverse under 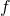 of the restriction of the order
of the restriction of the order 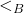 to
to 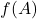 , that is
, that is 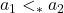 if and only if
if and only if 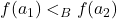 .Note in passing that the Order-Extension Principle implies that every set
.Note in passing that the Order-Extension Principle implies that every set 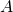 can be linearly ordered: simply consider a linear order that extends the empty partial order on
can be linearly ordered: simply consider a linear order that extends the empty partial order on 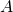 .
.
The compactness theorem for first-order logic has a great many other applications to model theory—as Keisler (1965, 113) puts it, “the most useful theorem in model theory is probably the compactness theorem”—as well as to set theory, other parts of logic, combinatorics, algebra, algebraic geometry; see Hodges (1997), especially chapter 5, for more.
4. Some Non-topological Proofs
In this section, we give three styles proofs of the compactness of propositional and first-order logic that do not draw on topology. These three proofs illustrate some important techniques, and could be broadly classified as deductive, syntactic, and semantic methods of proof.
a. Deductive: Proofs via Soundness and Completeness
We recall the definitions of soundness and completeness for a logic ![]() equipped with semantic consequence relation
equipped with semantic consequence relation ![]() and deductive consequence relation
and deductive consequence relation ![]() . The logic is complete iff for any set of well-formed formulas
. The logic is complete iff for any set of well-formed formulas ![]() and any well-formed formula
and any well-formed formula ![]() , if
, if ![]() then
then ![]() ; and it is sound iff the converse obtains: if
; and it is sound iff the converse obtains: if ![]() then
then ![]() .
.
If a logic has a sound and complete proof procedure, it is compact. A simple argument demonstrates this:
(1) ![]() Assumption
Assumption
(2) ![]() From (1) by Completeness
From (1) by Completeness
(3) ![]() From (2) by the finiteness of proofs
From (2) by the finiteness of proofs
(4) ![]() From (3) by Soundness
From (3) by Soundness
Here ![]() is some finite subset of
is some finite subset of ![]() . Anything deserving of the name of `proof procedure’ usually satisfies a host of syntactic requirements. Given soundness and completeness the only such requirement needed for the validity of the inference above is that the step from (2) to (3) be valid, namely that proofs draw only on finitely many premisses. The argument just given therefore applies to any logic which has a sound and complete proof procedure in this liberal sense.
. Anything deserving of the name of `proof procedure’ usually satisfies a host of syntactic requirements. Given soundness and completeness the only such requirement needed for the validity of the inference above is that the step from (2) to (3) be valid, namely that proofs draw only on finitely many premisses. The argument just given therefore applies to any logic which has a sound and complete proof procedure in this liberal sense.
Thus, no incompact logic can be completable by a sound proof procedure; second-order logic in particular cannot.
The proof of compactness via completeness is in an important respect unsatisfactory because it is based on properties incidental to the semantic property of interest. The proof derives compactness, a semantic property, from a property of the logic relating its syntax to its semantics. Thus Keisler (1965, 113): “unlike the completeness theorem, the compactness theorem does not involve the notion of a formal deduction, and so it is desirable to prove it directly without using that notion”. Indeed, from the perspective of a model theorist who sees talk of syntax as a heuristic for the study of certain relations between structures that happen to have syntactic correlates, proving compactness via completeness is tantamount to heresy (Poizat 2000, 53).
b. Syntactic: Henkin-Style Proofs
This proof is modelled on Henkin’s (1949b) proof of the completeness theorem for first-order logic, with its deductive core replaced by a semantic one. We begin with a relatively concrete argument for the simplest case of ![]() before passing to more abstract versions. Unlike the usual versions of the proof, our argument does not assume any particular set of truth-functional connectives, only that the set of sentences is countably-infinite (and thus the set of connectives is countable); the argument is usually simpler (but less general) when a particular set of connectives has been specified.
before passing to more abstract versions. Unlike the usual versions of the proof, our argument does not assume any particular set of truth-functional connectives, only that the set of sentences is countably-infinite (and thus the set of connectives is countable); the argument is usually simpler (but less general) when a particular set of connectives has been specified.
Let ![]() be an enumeration of the set of sentences of
be an enumeration of the set of sentences of ![]() . Given a finitely-satisfiable set
. Given a finitely-satisfiable set ![]() , define a denumerable sequence of sets
, define a denumerable sequence of sets ![]() as follows:
as follows:

By definition, ![]() is finitely-satisfiable for all
is finitely-satisfiable for all ![]() , hence
, hence ![]() is finitely-satisfiable since any finite subset of
is finitely-satisfiable since any finite subset of ![]() must be drawn from some
must be drawn from some ![]() .
.
From ![]() , define the valuation
, define the valuation ![]() by letting
by letting ![]() if and only if
if and only if ![]() , where
, where ![]() is a sentence letter. We now prove that
is a sentence letter. We now prove that ![]() is a valuation in which all the sentences in
is a valuation in which all the sentences in ![]() (not just the sentence letters) are true. Suppose towards a contradiction that
(not just the sentence letters) are true. Suppose towards a contradiction that ![]() for some
for some ![]() . Without loss of generality (renumbering sentence letters if necessary), let
. Without loss of generality (renumbering sentence letters if necessary), let ![]() be all the sentence letters in
be all the sentence letters in ![]() with truth-value 1 under
with truth-value 1 under ![]() and
and ![]() all the sentence letters in
all the sentence letters in ![]() with truth-value 0 under
with truth-value 0 under ![]() (one of these sets may be empty, in which case the argument to follow is easily modified). By the definition of
(one of these sets may be empty, in which case the argument to follow is easily modified). By the definition of ![]() , none of
, none of ![]() is in
is in ![]() so for each of these, let
so for each of these, let ![]() be a finite subset of
be a finite subset of ![]() such that
such that ![]() is unsatisfiable (
is unsatisfiable (![]() ); some such
); some such ![]() must exist given that
must exist given that ![]() was omitted in the construction of
was omitted in the construction of ![]() . Now consider the set
. Now consider the set
![Rendered by QuickLaTeX.com \[S := \df \{p_1, \ldots, p_k, \phi\} \cup \left( \bigcup_{i = k + 1}^n \Delta_i \right).\]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-9eb66f16985fe65d9d39c4ed31f4b26d_l3.png)
Any valuation in which all the elements of ![]() are true is one in which each of
are true is one in which each of ![]() is false, since
is false, since ![]() is unsatisfiable, and so any valuation in which
is unsatisfiable, and so any valuation in which ![]() and all elements of
and all elements of ![]() are true is one in which the sentence letters
are true is one in which the sentence letters ![]() have truth-value 0. It follows that any such valuation is one in which
have truth-value 0. It follows that any such valuation is one in which ![]() is false, since
is false, since ![]() contains no sentence letters other than
contains no sentence letters other than ![]() and
and ![]() . Hence
. Hence ![]() is unsatisfiable, contradicting the fact that this set is a finite subset of
is unsatisfiable, contradicting the fact that this set is a finite subset of ![]() . Having proved by reductio that any sentence in
. Having proved by reductio that any sentence in ![]() is true under
is true under ![]() , it follows that
, it follows that ![]() , which is a subset of
, which is a subset of ![]() , is satisfiable. It is obvious from its construction that
, is satisfiable. It is obvious from its construction that ![]() is a maximal finitely-satisfiable set, meaning that it is finitely-satisfiable and none of its proper extensions are finitely-satisfiable.
is a maximal finitely-satisfiable set, meaning that it is finitely-satisfiable and none of its proper extensions are finitely-satisfiable.
A more abstract version of the argument just presented runs as follows. Suppose ![]() is finitely-satisfiable. Order by inclusion the set
is finitely-satisfiable. Order by inclusion the set ![]() of finitely-satisfiable sets of sentences of the language containing
of finitely-satisfiable sets of sentences of the language containing ![]() .
. ![]() is non-empty, since it contains at least
is non-empty, since it contains at least ![]() . Any chain in
. Any chain in ![]() has an upper bound, obtained by taking the union of the elements in the chain: this union contains
has an upper bound, obtained by taking the union of the elements in the chain: this union contains ![]() as a subset since all the members of the chain do, and it is finitely-satisfiable since any of its finite subsets must come from some element of the chain, which by hypothesis is finitely-satisfiable. Zorn’s Lemma, provable in
as a subset since all the members of the chain do, and it is finitely-satisfiable since any of its finite subsets must come from some element of the chain, which by hypothesis is finitely-satisfiable. Zorn’s Lemma, provable in ![]() , states precisely that every partial order with the property that every chain has an upper bound has a maximal element. Since the conditions of Zorn’s Lemma are satisfied, we deduce from it that
, states precisely that every partial order with the property that every chain has an upper bound has a maximal element. Since the conditions of Zorn’s Lemma are satisfied, we deduce from it that ![]() has a maximal element, that is to say, a maximal finitely-satisfiable set extending
has a maximal element, that is to say, a maximal finitely-satisfiable set extending ![]() . We then reason as in the previous paragraph to show that all the elements of
. We then reason as in the previous paragraph to show that all the elements of ![]() are true under the valuation
are true under the valuation ![]() defined on sentence letters by
defined on sentence letters by ![]() if and only if
if and only if ![]() is a member of this maximal finitely-satisfiable set. Nowhere did we rely on the fact that the sentence letters are denumerably many, or on any assumption about the set of connectives. So this more general argument shows that
is a member of this maximal finitely-satisfiable set. Nowhere did we rely on the fact that the sentence letters are denumerably many, or on any assumption about the set of connectives. So this more general argument shows that ![]() is compact for any cardinal
is compact for any cardinal ![]() whatsoever.
whatsoever.
The abstract argument just given invoked Zorn’s Lemma, well known to be equivalent to the Axiom of Choice in ![]() . Is this use of a
. Is this use of a ![]() -equivalent of Choice necessary? No. A weaker principle than Zorn’s Lemma, namely the Ultrafilter Lemma, will do. (Section 7 has more on the relative strengths in
-equivalent of Choice necessary? No. A weaker principle than Zorn’s Lemma, namely the Ultrafilter Lemma, will do. (Section 7 has more on the relative strengths in ![]() of the Ultrafilter Lemma and Zorn’s Lemma. Consult Moore (1982) for more on the Axiom of Choice and its foundational significance.) To explain what the Ultrafilter Lemma is, we must first define the notion of a filter on a Boolean algebra. We denote the bottom, top, join, meet and complement in a Boolean algebra (with which we assume basic familiarity, see Givant and Halmos (2009) for an introduction) by the symbols
of the Ultrafilter Lemma and Zorn’s Lemma. Consult Moore (1982) for more on the Axiom of Choice and its foundational significance.) To explain what the Ultrafilter Lemma is, we must first define the notion of a filter on a Boolean algebra. We denote the bottom, top, join, meet and complement in a Boolean algebra (with which we assume basic familiarity, see Givant and Halmos (2009) for an introduction) by the symbols ![]() ; the derived strong and weak inequality symbols have their customary meanings (
; the derived strong and weak inequality symbols have their customary meanings (![]() means that
means that ![]() and so on). A filter on a Boolean algebra
and so on). A filter on a Boolean algebra ![]() is then a subset
is then a subset ![]() of
of ![]() such that:
such that:
- 1
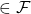 ;
; 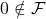 ;
; 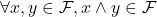 ;
;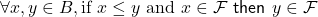 .
.
An ultrafilter ![]() is a maximal filter on
is a maximal filter on ![]() , or alternatively a filter on
, or alternatively a filter on ![]() that contains exactly one of
that contains exactly one of ![]() or
or ![]() for each
for each ![]() . The Ultrafilter Lemma, sometimes called the `Ultrafilter Theorem’ or `Ultrafilter Principle’, states that any filter on a Boolean algebra may be extended to an ultrafilter.
. The Ultrafilter Lemma, sometimes called the `Ultrafilter Theorem’ or `Ultrafilter Principle’, states that any filter on a Boolean algebra may be extended to an ultrafilter.
Armed with the notion of an ultrafilter, we may now modify the abstract proof of ![]() ‘s compactness to rely not on Zorn’s Lemma but on the
‘s compactness to rely not on Zorn’s Lemma but on the ![]() -weaker Ultrafilter Lemma instead. (Henceforth we assume that the set of propositional connectives is truth-functionally complete.) Consider the Boolean algebra
-weaker Ultrafilter Lemma instead. (Henceforth we assume that the set of propositional connectives is truth-functionally complete.) Consider the Boolean algebra ![]() whose domain is the set of equivalence classes of sentences of
whose domain is the set of equivalence classes of sentences of ![]() under logical equivalence, 0 and 1 being the equivalence class of a contradiction and tautology respectively,
under logical equivalence, 0 and 1 being the equivalence class of a contradiction and tautology respectively, ![]() ,
, ![]() and
and ![]() respectively denoting disjunction, conjunction and negation on the equivalence class representatives (easy check: this is well-defined); such a Boolean algebra is usually called a Lindenbaum algebra. To simplify notation, we denote the equivalence class of
respectively denoting disjunction, conjunction and negation on the equivalence class representatives (easy check: this is well-defined); such a Boolean algebra is usually called a Lindenbaum algebra. To simplify notation, we denote the equivalence class of ![]() by
by ![]() itself; observe that the equivalence of
itself; observe that the equivalence of ![]() and
and ![]() follows from the fact that
follows from the fact that ![]() and
and ![]() are logically equivalent if and only if
are logically equivalent if and only if ![]() .
.
Given a finitely-satisfiable set ![]() , form the set
, form the set ![]() consisting of all the sentences entailed by some finite subset of
consisting of all the sentences entailed by some finite subset of ![]() , that is,
, that is,
![]()
Clearly, ![]() is a subset of
is a subset of ![]() , and
, and ![]() also has the following three properties:
also has the following three properties:
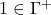 but
but 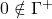 (since
(since 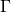 is finitely-satisfiable);
is finitely-satisfiable);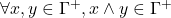 ;
;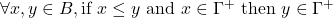 .
.
In other words, ![]() is a filter on the Boolean algebra of sentences of
is a filter on the Boolean algebra of sentences of ![]() . It is the smallest filter containing
. It is the smallest filter containing ![]() , that is to say,
, that is to say, ![]() is a filter-base for
is a filter-base for ![]() . By the Ultrafilter Lemma,
. By the Ultrafilter Lemma, ![]() may be extended to an ultrafilter. The alternative definition of an ultrafilter shows that this ultrafilter is a maximal finitely-satisfiable set of sentences containing
may be extended to an ultrafilter. The alternative definition of an ultrafilter shows that this ultrafilter is a maximal finitely-satisfiable set of sentences containing ![]() . The rest of the proof proceeds as above. We have thus proved the compactness of
. The rest of the proof proceeds as above. We have thus proved the compactness of ![]() using the Ultrafilter Lemma rather than Zorn’s Lemma.
using the Ultrafilter Lemma rather than Zorn’s Lemma.
The compactness of first-order logic may be demonstrated by a similar argument. We give two versions of the argument: the first and slightly more direct version uses the Axiom of Choice; the second uses only the weaker Ultrafilter Lemma. For the first version, let ![]() be the size of
be the size of ![]() where
where ![]() is the first-order language in which each of the sentences in our given finitely-satisfiable set
is the first-order language in which each of the sentences in our given finitely-satisfiable set ![]() is expressed,
is expressed, ![]() is the set of formulas of
is the set of formulas of ![]() , and
, and ![]() is
is ![]() ‘s set of variables. Add a distinct set of constants of size
‘s set of variables. Add a distinct set of constants of size ![]() to the language (usually known as nullary Skolem functions ), disjoint from
to the language (usually known as nullary Skolem functions ), disjoint from ![]() and to be used as a source of witnesses. Then
and to be used as a source of witnesses. Then ![]() also has size
also has size ![]() (since
(since ![]() for infinite
for infinite ![]() ), and so we can well-order both the set of formulas
), and so we can well-order both the set of formulas ![]() and the set of new constant symbols in order-type
and the set of new constant symbols in order-type ![]() . We now augment the set
. We now augment the set ![]() recursively by exploiting the well-ordering of
recursively by exploiting the well-ordering of ![]() and the well-ordering of the set of new constants (each well-ordering being of type
and the well-ordering of the set of new constants (each well-ordering being of type ![]() ). Let
). Let ![]() and
and ![]() for
for ![]() a limit. For the successor case, let
a limit. For the successor case, let
![]()
where ![]() denotes
denotes ![]() with
with ![]() substituted for any free occurrences of
substituted for any free occurrences of ![]() in
in ![]() , if
, if ![]() is the
is the ![]() formula in the ordering of
formula in the ordering of ![]() and
and ![]() is the first constant in the ordering of the set of constants not to appear in any element of
is the first constant in the ordering of the set of constants not to appear in any element of ![]() nor in
nor in ![]() ; otherwise (if the
; otherwise (if the ![]() formula is not existential) let
formula is not existential) let ![]() . Finally, let
. Finally, let ![]() and define
and define ![]() as the set of sentences entailed by any finite subset of
as the set of sentences entailed by any finite subset of ![]() , that is,
, that is,
![]()
An identical argument to the one in the propositional case now shows that ![]() is a filter on the Boolean algebra of the first-order
is a filter on the Boolean algebra of the first-order ![]() -sentences quotiented by logical equivalence. The only difference lies in the verification that
-sentences quotiented by logical equivalence. The only difference lies in the verification that ![]() , in other words, that
, in other words, that ![]() is finitely-satisfiable. For if
is finitely-satisfiable. For if
![]()
were unsatisfiable, with ![]() and
and ![]() is the greatest constant subject to their well-order (
is the greatest constant subject to their well-order (![]() and
and ![]() here are natural numbers, and the
here are natural numbers, and the ![]() and
and ![]() -indices are ordinals smaller than
-indices are ordinals smaller than ![]() ), then
), then
![]()
But if the premisses
![]()
are jointly satisfiable then they cannot entail both ![]() and
and ![]() . The reason is that if there is a model in which this premiss set and
. The reason is that if there is a model in which this premiss set and ![]() are satisfied, then there is a model in which the interpretation of
are satisfied, then there is a model in which the interpretation of ![]() may be chosen to witness the truth of
may be chosen to witness the truth of ![]() , since
, since ![]() does not appear in any other sentence than
does not appear in any other sentence than ![]() .
.
Having verified that ![]() is a filter, we invoke the Ultrafilter Lemma as before to extend
is a filter, we invoke the Ultrafilter Lemma as before to extend ![]() to an ultrafilter
to an ultrafilter ![]() . Note that
. Note that ![]() contains
contains ![]() and hence is witness-complete—every existential statement is satisfied by some constant. To show that
and hence is witness-complete—every existential statement is satisfied by some constant. To show that ![]() (and hence
(and hence ![]() ) is satisfiable, we construct a term model
) is satisfiable, we construct a term model ![]() . The term model’s domain consists of the closed terms of
. The term model’s domain consists of the closed terms of ![]() , quotiented by the relation of appearing in an identity statement of
, quotiented by the relation of appearing in an identity statement of ![]() , that is to say
, that is to say ![]() if and only if
if and only if ![]() . The interpretation
. The interpretation ![]() of the constant
of the constant ![]() is
is ![]() ‘s equivalence class, [
‘s equivalence class, [![]() ]; the interpretation
]; the interpretation ![]() of the function symbol
of the function symbol ![]() applied to
applied to ![]() is
is ![]() ; and for any
; and for any ![]() -place relation symbol
-place relation symbol ![]() and closed terms
and closed terms ![]() ,
, ![]() holds in the model if and only if
holds in the model if and only if ![]() is an element of
is an element of ![]() . A routine argument shows that this interpretation is well-defined and that the term model
. A routine argument shows that this interpretation is well-defined and that the term model ![]() is a model of
is a model of ![]() . It is an instructive exercise to determine where exactly the arguments just given break down in the case of second-order logic: see Paseau (2010a, 75–76) for details.
. It is an instructive exercise to determine where exactly the arguments just given break down in the case of second-order logic: see Paseau (2010a, 75–76) for details.
To see how to avoid the use of the Axiom of Choice, we show that turning ![]() into a Skolem set (a set containing a witness for every existential statement) does not in fact require the Well-Ordering Principle. In this alternative argument for the compactness of first-order logic, we construct a set
into a Skolem set (a set containing a witness for every existential statement) does not in fact require the Well-Ordering Principle. In this alternative argument for the compactness of first-order logic, we construct a set ![]() of constants disjoint from the set of constants of
of constants disjoint from the set of constants of ![]() , one for each ordered pair in
, one for each ordered pair in ![]() . (If we were to formalise this argument in our set-theoretic metatheory, say
. (If we were to formalise this argument in our set-theoretic metatheory, say ![]() , we may for instance code each constant
, we may for instance code each constant ![]() as
as ![]() . The point is that no Choice principles are required for this recursive definition.) Then add Skolem sentences
. The point is that no Choice principles are required for this recursive definition.) Then add Skolem sentences ![]() for every such ordered pair
for every such ordered pair ![]() . This gives us a new set of sentences
. This gives us a new set of sentences ![]() in a language
in a language ![]() . Iterate this process
. Iterate this process ![]() -times, constructing a chain of sets of sentences
-times, constructing a chain of sets of sentences ![]() , and a corresponding chain of languages
, and a corresponding chain of languages ![]() . By an inductive argument, each
. By an inductive argument, each ![]() is readily seen to be finitely-satisfiable (there is no need to assume the well-ordering of
is readily seen to be finitely-satisfiable (there is no need to assume the well-ordering of ![]() at this point), hence so is
at this point), hence so is ![]() . Finally, define
. Finally, define ![]() as the filter generated by
as the filter generated by ![]() . The rest of the argument, which defines a term model from the ultrafilter extending the filter
. The rest of the argument, which defines a term model from the ultrafilter extending the filter ![]() proceeds as above. The version of the argument sketched in this paragraph invoked the Ultrafilter Lemma and at no point did it use the Axiom of Choice.
proceeds as above. The version of the argument sketched in this paragraph invoked the Ultrafilter Lemma and at no point did it use the Axiom of Choice.
The set ![]() is an example of a Hintikka set, which is a set of first-order sentences
is an example of a Hintikka set, which is a set of first-order sentences ![]() that satisfies the following axioms. (For brevity, we use take
that satisfies the following axioms. (For brevity, we use take ![]() as primitive symbols in our first-order logic.)
as primitive symbols in our first-order logic.)
- For every atomic sentence
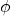 , if
, if 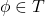 then
then 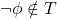 ,
, - For every closed term
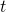 ,
, 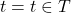 ,
, - If
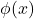 is an atomic formula with a single free variable
is an atomic formula with a single free variable 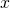 , and
, and 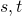 are closed terms such that
are closed terms such that 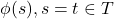 , then
, then 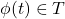 ,
, - If
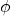 is a sentence and
is a sentence and  , then
, then 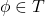 ,
, - If
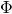 is a finite set of sentences, then
is a finite set of sentences, then
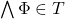 implies
implies 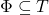 ,
,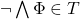 implies
implies 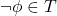 for some
for some 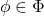 ,
,
- If
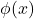 is a formula with a single free variable
is a formula with a single free variable 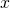 , then
, then  implies
implies 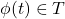 for every closed term
for every closed term 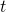 ,
,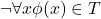 implies
implies 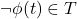 for some closed term
for some closed term 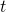 .
.
Given a Hintikka set ![]() , we can construct a term model (using the same definition given above) that satisfies
, we can construct a term model (using the same definition given above) that satisfies ![]() (Hodges 1997, 40–42).
(Hodges 1997, 40–42).
c. Semantic: Ultraproduct Proofs
In this subsection, we prove the compactness theorem for first-order logic from Łoś’ Theorem.
We recall the definition of an ultraproduct and state the theorem. For a proof, see Chang and Keisler (1990, p. 217, thm. 4.1.9) or Hodges (1997, p. 241–242, thm. 8.5.3).
Let ![]() be a collection of first-order structures of the same signature, indexed by
be a collection of first-order structures of the same signature, indexed by ![]() , and
, and ![]() an ultrafilter over this indexing set
an ultrafilter over this indexing set ![]() . In this context, the Boolean algebra is
. In this context, the Boolean algebra is ![]() with the subset ordering
with the subset ordering ![]() , so a filter
, so a filter ![]() is a set of subsets of
is a set of subsets of ![]() which does not contain the empty set and which is closed under finite intersection and upward containment. Denote the domain of each
which does not contain the empty set and which is closed under finite intersection and upward containment. Denote the domain of each ![]() by
by ![]() . When
. When ![]() is an ultrafilter over
is an ultrafilter over ![]() , defining
, defining ![]() by
by ![]() yields an equivalence relation over the product
yields an equivalence relation over the product
![Rendered by QuickLaTeX.com \[\prod_{i \in I} A_i = \Bigg\{f : I \to \bigcup_{i \in I} A_i \mid \forall i \in I, f(i) \in A_i\Bigg\}.\]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-a4669624950202fcead414be84efb356_l3.png)
(We tend to view elements of the product as generalised sequences ![]() .) The characteristic function
.) The characteristic function ![]() of
of ![]() is a finitely-additive full measure on
is a finitely-additive full measure on ![]() and thus intuitively the elements of
and thus intuitively the elements of ![]() are `large subsets of
are `large subsets of ![]() ‘: two functions in
‘: two functions in ![]() are identified by this relation precisely when they agree `
are identified by this relation precisely when they agree `![]() -almost-everywhere’. We define a new structure
-almost-everywhere’. We define a new structure ![]() as follows:
as follows:
- Domain of
 quotiented by
quotiented by 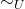 ;
; ![Rendered by QuickLaTeX.com [a]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-46276474876165ad906e954f72d71b61_l3.png) denotes the equivalence class of
denotes the equivalence class of  ;
; ![Rendered by QuickLaTeX.com c^\mathfrak{B} = [(\cdots, c^{\mathfrak{A}_i}, \cdots)]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-9d27e0669c09c36ccd42bb8e62785469_l3.png) ;
;![Rendered by QuickLaTeX.com f^{\mathfrak{B}}([a_1], \cdots, [a_k]) = [(\cdots, f^{\mathfrak{A}_i}(a_1(i), \cdots, , a_k(i)), \cdots)]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-8cd81009e408ce431ef619e13ae36c2f_l3.png) ;
;![Rendered by QuickLaTeX.com R^{\mathfrak{B}}([a_1], \cdots, [a_k])](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-315c983ae9f3c92a3bfeaf46b42f27bc_l3.png) if and only if
if and only if 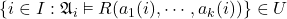 .
.
for any ![]() -place function and relation symbols
-place function and relation symbols ![]() and
and ![]() and any constant
and any constant ![]() of the first-order language in question. As may be checked, the fact that
of the first-order language in question. As may be checked, the fact that ![]() is a filter means that the definitions just given do not depend on the choice of representatives from
is a filter means that the definitions just given do not depend on the choice of representatives from ![]() . For
. For ![]() atomic we have by definition:
atomic we have by definition:
![]()
Łoś’ theorem, which is proved by induction on the complexity of ![]() , extends this to all
, extends this to all ![]() :
:
for all ![]() ,
, ![]() if and only if
if and only if ![]() .
.
The induction step for the universal / existential quantifier step does require some Choice. In fact, the Ultrafilter Lemma together with Łoś’ theorem imply the full Axiom of Choice (Howard 1975).
To prove the compactness theorem for first-order logic from Łoś’ Theorem, let ![]() be a finitely-satisfiable set of first-order sentences. Let
be a finitely-satisfiable set of first-order sentences. Let ![]() be the set of finite subsets of
be the set of finite subsets of ![]() and suppose we are given for each
and suppose we are given for each ![]() a model
a model ![]() for the sentences in
for the sentences in ![]() . For
. For ![]() let
let
![]()
The collection of ![]() is closed under finite intersection because
is closed under finite intersection because ![]() , hence
, hence ![]() is also closed under finite intersection; by definition,
is also closed under finite intersection; by definition, ![]() is closed under upward containment, and clearly
is closed under upward containment, and clearly ![]() does not contain the empty set. Thus
does not contain the empty set. Thus ![]() satisfies the conditions for being a filter and may therefore be extended to an ultrafilter
satisfies the conditions for being a filter and may therefore be extended to an ultrafilter ![]() . Now for any
. Now for any ![]() , we have
, we have ![]() and
and ![]() , from which it follows that
, from which it follows that ![]() . By Łoś’ theorem,
. By Łoś’ theorem, ![]() . This is true for every
. This is true for every ![]() , so
, so ![]() , in other words if
, in other words if ![]() is satisfiable. Intuitively, the model
is satisfiable. Intuitively, the model ![]() was designed so as to agree with
was designed so as to agree with ![]() on the `large subset’
on the `large subset’ ![]() of
of ![]() and in particular to agree with
and in particular to agree with ![]() on the truth-value of each element of
on the truth-value of each element of ![]() ; as this is true for all
; as this is true for all ![]() ,
, ![]() satisfies
satisfies ![]() . This completes the ultraproduct proof of the compactness of first-order logic.
. This completes the ultraproduct proof of the compactness of first-order logic.
For particular applications, we may not need the full strength of the Axiom of Choice to apply then ultraproduct method. For example, suppose we wish to use the ultraproduct method to construct a non-standard model of arithmetic (see Section 2c) with language ![]() and standard model
and standard model ![]() with domain
with domain ![]() . We extend the language to
. We extend the language to ![]() by introducing a new constant symbol
by introducing a new constant symbol ![]() and for each
and for each ![]() , let
, let ![]() be the
be the ![]() -expansion of
-expansion of ![]() given by interpreting
given by interpreting ![]() . Let
. Let ![]() be the filter of cofinite subsets of
be the filter of cofinite subsets of ![]() and let
and let ![]() be an ultrafilter that extends
be an ultrafilter that extends ![]() . Then the particular instance of Łoś’ Theorem can be proven for
. Then the particular instance of Łoś’ Theorem can be proven for ![]() and
and ![]() , utilising the well-foundedness of
, utilising the well-foundedness of ![]() in place of the Axiom of Choice. Thus
in place of the Axiom of Choice. Thus ![]() satisfies the same
satisfies the same ![]() -sentences as
-sentences as ![]() , and for all
, and for all ![]() ,
,
![]()
so by Łoś’ Theorem it follows that ![]() . Therefore
. Therefore ![]() is a non-standard model of arithmetic.
is a non-standard model of arithmetic.
5. Connection to Topology
Tarski (1952) article gives the compactness theorem its name (see theorems 13 and 17), observing its similarity with the finite-intersection-property definition of compactness in topologies.
Here we will demonstrate the topological connection in two stages. First, we show that the compactness theorem for a propositional logic is equivalent to the claim that its associated valuation space is compact. (Recall that an open cover of a topological space ![]() is a collection
is a collection ![]() of open subsets of
of open subsets of ![]() whose union is
whose union is ![]() , and that a space
, and that a space ![]() is compact if every open cover has a finite subcover—a finite subset that is also a cover. Equivalently, every collection of closed subsets with the finite-intersection property—every finite subset has non-empty intersection—has non-empty intersection. Intuitively, you cannot `escape’ a compact space; every collection of points will accumulate somewhere.) Second, we show that this space is indeed compact. We assume some basic knowledge of topology (Sutherland 2009; Willard 1970).
is compact if every open cover has a finite subcover—a finite subset that is also a cover. Equivalently, every collection of closed subsets with the finite-intersection property—every finite subset has non-empty intersection—has non-empty intersection. Intuitively, you cannot `escape’ a compact space; every collection of points will accumulate somewhere.) Second, we show that this space is indeed compact. We assume some basic knowledge of topology (Sutherland 2009; Willard 1970).
In this section, we spell out this reasoning for the case of propositional logic. We start with an argument that demonstrates the compactness of any ![]() , initially assuming for the sake of simplicity that the version of
, initially assuming for the sake of simplicity that the version of ![]() in question is equipped with a truth-functional set of connectives.
in question is equipped with a truth-functional set of connectives.
Let ![]() be the set of all valuations of
be the set of all valuations of ![]() . For each sentence
. For each sentence ![]() of
of ![]() define
define ![]() , the set of valuations in which
, the set of valuations in which ![]() is true. Since
is true. Since ![]() , the sets
, the sets ![]() form a basis for a topology on
form a basis for a topology on ![]() ; call this basis
; call this basis ![]() . (A basis
. (A basis ![]() for a topology
for a topology ![]() is a collection of open sets with the property that
is a collection of open sets with the property that ![]() if and only if
if and only if ![]() for some
for some ![]() . Given a collection
. Given a collection ![]() of subsets of
of subsets of ![]() , if its union is
, if its union is ![]() and for all
and for all ![]() ,
, ![]() for some
for some ![]() , then there exists a unique topology on
, then there exists a unique topology on ![]() with basis
with basis ![]() (Willard 1970, p. 38, thm. 5.3).) The topological space we shall be interested in has domain
(Willard 1970, p. 38, thm. 5.3).) The topological space we shall be interested in has domain ![]() and topology generated by the basis
and topology generated by the basis ![]() ; with this topology,
; with this topology, ![]() is the dual space of the Boolean algebra of sentences of
is the dual space of the Boolean algebra of sentences of ![]() . Thus properties of this space are determined only by the logical properties of valuations.
. Thus properties of this space are determined only by the logical properties of valuations.
Now consider any set of sentences ![]() of
of ![]() .
. ![]() is unsatisfiable if and only if any valuation assigns truth-value 0 to at least one of its members, or equivalently any valuation assigns truth-value 1 to at least one sentence
is unsatisfiable if and only if any valuation assigns truth-value 0 to at least one of its members, or equivalently any valuation assigns truth-value 1 to at least one sentence ![]() such that
such that ![]() . It follows that
. It follows that ![]() is unsatisfiable if and only if each valuation is in some open set of the form
is unsatisfiable if and only if each valuation is in some open set of the form ![]() where
where ![]() , or equivalently that
, or equivalently that ![]() is an open cover of the topological space
is an open cover of the topological space ![]() . The compactness of
. The compactness of ![]() is therefore equivalent to the following claim:
is therefore equivalent to the following claim:
if ![]() is an open cover of
is an open cover of ![]() then there is a finite subset
then there is a finite subset
![]() of
of ![]() such that
such that ![]() is an open cover of
is an open cover of ![]() .
.
Thus ![]() is compact if and only if
is compact if and only if ![]() is compact. (Note that any open set is the union of some basis sets and that any basis set
is compact. (Note that any open set is the union of some basis sets and that any basis set ![]() is identical to
is identical to ![]() for
for ![]() . Also, a space is compact if every open cover drawn from a fixed basis has a finite subcover.) It suffices, then, to show that
. Also, a space is compact if every open cover drawn from a fixed basis has a finite subcover.) It suffices, then, to show that ![]() is compact in the usual topological sense.
is compact in the usual topological sense.
The last claim is immediate from the fact that ![]() is homeomorphic to
is homeomorphic to ![]() with the (Tychonoff) product topology, when
with the (Tychonoff) product topology, when ![]() is given the discrete topology
is given the discrete topology ![]() . Recall that the product topology on the product
. Recall that the product topology on the product ![]() of a family of topological spaces (
of a family of topological spaces (![]() ) indexed by
) indexed by ![]() takes as its basic open sets
takes as its basic open sets ![]() , where
, where ![]() , and
, and ![]() for all but finitely elements
for all but finitely elements ![]() in
in ![]() . (For a finite collection (
. (For a finite collection (![]() ),
), ![]() , (
, (![]() , the product topology on
, the product topology on ![]() has basis {
has basis {![]() }. In general, the product topology is determined by the following universal property: for any space
}. In general, the product topology is determined by the following universal property: for any space ![]() and function
and function ![]() ,
, ![]() is continuous if and only if
is continuous if and only if ![]() is continuous for all
is continuous for all ![]() , where
, where ![]() is the projection map onto the
is the projection map onto the ![]() -th coordinate. If we remove the restriction that all-but-finitely-many
-th coordinate. If we remove the restriction that all-but-finitely-many ![]() ‘s are equal to
‘s are equal to ![]() , we obtain the box product topology. This coincides with the product topology for finite indexes, but varies drastically for infinite products.) Since
, we obtain the box product topology. This coincides with the product topology for finite indexes, but varies drastically for infinite products.) Since ![]() with the product topology is homeomorphic to the
with the product topology is homeomorphic to the ![]() (if the sentence letters in
(if the sentence letters in ![]() are
are ![]() for
for ![]() , then
, then ![]() defines a homeomorphism
defines a homeomorphism ![]() ) the latter is compact if and only if the former is. Now
) the latter is compact if and only if the former is. Now ![]() with the discrete topology is compact because finite spaces are trivially compact. Tychonoff’s Theorem, a ZF-equivalent of the Axiom of Choice, states that the product of compact spaces is compact. Putting the pieces together, it follows that
with the discrete topology is compact because finite spaces are trivially compact. Tychonoff’s Theorem, a ZF-equivalent of the Axiom of Choice, states that the product of compact spaces is compact. Putting the pieces together, it follows that ![]() with the product topology is compact. This proves the compactness of
with the product topology is compact. This proves the compactness of ![]() .
.
We do not in fact need the full power of Tychonoff’s Theorem. The weaker principle that the product of compact Hausdorff spaces is compact will do, because ![]() with the discrete topology is Hausdorff (any two of its elements—0 and 1—are contained in disjoint open sets
with the discrete topology is Hausdorff (any two of its elements—0 and 1—are contained in disjoint open sets ![]() and
and ![]() ). This weaker version of Tychonoff’s Theorem is in fact equivalent to the compactness theorem for propositional logic (and first-order logic), as discussed in Section 7.
). This weaker version of Tychonoff’s Theorem is in fact equivalent to the compactness theorem for propositional logic (and first-order logic), as discussed in Section 7.
The topological proof of ![]() ‘s compactness just given assumed that
‘s compactness just given assumed that ![]() ‘s set of connectives is truth-functionally complete. Without this assumption, there is no guarantee that the set
‘s set of connectives is truth-functionally complete. Without this assumption, there is no guarantee that the set ![]() is a basis for the product topology; for example, if a propositional logic cannot define negation, no element of
is a basis for the product topology; for example, if a propositional logic cannot define negation, no element of ![]() may correspond to the open set consisting of all elements of
may correspond to the open set consisting of all elements of ![]() with first coordinate 0, and if it cannot define conjunction then
with first coordinate 0, and if it cannot define conjunction then ![]() will not be closed under intersection and thus cannot be a basis. The compactness of a propositional logic with
will not be closed under intersection and thus cannot be a basis. The compactness of a propositional logic with ![]() sentence letters but without a truth-functional set of connectives is of course immediate from the fact that it is a sublogic of a truth-functionally complete propositional logic with the same
sentence letters but without a truth-functional set of connectives is of course immediate from the fact that it is a sublogic of a truth-functionally complete propositional logic with the same ![]() sentence letters. The topological way of seeing this is to endow the space
sentence letters. The topological way of seeing this is to endow the space ![]() with the topology which has
with the topology which has ![]() as a subbase and denote it by
as a subbase and denote it by ![]() .
.
(A subbase for a topological space (![]() ) is a collection of open sets
) is a collection of open sets ![]() such that
such that ![]() is a basis for (
is a basis for (![]() ).Given an arbitrary collection
).Given an arbitrary collection ![]() of subsets of a set
of subsets of a set ![]() , there is a unique topology
, there is a unique topology ![]() on
on ![]() which has
which has ![]() as a subbase. (Willard 1970, p. 39, thm. 5.6).) This topology is coarser than the dual space topology on
as a subbase. (Willard 1970, p. 39, thm. 5.6).) This topology is coarser than the dual space topology on ![]() : every open set in
: every open set in ![]() is open in the dual space topology. In general, if the topology
is open in the dual space topology. In general, if the topology ![]() on some set
on some set ![]() is coarser than the topology
is coarser than the topology ![]() on
on ![]() and (
and (![]() ) is compact, then so is
) is compact, then so is ![]() ). Intuitively, there are fewer means of `escaping’ (via the finite-intersection property) in
). Intuitively, there are fewer means of `escaping’ (via the finite-intersection property) in ![]() than in
than in ![]() , so if
, so if ![]() is compact then there are no such routes in
is compact then there are no such routes in ![]() . It follows that the topological space
. It follows that the topological space ![]() is compact, and thus any propositional logic is compact, whether or not its set of connectives is truth-functionally complete.
is compact, and thus any propositional logic is compact, whether or not its set of connectives is truth-functionally complete.
A `bare hands’ argument that avoids anything as strong as either the general Tychonoff Theorem or its compact Hausdorff version above may also be given for the compactness of ![]() . We present this argument, since
. We present this argument, since ![]() is the most common propositional logic.
is the most common propositional logic.
Suppose that some open cover ![]() of the space
of the space ![]() with the product topology lacks a finite subcover. We reduce this supposition to absurdity by constructing an element
with the product topology lacks a finite subcover. We reduce this supposition to absurdity by constructing an element ![]() of
of ![]() with the following property: the set of all elements of
with the following property: the set of all elements of ![]() extending an arbitrary finite initial segment of
extending an arbitrary finite initial segment of ![]() cannot be covered by any finite subset of
cannot be covered by any finite subset of ![]() . If
. If ![]() is a finite sequence of 0’s and 1’s, define
is a finite sequence of 0’s and 1’s, define ![]() as the set of elements of
as the set of elements of ![]() extending
extending ![]() . Let
. Let ![]() if
if ![]() does not admit a finite subcover from
does not admit a finite subcover from ![]() , and
, and ![]() otherwise. More generally, if
otherwise. More generally, if ![]() has been defined, let
has been defined, let ![]()
![]()
![]() if
if ![]() does not admit a finite subcover from
does not admit a finite subcover from ![]() , and
, and ![]()
![]()
![]() otherwise. Since by the assumption to be reduced to absurdity
otherwise. Since by the assumption to be reduced to absurdity ![]() does not admit a finite subcover from
does not admit a finite subcover from ![]() , an easy inductive argument shows that
, an easy inductive argument shows that ![]() does not admit a finite subcover from
does not admit a finite subcover from ![]() either, for any
either, for any ![]() . Letting
. Letting ![]() be the element of
be the element of ![]() whose restriction to
whose restriction to ![]() is
is ![]() (more formally,
(more formally, ![]() ), it follows from the fact that
), it follows from the fact that ![]() is an open cover of
is an open cover of ![]() that
that ![]() is an element of some basis set
is an element of some basis set ![]() , where
, where ![]() is an open set in
is an open set in ![]() . From
. From ![]() and the definition of the product topology, it further follows that for some
and the definition of the product topology, it further follows that for some ![]() ,
, ![]() , so that
, so that ![]() does in fact admit a finite subcover from
does in fact admit a finite subcover from ![]() , namely the open set
, namely the open set ![]() which contains
which contains ![]() as a subset. This contradicts our supposition and shows that
as a subset. This contradicts our supposition and shows that ![]() with the product topology is compact.
with the product topology is compact.
The argument just given, which constructs an infinite branch through a binary branching tree, did not require any version of Choice. The reason is that at each stage in the construction of ![]() we used the ordering on
we used the ordering on ![]() to extend
to extend ![]() by 0 if possible and 1 if not. An alternative argument for the compactness of
by 0 if possible and 1 if not. An alternative argument for the compactness of ![]() uses the fact that a countable product
uses the fact that a countable product ![]() of bounded (by 1) metric spaces (
of bounded (by 1) metric spaces (![]() ), is metrisable via the metric
), is metrisable via the metric
![]()
To say that ![]() is metrisable in this way is to say that the metric
is metrisable in this way is to say that the metric ![]() induces the product topology on
induces the product topology on ![]() . The rest of the argument turns on showing that the metric space
. The rest of the argument turns on showing that the metric space ![]() is compact, by exploiting the space’s metric properties. This argument cannot be generalised to show that
is compact, by exploiting the space’s metric properties. This argument cannot be generalised to show that ![]() ‘s valuation space is compact for any
‘s valuation space is compact for any ![]() : the uncountable product of metric spaces, each having at least two points, is not metrisable, as no point has a countable neighbourhood base.
: the uncountable product of metric spaces, each having at least two points, is not metrisable, as no point has a countable neighbourhood base.
Moving to arbitrary logics ![]() , we construct the space
, we construct the space ![]() of theories
of theories ![]() of
of ![]() -structures
-structures ![]() , topologised by the subbasic open sets
, topologised by the subbasic open sets ![]() for each formula
for each formula ![]() in
in ![]() . The compactness of
. The compactness of ![]() is then easily seen to be equivalent to the compactness of
is then easily seen to be equivalent to the compactness of ![]() with this topology (see Figure 1). In the case of propositional logic,
with this topology (see Figure 1). In the case of propositional logic, ![]() . (Note that unlike for bases, the implication that compactness of a space follows from every open cover drawn from a fixed subbase} has a finite subcover requires the Axiom of Choice. This is the Alexander subbase theorem (Willard 1970, p. 129, problem 17S).) However, the argument for first-order logic is more complicated than that for propositional logic and not as elementary as exhibiting a simple homeomorphism.
. (Note that unlike for bases, the implication that compactness of a space follows from every open cover drawn from a fixed subbase} has a finite subcover requires the Axiom of Choice. This is the Alexander subbase theorem (Willard 1970, p. 129, problem 17S).) However, the argument for first-order logic is more complicated than that for propositional logic and not as elementary as exhibiting a simple homeomorphism.
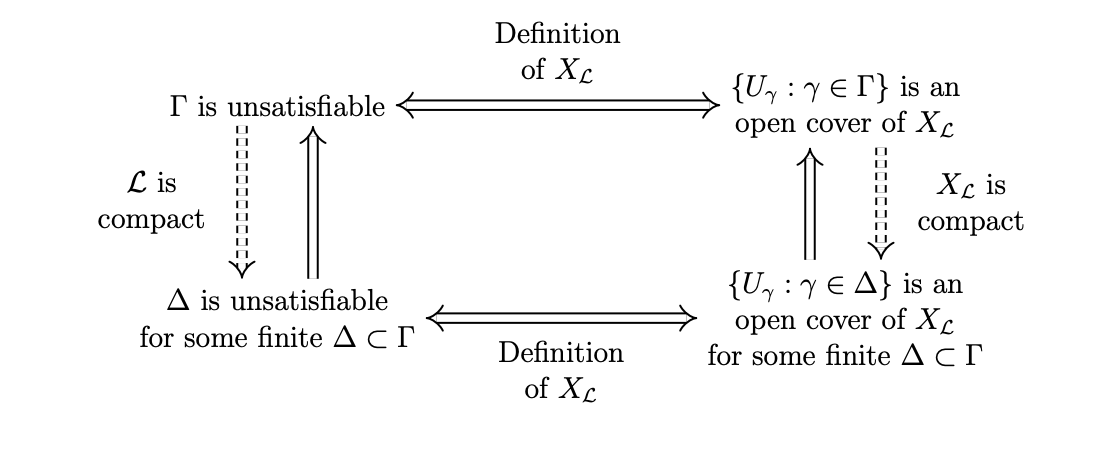
Figure 1: The connection between compactness of logics and its space of theories.
6. Extensions and Generalisations
The discussion of the compactness theorem in the most common logics, our concern here, could now ramify in several directions. There are two main dimensions of variation when considering a proof of compactness for a logic: we could vary the notion of compactness, or we could vary the logic. As an example of the latter, we might consider, for example, modal logics (![]() ); infinitary logics
); infinitary logics ![]() (
(![]() being the extension of first-order logic which allows for conjunctions and disjunctions of length less than
being the extension of first-order logic which allows for conjunctions and disjunctions of length less than ![]() and existential and universal quantifications of length less than
and existential and universal quantifications of length less than ![]() . Usually
. Usually ![]() : we use
: we use ![]() to represent no bound on the connectives / quantifiers respectively.); other extensions of first-order logic, such as logics with cardinality quantifiers.
to represent no bound on the connectives / quantifiers respectively.); other extensions of first-order logic, such as logics with cardinality quantifiers.
A rough rule of thumb is that infinitary logics are not compact. In particular, as demonstrated in Section 2 with the example of ![]() ,
, ![]() is not compact whenever
is not compact whenever ![]() . In contrast, logics extending first-order logic with generalised quantifiers tend to be compact, but not if they contain cardinality quantifiers. Roughly speaking, the quantifiers
. In contrast, logics extending first-order logic with generalised quantifiers tend to be compact, but not if they contain cardinality quantifiers. Roughly speaking, the quantifiers ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are interpretable as ‘there are exactly
are interpretable as ‘there are exactly ![]() ‘, ‘there are more than
‘, ‘there are more than ![]() ‘, ‘there are fewer than
‘, ‘there are fewer than ![]() ‘, ‘there are at least
‘, ‘there are at least ![]() ‘, and ‘there are no more than
‘, and ‘there are no more than ![]() ‘. Consider the set
‘. Consider the set
![]()
in an infinitary logic containing ![]() ; this set is finitely-satisfiable but unsatisfiable. (The arguments involving the other cardinality quantifiers are similar.) However, such logics tend to satisfy weaker notions of compactness. In particular, the logic that extends first-order logic with the quantifier
; this set is finitely-satisfiable but unsatisfiable. (The arguments involving the other cardinality quantifiers are similar.) However, such logics tend to satisfy weaker notions of compactness. In particular, the logic that extends first-order logic with the quantifier ![]() , interpreted as ‘there are uncountably many’, is countably-compact: that is, a countable set of sentences is satisfiable if and only if it is finitely-satisfiable (Keisler 1970).
, interpreted as ‘there are uncountably many’, is countably-compact: that is, a countable set of sentences is satisfiable if and only if it is finitely-satisfiable (Keisler 1970).
As an aside, it is worth observing that not all logics with higher-order (second-order or above) quantifiers are incompact. Second-order logic with non-standard (Henkin) semantics is compact (Enderton 2001, chap. 4), as is existential second-order logic, whose sentences are of the form ![]() , where
, where ![]() are second-order functions / relations, and
are second-order functions / relations, and ![]() is a first-order sentence in a language with symbols for
is a first-order sentence in a language with symbols for ![]() . (Via embeddings, this logic is equivalent to many first-order logics extended with extra quantifiers and game-theoretic semantics, such as Henkin’s quantifier, Hintikka-Sandu’s independence-friendly logic, and Väänänen’s dependence logic. However, these logics do not have a classical negation and the alternative form of compactness given in the introduction of this article is false: see section 2a of this article. For further details on these logics, consult Väänänen (2007) and Mann, Sandu, and Sevenster (2011)). As another example, consider what has been called pure second-order logic with identity, that is, second-order logic with neither functional nor first-order variables but with both second-order and first-order identity (as well as predicate variables and quantifiers). Pure second-order logic may be thought of as the complement of first-order logic relative to second-order logic in the following sense: first-order logic has object but not predicate quantifiers, pure second-order logic has predicate but not object quantifiers, and second-order logic combines the two. In other words, second-order logic merges first-order and pure second-order logic. As Paseau (2010b) shows, pure second-order logic with identity is compact; Denyer (1992) gives an argument that applies to pure second-order logic without identity. The moral is that the incompactness of second-order logic is not owed solely to the presence of second-order quantifiers, but to the combination of both first- and second-order quantifiers. Lindström’s Theorem tells us that any regular logical system weakly extending first-order logic satisfying both the downward Löwenheim-Skolem property (if a sentence is satisfiable, it is satisfiable in an at most countable model) and the compactness theorem is in fact identical to first-order logic itself (Lindström 1969, p. 8, thm. 2).
. (Via embeddings, this logic is equivalent to many first-order logics extended with extra quantifiers and game-theoretic semantics, such as Henkin’s quantifier, Hintikka-Sandu’s independence-friendly logic, and Väänänen’s dependence logic. However, these logics do not have a classical negation and the alternative form of compactness given in the introduction of this article is false: see section 2a of this article. For further details on these logics, consult Väänänen (2007) and Mann, Sandu, and Sevenster (2011)). As another example, consider what has been called pure second-order logic with identity, that is, second-order logic with neither functional nor first-order variables but with both second-order and first-order identity (as well as predicate variables and quantifiers). Pure second-order logic may be thought of as the complement of first-order logic relative to second-order logic in the following sense: first-order logic has object but not predicate quantifiers, pure second-order logic has predicate but not object quantifiers, and second-order logic combines the two. In other words, second-order logic merges first-order and pure second-order logic. As Paseau (2010b) shows, pure second-order logic with identity is compact; Denyer (1992) gives an argument that applies to pure second-order logic without identity. The moral is that the incompactness of second-order logic is not owed solely to the presence of second-order quantifiers, but to the combination of both first- and second-order quantifiers. Lindström’s Theorem tells us that any regular logical system weakly extending first-order logic satisfying both the downward Löwenheim-Skolem property (if a sentence is satisfiable, it is satisfiable in an at most countable model) and the compactness theorem is in fact identical to first-order logic itself (Lindström 1969, p. 8, thm. 2).
The other natural dimension of generalisation is the notion of compactness. A fairly obvious generalisation is:
![Rendered by QuickLaTeX.com \[\begin{quote} a logic is (\(\kappa\), \(\lambda\))-compact, where \(\kappa\) is an infinite cardinal or \(\infty\) and \(\lambda\) is an infinite cardinal \(\leq \kappa\), just when: whenever \(\Gamma\) is an unsatisfiable set of sentences of cardinality \(\leq \kappa\) there is an unsatisfiable \(\Gamma^{\lambda} \subset \Gamma\) of cardinality \(< \lambda\). (By convention \(\kappa < \infty\) for every cardinal \(\kappa\).) \end{quote}\]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-147766d011c90161e1181cf0c947d289_l3.png)
The ordinary notion of compactness is (![]() -compactness: whenever
-compactness: whenever ![]() is any unsatisfiable set of sentences (of any cardinality) there is an unsatisfiable
is any unsatisfiable set of sentences (of any cardinality) there is an unsatisfiable ![]() of cardinality
of cardinality ![]() , in other words of finite cardinality. A special case arises when
, in other words of finite cardinality. A special case arises when ![]() and the logic is
and the logic is ![]() . If this logic satisfies (
. If this logic satisfies (![]() -compactness, that is, if whenever
-compactness, that is, if whenever ![]() is an unsatisfiable set of sentences of cardinality
is an unsatisfiable set of sentences of cardinality ![]() then
then ![]() has an unsatisfiable subset of cardinality
has an unsatisfiable subset of cardinality ![]() , we say that it satisfies the Weak Compactness Theorem. One can show that for infinite cardinals, having the tree property is equivalent to satisfying the Weak Compactness Theorem, and either imply the weak inaccessibility of the cardinal. Cardinals satisfying the Weak Compactness Theorem are exactly those satisfying the combinatorial partition property
, we say that it satisfies the Weak Compactness Theorem. One can show that for infinite cardinals, having the tree property is equivalent to satisfying the Weak Compactness Theorem, and either imply the weak inaccessibility of the cardinal. Cardinals satisfying the Weak Compactness Theorem are exactly those satisfying the combinatorial partition property ![]() , and indeed the latter is the usual definition of a weakly-compact cardinal. For the definitions of the tree property and the partition property, and more on weakly-compact cardinals, consult chapters 9 and 17 of Jech (2003).
, and indeed the latter is the usual definition of a weakly-compact cardinal. For the definitions of the tree property and the partition property, and more on weakly-compact cardinals, consult chapters 9 and 17 of Jech (2003).
Another generalisation of the notion of compactness is strong compactness. An uncountable cardinal ![]() is strongly-compact if for any set
is strongly-compact if for any set ![]() , any
, any ![]() -complete filter on
-complete filter on ![]() can be extended to a
can be extended to a ![]() -complete ultrafilter on
-complete ultrafilter on ![]() . (A filter
. (A filter ![]() on a set is
on a set is ![]() -complete if
-complete if ![]() for every
for every ![]() with
with ![]() .) One may then show that
.) One may then show that ![]() is strongly-compact if and only if the logic
is strongly-compact if and only if the logic ![]() (or
(or ![]() ) has the property of (
) has the property of (![]() -compactness, that is, if
-compactness, that is, if ![]() is an unsatisfiable set of sentences then it has an unsatisfiable subset of cardinality
is an unsatisfiable set of sentences then it has an unsatisfiable subset of cardinality ![]() . (p. 366, lemma 20.2).
. (p. 366, lemma 20.2).
Both weakly- and strongly-compact cardinals are large cardinal properties. (A sentence ![]() is a large cardinal property if it satisfies the following:
is a large cardinal property if it satisfies the following: ![]() is equiconsistent with
is equiconsistent with ![]() ,
, ![]() , and the consistency strength of
, and the consistency strength of ![]() is strictly larger than
is strictly larger than ![]() , by which we mean the consistency of the former implies that of the latter, but there is no finitistic argument for the reverse implication, for example, if
, by which we mean the consistency of the former implies that of the latter, but there is no finitistic argument for the reverse implication, for example, if ![]() implies the arithmetised consistency of
implies the arithmetised consistency of ![]() , by Gödel’s second incompleteness theorem.) Another large cardinal property is the extendible cardinal property, which is defined in terms of elementary embeddings of levels in the von Neumann cumulative hierarchy. However, it was later discovered that extendibility of a cardinal
, by Gödel’s second incompleteness theorem.) Another large cardinal property is the extendible cardinal property, which is defined in terms of elementary embeddings of levels in the von Neumann cumulative hierarchy. However, it was later discovered that extendibility of a cardinal ![]() is equivalent to (
is equivalent to (![]() -compactness of
-compactness of ![]() , or the (
, or the (![]() -compactness of
-compactness of ![]() for each positive integer
for each positive integer ![]() (Kanamori 2009, p. 315, thm. 23.4).
(Kanamori 2009, p. 315, thm. 23.4). ![]() is the
is the ![]() th-order extension of
th-order extension of ![]() .
.
Generalising the argument in Section 5 above, it is easily shown that a logic ![]() is (
is (![]() -compact precisely when every subbasic open cover
-compact precisely when every subbasic open cover ![]() of
of ![]() , where
, where ![]() is a set of
is a set of ![]() -sentences of cardinality at most
-sentences of cardinality at most ![]() , has a subcover of cardinality less than
, has a subcover of cardinality less than ![]() . This is weaker than stating that
. This is weaker than stating that ![]() is (
is (![]() -compact, meaning every cover of cardinality at most
-compact, meaning every cover of cardinality at most ![]() has a subcover of cardinality less than
has a subcover of cardinality less than ![]() . For example, if
. For example, if ![]() is the extension of first-order logic with the quantifier
is the extension of first-order logic with the quantifier ![]() , then
, then ![]() is (
is (![]() -compact, but
-compact, but ![]() is not (
is not (![]() -compact. See Ebbinghaus (1985, sec. 5.1), Makowsky (1985, sec. 1.1), Mannila (1983), and Stephenson (1984) for more on (
-compact. See Ebbinghaus (1985, sec. 5.1), Makowsky (1985, sec. 1.1), Mannila (1983), and Stephenson (1984) for more on (![]() -compact logics and spaces.
-compact logics and spaces.
These remarks do no more than gesture at an extensive literature generalising the notion of compactness and connecting it to topics of set-theoretic interest. We would be remiss if we did not at least mention in passing the Barwise compactness theorem, which is as an important theorem in generalised recursion theory (Keisler and Knight 2004). The interested reader is invited to explore the references contained within this section.
7. Relative Strength
As we saw, the compactness theorem for both propositional and first-order logic may be proven in ![]() ; but as also indicated, all that is required for its proof, in the case of both propositional and first-order logic, is the Ultrafilter Lemma, which is in fact weaker than Choice relative to
; but as also indicated, all that is required for its proof, in the case of both propositional and first-order logic, is the Ultrafilter Lemma, which is in fact weaker than Choice relative to ![]() . Indeed, the Ultrafilter Lemma turns out to be equivalent to the compactness theorem in
. Indeed, the Ultrafilter Lemma turns out to be equivalent to the compactness theorem in ![]() . By the capitalised name `Compactness Theorem’ we hereafter understand the compactness theorem for both propositional and first-order logic, since these are of equivalent strength relative to
. By the capitalised name `Compactness Theorem’ we hereafter understand the compactness theorem for both propositional and first-order logic, since these are of equivalent strength relative to ![]() . The relative strength of these and related principles has been well-studied; in this section we report several of these results.
. The relative strength of these and related principles has been well-studied; in this section we report several of these results.
a. ZF-Equivalents
Tychonoff’s Theorem states that every product of compact spaces (with the product topology) is compact. In proving compactness earlier, we only required Tychonoff’s Theorem in the case when the product consisted of Hausdorff spaces. This weakened version is in fact equivalent to the Compactness Theorem. Some other equivalents are:
- The Boolean Prime Ideal Theorem: every Boolean algebra has a prime ideal.
- The Ultrafilter Lemma: every filter on a Boolean algebra can be extended to an ultrafilter.
- Stone’s Representation Theorem: every Boolean algebra is isomorphic to a field of sets.
- Alexander subbase theorem: if
 is a topological space with a subbase
is a topological space with a subbase  and every open cover
and every open cover 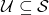 has a finite subcover, then
has a finite subcover, then 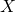 is compact (Rubin and Scott 1954).
is compact (Rubin and Scott 1954). - For every graph
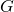 , if every finite subgraph of
, if every finite subgraph of 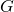 is 3-colourable then
is 3-colourable then 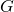 is also 3-colourable (Cowen 1990).
is also 3-colourable (Cowen 1990). - If
 is a set of propositional sentences consisting of a disjunction of at most three literals and every finite subset is satisfiable, then
is a set of propositional sentences consisting of a disjunction of at most three literals and every finite subset is satisfiable, then  is also satisfiable (Cowen 1990).
is also satisfiable (Cowen 1990).
The equivalences of the first three statements with the Compactness Theorem can be found in Jech (1973, chap. 2). For more information, consult Howard and Rubin (1998, form 14).
b. Principles Strictly ZF-Stronger Than the Compactness Theorem
It is known that the full Tychonoff Theorem is equivalent to the Axiom of Choice in ![]() (Kunen 2011, 72). To show that the Compactness Theorem does not imply Choice, we will briefly sketch the construction of a model where Choice fails but the Compactness Theorem holds. Suppose we are working in
(Kunen 2011, 72). To show that the Compactness Theorem does not imply Choice, we will briefly sketch the construction of a model where Choice fails but the Compactness Theorem holds. Suppose we are working in ![]() with a countably infinite set of atoms
with a countably infinite set of atoms ![]() (objects which do not contain any elements and are different from the empty set);
(objects which do not contain any elements and are different from the empty set); ![]() is a variant of
is a variant of ![]() with atoms (Jech 1973, sec. 4.1). We can develop all of our standard theory in this system, with some minor modifications (for example, the Axiom of Extensionality states that two sets are equal if they have the same elements). Let
with atoms (Jech 1973, sec. 4.1). We can develop all of our standard theory in this system, with some minor modifications (for example, the Axiom of Extensionality states that two sets are equal if they have the same elements). Let ![]() be a dense linear ordering on
be a dense linear ordering on ![]() without endpoints. Every permutation
without endpoints. Every permutation ![]() of
of ![]() has an extension
has an extension ![]() to the entire universe, define recursively by
to the entire universe, define recursively by ![]() for each set
for each set ![]() . Let
. Let ![]() be the group of order-preserving permutations of
be the group of order-preserving permutations of ![]() and for every set
and for every set ![]() define
define ![]() {
{ ![]() } and
} and ![]() }. We shall say that an object
}. We shall say that an object ![]() is symmetric if there is a finite set of atoms
is symmetric if there is a finite set of atoms ![]() such that
such that ![]() . Denote the class of hereditarily symmetric objects by
. Denote the class of hereditarily symmetric objects by ![]() .
.
If ![]() denotes the standard cumulative hierarchy in this theory, then it is easily seen that
denotes the standard cumulative hierarchy in this theory, then it is easily seen that ![]() . We may also show that
. We may also show that ![]() holds in
holds in ![]() . As the Axiom of Choice holds in
. As the Axiom of Choice holds in ![]() , a set
, a set ![]() is well-orderable, according to
is well-orderable, according to ![]() , precisely when there is a symmetric function mapping
, precisely when there is a symmetric function mapping ![]() to some set in
to some set in ![]() . This turns out to be the case precisely when there is a finite set of atoms
. This turns out to be the case precisely when there is a finite set of atoms ![]() such that
such that ![]() . Since for every finite set of atoms
. Since for every finite set of atoms ![]() , there is a non-identity order-preserving permutation of
, there is a non-identity order-preserving permutation of ![]() fixing
fixing ![]() , it follows that
, it follows that ![]() is not well-orderable according to
is not well-orderable according to ![]() . However, the Compactness Theorem still holds in
. However, the Compactness Theorem still holds in ![]() .
.
Although we worked in a theory with atoms, it is possible to translate this model to a model without atoms where Choice fails but the Compactness Theorem holds. The interested reader should consult (Jech 1973, pp. 44–54, chap. 4) for details of this proof. It now follows that, working in ![]() , Tychonoff’s Theorem is not implied from the Compactness Theorem.
, Tychonoff’s Theorem is not implied from the Compactness Theorem.
Here are some more examples of theorems equivalent to Choice (a principle we restate for the sake of completeness), and thus unprovable from the Compactness Theorem:
- Axiom of Choice: every family of non-empty sets has a choice function.
- Axiom of Multiple Choice: every collection of non-empty sets has a multiple choice function—a function that picks out a non-empty, finite subset from each set in the collection (Chapter 9).
- Well-Ordering Principle: every set can be well-ordered (Kunen 2011, 68).
- Zorn’s Lemma: every partial order in which every chain has an upper bound has a maximal element (68).
- Every vector space has a basis (Blass 1984).
- Every non-empty set can be endowed with a group operation (Hajnal and Kertész 1972).
See Howard and Rubin (1998, form 1) for more statements equivalent to the Axiom of Choice.
c. Principles Strictly ZF-Weaker Than the Compactness Theorem
The following is a small selection of Choice-like principles that are weaker than the Compactness Theorem. See Jech (1973) for the construction of models satisfying one of these statements but not the Compactness Theorem.
- Order-Extension Principle, and consequently the statement that every set can be linearly-ordered.
- Hahn-Banach theorem: If
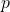 is a sublinear functional on a set
is a sublinear functional on a set 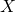 and
and 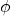 is a linear functional defined on a subspace
is a linear functional defined on a subspace 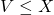 such that
such that  for all
for all 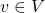 , then there exists a linear extension
, then there exists a linear extension 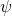 of
of 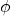 to all of
to all of 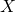 such that
such that  for all
for all 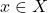 . In fact, the Hahn-Banach theorem is equivalent to the existence of a finitely-additive probability measure on every Boolean algebra (28). It is easily seen that a prime ideal gives rise to a finitely-additive,
. In fact, the Hahn-Banach theorem is equivalent to the existence of a finitely-additive probability measure on every Boolean algebra (28). It is easily seen that a prime ideal gives rise to a finitely-additive,  -valued probability measure on every Boolean algebra, and thus the Hahn-Banach theorem follows from the Boolean Prime Ideal Theorem.
-valued probability measure on every Boolean algebra, and thus the Hahn-Banach theorem follows from the Boolean Prime Ideal Theorem. - Every infinite set has a non-principal ultrafilter.
8. History of the Compactness Theorem
The first proof of a compactness theorem was published by Gödel:
Theorem X. For a denumerably infinite system of formulas to be satisfiable it is necessary and sufficient that every finite subsystem be satisfiable. (Gödel 1930, 118–19)
The formulas of the logic, called restricted (functional) calculus (103n3) or first-order predicate logic (Mal’cev 1936, 1), are those from first-order logic that do not contain any function, constant, nor equality symbols, but do contain propositional variables; these variables can only be interpreted as 1 (true) or 0 (false) in any model. Thus, this system extends that of propositional logic ![]() .
.
The central idea behind Gödel’s proof is to create an equivalent sequence (![]() of satisfiable formulas, where each
of satisfiable formulas, where each ![]() is a conjunction, with one of the conjuncts being
is a conjunction, with one of the conjuncts being ![]() , for each
, for each ![]() .
.
The models for each ![]() (in the language restricted to only those non-logical symbols that occur in
(in the language restricted to only those non-logical symbols that occur in ![]() ) form a finitely-branching tree of height
) form a finitely-branching tree of height ![]() , ordered by extension, which by König’s lemma must contain a branch. (Whilst König’s lemma in general requires some Choice to prove, if the tree is countable then it can be proven in
, ordered by extension, which by König’s lemma must contain a branch. (Whilst König’s lemma in general requires some Choice to prove, if the tree is countable then it can be proven in ![]() . A finitely-branching tree of height
. A finitely-branching tree of height ![]() is a countable union of finite sets, which is not necessarily countable in
is a countable union of finite sets, which is not necessarily countable in ![]() , even if the finite sets are pairs (Pincus 1974, 224).) The interpretations along this branch are consistent and form a model of the whole sequence (
, even if the finite sets are pairs (Pincus 1974, 224).) The interpretations along this branch are consistent and form a model of the whole sequence (![]() , which in turn models the original sequence. We have not included this approach to the compactness theorem in this entry—for details, see Paseau (2010a, 84).
, which in turn models the original sequence. We have not included this approach to the compactness theorem in this entry—for details, see Paseau (2010a, 84).
This result also proves the corresponding result for first-order logic with a countable infinity of symbols. Indeed, Gödel does extend his result to allow for equality symbols (Gödel 1930, p. 117, thm. VIII). To allow for constant and function symbols, we introduce new predicate symbols ![]() and
and ![]() of arity 1 and
of arity 1 and ![]() for each constant symbol
for each constant symbol ![]() and
and ![]() -ary function symbol
-ary function symbol ![]() , and make the following substitutions:
, and make the following substitutions:
- For a constant symbol
 occuring in a sentence
occuring in a sentence 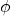 , replace each occurrence of
, replace each occurrence of  with a variable
with a variable 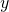 that does not occur in
that does not occur in 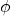 to obtain the formula. If
to obtain the formula. If 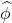 denotes this new sentence, we then replace
denotes this new sentence, we then replace 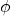 with
with 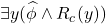 .
. - For an
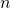 -ary function symbol
-ary function symbol 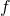 in a sentence
in a sentence 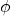 , replace each occurrence of
, replace each occurrence of
![Rendered by QuickLaTeX.com \[R(\sigma_1, \dots, \sigma_{k-1}, f(\tau_1, \dots, \tau_n), \sigma_{k+1}, \dots, \sigma_m)\]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-e25a97194580f9edd00f5522cff03745_l3.png)
with
![Rendered by QuickLaTeX.com \[\exists y (R(\sigma_1, \dots, \sigma_{k-1}, y, \sigma_{k+1}, \dots, \sigma_m) \wedge R_f(\tau_1, \dots, \tau_n, y)),\]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-9051486b47e7f36a7a96b1eb429ebb85_l3.png)
where
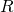 is an
is an 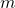 -ary predicate symbol,
-ary predicate symbol, 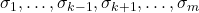 ,
, 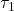 ,
,  are terms and
are terms and 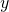 is a variable that does not occur in
is a variable that does not occur in 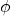 . Viewing equality as a binary predicate, we can perform the same procedure on subformulas of this form.
. Viewing equality as a binary predicate, we can perform the same procedure on subformulas of this form.
Repeating this procedure until there are no occurrences of constant nor function symbols, we obtain a new set of sentences ![]() . Appending to this set sentences of the form
. Appending to this set sentences of the form ![]() for each constant symbol
for each constant symbol ![]() and
and ![]()
![]() for each
for each ![]() -ary function symbol
-ary function symbol ![]() , we find that the satisfiability of this new set is equivalent to the satisfiability of
, we find that the satisfiability of this new set is equivalent to the satisfiability of ![]() , thus extending Gödel’s result to encompass languages with constant and function symbols.
, thus extending Gödel’s result to encompass languages with constant and function symbols.
Note that Gödel’s result is only applicable to the countable versions of propositional and first-order logic. In Gödel’s (1932) short paper, he proves the compactness theorem for propositional logic for arbitrary languages. Given a deductively-closed, consistent set ![]() of propositional formulas and a well-order on the set of propositional formulas, Gödel defines by transfinite recursion:
of propositional formulas and a well-order on the set of propositional formulas, Gödel defines by transfinite recursion:
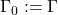 ,
,- for all ordinals
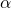 , if there is a formula
, if there is a formula 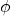 such that neither
such that neither 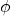 nor
nor  belong to
belong to 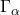 , let
, let 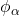 be the least such
be the least such 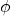 and define
and define
![Rendered by QuickLaTeX.com \[\Gamma_{\alpha + 1} \df := \{\psi : (\phi_\alpha \to \psi) \in \Gamma_\alpha\}.\]](https://iep.utm.edu/wp-content/ql-cache/quicklatex.com-03623f855ef5e6e6c0ac076cf587d678_l3.png)
Otherwise, define
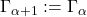 .
. - for all limit ordinals
 ,
,  .
.
For an ordinal ![]() where
where ![]() , it follows that the valuation
, it follows that the valuation ![]() defined as follows satisfies every formula in
defined as follows satisfies every formula in ![]() ,
,
![]()
Independently, Mal’cev (1936, thm. 1) also proved the compactness theorem for propositional logic, again using the full strength of the Axiom of Choice. His proof relies on transfinite induction, letting ![]() be an uncountable cardinal and assuming that the compactness theorem holds for sets of propositional sentences with cardinality strictly less than
be an uncountable cardinal and assuming that the compactness theorem holds for sets of propositional sentences with cardinality strictly less than ![]() . Let
. Let ![]() be a finitely-satisfiable set of sentences with cardinality
be a finitely-satisfiable set of sentences with cardinality ![]() and well-ordered in this order type. At each non-limit stage
and well-ordered in this order type. At each non-limit stage ![]() , he substitutes the
, he substitutes the ![]() th sentence
th sentence ![]() for a conjunction of literals. Supposing this has been done up to, but not including, stage
for a conjunction of literals. Supposing this has been done up to, but not including, stage ![]() , so we have a set
, so we have a set ![]() . The
. The ![]() th substitution is made according to the following rule: as the initial segments of
th substitution is made according to the following rule: as the initial segments of ![]() are satisfiable, we have a collection of
are satisfiable, we have a collection of ![]() -many models. One of the truth-value assignments to the variables that occur in
-many models. One of the truth-value assignments to the variables that occur in ![]() must coincide with
must coincide with ![]() -many of the assignments for these models. Replace
-many of the assignments for these models. Replace ![]() with
with ![]() , which is the conjunction of the letters in
, which is the conjunction of the letters in ![]() that are assigned true, together with the negation of the letters that are assigned false. By construction, the final set
that are assigned true, together with the negation of the letters that are assigned false. By construction, the final set ![]() is satisfiable, and any satisfying model is also a model of the original
is satisfiable, and any satisfying model is also a model of the original ![]() .
.
Mal’cev claimed to have extended this result to first-order logic in the same paper. However, his terminology is slightly ambiguous. What seems to be at issue is the claim that every sentence is `equivalent’ to a ![]() -sentence; one of the form
-sentence; one of the form ![]() , where
, where ![]() is an atomic formula. This is patently false: for instance, the arithmetical hierarchy does not collapse, so there exists a sentence that is not equivalent to a
is an atomic formula. This is patently false: for instance, the arithmetical hierarchy does not collapse, so there exists a sentence that is not equivalent to a ![]() -sentence, even over Peano Arithmetic. However, by `equivalent’ Mal’cev appears to mean equisatisfiable:
-sentence, even over Peano Arithmetic. However, by `equivalent’ Mal’cev appears to mean equisatisfiable:
![]()
This is also noted in a review of Mal’cev’s later articles (Henkin and Mostowski 1959, 57). Under this interpretation, the statement is true. Skolem’s normal form for satisfiability can be found in (Skolem 1920):
Theorem 1. If ![]() is an arbitrary first-order proposition, there exists a first-order proposition
is an arbitrary first-order proposition, there exists a first-order proposition ![]() in normal form with the property that
in normal form with the property that ![]() is satisfiable in a given domain whenever
is satisfiable in a given domain whenever ![]() is, and conversely. (255)
is, and conversely. (255)
Note that the languages of ![]() and
and ![]() are not in general the same. This result readily extends to sets of sentences and is a well-known tool in model theory. (Nowadays, Skolemisation of a theory usually refers to the introduction of function symbols directly in order to prove, amongst other things, the downward Löwenheim-Skolem (Skolem 1920, 257–59). As we do not require this theorem, the predicate approach has the added advantage of not requiring Choice.)
are not in general the same. This result readily extends to sets of sentences and is a well-known tool in model theory. (Nowadays, Skolemisation of a theory usually refers to the introduction of function symbols directly in order to prove, amongst other things, the downward Löwenheim-Skolem (Skolem 1920, 257–59). As we do not require this theorem, the predicate approach has the added advantage of not requiring Choice.)
The first explicit, publshed proofs of a compactness theorem from completeness were given independently by Henkin (1948, 1949b, 1950) and Robinson (1949, 1951). The logics considered in these dissertations are first-order logic / theory of simple types for Henkin, and restricted functional calculus for Robinson. However, the proof relies only upon the finitary nature of the deductive system and completeness of the logic. (The completeness theorem for propositional logic is independently proven by Bernays (1918, sec. 3)—see Zach (1999, 340–48) for a discussion on authorship—and Post (1921, 169). For the restricted functional calculus, it was first asked, for an empty set of premisses, in Hilbert and Ackermann (1928, 68). It was proven in the form of the model existence theorem—for countable sets in Gödel (1929, 96–101) and for arbitrary sets, using the Axiom of Choice, in Henkin (1949b, p. 164, cor. 2) and Robinson (1951, chap. 3). As noted above, this easily extends to completeness of first order logic.)
The compactness theorem finally receives its name in Tarski (1952) in two forms. The second form (p. 467, thm. 17) is the form we are familiar with. By ![]() , Tarski denotes the collection of arithmetical classes, which are classes of the form
, Tarski denotes the collection of arithmetical classes, which are classes of the form
![]()
where ![]() is a formula over a fixed first-order language
is a formula over a fixed first-order language ![]() , and the
, and the ![]() range over
range over ![]() -structures. In his terminology, the compactness theorem is the statement that if
-structures. In his terminology, the compactness theorem is the statement that if ![]() is a collection of
is a collection of ![]() -formulas and
-formulas and ![]() (which means
(which means ![]() is unsatisfiable) then there exists a finite set
is unsatisfiable) then there exists a finite set ![]() such that
such that ![]() (which means
(which means ![]() is not finitely-satisfiable). The first form (p. 466, thm. 13) is a generalisation that applies to types (Chang and Keisler 1990, 78–79; Hodges 1997, 130–31).
is not finitely-satisfiable). The first form (p. 466, thm. 13) is a generalisation that applies to types (Chang and Keisler 1990, 78–79; Hodges 1997, 130–31).
Whilst Tarski does not provide a topological argument for these theorems, relying upon completeness instead, he does draw some connection between a topological space based on ![]() and first-order logic. By defining a closure operator and then quotienting by equivalence of models, he obtains a space homeomorphic to the one constructed at the end of section 5 of this article. (There are some foundational issues at play here, since each equivalence class is a proper class, as are the open sets. Tarski takes only a set of models as opposed to the whole class. We avoided this issue in our construction by considering the space of theories. As the class of theories is a set, by taking enough representatives—using, for example, the Axiom of Collection—we find that Tarski’s space will be homeomorphic to our construction in section 5.) As he observes, the resulting space is a Stone space, noting that compactness of the space follows from the compactness of the logic. (Tarski uses the term bicompact for what we call compact. Compact used to refer to the countable compactness property (Willard 1970, 304).)
and first-order logic. By defining a closure operator and then quotienting by equivalence of models, he obtains a space homeomorphic to the one constructed at the end of section 5 of this article. (There are some foundational issues at play here, since each equivalence class is a proper class, as are the open sets. Tarski takes only a set of models as opposed to the whole class. We avoided this issue in our construction by considering the space of theories. As the class of theories is a set, by taking enough representatives—using, for example, the Axiom of Collection—we find that Tarski’s space will be homeomorphic to our construction in section 5.) As he observes, the resulting space is a Stone space, noting that compactness of the space follows from the compactness of the logic. (Tarski uses the term bicompact for what we call compact. Compact used to refer to the countable compactness property (Willard 1970, 304).)
The ultraproduct proof is given in Frayne, Morel, and Scott (1962, p. 216, thm. 2.10), which is based on Łoś’ Theorem (p. 213, lemma 2.1)—see Łoś (1971, 105, “(2.6)”) for the original statement (without proof). The argument is similar to the one given in Section 4c. Frayne, Morel, and Scott (1962, 195) acknowledge that Alfred Tarski suggested the use of ultraproducts, which had several applications in the literature already, in proving the compactness theorem. David Gale gave a topological proof of the compactness theorem for propositional logic (as credited by Henkin (1949a, 48n4)), whilst Beth (1951) gives a topological proof of the completeness theorem before deriving compactness as a corollary. A direct topological proof is given by Frayne, Morel, and Scott (1962, p. 225, ex. 2), using a combination of ultraproducts and Stone spaces.
More details on this history can be found in Dawson (1993) and the references therein.
9. References and Further Reading
- Barwise, J., and Solomon Feferman, eds. 1985. Model-Theoretic Logics. Perspectives in Mathematical Logic. New York: Springer.
- A book on the model-theory of many logics that extend first-order logic.
- Beall, J. C., and Greg Restall. 2006. Logical Pluralism. Oxford: Clarendon Press.
- The book that started the contemporary debate on whether there is one correct foundational logic (logical monism) or more than one (logical pluralism). The authors defend logical pluralism.
- Bernays, Paul. 1918. “Beiträge zur axiomatischen Behandlung des Logik-Kalküls.” In Ewald and Sieg 2013, 231–68.
- Bernays’ habilitiation thesis, in which he proves the completeness theorem for propositional logic, amongst other results related to the chosen propositional calculus.
- Beth, E. W. 1951. “A Topological Proof of the Theorem of Löwenheim-Skolem-Gödel.” Indagationes Mathematicae (Proceedings) 54:436–44. https://doi.org/10.1016/S1385-7258(51)50062-8.
- Beth presents a proof of the Löwenheim-Skolem-Gödel theorem: a set of first-order sentences Γ has a countable model if and only if Γ is consistent.
- Blass, Andreas. 1984. “Existence of Bases Implies the Axiom of Choice.” In Axiomatic Set Theory, edited by James E. Baumgartner, Donald A. Martin, and Saharon Shelah, 31–33. Contemporary Mathematics 31. Providence, RI: American Mathematical Society.
- Blass proves that if every vector space has a basis, then the Axiom of Choice holds, via the Axiom of Multiple Choice.
- Chang, C. C., and H. Jerome Keisler. 1990. Model Theory. 3rd ed. Studies in Logic and the Foundations of Mathematics 73. Amsterdam: North-Holland.
- A classic model theory text.
- Cowen, Robert H. 1990. “Two Hypergraph Theorems Equivalent to BPI.” Notre Dame Journal of Formal Logic 31 (2): 232–40. https://doi.org/ 10.1305/ndjfl/1093635418.
- Cowen proves that the Boolean Prime Ideal theorem (and thus the Compactness Theorem) is equivalent to the Compactness Theorem restricted to propositional formulas formed from a disjunct of at most 3 literals, and is also equivalent to the statement “a graph G is 3-colourable if every finite subgraph is 3-colourable”.
- Dawson, John W., Jr. 1993. “The Compactness of First-Order Logic: From Gödel to Lindström.” History and Philosophy of Logic 14 (1): 15–37. https://doi.org/10.1080/01445349308837208.
- Another article detailing the development and history of the compactness theorems.
- Denyer, Nicholas. 1992. “Pure Second-Order Logic.” Notre Dame Journal of Formal Logic 33 (2): 220–24. https://doi.org/10.1305/ndjfl/1093636099.
- Denyer proves that pure second-order logic (where formulas only have predicate variables) without identity is compact, whilst the corresponding logic with only functional variables is not.
- Ebbinghaus, H.-D. 1985. “Extended Logics: The General Framework.” In Barwise and Feferman 1985, chap. 2.
- Ebbinghaus presents a general framework for logics extending first-order logic and discusses various model-theoretic properties of these logics, in particular compactness and variations thereof.
- Enderton, Herbert B. 2001. A Mathematical Introduction to Logic. 2nd ed. San Diego: Harcourt/Academic Press.
- An introductory textbook on propositional, first-order, and second-order logic, as well as Gödel’s incompleteness theorems.
- Ewald, William, and Wilfried Sieg, eds. 2013. David Hilbert’s Lectures on the Foundations of Arithmetic and Logic: 1917–1933. Vol. 3 of David Hilbert’s Lectures on the Foundations of Mathematics and Physics: 1891–1933. Heidelberg: Springer.
- A collection of Hilbert’s works in the foundations of mathematics, with additional commentary and historical background, as well as a reproduction of Bernays’ habilitation thesis.
- Feferman, Solomon, John W. Dawson Jr., Stephen C. Kleene, Gregory H. Moore, Robert M. Solovay, and Jean van Heijenoort, eds. 1986. Publications 1929–1936. Vol. 1 of Kurt Gödel Collected Works. Oxford: Oxford University Press.
- A collection of many of Gödel’s important works, including his famous results on completeness, incompleteness, and compactness.
- Frayne, T., A. C. Morel, and Dana S. Scott. 1962. “Reduced Direct Products.” Fundamenta Mathematicae 51:195–228. https://doi.org/10.4064/fm-51-3-195-228.
- This paper presents several results on properties reduced products and ultraproducts.
- Givant, Steven, and Paul Halmos. 2009. Introduction to Boolean Algebras. Undergraduate Texts in Mathematics. New York: Springer.
- An introductory textbook on algebraic, order-theoretic, and topological aspects of Boolean algebras.
- Gödel, Kurt. 1929. “Über die Vollständigkeit des Logikkalküls.” Translated by Stefan Bauer-Mengelberg and Jean van Heijenoort. In Feferman, Dawson, Kleene, Moore, Solovay, and Van Heijenoort 1986, 60–101.
- Gödel’s doctoral dissertation, in which he proves the completeness of the restricted functional calculus.
- Gödel, Kurt. 1930. “Die Vollständigkeit der Axiome des logischen Funktionenkalküls.” Translated by Stefan Bauer-Mengelberg. In Feferman, Dawson, Kleene, Moore, Solovay, and Van Heijenoort 1986, 102–23.
- Based on his 1929 doctoral dissertation, Gödel proves the compactness (for countable sets of sentences) of restricted functional calculus from the completeness theorem.
- Gödel, Kurt. 1932. “Eine Eigenshaft der Realisierungen des Aussagenkalküls.” Translated by John W. Dawson Jr. In Feferman, Dawson, Kleene, Moore, Solovay, and Van Heijenoort 1986, 238–41.
- Gödel presents his proof of the compactness theorem in general for propositional logic.
- Goldblatt, Robert. 1998. Lectures on the Hyperreals: An Introduction to Nonstandard Analysis. Graduate Texts in Mathematics 188. New York: Springer.
- A graduate-level textbook on the subject of non-standard analysis, including the foundational and model-theoretic justification for its methods.
- Gonczarowski, Yannai A., Scott Duke Kominers, and Ran I. Shorrer. 2019. “To Infinity and Beyond: Scaling Economic Theories via Logical Compactness.” Harvard Business School Entrepreneurial Management Working Paper, no. 19–127, revised November 9, 2020. https://doi.org/10. 2139/ssrn.3409828.
- This substantial working paper demonstrates several applications of the compactness theorem in economics.
- Griffiths, O., and A. C. Paseau. 2022. One True Logic. Oxford: Oxford University Press.
- The authors argue that there is one correct foundational logic, and that it is highly infinitary.
- Hajnal, A., and A. Kertész. 1972. “Some New Algebraic Equivalents of the Axiom of Choice.” Publicationes Mathematicae Debrecen 19:339–40.
- The equivalence, under ZF, of the Axiom of Choice with the existence of groups structures (or other algebraic structures) on any set is proven in this short article.
- Henkin, Leon A. 1948. “The Completeness of Formal Systems.” PhD diss., Princeton University.
- Henkin’s doctoral dissertation which contains his proof of the completeness and compactness theorems for first-order functional calculus and the simple theory of types, as well as applications of the compactness theorem to algebra among other results. These results were published in Henkin (1949b, 1950).
- Henkin, Leon A. 1949a. “Fragments of the Propositional Calculus.” Journal of Symbolic Logic 14:42–48. https://doi.org/10.2307/2268976.
- Henkin demonstrates how to obtain complete axiomatisations for fragments of propositional logic.
- Henkin, Leon A. 1949b. “The Completeness of the First-Order Functional Calculus.” Journal of Symbolic Logic 14:159–66. https://doi.org/10. 2307/2267044.
- This article contains Henkin’s proof of the completeness and compactness theorems of first-order functional calculus, based on his doctoral dissertation.
- Henkin, Leon A. 1950. “Completeness in the Theory of Types.” Journal of Symbolic Logic 15:81–91. https://doi.org/10.2307/2266967.
- This article contains Henkin proves the completeness theorem for the theory of simple types, based on his doctoral dissertation.
- Henkin, Leon A., and Andrzej Mostowski. 1959. Review of Anatoliĭ Ivanovič Mal’cev. 1941. “Ob odnom obščém métodé polučéniá lokal’nyh téorém téorii grupp.” Ivanovskij Gosudarstvénnyj Pédagogičéskij Institut, Učényé zapiski, Fiziko-matématičéskié nauki 1 (1): 3–9 and “O prédstavléniáh modéléj.” 1956 by Anatoliĭ Ivanovič Mal’cev. Doklady Akadémii Nauk SSSR 108:27–29. Journal of Symbolic Logic 24 (1): 55–57. https://doi. org/10.2307/2964581.
- Henkin and Mostowski’s review of two of Mal’cev’s important papers on applications of the compactness theorems in algebra. English translations of these article are found in Mal’cev (1971, 15–26).
- Hilbert, D., and W. Ackermann. 1928. “Grundzüge der theoretischen Logik.” In Ewald and Sieg 2013, 809–915.
- A collection of Hilbert’s works in the foundations of mathematics, with additional commentary and historical background, as well as a reproduction of Bernays’ habilitation thesis.
- Hodges, Wilfrid. 1997. A Shorter Model Theory. Cambridge: Cambridge University Press.
- A comprehensive textbook on model theory.
- Howard, Paul E. 1975. “Łoś’ Theorem and the Boolean Prime Ideal Theo- rem Imply the Axiom of Choice.” Proceedings of the American Mathematical Society 49:426–28. https://doi.org/10.2307/2040659.
- In this paper, Howard proves the title statement and discusses the possibility of assumption of the Boolean Prime Ideal Theorem.
- Howard, Paul E., and Jean E. Rubin. 1998. Consequences of the Axiom of Choice. Mathematical Surveys and Monographs 59. Providence, RI: American Mathematical Society.
- A comprehensive source of the myriad Choice principles that occur throughout mathematics, organised by equivalence as well as topic. It also includes descriptions of the many models of set theory that demonstrate non-provable implications between the different forms of Choice.
- Jech, Thomas J. 1973. The Axiom of Choice. Studies in Logic and the Foundations of Mathematics 75. Amsterdam: North-Holland.
- A textbook on the Axiom of Choice and other Choice-like principles, which covers the standard permutation models used for proving the independence of one statement from another.
- Jech, Thomas J. 2003. Set Theory. 3rd ed. Springer Monographs in Mathematics. Berlin: Springer.
- A graduate-level textbook on axiomatic set theory, covering infinitary combinatorics, large cardinals, inner models, and forcing.
- Kanamori, Akihiro. 2009. The Higher Infinite: Large Cardinals in Set Theory from Their Beginnings. 2nd ed. Springer Monographs in Mathematics. Berlin: Springer.
- A graduate-level textbook on the large cardinal heirarchy.
- Keisler, H. Jerome. 1965. “A Survey of Ultraproducts.” In Logic, Methodology and Philosophy of Science II: Procedings of the 1964 International Congress, edited by Yehoshua Bar-Hillel, 112–26. Studies in Logic and the Foundations of Mathematics. Amsterdam: North-Holland.
- A survey on the use of ultraproducts in mathematics, including its relationship with the compactness theorem for first-order logic via Łoś’ theorem.
- Keisler, H. Jerome. 1970. “Logic with the Quantifier ‘There Exist Uncountably Many’.” Annals of Pure and Applied Logic 1:1–93. https://doi.org/ 10.1016/S0003-4843(70)80005-5.
- An extensive paper on the model-theoretic properties of logics that include the quantifier ‘there exist uncountably many’.
- Keisler, H. Jerome, and Julia F. Knight. 2004. “Barwise: Infinitary Logic and Admissible sets.” The Bulletin of Symbolic Logic 10 (1): 4–36. https: //doi.org/10.2178/bsl/1080330272.
- A survey of the Barwise compactness theorem of infinitary logic.
- Kunen, Kenneth. 2011. Set Theory. Studies in Logic 34. London: College Publications.
- A textbook on axiomatic set theory, covering infinitary combinatorics and forcing.
- Lindström, Per. 1969. “On Extensions of Elementary Logic.” Theoria 35:1– 11. https://doi.org/10.1111/j.1755-2567.1969.tb00356.x.
- Lindström proves his famous theorem characterising first-order logic via the (countable) compactness and Löwenheim-Skolem theorems.
- Łoś, Jerzy. 1971. “Quelques remarques, théorèmes et problèmes sur les classes définissables d’algèbres.” In Mathematical Interpretation of Formal Systems, 2nd ed., 16:98–113. Studies in Logic and the Foundations of Mathematics. Amsterdam: North-Holland.
- In this article (originally published in 1955), Łoś states without proof the theorem which bears his name.
- Makowsky, J. A. 1985. “Compactness, Embeddings and Definability.” In Barwise and Feferman 1985, chap. 18.
- Makowsky presents results on several model-theoretic properties of abstract logics, including generalised compactness properties.
- Mal’cev, Anatoliĭ Ivanovič. 1936. “Investigations in the realm of mathematical logic.” In Mal’cev 1971, 1–14.
- In this article, Mal’cev proves the compactness theorems for propositional and first-order logic.
- Mal’cev, Anatoliĭ Ivanovič. 1971. The Metamathematics of Algebraic Systems: Collected papers: 1936–1967. Edited and translated by Benjamin Franklin Wells III. Amsterdam: North-Holland.
- Translations of most of Mal’cev’s works on algebraic applications of mathematical logic.
- Mann, Allen L., Gabriel Sandu, and Merlijn Sevenster. 2011. Independence-Friendly Logic: A Game-Theoretic Approach. London Mathematical Society Lecture Note Series 386. Cambridge: Cambridge University Press.
- This monograph provides an introduction to independence-friendly logic, a logic with game-theoretic semantics.
- Mannila, Heikki. 1983. “A Topological Characterization of (λ, µ)∗-Compactness.” Annals of Pure and Applied Logic 25 (3): 301–5. https://doi.org/10.1016/0168-0072(83)90022-2.
- Mannila gives a model-theoretic characterisation of the (λ, µ)-compactness of the model space of a logic.
- Moore, Gregory H. 1982. Zermelo’s Axiom of Choice: Its Origins, Development, and Influence. Studies in the History of Mathematics and Physical Sciences 8. New York: Springer-Verlag.
- A comprehensive book detailing the history of Zermelo’s explication of the Axiom of Choice and the consequent controversy surrounding it in the early twentieth century.
- Paseau, A. C. 2010a. “Proofs of the Compactness Theorem.” History and Philosophy of Logic 31 (1): 73–98. https://doi.org/10.1080/014453409 03495340. Corrected in “Proofs of the Compactness Theorem.” History and Philosophy of Logic 32, no. 4 (2011): 407. https://doi.org/https://doi.org/10.1080/01445340.2011.618261.
- This article examines different proofs of the compactness theorem, including some of the ones included in the present article, and draws some philosophical conclusions.
- Paseau, A. C. 2010b. “Pure Second-Order Logic with Second-Order Identity.” Notre Dame Journal of Formal Logic 51 (3): 351–60. https://doi. org/10.1215/00294527-2010-021.
- Pure second-order logic is second-order logic without first-order or functional variables. In the context of second-order logic, it is therefore, in a sense, the complement of first-order logic. The article states and proves some metalogical results for this logic.
- Paseau, A. C., and Owen Griffiths. 2021. “Is English Consequence Compact?” Thought: A Journal of Philosophy 10 (3): 188–98. https://doi. org/10.1002/tht3.492.
- A detailed investigation of the validity of the ‘planets’ argument discussed in section 2b of the present article.
- Pincus, David. 1974. “The Strength of the Hahn-Banach Theorem.” In Victoria Symposium on Nonstandard Analysis: University of Victoria 1972, edited by Albert Hurd and Peter Loeb, 203–48. Lecture Notes in Mathematics 369. Berlin: Springer-Verlag.
- Pincus shows the consistency (relative to ZF) of the Hahn-Banach theorem holding whilst the Boolean Prime Ideal Theorem failing.
- Poizat, Bruno. 2000. A Course in Model Theory. Translated by Moses Klein. Universitext. An Introduction to Contemporary Mathematical Logic. New York: Springer.
- A graduate-level textbook on model theory.
- Post, Emil L. 1921. “Introduction to a General Theory of Elementary Propositions.” American Journal of Mathematics 43 (3): 163–85. https://doi. org/10.2307/2370324.
- Based on his doctoral dissertation, Post proves the completeness theorem for propositional calculus, as well as some results on many-valued logics.
- Putnam, Hilary. 1980. “Models and Reality.” Journal of Symbolic Logic 45 (3): 464–82. https://doi.org/10.2307/2273415.
- In this article, Putnam sets out the argument mentioned in section 3 of the present article.
- Richter, Marcel K. 1966. “Revealed Preference Theory.” Econometrica 34 (3): 635–45. https://doi.org/10.2307/1909773.
- Richter characterises the representability and rationality of consumers, where the latter proof uses the Order-Extension Principle.
- Robinson, Abraham. 1949. “On the Metamathematics of Algebraic Systems.” PhD diss., Birkbeck College, University of London.
- Robinson’s doctoral dissertation, which includes his proof of the completeness and compactness theorems for first-order functional calculus. These results were later published in Robinson (1951).
- Robinson, Abraham. 1951. On the Metamathematics of Algebra. Studies in Logic and the Foundations of Mathematics 4. Amsterdam: North-Holland.
- A monograph largely based on Robinson’s doctoral dissertation.
- Robinson, Abraham. 1966. Non-Standard Analysis. Studies in Logic and the Foundations of Mathematics 42. Amsterdam: North-Holland.
- A foundational text in non-standard analysis, providing a rigorous justification of its methods.
- Rubin, Herman, and Dana S. Scott. 1954. Some Topological Theorems Equivalent to the Boolean Prime Ideal Theorem. Presented at 503rd meeting of the American Mathematical Society, May 1, 1954. Abstract in W. Green. “The May Meeting in Yosemite.” Bulletin of the American Mathematical Society 60 (1954): 386–99. https://doi.org/10.1090/ S0002-9904-1954-09827-0.
- At this talk, several topological theorems are proven to be equivalent to the Boolean Prime Ideal Theorem.
- Shapiro, Stewart. 1991. Foundations without Foundationalism: A Case for Second-Order Logic. Oxford Logic Guides 17. Oxford: Clarendon Press.
- A detailed and extensive account of second-order logic, taking in its historical, mathematical and philosophical aspects.
- Shapiro, Stewart. 2014. Varieties of Logic. Oxford: Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199696529.001.0001.
- The author defends a more radical form of logical pluralism (the thesis that there is more than one correct foundational logic) than that of Beall and Restall (2006).
- Skolem, Thoralf. 1920. “Logico-Combinatorial Investigations in the Satisfiability or Provability of Mathematical Propositions: A Simplified Proof of a Theorem by L. Löwenheim and Generalizations of the Theorem.” Translated by Stefan Bauer-Mengelberg. In From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931, edited by Jean van Heijenoort, 254–63. Cambridge, MA: Harverd University Press.
- A translated extract from Skolem’s 1920 paper, in which he presents his normal form for formulas in first-order logic as well as presenting a fully-correct proof of the downward Löwenheim-Skolem theorem for countable sets of sentences, which uses his Axiom of Choice.
- Skolem, Thoralf. 1922. “Some Remarks on Axiomatized Set Theory.” Translated by Stefan Bauer-Mengelberg, 290–301.
- A translated transcript of Skolem’s address at the Fifth Congress of Scandinavian Address held in Helsinki 4th–7th July 1920, in which he discusses several foundational aspects of set theory, and in particular demonstrates his ‘paradox’.
- Stephenson, R. M., Jr. 1984. “Initially κ-Compact and Related Spaces.” In Handbook of Set-Theoretic Topology, edited by Kenneth Kunen and Jerry E. Vaughan, 603–32. Amsterdam: North-Holland.
- This article presents a survey of results on (κ, λ)-compactness of topological spaces.
- Sutherland, Wilson A. 2009. Introduction to Metric and Topological Spaces. 2nd ed. Oxford: Oxford University Press.
- An introductory textbook to topology. Chapter 13 on compactness is particularly relevant to this article.
- Szpilrajn, Edward. 1930. “Sur l’extension de l’ordre partiel.” Fundamenta Mathematicae 16:386–89. https://doi.org/10.4064/fm-16-1-386-389.
- In this short paper, Szpilrajn (also known as Marczewski) proves his Order Extension Principle.
- Tarski, Alfred. 1952. “Some Notions and Methods on the Borderline of Algebra and Metamathematics.” In Proceedings of the International Congress of Mathematicians: Cambridge, Massachussetts, U.S.A., August 30–September 6, 1950, 1:705–20. Providence, RI: American Mathematical Society.
- Tarski presents several results in the language of arithmetical classes (the classes of structures that satisfy a particular first-order sentence). Theorem 13 gives the compactness theorem its name.
- Väänänen, Jouko. 2007. Dependence Logic: A New Approach to Independence Friendly Logic. 70. Cambridge: Cambridge University Press.
- A monograph on dependence logic, and other logics with game-theoretic semantics.
- Willard, Stephen. 1970. General Topology. Reading, MA: Addison-Wesley.
- An introductory textbook on topology. Chapter 6 on compactness is particularly relevant to this article.
- Zach, Richard. 1999. “Completeness Before Post: Bernays, Hilbert, and the Development of Propositional Logic.” Bulletin of Symbolic Logic 5 (3): 331–66. https://doi.org/10.2307/421184.
- A historical article on Bernays and Hilbert’s role in development of mathematical logic, particularly focused on propositional logic.
Author Information
A. C. Paseau
Email: alexander.paseau@philosophy.ox.ac.uk
University of Oxford
United Kingdom
and
Robert Leek
Email: r.leek@bham.ac.uk
University of Birmingham
United Kingdom
