George Berkeley: Philosophy of Science
 George Berkeley announces at the very outset of Three Dialogues Between Hylas and Philonous that the goals of his philosophical system are to demonstrate the reality of genuine knowledge, the incorporeal nature of the soul, and the ever-present guidance and care of God for us. He will do this in opposition to skeptics and atheists.
George Berkeley announces at the very outset of Three Dialogues Between Hylas and Philonous that the goals of his philosophical system are to demonstrate the reality of genuine knowledge, the incorporeal nature of the soul, and the ever-present guidance and care of God for us. He will do this in opposition to skeptics and atheists.
A proper understanding of science, as Berkeley sees it, will be compatible with his wider philosophy in achieving its goals. His project is not to rail against science or add to the scientific corpus. Quite to the contrary, he admires the great scientific achievements of his day. He has no quarrel with the predictive power and hence the usefulness of those theories.
His project is to understand the nature of science including its limits and what it commits us to. A proper understanding of science will show, for example, that it has no commitment to material objects and efficient causation. Understanding this and other philosophical prejudices will undercut many of the assumptions leading to skepticism and atheism.
In exploring the nature of science, Berkeley provides insights into several of the central topics of what is now called the philosophy of science. They include the nature of causation, the nature of scientific laws and explanation, the nature of space, time, and motion, and the ontological status of unobserved scientific entities. Berkeley concludes that causation is mere regularity; laws are descriptions of fundamental regularities; explanation consists in showing that phenomena are to be expected given the laws of nature; absolute space and time are inconceivable; and at least some of the unobserved entities in science do not exist, though they are useful to science. Each of these topics is explored in some detail in this article.
Table of Contents
- Background
- Causation
- Laws of Nature
- Explanation
- Theories and Theoretical Entities
- References and Further Reading
1. Background
Philosophy of Science emerged as a specialized academic discipline in the mid-20th Century, but philosophers as early as Plato and Aristotle developed views about science that we recognize today as addressing central topics of the discipline. Philosophy of Science addresses the nature of science including its methods, goals, and institutions. Recent Philosophy of Science has drawn heavily from the history and sociology of science (Marcum). Typical topics are the structure of explanation, theories, confirmation, the objectivity of science, the role of values in science, and the difference between science and pseudoscience. It is especially important to reflect on science since it appears to give us our very best examples of knowledge and our best tools for understanding nature.
Periods of significant scientific change, such as the introduction of general relativity and quantum mechanics or Darwin’s theory of evolution, have and continue to provoke heightened philosophical reflection. George Berkeley had the good fortune of living during one of these periods. Through a critique of Scholasticism (an amalgam of Aristotelianism and Catholicism) what is now recognized as the beginning of modern science emerged. The period was roughly from 1550 to 1750. Its luminaries included Copernicus, Kepler, Galileo, Descartes, Boyle, Torricelli, and Newton. Berkeley had a broad understanding of the science of his day including what we now call the psychology of visual perception, medicine, biology, chemistry, and physics. He also had a keen grasp of current mathematics.
Building or elaborating scientific theories was not Berkeley’s goal. He had no quarrels with the empirical content of the best theories. He welcomed their usefulness in bettering our lives. His project was to critique mistaken philosophical interpretations and mistaken popularizations of some theories, especially those that led to skepticism and atheism. His philosophical system is largely a reaction to the materialistic mechanism as espoused by many scientists and philosophers, in particular, Descartes and Locke. Berkeley’s critique rejects a key provision of the theory: an ordinary object (apple or chair) is a material substance—an unthinking something that exists independently of minds. Berkeley’s ontology only includes spirits or minds and ideas. Our senses are to be trusted and all physical knowledge comes by way of experience (3Diii 238, DM ϸ21).
This is an oversimplification, but here is not the place to consider his arguments and qualifications for immaterialism (Flage).
In the course of his reaction to materialistic mechanism and other scientific theories, Berkeley made important and novel contributions to understanding concepts crucial to the nature of science. For example, causation, laws of nature, explanation, the cognitive status of theoretical entities, and space and time. His contribution to these topics is examined below. Berkeley’s reflection on science occurs throughout his many works, from Essay on Vision to Sirus (S), but the bulk of his thought is contained in The Principles of Human Knowledge (PHK), Three Dialogues Between Hylas and Philonous (3D), and De Motu (DM). His views, on the important topics mentioned, continued to evolve throughout his writings, becoming more sensitive to actual scientific practice.
2. Causation
a. Physical Causation
Causal claims occur throughout ordinary language and science. Overcooking caused the chicken to be tough. Salt caused the freezing point of the water to rise. Diabetes is caused by insulin insufficiency. Causes as commonly understood, make their effects happen. Many verbs in English, such as the terms ‘produce’ or ‘bring about’, capture the “make happen” feature of causation.
Berkeley’s account of causation plays a central role in his philosophical system and his understanding of the methods, goals, and limits of science. Take the example of fire causing water to boil. When one examines the case, according to Berkeley, ideas of yellow, orange, and red in shimmering motion are followed by ideas of a translucent bubbly haze. In short, one set of ideas is accompanied by another set of ideas. The crucial point is that no “making happen” or “producing” is available to the senses.
All our ideas, sensations, or the things which we perceive, . . . are visibly inactive: there is nothing of power or agency included in them. So that one idea or object of thought cannot produce or make any alteration in another. To be satisfied of the truth of this, there is nothing else requisite but a bare observation of our ideas. (PHK ϸ25)
The basic argument is as follows:
-
- Efficient causes are active.
- Ideas are inert (inactive).
- Therefore, ideas are not efficient causes.
The justification for b is d.
-
- Ideas when observed are found to be inert.
Ideas do undergo changes and we do have ideas of motion, but none of this counts as activity for Berkeley. What constitutes activity in an idea? Could there not be some feature or aspect of ideas that are hidden from sense, some feature that is active? Berkeley’s answer is no.
-
- Ideas exist only in the mind.
- Therefore, there is nothing in them but what is perceived.
Causation in the physical world amounts to one set of ideas regularly followed by another set of ideas. Berkeley uses a variety of terms to mark the contrast with efficient causation: ‘natural causes,’ ‘second causes,’ ‘material causes,’ ‘instruments,’ ‘physical causes,’ and ‘occasional causes’ (S ϸ160, 245; PC Berkeley to Johnson ϸ2). There is no necessary connection between the relata in a causal relation. Berkeley suggests that a better way to conceive of the regularity among ideas in a “causal” relation is as of signs to things signified. Fire is a sign of boiling water. Additionally, signs do not make happen what they signify. The appropriateness of the sign/thing signified relation is further explored in a later section.
This account does not fit our common understanding of causation. Berkeley recognizes this and has no desire to propose that we speak differently in ordinary affairs. In fact, he often lapses into the vernacular. Our common speech presents no problems in ordinary practical affairs, but the philosopher, when being careful, knows that physical causes do not make their effects happen.
b. Efficient Causation
There is a domain where real or efficient causes occur as opposed to the mere physical regularities described above. When one intends to raise her arm and by force of will raises it, stands as an example of efficient causation. Real causation is carried out by an act of mind. Considering the example, Berkeley believes we know this is efficient causation containing the active requirement for causation, though he thinks we have no sensible idea of it.
Returning to the physical causation, the regularities among ideas are created and maintained by God’s will. Although we as creatures with minds have the ability to will certain ideas, many ideas are forced upon us, independently of our will. These are caused by God.
An important consequence of the distinction between physical and efficient causes is what natural philosophy should and should not study. Natural philosophy should focus on understanding the world in terms of physical causes. Efficient causation is the business of theology and metaphysics. Only these disciplines should consider explanations invoking efficient causation (DM ϸ41).
It is not known to what extent Berkeley influenced David Hume. Hume, the third member of the British Empiricists along with John Locke and Berkeley, developed a more detailed version of a regularity theory of causation. Though Berkeley denies any necessary connection between the causal relata in physical causation, he provides no account of our strong tendency to believe that the relation between the relata is more than constant conjunction. For Hume, the power or necessity in causation is produced from our experience; it is in us not in the objects themselves. He also speaks to the temporal and spatial requirements for the relation between cause and effect and considers what counts as an appropriate regularity (Lorkowski). Hume’s theory is importantly different from Berkeley’s in that he holds that all causation is mere regularity. Acts of the will are no exception. Using Berkeley’s terminology, on Hume’s account, all causes are physical causes.
3. Laws of Nature
The early account of laws of nature in The Principles of Human Knowledge treats them as the regularities discussed under causation:
The ideas of sense . . . have likewise a steadiness, order and coherence, and are not excited at random, . . . but in a regular train or series . . . Now the set rules, or established methods, wherein the Mind we depend on excites in us the ideas of Sense, are called the laws of nature; and these we learn by experience, which teaches us that such and such ideas are attended with such and such other ideas, in the ordinary course of things (PHK ϸ30).
The same account is repeated in the Three Dialogues. Laws are “no more than a correspondence in the order of Nature between two sets of ideas, or things immediately perceived” (3Diii 24).
Here laws of nature are low-level empirical generalizations that assert a regularity between phenomena or aspects of phenomena. They are learned by experience by both natural philosophers and ordinary people alike and are found useful in guiding their lives. Berkeley emphasizes that the relation between the relata in a law of nature is not a necessary relation. God has conjoined smoke with fire, but he could have conjoined fire with a high-frequency tone or anything else He pleased. Though Berkeley is not explicit on this matter, it does appear that laws of nature are not restricted to a universal logical form, that is, the form whenever phenomena of type A occur without exception, phenomena of type B occur. Statements expressing probabilities count as laws as well. So, both “breeding albatrosses lay one egg per year” and “most people with lung cancer are smokers” are laws. Berkeley persistently stresses that the important feature of laws is that they are useful. For Berkeley, this usefulness attests to the wisdom and benevolence of God, who has created and maintains them.
In addition to laws of modest scope whose terms refer to what is immediately perceived, “there are certain general laws that run through the whole chain of natural effects . . .” (PHK ϸ61). An example is Galileo’s Law: Any body falling from rest freely to earth covers a distance proportional to the square of the time it has spent falling. These general laws and sets of general laws such as Newton’s Laws of Motion provide a “largeness of comprehension” that occupy the attention of the natural philosopher. They enable one to see the unity in apparently diverse phenomena. For example, the unity in falling bodies, tides, and planetary orbits. Some very general and fundamental laws allow for the explanation of other laws.
In mechanical philosophy those are to be called principles, in which the whole discipline is grounded and contained, these primary laws of motion which have been proved by experiments, elaborated by reason and rendered universal. These laws of motion are conveniently called principles, since from them are derived both general mechanical theorems and particular explanations of phenomena (DM ϸ36).
These more fundamental laws are no longer simple correlations or inductive generalizations perceived and learned by experience. Instead, they are laws of great generality containing theoretical terms (such as “force”) and proved by experiments.
4. Explanation
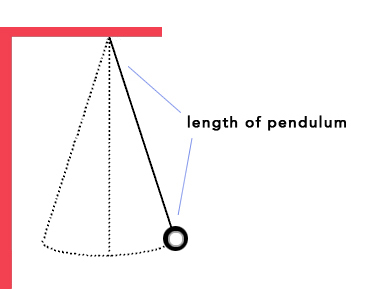
To explain phenomena, they must be “reduced to general rules” (PHK ϸ 105) or alternatively be shown to conform to the laws of nature (PHK ϸ61). This account is a very early version of what is now called the covering law account of explanation. The sentence describing the phenomenon or event to be accounted for is called the explanandum. The sentences describing the information that does the explaining is called the explanans. According to Berkeley’s account, the explanans must contain a law of nature (DM ϸ37). It will typically also contain sentences describing a number of facts. Consider a simple example that would have been quite familiar to Berkeley: Suppose a pendulum oscillates for a period of 6.28 seconds. The explanandum, a period of 6.28 seconds, must be shown to be in conformity with a law. The relevant law is T=2π√(L/g) where T is the period, L is the length of the pendulum, and g is the acceleration due to gravity (10 meters per second2). If L is 10 meters, the period will be 6.28 seconds. The explanandum follows deductively from the explanans. The length of the pendulum being 10 meters and the law cited, explain the period being 6.28 seconds.
| Explanans | (1) | T = π√L/g |
| (2) | L = 10 meters | |
| ———————- | ||
| Explanandum | T = 6.28 seconds |
There is nothing puzzling about the period once the law and pendulum length are known. The period was to be expected.
Figure 1. Diagram of simple pendulum.
An important difference between the contemporary covering law account of explanation and Berkeley’s version is that the contemporary account requires that the sentences making up the explanans, including the law(s), be true (Hempel 89-90). As discussed in the next section, Berkeley regards some laws of nature, most notably Newton’s laws of motion, as neither true nor false. They are not the sort of things that can be true or false. They are guides, calculating devices, and useful fictions. This is not to disparage them. Berkeley regards Newton’s laws as the greatest achievement in natural philosophy and a model for future science (PHK ϸ110, S ϸ243, 245). The role of laws is to enable us to expect what will happen. Newton’s laws are remarkably successful at this goal.
Berkley argues that the goal of science is not necessarily to uncover true laws, nor will true laws be better at helping us expect phenomena. The goal of mature science is to produce general laws. They are easy to use, few in number, and give predictive control of a wide range of phenomena. The virtue of laws and the explanations they enable is serving these practical goals. His insight is that true laws may be in tension with these practical virtues. True laws may be too complex, too cumbersome to apply, too numerous to serve the practical goal of simplicity, and so forth. The first objective of laws and explanations is usefulness.
The covering law account of explanation has received a range of criticisms. This is not the place to rehearse these criticisms and evaluate their force. But there is one prominent criticism that deserves consideration. Seeing how Berkeley would respond brings together his positions on causation, laws of nature, and explanation.
Consider the pendulum example again: Intuitively there is an asymmetry between explaining the period in terms of the length of the pendulum verses explaining the length in terms of the period. L explains T. T does not explain L, but T can be calculated from L and L can be calculated from T. Using Berkeley’s position on how explanations make phenomena intelligible, given L, T is expected and given T, L is expected. So, it appears that the covering law view of explanation cannot account for the asymmetry. The covering law view lets in too much. It sanctions T explains L, yet this conflicts with strong intuitions. The problem is not merely an artifact of the pendulum case. It arises with many natural laws including Boyle’s Law, Ohm’s Law, and the laws of geometric optics, along with others.
In response to this, Berkeley would insist that there are no efficient causes in nature. The alleged asymmetry is a relic of the mistaken view that the length of the pendulum causes its period, but the period does not cause the length of the pendulum. Causal relations and laws of nature describe regularities, not what makes things happen:
. . . the connexion of ideas does not imply the relation of cause and effect, but only the mark of sign and thing signified. The fire which I see is not the cause of the pain I suffer upon my approaching it. In like manner the noise that I hear is not the effect of that motion or collision . . . , but the sign thereof (PHK ϸ65).
In customary talk, there may be an asymmetry where causes can explain effects but not vice versa, but when efficient causation is replaced with regularities between sign and thing signified, the asymmetry disappears. “Causes” can be signs of “effects” and, as in the above quotation, “effects” can be signs of “causes”. Noise is the sign of a collision.
The Berkeleyan defense of the covering law account rests on the claim that the way in which explanations make phenomena intelligible is by giving one reason to expect them or to calculate their occurrence (PHK ϸ31, S ϸ234). This is undoubtedly Berkeley’s official position. Carl Hempel, the leading contemporary defender of the covering law account of explanation, would agree with Berkeley on the point of explanation and how to handle the asymmetries. The asymmetries according to Hempel are due to “preanalytic causal and teleological ideas” (Hempel 95). These ideas are hardly the basis for a systematic and precise analysis of explanation.
In De Motu Berkeley hints at a very different account of how explanations make phenomena intelligible:
For once the laws of nature have been found out, then it is the philosopher’s task to show that each phenomenon is in constant conformity with those laws, that is, necessarily follows from those principles. In that consist the explanation and solution of phenomena and assigning their cause, i. e. the reason why they take place (DM ϸ37).
There are two issues of concern here: 1) Berkeley asserts that the explanandum must follow necessarily from the explanans. This is inconsistent with allowing statistical laws in explanations. As has been suggested, there is no reason Berkeley cannot allow this. God created and maintains the laws of nature to help us know what to expect. Their practical nature is well served by statistical laws. 2) Much more importantly, he invokes a different rationale for how explanations make phenomena intelligible. There is a significant difference between providing grounds for expecting or calculating events and providing “the reason why they take place.” In the pendulum example, the period allows for the calculation of the length, but it does not provide the cause or reason why it is 10 meters. That rests with the designer of the pendulum or the manufacturing process.
Perhaps Berkeley has misspoken or is speaking not as a philosopher, or perhaps he is under the spell of the very view of causation he has rejected. If Berkeley wants to maintain the requirement that explanations tell us why events take place, he will need an account of the asymmetry discussed. Of course, he must do this without appeal to efficient causation. There are numerous ways to do this. For one, the length of the pendulum can be given a covering law explanation independently of the period, but an explanation of the period appears to require appeal to the length of the pendulum (Jobe). This suggestion and others, need careful development including an account of their relevance to the larger issue of explanation. The point here is that answers to the asymmetry problem might be available that do not invoke efficient causation.
5. Theories and Theoretical Entities
a. Scientific Instrumentalism and Newtonian Forces
Much of De Motu is an argument for how to understand the status of forces in Newton’s theories of motion and gravitation. In the first section Berkeley warns the reader of “. . . being misled by terms we do not rightly understand” (DM ϸ1). The suspect terms at issue occur in the science of motion. They fall into two groups: The first includes ‘urge,’ ‘conation,’ and ‘solicitation.’ These play no role in the best accounts of motion and have no legitimate role in physical science. They are “of somewhat abstract and obscure signification” (DM ϸ2) and on reflection clearly apply solely to animate beings (DM ϸ3). The second group includes ‘force,’ ‘gravitation,’ and allied terms. Berkeley’s attention is focused on this group. He expresses a worry about these terms by way of an example. When a body falls toward the center of the earth it accelerates. Some natural philosophers are not satisfied with simply describing what happens and formulating the appropriate regularity. In addition, a cause of the acceleration is assigned—gravity.
A major motivation for Berkeley writing De Motu was to resist treating forces and gravitation as efficient causes. Some of Newton’s followers and perhaps Newton himself held this view. Given the prestige of Newton’s physics, it was particularly important for Berkeley to respond. Treating forces as efficient causes would undermine Berkeley’s immaterialism, but Berkeley is not merely defending his own philosophical territory. Regardless of one’s commitment, or lack of it, to immaterialism, Berkeley raises significant issues about forces.
One could simply argue that there are no forces. So, force-talk should be abandoned. This would certainly rid the scene of forces as causes. Much the same has happened with caloric, phlogiston, ether, and witches. The terms have disappeared from highly confirmed theories along with any causal role assigned to the entities. Berkeley’s view is more subtle than this. His general thesis is that “force,” “gravity,” and allied terms lack the significance required to indicate the real nature of things. The terms are not meaningless, as they have a useful role to play in scientific theories, but they lack the sort of significance needed to support a realistic understanding of forces. They fail to indicate distinct entities or qualities.
Lisa Downing has detailed Berkeley’s argument for an anti-realistic understanding of forces (Downing 1996, 2005 238-249). The key premise is as follows:
P. Forces are unknown qualities of bodies, that is, unsensed.
From this he concludes:
C. Force terms (‘force,’ ‘gravity,’ ‘attraction’) fail to indicate (refer to) distinct qualities.
Though Berkeley takes P as obvious, he does have an argument for it. Forces as efficient causes are active qualities of bodies. They must be unsensed, for on careful examination all the sensed qualities of bodies are passive.
What licenses the move from P to C? Naming or referring to forces requires conceiving of forces. To conceive of physical entities requires a sense-based idea of them (Downing 2005 247).
Berkeley does not hold that all meaningful words stand for ideas. This view, often attributed to John Locke, is aggressively criticized by Berkeley (Pearce 194-196). Words need not bring a distinct idea to the speaker’s or hearer’s mind. In fact, force terms without standing for ideas are meaningful. Their significance comes from the usefulness they provide in Newtonian dynamics. A system of mathematical rules that employ force terms allow for precise predictions. This is accomplished lacking the kind of significance needed to secure reference. With ‘force’ failing to name anything, forces cannot be understood realistically.
Berkeley’s examination of forces is not only destructive. He had a great appreciation of the explanatory success of Newtonian dynamics. He saw that force terms play an important role in the theory. He interprets those terms instrumentally. They do not “indicate so many distinct qualities,” but they are useful in reasoning about motion:
Force, gravity, attraction and terms of this sort are useful for reasonings and reckonings about motion . . . As for attraction, it was certainly introduced by Newton, not as a true physical quantity, but only as a mathematical hypothesis (DM ϸ17).
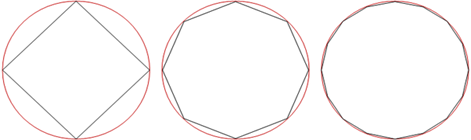
Berkeley gives perspicuous illustrations of what he means by mathematical hypotheses and being useful in reasoning. The first occurring after the above quote concerns the parallelogram of forces. This mathematical technique allows for the computation of the resultant force. But this force is not proffered as a “true physical quantity” though it is very useful for predicting the motion of bodies (DM ϸ18). The second illustration reminds us of how considering a curve as an infinite number of straight lines (though it is not in reality) can be of great utility. For instance, it allows a geometrical proof of the common formula for the area of a circle—A = π r2, and in mechanics, it is also useful to think of circular motion as “arising from an infinite number of rectilinear directions” (DM ϸ61).
Figure 2
For numerous practical purposes a circle can be regarded as composed of many straight lines.
b. Scientific Realism and Corpuscularianism
Corpuscularianism was the dominant theoretical framework for the physical sciences in the 17th century. The basic position is a form of atomism. Bodies are material objects existing independently of human minds and composed of minute particles (corpuscles) that are unobservable. Their properties are restricted to size, shape, position, and motion (the primary qualities). Corpuscles explain the properties of bodies including their color, smell, temperature, and sound (the secondary qualities).
Given the prominence of the corpuscularian theoretical framework and Berkeley’s intimate familiarity with the works of many of the theory’s proponents (notably Rene Descartes, Robert Boyle, and John Locke), it is appropriate to ask how he understood the status of the framework’s fundamental entities—corpuscles. The received view has been that Berkeley must hold instrumentalism for all theoretical entities (Popper; Warnock 202; Newton-Smith 152; Armstrong 32-34). This position is encouraged by at least two considerations: (1) When Berkeley explicitly addresses the cognitive status of theoretical entities it is always to argue against realism. He never offers arguments for a realistic understanding of some theoretical entities. (2) Berkeley’s immaterialism maxim, esse est percipi, (to be is to be perceived) was thought to be incompatible with realism for theoretical entities.
More recent scholarship attempts to show that a realistic understanding of corpuscles is compatible with Berkeley’s wider philosophical position, if not embraced by him (Downing 1995, 2005 230-235; Garber; Winkler 238-275). Berkeley’s immaterialist version of corpuscularianism must be qualified in several important ways: First, corpuscles are not bits of matter that are mind independent. They are sets of ideas just as ordinary objects are. Second, corpuscles do not cause anything, but they can be signs of things signified. Third, Berkeley does not endorse the primary/secondary quality distinction. The ideas that make up corpuscles have the same range of qualities as the ideas that make up ordinary objects. This does not prohibit him from recognizing that the primary qualities may be more useful in formulating laws with predictive power. Fourth, corpuscles are in principle sensible. This qualification was accepted by many practicing corpuscularian scientists. Sensing corpuscles is neither logically nor scientifically impossible. It allows a response to the charge that esse est percipi rules out a realistic account of corpuscles.
At the beginning of the Principles, Berkeley spells out his account of ordinary physical objects—apples, stones, books, and so forth. A group of ideas are ‘’observed to accompany each other”, given a name and regarded as one thing (P ϸ1). An apple has a certain odor, color, shape, and texture associated with it. Berkeley immediately recognizes a problem. If things are sets or bundles of ideas, what happens to the existence of things when not sensed? “The table I write on I say exists; that is, I see and feel it: and if I were out of my study I should say it existed; meaning thereby that if I was in my study I might perceive it . . .“(P ϸ3). The counterfactual account is not just needed to explain the continuity of physical objects when unsensed. Apples have a backside and a core. When held in one’s hand only a part of the apple is seen. But under certain conditions, according to Berkeley, one would see the backside and the core. Consider an apple that has fallen from a tree and rolled under leaves never to be sensed by anyone. Quite plausibly there are such apples. Again, Berkeley can use his counterfactual analysis to deal with their existence. If one were walking through the orchard and removed the leaves, she would perceive the apple. This account of the continuity of ordinary objects is clear, but unfortunately it appears to violate common sense—something Berkeley claims to champion. Berkeley’s table goes in and out of existence. To say he would see it when he enters his study is not to say it exists when he is absent from his study. Berkeley sees this as problematic and considers various approaches to continuity in his writings. There is disagreement among scholars on what Berkeley’s preferred position is and on what position fits best with the core principles of his immaterialism (Pitcher 163-179; Winkler 207-244).
In the Three Dialogues, Berkeley hints at a position that both elaborates the counterfactual account and speaks directly to what entities actually exist. Hylas, the spokesperson for materialism, claims that immaterialism is incompatible with the scriptural account of creation. Everything exists eternally in the mind of God; hence everything exists from eternity. So how can entities both exist from eternity and be created in time? Berkeley agrees with Hylas that nothing is new or begins in God’s mind. The creation story must be relativized to finite minds. What actually exists is what God has decreed to be perceptible in accord with the laws of nature. He has made his decrees in the order of the biblical account. If finite minds would have been present, they would have had the appropriate perceptions (3Diii 253).
Obviously, God has decreed that apples are perceivable by finite minds. Given the laws of nature, the core, the backside, and buried apples, would be perceived given one is in the right location. Once God has decreed that something is perceivable, the relevant counterfactuals are supported by the laws of nature, which God created and maintains.
Berkeley’s account is situational. It depends on the observer being in the right place at the right time with no barriers interfering with the light and the observer having well-working visual faculties. If corpuscles exist God has decreed that they are observable under certain conditions. Perhaps corpuscles are analogous to the apple under the leaves. Though neither has been observed they are both observable in principle. Observing the buried apple requires removing the leaves. Observing corpuscles requires being in the right place with a sufficiently powerful microscope. It is not required that the appropriate microscope ever be invented. Economic conditions, for example, may prevent its development. What is required is that the scope is scientifically possible.
The analogy is not perfect. First, in the 18th century, some apples had been observed; no corpuscles had been observed. Second, a special apparatus is not required to see apples. Seeing corpuscles requires a very powerful microscope.
The fact that apples have generic observability (some apples have been observed) whereas no corpuscles have been observed, will only be damning if this provides a reason for corpuscles being inconceivable. As is discussed, it does not. The need for a special apparatus in the case of corpuscles can be answered. Surely eyeglasses are a permissible apparatus. The principles by which light microscopes work are known. They work basically in the same way eyeglasses work. Microscopes do not enable one to merely detect some entity or see the effects of the entity; they, like eyeglasses, enable one to see the entity.
This raises the question of how can corpuscles be treated realistically when forces cannot? In both cases, they are unsensed. There are two important differences for Berkeley: (1) Forces are unperceivable in principle whereas corpuscles are not; (2) Corpuscles can be imagined, and forces cannot be. For Berkeley, imagining is a kind of inner perceiving. Images are constructed by us from ideas that are copies of ideas originally “imprinted on the senses” (PHK ϸ1). One can imagine elephants with train wheels for legs moving about on tracks. Similarly, scientists can imagine corpuscles as tiny objects with a certain shape, size, and texture. Berkeley does not think a construction of any sort is available for forces (DM ϸ6). So, though no corpuscles have been perceived, they are conceivable and the term ‘corpuscle’ is not without meaning.
The textual evidence for Berkeley endorsing corpuscularianism comes from Principles (ϸ60-66) where Berkeley answers a particular objection to his philosophy. What purpose do the detailed mechanisms of plants and animals serve when those mechanisms are ideas caused by God and of no causal power? Similarly, why the inner wheels and springs of a watch? Why does not God simply have the hands turn appropriately without internal complexity?
Berkeley’s answer is that God could do without the inner mechanisms of watches and nature, but he chooses not to do so in order for their behavior to be consonant with the general laws that run throughout nature. These laws of manageable number have been created and maintained by God to enable us to explain and anticipate phenomena. A world without internal mechanisms would be a world where the laws of nature would be so numerous to be of little use.
Berkeley describes the mechanisms as “elegantly contrived and put together” and “wonderfully fine and subtle as scarce to be discerned by the best microscope” (P ϸ60). Admittedly he does not explicitly mention corpuscularian mechanisms, but Garber (182-184) gives several reasons why Berkeley included them. Nowhere does Berkeley deny the existence of the subtle mechanisms or suggest that they should be treated instrumentally. His descriptions of the mechanisms often mirror those of John Locke speaking of corpuscles. Perhaps most importantly, if the science of Berkeley’s day is to explain various phenomena including heat combustion and magnetism, it must refer to hidden mechanisms including corpuscles.
Siris is Berkeley’s last major work. It provides textual support for corpuscularian realism. Siris is a peculiar work. Much of it is devoted to praising the medicinal virtues of tar water (a mixture of pine tar and water), and explaining the scientific basis for its efficacy. The latter project explores parts of 18th century chemistry drawing on a number of corpuscularian hypotheses. The key point is that Berkeley never raises anti-realistic concerns about the relevant entities. He does this in the context of affirming his immaterialism and pointedly repeating his instrumental account of Newtonian forces found in De Motu (Downing 205).
 Figure 3: Cartesian diagram showing how screw shaped particles accounted for magnetism.
Figure 3: Cartesian diagram showing how screw shaped particles accounted for magnetism.
Berkeley’s familiarity with the advances in microscopy provides further indirect support for immaterialistic corpuscularianism. Berkeley knew that there were many entities that were unobservable at one time and later became observable. There was no reason to believe that progress in microscope technology would not continue revealing further mechanisms. In fact, some of Locke’s contemporaries believed that microscopes would improve to a point where corpuscles could be seen.
The general point, one supporting realism, is that mere current unobservability does not speak against realism. To the contrary, the progressive unveiling of nature supports realism.
If Berkeley is a scientific realist about corpuscles, aether, and other entities, this might explain his lack of an argument for realism. He thought that all that was valuable in the best science was not incompatible with immaterialism. Immaterialism along with realism about entities is perhaps regarded as the norm. The outlier is Newtonian forces. They require special argument.
c. Absolute Space and Motion
Absolute motion and absolute space are not understood realistically or instrumentally by Berkeley. He recommends that natural philosophers dismiss the concepts. Relative space and motion will more than adequately serve the purposes of physics. The debate about absolute motion and space has a long and complex history. Berkeley’s critique is often regarded as an anticipation of that of Ernest Mach (Popper).
According to Newton, absolute space “. . . in its own nature and without regard to anything external, always remains similar and immovable.” Absolute space is not perceivable. It is known only by its effects. It is not a physical object or a relation between physical objects. It is a “container” in which motions occur. Absolute motion is the motion of a physical object with respect to absolute space. Relative space, as Berkeley understood it, is “. . . defined by bodies; and therefore, an object of sense” (DM ϸ52). Relative motion requires at least two bodies. One body changes its direction and distance relative to another body (DM ϸ58). If all bodies were annihilated but one, it could not be in motion.
Newton had many reasons, including theological, for endorsing absolute space. In Newtonian physics a special frame of reference must be stipulated in order to apply the laws of motion. There are many possible frames of reference—the earth, the sun, our galaxy, and so on. Are they all equally adequate? A falling object will have a different acceleration and trajectory depending on the chosen reference frame. The differences may be slight and of minimal practical importance, but present a significant theoretical problem. If Newton’s laws are to apply in every reference frame, various forces will need to be postulated from frame to frame. This appears ad hoc and leads to great complexity. To blunt the problem, Newton thought a privileged frame was needed—absolute space (Nagel 204 -205).
Berkeley argued against Newton’s position from his early writings in The Notebooks, The Principles of Human Knowledge, and De Motu. As with forces, he wanted to reject absolute space as an efficient cause, but he also had theological motivations. He found the view that absolute space necessarily exists, is uncreated, and cannot be annihilated, abhorrent. It put absolute space in some respects on the level of God. Nevertheless, Berkeley’s arguments against absolute space do not involve theological principles. The focus here is on the critique in De Motu, Berkeley’s last and most thorough treatment of the topic.
Berkeley has two lines of criticism of absolute space and in turn absolute motion. The first is a general argument from his theory of language; the second responds to Newton’s demonstration of absolute space. On the first line of criticism, imagine all bodies in the universe being destroyed. Supposedly what remains is absolute space. All its qualities (infinite, immovable, indivisible, insensible and without relation and distinction) are negative qualities (DM ϸ53). There is one exception. Absolute space is extended, a positive quality. But Berkeley asks what kind of extension can neither be measured nor divided nor sensed nor even imagined? He concludes that absolute space is pure negation, a mere nothing. The term “absolute space” fails to refer to anything since it is neither sensible nor imaginable (DM ϸ53). This reasoning is similar to the argument against forces, though absolute space has no instrumental value in theorizing.
In the second line of criticism, two thought experiments of Newton designed to demonstrate the existence of absolute space and motion are examined. Though Newton admitted that absolute space was insensible, he thought it could be known through its effects. It was essential that Berkeley take up these experiments. Even though the first line of criticism showed, if cogent, that ‘absolute space’ fails to name anything in nature, further argument was required to show that it was not needed, even instrumentally, for an adequate physical account of motion.
The first thought experiment involves two globes attached by a cord spinning in circular motion. No other physical bodies exist. There is no relative motion of the globes but there is a tension in the cord. Newton believes the tension is a centrifugal effect and is explained by the globes being in motion with respect to absolute space. Berkeley’s response is to deny the conceivability of the experiment. The circular motion of the globes “cannot be conceived by the imagination” (DM ϸ59). In other words, given Newton’s description of the experiment there can be no motion of the globes. Berkeley then supposes that the fixed stars are suddenly created. Now the motion of the globes can be conceived as they approach and move away from different heavenly bodies. As for the tension in the cord, Berkeley does not speak to it. Presumably, there is no tension or motion until the stars are created.
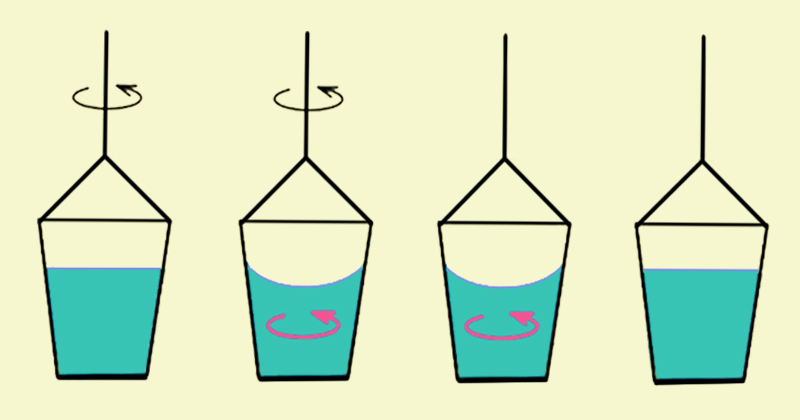
In the much-discussed second thought experiment, a bucket half-filled with water is suspended from a tightly twisted cord. In Phase 1 the bucket is allowed to start spinning. The surface remains a plane and the sides of the bucket accelerate relative to the water. In Phase 2 the water rotating catches up with the bucket sides and is at rest relative to them. Now the surface of the water is concave having climbed the sides of the bucket. In Phase 3 the bucket is stopped. The water remains concave and is accelerated relative to the sides of the bucket. In Phase 4 the water ceases to rotate and is at rest relative to the sides.
On Newton’s understanding, the shape of the water does not depend on the water’s motion relative to the sides of the bucket. It is a plane in Phase 1 and Phase 4 and concave in Phase 2 and Phase 3. However, the concave shape of the water demands explanation. A force must be responsible for it. According to his second law (the force acting on an object is equal to the mass of the object times its acceleration), a force indicates an acceleration. Since the acceleration is not relative to the bucket sides, it must be relative to absolute space (Nagel 207-209).
Figure 4: Relevant phases in bucket experiment.
Berkeley has a response. Given a body moving in a circular orbit, its motion at any instant is the result of two motions: One along the radius and one along the tangent of the orbit. The concave shape of the water in phase 2 is due to an increase of the tangential forces on the particles of water without a corresponding force along its radius. Though Berkeley’s account of the deformation of the water by factors internal to the bucket system is an appropriate strategy for undermining Newton (showing that absolute space is unnecessary), it fails because his alternative explanation does not in fact correctly explain the deformation (Suchting 194-195, Brook 167-168).
Following Berkeley’s “solution” to the bucket experiment, he points out that given relative space, a body may be in motion relative to one frame of reference and at rest with respect to another. To determine true motion or rest, remove ambiguity, and to serve the purposes of natural philosophers in achieving a widely applicable account of motion, the fixed stars regarded at rest will serve admirably. Absolute space will not be needed (DM ϸ64).
The fixed stars are not explicitly invoked to account for the centrifugal effect in the bucket experiment as they were in the two globes experiment. It is a promising solution available to Berkeley. Karl Popper and Warren Asher, among others, assume that Berkeley understands it as a cogent response to the bucket experiment (Popper 232, Asher 458).
d. General Anti-Realism Arguments
In two very brief passages, one in De Motu and one in Siris, Berkley appears to offer arguments that would undermine realism not only for corpuscles, but for all theoretical entities. These arguments are difficult to interpret given that they are not amplified in any other works. They are intriguing for they hint at widely discussed issues in contemporary philosophy of science.
Berkeley briefly examines a pattern of inference, the hypothetico-deductive method, commonly used to justify theoretical hypotheses. The pattern of inference, as he understands it, is to derive certain consequences, C, from a hypothesis, H. If the consequences are born out (observed to occur), then they are evidence for H. Berkeley expresses skepticism that the method allows for the discovery of “principles true in fact and nature” (S ϸ228). He defends his position by making a logical point and giving an example: If H implies C, and H is true, then one can infer C. But from H implies C and C, one cannot infer H. The Ptolemaic systems of epicycles has as a consequence the movements of the planets. This, however, does not establish the truth of the Ptolemaic system.
Berkeley’s description of the hypothetico-deductive method is overly simplified. In actual scientific practice many factors are considered in accepting a hypothesis, including the number of positive predictions, the existence of negative predictions, the riskiness of the predictions, plausibility of competing hypotheses, and the simplicity of the hypothesis. Nevertheless, the method in its most refined form does not guarantee the truth of the hypothesis under consideration. If this is Berkeley’s point, it is well taken. A certain caution is warranted. But if anti-realism is to follow from the lack of certainty that the hypothesis is true, additional argument is required, including how corpuscularianism escapes anti-realism.
The passage is important in another regard. It reinforces Berkeley’s pragmatic understanding of explanation. Though the Ptolemaic system is not “true in fact”, it “explained the motions and appearances of the planets” (S ϸ238). Whether true or not, it has significant predictive power. It helps us expect how the planets will move.
A fascinating and complex passage in De Motu (section 67) has been interpreted by at least one commentator as offering an argument for instrumentalism based on the underdetermination of theory by data (Newton-Smith). For any theory, T, there is another theory, T*. T and T* are both about the same subject manner, logically incompatible, and fit all possible evidence. This lands in skepticism. Which theory is true is beyond our grasp. Berkeley cannot accept this result. A chief motivation for his philosophical system is to avoid skepticism. Skepticism, for Berkeley, is the thesis that our sense experience is not reliable. It is insufficient to determine the true nature of physical reality and often outright misleads us as to that reality. According to the underdetermination thesis, despite complete observational evidence (evidence provided by the senses) the correct theory can still not be sorted.
But given instrumentalism, the skeptical consequences of the underdetermination thesis can be avoided. Since theories are understood as calculating devices, not a set of propositions that are true or false, logical incompatibility can be avoided, and skepticism as well.
In an effort to strengthen his instrumental account of forces, Berkeley does appear to offer an underdetermination argument. “…great men advance very different opinions, even contrary opinions…and yet in their results attain the truth” (DM ϸ67). He provides an illustration: When one body impresses a force on another, according to Newton, the impressed force is action alone and does not persist in the body acted upon. For Torricelli, the impressed force is received by the other body and remains there as impetus. Both theories fit the observational evidence.
A sketch of one example hardly establishes the underdetermination thesis; an argument for the underdetermination thesis is needed. Perhaps a crucial experiment will settle the Newton/Torricelli disagreement. Perhaps the two theories differ only verbally.
Berkeley was aware that at certain moments in the history of science two or more competing theories were consistent with the known evidence, but it is a much stronger thesis to claim that the theories are compatible with all possible evidence. Although there is no textual indication that Berkeley holds this strong thesis, without it, the argument from underdetermination for instrumentalism fails.
Margaret Atherton provides an alternative to Newton-Smith’s analysis (Atherton 248-250). She does not see Berkeley employing the underdetermination thesis. Rather he is explicating how natural philosophers use mathematical hypotheses. Newton and Torricelli “attain the truth” while supposing contrary theoretical positions on how motion is communicated.
Despite Newton and Torricelli sharing the same set of observations—the same sense-based descriptions of how bodies actually move, “They use different pictures to describe what links instances of this sort together….” (Atherton 249). The same regularities are discovered regardless of which picture is operative.
This raises questions about the cognitive status of the pictures. Do they differ only verbally? Are they shorthand descriptions for the movements of bodies? If they are genuinely different calculating devices what guarantees that they will continue to fit or predict the same future observations? How to understand De Motu ϸ67 as well as Siris ϸ228 remains contentious.
6. References and Further Reading
- Armstrong, David. “Editor’s Introduction” in Berkeley’s Philosophical Writings, edited by David Armstrong, Collier Books, New York, 1965, pp 7-34.
- Contains a very brief introduction to the whole of Berkeley’s philosophy including his philosophy of science.
- Asher, Warren O. “Berkeley on Absolute Motion.” History of Philosophy Quarterly. 1987, pp 447-466.
- Examines the differing accounts of absolute motion in the Principles and De Motu.
- Atherton, Margaret. “Berkeley’s Philosophy of Science” in The Oxford Handbook of Berkeley, edited by Samuel C. Rickless, Oxford University Press, Oxford, 2022, pp 237-255.
- Berkeley, George. Philosophical Works, Including the Works on Vision. Edited by Michael R. Ayers. Everyman edition. London: J.M. Dent, 1975.
- This is a readily available edition of most of Berkeley’s important works. When a text is without section numbers the marginal page numbers refer to the corresponding page in The Works of George Berkeley.
- Berkeley, George. The Works of George Berkeley, Bishop of Cloyne. Edited by A.A. Luce and T.E. Jessop. Nine volumes. London: Thomas Nelson and Sons, 1948-1957.
- Standard edition of Berkeley’s works. All references are to this edition.
- Brook, Richard. “DeMotu: Berkeley’s Philosophy of Science” in The Bloomsbury Companion to Berkeley, edited by Richard Brook and Bertil Belfrage, Bloomsbury, London, 2017, pp 158-173.
- Brief survey of Berkeley’s philosophy of science. Includes references to important scholarly work on the topic.
- Dear, Peter. Revolutionizing The Sciences. Second Edition. Princeton University Press, Princeton, 2009.
- Downing, Lisa. “Berkeley’s Case Against Realism about Dynamics” in Berkeley’s Metaphysics: Structural, Interpretive, and Critical Essays, edited by Robert Muehlmann, Pennsylvania State University press, University Park, PA, 1996, pp 197-214.
- Detailed treatment of Berkeley’s antirealism for Newtonian forces.
- Downing, Lisa. “Berkeley’s Natural Philosophy and Philosophy of Science” In The Cambridge Companion to Berkeley, edited by Kenneth P. Winkler, Cambridge University Press, Cambridge, 2005, pp 230-265.
- Downing, Lisa. “’Siris’ and the Scope of Berkeley’s Instrumentalism”. British Journal for the History of Philosophy, 1995, 3:2, pp 279-300.
- Looks at the realism/antirealism issue in the context of Siris. Argues that corpuscular theories are not subject to the anti-realism consequences of the hypothetico-deductive method.
- Flage, Daniel E. “Berkeley” in Internet Encyclopedia of Philosophy.
- Provides a broad discussion of Berkeley’s philosophy.
- Garber, Dan. “Locke, Berkeley, and Corpuscular Scepticism” in Berkeley: Critical and Interpretative Essays, edited by Colin M. Turbayne, University of Minnesota Press, Minneapolis, 1982, pp 174-194.
- Defense of realism for corpuscles in Berkeley.
- Hempel, Carl. “Deductive-Nomological versus Statistical Explanation” in The Philosophy of Carl G. Hempel, edited by James H. Fetzer, Oxford University Press, New York, 2001, pp 87-145.
- Jobe, Evan K. “A Puzzle Concerning D-N Explanation”. Philosophy of Science, 43:4, pp 542-547.
- Lorkowski, C. M. “David Hume: Causation” in Internet Encyclopedia of Philosophy.
- Thorough discussion of Hume’s account of causation.
- Marcum, James A. “Thomas S. Kuhn” in Internet Encyclopedia of Philosophy.
- Reviews the work of historian and philosopher of science Thomas Kuhn. Kuhn was instrumental in initiating a historiographical turn for many philosophers of science. His work challenged prevailing views on the nature of science, especially accounts of scientific change.
- Nagel, Ernest. The Structure of Science. Harcourt, Brace and World, New York, 1961.
- Classic introduction to the philosophy of science. Excellent on the cognitive status of theories of space and geometry.
- Newton-Smith, W. H. “Berkeley’s Philosophy of Science” in Essays on Berkeley, edited by John Foster and Howard Robinson, Clarendon Press, Oxford, 1985, pp 149-161.
- Argues that Berkeley gives an argument for instrumentalism from the underdetermination of theories.
- Pearce, Kenneth L. “Berkeley’s Theory of Language” in The Oxford Handbook of Berkeley, edited by Samuel C. Rickless, Oxford University Press, Oxford, 2022, pp 194-218.
- Discusses four accounts of Berkeley’s theory of language. Defends the use theory.
- Pitcher, George. Berkeley. Routledge & Kegan Paul, London, 1977.
- Account of Berkeley’s main philosophical positions.
- Popper, Karl. “A Note on Berkeley as Precursor of Mach and Einstein” in Conjectures and Refutations, Routledge, London, 2002, pp 224-236.
- Early explication of Berkeley’s instrumentalism by an influential philosopher of science.
- Suchting, W. A. “Berkeley’s Criticism of Newton on Space and Motion”. Isis, 58:2, pp 186-197.
- Warnock, G.J. Berkeley. Penguin Books, Baltimore, 1953.
- Introduction to Berkeley’s thought.
- Wilson, Margaret D. “Berkeley and the Essences of the Corpuscularians” in Essays on Berkeley, edited by John Foster and Howard Robinson, Clarendon Press, Oxford, 1985, pp 131-147.
- Raises concerns about interpreting Berkeley as a scientific realist for corpuscles.
- Winkler, Kenneth. Berkeley An Interpretation. Clarendon Press, Oxford, 1989.
- Thorough discussions of both the continuity of physical objects and corpuscularianism.
Author Information
A. David Kline
Email: akline@unf.edu
University of North Florida
U. S. A.