Charles Sanders Peirce: Logic

Charles Sanders Peirce (1839-1914) was an accomplished scientist, philosopher, and mathematician, who considered himself primarily a logician. His contributions to the development of modern logic at the turn of the 20^th century were colossal, original and influential. Formal, or deductive, logic was just one of the branches in which he exercized his logical and analytical talent. His work developed upon Boole’s algebra of logic and De Morgan’s logic of relations. He worked on the algebra of relatives (1870-1885), the theory of quantification (1883-1885), graphical or diagrammatic logic (1896-1911), trivalent logic (1909), higher-order and modal logics. He also contributed significantly to the theory and methodology of induction, and discovered a third kind of reasoning, different from both deduction and induction, which he called abduction or retroduction, and which he identified with the logic of scientific discovery.

Philosophically, logic became for Peirce a broad discipline with internal divisions and external architectonic relations to other parts of scientific inquiry. Logic depends upon, or draws its principles from, mathematics, phaneroscopy (=phenomenology), and ethics, while metaphysics and psychology depend upon logic. One of the most important characters of Peirce’s late logical thought is that logic becomes coextensive with semeiotic (his preferred spelling), namely the theory of signs. Peirce divides logic, when conceived as semeiotic, into (i) speculative grammar, the preliminary analysis, definition, and classification of those signs that can be used by a scientific intelligence; (ii) critical logic, the study of the validity and justification of each kind of reasoning; and (iii) methodeutic or speculative rhetoric, the theory of methods. Peirce’s logical investigations cover all these three areas.

Logic among the Sciences
Logic as Semeiotic
Peirce’s Logic in Historical Perspective
References and Further Reading

1. Logic among the Sciences

Peirce’s idea of logic is guided by finding the location of logic in the map of the sciences. Peirce’s mature classification of the sciences (CP 1.180-202, 1903; see Brent 1987), which is a “ladder-like scheme” (MS 328, p. 20, c. 1905), takes superordinate sciences to provide principles to subordinated sciences, forming a ladder of decreasing generality.

According to Peirce’s 1903 scheme, which he as late as 1911 considered a satisfactory account (MS 675), sciences are either sciences of discovery, sciences of review, or practical sciences. Logic is a science of discovery. The sciences of discovery are divided into mathematics, philosophy and idioscopy. Mathematics studies the necessary consequences of purely hypothetical states of things. Philosophy, by contrast, is a positive science, concerning matters of fact. Idioscopy embraces more special physical and psychical sciences, and depends upon philosophy. Philosophy in turn divides into phaneroscopy, normative sciences and metaphysics. Phaneroscopy is the investigation of what Peirce calls the phaneron: whatever is present to the mind in any way. The normative sciences (aesthetic, ethics, and logic) introduce dichotomies, in that they are, in general, the investigation of what ought and what ought not to be. Metaphysics gives an account of the universe in both its physical and psychical dimensions. Since every science draws its principles from the ones above it in the classification, logic must draw its principles from mathematics, phaneroscopy, aesthetics and ethics, while metaphysics, and a fortiori psychology, draw their principles from logic (EP 2, pp. 258-262, 1903).

In sharp contrast to the logicist hypothesis, Peirce did not believe that mathematics depends upon deductive logic. On the contrary, in a sense it is deductive logic that depends upon mathematics. For Peirce, mathematics is the practice of deduction, logic its description and analysis: Peirce’s father Benjamin Peirce had defined mathematics as the science which draws necessary conclusions (B. Peirce 1870, p. 1). Hence deductive logic for Charles became the science of drawing necessary conclusions (CP 4.239, 1902). Logic cannot furnish any justification of a piece of deductive reasoning: deduction in general is in the first place mathematically, rather than logically, valid. And deductive logic is at any rate only a part of logic: “logic is the theory of all reasoning, while mathematics is the practice of a particular kind of reasoning” (MS 78, p. 4; see Haack 1993 and Houser 1993). Logic rather draws its principles from phaneroscopy, as the latter analyzes the structure of appearance but does not pronounce upon the veracity of such appearance. Logic also draws its principles from the normative sciences of ethics and esthetics (Peirce’s preferred spelling), which precede normative logic in the ladder of generality. Ethics depends on esthetics because ethics draws from esthetics the principles involved in the idea of a summum bonum, the highest good. Since ethics is the science that distinguishes good from bad conduct, it must be concerned with deliberate, self-controlled, conduct, because only by deliberate conduct is it possible to say whether the conduct is good or bad. Logic treats of a special kind of deliberate conduct, thought, and distinguishes good from bad thinking, that is, valid from invalid reasoning. Since deliberate thought is a species of deliberate conduct, logic must draw its principles form ethics (CP 5.120-50; EP 2, pp. 196-207, 1903)

Of the sciences down the ladder of generality, metaphysics and psychology come out next. Peirce had learnt from Kant that metaphysical conceptions mirror those of formal logic. Peirce’s criticism ever since the 1860s had been that Kant’s table of categories was mistaken not because he based them upon formal logic but because the formal logic that Kant had used was itself poor and ultimately wrong (see NEM 4, p. 162, 1898). The only way to arrive at a good metaphysics is to begin with a good logical theory (EP 2, pp. 30-31, 1898). Psychology, too, depends upon logic. According to Peirce, different versions of logical psychologism characterized the logics of his time, especially in Germany. Logic for Peirce considers not what or how we in fact think but how we ought to think; logic is a normative, not a descriptive, science. The validity of an argument consists in the fact that its conclusion is true, always or for the most part, when its premises are true; it has nothing to do with reference to a mind. Logical necessity is a necessity of (non-empirical) facts, not a necessity of thinking. No appeal to psychology is thereby of any aid in logic. On the contrary, it is psychology that stands in the need of a science of logic (EP 2, pp. 242-257, 1903).

2. Logic as Semeiotic

In the 1890s (MS 595, 787), Peirce divided logic into three branches: speculative grammar (also called stechiology), logical critics (or just critics) and methodeutic (also called speculative rhetoric). The division echoes the three sciences of the medieval Trivium: grammar, dialectic and rhetoric.

Perhaps the most salient character of Peirce’s logic as a whole is that in his later works (MS L 75, 1902; MS 478, 1903; MS 693, 1904; MS 640, 1909) logic is identified with semeiotic, the science and philosophy of signs and representations. Already in his early works on the theory of inference Peirce had affirmed that logic is the branch of semeiotic that treats of one particular kind of representations, namely symbols, in their reference to their objects (W1, p. 309, 1865). By the beginning of the 20^th-century, he had shifted from the idea of “logic-within-semeiotic” to that of “logic-as-semeiotic.” He thus needed to distinguish between logic in the narrow sense, which he now calls logical critics, and logic in the wide sense; the latter is made coextensive with semeiotic. “Logic, in its general sense, is, as I believe I have shown, only another name for semiotic (σημειωτική), the quasi-necessary, or formal, doctrine of signs” (CP 2.227, c.1897; cf. Fisch 1986, pp. 338-341).

According to Peirce’s mature views, an enlargement of logic to cover all varieties of signs was a valuable methodological guidance to the building of an objective, anti-psychological and formal logical theory: “The study of the provisional table of the Divisions of Signs will, if I do not deceive myself, help a student to many a lesson in logic” (MS S 46, 1906; cf. MS 283, c. 1905; MS 675-676, 1911; MS 12, 1912). Therefore, his logic contains, as a proper part of it, a study of its own scope and expansions. In homage to Thomas of Erfurt’s grammatica speculativa, which at Peirce’s times was misattributed to Duns Scotus, Peirce names this part of logic “speculative grammar.”

a. Speculative Grammar

In the 1890s Peirce regarded speculative grammar as an analysis of the nature of assertion (MS 409-8, 1894; CP 3.432, 1896, MS 787, c. 1897). Starting with the Syllabus of his 1903 Lowell Lectures (A Syllabus of Certain Topics of Logic, MS 478, MS 540), speculative grammar becomes a classification of signs. In the Syllabus Peirce defines a Sign or Representamen as

the first Correlate of a triadic relation, the second Correlate being termed its Object, and the possible Third Correlate being termed its Interpretant, by which triadic relation the possible Interpretant is determined to be the first correlate of the same triadic relation to the same Object, and for some possible Interpretant. (MS 540, CP 2.242; EP 2, p. 290).

A sign for Peirce is something that represents an independent object and which thereby brings another sign, called interpretant, to represent that object as the sign does. According to a long tradition in the history of logic, Peirce declares that the principal classes of signs that logic is concerned with are terms, propositions, and arguments. But by 1903 these three elements become parts of a larger taxonomic scheme.

Since the Syllabus and until at least 1909 Peirce continued experimenting with principles and terminologies, without however settling on any definitive division. This section presents the main principles of the Syllabus classification.

Signs are divisible by three trichotomies; first, according as the sign in itself is a mere quality, is an actual existent, or is a general law; secondly, according as the relation of the sign to its Object consists in the sign’s having some character in itself, or in some existential relation to that Object, or in its relation to an Interpretant; thirdly, according as its Interpretant represents it as a sign of possibility, or as a sign of fact, or a sign of reason. (CP 2.243, 1903)

The first trichotomy considers signs as (i) tones, when taken in their material qualities (such as the blueness of the ink), as (ii) tokens (such as any instance of the word “the”), and as (iii) general types (such as the word “the”). The second trichotomy is the best known, namely that of (i) icons, or signs that bear similarity or resemblance to their objects, (ii) indices, which have factual connections to their objects, and (iii) symbols, which have rational connections to their objects. The third trichotomy divides signs into terms, propositions, and arguments: Through his work on the logic of relatives (see § 2.b.iii.), Peirce had come to consider the terms as (i) rhemas, which are unsaturated predicates with logical bonds or subject-positions, in some ways similar to Frege’s Begriff and Russell’s propositional function; (ii) propositions, which unify subject and predicate and thus assert, or as in the Syllabus are dicisigns, signs that tell, and (iii) arguments, which embody the ultimate perfection and end of signs as a representation of facts that are signs of other facts, such as the premises being the sign of the conclusion. [Peirce’s theory of the proposition is articulated and highly original and has been thoroughly investigated in Hilpinen 1982, 1992; Ferriani 1987; Chauviré 1994; Stjernfelt 2014.]

There are cross-divisions of these three trichotomies across speculative grammar. A term or rhema is a symbol which is represented by its interpretant as an icon of its object, while a proposition or dicisign is a symbol which is represented by its interpretant as an index of its object. Arguments themselves are considered as symbols that represent their conclusion in three different ways: iconically in abduction, indexically in deduction, and symbolically in induction. (In an early cross-division proposed in 1867 these last two were interchanged. See W2, p. 58). Other outcomes of the classifications consisted in further divisions of objects and interpretants into various subtypes. [For more on Peirce’s classifications, see Weiss & Burks 1945; Short 2007, chs. 7-9; and Burch 2011.]

Grammatical taxonomy shows that there are three kinds of arguments, each manifesting a different semiotic principle. But it is up to the second branch of logic, critics, to investigate the question of logical validity and justification of such arguments. The analysis of the conditions of validity of these three kinds of reasoning is a critical, not grammatical, question.

b. Logical Critics

i. From Three Types of Inference to Three Stages of Inquiry

Logical critics is the heart of Peirce’s logic. It cover what usually goes under the name of logic proper, that is, the investigation of inference and arguments. Many 19^th-century logicians (for example, John S. Mill, George Boole, John Venn and William Stanley Jevons) took the range of logic to include deductive as well as inductive logic. As appears from the classification, the remarkable novelty of Peirce’s logical critics is that it embraces three essentially distinct though not entirely unrelated types of inferences: deduction, induction, and abduction. Initially, Peirce had conceived deductive logic as the logic of mathematics, and inductive and abductive logic as the logic of science. Later in his life, however, he saw these as three different stages of inquiry rather than different kinds of inference employed in different areas of scientific inquiry.

Peirce had formulated a definite theory of logical leading principles early in the late 1860s. His argument is roughly as follows. In any inference, we pass from some fact to some other fact that follows logically from it. The former is the premise (for in cases where there is more than one they may be colligated or compounded into one copulative premise), the latter is the conclusion.

P
∴C

The conclusion follows from the premise logically, that is, according to some leading principle, L. As logic supposes inferences to be analyzed and criticized, as soon as the logician asks what is it that warrants the passing from such premise to the conclusion she is obliged to express the leading principle L in a proposition and to lay it down as an additional premise:

P
L
∴C

This gives what Peirce calls a complete argument, in opposition to incomplete, rhetorical or enthymematic arguments. This second argument has itself its own leading principle L₁, which may again be expressed in a proposition and laid down as a further premise:

P
L
L₁∴C

When L₁is not a substantially different leading principle than L, then L is said to be a logical leading principle. In Peirce’s words:

This second argument has certainly itself a leading principle, although it is a far more abstract one than the leading principle of the original argument. But you might ask, why not express this new leading principle as a premise, and so obtain a third argument having a leading principle still more abstract? If, however, you try the experiment, you will find that the third argument so obtained has no more abstract a leading principle than the second argument has. Its leading principle is indeed precisely the same as that of the second argument. This leading principle has therefore attained a maximum degree of abstractness; and a leading principle of maximum abstractness may be termed a logical principle. (NEM 4, p.175, 1898)

A logical leading principle is therefore a formal or logical proposition which, when explicitly stated, adds nothing to the premises of the inference which it governs. The central question of logical critics becomes that of determining different kinds of logical leading principles.

Peirce’s initial strategy to prove that there are three and only three irreducible kinds of reasoning was to use syllogism. He gave the demonstration that the second and the third figure are reducible to the first only through the employment of the very figure that is to be reduced. The principles involved in the three syllogistic figures cannot then be reduced to a combination of other, more primitive principles, as they invariably enter as parts into the reduction proof itself. From this Peirce drew the broader conclusion that the three figures of syllogism correspond to the three kinds of inference in general: deduction corresponds to the first figure, abduction to the second, and induction to the third:

In Peirce 1878 and Peirce 1883, abduction and induction are described as inversions of a deductive syllogism. If we call the major premise of a syllogism in the first figure Rule, its minor premise Case, and its conclusion Result, then abduction may be said to be the inference of a Case from a Result and a Rule, while induction may be said to be the inference of a Rule from a Case and a Result:

Later in 1903 Peirce had come to the conclusion that the three kinds of reasoning are in fact three stages in scientific research. First comes abduction, now often also called retroduction, by which a hypothesis or conjecture that explains some surprising fact is set forth. Then comes deduction, which traces the necessary consequences of the hypothesis. Lastly comes induction, which puts those consequences to test and generalizes its conclusions.

Any inquiry is for Peirce bound to follow this pattern: abduction–deduction–induction. Each kind of inference retains its validity and modus operandi and is logically irreducible to either of the others; yet all three of them are necessary in any complete process of inquiry. Of the three methods, Peirce took deduction to be the most secure and the least fertile, while abduction is the most fertile and the least secure.

All these three departments of critics epitomize the originality of Peirce’s contributions. The following sections deals with Peirce’s abductive, deductive, and inductive logics, respectively.

ii. Abductive Logic

The central question of abductive or retroductive logic is: is there a logic of scientific discovery? If yes, what are its justification and method?

Initially, Peirce described abduction as the inference of a Case from a Rule and a Result:

Hypothesis proceeds from Rule and Result to Case; it is the formula of the […] process by which a confused concatenation of predicates is brought into order under a synthetizing predicate. (Peirce 1883, p. 145)

Its general formula is this:

Result: S is M₁ M₂ M₃ M₄Rule: P is M₁ M₂ M₃ M₄Case: Therefore, S is P.

A certain number of surprising facts have been observed which call for explanation, and a single predicate embracing all of them is found which would explain them. When I notice that light manifests such-and-such complicated and surprising phenomena, and I know that ether waves exhibits those same phenomena, I conclude abductively that, if light were ether waves, it would be normal for it to manifest those phenomena. This offers rational ground for the hypothesis that light is ether waves.

In 1900, Peirce began viewing this description of abduction as inadequate. What he in 1883 had called hypothesis or abduction was actually induction about characters instead of things and is therefore better to be called qualitative induction (see § 2.b.iv): its leading principle is inductive and not abductive. Abduction is no longer constrained by the syllogistic framework. Most generally, it is the non-inductive process of forming an explanatory hypothesis. In Peirce’s words, abduction “is the only logical operation which introduces any new idea” (CP 5.172, 1903). Although abduction asserts its conclusions only conjecturally, it has a definite logical form. The following has become its standard, albeit not the ultimately satisfactory, description after Peirce’s pronouncement of it in the seventh of the Harvard Lectures of 1903:

The surprising fact, C, is observed;
But if A were true, C would be a matter of course,
Hence, there is reason to suspect that A is true. (CP 5.189, 1903)

This schema reveals why abduction is also called retroduction: it is reasoning that leads from a consequent of an admitted consequence to its antecedent.

Another description of the logical form of abduction is contained in a later, unpublished manuscript:

In the inquiry, all the possible significant circumstances of the surprising phenomenon are mustered and pondered, until a conjecture furnishes some possible Explanation of it, by which I mean a syllogism exhibiting the surprising fact as necessarily following from the circumstances of its occurrence together with the truth of the conjecture as premisses. (MS 843, p. 41, 1908)

The explaining syllogism is the inversion of the 1903 formula:

If A were true, C would be observable.
A is true.
Therefore, C is observable.

One more and hitherto unknown formulation of retroduction is found in an unpublished letter to Lady Welby:

[The] “interrogative mood” does not mean the mere idle entertainment of an idea. It means that it will be wise to go to some expense, dependent upon the advantage that would accrue from knowing that Any/Some S is M, provided that expense would render it safe to act on that assumption supposing it to be true. This is the kind of reasoning called reasoning from consequent to antecedent. For it is related to the Modus Tollens thus:

Instead of “interrogatory”, the mood of the conclusion might more accurately be called “investigand”, and be expressed as follows:

It is to be inquired whether A is not true.

The reasoning might be called “Reasoning from Surprise to Inquiry..” (Peirce to Welby, July 16, 1905, LoF, pp. 907-908)

The whole course of thought, consisting in noticing the surprising phenomenon, searching for pertinent circumstances, asking a question, forming a conjecture, remarking that the conjecture appears to explain the surprising phenomenon, and adopting the conjecture as plausible, constitutes the first, abductive stage of inquiry. Nonetheless, its crucial phase is that of forming the conjecture itself. This is often described by Peirce as an act of insight, or an instinct for guessing right, or what Galileo called il lume naturale. [That Peirce actually got the phrase from Galileo has sometimes been contested. But see the story by Victor Baker in Bellucci, Pietarinen & Stjernfelt (2014) on the “Myth of Galileo.” Baker refers to Jaime Nubiola’s finding of Peirce’s copy of Galileo’s Opere that had that phrase underlined in Peirce’s hand. That fifteen volumes edition was at least in 2012 still to be found at the Robbins Library at the Department of Philosophy, Harvard University.]

However, to pronounce reasoning to be instinctive would amount to excluding it from the realm of logic. For logic only considers reasoning, and reasoning is a deliberate act subject to self-control. According to Peirce, abduction is an inference type based upon a logical principle. In its most abstract shape, such logical principle gives abduction its justification, and the justification of abduction is the bottom question of logical critics (EP 2, p. 443, 1908).

According to Peirce, abduction “consists in studying the facts and devising a theory to explain them” (CP 5.145, 1903). Its only justifications are that “if we are ever to understand things at all, it must be in that way,” and that “its method is the only way in which there can be any hope of attaining a rational explanation” (CP 2.777, 1902). The only justification for a hypothesis is that it might explain the facts. But in general, an inference is valid if its leading principle is an instance of a logical principle which is conducive to the acquisition of new information. Therefore, the logical leading principle of all abductions is that nature, in general, is explainable. To suppose something inexplicable is contrary to the principles of logic: such supposition only has the appearance of an explanation conducive to the acquisition of new information, but to really suppose something inexplicable is to renounce knowledge.

That nature is explicable is therefore the primary abduction underlining all possible abductions. Human powers of insight may well be justified also inductively, that is, as testified by the history of science. But abduction’s primary justification is abductive rather than inductive: if we are to acquire new knowledge at all, sooner or later we must reason abductively. [See Bellucci & Pietarinen 2014; Burks 1946; Fann 1970; Kapitan 1992; Kapitan 1997; Paavola 2004 for further details on Peirce’s theory of abduction or retroduction, and Ma & Pietarinen 2015 for a dynamic logic approach to Peirce’s interrogative abduction.]

Of these three stages of reasoning, abduction is the most fertile but the least secure. For this reason, Peirce affirms that abduction is the principal kind of reasoning in which, after logical critics has pronounced it valid, it remains to be inquired whether and how it is advantageous. To carry out such tasks pertains to the third branch of logic, methodeutic, which is discussed in § 2.c below.

iii. Deductive Logic

The works of George Boole and Augustus De Morgan provided the essential backdrop for Peirce’s development of deductive logic. Also Benjamin Peirce’s Linear Associative Algebra (B. Peirce 1870) influenced his son’s early development of algebraic logic of relatives. Peirce’s dissatisfaction with how Boole represented syllogisms as algebraic equations led him to develop new algebraic approaches to logic, which he did by combining Boole’s calculus (Boole 1847, 1854) with De Morgan’s treatment of relations (De Morgan 1847, 1860).

Some of Peirce’s most important contributions to the development of modern logic are highlighted below.

1867: In the paper “An Improvement in Boole’s Calculus of Logic” published in the Proceedings of the American Academy of Arts and Sciences (Peirce 1867), Peirce subscribed all operation symbols with a comma to differentiate the logical from the arithmetical interpretation. He also made Boole’s union operator inclusive rather than exclusive (he was anticipated in this by Jevons 1864). Peirce became aware of the limitations of Boole’s algebraic logic, such as that it cannot express categorical propositions (Some X is Y), so it fails to properly represent quantification.

1870: Peirce’s development of De Morgan’s theory of relations is fully exposed in his paper “Description of a Notation for the Logic of Relatives, resulting from an Amplification of the Conceptions of Boole’s Calculus of Logic” (Peirce 1870), which was communicated to the American Academy of Arts and Sciences in January 1870. In this paper, Peirce combines De Morgan’s theory with Boole’s calculus. The result is a logical algebra equivalent in expressive power to first-order predicate logic without identity. Peirce’s paper introduces a number of original innovations. Among them is a new process of logical differentiation, explained in Welsh (2012, pp.166-180). Peirce also introduces the copula of inclusion, , later also termed the sign of illation and expressed in cursive form as . Inclusion is for Peirce a wider and logically simpler concept than that of equality. This difference marks another important departure from Boole’s mathematical algebra towards new types of logical algebras. Beginning with C. I. Lewis’s (1918) comments on Peirce’s algebra, the literature has discussed whether in this 1870 paper what Peirce calls relative terms are to be equated with relations (see Merrill 1997 for a summary and further references). It appears that in the very least they are what verbs and phrases express linguistically, such as lover of___, whatever is a lover of____, or buyer of____for____from____. Here blanks stand for nouns that are required to complete the expressions. Beginning in 1882, Peirce comes to define relative terms as classes of ordered pairs ( later understood as being relations). He denotes such terms by rhemas with blanks for expressions standing for subjects, such as ____is a lover of____, whatever____is a lover of____ and so forth. Of note is that the algebra of Peirce’s 1870 paper is able to express various forms of quantification although the term “quantifier” and its modern conception was to emerge only later in his works after the early 1880s.

1880a: The long paper “On the Algebra of Logic” (Peirce 1880a), which was published in the American Journal of Mathematics, introduces a number of further developments of which the following six are listed here:

(1) The copula, expressed as a binary relation between classes of propositions, P_i C_i, is now understood to express the notion of the semantic consequence, namely that “every state of things in which a proposition of the class P_i is true is a state of things in which the corresponding propositions of the class C_i are true” (W4, p. 166). The binary relation here is thus a truth-functional implication. Moreover, the remarks in his Logic Notebook published in W4 (p. 216) were written in the same year and appear to be the first instance presenting variables v and f to denote the truth values true and false.

(2) A dash over a symbol is used to denote a negative of the symbol. A dash over the sign of illation in P_i C_i indicates the class complement. Constants ∞ and 0 are taken to mean the values of the possible and the impossible. An important modal component which Peirce would develop later on is thus emerging in this work.

(3) The totality of all that is possible is according to Peirce the “universe of discourse, and may be very limited,” that is, limited to that which “actually occurs,” rendering “everything which does not occur” impossible (W4, p. 170). The important idea of working with variable and restricted domains makes a marked difference not only to Frege who is well-known to have his logic to quantify over the entire “logical thought”, but also to Schröder, who though also working on the algebra of logic had nonetheless rendered Peirce’s 1885 (see below) algebra of logic so as to quantify, in a Fregean fashion, what Peirce had later in 1903 remarked to be “the whole universe of logical possibility” (MS 478, pp. 163-4).

(4) A new operation on relatives, which Peirce termed transaddition (º) is then introduced (W4, p.204). Taking two relatives, such as being lover of___ (l) and being servant of___ (s), their relative product ls denotes whatever is lover of a servant of___. Their transaddition l º s denotes whatever is not a lover of everything but servants of___, that is, it denotes a complement of the complements of the relative product of the two terms l and s.

(5) The 1880 paper is also the first in which the idea of a relative sum, which is the complement of the transaddition and which Peirce in 1882 will denote by the dagger (†), is employed. For example, l † s reads lover of everything but servants of___. Hence this 1880 paper marks a decisive move towards a theory of quantification which will see its emergence in his 1883 Note B in the Studies in Logic (see below) and which comes to be completed in his 1885 “Algebra of Logic” paper (see below).

(6) The 1880 paper also suggests a mathematical theory of lattices for the treatment of the algebra of logic (W4, pp. 183-188).

Arthur Prior (1958, 1964) showed that Peirce’s 1880 paper provides a complete basis for propositional logic.

1880b: In an unpublished manuscript (MS 378, Peirce 1880b) entitled “A Boolian Algebra with One Constant”, which still in 1926 was tagged “to be discarded” at the Department of Philosophy at Harvard University, Peirce reduces the number of logical operations to one constant. He states that “this notation … uses the minimum number of different signs … shows for the first time the possibility of writing both universal and particular propositions with but one copula” (W4, p.221). Peirce’s notation was later termed the Sheffer stroke, and is also well-known as the NAND operation, in Peirce’s terms the operation by which “[t]wo propositions written in a pair are considered to be both denied” (W4, p.218). In the same manuscript, Peirce also discovers what is the expressive completeness of the NOR operation, indeed today rightly recognized as the Peirce arrow.

1881: “On the Logic of Number” (Peirce 1881), published in American Journal of Mathematics and read before the National Academy of Sciences, was noted by Gerrit Mannoury (1909, pp. 51, 78) to be the first successful axiomatization of natural numbers. Shields (1981/2012) has shown Peirce’s axiom system to be equivalent to the better-known systems of Dedekind (1888) and Peano (1889). Peirce’s paper formulates, presumably for the first time, the notions of partial and total linear orders, recursive definitions for arithmetical operations, and the general definition of cardinal numbers in terms of ordinals. The paper also provides a purely cardinal definition of a finite set (Dedekind-finite) by checking whether De Morgan’s syllogism of transposed quantity is valid. [The syllogism of transposed quantity is expressed in the following mode of inference: Every Texan kills a Texan; Nobody is killed by but one person; Hence, every Texan is killed by a Texan.] Peirce then derives in this paper the latter property of finiteness from the ordinal one. Doing the converse assumes the axiom of choice.

During 1881-2, Peirce edited a book, published in 1883 and entitled Studies in Logic by Members of the Johns Hopkins University (Peirce 1883). It contained significant graduate work by his students Benjamin I. Gilman, Christine Ladd(-Franklin), Allan Marquand and Oscar Howard Mitchell. Peirce contributed to the volume a paper “A Theory of Probable Inference”, together with Note A, “A Limited Universe of Marks”, and Note B, “The Logic of Relatives.” Some developments in Mitchell’s paper as well as in Note B are worth highlighting.

Mitchell’s “On a New Algebra of Logic” was hailed by his teacher as “one of the greatest contributions that the whole history of logic can show” (MS 492; LoF, p. 225). Peirce attributed to Mitchell two major discoveries: first, the invention of the basic form of proof transformation and second, the interpretation of quantifiers in multiple dimensions, one of which is time. The former is similar to the resolution rule in logic programming, and consists of a series of insertions (by adding to premises) and erasures (by elimination of consequents). In Peirce’s words, “the passage from a premiss or premisses … to a necessary conclusion in the manner to which is alone usually called necessary reasoning, can always be reached by adding to the stated antecedents and subtracting from stated consequents, being understood that if an antecedent be itself a conditional proposition, its antecedent is of the nature of a consequent” (MS 905; LoF, pp. 731-732). The latter discovery—universes in multiple dimensions—has its correlate in the idea of interpreted domains and in the modern notion of temporal logics and many-sorted quantification. It can also be seen as a development of new languages that take the role of indices in the quantifiers to be mappings from contexts to values in universes of discourse. Having in mind Mitchell’s pioneering idea of logical dimensions, Peirce goes on to mention that the study of Mitchell’s paper was for him necessary in order to break “ground in the gamma [modal logic] part of the subject” of existential graphs (MS 467; LoF, p. 332; see below). Years later, Peirce defines the term “dimension” in the Dictionary of Philosophy and Psychology by noting that it is

an element or respect of extension of a logical universe of such a nature that the same term which is individual in one such element of extension is not so in another. Thus, we may consider different persons as individual in one respect, while they may be divisible in respect to time, and in respect to different admissible hypothetical states of things, etc. This is to be widely distinguished from different universes, as, for example, of things and of characters, where any given individual belonging to one cannot belong to another. The conception of a multidimensional logical universe is one of the fecund conceptions which exact logic owes to O. H. Mitchell. Schröder, in his then second volume, where he is far below himself in many respects, pronounces this conception ‘untenable’. But a doctrine which has, as a matter of fact, been held by Mitchell, Peirce, and others, on apparently cogent grounds, without meeting any attempt at refutation in about twenty years, may be regarded as being, for the present, at any rate, tenable enough to be held. (DPP 2, p. 27)

Mitchell develops, for the first time, the idea and the notation for existential and universal quantifiers, and notices that it is by from alternations of these quantifiers that logic derives its expressive power. Peirce testifies in the same dictionary entry that placing Σ and Π in alternating orders “was probably first introduced by O. H. Mitchell in his epoch-making paper” (DPP 2, p. 650). However, being limited to monadic predicates, Mitchell’s language was deprived of some expressive power.

Having supervised and perused Mitchell’s paper, in Note B of the Studies in Logic, Peirce generalizes the groundwork Mitchell had laid on the theory of quantification. His theory of relatives adds indices as individual variables to the operators Σ and Π to denote individual objects. Relative products and relative sums are then defined as (lb)_ij = Σx(l)_ix(b)_xj and (l † b)_ij = Π_x{(l)_ix+ (b)_xj}, thus becoming species of existential and universal quantification: the lover of a benefactor is “a particular combination, because it implies the existence of something loved by its relate and a benefactor of its correlate.” The lover of everything but benefactors is “universal, because it implies the non-existence of anything except what is either loved by its relate or a benefactor of its correlate” (Peirce 1883, p. 189). Peirce had already had the relative sum at his disposal and the idea of it expressing the non-existence of exceptions naturally led to its dual of the existential quantification. Towards the end of Note B Peirce writes something is a lover of something as Σ_i Σ_aj l_ij, everything is a lover of something as Π_iΣ_j l_ij, there is something which stands to something in the relation of loving everything except benefactors of it as Σ_iΣ_kΠ_j (l_ij+ b_jk), and so on. Taking α to denote accuser to___of___, ε excuser to___of___, and π preferrer to___of___, Π_iΣ_jΣ_k (α)_ijk (ε_jki + π_kij) means that “having taken any individual i whatever, it is always possible so to select two, j and k, that i is an accuser to j of k, and also is either excused by j to k or is something to which j is preferred by k” (Peirce 1883, p. 201). The phrasing Peirce uses here (such as “having taken any individual”, “it is always possible so to select”) is indicative of a new semantic treatment of quantifiers and sequences of quantifiers which he goes on to pursue further in later papers, and which in Hilpinen (1982), Hintikka (1996) and Pietarinen (2006) have shown to agree with game-theoretic semantics. Interestingly, Peirce’s examples are all stated in prenex normal form, which highlights the idea of sequences of dependent quantifiers. Peirce’s quantifiers bind variables ranging over interpreted domains. In this 1883 paper, he provides the basic inference rules, such as Σ_iΠ_j Π_jΣ_i, for manipulating the strings of quantifiers. The language is not inductively defined, it lacks notation for functions, and it uses neither constants nor an equality sign, but in other respects it coincides with that of first-order predicate calculus.

Alfred Tarski’s summary concerning Peirce’s contributions to the logical theory of relatives is illuminating:

[t]he title of creator of the theory of relations was reserved for C. S. Peirce. In several papers published between 1870 and 1882, he introduced and made precise all the fundamental concepts of the theory of relations and formulated and established its fundamental laws. Thus Peirce laid the foundation for the theory of relations as a deductive discipline; moreover he initiated the discussion of more profound problems in this domain. In particular, his investigations made it clear that a large part of the theory of relations can be presented as a calculus which is formally much like the calculus of classes developed by G. Boole and W. S. Jevons, but which greatly exceeds it in richness of expression and is therefore incomparably more interesting from the deductive point of view. (Tarski 1941, p. 73)

However, it is his 1885 theory of quantification that Peirce calculated to settle the problems of deductive logic and logical analysis in a way that decidedly brought him beyond the algebraic approach to the logic of relatives.

1885: Peirce’s logic of quantifiers comes to a full blossom in his paper, written in summer 1884, “On the Algebra of Logic: A Contribution to the Philosophy of Notation”, and published in the American Journal of Mathematics in the following year (Peirce 1885). This massive paper defies any condensed exposition; but in summary, it contains Peirce’s “five icons of algebra” as a system of natural deduction based on introduction and elimination rules. Peirce had repeatedly stated that his having supervised and examined Mitchell’s paper was essential in order to arrive at the idea of these two basic operations. There is an abundant use of truth-functional propositions and an anticipation of the truth-table method to test tautologies. One of the examples comes close to the tableaux method, later proposed by Evert Beth and Jaakko Hintikka, that spells out a systematic search for counter-models by deriving contradictions from the negations of the formula to be proved. In order “to find whether a formula is necessarily true,” he says, “substitute f and v for the letters and see whether it can be supposed false by any such assignment of values” (Peirce 1885, p. 224; Pietarinen 2006; Anellis 2012a).

When he moves on to the first-order (“first-intentional”) logic, Peirce seeks to devise a notation that is as iconic as possible, building on his semiotic insight that the more iconic a notation is, the better suited it would be for logical analysis. He starts by using “Σ for some, suggesting a sum, and Π for all, suggesting a product” (1885, p. 180). Once again, Peirce credits Mitchell, now for the method of separating the “quantifying part”—which he later termed the “Hopkinsian” to honour its place of discovery (MS 515, 1902)—from the pure Boolean expression: the latter refers to an individual by its use of indices (like pronouns in language) while the former states what that individual is. The quantifying operators are, however, “only similar to a sum and product,…because the individuals of the universe may be denumerable” (1885, p. 180). Peirce’s consideration illustrates similar lines of thought as those that prompted Löwenheim to formulate his famous 1915 theorem: if a first-order sentence has a model then it has also a countable model, or generally, models for sets of formulas being of some cardinality imply models of some other infinite cardinality (Badesa 2004). (Associating infinite products and sums with conjunctions and disjunctions was what Wittgenstein took to be his own biggest mistake in logic.) The 1885 paper continues introducing rules for quantifier manipulation, including “putting the Σs to the left, as far as possible” (1885, p. 182), which is a prelude to the idea of Skolem normal forms. One could say that it is the sequences of quantifiers, especially those of dependent quantifiers, that contribute to a linear logic notation as being maximally iconic, and that it is the prenex and Skolem normal forms that bring out maximal analyticity which logical icons exploit. The 1885 paper then presents many examples drawn from natural language to be analyzed logically with this new notation. The paper also extensively deals with issues having to do with the representation of mathematical notions such as one-to-one correspondence and identity in the second-intentional logic, developed in the third part of the paper, and in which variables range over relations. There is an early attempt at axiomatizing set theory as well as some profound philosophical consideration on the possibility of developing a “method for the discovery of methods in mathematics,” which is to be based on these new approaches that aim at formulating a general theory of deductive logic.

Thanks to the volumes that have appeared in the Chronological Edition of the Writings between 1982 and 2010, and which have covered Peirce’s work up to 1892, these earlier phases of Peirce’s deductive logic are now relatively well understood. But the research from that point on has been hampered by the unavailability of systematic editions concerning Peirce’s later logical writings. Yet the mid-1890s marks only the beginnings of a new and by far the most productive era in Peirce’s logical investigations, which were to last until the last months of his life. This situation has by no means been adequately reflected in the secondary literature.

Although Peirce would continue his investigations on the algebra of logic throughout his life, the algebraic element would no longer assume a central position in his overall oeuvre:

In 1895 Schröder published the third huge volume of his logic, which consisted mainly of a vast elaboration in detail of the logical algebra of my Note B. That I never considered that algebra to be a great masterpiece is sufficiently shown by my giving my exposition of it no other title than “Note B.” The perusal of Schröder’s book convinced me that the algebra was not what was wanted, and in the Monist for January 1897 I produced a system of graphs which I now term Entitative Graphs. I shortly after abandoned that and took up Existential Graphs” (MS 467; LoF, p. 332).

Although it was Schröder’s elaboration that was to influence the works of the early model theorists such as Löwenheim and Skolem (Brady 2000), it was Peirce’s and Mitchell’s works that germinated the concept of first-order statements being true-in-a model (Pietarinen 2006; Bellucci & Pietarinen 2015a). Moreover, Peirce’s incessant hunt for new logical notations and methods was much more ambitious and philosophical than his early algebraic investigations revealed.

What was to take the place of algebra were the ideas that emerged from diagrammatic, iconic and topological considerations on logical representation and reasoning. These considerations were at first prompted by logical analogues to algebraic invariants in chemistry first developed by Peirce’s John Hopkins colleague J. J. Sylvester (1878) and investigated in Kempe (1886). Peirce was initially fascinated by the analogy in which a chemical atom is like a relative “in having a definite number of loose ends or “unsaturated bonds”, corresponding to the blanks of the relative” (CP 3.469, 1897). But the continual search for better and better notations for the overall purposes of logical analysis would also reveal the reasons why Peirce had to overcome this analogy between logic and chemistry.

Peirce’s theory of Existential Graphs (EGs), first conceived in summer 1896 and developed in subsequent years (for example Peirce 1897, 1906), was in part motivated by his need to respond to the expressive insufficiency and lack of analytic power of the systems described in his Note B, which he later termed the algebra of dyadic (dual) relatives, and in the 1885 general (universal) algebra of logic. The analytic power comes from the idea of subsuming what the algebraic operations do when composing concepts under one mode of composition. This composition of concepts is effected in the theory of EGs by the device of ligatures. A ligature is a complex line, composed of what Peirce terms the lines of identities, which connects various parts and areas of the graphs: [See e.g. Zeman 1964; Roberts 1973; Shin 2002; Dipert 2006; Pietarinen 2005, 2006, 2011, 2015a.]

Fig. 1

Fig. 2

Fig. 3

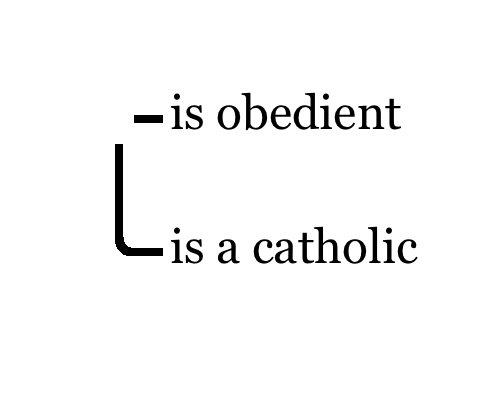
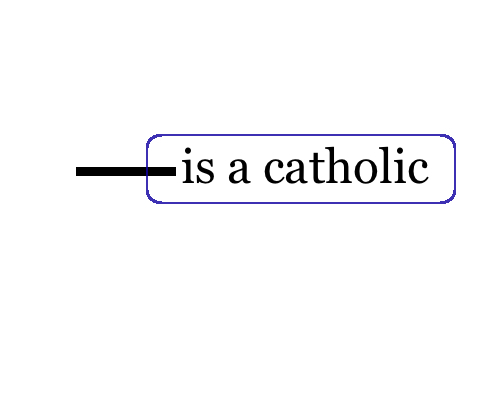
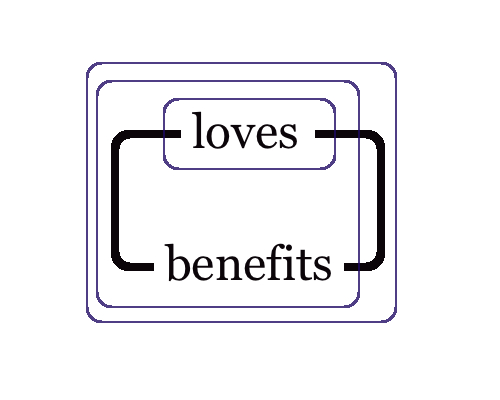
The meaning of these lines is that the two or more descriptions apply to the same thing. For example, in Figure 2 there is a horizontal line attached to the predicate term “is obedient.” It means that “something exists which is obedient.” There is also another line which connects to the predicate term “is a catholic,” and that composition means that “something exists which is a catholic”, which is equivalent to the graph-instance in Figure 3. Since in Figure 1 these two lines are in fact connected by a continuous line, the graph-instance in Figure 1 means that “there exists a catholic which is obedient,” that is, “there exists an obedient catholic.” Ligatures, representing continuous connections composed of two or more lines of identities, stand for quantification, identity and predication, all in one go.

These EGs are drawn on a sheet of assertion that represents what the modeller knows or what mutually has been agreed upon to be the case by those who undertake the investigation of logic. The sheet thus represents the universe of discourse. The graph that is drawn on the sheet puts forth an assertion, true or false, that there is something in the universe to which it applies. This is the reason why Peirce terms these graphs existential. Drawing a circle around the graph, or alternatively, shading the area on which the graph-instance rests, means that nothing exists of the sort of description intended. In Figure 4, the assertion “something is a catholic” is denied by drawing an oval around it and thus severing that assertion from the sheet of assertion:

Fig. 4

The graph-instance depicted in Figure 4 thus means that “something exists that is not catholic.”

Peirce aimed at a diagrammatic syntax that would use a minimal number of logical signs but at the same time be maximally expressive and as analytic as possible. His ovals, for instance, have different notational functions: “The first office which the ovals fulfill is that of negation. […] The second office of the ovals is that of associating the conjunctions of terms. […] This is the office of parentheses in algebra” (MS 430, pp. 54-56, 1902). The ovals are thus not only the diagrammatic counterpart to negation but also serve to represent the compositionality of a graph-formula. He held (MS 430, 1902; MS 670, 1911) that a notation that does not separate the sign of truth-function from the representation of its scope is more analytic than some other notation, such as that of an ordinary “symbolic” language, where such a separation is needed to force a one-dimensional notation. The role of ovals as denials is in fact a derived function from more primitive considerations of inclusion and implication (Bellucci & Pietarinen 2015; MS 300, 1908).

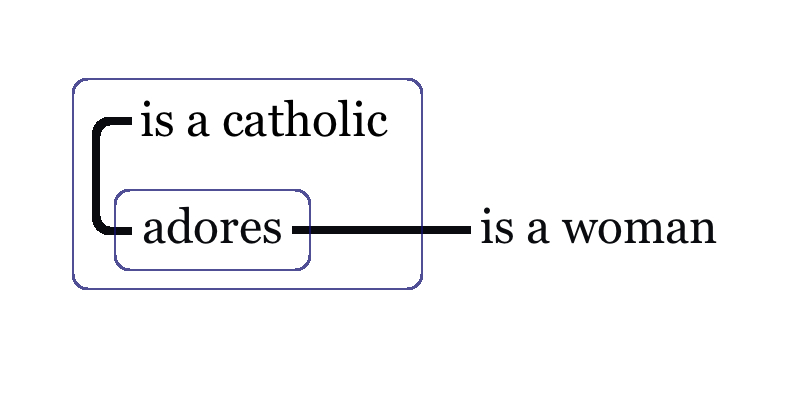
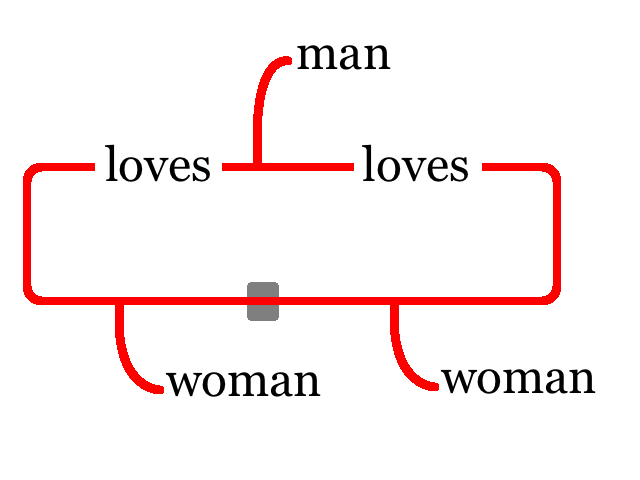
As to expressivity, Peirce had already recognized that the notion of dependent quantification was essential in any system expressive enough to serve the purposes of logical analysis of any assertions. The nested system of ovals in EGs effectuate this in a natural way, much in contrast to algebras that resort to an explicit use of parentheses and other punctuation devices. For example, the graph in Figure 5 means that “Every Catholic adores some woman.” The graph in Figure 6 means that “Some woman is adored by every Catholic.” Peirce notes that the latter asserts more since it states that all Catholics adore the same woman, whereas the former allows different Catholics to adore different women.

Fig. 5

Fig. 6

The graph in Figure 7 means that “anything whatever is unloved by something that benefits it,” that is, “everything is benefitted by something or other that does not love it”:

Fig. 7

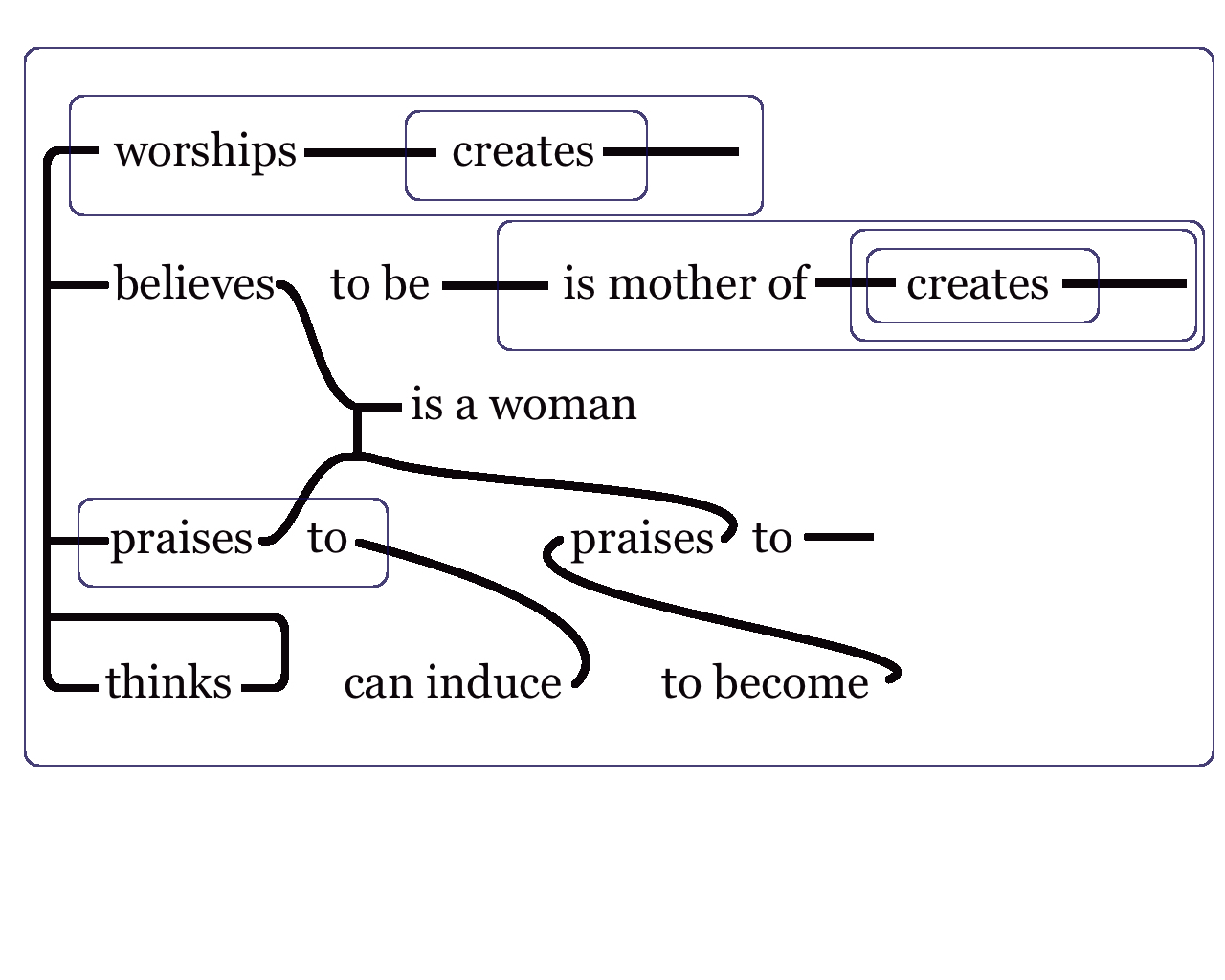
Lastly, Figure 8 provides an example of a very complex graph taken from MS 504 (1898):

Fig. 8

Peirce provided the meaning in natural language this way:

Every being unless he worships some being who does not create all beings either does not believe any being (unless it be not a woman) to be any mother of a creator of all beings or else he praises that woman to every being unless to a person whom he does not think he can induce to become anything unless it be a non-praiser of that woman to every being.

It is on the level of semantics where the power of dependent quantification comes to the fore. Peirce carried the semantics out in terms of defining the basics of what today is recognized as two-player zero-sum semantic games. For Peirce these games take place between the Graphist/Utterer and the Grapheus/Interpreter. [Sometimes, especially in Peirce’s model-building games, these roles split so that the Grapheus and the Interpreter are playing separate roles, see Pietarinen 2013.] Peirce’s semantic games were not limited to EGs; he applied the same idea also to interpret quantificational expressions and connectives in his general algebra of logic.

It speaks to the superiority of EGs over algebraic systems that in it deduction, following Mitchell’s work, is reduced to a minimum number of permissive operations. Peirce termed these operations illative rules of transformation, and in effect they consist only of two: insertions (permissions to draw a graph-instance on the sheet of assertion) and erasures (permissions to erase a graph-instance from the sheet). More precisely, the oddly enclosed areas of graphs (areas within an odd number of enclosures) permit inserting any graph on that area, while evenly enclosed areas permit erasing any graph from that area. A copy of a graph-instance is permitted to be pasted on that same area or any area deeper within the same nest of enclosures (the rule of iteration), and a copy thus iterated is permitted to be erased (the converse rule of deiteration). An interpretational corollary is that the double enclosure with no intervening graphs in the middle area can be inserted and erased at will.

A more detailed exposition of these illative rules of transformation would need to show their application to quantificational expressions, namely applying insertions and erasures to ligatures. A flavor of such proofs is given by inspecting the Figures 1, 2 and 3: an application of a permissible erasure on the line of identity in Figure 1 amounts to the graph-instance in Figure 2, and that another application of a permissible erasure on the upper part of the graph-instance in Figure 2 amounts to the graph-instance depicted in Figure 3. Thus what is represented in Figure 2 is a logical consequence of the graph-instance in Figure 1, and what is represented in Figure 3 is a logical consequence of the graph-instance given in Figure 2.

Roberts (1973) was the first to prove that these transformation rules, first given by Peirce in 1898, form a semantically complete system of deduction. Roberts did not mention, however, that Peirce had demonstrated their soundness in 1898 and again in 1903 and that he had argued for their completeness in terms of what he termed the “perfect archegetic rules of transformation” in the unpublished parts of the Syllabus for the Lowell Lectures that Peirce delivered in 1903.

The polarity of the outermost ends or portions of ligatures determines whether the quantification is existential (that end or portion resting on even/positive areas) or universal (if it rests on odd/negative area). Unlike in the Tarski-type semantics, but just as what happens in game-theoretic semantics, the preferred rule of interpretation of the graphs is what Peirce termed “endoporeutic”: one looks for the outermost portions of ligatures on the sheet of assertions first, assigns semantic values to that part, and then proceeds inwards into the areas enclosed with ovals. In non-modal contexts, ligatures are not well-formed graphs because they may cross the enclosures.

The diagrammatic nature of EGs consists in the iconic relationship between forms of relations exhibited in the diagrams and the real relations in the universe of discourse. Peirce was convinced that, since these graphical systems exploit a proper diagrammatic syntax, they—together with any of their extensions that would be introduced to cover modalities, non-declarative expressions, speech acts, and so forth—can express any assertion, however intricate. Guided by the precepts laid out by the diagrammatic forms of expression, and together with the simple illative permissions by which deductive inference proceeds, the conclusions from premises can be “read before one’s eyes”; these graphs present what Peirce believed is a “moving picture of the action of the mind in thought” (MS 298; LoF, p. 655; late 1906-1907).

If upon one lantern-slide there be shown the premisses of a theorem as expressed in these graphs and then upon other slides the successive results of the different transformations of those graphs; and if these slides in their proper order be successively exhibited, we should have in them a veritable moving picture of the mind in reasoning. (MS 905; LoF, p. 723; late 1907-1908)

The theory of EGs that uses only the notation of ovals and the spatial notion of juxtaposition of graphs is termed by Peirce the Alpha part of the EGs, and it corresponds to propositional logic. The extension of the alpha part with ligatures and rhemas (also termed spots by Peirce) gives rise to the Beta part, and it corresponds to fragments of first-order predicate calculus. What Peirce termed the Gamma part was a boutique of a number of developments, including various modalities such as metaphysical, epistemic and temporal modalities, as well as extensions of such graphs with ligatures. In Peirce’s writings, there are developments of graphical systems for higher-order logics and abstraction (Peirce’s “logic of potentials”), the logic of collections, and investigation of meta-logical expressions that use the language of graphs to talk about notions and properties of the graphs in that language (Peirce’s “graphs of graphs”). He mentions late in 1911 that the Delta part would also need to be added, most likely because of the ever-expanding systems that had been mushrooming in the Gamma part.

Peirce’s further contributions to deductive logic. While the development of the theory of the logic of existential graphs was his chief contribution, Peirce’s other contributions to the development of modern logic were numerous. In the Logic Notebook (1909) he defined a number of operations for three-valued logic and gave semantics for them in terms of defining truth-tables for such new connectives (Fisch & Turquette 1966). In these systems, which he called triadic logic, the third value is “the limit” between “true” and “not true,” and it applies to what Lane (1999) has identified as boundary-propositions: in Peirce’s terms, boundary-propositions have “a lower mode of being” which can “neither be determinately P, nor determinately not-P,” but are “at the limit between P and not P” (MS 399, p. 344r, 1909). Peirce defined several connectives to realize this idea in alternative ways, including four one-place connectives which were later reinvented as strong negation, two Post negations and the Tertium function, as well as six two-place connectives, including one that pertains to the logic of ordinary discourse.

Generally, Peirce divided deduction in two: on the one hand, deduction is either necessary or probable (deductive reasoning about probabilities), and on the other hand, deduction is either corollarial or theorematic. Corollarial deduction is reasoning “where it is only necessary to imagine any case in which the premisses are true in order to perceive immediately that the conclusion holds in that case.” Theorematic deduction “is deduction in which it is necessary to experiment in the imagination upon the image of the premiss in order from the result of such experiment to make corollarial deductions to the truth of the conclusion” (MS L 75, 1902). He considered the theorematic/corollarial distinction his first real discovery in the philosophy of mathematics. Theorematic deductions can be of different kinds and degrees of complexity, and he took the classification of various types of theorematic deductions to be of the utmost value in the theory of logic (MS 617; MS 201; Peirce 1908). Stjernfelt (2014) proposes a new classification of theorematic inferences. Hintikka (1980) has argued that reasoning is theorematic if it increases the number of layers of quantifiers, and that an argument is the more theorematic the more new individuals are used in it (see also Ketner 1985; Zeman 1986; Hoffmann 2010).

Zooming into some of the details of Peirce’s systems of logic, including those of diagrammatic logics, one finds a treasury of developments the meaning of which is only beginning to unravel over a century later (Bellucci, Pietarinen & Stjernfelt 2014). In 1886, Peirce suggested in a letter to his former student Allan Marquand, who had designed mechanical logic machines for syllogistic reasoning, that “it is by no means hopeless to expect to make a machine for really difficult problems. But you would have to proceed step by step. I think electricity would be the best thing to rely on” (L 269, Peirce to Marquand, 30 December, 1886; W5, p. 422). He then showed how switching circuits can be connected serially and in parallel, noting that these two configurations correspond to multiplication (algebraic sum as logical disjunction) and addition (algebraic product as logical conjunction) in logic. In addition to the idea of real logical machines running on electricity, Peirce was also very interested in the philosophical question of whether living intelligence is required in performing deductive reasoning, an issue of continuing relevance to A.I. and to the prospects of automatized theorem proving. In 1902 he developed two notational systems with sixteen binary connectives to map out all of the possible truth functions of the binary propositional calculus (Clark 1997; Zellweger 1997). According to Max Fisch, “No other logician compares with Peirce in attention to systems of notation and to sign-creation” (Fisch 1982, p. 132). Peirce’s work on these notational systems foresaw geometrical structures of logic, including spaces revealed by the study of the geometry of negation and other operators. Based on Peirce’s conceptual and sign-theoretic considerations, an apparatus for displaying and performing a complete set of the sixteen binary connectives in a two-valued propositional logic was patented in the U.S.A. in 1981 by Shea Zellweger.

Peirce also worked on early forms of topology (Havenel 2010), including studies on what might be recognized as rudimentary versions of homologies and knots, in his attempts to find pathways not only to logical issues but also to questions in philosophy of mathematics (Murphey 1961; Moore 2010).

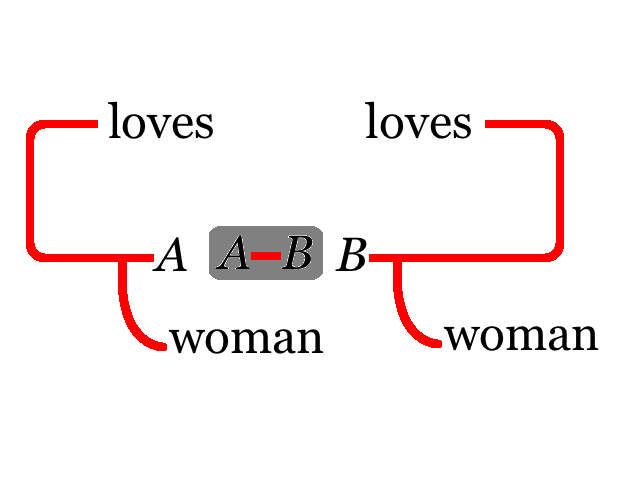
Moreover, his diagrammatic systems of modal logic included suggestions for defining several types of multi-modal logics in terms of tinctures of areas of graphs. Tinctures enable logic to assert, among others, modalities including necessities and metaphysical possibilities, and so call for changes in the nature of how the corresponding logics behave, including the identification of individuals at the presence of multiple universes of discourses. He defined epistemic operators in terms of subjective possibilities, which, just as in contemporary epistemic logic, are epistemic possibilities defined as duals of knowledge operators. He analyzed the meaning of identities between actual and possible objects in quantified multi-modal logics. As an example, the two graphs given in Figures 9 and 10 that he presented in a 1906 draft of the Prolegomena paper (MS 292) illustrate the nature of the interplay between epistemic modalities and quantification.

Fig. 9

Fig. 10

The graph in Figure 9 is read “There is a man who is loved by one woman and loves a woman known by the Graphist to be another.” The reason is this. In the equivalent graph depicted in Figure 10 the woman who loves is denoted by the name A, and the woman who is loved is denoted by the name B. The shaded area is a tincture that refers to the modality of subjective possibility. Thus the graph in Figure 10 means that it is subjectively impossible, by which Peirce means that “it is contrary to what is known by the Graphist” (= the modeller of the graph), that A should be B. In other words, the woman who loves and the woman who is loved (whom the graph does not assert to be otherwise known to the Graphist) are known by the Graphist not to be the same person.

Peirce’s work highlights the philosophical signiﬁcance of ideas that were rediscovered later and largely after the mid-twentieth century, though often in different clothes: in Peirce’s largely unpublished works one finds him addressing such topics as multi-modal logics and possible-worlds semantics, quantiﬁcation into modal contexts, cross-world identities (in MS 490 he termed these special relations connecting objects in different possible worlds (for references, see Pietarinen 2005), cumulative and branching quantifiers (the latter being related to independence-friendly logic, see Pietarinen 2015b), as well as what later on became known as “Peirce’s Puzzle” (Dekker 2001; Hintikka 2011; Pietarinen 2015b), namely the question of the meaning of indeﬁnites in conditional sentences, which Peirce himself analyzed in quantified modal extensions of EGs.

Far from merely anticipating later discoveries, thus, Peirce’s logic in general puts what later on came to be explored in the fields of philosophical logic, formal semantics and pragmatics, philosophy of logic, mathematics, mind and language, cognitive and computing sciences, and history and philosophy of science, into a systematic logico-semeiotic perspective. From time to time, his ideas even surpass stagnated contemporary discussions, especially in the philosophy of logic and mathematics. [See for example Bellucci, Pietarinen & Stjernfelt 2014; Lupher & Adajian 2015; Sowa 2006; Zalamea 2012a; Zalamea 2012b; PM. For further details on Peirce’s deductive logic, see the collection of Houser and others, eds. 1997. Hilpinen 2004 provides a useful overview.]

iv. Inductive Logic

In 1865 (W1, pp. 263-64) Peirce defines induction as inference from Case and Result to Rule. Its general form is:

Case: M₁ M₂ M₃ M₄are S
Result: M₁ M₂ M₃ M₄are P
Rule: Therefore, all S are P.

A certain number of objects (M₁ M₂ M₃ M₄), known to belong to a certain class (S), possess a certain character (P); therefore, it can be infered inductively that the whole class S possesses that character. I notice that neat, swine, sheep, and deer, which I know are cloven-hoofed, are herbivores. Therefore, I infer inductively that all cloven-hoofed animals are herbivores.

Later, Peirce came to divide induction into three principal kinds. Crude induction is the lowest form of induction, based upon the common practice of generalizing about future events on the ground of previous experience. For example, “No instance of a genuine power of clairvoyance has ever been established: So I presume there is no such thing”; “cancer is incurable, because every known case has proved to be so.” Its general form is “All observed As are B. Therefore, All As are B.” It is the weakest form of inductive reasoning in terms of security. Qualitative induction is the intermediate kind in terms of security. It is what Peirce had earlier called hypothetical reasoning or abduction. It consists in testing a hypothesis by sampling the possible predications that may be made on the basis of it (CP 7.216). Qualitative abduction is reasoning that tests hypotheses already formulated. It should not be confused with abduction, which is reasoning that originates new hypotheses. Quantitative induction is the highest form of induction in terms of security. It investigates the real probability that a member of a certain class will have a certain character. Its procedure consists in finding a representative sample of the class and noting the proportion of them that possess the character P. Then, the inference is drawn that the proportion holds for the whole class. Its logical form is

S₁S₂S₃S₄and so forth, are taken at random from the Ms.
The proportion p of S₁S₂S₃S₄is P.
Hence, probably and approximately, the same proportion p of the Ms are P.

The inversion of a quantitative induction gives us a statistical deduction, whose form is

The proportion p of the Ms are P.
S₁S₂S₃S₄and so forth, are taken at random from the Ms.
Hence, the proportion p of them is P.

Although crude, qualitative, and quantitative induction are different in kind, their justification is, according to Peirce, the same:

The validity of Induction consists in the fact it proceeds according to a method which though it may give provisional results that are incorrect will yet if steadily pursued, eventually correct any such error. […] all Induction possesses this kind of validity, and […] no Induction possesses any other kind that is more than a further determination of this kind. (MS 293, 1907)

The validity rests upon induction being self-corrective: in the long run induction is bound to lead us ever closer to the correct representation of reality. Its validity is therefore linked to esse in futuro, to the possibility of self-correction of the very method itself. Any actual induction that is performed may well be wrong or partly wrong, but it remains valid because its leading principle is valid, that is, is conducive to truth in the long run.

Peirce’s polemic target was a theory that would make the validity of induction rest upon some principles of uniformity or regularity in nature. According to Peirce, that was how John S. Mill and Philodemus of Gadara (ca.110–ca.30 B.C.E.) attempted, unsoundly, to justify induction. Of the several objections that Peirce raised from time to time against this way of justifying induction, one is worth reporting. Mill argues that a universe without any regularity is imaginable, and that in that universe inductions would be invalid. But the absence of uniformity, that is, the absence among certain objects S of the character P, is itself a uniformity. No universe is imaginable in which induction is not valid. According to Peirce, “even if nature were not uniform, induction would be sure to find it out, so long as inductive reasoning could be performed at all” (CP 2.775).

Cheng 1969, Goudge 1946, Merrill 1975 and Forster 1989 provide further details on Peirce’s inductive logic.

c. Methodeutic

The third branch of Peirce’s logic is methodeutic, which he also called speculative rhetoric. He defined it to be “the study of the proper way of arranging and conducting an inquiry” (MS 606, p. 17), depicting it as being “not so exact in its conclusions as is critical logic” (MS L 75, 1902) and as involving “certain psychological principles” (MS 633, 1909). But it nevertheless is a theoretical study and not an art. Methodeutic is based upon critics, and considers not what is admissible (logical validity) but what is advantageous (logical economy). It is a “theoretical study of advantages” (MS L 75, 1902).

Abduction is of special interest to methodeutic, because abduction is the only mode of inference that can initiate a scientific hypothesis. But being justifiable is not a sufficient property of good hypotheses:

Any hypothesis which explains the facts is justified critically. But among justifiable hypotheses we have to select that one which is suitable for being tested by experiment. (MS L 75, 1902)

Among critically equivalent hypotheses (that is, hypotheses that explain the facts), one should be able to select for testing those that are capable of experimental verification. [Being capable of experimental verification is in Peirce’s philosophy of science to be conceived in the wide sense, including mental experimentation and imaginative activities in our thoughts (Bellucci & Pietarinen 2015b). It is not the same thing as the empirical verification criterion of the positivists, which Peirce often criticized.] This is the core of Peirce’s philosophy of pragmati(ci)sm, which teaches that the whole meaning of a hypothesis is in its conceivable practical (that is, experienceable) effects; pragmaticism therefore is “nothing else than the question of the logic of abduction” (CP 5.196, 1903).

In turn, among “pragmatistically” equivalent hypotheses (that is, hypotheses that are capable of experimental verification) one should select those that in the sense of Peirce’s economy of research are the cheapest ones. His argument for the economic character of methodeutic is roughly as follows: the logical validity of abduction presupposes that nature be in principle explainable. This means that to discover is simply to expedite an event that would sooner or later occur. Therefore, the real service of a logic of abduction is of the nature of an economy. Economy itself depends on three factors: cost (of money, time, energy, thought), the value of the hypothesis itself, and its effects upon other projects and hypotheses (MS L 75, 1902; MS 690, CP 7.164-231, 1901).

Although primarily concerned with abduction, methodeutic also has an interest in deduction and induction. Theorematic deductions (see §2.b.iii) manifest peculiar logical steps that are abductive rather than deductive. In order to overcome the lack of critical instruments for the investigation of those steps, Peirce emphasizes the need to have an inventory and logical classification of valuable steps in the history of mathematics which would become part of a methodeutic of necessary reasoning (Peirce 1908, MS 200-201).

Peirce also considered the study of the properties of different logical and mathematical notations and symbolisms as belonging to the department of methodeutic. In this respect, he coined the maxim of the ethics of terminology and of notation:

The person who introduces a conception into science has both the right and the duty of prescribing a terminology and a notation for it; and his terminology and notation should be followed except so far as it may prove positively and seriously disadvantageous to the progress of science. If a slight modification is sufficient to remove the objection, a much greater one should be avoided. (MS 530, 1902)

Induction too has its methodological side. The methods of the three classes of inductions are all based on “samples,” and they all presuppose that the samples are representative of the class from which they are sampled: methodeutic should therefore teach methods of producing fair samplings. His own experimental work is exemplary in that it develops new statistical methods to ascertain that truly randomized samples are achieved and that fully blinded testing conditions are secured. He emphasizes the method of predesignation, which prescribes that the characters concerning which class is sampled are to be chosen beforehand so that the sampler would not be influenced by any agreement among the members of the sample (see Goudge 1946).

Other things Peirce considers to pertain to methodeutic include the principles of definition, the methods of classification in general, and the doctrine of the clearness of ideas.

Peirce’s logic, conceived as semeiotic, characterizes a broad philosophical, methodological and scientific area of investigation. Although the present article has exposed a number of developments in Peirce’s studies in deductive logic, the deductive part is only a fraction of the wider project of semeiotic, the theory and philosophy of signs, and the logic of science. From a contemporary perspective, deductive, formal, and mathematical logic may have become the mainstay of logic as such, but for Peirce other areas of logic, such as speculative grammar and the critics and methodeutic of abduction and induction, are at least as important as the deductive part of logic.

3. Peirce’s Logic in Historical Perspective

Peirce’s algebraic work in formal logic influenced Ernst Schröder (1841–1902), who drew heavily upon Peirce’s work in the three volumes of his Vorlesungen über die Algebra der Logik (Schröder 1890–1905). Peirce also successfully initiated a school in logic during his Johns Hopkins period (1879–1884), whose most evident manifestation is the richness and originality of the papers contained in the Studies in Logic (Peirce 1883). For the main part of his career, Peirce had been in contact and correspondence with the most prominent logicians, mathematicians and scientists of the time, and his works appeared in leading scientific journals and proceedings.

All these facts notwithstanding, the reception of Peirce’s deductive logic has been strangely erratic, even in the early days. Especially in his later period (1892–1914), Peirce worked virtually alone in an adverse environment and without much intellectual and material support. It is true that the recognition of his contributions has suffered from a long-term unavailability of his vast Nachlass of over 100,000 surviving pages of manuscripts and correspondence. In some cases at least, the explanation may be found in the unprecedented technical and mathematical standard and rigor characterizing his work. But what is certainly a chief reason behind the general neglect of Peirce’s logic is the rise, at the end of the 19^th century, of what has later been named the Frege-Russell tradition in logic.

The historiography of logic seems to have accepted the idea, initially promoted by Bertrand Russell and subsequently canonized by historian of logic Jean van Heijenoort (1912–1986), of a “Fregean revolution” in logic. In this narrative, modern mathematical logic (also deceptively called symbolic logic) has replaced traditional or Aristotelian logic. According to such a picture, the work of the “algebraists,” (including Boole, De Morgan, Peirce and Schröder) belongs to the pre-Fregean logical paradigm.

Anellis (2012b) identified seven features of such a “Fregean” revolution: (1) A propositional calculus with a truth-functional definition of connectives, especially the conditional. (2) Decomposition of propositions into function and argument instead of into subject and predicate. (3) A quantification theory, based on a system of axioms and inference rules. (4) Definitions of infinite sequence and natural number in terms of logical notions (that is the logicization of mathematics). (5) Presentation and clarification of the concept of a formal system. (6) Relevance and use of logic for philosophical investigations (especially for philosophy of language). (7) Separating singular propositions, such as “Socrates is mortal” from universal propositions such as “All Greeks are mortal.” All these characteristics, Anellis argued, can be found in Peirce’s work, which therefore falls within the parameters of van Heijenoort’s conception of the Fregean revolution and the definition of mathematical logic. One also needs to remember that there are many characteristics of Peirce’s logic and philosophy of logic, vitally important to his logical vision, that either add to, modify or reject those that have been taken to typify the Fregean tradition. What may be ill-named as a Fregean revolution is found in a different, and perhaps more penetrating and consequential shape in Peirce’s work.

Peirce and Frege discovered quantificational theory around the same time (1879–1883). Frege’s work was at the time largely ignored. Russell credited Frege a posteriori with having founded modern logic in the Begriffsschrift (Frege 1879). However, while Frege’s notation was hardly ever used, the Peirce-Schröder notation was largely adopted by others. The important results of Löwenheim and Skolem at the beginning of the 20^th century were presented in the Peirce-Schröder system without any trace of influence by Frege or Russell. Peano’s use of the existential and universal quantifiers derives from Schröder and Peirce, not from Frege. Unlike Frege, Peirce recognized the utmost importance of dependent quantifiers and experimented with that idea in various ways in the algebra of logic and in existential graphs, and proposed new systems and dimensions of quantification that involve independent quantification (MS 430). Peirce’s overall influence upon the development of modern logic was considerable though its nature and scope had remained ill-understood for a long time (Putnam 1982; Dipert 1995; Pietarinen 2015a).

Peirce’s philosophy of logic had no better fate. Aside from Josiah Royce and especially Lady Victoria Welby with whom Peirce corresponded on the logic of signs and semiotics during 1903-1910, Peirce’s radical idea of “logic as semeiotic” largely passed by unnoticed. In the 1930s Charles Morris took, misleadingly, Peirce’s trivium of speculative grammar, critics and methodeutic to correspond to the division of the study of language into syntax, semantics, and pragmatics (Morris 1938, pp. 21-22). Carnap (1942) adopted Morris’ trichotomy and made it popular. Peirce’s philosophy of signs has since been studied by semioticians, led by the pioneering explorations by Roman Jakobson and Umberto Eco (see Eco 1975; Jakobson 1977; Eco 1984). Other aspects of Peirce’s philosophy of logic, such as the distinction between corollarial and theorematic deduction, his ideas on diagrammatic reasoning, and the evolution of new logical notations and meanings, is gaining the interest, not only of logicians and historians of logic, but also of philosophers of science, cognitive scientists as well as many scholars, scientists, artists and practitioners looking for ways to overcome boundaries of narrow conceptions of logic, reasoning and representation, as well as the outdated 20^th-century scientific methodologies that have characterized their respective fields. [See for example the 2014 Peirce Centennial Conference at Lowell as well as the Applying Peirce Conference series at Helsinki in 2007 and 2014, which have brought together scholars and scientists interested in Peirce’s thought virtually on any field of science.]

From the perspectives of the history and philosophy of modern logic, it may not be entirely right to talk in strict terms about the two traditions in logic, namely those of the algebraic and the symbolic ones. On the one hand, Peirce’s line of work in the algebra of logic led to the invention of a spectrum of methods in the semantic and model-theoretic tradition while the logic that Schröder, for example, preferred was to quantify over the entire universe and was thus at bottom a universalist one, thereby sharing the same preference as Frege. On the other hand, Peirce’s continuous search for new notations for the purposes of logical analysis and representation made what others may have considered to be the subject of symbolic notations really the subject of diagrams and icons. Algebraic notations were for Peirce iconic and often even very graphically so. What mattered to him was to remain clear of the significations of logical signs. Logical signs were to be interpreted in proper contexts and according to the purposes of investigation at hand. Thus, Peirce’s philosophy of logic stands in stark contrast to purely formal, mathematical and proof-theoretic approaches to logic, which do not care so much for signification. Peirce should accordingly be counted in the pragmatic, rather than just the semantic, tradition in philosophy of logic and language (Pietarinen 2006; Tiercelin 1991).

The famous van Heijenoort–Hintikka distinction between “logic as calculus” and “logic as a universal medium” is nonetheless instructive here (van Heijenoort 1967; Hintikka 1997; Peckhaus 2004). According to the former view of logic as calculus, methods and languages are many, they are reinterpretable according to the context and purposes at hand, and they admit of many and varying universes as well as modal and intensional considerations. The latter, universalist position means, in contrast, that there is one logic to “rule them all,” and so our thought is bounded by what that logic can express. Peirce fits squarely into the former camp. Here again it is not that all who worked on the algebra of logic would be members of that same camp (Schröder is a counterexample), or that all of those who in the literature have been tagged as formalists would share the universalist presuppositions (David Hilbert may serve as another kind of a counterexample). It may be one of the lessons of Peirce’s pragmaticism and the methodological pluralism which he exercised in his logic that one does not fix in advance what may in the future be considered to fall within the scope of logic.

4. References and Further Reading

Peirce’s works
1867. An Improvement in Boole’s Calculus of Logic. Proceedings of the American Academy of Arts and Sciences 7, pp. 249-261.
1870. Description of a Notation for the Logic of Relatives. Memoirs of the American Academy of Arts and Sciences 9, pp. 317-378.
1880a. On the Algebra of Logic. American Journal of Mathematics 3, pp. 15–57.
1881. On the Logic of Number. American Journal of Mathematics 4, pp. 85-95.
1883 (ed.). Studies in Logic by Members of the Johns Hopkins University. Boston: Little, Brown, and Co. 1883.
1885. On the Algebra of Logic. A Contribution to the Philosophy of Notation. American Journal of Mathematics 7, pp. 197–202.
1897. The Logic of Relatives. The Monist 7, pp. 161–217.
1901-1902. Entries in Dictionary of Philosophy and Psychology, 3 vols, edited by Baldwin, James Mark. Cited as DPP followed by volume and page number.
1906. Prolegomena to an Apology for Pragmaticism. The Monist 16, pp. 492–546.
1908. Some Amazing Mazes. The Monist 18 (3), pp. 416-464.
1931–1966. The Collected Papers of Charles S. Peirce, 8 vols., ed. by Hartshorne, C, Weiss, P. and Burks, A. W. Cambridge: Harvard University Press. Cited as CP followed by volume and paragraph number.
1967. Manuscripts in the Houghton Library of Harvard University, as identified by Richard Robin, “Annotated Catalogue of the Papers of Charles S. Peirce,” Amherst: University of Massachusetts Press, 1967, and in “The Peirce Papers: A supplementary catalogue,” Transactions of the C. S. Peirce Society 7 (1971): 37–57. Cited as MS followed by manuscript number and, when available, page number.
1976. The New Elements of Mathematics by Charles S. Peirce, 4 vols., ed. by Eisele, C. The Hague: Mouton. Cited as NEM followed by volume and page number.
1982 – …. Writings of Charles S. Peirce: A Chronological Edition, 7 vols., ed. by. Moore, E. C., Kloesel, C. J. W. et al. Bloomington: Indiana University Press. Cited as W followed by volume and page number.
2010. Philosophy of Mathematics: Selected Writings, ed. by M. E. Moore, Bloomington and Indianapolis, IN: Indiana University Press. Cited as PM.
2015. Logic of the Future. Peirce’s Writings on Existential Graphs, ed. by A.-V. Pietarinen, Bloomington: Indiana University Press. Cited as LoF.
Other works
Anellis, I. 2012a. Peirce’s Truth-Functional Analysis and the Origin of the Truth Table. History and Philosophy of Logic 33, pp. 37–41.
Anellis, I. 2012b. How Peircean was the ‘Fregean’ Revolution in Logic? arXiv:1201.0353.
Badesa, C. 2004. The Birth of Model Theory: Löwenheim’s Theorem in the Frame of the Theory of Relatives, Princeton: Princeton University Press.
Bellucci, F. & Pietarinen, A.-V. (2014). New Light on Peirce’s Concept of Retroduction and Scientific Reasoning, International Studies in the Philosophy of Science 28(2), pp. 1-21.
Bellucci, F. & Pietarinen, A.-V. (2015). Existential Graphs as an Instrument of Logical Analysis. Part I: Alpha, to appear.
Bellucci, F., Pietarinen, A.-V. & Stjernfelt, F. eds. 2014. Peirce: 5 Questions. VIP/Automatic Press.
Boole, G. 1847. The Mathematical Analysis of Logic. Cambridge: Macmillan, Barclay, & Macmillan.
Boole, G. 1854. An Investigation of the Laws of Thought. Cambridge: Walton & Maberly.
Brady, G. 2000. From Peirce to Skolem. Amsterdam: Elsevier Science.
Brent, B. 1987. Charles S. Peirce. Logic and the Classification of the Sciences, Kingston/Montreal: MacGill-Queen’s University Press
Burch, R. W. 2011. Peirce’s 10, 28, and 66 Sign-Types: The Simplest Mathematics. Semiotica 184, pp. 93–98.
Burks, A. W. 1946. Peirce’s Theory of Abduction. Philosophy of Science 13, pp. 301-306.
Carnap, R. 1942. Introduction to Semantics, Cambridge, Mass: MIT Press.
Chauviré, Ch. 1994. Logique et Grammaire Pure. Propositions, Sujets et Prédicats Chez Peirce. Histoire Epistémologie Langage 16, pp. 137–175.
Cheng, C.-Y. 1969. Peirce’s and Lewis’s Theories of Induction, The Hague: Martinus Nijhoff.
Clark, G. 1997. New Light on Peirce’s Iconic Notation for the Sixteen Binary Connectives. In Houser and others 1997, pp. 304-333.
Dedekind, R. 1888. Was sind und was sollen die Zahlen. Braunschweig: Vieweg.
Dekker, Paul 2001. Dynamics and Pragmatics of ‘Peirce’s Puzzle’, Journal of Semantics 18, pp. 211-241.
De Morgan, A. 1847. Formal Logic. London: Taylor and Walton.
De Morgan, A. 1860. On the Syllogism IV; and on the Logic of Relations. Transactions of the Cambridge Philosophical Society 10, pp. 331-358.
Dipert, R. 1995. Peirce’s Underestimated Place in the History of Logic: A Response to Quine. In Ketner, K. L. ed. Peirce and Contemporary Thought. New York: Fordham University Press, pp. 32-58.
Dipert, R. 2006. Peirce’s Deductive Logic: Its Development, Influence, and Philosophical Significance. In: Misak, C. (ed.). The Cambridge Companion to Peirce. Cambridge: Cambridge University Press, pp. 287-324.
Eco, U. 1975. Trattato di semiotica generale. Milano: Bompiani.
Eco, U. 1984. Semiotica e filosofia del linguaggio. Torino: Einaudi.
Fann, K. T. 1970. Peirce’s Theory of Abduction. The Hague: Martinus Nijhoff.
Ferriani, M. 1987. Peirce’s Analysis of the Proposition: Grammatical and Logical Aspects. In Ferriani, M. & Buzzetti, D. (eds.), Speculative grammar, universal grammar and philosophical analysis of language. Amsterdam: Benjamins, pp. 149-172.
Fisch, M. H. 1982. The Range of Peirce’s Relevance, The Monist 65, pp. 123-141. Reprinted in Fisch 1986, pp. 422-448.
Fisch, M. H. 1986. Peirce, Semeiotic and Pragmatism. Ed. by K. L. Ketner and C. J. W. Kloesel, Bloomington: Indiana University Press.
Fisch, M. H. & Turquette, A. 1966. Peirce’s Triadic Logic. Transactions of the Charles S. Peirce Society 2, pp.71-85.
Forster, P. 1989. Peirce on the Progress and Authority of Science. Transactions of the Charles S. Peirce Society 25, pp. 421–452.
Frege, G. 1879. Begriffsschrift: eine der arithmetischen nachgebildete Formelsprache des reinen Denkens. Halle: Louis Nebert.
Goudge, T. 1946. Peirce’s Treatment of Induction. Philosophy of Science 7, pp. 56-68.
Haack, S. 1993. Peirce and Logicism: Notes Towards an Exposition. Transactions of the Charles S. Peirce Society 29, pp. 33–56.
Havenel, J. 2010. Peirce’s Topological Concepts. In Moore 2010, pp. 283-322.
Hilpinen, R. 1982. On C. S. Peirceʼs Theory of the Proposition: Peirce as a Precursor of Game-Theoretical Semantics. The Monist 65, pp. 182-188.
Hilpinen, R. 1992. On Peirce’s Philosophical Logic: Propositions and Their Objects. Transactions of the Charles S. Peirce Society 28, pp. 467–488.
Hilpinen, R. 2004. Peirce’s Logic, in Gabbay, D.M., and J. Woods. 2004. Handbook of the History of Logic. Vol. 3: The Rise of Modern Logic From Leibniz to Frege. Vol. 3. Amsterdam: Elsevier North-Holland, pp. 611-658.
Hintikka, J. 1980. C. S. Peirce’s ‘First Real Discovery’ and Its Contemporary Relevance. Monist 63, pp. 304-315.
Hintikka, J. 1996. The Place of C. S. Peirce in the History of Logical Theory. In J. Brunning, J. & Forster, P. eds. The Rule of Reason: The Philosophy of Charles Sanders Peirce, Toronto: University of Toronto Press, pp. 13–33.
Hintikka, J. 1997. Lingua Universalis vs. Calculus Ratiocinator: An Ultimate Presupposition of Twentieth Century Philosophy. Dordrecht: Kluwer.
Hintikka, J. 2011. What the bald man can tell us. In: Biletzky, A. (ed.) Hues of Philosophy: Essays in Memory of Ruth Manor. London: College Publications.
Hoffmann, M. 2010. Theoric Transformations. Transactions of the Charles S. Peirce Society 46, pp. 570–590.
Houser, N. 1993. On ‘Peirce and Logicism’: A Response to Haack. Transactions of the Charles S. Peirce Society 29, pp. 57–67.
Houser, N., Roberts, D., Van Evra, J. eds. 1997. Studies in the Logic of Charles S. Peirce. Bloomington and Indianapolis: Indiana University Press.
Jakobson, R. 1977. A Few Remarks on Peirce, Pathfinder in the Science of Language. MLN 92, pp. 1026–1032.
Kapitan, T. 1992. Peirce and the Autonomy of Abductive Reasoning. Erkenntnis 37, pp. 1–26.
Kapitan, T. 1997. Peirce and the Structure of Abductive Inference. In Houser and others eds. 1997, pp. 477-496.
Kempe, A. B. 1886. A Memoir on the Theory of Mathematical Form. Philosophical Transactions of the Royal Society of London 177, pp. 1-70.
Ketner, K. L. 1985. How Hintikka Misunderstood Peirce’s Account of Theorematic Reasoning. Transactions of the Charles S. Peirce Society 21, pp. 407–418.
Lane, R. 1999. Peirce’s Triadic Logic Revisited. Transactions of the Charles S. Peirce Society 35, pp. 284–311.
Lewis, C. I. 1918. A Survey of Symbolic Logic. Berkeley: University of California Press.
Lupher, T. and Adajian, T. eds. 2015. Philosophy of Logic: 5 Questions. Copenhagen: Automatic Press.
Ma, Minghui & Pietarinen, A.-V. 2015. A dynamic approach to Peirce’s interrogative construal of abductive reasoning, IFCoLog Journal of Logics and their Applications, in press.
Mannoury, G. 1909. Methodologisches und Philosophisches zur Elementar-Mathematik. Haarlem: P. Visser.
Merrill, D. D. 1997. Relations and Quantification in Peirce’s Logic, 1870-1885. In Houser et. al. eds. 1997, pp. 158-172.
Merrill, G. H. 1975. Peirce on Probability and Induction. Transactions of the Charles S. Peirce Society 11, pp. 90–109.
Moore, M. ed. 2010. New Essays on Peirce’s Mathematical Philosophy. Chicago: Open Court.
Morris, C. W. 1938. Foundations of the Theory of Signs. In Morris, C. 1971. Writings on the General Theory of Signs. The Hague: Mouton.
Murphey, M. G. 1961. The Development of Peirce’s Philosophy, Cambridge, Mass: Harvard University Press, 2^nd ed. 1993, Indianapolis: Hackett.
Paavola, S. 2004. Abduction as a Logic and Methodology of Discovery: The Importance of Strategies. Foundations of Science 9, pp. 267–283.
Peano, G. 1889. Arithmetices Principia. Nova Methodo Exposita. Torino: Bocca.
Peckhaus, V. 2004. Calculus Ratiocinator vs. Characteristica Universalis? The Two Traditions in Logic, Revisited. History and Philosophy of Logic 25, pp. 3-14.
Peirce, B. 1870. Linear Associative Algebra. Litographated ed., Washington D.C.
Pietarinen, A.-V. 2005. Compositionality, Relevance and Peirce’s Logic of Existential Graphs. Axiomathes 15, pp. 513-540.
Pietarinen, A.-V. 2006. Signs of Logic: Peircean Themes on the Philosophy of Language, Games and Communication. Dordrecht: Springer.
Pietarinen, A.-V. 2011. Existential Graphs: What a Diagrammatic Logic of Cognition Might Look Like. History and Philosophy of Logic 32, pp. 265–281.
Pietarinen, A.-V. 2013. Logical and Linguistic Games from Peirce to Grice to Hintikka (with comments by J. Hintikka). Teorema 33, pp. 121-136.
Pietarinen, A.-V. 2015a. Exploring the Beta Quadrant. Synthese 192, pp. 941-970.
Pietarinen, A.-V. ed. 2015b. Two Papers on Existential Graphs by Charles S. Peirce: 1. Recent Developments of Existential Graphs and their Consequences for Logic (MS 498, 499, 490, S-36, 1906), 2. Assurance through Reasoning (MS 669, 670, 1911). Synthese 192, pp. 881-922.
Pietarinen, A.-V. & Bellucci, F. 2015a. Habits of Reasoning: On the Grammar and Critics of Logical Habits. In D. E. West & M. Anderson eds. Consensus on Peirce’s Concept of Habit: Before and Beyond Consciousness. Dordrecht: Springer.
Pietarinen, A.-V. & Bellucci, F. 2015b. The Iconic Moment: Towards a Peircean Theory of Diagrammatic Imagination. In J. Redmond, A. N. Fernàndez, O. Pombo eds. Epistemology, Knowledge, and the Impact of Interaction, Dordrecht: Springer.
Prior, A. N. 1958. Peirce’s Axioms for Propositional Calculus. The Journal of Symbolic Logic 23, pp. 135–136.
Prior, A. N. 1964. The Algebra of the Copula. In Moore, E. & Robin, R. eds. Studies in the Philosophy of Charles Sanders Peirce. Amherst: The University of Massachusetts Press, pp. 79-94.
Putnam, H. 1982. Peirce the Logician. Historia Mathematica 9, pp. 290-301.
Roberts, D. D. 1973. The Existential Graphs of Charles S. Peirce. The Hague- Paris: Mouton.
Schröder, E. 1890-1905. Vorlesungen über die Algebra der Logik, 3 vols. Leipzig: Teubner.
Shields, P. 1981. Charles S. Peirce on the Logic of Number, 2^nd ed. Boston: Docent Press, 2012.
Shin, S.-J. 2002. The Iconic Logic of Peirce’s Graphs. Cambridge, MA: MIT Press.
Short, T. L. 2007. Peirce’s Theory of Signs. Cambridge: Cambridge University Press.
Sowa, J. 2006. Peirce’s Contributions to the 21st Century, 14th International Conference on Conceptual Structures, Aalborg, Denmark, July 16-21, Lecture Notes in Computer Sceince, 4068, pp. 54-69.
Stjernfelt, F. 2014. Natural Propositions. The Actuality of Peirce’s Doctrine of Dicisigns, Boston: Docent Press.
Sylvester, J. J. 1878. On an Application of the New Atomic Theory to the Graphical Representation of the Invariants and Covariants of Binary Quantics. American Journal of Mathematics 1, pp. 64-104.
Tarski, A. 1941. On the Calculus of Relations. Journal of Symbolic Logic 6, pp. 73-89.
Tiercelin, C. 1991. Peirce’s Semiotic Version of The Semantic Tradition in Formal Logic. In New Inquiries into Meaning and Truth, N. Cooper & P. Engel eds. Harverest Wheatsheaf: St. Martin’s Press, pp. 187–210.
Van Heijenoort, J. 1967. Logic as Calculus and Logic as Language. Synthese 17, pp. 324–330.
Walsh, A. 2012. Relations between Logic and Mathematics in the Work of Benjamin and Charles S. Peirce. Boston: Docent Press.
Weiss, P. & Burks, A. 1945. Peirce’s Sixty-Six Signs. The Journal of Philosophy 42, pp. 383–388.
Zalamea, F. 2012a. Synthetic Philosophy of Contemporary Mathematics, Urbanomic.
Zalamea, F. 2012b. Peirce’s Logic of Continuity: A Mathematical and Conceptual Approach, Docent Press.
Zellweger, S. 1997. Untapped Potential in Peirce’s Iconic Notation for the Sixteen Binary Connectives. In Houser and others eds. 1997, pp. 334-386.
Zeman, J. 1964. The Graphical Logic of Charles S. Peirce, Ph.D. dissertation, University of Chicago.
Zeman, J. 1986. Peirceʼs Philosophy of Logic. Transactions of the Charles S. Peirce Society 22, pp. 1-22.

Author Information

Francesco Bellucci
Email: bellucci.francesco@gmail.com
Tallinn University of Technology
Estonia

and

Ahti-Veikko Pietarinen
Email: ahti-veikko.pietarinen@ttu.ee
Tallinn University of Technology
Estonia

Internet Encyclopedia of Philosophy