Intuitionism in Mathematics

In the philosophy of mathematics, intuitionism stems from the view originally developed by L. E. J. Brouwer that mathematics derives from intuition and is a creation of the mind. This view is prefigured most notably by Kant, Kronecker, Poincaré, Borel, and Lebesgue. Intuitionism maintains that a mathematical object exists only if it has been constructed and that a proposition is true only if a certain construction that realizes its truth has been carried out. Thus, intuitionism generally entails a form of anti-realism in ontology and truth-value, for mathematical objects exist and mathematical propositions have truth-values but never independently of our limited human cognitive faculties.

Intuitionism can also be understood as a reaction to Cantor’s set theory due to its attempt to tame the infinity in mathematics by accepting only potentially infinite objects, namely, actually finite objects which can always be extended into larger finite objects. In this respect, intuitionism preserves the spirit of ancient Greek mathematics, where actual infinity used to be avoided by techniques such as the method of exhaustion. In his systematic development of a new foundation of mathematics without actually infinite collections, Brouwer was famously led to abandon the law of excluded middle and to introduce a new finitary class of objects called “choice sequences” in order to reconstruct the theory of the continuum.

Intuitionism is one of the three major views that dominated debates in the foundations of mathematics during the first half of the 20^th century, along with logicism and formalism. It maintains against logicism that logic is merely a part of mathematics and against formalism that mathematics has meaning and is unformalizable. Intuitionism is also the only school among the three that was in effect largely reinforced by Gödel’s incompleteness results. Although it is classical mathematics and not intuitionistic mathematics that remains widely practiced, intuitionism has born many fruits in philosophy, mathematics, and computer science. Moreover, in addition to the historical significance of intuitionism, topics in its mathematics, logic, and philosophy continue to be actively explored.

This article surveys intuitionism as a philosophy of mathematics, with emphasis on the philosophical views endorsed by Brouwer, Heyting, and Dummett. Some preliminary remarks are in order. The term “intuitionism” is not synonymous with “constructivism”, an umbrella term that roughly refers to any particular form of mathematics that adopts “we can construct” as the appropriate interpretation of the phrase “there exists”. However, intuitionism remains one of the most prominent varieties of constructive mathematics. The curious reader can see the related article constructive mathematics for background. For more on the intuitionistic rejection of actual infinities, see also the article on the infinite. Finally, because intuitionism advocates a revision of classical mathematics, a certain amount of mathematical knowledge is required to fully appreciate some parts of this article, most importantly in the section on intuitionistic analysis. Readers can check any introductory textbook on classical real analysis or topology if they are not familiar with the terminology. Some familiarity with basic set theory is also presupposed in the first section on Brouwer, in particular regarding transfinite ordinals and uncountable cardinalities. Since the focus is intuitionistic mathematics, intuitionistic logic is not presented in this article. But for reference the appendix includes a list of notable theorems and non-theorems of intuitionistic logic.

Brouwer
Heyting
Dummett
Appendix: Intuitionistic Logic
1. Theorems of Intuitionistic Logic
2. Classical Theorems Unprovable in Intuitionistic Logic
References and Further Reading
1. Further Reading
2. References

1. Brouwer

The development of non-Euclidean geometry in the eighteen century put some serious pressure on the status of space as a pure form of intuition, for it is hard to determine which geometry best describes the space of our experience. Intuitionism represents Brouwer’s attempt to revise Kant’s philosophy of mathematics by renouncing the intuition of space altogether and developing a stronger commitment to the pure intuition of time. Simply put, Brouwer views all his intuitionistic mathematics as a product of temporal intuition. This means in particular that Brouwer is open to the use of the tools of analytic geometry to found geometry on real-number coordinates without appeal to spacial intuition.

According to Brouwer, mathematics is a human mental activity independent of language; mathematical objects exist only as mental constructions given in intuition; and there are no mathematical truths which are not graspable by intuition. This means that Brouwer is committed to a radical version of anti-realism better characterized as a form of mathematical idealism in ontology and truth-value: both the existence of mathematical objects and the truth-values of mathematical propositions depend on the mind.

Brouwer proposed various articulations of intuitionism throughout his career. The germ of his basic views on mathematical intuition, logic, and language can be traced back as far as his dissertation on the foundation of mathematics (Brouwer 1907). This section concentrates on the presentations found in Brouwer’s late writings. Their main distinctive feature is that the development of intuitionistic mathematics out of intuition is more methodically described by means of two acts (Brouwer 1952, 1954, 1981). These two acts are performed by an idealized mind known as the creating subject. The most comprehensive formulations of the background philosophy that he adopted to justify his two acts of intuitionism can be found in (Brouwer 1905, 1929, 1933, 1948b). The following sections examine each one of these acts in turn and discuss the role they play in Brouwer’s philosophical justification of his intuitionistic mathematics.

a. The First Act of Intuitionism

Intuitionistic mathematics is a creation of the mind and independent of language. Brouwer emphasizes this mental dimension of intuitionism with the first act, which at the same time separates mathematics from language and introduces the “intuition of twoity” as the foundation on which the whole edifice of intuitionistic mathematics rests:

[…] Intuitionistic mathematics is an essentially languageless activity of the mind having its origin in the perception of a move of time. This perception of a move of time may be described as the falling apart of a life moment into two distinct things, one of which gives way to the other, but is retained by memory. If the twoity thus born is divested of all quality, it passes into the empty form of the common substratum of all twoities. And it is this common substratum, this empty form, which is the basic intuition of mathematics (Brouwer 1981, pp. 4-5).

As this is a rather brief and difficult passage, the rest of this subsection takes a closer look at the mental construction of mathematical objects according to the intuition of twoity and explores the autonomy of intuitionistic mathematics from logic and language. This article draws from other works by Brouwer to clarify these aspects of the first act.

i. Mental Construction in Intuition

The empty twoity is the form “one thing and then another thing” shared by all twoities, where a twoity is a pair of a first sensation followed by a second one. We intuit a twoity by perceiving the succession of two experiences in time, which is understood not in the external sense of scientific time but in the internal sense of our time consciousness. For example, suppose that we listen to the sounds of two successive ticks of a clock. One tick is heard at the initial present stage of our awareness, then as the second tick is heard at a new stage, the first tick does not completely disappear from consciousness but is retained in our memory as just past. Finally, a twoity that pairs these sounds is experienced by thinking of both ticks together:

[…] The basic intuition of mathematics (and of every intellectual activity) as the substratum, divested of all quality, of any perception of change, a unity of continuity and discreteness, a possibility of thinking together several entities, connected by a ‘between’, which is never exhausted by the insertion of new entities. Since continuity and discreteness occur as inseparable complements, both having equal rights and being equally clear, it is impossible to avoid one of them as a primitive entity, trying to construe it from the other one, the latter being put forward as self-sufficient; in fact it is impossible to consider it as self-sufficient (Brouwer 1907, p. 8).

Some comments on the passage quoted above are needed. The same formulation of the intuition of twoity found in Brouwer’s statement of the first act is paraphrased in almost verbatim style multiple times in his later writings, but, as we can see above, he maintained the ideas already in his dissertation (Brouwer 1907, p. 9). The greatest difference is that in these early formulations he puts emphasis on a “between” that connects the two elements of our perception of two things in time and he insists that the discrete and continuum are both inseparable primitive complements of each other. From Brouwer’s introduction of the second act on, he almost never speaks of the irreducible continuum, but still stresses the creation of the between with a twoity (Brouwer 1981, p. 40). The postulation of choice sequences and species with the second act merely allows Brouwer to recognize the intuitive continuum as a “matrix of ‘point cores’” and study it mathematically.

Intuitionistically, the positive integers 1, 2, 3, … are represented in terms of finite ordinals. The intuition of twoity generates in the first instance the ordinal numbers two and one, as well as all other finite ordinal numbers by the indefinite repetition of the process. As the empty twoity is the form of two paired things, it can be viewed as a pair of units. One of its elements is defined as the number 1 and the empty twoity itself is the number2. The discrete fragment of intuitionistic mathematics arises from the basic operation of mentally constructing new twoities in intuition by pairing the empty twoity and its units:

This empty two-ity and the two unities of which it is composed, constitute the basic mathematical systems. And the basic operation of mathematical construction is the mental creation of the two-ity of two mathematical systems previously acquired, and the consideration of this two-ity as a new mathematical system (Brouwer 1954, p. 2).

We should stress that, as for Brouwer the empty twoity is intuited before its elements are, the number 2 is constructed before the number 1 in his mathematical universe. This is because 1 can only be constructed by projecting a unit out of the empty twoity. The intuitive nature of projection is often emphasized by van Atten (2004, §1.1; 2024, p.63). Brouwer thinks we could not have an empty unity as the starting point because the operation of adding another unit would already presuppose the intuition of twoity to form a pair of units:

The first act of construction has two discrete things thought together […] F. Meyer […] says that one thing is sufficient, because the circumstance that I think of it can be added as a second thing; this is false, for exactly this adding (i.e. setting it while the former is retained) presupposes the intuition of two-ity; only afterwards this simplest mathematical system is projected on the first thing and the ego which thinks the thing (Brouwer 1907, p. 179, fn. 1).

Indeed, the construction of all the positive integers proceeds as follows:

The inner experience (roughly sketched):
twoity;
twoity stored and preserved aseptically by memory;
twoity giving rise to the conception of invariable unity;
twoity and unity giving rise to the conception of unity plus unity;
threeity as twoity plus unity, and the sequence of natural numbers;
mathematical systems conceived in such a way that a unity is a mathematical system and that two mathematical systems, stored and aseptically preserved by memory, apart from each other, can be added; etc. (Brouwer 1981, p. 90).

It is important to note that Brouwer omits the construction of the number zero here. It is unclear whether this has to do with its lack of a direct representation in intuition, since it was common to exclude zero as a natural number during his time. In any event, Brouwer introduces zero into his mathematical ontology later as an integer. Kuiper (2004, ch. 2) proposes alternative ways to accommodate zero and describes constructions of the natural numbers and rationals from the intuition of twoity relying on the early notion of betweenness advocated in Brouwer’s dissertation. A recent interpretation of the construction of the positive integers based on Brouwer’s mature writings is developed by Bentzen (2023b, section 3.1) based on intuitive operations of pairing, projecting, and recollecting.

The intuition of twoity does not just yield the positive integers. Brouwer maintains that the first infinite ordinal number $\omega$ and all subsequent countable ordinals can be obtained by the indefinite repetition of the creation of twoities in time (Brouwer 1907, pp. 144-145). The first act of intuitionism is therefore also able to produce the sequence of mathematical objects $\omega,\omega+1,\omega+2,…,\omega + \omega, …,\omega \times \omega,\omega \times \omega + 1,…$, but it excludes uncountable ordinals. In fact, in his early writings, Brouwer can be found stressing that intuitionistic mathematics only recognizes the existence of countable sets (Brouwer 1913, p. 58). Recall that a set is countable if its elements can be put in a one-to-one correspondence with the elements of a subset of the set of natural numbers. Just as in classical mathematics, the continuum also remains uncountable intuitionistically. Of course, this does not mean that Brouwer is prepared to deny the existence of the continuum, but only that it cannot be reduced to a totality that is supposed to exist as a whole (Brouwer 1907, pp. 144-149). Intuitionistically, we can only make sense of an uncountable set as a “denumerably unfinished set”, namely, a set such that as soon as we think we have constructed more elements than those in a countable subset of it, we can immediately find new elements which should also belong to it. Notice that, after the introduction of the second act, this vague notion of set assumed in Brouwer’s early writings is abandoned in favor of his mature conception of species. In his later works the word “set” (Menge) is reserved for a spread, a particular kind of species of choice sequences. Choice sequences and spreads are examined in a later section.

ii. Logic and Language

Brouwer stresses that language can only play a non-mathematical auxiliary role in the construction of objects out of the intuition of twoity. For example, language can be used as a memory aid and to communicate some mathematical constructions to others, but what is written down can only be justified as an expression of our mental acts. This is why Brouwer maintains against Hilbert that freedom from contradiction can never guarantee existence. From the intuitionistic standpoint, to exist is to be constructed in intuition:

It is true that mathematics is quite independent of the material world, but to exist in mathematics means: to be constructed by intuition; and the question whether a corresponding language is consistent, is not only unimportant in itself, it is also not a test for mathematical existence (Brouwer 1907, p. 177).

In its purest form, intuitionistic mathematics consists of acts of construction in intuition. Logic and language only come into play later in its communication. This independence of mathematics from logic immediately leads to a repudiation of logicism, for, intuitionistically, mathematics is not part of logic. Rather, it is logic that is a part of mathematics:

While thus mathematics is independent of logic, logic does depend upon mathematics: in the first place intuitive logical reasoning is that special kind of mathematical reasoning which remains if, considering mathematical structures, one restricts oneself to relations of whole and part; the mathematical structures themselves are in no respect especially elementary, so they do not justify any priority of logical reasoning over ordinary mathematical reasoning (Brouwer 1907, p. 127).

Despite Brouwer’s general downplay of logic, he often stresses that if our mathematical constructions are put into words, the logical principles of the law of identity, the law of noncontradiction, and the Barbara syllogism can always be used to arrive at linguistic descriptions of new constructions (Brouwer 1908, pp. 155-156).. Nevertheless, he notes that in general this cannot be said of the law of excluded middle as well, namely, the principle that states that either a proposition or its negation holds, for any proposition. The law of excluded middle must be rejected in intuitionistic mathematics because it is taken to mean that every mathematical proposition can either be proved or refuted. The constant presence of open problems in mathematics indicates that this is not the case:

The question of the validity of the principium tertii exclusi is thus equivalent to the question concerning the possibility of unsolvable mathematical problems. For the already proclaimed conviction that unsolvable mathematical problems do not exist, no indication of a demonstration is present (Brouwer 1908, p. 156).

The rejection of the law of excluded middle is very subtle. To avoid confusion, notice that intuitionism simply does not accept that this law is generally valid for every proposition. It is not denied that the law might hold for certain propositions. Indeed, Brouwer insists that there will always be admissible uses of the law of excluded middle when dealing with properties about finite sets (Brouwer 1981, pp. 5-6). This is because an exhaustive verification running through the elements of the set one by one will always terminate. This leads to a proof or refutation of the finitary proposition in question. But we have to be careful when working with infinite sets because an exhaustive verification is not available to us. The repudiation of the law of the excluded middle for infinite domains is a direct product of Brouwer’s view of intuitionistic mathematics as an activity of the finite human mind.

When discussing logic in the first act of intuitionism, Brouwer often connects the rejection of the law of excluded middle to the existence of what he calls “fleeing” properties. Roughly, a fleeing property is a property of the natural numbers such that for every individual number it can be decided whether it holds or not, but we do not know a particular number for which it holds, nor that there is no number for which it holds. Now, Brouwer often refused to adopt logical symbolism in his writings perhaps due to his aversion to formalization, but we will not hesitate to employ formal notation in this entry for more precision. We say that a property $A$ on the natural numbers is fleeing if the following three conditions are met:

we know that $\forall n (A(n) \lor \neg A(n))$;
it is not known so far whether $\exists n A(n)$;
it is not known so far whether $\neg
\exists n A(n)$.

Every fleeing property therefore provides an unsettled instance of the excluded middle. Some properties may cease to be fleeing the moment it is found an $n$ such that $A(n)$ or if there emerges a proof that no such number exists, in which case $\exists n A(n) \lor \neg \exists n A(n)$ is decided. But there will always be other fleeing properties available to us. In fact, every open problem about the natural numbers naturally gives rise to a fleeing property, as shown in the following example. Suppose that $A(n)$ holds iff $n$ is a counterexample to Goldbach’s Conjecture, which states that every even natural number greater than $2$ is a sum of two primes. Since as of this writing this proposition remains a conjecture, we cannot tell whether there exists a counterexample nor whether it is impossible that a counterexample might exist. Yet, given any particular number we can, at least in principle, ignoring practical limitations of time, verify whether it is a counterexample or not because, once again, we are dealing with a decidable property over the natural numbers. Put differently, there exists an effective method for checking whether the property holds or not for each number.

Intuitionistic arithmetic is not quite different from its classical counterpart. One reason for their similarity is that equality between natural numbers is decidable, so $\forall n \forall m (n = m \lor \neg n = m)$ is an intuitionistically valid instance of the law of excluded middle. This is why Brouwer repeatedly insists that on the basis of the first act alone classical discrete mathematics “can be rebuilt in a slightly modified form” (Brouwer 1952, p. 142). Yet, there remains several theorems from classical number theory that cannot be proved intuitionistically. Perhaps the most notable case in point is the absence of the least number principle, which asserts that if a property on the natural numbers has a witness then it has a least one. To be exact, it can be expressed symbolically as $\exists n A(n) \to \exists n (A(n) \land \forall i (i < n \to \neg A(i)))$. Its failure in intuitionistic arithmetic is due to the presence of fleeing properties. To see this, let $B$ be a property such that $B(n)$ holds for all $n > 0$ but $B(0)$ holds iff $\exists n A(n)$, where $A$ is the property considered above tracking counterexamples to Goldbach’s Conjecture. If this conjecture is settled one day we can just pick another open problem to replace $A$. If the least number principle were to hold for $B$, we would already know whether $\exists n A(n)$ or not. ==Given that $A$ is a fleeing property, this is currently undecided (Posy 2020, section 2.2.1). Clearly there are some properties for which the least number principle holds. It is just not valid for every property in the intuitionistic setting as it is in classical number theory.

b. The Second Act of Intuitionism

We have seen that the first act of intuitionism postulates the construction of the positive integers in intuition as finite ordinals and all countable infinite ordinals. We also saw that intuitionistic arithmetic already diverges to some extent from classical arithmetic. It is however in its distinctive treatment of the continuum that the greatest differences between classical and intuitionistic mathematics begin to show. To arrive at a satisfactory approach to real analysis from the intuitionistic standpoint, Brouwer thought more powerful tools than those introduced in the first act are required. The second act postulates the admission of species and choice sequences into the domain of intuitionistic mathematical objects:

Admitting two ways of creating new mathematical entities: firstly in the shape of more or less freely proceeding infinite sequences of mathematical entities previously acquired (so that, for example, infinite decimal fractions having neither exact values, nor any guarantee of ever getting exact values are admitted); secondly in the shape of mathematical species, i.e. properties supposable for mathematical entities previously acquired, satisfying the condition that if they hold for a certain mathematical entity, they also hold for all mathematical entities which have been defined to be ‘equal to it, definitions of equality having to satisfy the conditions of symmetry, reflexivity and transitivity (Brouwer 1981, p. 8).

Once again, this is not an entirely clear formulation. In particular, Brouwer tends to be rather briefly worded in his articulations of what precisely a choice sequence is. The first place where choice sequences are accepted is (Brouwer 1914). However, it is not until later that they begin to be put to use in the intuitionistic modeling of the continuum by means of spreads. Without spending much time discussing these novel ideas, Brouwer simply introduces choice sequences as the paths through a spread (Brouwer 1918, p. 3). The notion of spread is examined more carefully when looking at species in a later section, but for now it will suffice to think of a spread as an infinitely branching tree described according to a certain law, where of course infinity is understood only in the sense of potential infinity. So, a choice sequence is viewed as a path of nodes growing indefinitely with some degree of freedom. While Brouwer does not go far beyond this initial vague explanation, he later revisits this characterization of choice sequences adding that we can restrict their freedom of continuation by a law after each choice as we wish (Brouwer 1925, fn. 3). Multiple passing remarks intended to elaborate on law restrictions can be found in his writings. For a period, Brouwer even hesitated about accepting higher-order restrictions, which allow for a restriction imposed on restrictions of choice of elements, and so on. But the details are unimportant for our purposes in this entry, given that the idea, first introduced in Brouwer 1942), was ultimately abandoned a decade later (Brouwer 1952, p. 142 fn.*). We shall therefore focus on the ordinary conception of choice sequence with first-order restrictions here. Readers interested in higher-order restrictions can see (van Atten and van Dalen 2002, pp. 331-335).

The above articulation of the second act also leaves out the two special ingredients that Brouwer invokes in his intuitionistic approach to real analysis, namely, his principles of continuity and bar induction. It is unclear whether Brouwer omitted them from his formulation of the second act because he viewed them as mere consequences of it. In any case, he never attempted to offer a justification for these principles in his writings, though as we shall see in the remainder of this section, they are far from being obvious. Regardless, the principles of continuity and bar induction are so important to intuitionistic analysis that it cannot be done without them. They are the ingredients that lead to notable results such as the uniform continuity theorem that actually contradict classical analysis. In the literature results like this are referred to as “strong counterexamples” because they reveal that intuitionistic analysis is not a merely restriction of its classical counterpart, as in the case of intuitionistic and classical arithmetic, but rather an incomparable alternative to it.

i. Choice Sequences and Continuity

Choice sequences are potentially infinite sequences of mathematical objects. That is, at every stage in time only a finite initial segment of the sequence has been constructed, but the sequence can always be continued with the inclusion of a new element. For example, if so far the creating subject has only constructed some initial segment $\langle 7, 5, 12, 8, 23 \rangle$, they can later pick another number of their choosing to extend the sequence with, say $42$. It is not possible to make an actually infinite number of choice of elements. Due to the inherently finite nature of the human mind the construction process can never be finished.

What is special about choice sequences and distinguishes intuitionism from all other variants of constructive mathematics such as Bishop’s brand of constructivism is that it is explicitly admitted that their elements need not be given by some law. Simply put, a law is any procedure that our minds can express by means of an algorithm. The notion of choice sequence also admits in addition to elements determined algorithmically a unique method of free choice that arbitrarily selects a new element. We sometimes say that these elements are chosen by the free will of the creating subject. In all his career Brouwer saw free choice as a necessary ingredient to go beyond the computable reals, the real numbers which can be computed by an algorithm and are classically countable. Heyting (1975, p. 607) notes that this conviction was invalidated when Bishop showed that the set of computable reals remains uncountable constructively if all functions admitted are algorithmic. In any case, choice sequences remain significant for their philosophical and mathematical interest.

It is time to take a closer look at what choice sequences are. Although, as we saw earlier, Brouwer does not actually say much about them, it is common in the literature to think of a choice sequence as a generalization of an algorithmic sequence (Troelstra 1977, section 1.7), that is, a sequence whose elements are all determined by an algorithm. Unless explicitly stated otherwise, we shall follow the usual convention of denoting algorithmic sequences using the small Latin letters $f, g, …$ and choice sequences using the small Greek letters $\alpha, \beta, …$ Now, to see how this generalization works, note that, given any algorithmic sequence $f$, an algorithm determines exactly one value $f(n)$ for every positive integer $n$. In contrast, given a choice sequence $\alpha$, we still retain $\alpha(n)$ as a value assigned for each $n$, but we cannot require that this value be effectively calculable by an algorithm. In general, at every stage only an initial segment may be known. But recall that Brouwer (1925, 1942, 1952) does emphasize that law restrictions can be imposed at will to the freedom of continuation of the sequence after each step of its construction. To express this more precisely, we may demand that for any finite initial segment $\langle \alpha(1), …, \alpha(n) \rangle$ for some positive integer $n$, there is an algorithm determining a non-empty range of possible values for $\alpha(n+1)$ onward. Simply put, instead of stipulating that an algorithm determines exactly one value, as in the case of algorithmic sequences, we just require that at each stage of the construction of a choice sequence its range of possible further values be determinable algorithmically. We can calculate the restrictions and even subject them to further restrictions at some later point in the ever-unfinished construction of the sequence. What need not be calculable ahead of time is the exact value of $\alpha(n)$ for every $n$. In sum, a choice sequence is given by an initial finite segment and a law that determines at every subsequence step of the sequence its range of possible future values. From this it immediately follows that, from the intuitionistic standpoint, an algorithmic sequence is nothing but a special case of a choice sequence in which its range of possible values always has exactly one element.

Now, let us look at some examples of choice sequences to illustrate the idea. The common practice in the literature is to distinguish between at least two different kinds of choice sequences depending on the information available to the creating subject:

lawlike sequences are choice sequences that are algorithmic. The simplest example is the sequence of positive integers, whose elements are completely determined by the number one and an effective rule that repeatedly applies the successor operation. But any more complex sequence calculable by an algorithm will do.
lawless sequences are choice sequences subject to no law restrictions. At each stage in their construction only a finite initial segment of them can be known. More precisely, after a fixed initial segment of the sequence is stipulated at the outset, there is no law limiting the range of possible future values. Perhaps the most well-known example is that of a sequence obtained by throwing a die with six faces $\{1,2,3,4,5,6\}$. For example, if we let $\alpha(1)=1$ be its initial segment, from this point on we cannot know in advance nothing more than that $\alpha(i) \in \{1,2,3,4,5,6\}$ for all $i > 1$. The terminology “lawless” was suggested by Gödel and introduced by (Kreisel 1968).

Some remarks are in order to avoid confusion. First, note that lawlike sequences are to be distinguished from general recursive sequences, for, as Heyting (1966) observes, the intuitionist does not accept Church’s thesis with respect to laws, which essentially states that every lawlike sequence can be computed by a Turing machine. Even if it might be compelling to identify “mechanically computable” with “calculable by a Turing machine”, there are still good reasons to abstain from Church’s thesis. Given that intuitionism is a product of the human mind, a law is understood as what is humanely computable, and that is to be distinguished from a mechanically computable process (Troelstra 1977, section 1.3). From the intuitionistic perspective, as the states of a mental calculation involve intentional aspects having to do with the basic mathematical intuition, for all we know, they might go beyond the artificial states of a Turing machine (Tieszen 1989, p. 81). In Brouwer’s work the notion of a law is accepted as primitive and left without a rigorous definition. His introduction of choice sequences predates the work of Church and Turing by nearly two decades, but even after that it appears that he never has commented on the status of Church’s thesis. For more on the acceptance of this thesis, see (McCarty 1987). Although most intuitionists tend to reject Church’s thesis, McCarty provides a systematic investigation of different ways in which it can be understood in intuitionistic mathematics. The alternative variety of constructivism that accepts this thesis is known as recursive constructivism.

Second, in the example given above of a lawless sequence, we have limited ahead of time the domain of the sequence to a proper subset of the positive integers. Put it differently, we have restricted all elements of the sequence to $\{1, 2, 3, 4, 5, 6\}$ from the very beginning, ruling out any other positive integers from the lawless sequence. However, how can this be possible if lawless sequences are supposed to be subject to no law restrictions? There is no contradiction, for our freedom to create a lawless sequence guarantees that the range of the sequence can be any range we want. We are always allowed to impose a “general a priori restriction” that all values belong to a certain domain (Troelstra 1977, section 2.2). It is conceivable, for instance, to have a lawless sequence of coin tosses that only has values in $\{1, 2 \}$ depending on whether we get heads or tails. What we cannot do is to impose a law during the construction of a lawless sequence to further restrict that domain.

Finally, the distinction between lawlike and lawless sequences is not exhaustive. It is a very common mistake to assume that all non-lawlike sequences are lawless. We simply call a sequence non-lawlike if it is a choice sequence that is not lawlike. Of course, every lawless sequence is non-lawlike by definition, but the converse is false. The following example illustrates why. Given two lawless sequences $\alpha$ and $\beta$, define a new choice sequence $\gamma$ by $\gamma(k)=\alpha(k)+\beta(k)$. Then $\gamma$ is subject to a law restriction, but is not given algorithmically. Another example is the choice sequence $\delta$ which oscillates between $\alpha$ and $\beta$ on even and odds arguments, that is, $\delta(2k)=\alpha(k)$ and $\delta(2k+1)=\beta(k)$. In general, non-lawlike sequences enjoy an intermediate degree of freedom, involving both law restrictions and free choice. The best well-known example of a class of choice sequences that exhibit this intermediate nature is that of hesitant sequences (Troelstra and van Dalen 1988, section 4.6.2), namely, choice sequences that start out lawless but a law may or may not be adopted to determine future values. If a law is accepted from the very beginning or never accepted then the particular sequence is in fact lawlike or lawless respectively, but it remains neither if the antecedent is not the case.

Continuity
Since choice sequences are permanently in a process of growth and can never be admitted as completed mathematical objects, how can we do mathematics with them? First of all, when dealing with choice sequences, we must carefully distinguish between intensional and extensional equality. As one might expect, two choice sequences $\alpha$ and $\beta$ are extensionally equal iff they have the same values for the same arguments: \[\alpha = \beta \leftrightarrow \forall n \alpha (n) = \beta (n).\]

Strictly speaking, however, we should also distinguish between the laws according to which the sequence might be given to us (Dummett 1977, section 3.1). Simply put, two sequences might be extensionally equal but still be intensionally different if they are given by different laws. We commonly write $\alpha \equiv \beta$ to indicate that $\alpha$ and $\beta$ are intensionally equal. We are often especially interested in properties that respect extensionality in intuitionistic mathematics. We say that a property $A$ of choice sequences is extensional iff the following holds: \[\forall \alpha \forall \beta (A(\alpha) \land \alpha = \beta \to A(\beta) ).\]

It is worth noting that a choice sequence might be extensionally equal to a lawlike sequence but not necessarily given as a lawlike one. It is not even generally possible to determine when a supposedly lawless sequence actually turns out to determine a lawlike sequence extensionally. To borrow Borel’s metaphor, if we give an infinite amount of time to a monkey hitting number keys at random in a typewriter, then in principle the monkey could end up reproducing the Fibonacci sequence, for instance. That is to say, the creating subject cannot be certain that they are not following an unknown law when constructing a choice sequence until the very end, and yet the construction will never end. Let me clarify that this does not mean that a lawless sequence can in fact be lawlike. We may say the sequence is intensionally lawless but extensionally lawlike in the sense above. In the remainder of this subsection, it is assumed that all properties are extensional. Now, to motivate Brouwer’s principle of continuity, it might be useful to start with some general remarks on the acceptance of the axiom of choice in intuitionism. The simplest version of the axiom states that if for every natural number $n$ there is some $m$ such that $A(n,m)$, there exists a function $f$ such that $A(n,f(n))$ for every $n$. In symbols: \[\forall n \exists m A(n,m) \to \exists f \forall n A(n,f(n)).\]

To avoid confusion, we stress that here $f$ denotes a function and not a lawlike sequence. The above principle is in fact perfectly valid intuitionistically. It is a direct consequence of the meaning of the intuitionistic logical constants, for the antecedent has a form $\forall x \exists y A(x,y)$ and its truth presupposes a procedure that ransforms every object $x$ into a pair that contains a specific $y$ and a proof that $A(x,y)$. We will look more closely at this informal semantics when studying Heyting’s meaning explanations in 2.2. The point is that the constructive meaning of existence yields an “operation” that in this particular case serves as a choice function because intensional and extensional equality coincide. Therefore, controversies surrounding the axiom of choice arise in intuitionistic mathematics only when intensional and extensional equality diverge. The reader is referred to (McCarty et. al. 2023) for a comprehensive overview of the status of the axiom of choice in various intuitionistic and constructivist systems. In the general version of the axiom of choice, we drop the above restriction to the natural numbers and consider any set (or rather species). In this form, the axiom is false because intensional and extensional equality need not always agree. We have already seen that that is not the case for choice sequences in general.

What does this have to do with continuity? We can think of a continuity principle as a more assertive version of the axiom choice that tells us how to manipulate choice sequences. If instead of the natural number $n$ we consider a choice sequence $\alpha$ in the above formula, the resulting version of the axiom of choice $\forall \alpha \exists m A(\alpha,m) \to \exists f
\forall \alpha A(\alpha,f(\alpha))$ is false. Even when $A$ is an extensional property, the function $f$ need not respect extensional equality. So, if $\alpha = \beta$ then $f(\alpha) = f(\beta)$ might not hold, unless $\alpha \equiv \beta$ also holds (Dummett 1977, p. 57). It is possible that $A(\alpha,f(\alpha))$ is true but not $A(\beta,f(\beta))$ or vice-versa, contradicting the assumption that $A$ is an extensional property. To overcome this obstacle, intuitionists need to impose an additional requirement to the admissible choice functions to guarantee the preservation of extensional propertiesand this is where continuity enters the picture. One solution is to restrict them to those belonging to a class of “neighborhood functions” $\mathbf{K}$ that allow us to determine their value in a finitistic way. They are usually denoted by the letter “$e$” rather than “$f$” in the literature because of their special status. If $e \in \mathbf{K}$, then $e(\alpha)$ is calculable from a finite amount of information known about $\alpha$, such as the finite initial segment of the sequence or the law restrictions imposed up until a certain stage. The value $e(\alpha)$ never depends on all the elements of the sequence, but only from what we know about $\alpha$ at some point. This means that such a function $e$ is in effect only ever applied to initial segments.

So, as the domain of a neighborhood function actually consists of finite sequences, strictly speaking, the notation “$e(\alpha)$” makes a category mistake. However, we can treat $e(\alpha)$ as an abbreviation for the value of $e$ on the smallest sufficiently long initial segment of $\alpha$. Put another way, if, intuitively, $e(\overline{\alpha}(n))=0$ means that the initial segment $\overline{\alpha}(n)$ is not sufficiently long enough to compute the value of $e$ for $\alpha$, then \[e(\alpha) \text{ is defined iff } \exists n (e(\overline{\alpha}(n)) > 0),\] \[e(\alpha)=k \text{ iff } \exists n (\overline{\alpha}(n) = k + 1) \land \forall m (m < n \to \overline{\alpha}(n) = 0).\]

Now, $e(\alpha)=e(\beta)$ holds because $e$ is continuous in a precise sense (Dummett 1977, p. 58). Although this is not to place to enter into detail, the basic idea is this. Suppose for the moment that we are dealing only with arbitrary, unrestricted choice sequences. Then the topological space in question can be studied as a Baire space, whose neighborhoods consist of all species of choice sequences sharing the same initial segment of some length. Readers need not worry if the concept of a Baire space is unfamilar to them, for it essentially describes the universal spread soon to be discussed in 1.2.2. Topologically, $e$ serves as a continuous function from this Baire space to the natural numbers with the discrete topology, the space consisting of every subset of the natural numbers as a neighborhood. Continuity means that, given any choice sequence $\alpha$, for every neighborhood $N(e(\alpha))$, there exists a neighborhood $M(\alpha)$ such that if $\beta \in M(\alpha)$ then $e(\beta) \in N(e(\alpha))$. The equality $e(\alpha)=e(\beta)$ immediately follows because, under the discrete topology, the singleton $\{ e(\alpha) \}$ is a neighborhood of its element. Notice that we only focused our attention on the universal spread in the example above for the sake of simplicity, but similar considerations also apply to neighborhood functions associated with choice sequences that admit restrictions.

Once again, it is not our interest to dive into topology in this survey. As far as intuitionism is concerned in the philosophy of mathematics, the important thing to keep in mind is that such a $\forall\alpha\exists n$-continuity principle results from the imposition of continuity to the otherwise problematic choice principle $\forall \alpha \exists m A(\alpha,m) \to \exists f \forall \alpha A(\alpha,f(\alpha))$ mentioned above. The antecedent remains unchanged, but the consequent states that there exists a neighborhood function $e$ such that for every $\alpha$ for which $e$ is defined, $A(\alpha, e(\alpha)$ holds. If we write $e(\alpha) > 0$ to mean that $e$ is defined for $\alpha$, then the resulting principle can be stated as follows:

\[\tag{C-N} \label{cn} \forall \alpha \exists n A(\alpha, n) \to \exists e \in \mathbf{K} \forall \alpha (e(\alpha) > 0 \to A(\alpha, e(\alpha))).\]

This is one of the formulations of Brouwer’s continuity principle. It is commonly described as the full version of continuity to distinguish it from a weaker formulation for the natural numbers that can be derived from it. Let the equality $\overline{\alpha}(m) = \overline{\beta}(m)$ abbreviate the fact that the initial segments of length $m$ of $\alpha$ and $\beta$ agree, which we can symbolically represent as $\forall i < m (\alpha(i) = {\beta}(i))$. We can state the weak continuity principle as:

\[\tag{WC-N} \label{wcn} \forall \alpha \exists n A(\alpha, n) \to \forall \alpha \exists m \exists n \forall \beta (\overline{\beta}(m) = \overline{\alpha}(m) \to A(\beta, n)).\]

The only difference between these two principles is the consequent. Indeed, in (WCN) the requirement that there be a neighborhood function is dropped. Informally, the consequent says that given an $\alpha$, we can find a fixed length $m$ such that for some $n$ and any $\beta$ whose the initial segments of length $m$ agrees with $\alpha$, $A(\beta,n)$ holds. As van Atten and van Dalen (2002) note, Brouwer used this continuity principle for the first time to show that the set of numerical choice sequences is not enumerable. They also investigate justifications for versions of the weak continuity principle (WC-N). As they point out, this principle is evident for lawless sequences because we never know more than a finite segment of them in advance. But for lawlike sequence it is less obvious since law restrictions might be taken into account.

These are not the only continuity principles considered in intuitionism. An even stronger form of continuity is usually discussed under the name of $\forall\alpha\exists\beta$-continuity. It can be regarded as a generalization of the full continuity principle (C-N) where the existential statement about numbers is instead about choice sequences. It is articulated by considering a partial higher-order function $|$ that given a neighborhood function $e$ and choice sequence $\alpha$ returns a choice sequence $e|\alpha$ if it satisfies some technical conditions (Dummett 1977, p. 60):

\[\tag{SC-N} \forall \alpha \exists \beta A(\alpha, \beta) \to \exists e \in \mathbf{K} \forall \alpha A(\alpha, e | \alpha).\]

The status of the $\forall\alpha\exists\beta$-continuity principle is more controversial. Dummett (1977, p. 222) sees this it as a dubious principle, as “it is far from plain that it is intuitionistically correct”. While it might initially be seen that $\forall\alpha\exists\beta$-continuity leads to contradictions in creating subject contexts, Posy (2020, pp. 73-74) explains that it is valid intuitionistically and that the clash only arises if one forgets about the restriction to extensional properties.

Continuity principles allow us to refute some classical theorems. It provides us with theorems that contradict results in classical mathematics. Iemhoff (2024) stresses that even the weak continuity principle implies the negation of a quantified version of the law of excluded middle $\neg\forall \alpha (\forall n \alpha(n)=0 \lor \neg \forall n \alpha(n)=0)$. More precisely, unlike intuitionistic logic, which is not incompatible with classically valid principles, intuitionistic mathematics actually refutes classical logic (not just classical mathematics)! The full continuity principle can be used to prove that every total real function is continuous in intuitionistic analysis. The intuitionistic construction of the real numbers is discussed in the next sub-section. To be clear, however, it should be emphasized that discontinuous functions can be defined, but they are not total (Posy 2020, p. 35). For an overview of these and other consequences of the continuity principles, such as a derivation of weak continuity (WC-N) from full continuity (C-N), see (Dummett 1977, pp. 60-67). A more general mathematical account is given by (Veldman 2021, sections 12-13).

ii. Species, Spreads, and Bar Induction

Species are the closest analog in intuitionism to sets as used in classical mathematics. But at the same time they exhibit significant differences that should be emphasized. In a nutshell, a species is a property that previously constructed mathematical objects may possess. When a species $S$ is defined by a certain property $A$, we write $S=\{x \mid A(x)\}$. If $A(a)$ holds, we say that a formerly obtained object $a$ is an element of $S$ and we write $a \in S$. Brouwer always highlights the following facts when introducing the notion of species in the second act:

1. a species can be an element of another species, but never an element of itself. That is to say that predicativity is a built-in feature of species. This is how the intuitionist is able to circumvent circularities like Russell’s paradox. In a sense, there is a clear resemblance with the theory of types (Heyting 1956b, section 3.2.3). The universe of species can be stratified into a hierarchy depending on their order: first-order species may only have elements which are not themselves given as species; second-order species may only have as elements objects given as first-order species and so on.

2. a species always has an equality relation defined among its elements. The equality associated with the definition of a species $S$ must always be an equivalence relation $R$ such that if $a \in S$ and $R(a,b)$ then $b \in S$. We write $a =_S b$ to denote $R(a,b)$. This ternary equality relation is to be distinguished from the binary relations of intensional and extensional identity considered previously for choice sequences, for instance.

3. we can redefine the same species time and again. To understand why this is useful, recall that only for entities constructed prior to the definition of a species may we ask if they possess the corresponding property. When a species $S$ is introduced no other mathematical object $b$ constructed after this point in time can be a member of it, even if they turn out to satisfy the same property $A$ that defined $S$! In order to accommodate this missing element, we can redefine the species $S$ again after constructing $b$. Thus, roughly speaking, a species can change their membership relation over time. We never lose its former elements but we might gain new ones after the redefinition.

Just as with the notion of a choice sequence, which necessarily grow over time, with species temporality is witnessed in the second act of intuitionism. This should not come as a surprise, for, as already seen earlier, intuitionistic mathematics is based on the intuition of time. Besides, like choice sequences, species are intrinsically intensional since two species are in fact one and the same only when given by the same property (van Atten 2004, pp. 6-7).

How are species used to construct the intuitionistic continuum? First, let us remark that the classical constructions of the set of integers $\mathbb{Z}$ and rationals $\mathbb{Q}$ are essentially acceptable intuitionistically, except that we are dealing with species instead. Moreover, it should be noted that they are not regarded as a finished totality. They can be defined with the usual equivalence relations by considering the equivalence classes as species. But due to the intensionality that species carry with them, we need to maintain some fine grained distinctions not present in classical set theory. For example, the subset of natural numbers in the integers $\mathbb{N}_\mathbb{Z}$ and in the rationals $\mathbb{N}_\mathbb{Q}$ are not identical species. The construction of the species $\mathbb{R}$ is sometimes said to be analogous to the construction of the reals in terms of Cauchy sequences in classical mathematics. This is true in a sense, but the description downplays the role of choice sequences. In the intuitionistic approach to mathematics, the notion of choice sequence first comes into play in the definition of $\mathbb{R}$ as the species of equivalence classes of convergent choice sequences of rationals (Heyting 1956b, section 3.1.1. Let $\alpha=\langle r_i \rangle_i$ be a choice sequence of rational numbers. We say that $\alpha$ is convergent iff its elements eventually get closer and closer to one another. More precisely, \[\forall k \exists n \forall m (|r_n – r_{n+m}| <_{\mathbb{Q}} 2^{-k}).\]

Two choice sequences $\alpha=\langle r_i \rangle_i$ and $\beta=\langle s_i \rangle_i$ coincide, in symbols, $\alpha \simeq \beta$, when their own elements eventually get closer and closer to one another: \[\forall k \exists n \forall m (|r_{n+m} – s_{n+m}| <_{\mathbb{Q}} 2^{-k}).\]

We call a convergent choice sequence of rational numbers a real number generator. Now, let a real number be the equivalence class $\{ \beta \mid \alpha \simeq \beta \}$ for some real number generator $\alpha$. Finally, the species $\mathbb{R}$ is simply defined as the species of all real numbers. For accessible accounts of the intuitionistic continuum, see (Dummett 1977, section 2.2) or (Posy 2020, section 2.2.2). It is worth emphasizing that, unlike in Bishop’s constructive mathematics, for example, intuitionistically the real numbers are not convergent sequences of rational numbers themselves. Real numbers remain treated as equivalence classes in intuitionism just as they are in classical mathematics. In this sense, intuitionism stays relatively closer to classical mathematics.

Spread

In fact, a species of choice sequences of rationals is what we call a spread. We can view a spread as a tree in which each node is a finite sequence but every path is infinite. As we mentioned earlier, a choice sequence can be identified with the paths of the tree. So spreads are essentially species of choice sequences sharing a law restriction. Although in the contemporary literature one often reduces the notion of spread to that of species, spreads were originally introduced by Brouwer as primitive mathematical objects. To be exact, a spread is defined by a spread law and a complementary law (Heyting 1956b, section 3.1.2). As shown below, the former serves to determine the admissible finite sequences of natural numbers, and the latter is used to map them to other mathematical objects.

The spread law classifies finite sequences into admissible and inadmissible. This law dictates the overall structure of the spread with an exhaustive account of all different admissible ways the finite sequences of natural numbers keep growing in time. Because it is exhaustive, it is possible to decide when a finite sequence is admissible or not, meaning that the excluded middle actually holds for finite sequences as far as the spread law is concerned. Moreover, the spread law always begins by including the empty sequence $\langle\rangle$ as admissible and from then on proceeds by determining what its admissible extensions are. We say that the finite sequence $\langle n_1, …, n_k, n \rangle$ is an extension of the finite sequence $\langle n_1, …, n_k \rangle$. So, to sum up, every spread law has to satisfy the following four conditions:

1. the empty sequence is admissible;

2. either a finite sequence is admissible or not admissible;

3. at least one extension of an admissible sequence is admissible;

4. no extension of an inadmissible sequence is admissible.

The complementary law assigns mathematical objects to the non-empty finite admissible sequences. In effect, it maps numeric choice sequences to choice sequences of elements of some species. For example, recall that in the construction of the continuum sketched above we work with choice sequences of rational numbers. Given that the species of real number generators is actually treated as a spread, as we already explained, in this case the complementary law assigns rational numbers to the non-empty finite sequences. Roughly, if the spread law provides an endoskeleton that supports the spread, the complementary law supplies the body tissue that reveals how it looks like. Spreads with only a spread law are called naked and those with a complementary law are called dressed. For example, the so-called “universal spread” is a naked spread of all finite sequences of natural numbers. It can be helpful to illustrate its tree structure diagrammatically. We start from the empty sequence as the root and then include its admissible extensions as its nodes: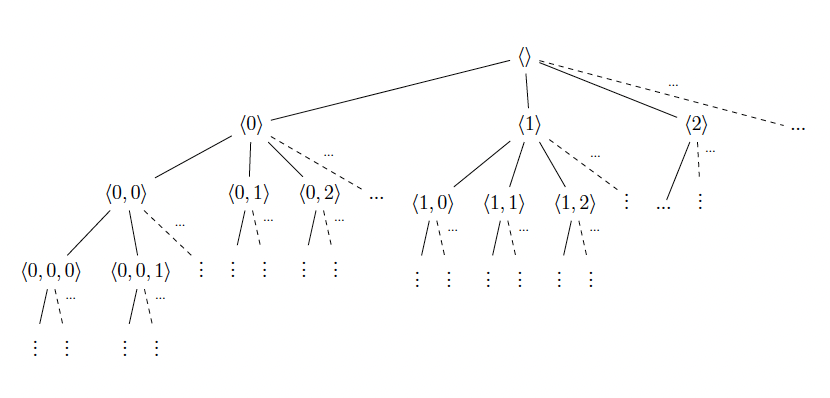The species of real number generators mentioned above is an example of a dressed spread. But for a more concrete example, consider the spread of binary sequences (Posy 2020, p. 31). The spread law specifies that for every admissible sequence $\langle b_1,…,b_k \rangle$, there are exactly two extensions $\langle b_1,…,b_k,0\rangle$ and $\langle b_1,…,b_k,1 \rangle$. The complementary law maps the sequence $\langle b_1,…,b_k\rangle$ to its last binary digit $b_k$. The spread can thus be visualized as follows: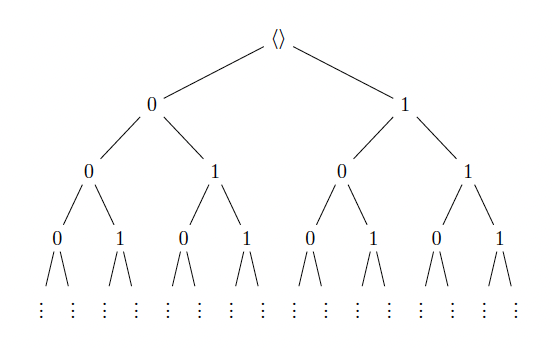Finally, what does it mean for a choice sequence $\alpha$ to be an element of a spread $M$? We write $\alpha \in M$ iff for every $n$, the complementary law assigns $\alpha(n)$ to an admissible sequence. In the simpler case of naked spreads, $\alpha \in M$ iff for every $n$, $\overline{\alpha}(n)$ is admissible. It should be noted this treatment of membership is just a particular case of species membership.

Fan

Fans are finitary spreads. Informally speaking, the paths along the tree structure of a fan remain infinite, but the tree admits only finite branching. The spread of binary sequences illustrated above is an example of a fan. Note also that the binary fan has uncountably infinitely many infinite paths in the form of all sequences of zeros and ones. So despite the finite branching, fans need not even have a countable number of paths. We may characterize a fan as a spread that imposes an additional requirement that, for every admissible sequence, the spread law specifies that only a finite number of extensions is admissible.

One of the most important results in intuitionism is the so-called “fan theorem”. It can be understood as the intuitionistic counterpart of König’s lemma in classical graph theory, which states that if there is no finite upper bound to the paths of a finitely branching tree then the tree has at least one infinite path. Classically, its contrapositive thus states that if every path in a finitely branching tree is finite then there exists a longest finite path. That is precisely what the fan theorem says in intuitionistic mathematics, except that “there exists” must be interpreted constructively and the context is transposed to fans. One difficulty is that, strictly speaking, the intuitionist cannot have a finite path in a fan, since every path in a spread is identified with a choice sequence and is thus infinite. To make sense of the idea that a path terminates in another way, Brouwer introduced the concept of a bar. Simply put, a bar $R$ is a species of “nodes” such that each path in a spread $M$ is intersected. To be exact, $R$ is a bar if every choice sequence in $M$ has some initial segment of some length in $R$: \[\forall \alpha \in M \exists n \overline{\alpha}(n) \in R.\]

Since the bar associates every choice sequence with a number, it in essence simulates some kind of oracle device telling us the lengths where the paths terminate. This captures the intuition that a finitely branching tree is finite. That is what a barred fan is. Now, in this intuitionistic terminology, we can express the idea that the fan has a finite path, namely, the consequent of König’s lemma, if we can determine a length such that every choice sequence in $M$ has initial segment no longer than this length in $R$: \[\exists m \forall \alpha \in M \exists n (n \leq m \land \overline{\alpha}(n) \in R).\]

We are now in a position to state the fan theorem:

Theorem 1 (Fan theorem). Let $M$ be a fan and $R$ be a species of finite sequences. If every $\alpha \in M$ has an initial segment of length $n$ in $R$, then there exists a longest length $m$ such that every $\alpha \in M$ has an initial segment no longer than $m$ in $R$:

\[
\tag{FT}
(\forall \alpha \in M \; \exists n \; \overline{\alpha}(n) \in R)
\;\to\;
(\exists m \; \forall \alpha \in M \; \exists n \; (n \leq m \;\land\; \overline{\alpha}(n) \in R)).
\]

But how is the fan theorem proved? The classical proof of König’s lemma makes use of an intuitionistically invalid inductive argument to show the existence of $m$ (Dummett 1977, p. 51). The intuitionist must therefore appeal to a different argument.

The proof of the fan theorem relies on an original argument known as the principle of bar induction. It can be stated without loss of generality for the universal spread $M$. Let $A$ be a subspecies of admissible sequences of $M$. Call $A$ *upward hereditary* if whenever every extension by one element of a finite sequence is in $A$, then so is the finite sequence itself.

In the unrestricted form conceived by Brouwer, the principle of bar induction states that, if $R$ is a bar, $R$ is a subspecies of $A$, and $A$ is upward hereditary, then the empty sequence belongs to $A$:
\[
\tag{BI}
\bigl(\forall \alpha \in M \; \exists n \; \overline{\alpha}(n) \in R \; \land\;\\
\forall u \,(u \in R \lor u \notin R) \;\land\; \forall u \,(u \in R \to u \in A) \; \land\;\\
\forall u \,(\forall n \,(u \cdot \langle n \rangle \in A) \to u \in A)\bigr) \;\to\; \langle \rangle \in A.
\]

Here $u \cdot \langle n \rangle$ denotes the extension of a finite sequence $u$ by one element $n$. It helps to think of $A$ as the species of those finite sequences for which we can find the length required by the consequent of the fan theorem. Indeed, the proof proceeds by instantiating $A$ with such a species $\{ u \mid \exists m \forall \alpha \in M \exists n (n < m \land \overline{\alpha}(n) \in R) \land \exists k \; u = \alpha(k) \}$.

Another key result in intuitionistic mathematics goes by the name of the “bar theorem”. The fan theorem can be easily confused with this theorem because it is also a result about bars. In fact, the bar theorem is simply the statement that bar induction holds. It should be noted that in bar induction the restriction that the spread must be finitary is dropped. So bar induction is maintained not just for fans but spreads in general. Brouwer originally derived the fan theorem using the principle of bar induction as a corollary of the bar theorem. The proof of the bar theorem is presented in three different articles (Brouwer 1924, 1927, 1954). His proofs have been extensively studied because they inaugurate a proof-theoretic method of analysis of the structure of canonical proofs. The bar theorem has even found applications in repairing Gentzen’s original proof of the consistency of arithmetic. But a careful study would be outside the scope of this introductory article. The reader is referred to Dummett (1977, section 3.4), Martino and Giaretta (1981), and Sundholm and van Atten (2008) for more on Brouwer’s proof and to Tait (2015) for connections with Gentzen’s original consistency proof.

It should be emphasized, however, that the principle (BI) originally formulated by Brouwer turns out to be false intuitionistically (Kleene and Vesley 1965, section 7.14). In this unrestricted form, bar induction implies a quantified version of the law of excluded middle and thus, as it can be inferred from 1.2.1.1, it must be inconsistent with the continuity principle. To fix this, Kleene proposes that we add an additional requirement that $R$ is decidable:

\[
\tag{BI$_D$}
\bigl(\forall \alpha \in M \; \exists n \; \overline{\alpha}(n) \in R \; \land\; \\ \forall u \,(u \in R \lor u \notin R) \;\land\; \\ \forall u \,(u \in R \to u \in A) \;\land\;\\ \forall u \,(\forall n \,(u \cdot \langle n \rangle \in A) \to u \in A)\bigr)
\;\to\; \langle \rangle \in A.
\]

(Van Atten 2004, section 4.3) argues that the decidability condition is implicit in Brouwer’s earlier proofs from 1924 and 1927, though not in the 1954 proof. Another intuitionistically valid formulation introduces a requirement of monotonicity. $R$ is monotonic if the fact that $u \in R$ and $v$ is an extension of $u$, $u \preceq v$, implies that $v \in R$:

\[
\tag{BI$_M$}
\bigl(\forall \alpha \in M \; \exists n \overline{\alpha}(n) \in R \land\ \\
\forall u (u \in R \land u \preceq v \to v \in R) \land\ \\
\forall u (u \in R \to u \in A) \land\ \\
\forall u (\forall n (u \cdot \langle n \rangle \in A) \to u \in A)\bigr) \to \langle \rangle \in A.
\]

Brouwer’s “proof” of the bar theorem is not actually a proof. Surely, it must be erroneous since the unrestricted form of bar induction used does not hold intuitionistically. But even if we correctly derive the bar theorem from decidable or monotonic bar induction, these principles are no less in need of justification than the statement to be proved. Still, despite its mathematical shortcomings, Brouwer’s argument remains philosophically significant in that it serves to shed light on the intuitive content of the bar theorem. Before concluding this discussion of Brouwer’s views, it should be remarked that the fan and bar theorems were primarily motivated by him as tools to prove the uniform continuity theorem, which states that every total real function is uniformly continuous. This is an even stronger counterexample than the continuity result mentioned in 1.2.1. Finally, we note that the fan theorem is incompatible with Church’s thesis (Dummett 1977, p. 53).

c. The Creating Subject

Intuitionism is the product of the activity of the creating subject, an idealized mind carrying out constructions and experiencing truths at discrete stages of time. (Brouwer 1948a) starts introducing in print arguments relying on the creating subject to construct weak and strong counterexamples to classical principles based on the solvability of open problems. Such arguments are ultimately grounded in Brouwer’s conception of truth, according to which a proposition is true if it has been experienced by the creating subject:

[…] truth is only in reality i.e. in the present and past experiences of consciousness. Amongst these are things, qualities of things, emotions, rules (state rules, cooperation rules, game rules) and deeds (material deeds, deeds of thought, mathematical deeds). But expected experiences, and experiences attributed to others are true only as anticipations and hypotheses; in their contents there is no truth (Brouwer 1948b, p. 1243).

At this stage [of introspection of a mental construction] the question whether a meaningful mathematical assertion is correct or incorrect, is freed of any recourse to forces independent of the thinking subject (such as the external world, mutual understanding, or axioms which are not inner experience) and becomes exclusively a matter of individual consciousness of the subject. Correctness of an assertion then has no other meaning than that its content has in fact appeared in the consciousness of the subject (van Stigt 1990, p. 450).

[…] in mathematics no truths could be recognized which had not been experienced […] (Brouwer 1955, p. 114).

There has been much debate about the exact nature of the creating subject. Brouwer is frequently accused of psychologism, subjectivism, or even solipsism. Placek (1999, section 2.4.1) defends Brouwer against the charges of psychologism and subjectivism by maintaining that the creating subject is a transcendental subject in Kant’s sense. The transcendence is hinted at in passages such as the above, where Brouwer stresses that all our physical and psychological limitations as human subjects are abstracted away, such as our finite lifespan, imperfect memory, mental state, mathematical proficiency. Although Brouwer does argue against the plurality of minds (Brouwer 1948b, pp. 1239-1240), Placek notes that there is still some room left for intersubjectivity, which allows for the possibility of communication with other minds equally equipped with all the cognitive structure assumed by Brouwer.

There is also some dispute as to whether the transcendental status of Brouwer’s creating subject is better understood from Kant’s or Husserl’s perspective. Perhaps because of the way Brouwer himself explicitly acknowledges his debt to Kant, the received view is the Kantian interpretation assumed by (Placek 1999). Similarities between Brouwer and Kant in the context of their transcendental philosophies are most systematically drawn by Posy (1974, 1991, 1998). At the same time, however, there are other similarities between Brouwer and Husserl that are just as difficult to ignore. Drawing from the phenomenology of inner-time awareness, van Atten (2004, section 6.2) argues that Brouwer’s creating subject is best analyzed using Husserl’s phenomenology. Further connections between Brouwer’s intuitionism and Husserl’s phenomenology have been explored especially by Tieszen (1989, 1995, 2008) and van Atten (2006, 2017, 2024). 2.2 shows that this phenomenological interpretation of intuitionism is originated by the meaning explanations advanced by Heyting in terms of fulfillments of intentions.

Creating Subject Argument:

It is time to return to the creating subject arguments. Brouwer realized that the way the creating subject experiences truths about open problems could be used to define choice sequences and generate counterexamples to emphasize the elements of indeterminacy in intuitionistic analysis. To see how this can be done, it might be instructive to examine a simple argument used by Brouwer as a weak counterexample to $\forall r \in \mathbb{R}(r \neq 0 \to r > 0 \lor r < 0)$ (Brouwer 1948a, p. 322). We say that a proposition $A$ is testable if the instance of the weak law of excluded middle $\neg A \lor \neg\neg A$ holds. Given a proposition $A$ not known to be testable, Brouwer maintains that the creating subject can construct a choice sequence $\alpha$ of rationals by making the following choices:

if during the choice of $\alpha(n)$ the creating subject has neither experienced the truth of $A$ nor its absurdity then choose $\alpha(n) = 0$;
if as soon as between the choice of $\alpha(k-1)$ and $\alpha(k)$, the creating subject has
experienced the truth of $A$ then choose $\alpha(k+n) = 2^{-k}$ for every $n$;
if as soon as between the choice of $\alpha(k-1)$ and $\alpha(k)$, the creating subject has
experienced the absurdity of $A$ then choose $\alpha(k+n) = -2^{-k}$ for every $n$.

Let us introduce some notation to make this definition a bit more mathematically precise. Brouwer’s tenet that “there are no non-experienced truths” can be understood as saying that, if a proposition $A$ is true, then it is not possible that there is no stage at which the creating subject is going to experience the truth of $A$. In the presence of a special notation $\Box_n A$ to express that “the creating subject has experienced the truth of $A$ at stage $n$”, then this fundamental tenet can be put into symbolic notation as:

\[A \to \neg
\neg \exists n \Box_n A.\]
The above definition can then be more rigorously stated as:

\[
\alpha(n) =
\begin{cases}
0 & \text{if } \neg \Box_n (A \lor \neg A) \\[6pt]
2^{-k} & \text{for all } n \geq k \text{ if } \Box_k A \text{ and } \neg \Box_{k-1}(A \lor \neg A) \\[6pt]
-2^{-k} & \text{for all } n \geq k \text{ if } \Box_k \neg A \text{ and } \neg \Box_{k-1}(A \lor \neg A).
\end{cases}
\]

$\alpha$ is convergent and thus a real-number generator. Yet, the real number $r$ generated by $\alpha$ cannot be $0$ because that would lead to a contradiction. If that were the case, $\alpha(n)=0$ for all $n$, meaning that $\forall n \neg \Box_n (A \lor \neg A)$. Intuitionistically, the De Morgan law $(\forall x \phi(x)) \to (\neg \exists x \neg \phi(x))$ and contraposition $(\phi \to \psi) \to (\neg \psi \to \neg\phi)$ are valid schemes. See the appendix for more information. The contradiction $\neg A \land \neg\neg A$ follows from the contrapositive of Brouwer’s tenet, $\neg \exists n \Box_n (A \lor \neg A) \to \neg (A \lor \neg A)$. This shows that $r \neq 0$. Yet, if $r > 0$, there is a $k$ such that $\alpha(n) = 2^{-k}$ and thus the truth of $A$ has been experienced, contradicting our assumption that $A$ is not known to be testable. Since the same can be said mutatis mutandis for $r < 0$, we have established that $r < 0 \lor r > 0$ does not hold. For an overview of this and other examples given by Brouwer, see (van Atten 2018).

Creating subject arguments tend to be seen as a controversial aspect of intuitionism because it is not clear how they qualify as mathematical arguments (Heyting 1956b section 8.12.1). In spite of the doubts surrounding them, they have been studied in the literature and different formalizations have been offered to make precise the assumptions underlying them. We conclude this section by presenting the two most influential proposals:

Kripke’s Schema:
\[\tag{KS} \label{wks}
\exists \alpha ((\neg A \leftrightarrow \forall n \alpha(n)=0)
\land (\exists n \alpha(n)\neq 0 \to A)).\]

This schema was proposed by Kripke in a letter to Kreisel around 1965 (Kripke 2019, fn. 8). This letter led Kreisel to formulate the theory of the creating subject to be seen soon. The schema is intended to describe the generation of a choice sequence $\alpha$ out of the truth or absurdity of a proposition $A$ experienced by the creative subject. Though Kripke originally formulated it in what is known as its weak form, there is a stronger and simpler form:

\[\tag{KS+} \label{sks} \exists \alpha (A \leftrightarrow \exists n \alpha(n)=1).\]

Van Atten (2018) stresses that both schemes are present in Brouwer’s published work.

The Theory of the Creating Subject:

\[
\begin{align*}
\tag{CS1} & \forall n (\Box_n A \lor \neg \Box_n A) \\
\tag{CS2} & \forall n (\Box_n A \to \Box_{n+m} A) \\
\tag{CS3} & \forall n (\Box_n A \to A) \\
\tag{CS4} & A \to \neg \neg \exists n \, \Box_n A.
\end{align*}
\]

The theory of the creating subject was originally proposed by Kreisel (1967, secton 3) and subsequently refined by Troelstra (1969, section 16). In their expositions they employ a turnstile notation to represent the creating subject and omit the universal quantifiers. The modal notation used here is introduced by Troelstra and van Dalen (1988, p. 236). The four axioms above emphasize that the creating subject continuously performs their mental activities one after another at stages of time. (CS1) states that $\Box_n A$ is decidable at every stage $n$, for the creating subject either experiences a truth or not. (CS2) expresses that truths experienced in past stages are never forgotten at subsequent stages. (CS3) encapsulates the plausible principle that experienced truths are indeed truths. At any stage $n$, if the creating subject has experienced the truth of $A$, then $A$ is true. (CS4) expresses the already familiar tenet discussed before. Importantly, (KS) is derivable from these four axioms. It can be derived with the strengthening of (CS4) proposed by Troelstra (1969, pp. 95-96): \[\tag{CS4+} \label{cs4plus} A \leftrightarrow \exists n \Box_n A.\]

For additional readings the reader is referred to (Posy 2020, sections 2.2.3 and 3.2.4).

2. Heyting

Although Brouwer downplays the roles of logic and language in his intuitionism, the development of intuitionistic logic by his student Arend Heyting and others has ironically made intuitionism more accessible and generated a growing interest. Historically, intuitionistic logic came into being when the Dutch Mathematics Society held a contest involving the formalization of intuitionistic logic and mathematics, and developed the first full axiomatization of intuitionistic first-order logic by isolating the set of intuitionistically acceptable axioms of Principia Mathematica. Heyting begins the undertaking with the following remark that echoes Brouwer’s attitude about language:

Intuitionistic mathematics is a mental activity, and for it every language, including the formalistic one, is only a tool of communication. It is in principle impossible to set up a system of formulas that would be equivalent to intuitionistic mathematics, for the possibilities of thought cannot be reduced to a finite number of rules set up in advance (Heyting 1930a, p. 191).

Perhaps because of Brouwer’s tendency towards anti-formalism, there is a popular narrative that his initial reaction to Heyting’s formalization work was negative. However, in reality Brouwer was very pleasantly surprised (van Stigt 1990, section 5.12.2-3). This survey article does not delve into intuitionistic logic and its formal developments. Instead, we refer the interested reader to the appendix for a list of notable theorems in intuitionistic logic and classical theorems that turn out unprovable within intuitionistic logic. Our focus is on the philosophical views that underlie Heyting’s presentation of intuitionistic mathematics. While they continued to be true to the spirit of his teacher’s intuitionism as a mental creation independent of language, his thought has evolved in many interesting directions. His liberalism and anti-metaphysics, meaning explanations for the logical connectives, and hierarchy of grades of evidence are some major contributions worth stressing.

a. Intuitionism Without Philosophical Subtleties

Perhaps the most relevant contrast in attitude is that Brouwer is a strong mathematical revisionist that sees classical mathematics as unjustified. Without making compromises, Brouwer was determined to make intuitionism prevail over formalism. Heyting, on the other hand, expresses a more liberal stance in the foundational debate, and is even willing to see intuitionistic mathematics as standing alongside classical mathematics. He is interested in promoting intuitionism so that working mathematicians could engage with its practice and not in witnessing the end of classical mathematics. In order to popularize intuitionism and minimize conflict with formalists, Heyting decided to present it as a simple program that banishes metaphysics from mathematics.

Brouwer’s own account of intuitionism is actually inseparable from a mystical perspective towards life that supports the intuition of twoity. This rather arcane doctrine states how consciousness moves away from its deepest home to the exterior world of the subject. The reader can refer to for an easy-to-follow overview of it. Given that these mythicist elements understandably tend to unsettle mathematicians, it is hardly surprising that these ideas are largely marginalized in Heyting’s work. Heyting emphasizes that to properly understand intuitionistic mathematics we do not need to adhere to this peculiar “psychological theory concerning the origination of knowledge”:

Brouwer’s explanations are incorporated in an exposition of his views on science in general and of an all-embracing conception of life and the world. Fortunately, in order to understand intuitionistic mathematics, it is not necessary to adhere to philosophic and psychological theories (Heytng 1958b, p. 102).

Heyting also dismisses the Kantian roots of intuitionism. Like Brouwer, Heyting stresses that intuitionism is an activity rather than a doctrine. It thus cannot be adequately described by means of a set of premises. Heyting sees this as reason to avoid looking for a basis for intuitionistic mathematics within some form of Kantian philosophical framework. He thinks the foundations of intuitionism should be erected on simple ordinary concepts that do not require any definite metaphysical considerations. For Heyting, intuitionism does not stand as a philosophical system on par with “realism, idealism, or existentialism”. In his view “the only philosophical thesis of mathematical intuitionism is that no philosophy is needed to understand mathematics” (Heyting 1974, p. 79). One might wonder how he may retain the mind-dependence of mathematical objects and truths without committing intuitionistic mathematics to a form of mathematical idealism. As we shall see, his answer seems to be that to practice intuitionism we do not need to pay attention to such questions.

Despite the rejection of any kind of philosophical system, Heyting still maintains the view that the intuition of twoity is the starting point of intuitionistic mathematics. The “two fundamental facts” of the “mental conception of an abstract entity, and that of an indefinite repetition of the conception of entities” is described not as part of a theory of knowledge but as a natural phenomenon of our daily lives. Everyone “knows how to build up mentally the natural numbers” from these two concepts and “knows what it means that their sequence can be made to proceed indefinitely” (Heyting 1958b, p. 102). Heyting stresses that the considerations about intuition are not metaphysical per se, for in intuitionistic mathematics we do not need to inquire how these two fundamental concepts are obtained:

They become so if one tries to build up a theory about them, e.g., to answer the question whether we form the notion of an entity by abstraction from actual perceptions of objects, or if, on the contrary, the notion of an entity must be present in our mind in order to enable us to perceive an object apart from the rest of the world. But such questions have nothing to do with mathematics. We simply state the fact that the concepts of an abstract entity and of a sequence of such entities are clear to every normal human being, even to young children (Heyting 1956b, p. 13).

b. The Meaning Explanations of the Intuitionistic Logical Constants

Brouwer viewed logic as a mere part of mathematics, never paying much attention to the study of intuitionistic logic as an independent discipline. He entrusted this task to Heyting, limiting himself to only a few scattered remarks on the proper interpretation of the intuitionistic logical connectives and the intuitionistic nature of truth in his work. In essence, according to intuitionism, a subject may only claim that a proposition is true when a construction required by the proposition has been carried out (Heyting 1958c, p. 278). Since truth requires an “introspective realization” of a mathematical construction, no subject-independent notion of truth is recognized in intuitionistic mathematics.

There was a heated debate in the twenties about the nature of intuitionistic logic, including contributions by Glivenko, Barzin and Errera, and others. Heyting developed in a series of papers his “meaning explanations” to address questions about the meaning of expressions occurring in a formal system of intuitionistic logic (Heyting 1930b, 1931, 1934). The meaning explanations serve as an informal semantics that endows every compound mathematical proposition formed by the intuitionistic logical connectives with meaning by establishing the intended interpretation of these connectives. It has led to the consolidation of what is today known as the BHK explanation of the logical connectives (Troelstra and van Dalen 1988, section 3.1). The acronym is a reference to its originators, Brouwer, Heyting, and Kolmogorov. Note that sometimes this explanation is described as an interpretation instead. There are good reasons to avoid this terminology since interpretations are commonly associated with formal semantics. The constructions that realize the truth of a propositions can be informally regarded as proofs. For this reason, the BHK explanation is also known as the proof explanation as well:

a proof of $A \land B$ is a pair containing a proof of $A$ and a proof of $B$;
a proof of $A \lor B$ is a either a proof of $A$ or a proof of $B$, plus the information of whether the left or right disjunct is the one being proved;
a proof of $A \to B$ is a method that transforms any proof of $A$ into a proof of $B$;
a proof of $\bot$ is not possible; $\neg A$ is defined as $A \to \bot$;
a proof of $\forall x \in A\, B(x)$ is a method that transforms any $x \in A$ into a proof of $B(x)$;
a proof of $\exists x \in A\, B(x)$ is a pair containing an $x \in A$ and a proof of $B(x)$.

By themselves these conditions have no explanatory power as a formal semantics. Whether or not they can invalidate the law of excluded middle, for example, depends on a concrete interpretation of “proof” and “method” (Troelstra and van Dalen 1988, ex. 1.3.4). Note also that the domain of quantification is a species. It can be omitted when the species is simple enough that $x \in A$ does not require a proof and we know the domain that $B$ ranges over. This was done above in formulas about numbers or numeric sequences. But even when this is not made explicit, quantification is always restricted to a domain. Intuitionism sees the totality of mathematical constructions as open-ended (Brouwer 1907, pp. 148-149). It cannot make sense of an unrestricted quantification over all mathematical objects.

It is important to distinguish the BHK explanation as presented above from Heyting’s own original ideas advanced in his meaning explanations. It is especially worth noting that he says nothing about the intuition of twoity. One might think that this is related to his general aversion to intricate philosophical considerations. Yet, in his explanations Heyting does borrow key concepts from Husserl’s theory of intentionality. This connection was first emphasized by Martin-Löf (1985) and Tieszen (1984). By interpreting proofs of propositions as fulfillments of intentions, Heyting alludes to the view of proofs as objects of intuition in Husserl’s sense. This suggests that the meaning explanations are elucidated in terms of intuition in the phenomenological sense of intentional fulfillments:

A mathematical proposition expresses a certain expectation; e.g. the proposition “The Euler constant $C$ is rational” means the expectation that one can find two integers $a$ and $b$ in such a way that $C = a / b$. Perhaps the word “intention” coined by the phenomenologists expresses even better what is meant here than the word “expectation”. I also use the word “proposition” for the intention expressed by the proposition. […] The assertion of a proposition means the fulfillment of the intention, e.g. the assertion “$C$ is rational” would mean that one has actually found the wanted integers (Heyting 1931, p. 113, our translation).

Unfortunately, Heyting does not say much more about the idea. But since then connections between intuitionism and phenomenology have been extensively explored in the literature. This propositions-as-intentions explanation in particular has been further extended by Tieszen (1989) to accommodate intuitions of natural numbers and finite sets and by van Atten (2004, 2006, 2017) to justify choice sequences as objects of intuition. It has also been severely criticized due to incompatibilities between Husserl’s strong platonist tendencies and other idealist aspects of Brouwer’s thought (Rosado Haddock 2010) (Hill 2010). In 2023, a stronger objection that, even if we overlook these tensions, propositions cannot be intentions and proofs cannot be fulfillments, has been raised: while intentions have to be directed to a unique object and can only be fulfilled with their presence, propositions, such as disjunctions and existential statements, can have different proofs (Bentzen 2023a, section 6.4).

Another significant contrast is that, as observed by Prawitz (2012), the term “proof” does not systematically appear in Heyting’s meaning explanations. Although in the BHK explanation the notion of provability is employed in every condition, Heyting himself only introduces proofs in his explanation of the clause for implication, writing that $A \to B$ means the intention of a construction which leads from every proof of $A$ to a proof of $B$. Even so, a proof of a proposition is explained as the realization of the construction required by it, a mathematical construction which can itself be treated mathematically (Heyting, 1934 p.14; 1931, p.114). That is, provability is not accepted as a primitive notion. This suggests that, in contrast to the formulation of the BHK explanation given above, proofs does not play a central semantic role in Heyting’s view. For him, proofs can be seen to receive their Brouwerian reduction to mental constructions given in intuition through their identification with intentional fulfillments. One difficulty with this strategy is that proofs are treated as objects, while fulfillments are mental processes. Tieszen (1989, pp. 86-87) argues that the objectification of a mental process can be achieved through an act of reflection, a higher-order intentional act that one directs at one’s own intentional experiences.

Heyting rejects the rather widespread explanation of “$A$ is true” as “$A$ is provable”. He sees the latter as equivalent to the phrase “there exists a proof of $A$”, which implies the idea of mind-transcendent existence of proofs. Intuitionistically, truth is understood as the establishment of an “empirical fact” about realization of expectations or fulfillment of intentions. It does not have to do with a state-of-affairs, but only with one’s own experiences. To assert the truth of a proposition $A$ is thus to maintain “we know how to prove $A$” (Heyting 1930b, p. 959).

c. The Hierarchy of Grades of Evidence

Brouwer developed intuitionism as a response to the paradoxes of set theory, ensuring that every theorem possesses intuitive content to guarantee the absence of contradictions. But for Heyting not even in intuitionistic mathematics can we achieve absolute certainty. He proposed a hierarchy that classifies what is intuitively clear in a descending order:

It has proved not to be intuitively clear what is intuitively clear in mathematics. It is even possible to construct a descending scale of grades of evidence. The highest grade is that of such assertions as $2 + 2 = 4$. $1002 + 2 = 1004$ belongs to a lower grade; we show this not by actual counting, but by a reasoning which shows that in general $(n + 2) + 2 = n + 4$. Such general statements about natural numbers belong to a next grade. They have already the character of an implication: ‘If a natural number $n$ is constructed, then we can effect the construction, expressed by $(n + 2) + 2 = n + 4$’. This level is formalized in the free-variable calculus. I shall not try to arrange the other levels in a linear order; it will suffice to mention some notions which by their introduction lower the grade of evidence.

The notion of the order type $\omega$, as it occurs in the definition of constructible ordinals.

The notion of negation, which involves a hypothetical construction which is shown afterwards to be impossible.

The theory of quantification. The interpretation of the quantifiers themselves is not problematical, but the use of quantified expressions in logical formulas is.

The introduction of infinitely proceeding sequences (choice sequences, arbitrary, functions).

The notion of a species, which suffers from the indefiniteness of the notion of a property. The natural numbers form a species; all species do not. It is doubtful whether all species of natural numbers form a species; therefore I prefer not to use this notion (Heyting 1966, p. 195).

Let us go over his hierarchy from the highest to the lowest grades of evidence. First, we have particular propositions about small numbers. They have the highest grade because they are immediately evident (Heyting 1958a, p. 335-336). The second highest grade of evidence is that of particular propositions about larger numbers. Heyting maintains that there is loss in evidence because they tend to be demonstrated as instances of a general rule. For example, when asked to show that $135664 + 37863 = 37863 + 135664$ most people will appeal to the fact that $n + m = m + n$ for every $n$ and $m$ instead of counting. The third highest grade of evidence is that of such general numeric propositions. The issue at stake here is that such a general proposition has a hypothetical nature. Heyting does not elaborate, but the fact that general numeric propositions cannot be verified by calculation and need to be proved by induction presumably has to do with the loss of evidence. What about the lowest grade described in (1)–(5)? Heyting follows Griss (1946) in admitting that we descend into an even lower grade when we introduce negations, since the implication is less certain when the hypothetical constructions cannot be carried out. He also mentions the theory of quantification, but since general propositions have already been placed one level above, it is not entirely clear what kind of propositions he has in mind. Infinity is also found at the bottom of the hierarchy in the form of the introduction of $\omega$ and choice sequences. Heyting places the notion of species in the lowest grade, for there is no precise definition of what a property is. Note that each one of these represent a different and incomparable lowest grade.

3. Dummett

Mental constructions in intuition play a key role in the writings of Brouwer and Heyting. Dummett’s seminal work marked a notable departure from their tradition. Restricting his attention to only logic and not all of intuitionistic mathematics, he wishes to justify the rejection of classical logic in favor of intuitionistic logic. This is done by means of an original meaning-theoretic argument where intuition is replaced by provability as the fundamental notion that grounds meaning and truth (Dummett 1975, pp. 6-7, 16-17). More generally, unlike Brouwer and Heyting, Dummett denies the mind-independence of both mathematical objects and truths without maintaining their mind-dependence. This position leads to an intuitionism without intuition that subscribes only to anti-realism and not to idealism.

a. The Meaning-Theoretic Turn

For Dummett, the meaning of a sentence is manifested in its use. Dummett concludes from this that meaning should be given in terms of proof, given that in ordinary mathematical practice using a sentence expressing a theorem is the same as using a proof of it or at least recognizing such a proof when we are presented with one. Dummett’s program can be seen as a rearticulation of the meaning explanations proposed by Heyting through the late Wittgenstein’s idea that the meaning of a word can be determined by its use.

Dummett forcefully rejects Brouwer’s views. Dummett sees the meaning of a sentence as a product of its function as an instrument for communication. An individual cannot assign a personal mental image to the meaning of a sentence that cannot be observed by its communication. For him explaining meaning by appealing to a subjectivist notion of mental construction in intuition invites the threat of solipsism. In fact, Dummett describes Brouwer’s philosophy as “psychologistic through and through” (Dummett 1980). We must understand meaning in terms of mind-independent verifiability conditions.

Realism violates the principle that use exhaustively determines meaning, for it determines meaning by truth-conditions which are in general not verifiable. The roots of Dummett’s rejection of realism and general appreciation of the intuitionistic standpoint can already be found in his earlier investigations about truth (Dummett 1959, pp. 160-162). The principle that meaning is use is perfectly consistent with the BHK explanation. Dummett observes that to conform with this principle we must also replace the notion of truth by that of proof. How should this meaning-theoretic argument for intuitionism analyze truth in such terms? There are two fundamental principles that in his view the notion of truth should satisfy:

(K) If a statement is true, it must be in principle possible to know that it is true.

The first principle can be traced back to classical correspondence theories of truth. It is also valid intuitionistically as long as the truth-makers are identified with proofs. The second principle requires commitment to anti-realism. How to satisfy these principles? This raises several difficult questions about existence, temporality, and provability which Dummett acknowledges but does not offer a conclusive answer for. Consider how the truth of the proposition $598017 + 246532 = 844549$, for example, may be verified. Dummett writes:

We may perform the computation, and discover that $598017 + 246532$ does indeed equal $844549$: but does that mean that the equation was already true before the computation was performed, or that it would have been true even if the computation had never been performed? The truth-definition leaves such questions quite unanswered, because it does not provide for inflections of tense or mood of the predicate ‘is true’: it has been introduced only as a predicate as devoid of tense as are all ordinary mathematical predicates (Dummett 1975, pp. 24-25).

Should one reduce “$A$ is true” to “$A$ is provable” or “$A$ has been proved”? This introduces in Dummett’s rearticulation of intuitionism what Raatikainen (2004) calls the distinction between the actualist and possibilist conceptions of truth. To endorse the actualist view is to introduce tense in mathematics, as Dummett admits, while under the possibilist view truth remains timeless just as it is in a classical account. We should stress that the ambiguous modality involved in “provable” further complicates the possibilist view. In his attempts to elucidate the possibility of proof existence involved in the account, Prawitz even goes as far as endorsing ontological realism for proofs (Prawitz 1987, pp. 153-154). Dummett fears that allowing for the existence of unknown proofs in such a static mathematical reality leads to the validation of the excluded middle and thus cannot accept the proposal. Dummett does not consistently subscribe to either the actualist or possibilist conception in his writings. Unlike the account of truth envisioned by Brouwer and Heyting seen in the previous sections, in Dummett there is no reference to intentional content because truth has been desubjectivized. It is no longer, so to speak, a first-person notion that appeals to the creating subject, as it was since Brouwer, but a notion analyzed strictly from a third-person perspective.

One of Dummett’s major contributions to intuitionism is the introduction of a crucial distinction between canonical and non-canonical proofs. Roughly, a canonical proof has an explicit form by which it can be directly checked that it proves a proposition; a proof is non-canonical if it is not in canonical form, but an effective method can reduce it to a canonical proof in a finite period of time (Dummett 1975, pp. 31-35). The notion of proof presupposed in the BHK explanation has to be limited to that of canonical proof. Clearly, even in intuitionistic mathematics, a proof of a conjunction $A \land B$, for example, need not consist in a pair of proofs of $A$ and $B$ explicitly. We may prove the conjunction indirectly, say, by modus ponens, if we have proofs $C \to A \land B$ and $C$ in hand. Dummett also contemplates connections between canonical proofs and normalized proofs in proof systems of natural deduction, on the one hand, and canonical proofs and Brouwer’s fully analyzed proofs in his proof of the bar theorem, on the other.

The notion of canonical proof has been instrumental in the further development of mathematical constructivism with the Swedish school led by Prawitz, Martin-Löf, and Sundholm, which pushed forward the meaning-theoretic approach inaugurated by Dummett in different directions. Prawitz founded proof-theoretic semantics as an attempt to convert the BHK explanation into a formal semantics complete with respect to intuitionistic logic (Prawitz 1971, 1973, 1974). Martin-Löf kept the explanation informal but extended its scope to offer a philosophical justification for the axioms and rules of inference of his constructive type theory (Martin-Löf 1984), a formal system developed to establish a rigorous foundation for Bishop’s brand of constructive mathematics. The formalism is based on a correspondence between propositions and types sometimes known as the Curry–Howard isomorphism. See (Sundholm 2004) for an overview of anti-realism in this type-theoretic tradition.

b. Against the Ontological Route

Dummett (1975, pp. 38-40) argues that the meaning-theoretic argument outlined above is the only correct route to the justification of intuitionistic logic. Of course, questions of meaning were already considered to some extent in the works of Brouwer and Heyting. But their main focus has always been epistemological: their intuitionism reflects the mental activity of the creating subject carrying out constructions in intuition. With Dummett, the matter of how mathematical objects are given to us is given a semantic answer: what in analytic philosophy is known as Frege’s linguistic turn is replicated in intuitionistic mathematics. In other words, intuitionism ceases to be primarily a theory of knowledge with semantic overtones and becomes primarily a theory of meaning with epistemic overtones.

Part of the strength of Dummett’s meaning-theoretic turn derives from his rejection of another argument for intuitionistic logic that is ontological in nature. It starts with the doctrine that natural numbers are the creations of human thought (Dummett 1975, pp. 18-19). Without presupposing any sort of theory of meaning, he implies that we may only elucidate truth for decidable arithmetical statements by means of actually performed computations:

[…] it has now become apparent that there is one way in which the thesis that natural numbers are creations of the human mind might be taken, namely as relating precisely to the appropriate notion of truth for decidable statements of arithmetic, which would provide a ground for rejecting a platonistic interpretation of number-theoretic statements generally, without appeal to any general thesis concerning the notion of meaning. This way of taking the thesis would amount to holding that there is no notion of truth applicable even to numerical equations save that in which a statement is true when we have actually performed a computation (or effected a proof) which justifies that statement. Such a claim must rest, as we have seen, on the most resolute scepticism concerning subjunctive conditionals: it must deny that there exists any proposition which is now true about what the result of a computation which has not yet been performed would be if it were to be performed (Dummett 1975, p. 40).

The problem with this “hard-headed” view, according to Dummett, is that it entails a strong form of skepticism about subjunctive conditionals. If we can only explain truth for decidable arithmetical statements by appealing to actual computations, Dummett thinks we necessarily rule out the existence of propositions which are now true about the result of a yet-to-be-performed computation. For example, it is easy to tell now that $10^{100} + 10^{10} = 10^{10} + 10^{100}$ is true even before performing the calculations involved in the equation. Dummett sees ontological intuitionism as an unattainable position because, in his view, it must reject such kind of reasoning about subjunctive conditionals. One might resist Dummett’s argument by noting that actual computations need not play a decisive role in determining truth. If numbers are the creations of human thought, then some truth-makers of propositions may also come into being in time. Van Atten (2022) presents an excellent reconstruction of Dummett’s arguments and launches a defense of the ontological route in this direction.

c. Sense and Reference

Dummett (2021) also considers a sense-reference distinction for constructive semantics. In a nutshell, the basic insight behind his distinction is that the sense of an expression is related to its reference as a program is related to its execution. That is, under an intuitionistic point of view, the sense of an expression must be an effective method for computing its reference, whereas the reference must be what results after the method is fully carried out. The idea has its roots in Dummett’s early commentaries on Frege’s own semantic distinction:

Frege’s argument about identity statements would be met by supposing the sense of a singular term to be related to its reference as a programme to its execution, that is, if the sense provided an effective procedure of physical and mental operations whereby the reference would be determined (Dummett 1978, p. 133).

How to implement such a distinction? Dummett classifies expressions in two main groups, namely, that of predicates, relational expressions, and logical constants, on the one hand, and that of singular terms and functional expressions, on the other. To specify the meaning of predicates, relational expressions, and logical constants we must rely on the notion of proof, but a semantic analysis of singular terms and functional expressions can be done directly without explicit mention of proofs (Dummett 2021, pp. 489-494). Predicate-like functional expressions in the Fregean sense are excluded from the second group. The meaning of the logical constants is fixed by the BHK explanation. Dummett adds that the meaning of a predicate consists in a means of recognizing a proof that the predicate applies to a given object. Dummett relates this conception of meaning to sense and reference as follows:

We grasp the meaning of a predicate when we know how, for any element of the domain over which it is defined, to classify mathematical constructions into those that do and those that do not prove that it satisfies the predicate; and just that principle of classification is the semantic value of the predicate (Dummett 2021, p. 490).

What we grasp when we understand a predicate is its sense. Here “semantic value” is simply Dummett’s word for the intuitionistic counterpart of reference. Dummett concludes from this that there is no room for a sense-reference distinction for predicates, for “the semantic value of the predicate and what we grasp when we understand it are one and the same” (p.491). He sees the problem as the explanation of the meaning of a predicate in terms of proofs. Given that the same can be said of the meaning of relational expressions and logical constants, there can be no distinction between sense and reference for them either.

What about singular terms and functional expressions? Dummett argues that insofar as we are dealing with natural numbers or other finitely presented mathematical objects, we can distinguish the sense and reference of their corresponding expressions. To illustrate this, he points out that the same natural number may be given in different ways. The number thirteen can be presented to us as $13$ or $4 + 3^2$, for example, and the equality $13 = 4 + 3^2$ may even extend our knowledge, if analytic judgments are allowed to be ampliative. We may thus regard numerals as “aiming at natural numbers by varying routes” (p.493). Yet, we cannot do the same for expressions for real numbers or other not finitely given mathematical objects. The particular way a real number is given to us might affect what counts as a proof of a proposition about it. As a result, their sense is part of their semantic value:

A real number, such as $\pi$, can be given in different, even though provably equivalent, ways. For classical mathematicians and constructivists alike, the specific way in which the number $\pi$ is given affects what is required for a proof of a statement about it, at least until the different possible definitions have been proved equivalent; that is why the sense of an expression, and not just its reference, must be something common to all. In classical semantics, however, the semantic value of a term denoting $\pi$ will be its contribution to what determines, not what is required to prove a statement in which it occurs, but its truth-value, and that is just the denotation of the term, the number $\pi$ itself; that is why its sense is not part of its semantic value. In a constructivist meaning-theory, by contrast, the semantic value of the term is, precisely, its contribution to determining what is to count as a proof of any statement in which it occurs; and therefore the way in which the denotation is given to us is an integral ingredient of its semantic value (Dummett 2021, p. 494).

These considerations also extend to functional expressions, since infinite sequences may be regarded as functions from the natural numbers. In sum, for Dummett the intuitionist cannot generally maintain a sense-reference distinction not even for singular terms or functional expressions because of the intensional treatment that infinitary objects receive. A more optimistic rearticulation Dummett’s semantic views is proposed by Martin-Löf (2021) against the background of constructive type theory. Bentzen (2020, 2022) advances yet another type-theoretic reformulation of the sense-reference distinction. See (Klev 2022) for a comprehensive account of identity in constructive type theory.

4. Appendix: Intuitionistic Logic

Intuitionistic logic can be roughly viewed as classical logic without the law of excluded middle. Below is a non-exhaustive list of some notable theorems of intuitionistic logic as well as some notable classical theorems that are not provable in intuitionistic logic. Some of them have been important enough in the literature to deserve their own names. Others have been grouped together under a certain theme. If you see an implication but not a biconditional in the intuitionistic theorems, it is typically because the converse fails.

a. Theorems of Intuitionistic Logic

$\phi \to \neg\neg\phi$ (double negation introduction)
$\neg (\phi \land \neg \phi)$ (law of non-contradiction)
$\neg\neg (\phi\lor \neg \phi)$ (double negative law of excluded middle)
$\neg\neg\neg \phi\leftrightarrow \neg \phi$ (law of triple negation)
$(\phi\lor \neg \phi) \to (\neg\neg \phi\to \phi)$ (excluded middle implies double negation elimination)
$\phi \to (\neg \phi \to \psi)$ (ex falso quodlibet)
$(\phi \to \psi) \to ((\phi \to \neg \psi) \to \neg \phi)$
$(\phi \to \psi) \to (\neg \psi \to \neg\phi)$ (contraposition)
$(\phi \to \neg\psi) \to (\psi \to \neg\phi)$
$(\phi \to \psi) \to \neg (\phi \land \neg \psi)$
$\phi \land \neg \psi \to \neg (\phi \to \psi)$
$(\phi \to \neg\psi) \leftrightarrow \neg (\phi \land \psi)$
$\neg (\phi \to \psi) \to \neg\neg \phi \land \neg \psi$
$(\phi \lor \psi) \to (\neg \phi \to \psi)$ (disjunctive syllogism)
$(\neg\phi \lor \psi) \to (\phi \to \psi)$
$(\neg\neg \phi \to \neg\neg \psi) \leftrightarrow \neg\neg (\phi \to \psi)$ (double negation distribution)
$\neg\neg (\phi \to \psi) \to (\phi \to \neg\neg \psi)$
$(\neg\neg \phi \to \neg\neg \psi) \leftrightarrow (\phi \to \neg\neg\psi)$
$(\neg\neg \phi \land \neg\neg \psi) \leftrightarrow \neg\neg (\phi \land \psi)$
$(\neg\neg \phi \lor \neg\neg \psi) \to \neg\neg (\phi \lor \psi)$
$(\neg (\phi\lor \psi)) \leftrightarrow (\neg \phi\land \neg \psi)$ (de Morgan laws)
$(\neg \phi \lor \neg \psi) \to (\neg (\phi \land \psi))$
$(\phi\lor \psi) \to \neg (\neg \phi\land \neg \psi)$
$(\phi \land \psi) \to \neg (\neg \phi \lor \neg \psi)$
$((\phi\lor \neg \phi) \to \neg \psi) \leftrightarrow \neg \psi$ (the excluded middle dictates falsity)
$(\phi \lor \forall x \psi(x)) \to (\forall x (\phi\lor \psi(x)))$ (universal distribution of disjunction)
$(\phi \land \exists x \psi(x)) \leftrightarrow (\exists x (\phi \land \psi(x)))$ (existential distribution of conjunction)
$(\neg\neg \forall x \phi(x)) \to (\forall x \neg\neg \phi(x))$ (converse of double negation shift)
$(\exists x \neg\neg \phi(x)) \to (\neg\neg \exists x \phi(x))$
$(\neg \exists x \phi(x)) \leftrightarrow (\forall x \neg \phi(x))$ (generalized de Morgan laws)
$(\exists x \neg \phi(x)) \to (\neg \forall x \phi(x))$
$(\forall x \phi(x)) \to (\neg \exists x \neg \phi(x))$
$(\exists x \phi(x)) \to (\neg \forall x \neg \phi(x))$
$(\exists x \phi \lor \psi(x)) \to (\neg \phi \to \exists x \psi(x))$
$(\exists x (\phi \to \psi(x))) \to (\phi \to \exists \psi(x))$
$(\exists x (\phi(x) \to \psi)) \to (\forall x \phi(x) \to \psi)$
$\phi \lor \neg\phi \to ((\phi \to \exists x \psi(x)) \to \exists x (\phi \to \psi(x)))$

b. Classical Theorems Unprovable in Intuitionistic Logic

$\neg\neg\phi \to \phi$ (double negation elimination)
$\neg (\phi \land \neg \phi) \to (\phi \lor \neg \phi)$ (non-contradiction implies excluded middle)
$\phi\lor \neg \phi$ (law of excluded middle)
$\neg\neg \phi \lor \neg \phi$ (weak law of excluded middle)
$(\neg\neg \phi \to \phi) \to (\phi \lor \neg \phi)$ (double negation elimination implies excluded middle)
$((\phi \to \psi) \to \phi)\to \phi$ (Peirce’s law)
$(\neg\phi \to \psi) \to ((\neg\phi \to \neg \psi) \to \phi)$
$(\phi \to \psi) \lor (\psi \to \phi)$
$(\neg \phi \to \psi \lor \chi) \to ((\neg\phi \to \psi) \lor (\neg\phi \to \chi))$ (Harrop’s rule)
$(\neg \psi \to \neg\phi) \to (\phi \to \psi)$ (converse of contraposition)
$(\neg \phi \to \psi) \to (\phi \lor \psi)$ (converse of disjunctive syllogism)
$(\psi \to \phi) \to (\neg \phi \lor \psi)$
$\neg (\phi \land \neg \psi) \to (\phi \to \psi)$
$\neg (\phi \to \psi) \to \phi \land \neg \psi$
$(\phi \to \neg\neg \psi) \to \neg\neg (\phi \to \psi)$
$\neg\neg (\phi \lor \psi) \to (\neg\neg \phi \lor \neg\neg \psi)$ (double negation distribution over disjunction)
$(\neg (\phi \land \psi)) \to (\neg \phi \lor \neg \psi)$ (de Morgan law)
$\neg (\neg \phi\land \neg \psi) \to (\phi\lor \psi)$
$((\phi\lor \neg \phi) \to \psi) \leftrightarrow \psi$ (the excluded middle dictates truth)
$(\forall x (\phi \lor \psi(x))) \to (\phi \lor \forall x \psi(x))$
$(\forall x \neg\neg \phi(x)) \to (\neg\neg \forall x \phi(x))$ (double negation shift)
$(\neg\neg \exists x \phi(x)) \to (\exists x \neg\neg \phi(x))$
$(\neg \forall x \phi(x)) \to (\exists x \neg \phi(x))$ (generalized de Morgan law)
$(\neg \exists x \neg \phi(x)) \to (\forall x \phi(x))$
$(\neg \phi \to \exists x \psi(x)) \to (\exists x (\phi \lor \psi(x)))$
$(\forall x \phi(x) \to \psi) \to \exists x (\phi(x) \to \psi)$
$(\phi \to \exists x \psi(x)) \to \exists x (\phi \to \psi(x))$ (independence of premise principle)
$\exists x (\phi(x) \to \forall y \phi(y)))$ (drinker paradox)
$\neg\neg \forall x (\phi(x) \lor \neg \phi(x))$
$\neg \neg \forall x \forall y (x=y \lor x \neq y)$
$\forall x \exists y \phi(x,y) \lor \exists x \forall y \neg \phi(x,y)$
$\forall x \phi(x) \lor \exists x \neg \phi(x)$ (principle of omniscience)

5. References and Further Reading

a. Further Reading

(Van Atten 2004) is one of the best entry points into Brouwer scholarship for philosophy students without extensive mathematical training. The canonical introduction to intuitionism and constructivism in general is (Troelstra and van Dalen 1988). For additional sources, philosophers and logicians may consult (Dummett 1977) and Posy 2020) . For historical accounts of Brouwer’s development of his intuitionism see (van Stigt 1990). More mathematically-oriented sources can be found in (Troelstra 1969), (Moschovakis and Valfeiadou 2020) and (Veldman 2021). (Heyting 1956b) remains a mostly readable introduction to the subject despite its unusual dialogue-driven style. Readers interested in more about Brouwer’s life can have a look at the biography in (van Dalen 2012) as well as an edited collection of Brouwer’s correspondence in (van Dalen 2011).

b. References

Bentzen, Bruno. 2020. “Sense, Reference, and Computation.” Perspectiva Filosofica 47 (2): 179–203. http://philsci-archive.pitt.edu/17408/.
Bentzen, Bruno. 2022. “On Different Ways of Being Equal.” Erkenntnis 87 (4). https://doi.org/10.1007/s10670-020-00275-8.
Bentzen, Bruno. 2023a. “Propositions as Intentions.” Husserl Studies 39: 143–60. https://doi.org/10.1007/s10743-022-09323-3.
Bentzen, Bruno. 2023b. “Brouwer’s Intuition of Twoity and Constructions in Separable Mathematics.” History and Philosophy of Logic 45 (3): 341–61. https://doi.org/10.1080/01445340.2023.2210908.
Brouwer, L. E. J. 1905. “Leven, Kunst en Mystiek.” Delft: Waltman.
Brouwer, L. E. J. 1907. “Over de Grondslagen der Wiskunde.” PhD thesis, Universiteit van Amsterdam. https://eprints.illc.uva.nl/id/eprint/1852/2/HDS-20-LEJBrouwer.text.pdf.
Brouwer, L. E. J. 1908. “De Onbetrouwbaarheid der Logische Principes.” Tijdschrift Voor Wijsbegeerte 2: 152–58.
Brouwer, L. E. J. 1913. “Intuitionism and Formalism.” Bulletin of the American Mathematical Society 20 (2): 81–96. https://www.ams.org/journals/bull/2000-37-01/S0273-0979-99-00802-2/S0273-0979-99-00802-2.pdf.
Brouwer, L. E. J. 1914. “A. Schoenflies und H. Hahn, Die Entwickelung der Mengenlehre und ihrer Anwendungen.” In Jahresbericht Der Deutschen Mathematiker-Vereinigung, 23:78–83.
Brouwer, L. E. J. 1918. “Begründung der Mengenlehre unabhangig vom logischen Statz vom ausgeschlossenen Dritten. Erster Teil: Algemeiner Mengenlehre.” Verhandelingen Der Koninklijke Nederlandsche Akademie van Wetenschappen Te Amsterdam 12. https://doi.org/10.1016/B978-0-7204-2076-0.50015-5.
Brouwer, L. E. J. 1924. “Beweis, dass jede volle Funktion gleichmässig stetig ist.” Koninklijke Nederlandse Akademie van Wetenschappen 27: 189–93. https://doi.org/10.1016/B978-0-7204-2076-0.50027-1.
Brouwer, L. E. J. 1925. “Zur Begründung der intuitionistischen Mathematik. I.” Mathematische Annalen 93 (1): 244–57. https://doi.org/10.1007/BF01449963.
Brouwer, L. E. J. 1927. “Über Definitionsbereiche von-Funktionen.” Mathematische Annalen 97: 60–75. https://doi.org/10.1007/BF01447860.
Brouwer, L. E. J. 1929. “Mathematik, Wissenschaft und Sprache.” Monatshefte Für Mathematik Und Physik 36: 153–64. https://doi.org/10.1016/B978-0-7204-2076-0.50041-6.
Brouwer, L. E. J. 1933. “Willen, Weten, Spreken.” Euclides 9: 177–93.
Brouwer, L. E. J. 1948a. “Essentieel Negatieve Eigenschappen.” Indagationes Mathematicae 10: 322–23. https://doi.org/10.1016/B978-0-7204-2076-0.50053-2.
Brouwer, L. E. J. 1948b. “Consciousness, Philosophy, and Mathematics.” Proceedings of the 10th International Congress of Philosophy, Amsterdam, 1235–49. https://doi.org/10.1016/B978-0-7204-2076-0.50054-4.
Brouwer, L. E. J. 1952. “Historical Background, Principles and Methods of Intuitionism.” South African Journal of Science 49: 139–46. https://doi.org/10.1016/B978-0-7204-2076-0.50062-3.
Brouwer, L. E. J. 1954. “Points and Spaces.” In Philosophy and Foundations of Mathematics (1975), 522–38. Elsevier. https://doi.org/10.1016/B978-0-7204-2076-0.50065-9.
Brouwer, L. E. J. 1955. “The Effect of Intuitionism on Classical Algebra of Logic.” Proceedings of the Royal Irish Academy 57: 113–16.
Brouwer, L. E. J. 1996. “Life, Art, and Mysticism.” Notre Dame Journal of Formal Logic 37 (3): 389–429. https://doi.org/10.1305/ndjfl/1039886518.
Brouwer, L. E. J. 1981. Brouwer’s Cambridge Lectures on Intuitionism. Cambridge: Cambridge University Press.
Dummett, Michael. 1959. “Truth.” Proceedings of the Aristotelian Society 59 (1): 141–62. https://doi.org/10.1093/aristotelian/59.1.141.
Dummett, Michael. 1975. “The Philosophical Basis of Intuitionistic Logic.” Studies in Logic and the Foundations of Mathematics 80: 5–40. https://doi.org/10.1016/S0049-237X(08)71941-4.
Dummett, Michael. 1977. Elements of Intuitionism. Oxford University Press.
Dummett, Michael. 1980. “Critical Notice. L. E. J. BROUWER: Collected Works, Amsterdam and Oxford: North-Holland Publishing Company, New York: American Elsevier Publishing Company. Volume I, Philosophy and Foundations of Mathematics. Edited by A. HEYTING, 1975. Pp. xv+628. Volume 2, Geometry, Analysis, Topology and Mechanics. Edited by HANS FREUDENTHAL, 1976. Pp. xxvii+706. Dfl. 250, £110, per volume.” Mind LXXXIX (356): 605–16. https://doi.org/10.1093/mind/LXXXIX.356.605.
Dummett, Michael. 1978. “Frege’s Distinction Between Sense and Reference.” In Truth and Other Enigmas, 116–44. Cambridge: Harvard Univ. Press.
Dummett, Michael. 2021. “Sense and Reference from a Constructivist Standpoint.” The Bulletin of Symbolic Logic 27 (4): 485–500. https://doi.org/10.1017/bsl.2021.60.
Franchella, Miriam. 1994. “Heyting’s Contribution to the Change in Research into the Foundations of Mathematics.” History and Philosophy of Logic 15 (2): 149–72. https://doi.org/10.1080/01445349408837229.
Griss, G. F. C. 1946. “Negationless Intuitionistic Mathematics i.” Indagationes Mathematicae 8: 675–81. https://doi.org/10.1016/S1385-7258(51)50064-1.
Heyting, Arend. 1930a. “Die formalen Regeln der intuitionistischen Logik.” Sitzungsberichte Der Preussischen Akademie Der Wissenschaften, 42–56.
Heyting, Arend. 1930b. “Sur La Logique Intuitionniste.” Académie Royale de Belgique, Bulletin de La Classe Des Science 16: 957–63.
Heyting, Arend. 1931. “Die intuitionistische Grundlegung der Mathematik.” Erkenntnis 2 (1): 106–15. https://doi.org/10.1007/BF02028143.
Heyting, Arend. 1934. Mathematische Grundlagenforschung, Intuitionismus, Beweistheorie. Berlin: Springer.
Heyting, Arend. 1935. “Intuitionistische Wiskunde.” Mathematica B (Leiden).
Heyting, Arend. 1956a. “La Conception Intuitionniste de La Logique.” Les Etudes Philosophiques, January, 226–33.
Heyting, Arend. 1956b. Intuitionism: An Introduction. North-Holland.
Heyting, Arend. 1958a. “Blick von den intuitionistischen Warte.” Dialectica 12: 332–45. https://doi.org/10.1111/j.1746-8361.1958.tb01468.x.
Heyting, Arend. 1958b. “Intuitionism in Mathematics.” In Philosophy in the Mid-Century. A Survey, i Logic and Philosophy of Science, edited by Raymond Klibansky, 101–15. Florence: La Nuova Italia Editrice.
Heyting, Arend. 1958c. “On Truth in Mathematics.” Verslag van de Plechtige Viering van Het Hondervijftigjarig Bestaan Der Koninklijke Nederlanse Akademie van Wetenschappen Met de Teksten Der Bij Die Gelegenheid Gehouden Redevoenmgen En Voordrachten 12: 227–79.
Heyting, Arend. 1966. “After Thirty Years.” In Studies in Logic and the Foundations of Mathematics, 44:194–97. Elsevier. https://doi.org/10.1016/S0049-237X(09)70586-5.
Heyting, Arend. 1974. “Intuitionistic Views on the Nature of Mathematics.” Synthese 27 (1-2): 79–91. https://www.jstor.org/stable/20114907.
Heyting, Arend, ed. 1975. L. E. J. Brouwer Collected Works 1. Philosophy and Foundations of Mathematics. Amsterdam: North-Holland. https://doi.org/10.1016/C2013-0-11893-4.
Hill, Claire Ortiz. 2010. “Husserl on Axiomatization and Arithmetic.” In Phenomenology and Mathematics, 195:47–71. Dordrecht: Springer. https://doi.org/10.1007/978-90-481-3729-9_3.
Iemhoff, Rosalie. 2024. “Intuitionism in the Philosophy of Mathematics.” In The Stanford Encyclopedia of Philosophy, edited by Edward N. Zalta and Uri Nodelman, Summer 2024. Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/archives/sum2024/entries/intuitionism/.
Kleene, Stephen, and R. E. Vesley. 1965. The Foundations of Intuitionistic Mathematics, Especially in Relation to Recursive Functions. Amsterdam: North-Holland.
Klev, Ansten. 2022. “Identity in Martin-Löf Type Theory.” Philosophy Compass 17 (2): e12805. https://doi.org/10.1111/phc3.12805.
Kreisel, Georg. 1968. “Lawless Sequences of Natural Numbers.” Compositio Mathematica 20: 222–48. http://www.numdam.org/item/CM_1968__20__222_0/.
Kreisel, Georg. 1970. “Church’s Thesis: A Kind of Reducibility Axiom for Constructive Mathematics.” In Studies in Logic and the Foundations of Mathematics, 60:121–50. Elsevier.
Kripke, Saul A. 2019. “Free Choice Sequences: A Temporal Interpretation Compatible with Acceptance of Classical Mathematics.” Indagationes Mathematicae 30 (3): 492–99. https://doi.org/10.1016/j.indag.2019.01.003.
Kuiper, Johannes John Carel. 2004. “Ideas and Explorations: Brouwer’s Road to Intuitionism.” PhD thesis, Utrecht University. https://dspace.library.uu.nl/handle/1874/90.
Mancosu, Paolo. 1997. From Brouwer to Hilbert: The Debate on the Foundations of Mathematics in the 1920s. Oxford University Pres.
Martin-Löf, Per. 1984. Intuitionistic Type Theory. Vol. 1. Studies in Proof Theory. Lecture Notes. Bibliopolis, Naples.
Martin-Löf, Per. 1985. “On the Meanings of the Logical Constants and the Justifications of the Logical Laws.” In Atti Degli Incontri Di Logica Matematica. Scuola Di Specializzazione in Logica Matematica, 2:203–81. Universitá di Siena. https://ncatlab.org/nlab/files/MartinLofOnTheMeaning96.pdf.
Martin-Löf, Per. 2021. “The Sense/Reference Distinction in Constructive Semantics.” Bulletin of Symbolic Logic 27 (4): 501–13. https://doi.org/10.1017/bsl.2021.61.
Martino, Enrico, and Pierdaniele Giaretta. 1981. “Brouwer, Dummett and the Bar Theorem.” In Atti Del Congresso Nazionale Di Logica, Montecatini Terme, 1–5 Ottobre 1979, edited by Sergio Bernini. Napoli: Bibliopolis.
Martino, Enrico, and Pierdaniele Giaretta. 2018. “Brouwer, Dummett and the Bar Theorem.” Intuitionistic Proof Versus Classical Truth: The Role of Brouwer’s Creative Subject in Intuitionistic Mathematics, 1–14. https://doi.org/10.1007/978-3-319-74357-8_1.
McCarty, Charles. 1987. “Variations on a Thesis: Intuitionism and Computability.” Notre Dame Journal of Formal Logic 28 (4): 536–80.
McCarty, Charles, Stewart Shapiro, and Ansten Klev. 2023. “The Axiom of Choice Is False Intuitionistically (in Most Contexts).” Bulletin of Symbolic Logic 29 (1): 71–96. https://doi.org/10.1017/bsl.2022.22.
Moschovakis, J. R., and G. Vafeiadou. 2020. “Intuitionistic Mathematics and Logic,” 1–28. https://arxiv.org/pdf/2003.01935.
Placek, Tomasz. 1999. Mathematical Intuitionism and Intersubjectivity: A Critical Exposition of Arguments for Intuitionism. Vol. 279. Springer Science & Business Media. https://doi.org/10.1007/978-94-015-9315-1.
Posy, Carl J. 1974. “Brouwer’s Constructivism.” Synthese 27 (1-2): 125–59. https://doi.org/10.1007/BF00660893.
Posy, Carl J. 1991. “Mathematics as a Transcendental Science.” In Phenomenology and the Formal Sciences, 107–31. Springer.
Posy, Carl J. 1998. “Brouwer Versus Hilbert: 1907–1928.” Science in Context 11 (2): 291–325. https://doi.org/10.1017/S0269889700003021.
Posy, Carl J. 2020. Mathematical Intuitionism. Cambridge University Press. https://doi.org/10.1017/9781108674485.
Prawitz, Dag. 1971. “Ideas and Results in Proof Theory.” In Proceedings of the Second Scandinavian Logic Symposium, edited by J. E. Fenstad, 63:235–307. Studies in Logic and the Foundations of Mathematics. Elsevier. https://doi.org/10.1016/S0049-237X(08)70849-8.
Prawitz, Dag. 1973. “Towards a Foundation of a General Proof Theory.” In Proceedings of the Fourth International Congress for Logic, Methodology and Philosophy of Science, Bucharest, 1971, edited by Patrick Suppes, Leon Henkin, Athanase Joja, and Gr C. Moisil, 74:225–50. Studies in Logic and the Foundations of Mathematics. Elsevier. https://doi.org/10.1016/S0049-237X(09)70361-1.
Prawitz, Dag. 1974. “On the Idea of a General Proof Theory.” Synthese 27 (1/2): 63–77. http://www.jstor.org/stable/20114906.
Prawitz, Dag. 1987. “Dummett on a Theory of Meaning and Its Impact on Logic.” In Michael Dummett: Contributions to Philosophy, edited by Barry M. Taylor, 117–65. Dordrecht: Springer Netherlands. https://doi.org/10.1007/978-94-009-3541-9_5.
Prawitz, Dag. 2012. “Truth and Proof in Intuitionism.” In Epistemology Versus Ontology, 27:45–67. Dordrecht: Springer. https://doi.org/10.1007/978-94-007-4435-6_3.
Raatikainen, Panu. 2004. “Conceptions of Truth in Intuitionism.” History and Philosophy of Logic 25 (2): 131–45. https://doi.org/10.1080/014453401625669.
Rosado Haddock, Guillermo. 2010. “Platonism, Phenomenology, and Interderivability.” In Phenomenology and Mathematics, 195:23–46. Dordrecht: Springer. https://doi.org/10.1007/978-90-481-3729-9_2.
Sundholm, Göran. 2004. “Antirealism and the Roles of Truth.” In Handbook of Epistemology, edited by I. Niiniluoto, M. Sintonen, and J. Woleński, 437–66. Netherlands: Kluwer Academic Publishers.
Sundholm, Göran, and Mark van Atten. 2008. “The Proper Explanation of Intuitionistic Logic: On Brouwer’s Demonstration of the Bar Theorem.” In One Hundred Years of Intuitionism (1907–2007) the Cerisy Conference, 60–77. Birkhäuser Basel. https://doi.org/10.1007/978-3-7643-8653-5_5.
Tait, William W. 2015. “Gentzen’s Original Consistency Proof and the Bar Theorem.” Gentzen’s Centenary: The Quest for Consistency, 213–28. https://doi.org/10.1007/978-3-319-10103-3_8.
Tieszen, Richard. 1984. “Mathematical Intuition and Husserl’s Phenomenology.” Nous, 395–421. https://doi.org/10.2307/2215219.
Tieszen, Richard. 1989. Mathematical Intuition: Phenomenology and Mathematical Knowledge. Dordrecht: Kluwer. https://doi.org/10.1007/978-94-009-2293-8.
Tieszen, Richard. 1995. “What Is the Philosophical Basis of Intuitionistic Mathematics?” In Studies in Logic and the Foundations of Mathematics, 134:579–94. Elsevier. https://doi.org/10.1016/S0049-237X(06)80064-9.
Tieszen, Richard. 2008. “The intersection of intuitionism (Brouwer) and phenomenology (Husserl).” In One Hundred Years of Intuitionism (1907–2007), 78–95. Springer. https://doi.org/10.1007/978-3-7643-8653-5_6.
Troelstra, Anne S. 1969. Principles of Intuitionism. Vol. 95. Springer Lecture Notes. Berlin–Heidelberg–New York: Springer.
Troelstra, Anne S. 1977. Choice Sequences: A Chapter of Intuitionistic Mathematics. Clarendon Press Oxford.
Troelstra, Anne S., and Dirk van Dalen. 1988. Constructivism in Mathematics. Vol. I. Vol. 121. Studies in Logic and the Foundations of Mathematics. Amsterdam: North-Holland.
van Atten, Mark. 2004. On Brouwer. Belmont, CA: Wadsworth/Thomson Learning.
van Atten, Mark. 2006. Brouwer Meets Husserl: On the Phenomenology of Choice Sequences. Vol. 335. Springer Science & Business Media. https://doi.org/10.1007/978-1-4020-5087-9.
van Atten, Mark. 2017. “Construction and Constitution in Mathematics.” In Essays on Husserl’s Logic and Philosophy of Mathematics, 384:265–315. Dordrecht: Springer. https://doi.org/10.1007/978-3-319-10031-9_12.
van Atten, Mark. 2018. “The Creating Subject, the Brouwer–Kripke Schema, and infinite proofs.” Indagationes Mathematicae 29 (6): 1565–1636. https://doi.org/10.1016/j.indag.2018.06.005.
van Atten, Mark. 2022. “Dummett’s Objection to the Ontological Route to Intuitionistic Logic: A Rejoinder.” Inquiry 65 (6): 725–42. https://doi.org/10.1080/0020174X.2019.1651091.
van Atten, Mark. 2024. “Intuition, Iteration, Induction.” Philosophia Mathematica 32 (1): 34–81. https://doi.org/10.1093/philmat/nkad017.
van Atten, Mark, and Göran Sundholm. 2017. “L. E. J. Brouwer’s ‘Unreliability of the Logical Principles’: A New Translation, with an Introduction.” History and Philosophy of Logic 38 (1): 24–47. https://doi.org/10.1080/01445340.2016.1210986.
van Atten, Mark, and Dirk van Dalen. 2002. “Arguments for the Continuity Principle.” Bulletin of Symbolic Logic 8 (3): 329–47. https://doi.org/10.2178/bsl/1182353892.
van Dalen, Dirk. 1998. “From a Brouwerian point of view.” Philosophia Mathematica 6 (2): 209–26. https://doi.org/10.1093/philmat/6.2.209.
van Dalen, Dirk. 2011. The Selected Correspondence of L. E. J. Brouwer. London: Springer. https://doi.org/10.1007/978-0-85729-537-8.
van Dalen, Dirk. 2012. L. E. J Brouwer Topologist, Intuitionist, Philosopher : How Mathematics Is Rooted in Life. Springer. https://doi.org/10.1007/978-1-4471-4616-2.
van Dalen, Dirk. 2005. Mystic, Geometer, and Intuitionist: The Life of LEJ Brouwer. Volume 2: Hope and Disillusion. Oxford: Clarendon Press.
Walter P van Stigt. Brouwer’s intuitionism. North-Holland Amsterdam, 1990.
Veldman, Wim. 2021. “Intuitionism: An Inspiration?” Jahresbericht Der Deutschen Mathematiker-Vereinigung 123: 221–84.

Author Information

Bruno Bentzen
Email: b.bentzen@hotmail.com
Zhejiang University
China

Internet Encyclopedia of Philosophy