The Port Royal Logic

Logic or the Art of Thinking, commonly known as The Port Royal Logic, was written by Antoine Arnauld and Pierre Nicole and first published in 1662. Although it was a textbook containing much worked-over material, the Logic was extremely influential, certainly the most important textbook in logic for the next two hundred years. Part of its influence was due to its accessibility: it was short for a logical treatise and the first logic textbook in a vernacular language. It was quickly translated, had numerous editions, and was popular throughout Europe and the U.S. well into the 19^th century. Its technical logic, however, is unoriginal. From a modern perspective the Logic’s interest is twofold: it harmonizes Cartesian dualism with standard doctrines of late medieval logic, and for the first time it gives intentional content a central role in semantics. The two are related. Because dualism was inconsistent with the standard medieval theory of reference, it was necessary to forge a new foundation. To do so, the Logic’s authors relocated objective being, an early version of intentional content, to the center of logical theory. This article focuses on the Logic’s innovations in semantics, especially the role of intentional content, and on the place of its innovations in the history of logic, both where they came from and how they evolved.

As a result of its commitment to dualism, the Logic faced four tasks: (1) to explain anew how terms in mental language “signify” things in the world, (2) to reformulate truth-conditions in a way compatible with its new definition of signification, (3) to preserve the standard proof theory of late medieval logic, and (4) to explain how logical demonstration contributes to scientific knowledge in the context of Cartesian rationalism. These tasks correspond to the four “parts” of the Logic. Parts I to III correspond to the standard books of earlier logical treatises, which follow a division loosely modeled on Aristotle’s Organon: the logic of terms, the logic of propositions, and the logic of arguments. Part IV concerns method, a topic of special interest in the 17^th century.

The Logic of Terms
The Logic of Propositions
The Logic of Arguments
Method
References and Further Reading
1. Primary Sources
2. Secondary Sources

1. The Logic of Terms

a. Summary

(The original edition of Port Royal Logic is hereafter referred to as Logic; Arnauld 2003, hereafter KM, Logic is vol. 5., 99–413. English translation: Arnauld 1996, hereafter B.) In Book I, the authors lay out the fundamental assumptions and concepts of their semantic theory. These include a substance-mode ontology with its dualistic division into matter and spirit (Logic, Part I, Chapter 2, hereafter I:2); a theory of mental language (I:1, 4); ideas and their causes, including abstraction and restriction (I:1, 5, 8); the traditional ten categories (I:3) and five predicables including genera and species (I:7); false ideas and error (9–11); and essential definitions (I:12–15). Most importantly they explain their theory of reference (I:6). The key concepts possess a definitional order. First, every term possesses by nature an intentional content. This content determines what the term signifies in the world. What it signifies in turn determines its inferior ideas. Inferior ideas then combine to form the term’s extension. Extension will then be the key concept in the definition of truth in Part II. At multiple points in both the introductory Discours and Part I the authors point out the intellectual and moral dangers lurking in equivocation and false ideas.

b. Ontology

In the introduction the authors decline to engage in the realism/nominalism debate, on whether, as they put it, universals exist a parte rei, because they judge the issue uninteresting and useless (Discours I, KM V 112–113, B 11–12). In Part I, nevertheless, they assume a basic substance-mode ontology that is roughly Aristotelian. They divided being into two kinds: substances, which can be conceived as existing independently, and modes (attributes, qualities), which can only be conceived of as existing instantiated in substances (I:2).

c. Dualism, Ideas

To this Aristotelian foundation the Logic adds Cartesian dualism. Substances and their modes divide into two kinds: spiritual and material. The essential property of material substances is extension and that of souls is thought. In the Logic the modes attributed to material substances are those described in Cartesian physics; for example, relative size, position, motion, and shape. Modes attributed to the soul include sensory qualities, ideas, and mental operations. These operations include the three traditionally listed in medieval logic: conception (concevoir), judgment (affirmation and denial, juger), and reason (logical deduction, raisonner), and a fourth, the methodological organization of knowledge (ordoner), which was considered important in 17^th century logic (I:Introduction, KM V 125, B 23). These four operations correspond to the four parts of the Logic. Although the authors sometimes used idea loosely to refer to any spiritual mode, in more precise contexts an idea is a mental mode that functions as a term in mental language, or what medieval logicians and Descartes call a concept.

d. Mental Language

The Logic discusses grammar piecemeal (I:1–6 and II). It does not provide an exhaustive breakdown of spoken language into basic parts of speech, nor does it attempt to formulate precise grammar rules for complex expressions like those of a modern generative grammar. As in medieval logic, the spoken language in which logic is conducted (and which the Logic discusses) turns out to be a rather stylized fragment of natural language (I:1, 4). Chomsky surprised the linguistic community in the 1960s by pointing out in Cartesian Linguistics that Logic posits a mental language parallel to speech and suggested that their distinction anticipates his between surface and deep structure (Chomsky 1966, 31 and following). It is more accurate to say that medieval logicians had been working out the theory of mental language for centuries, in which spoken words and phrases were conventional signs for a language of thought that was prior to speech and had its own grammar and semantics. The basic linguistic operations are conceptualization, judgment, and reasoning.

Conceptualization is the act of instantiating in the soul an idea that serves as a basic term in mental grammar. These ideas have semantics. An idea by its nature has an intentional content that the soul is aware of more or less clearly during the act of conceptualization. This intentional content determines what the idea signifies in the world. What it signifies in turn determines other ideas that are “inferior” to it. The set of its inferiors constitute its “extension” in the special sense peculiar to the Logic. An idea that fails to signify anything real (that fails of reference) is called a false idea.

Judgment is the act in which the soul affirms or denies propositions, which are grammatical complexes in which ideas occur as terms. Reasoning is the act where the soul draws a conclusion from other propositions as premises. Part II explains the truth-conditions of propositions, and Part III explains which reasoning patterns are valid.

Substantives and adjectives are the two basic kinds of referring terms in mental propositions. The Logic has no single technical term for reference. Sometimes it is called expression, sometimes representation, but most frequently it is called signification, which was the standard term in earlier logic. Fundamental to the Logic’s semantics is the thesis that signification is explained by intentional content (I:2, 5–6).

e. Intentional Content

As mentioned above, one of the challenges faced by the Logic was how to reconstruct the medieval theory of reference. In earlier Aristotelian accounts, reference is explained by the transmission of a property from the world to the soul. By sensation and abstraction, the view held, an external property was causally transmitted via the sense organs to the brain and from there to the intellect. Once in the intellect it serves as a concept or term in mental language. This term was then said to signify those objects outside the mind that instantiate the transmitted property. Dualism, however, makes this mechanism impossible. If dualism is true, no property can be instantiated in both matter and the soul.

To explain reference, the Logic appeals to intentional content. Intentional content was far from a new idea. Versions had been used throughout the Middle Ages to explain various semantic phenomena (Pasnau 1997). Peter Aureol holds that what we see when we have an illusion, like the apparent movement of the trees from a passing boat, is not something that really exists outside the mind but rather a third entity that only exists “in the eye objectively” and “intentionally.” At some points in his career, Ockham calls “what we understand” when we grasp an abstract noun a “fictum” having esse objectivum and esse cogitum (Willam of Ockham 1978, §10.) Scotus calls something’s nature an “intelligible being” distinct from the thing itself. By the 16^th century, it was common for logicians to distinguish between the “formal” and “objective” being of a concept (Cronin 1966). A concept has formal being inasmuch as it is a mode of the soul and as such is part of its “form.” It exhibits objective being because it carries with it the understanding of an object—it “throws” the object “against” the mind. Suárez, for example, holds that an essential definition is true timelessly, even prior to creation, because it signifies objective being. Toletus explains “beings of reason” like a chimera and non-referring terms like antichrist that do not refer to existing things as signifying objective being. By Descartes’ time, the distinction was commonplace in the logic books studied in schools and universities, including the schools attended by Descartes, Arnauld, and Nicole. It is prominent, for example, in treatises by Toletus, Raconis, Fonseca, and Eustache de Saint-Paul. (Toletus S.J. 1596, 3, 30; Raconis 1651, De principis entis, a. 3, §1a, 827; Fonseca S.J. 1599, q. ii, §1; Eustachio-De-S.-Paulo 1648 Metaphysia, De natural entis, de conceptus formali et objectivo, 1; see also Cronin 1966). Descartes appeals to the objective being of the idea of God in his famous ontological argument of Meditation III (§§ 21–22). The Logic prefers to speak about an idea’s content, but Arnauld uses the medieval terminology objective realty or objectively being in On True and False Ideas. (See Arnauld 1813, vol. I, hereafter VFI, Ch. 5, 6; KM I, 202, 205; English translation Arnauld 1990 [1683], hereafter G, 69, 71–127). In the Logic objective being is used to explain not only of signification, but also extension, abstraction, restriction, privative negation, essential definition, ambiguity, equivocation, clear and distinct ideas, and perception.

The explanatory role of intentional content (I:6–7) begins with substantives. Grammatically, substantives are ideas that serve as the subjects or predicates of categorical propositions. Semantically, a substantive is distinguished by its intentional content, which in the case of a substantive is called its comprehension. Comprehension is explained by appeal to substance-mode ontology. A substantive’s comprehension is a series of modes. It modern terms it may be thought of as a set of modes. These form the idea’s content and provide its identity criteria. Two substantives are identical if and only if they have the same comprehensions. Signification is then defined in terms of comprehension. A substantive signifies all and only those entities that satisfy all the modes in its comprehension. The theory is not unlike—indeed it is a remote ancestor of—Frege’s view that sense determines reference. A substantive that signifies many individuals is a common or abstract noun. One that signifies a single individual is a proper noun. Normally, a substantive signifies substances, but it can also signify modes, like whiteness. If a substantive signifies another idea, which is a mode of the soul, it is a term of second intention.

Adjectives too have intentional content, but the terminology is different. Grammatically, adjectives serve as the predicates of categorical propositions or as modifiers of substantives in longer noun phrases. Semantically, an adjective has as its intentional content a mode or sometimes multiple modes. In the case of an adjective these are called its secondary signification. This content determines the objects the adjective is true of or “signifies in the primary sense”: an adjective signifies primarily all and only the entities that instantiate all the modes in its secondary signification. Again, intentional content provides identity conditions: two adjectives are identical if and only if they have the same secondary signification. Following medieval usage, an adjective is called a connotative term (I:8; KM V 152; B 46). It directly signifies a mode and indirectly connotes the individuals in which they inhere. Substantives differ semantically from adjectives in that a substantive’s primary function is to signify an entity in abstraction from its modes. An adjective, however, draws attention to entities by first drawing attention to the mode or modes in its secondary signification. (The primary and secondary terminology derives from Aristotelian metaphysis in which substances are ontologically prior to modes because a mode must exist in a substance.) Because a substantive signifies objects directly but an adjective signifies objects indirectly by first signifying a mode, a substantive is called absolute and adjective relational.

It is clear that the Logic’s authors regarded intentional mode-sets as part of its explanation of conceptualization or of “what it is to understand an idea.” Details are fleshed out in Part IV in the discussion of clear and distinct ideas, and sensation. Like some nominalists who believed in objective being, the Logic’s authors make the point that objective being is not some kind of representative entity between, or in addition to, the soul and the external world. It is a fact of psychology, they hold, that when a perception is experienced during sensation or when an idea is clearly conceived in thought, the soul is aware of the modes that make up its content. No mode of matter experienced in the content of a perception or idea, however, can be true of the soul itself. They are true rather of the material substance outside the soul that is the object of sensation or that the idea signifies.

f. Kinds of Ideas, Occasionalism

Like Descartes (Meditations III.7), the authors hold that there are three kinds of ideas that differ by how they are caused. They are adventitious, innate, and factitious.

Adventitious ideas are those caused by God on the occasion of a bodily sensation. Sensation is more fully explained in Part IV. Because material modes cannot be instantiated in the soul, the Logic is forced to reject the usual Aristotelian account of sensation and concept formation. The material transfer of modes in sensation only goes as far as the brain. The properties of a material substance travel from the object being sensed to perceiver’s sense organs, and from there to the brain, but they stop there. Material modes cannot then be transferred “intentionally” to the soul itself to become consciously perceived. The Logic’s alternative explanation is a form of occasionalism. (On occasionalism in the Logic see I:1, KM V 132–33, B 29-30; I:9, KM V 157–78, B 9–50; I:12, KM V 168–170, B 58–60; VFI 6, KM I 204, G 71–71; VFI 27, KM I 349–50, G 208. For broader accounts in Cartesianism generally, see Nadler 2011, Nadler 1989, and Garber 1993.)

On the occasion of bodily sensation in which a material object transfers its modes to the perceiver’s brain in the form of physical motion, God simultaneously causes to be instantiated in the soul a mental mode. This mode is adventitious and is called a perception in a narrow sense. A perception, moreover, has an intentional content of which the soul is aware with varying degrees of vividness, clarity, and distinctness. Some of these modes, like motion, relative position, and shape, are material and are true of the object outside the mind causing the sensation. Other modes in the perception’s content are sensory. They are true of the soul itself, like colors, tastes, smells, textures, sounds, and feelings of pleasure and pain.

Innate ideas are ideas directly instantiated in the soul by God apart from sensation. They include the idea of infinity and of God himself.

Factitious ideas are caused by the soul itself through one of two mental operations: restriction or abstraction. Both operations were standard topics in earlier logic. The Logic’s account is novel in that it explains their mechanisms in terms of intentional content.

g. Determinative and Explicative Restriction

Grammatically, restriction is a mental operation by which the soul forms a longer substantive phrase by modifying a substantive with an adjective or relative clause. Semantically, a relative clause functions like an adjective: it has a primary and secondary signification. In restriction a new idea is formed. Its comprehension is the intersection of the comprehensions of the two contributing ideas. Since the new comprehension contains more modes than either the substantive or its modifier, it will frequently be true of fewer things and will then be less general. If the restricted phrase signifies fewer individuals than the substantive alone, it is said to be determinative. On the other hand, if the restriction does not signify fewer things but simply adds extraneous information, it is called explicative.

Because an explicative restriction does not reduce the significance range of the modified substantive, the proposition expressed is equivalent to a conjunction of propositions. In one of these, the extraneous modifier is deleted, and in the other, the modifier is predicated of the original substantive. For example, in the Pope, who is the Vicar of Christ, resides in Rome, the relative clause who is the Vicar of Christ does not further restrict the significance range of the subject the Pope. The proposition is therefore equivalent to a conjunction of two propositions: The Pope resides in Rome and the Pope is the Vicar of Christ (I:8, KM V 151–52, B 44–45). This distinction between determinative and restrictive relative clauses had been made frequently in earlier logic. (See, for example, Buridan 2001, 286; Parsons 2014, 5.6.) The Logic adds its explanation in terms of content. The distinction is also made in modern grammar using the terminology restrictive and non-restrictive relative clauses.

h. Indeterminate Restriction

The Logic also recognizes what some commentators call a special type of restriction called indeterminate restriction (II:6, KM V 145, B 40; I:7, KM V 147–48, B 41–42; I:7, KM V 150, B 44; II:3, KM V 199, B 83). (Pariente 1985, 247–238, Auroux 1993, 74.) This is not really a second type of restriction but rather a way of referring to restriction in the metalanguage using an existential quantifier. Indeterminate restriction is important in Part II where it is used to state the truth-conditions of particular affirmative propositions. As explained there, a particular affirmative some S is P is true if there is some third term, call it Q, by which both terms S and P are restricted with the result that the restricted terms have the same extension. As in a similar analysis of Aristotle’s called ecthesis (see, for example, Prior Analytics 28a23–26, 30a9–14), the common subset shared by S and P is “exhibited” by the two restricted terms. In the precise statement of the truth-conditions, restriction occurs in its univocal sense but in such a way that there is an existential quantification in the metalanguage over the restricting term: some S is P is true if and only if there is some idea Q so that restrictions of S by Q and P by Q have the same extension.

i. False Ideas

If the combination of modes in an idea’s comprehension are not jointly true of any actual object, then the idea is said to be false.

If the objects represented by these ideas, whether they be substances or modes, are represented to us as they are in fact, one calls them true [véritables]. If they are not such, they can only be false [elles sont fausses en la maniere qu’elles les peuvent être], and this is what one calls in the School beings of reason, which usually consist of the combination that the soul makes from two ideas real in themselves, but which are not joined in truth to form a single idea. An example is the one that can be formed from a mountain of gold. It is a being of reason, because it is composed of two ideas, of mountain and of gold, which it represents as one even though they would not really be so. (I:2, KM V 136, B 32, author’s translation. See also Discours I, KM V 110, B 9–10; I:9, KM V 157–78, B 49–50; I:11, KM V, 168–170, B 58–60.)

Many of the examples of false ideas given in the Logic are not just false but impossible, either because their contents contain contrary modes or because the laws of nature prevent their joint satisfaction. In earlier logic it was common to call such a non-existing thing a being of reason. It was often said to have objective being and to have some status in reality distinct from the soul and real beings (esse reale, in re). (See, for example, Willam of Ockham 1978 §10, and Suárez 1995.) A standard example was an impossible being like a chimera, goat stag, or golden mountain, as well as a planned but incomplete possible being like a castle, house, or city. The authors of the Logic, however, reject the view that a being of reason possesses a reality independent of the soul, and regard objective being rather as a property of ideas. An idea has objective being to the extent that the soul is aware of the modes in the idea’s intentional content when the idea is instantiated in the soul. As egregious examples of false ideas the Logic cites those with comprehensions that combine spiritual and material modes. Examples include a red, blue and orange rainbow (of water drops); pain caused by fire; heaviness caused gravitational attraction; happiness as caused by material wealth; courage as feats of valor; lack of physical pleasure as evil; and spatial solitude as misery. Some ideas, however, are only contingently false. The Logic remarks, for example, that Alexander, the son of Philip would be a false idea if Alexander had not been Philip’s son. The idea the bent stick in the water would be false if the stick were straight, but true if not. Peter, the denier of Christ happens to be a true idea, but since Peter was free, it might well have been a false idea.

Following Descartes, the Logic places false ideas at the center of its explanation of error, especially the errors characteristic of Aristotelian psychology and various moral failings. Aristotelian accounts of perception err because a mode true of matter cannot travel via sensation and abstraction to become instantiated in the soul. Rather, the material world, which consists of Cartesian extension modified by geometric and mechanical modes, is entirely separate from the soul, which is modified by modes of sensations, feelings, and morals. Ideas that combine the two are false. In addition, many moral failings are grounded in false ideas. When young, we mistakenly believe that moral qualities, which are true of the soul, are caused by material circumstances. We err when we combine them into a single idea, for example, when we combine virtue and worldly wealth.

False ideas are important to logic because they have implications for the theory of truth. Semantically, false ideas are nonreferring terms—they fail of existential import. What are the truth-conditions of an affirmative categorical proposition with a false idea as subject term? Medieval logicians had divided on whether this failure makes the position false. The quotation above, and others in the Logic, strongly suggest that in Arnauld and Nicole’s view an affirmation with a false idea as subject is false. The issue recurs in Part IV’s account of necessary and contingent truth. (See Martin 2012.)

j. Abstraction

The second way in which the soul causes new ideas is by abstraction. Various accounts of abstraction had been part of logic since Aristotle, but the Logic’s version had to be made consistent with dualism. (For a standard medieval account see Aquinas, Summa Theologica I.I, Q. 85.) To do so, the authors explain its mechanism as a manipulation of intentional content. (I:5, KM V 142–43, B 37–38; I:11, KM V 168–170, B 58–59; VFI 6, KM I 207–210, G 74–76; VFI 11, KM I 234–235, G 98–100.)

Abstraction is either from a sensation or a prior idea. On the occasion of sensation, God causes the soul to experience a vivid awareness of a modal content. Some of these modes, like extension, relative position, and motion, are true of the material object that is the external correlate of the experience and that has caused the corresponding movements in the perceiver’s brain. Other of these modes, like colors, tastes, weight, sounds, and associated feelings, are true of the soul. When attending to this broad content, the perceiver may form an idea from this content. The soul does so by selecting as the idea’s comprehension a subset of modes evident in the perceptual experience.

The second kind of abstraction is from a prior idea. While attending to the comprehension of a prior idea, the perceiver may form a new idea with a new comprehension by selecting a subset of modes from the prior idea’s comprehension. Because the new content contains fewer modes, it is generally true of more things and is therefore more general.

The Logic describes the accumulation of abstract ideas as progressive, starting with abstractions from sensory experience and proceeding to increasingly more general ideas. In earlier logic, abstraction was usually described as progressing in the reverse order (for example, in Aquinas above), starting with abstraction to the most general ideas and then progressing by steps of restriction to more concrete ideas.

k. The Categories and Predicables

Following the logical tradition, the Logic endorses Aristotle’s categories (I:3) and Porphyry’s predicables (I:7). Its list of the ten categories is standard: substance, quantity, quality, relation, activity, passivity, place, time, position, and state. The book later scarcely mentions the distinctions among the various nonsubstance categories. Like some late medieval logicians, the authors evidently regarded distinctions among mode types as unimportant. In particular, the Logic rarely speaks of relations as such, although it recognizes that some modes are internal to a substance and others external. In the medieval fashion, external modes are another name for relations, and are so-called because they hold of a substance only by reference to another substance.

The authors also endorse the five predicables, a standard topic in logic since Porphyry: genus, species, deference, property, and accident. These classify mental predicates according to their degree of necessity. These distinctions, unlike those among type of modes, are important in the Logic.

Genera and species are common nouns in mental language (I:4–6). As such they have comprehensions and signify individuals. In the normal case they signify substances, but as terms of second intention, they may also signify modes. Differences, properties, and accidents too are terms in mental language, but they are adjectives. As such they signify secondarily a mode or modes, and signify primarily the individuals that satisfy these modes. Thus, viewed ontologically, genera and species differ from difference, property, and accident as substances differ from modes. Corresponding to genera and species are the individuals they signify, which in general are substances. Corresponding to differences, properties and accidents are the modes they signify directly and the objects in which the modes inhere indirectly.

The Logic uses the predicables to articulate its account of essential definition. The details follow earlier standard accounts. Every species has an essential or real definition, as distinct from a nominal definition (1:12–014). A nominal definition lays down a convention in which a spoken sound is paired with an idea. (This relation is also called signification, but in this sense it is distinct from signification in the sense of reference, a natural relation between an idea and what it stands for outside the mind. The dual senses were common in medieval logic.) A real or essential definition is a universal affirmative proposition in which a species is the subject term and its genus restricted by a distinguishing adjective is the predicate. The adjective is called the species’ difference (differentia). An essential definition is necessarily true and describes the species’ nature. Part IV assigns a major role in scientific knowledge to essential definitions.

It follows from the account of essential definition that species fall into a structure. Every genus except the highest is itself a species and has its own essential definition. The highest genus, which has no definition, is referred to as being or substance. A species that is not a genus is an infima species. At several places, the Logic mentions the traditional doctrine of differentiation by privation. This is the case in which a genus divides into two species which are such that the difference of the second is the privative negation of the difference of the first. (I:7, KM 148, B 42; II:15, KM 242, B 124.) The species animal, for example, is said to divide into the species human with the difference rational and the species brute with the privative difference irrational. Although the authors do not draw attention to the fact, the account entails genera and species’ conforming to a finite finitely branching tree-structure, which is traditionally called the tree of Porphyry. (See Structure of Ideas below.)

A property (proprium) is an adjective that is not the difference of any species but that nevertheless signifies secondarily a mode necessarily true of a species. As an example, the Logic cites a mode that is necessarily true of a circle but not part of its definition: all lines from the center to the circumference are equal. An accident is such that any species “can be conceived without it.” More precisely, an accident is an adjective that is not a difference or a property. An accident connotes a mode that is true but not necessarily true of what it signifies. It is either not true of every member of a species, or not always true of them.

l. Nominalism-Realism

Like some medieval logicians, the Logic explains genera and species nominalistically. Ontologically genera and species are not classified as some special kind of entity in addition to matter and its modes, or souls and their modes, as some realists had suggested. They are simply ideas, which are modes of the soul. On the other hand, the Logic treats differences, properties, and accidents realistically. Strictly speaking, these too are ideas in mental language (I:7). But they are also adjectives, and as such they signify modes secondarily. Frequently the Logic muddles use-mention and uses difference, property, and accident to refer to these modes themselves. For example, the difference of the species human sometimes means the adjective rational and sometimes the mode rationality. The context makes clear which is intended. The Logic’s overall metatheory is basically realistic because it assumes a fundamental substance-mode ontology in which modes have real existence. Thus, although the Logic’s ontology is basically realistic, which is evident in what it has to say about difference, property, and accident, it adopts the nominalistic move of some earlier logicians of avoiding positing special entities for genera and species by identifying them with modes of the soul.

m. Comprehension as a Generalization of Essence

In the Logic’s technical vocabulary, the collected differences of a species’ higher genera constitute the species’ comprehension, which is its intentional content. Indeed, it is not an exaggeration to say that the Logic’s entire theory of reference via intentional content—comprehension in the case of substantives and secondary signification in the case of adjectives—is a generalization of the Aristotelian theory of essential definition. Available in that theory was the generalization that a species comprises those individuals that satisfy its difference and those of its higher genera. In the Logic, it is these modes that determine what a species term signifies. In other words, a species signifies those individuals that satisfy the modes in its intentional content. It is a small step to attributing a content to all terms and explaining their signification similarly.

n. Species and Difference

The Logic holds an odd view about species. A species and its difference, it holds, are semantically equivalent. They both signify the same individuals and therefore have the same extension (I:7, KM V 147–48, B 42). The authors are here following Aristotle, who maintained that each species has a unique difference. No two species, in other words, have the same difference. (See, for example, Parts of Animals 3, 642b20–643a20.) Moreover, if a difference, which is an adjective, is read as a substantive, the species and the difference signify the same individuals. It is perfectly normal in Latin to read an adjective as a noun when it is not used to modify another noun. The Logic’s example is the word album (white) which may be understood as either an adjective or a noun. Likewise, rationalis is an adjective in animal rationalis, but a noun signifying the same individuals as homo when it occurs alone as a noun. Thus, the signification of the noun is the primary signification of the adjective. In the Logic’s terminology, the secondary signification of the difference when construed as an adjective is identical to its comprehension when construed as a noun. It is for this reason that the Logic at times says that a species and its difference are the same thing.

o. Signification and Extension

Extension is probably the most interesting concept in the Logic’s semantics. Truth is defined in terms of extension but extension is defined in terms of ideas. The result has the appearance of a kind of idealism in which truth is defined independently of the external world. The appearance, however, is misleading. Although the authors are dualists and revolutionaries of a sort who want to define truth using only mental categories, they are also conservative in the sense that they want to maintain a correspondence theory of truth. To do so, they defined extension so that it tracks what happens in the world outside the mind. A universal affirmative, to be sure, is true if the extension of its subject term is contained in the extension of the predicate. Moreover, extension here consists of ideas. But subordination among these ideas corresponds, it turns out, to subordination among things in the world.

The story is somewhat indirect due to the authors’ loose mathematical style. They fail to give what we would regard today as a clear definition of extension. The best they have to say is that a term’s extension consists of its “inferior subjects.” (I:6) They make clear that by “subjects” here they mean ideas. From these two remarks it is possible to piece together a definition: the extension of an idea consists of all its inferior ideas. The problem, however, is that they do not define “inferior.” They do give an example. Various types of triangles, they say, are inferior to the genus triangle. This reading, moreover, conforms with prior usage in medieval logic. The suggestion is that the extension of A is the set of all ideas B such that all the modes in the comprehension of A are included in the comprehension of B. Several things follow: First, the extension of B would be included in that of A if and only if all the ideas defined in terms of B are a subset of all the ideas defined in terms of A. Second, all the ideas defined in terms of B are a subset of all the ideas defined in terms of A if and only if the comprehension of A is a subset of the comprehension of B. It follows that whether a species is inferior to a genus would be a function of the essential definitions. The definition of inferiority would entail that every S is P is true if and only if the comprehension of P is a subset of that of S. A true universal affirmative would then be a matter of conceptual inclusion and, as such, necessary. A plausible example would be every animal is a living being. It would be true because the species animal is included in the genus of living being or, equivalently, animal is defined in terms of living being. Being an essential definition it is also necessary.

This reading, however, is much too narrow to fit other views within the Logic’s more general metatheory. It excludes, for example, the possibility of contingent truth. In particular, it entails the wrong truth-conditions for propositions that affirm accidental predicates. Accidents, of course, are not species. They have no “inferiors” in the proposed sense. On the other hand, contingent propositions like Peter denied Christ and every student in the classroom is asleep can be true, yet the intentional content of the predicate is not contained in that of the subject. Similarly as a contingent matter a universal negative like no doctor is a thief can be true and no doctor is poet false, yet in that case both can be made false as function of ideas. The set of ideas defined in terms of doctor and poet is non-empty if the idea doctor-poet is formed by restriction Likewise the set of ideas defined in terms of doctor and thief is non-empty if it contains doctor-thief. (See Auroux 1993, 135, and Martin 2017.) The reading also poses problems for the Logic’s doctrine of false idea. As explained above, the Logic attributes errors in philosophy and morality to believing propositions that have false ideas as subjects. These are ideas that fail to signify any existing thing, like pain caused by fire or virtuous rich man. Affirmative propositions with false ideas as subjects—that is, affirmatives with subject terms that have no existential import—are supposed to be false. On the other hand, the intentional content of mountain is contained in that of golden mountain, and anything defined in terms of golden mountain would be defined in terms of mountain. It would seem, then, that a trivial but empty proposition like every golden mountain is a mountain would be true despite have a false idea as subject. The issue is important in Part IV (see Martin 2012).

The broader context makes clear the correct definition of inferiority. The key is to define inferiority in terms of signification: idea A is inferior to B if and only if every individual that A signifies B signifies. Equivalently, A is inferior to B if and only if all the individuals that satisfy the modes in the intentional content of A also satisfy all the modes in the intentional content of B. The extension of idea A, or Ext(A), is defined as the set of ideas B that signify only individuals that B signifies. It follows that the ideas in a term’s extension, which is the set of its inferiors, signify what the term signifies but do so in finer detail. Let the significance range of idea A, or Sig(A), be the set of all individuals that A signifies. In short, Ext(A) is the set of ideas B such that Sig(B)⊆Sig(A).

The mappings Ext and Sig stand in one-to-one correspondence and as a result the definition of extension insures that a term’s extension provides an indirect way of referring to individuals “outside the mind.” Ext(A) determines Sig(A) because Sig(A) is the set of all individuals that are in any idea in Ext(A). Conversely, Sig(A) determines Ext(A) because Ext(A) is the set of all ideas inferior to A that signify only individuals in Sig(A). Moreover, their inclusion relations mirror one another: Sig(A)⊆Sig(B) if and only if Ext(A)⊆Ext(B). A correspondence theory of truth follows. As Part II explains, the truth-conditions of the universal affirmative are stated in terms of extensional inclusion: every S is P is true if and only if Ext(S)⊆Ext(P). But this holds exactly when Sig(S)⊆Sig(P).

The reader should be warned that the definition of extension in the Logic is rather different from the usual one in modern logic. Modern usage, which follows Leibniz and Frege, identifies the extension of A with Sig(A). That is, in modern usage the extension of A is a set of individuals, not ideas. Although the Logic’s usage has fallen into desuetude, it has historical priority.

p. The Structure of Ideas

The ordering relations on ideas and extensions have suggested to some commentators that the Logic anticipates 19^th century Boolean algebra. (See Dominicy 1984, Auroux 1982, and Auroux 1993.) The suggestion is intriguing but overblown. It is true that intentional content seems to be a set of modes and sets are ordered by the subset relation. This ordering, moreover, induces a containment relation on ideas: idea A is contained in idea B (briefly A≤B) if and only if the intentional content of B is a subset of the intentional content of A. In addition, every idea determines a significance range. The mapping from ideas to significance ranges is, moreover, many-one because distinct ideas may signify the same individuals. For example, a species-difference and its proprium would have the same significance range, as do the two terms Peter and the man who denied Christ three times. The mapping, moreover, is antitonic—it reverses the ordering: if A≤B, then Ext(B)⊆Ext(A). As pointed out above, there is also a one-one order preserving mapping from significance ranges to extensions. It follows that there is a many-one antitonic mapping from ideas to extensions: if A≤B, then Ext(B)⊆Ext(A). Thus, as Leibniz later observed, the order of extensions reverses the order of ideas. These are all genuine algebraic properties in the modern sense, and they are in some sense implicit in the Logic. On the other hand, these properties were not remarked upon by the Logic’s authors themselves.

In their own pre-algebraic language about containment, signification, and extension, the authors do remark on order and correspondence. It is an exaggeration, however, to say they noticed duality or the properties of a Boolean algebra (see Martin 2016c). They do not comment on the fact that the order of extensions reverses that of ideas, a necessary condition for duality. They do not point out that ≤ and ⊆ are reflexive, transitive, or asymmetric. Much less do they claim that abstraction and restriction satisfy the conditions for meet and join operations. Abstraction, for example, is treated as a one-place operation, and there is no suggestion that the set of ideas is “closed” under either abstraction or restriction. There is no textual evidence that they envisaged a maximal idea, which would have as its intentional content the set of all modes. It is also unclear whether being, the highest genus, should be regarded as a minimal idea. Is being in the comprehension of golden mountain or square circle? The authors avoid such issues. The few times they refer to a negation as an operation it is as the medieval notion of privative negation rather than as a complementation operation in the modern sense. (I:7, KM 148, B 42; II:15, KM 242, B 124. See Martin 2016b.) They do not even say explicitly that genera and species exhibit the structure of the tree of Porphyry. (See Auroux 1992, Auroux 1993.) All in all, the discussion of structure in the Logic is pre-algebraic, like discussions of structure found in medieval logic, of which the Logic is a continuation.

2. The Logic of Propositions

a. Summary

Part II discusses the properties of expressions in spoken language. Among other expressions it discusses nouns, pronouns, and verbs (II:1), the four categorical propositions (II:3), gappings (II:4-5), false ideas (II:7), exclusives such as only (II:10:1) and exceptives such as except (II:10:2), the alethic modalities (II:8), comparative adjectives (II:10:3), various compound sentences (II:9), and definitions (II:16). Expressions in spoken language represent propositions in mental language, essentially the categorical propositions of the syllogistic and their truth-functions. Part II concludes with the truth-conditions for categorical propositions (II:17–20) and conversion. Much of the material is unoriginal or of slight logical interest. Remarks here are limited to modality and the truth-conditions for categorical propositions.

b. Modality

The alethic modalities—possible, contingent, impossible, and necessary—are discussed briefly and characterized syntactically as verbal modifiers. There is no attempt to provide semantic analysis or truth-conditions. A point of interest is that in a series of mnemonic names setting out four squares of oppositions, one for each of the four modalities, they conflate contingent with possible. That is, they identify contingency with so-called “single-sided” possibility: it is contingent that P means it is possible that P. They are probably following the commentary tradition. At some points in the De Interpretatione Aristotle explains contingency in the single-sided sense, a conflation that had been regularly remarked upon by later commentators. The Logic’s authors may in fact be copying a virtually identical discussion of the mnemonic names from the logic of Eustache de Saint-Paul in which he makes the same conflation using the same names and squares. Fonseca in his logic of roughly the same period is more revealing. He reports Aristotle’s conflations of contingency with single-sided possibility and remarks that in 17^th century logical discourse contingency had evolved to its double-sided sense. He nevertheless goes on in his text to provide a list that follows Aristotle and identifies the contingent with the possible. Regardless of the mnemonics at II:8, where the authors themselves actually use the word contingent or contingency in the Logic to state their own views, they use contingent in the double-sided sense following the general usage of the period. For example, in Part IV they describe knowledge of historical and human events, which is based on sensation, as “contingent” with the understanding that the events might have been otherwise.

c. Distributive and Confused Supposition

Part II concludes with sections laying out “axioms” for the truth-conditions for the categorical propositions of the syllogistic. These sections are some of the most interesting parts of the book. The account is not really axiomatic in the modern sense: it is rather a series of informal definitions. From the “axioms” and the explanatory remarks that accompany them, however, it is possible to abstract clear truth-conditions in the modern sense. What is interesting from a modern perspective is that truth is defined as a function of the semantic interpretations of a proposition’s parts, much as in a modern recursive definition. The particular way they do so is also of historical interest because it draws on ideas from medieval supposition theory.

In the theory of supposition, medieval logicians had distinguished various ways in which categorical terms refer. Depending on the type of propositions in which it occurs and its position, a term signifies either all the individuals in its scope, in which case it was said to have distributive supposition, or just some individuals, in which case it was said to have confused supposition. These species of supposition were explained in terms of characteristic entailments that hold between the proposition itself and specific conjunctions and disjunctions of multiple identity statements. (See Parsons 2014, Chapter 7.) There are four cases, one for each of the four types of categorical proposition. It is assumed that there are proper names for each of the individuals that a term signifies:

A universal affirmative is equivalent to a long conjunction of disjunctions. For each individual in the subject’s scope there is a conjunct, and this conjunct consists of a disjunction that affirms of that individual that it is identical to one or the other of the individuals in the predicate’s scope.
A particular affirmative is equivalent to a long disjunction of disjunctions. For each individual in the subject’s scope there is a disjunct, and this disjunct consists of a disjunction that affirms of that individual that it is identical to one or the other of the individuals in the predicate’s scope.
A universal negative is equivalent to a long conjunction of conjunctions. For each individual in the subject’s scope there is a conjunct, and this conjunct consists of a conjunction that denies of that individual that it is identical to each of the individuals in the predicate’s scope.
A particular negative is equivalent to a long disjunction of conjunctions. For each individual in the subject’s scope there is a disjunct, and this disjunct consists of a conjunction that denies of that individual that it is identical to each of the individuals in the predicate’s scope.

These equivalents can be stated briefly in the notation of sentential logic. Let us assume that the constants s₁,…,s_nname all the individuals in the scope of the subject S, and that p₁,…,p_nname all the individuals in the scope of the predicate P. The entailments for the four propositional forms are then:

By reference to these equivalents it is possible to give a semantic definition of distributive supposition. The definition depends on whether the term is a subject or predicate. A subject term is distributive if the proposition in which it occurs is equivalent to a conjunction of conjunctions or disjunctions and is non-distributive otherwise. A predicate is distributive if the proposition in which it occurs is equivalent to a conjunction or disjunction of conjuncts and is non-distributive otherwise:

	Subject	Predicate
A	Distributive	Non-Distributive
E	Distributive	Distributive
I	Non-Distributive	Non-Distributive
O	Non-Distributive	Distributive

d. Truth-Conditions for Categorical Propositions

What makes the entailments relevant to truth-conditions is that they suggest a way to characterize truth according to distributional properties. For example, a universal affirmative is true if the subject is truly distributive and the predicate non-distributive. From the perspective of modern truth-theory, however, any definition of truth in terms of the medieval notions of distribution and non-distribution would be flawed because it would be circular. Truth cannot be defined in terms of distribution because distribution is defined in terms of entailment, and entailment in terms of truth. Medieval logicians were not troubled about circularity because the distinction between distributive and non-distributive supposition was part of a system of classifying the different ways terms refer. There was no intention of incorporating supposition into a definition of truth, recursive or otherwise.

Arnauld and Nicole, however, in effect noticed that is possible to explain distribution and non-distribution directly without reference to the entailments of “descent and ascent.” It is then possible to use the distinction to state truth-conditions in a non-circular way. More precisely, it is possible to say in the metalanguage, without referring to object language identity statements, that in a true universal affirmative each referent in the extension of the subject is identical to some referent in the extension of the predicate, and so forth for the other propositional types. (See Martin 2013 and Martin 2016a. Compare Pariente 1985, who questions the influence of supposition theory.)

To explain the authors’ metalinguistic approach, it is useful to make use of the notation of restricted quantification. The notation attaches a subscript to the quantifier symbol naming its “extension.”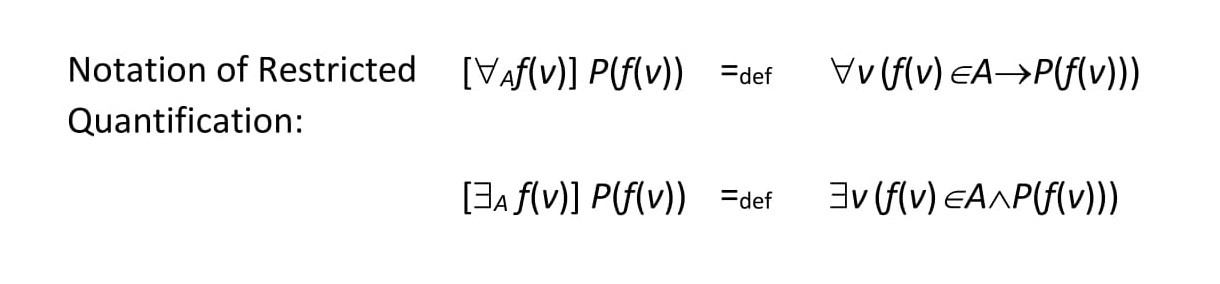

Here f(v) is a functor f applied to a variable v, and P(f(v)) is an open sentence saying something about f(v); [∀_A f(v)] P(f(v)) is read as for any f(v) in A, P(f(v)); and [∃_A f(v)] P(f(v)) is read as for some f(v) in A, P(f(v)).

The truth-conditions for the categorical propositions are easily stated in the metalanguage as facts about the identity or non-identity of all or some of the referents to individuals in the subject’s relevant extension to those in the predicate’s. In the notation below, the individual signified by term v, briefly Sig(v), is referred to as being in either the extension of the subject S, briefly Ext(S), or in the extension of the predicate P, briefly Ext(P), or in the intersection of the two extensions, briefly Ext(S) ∩ Ext(P):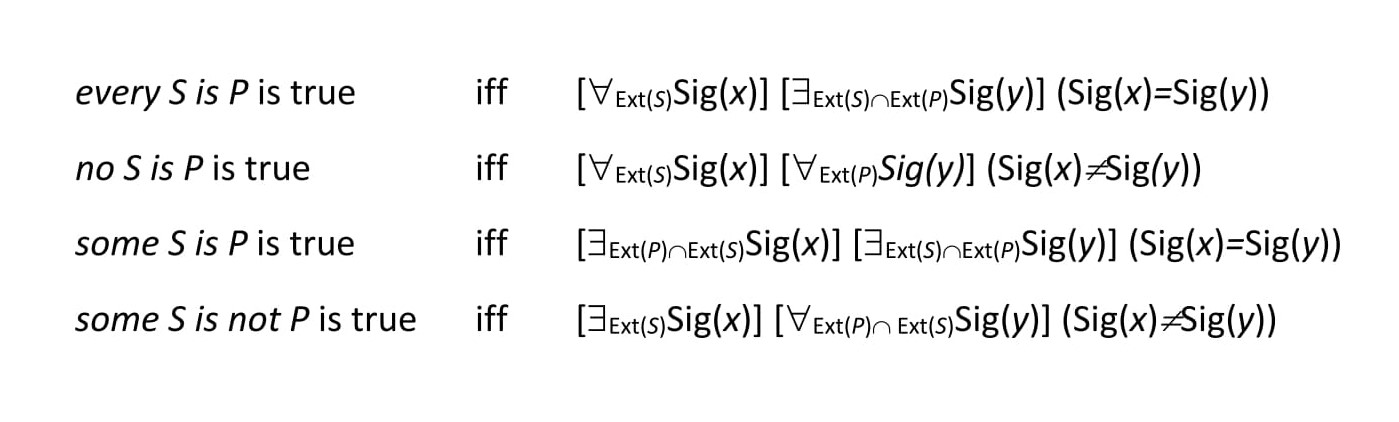
In the formulas above let the right hand side be called the truth-conditions of the categorical proposition on the left. Let the outer (left-most) quantifier in the truth-conditions, which has the broader scope, be called the subject quantifier, and let the inner (right-most) quantifier, which has narrower scope, be called the predicate quantifier. It is then possible to define distributive term semantically. A term is used distributively in a proposition if the proposition is true and its quantifier in its truth-conditions is universal, and non-distributively if it is true and its quantifier is existential.

The Logic’s authors make the same distinction using different terminology. They prefer to use universal for distributive and particular for non-distributive, a common variant in earlier logic. They also noticed that the relevant extension of a term varies by its position. A term’s relevant extension is its entire extension if the term is the subject of universal affirmative, universal negatives, or particular negatives, or it is the predicate of a universal negative. In all other cases, a term’s relevant extension is the intersection of the extensions of the proposition’s two terms. (In modern general quantification theory, similar distinctions are made in terms of whether the proposition’s quantifier is monotonic.) Recall that in the Logic, a term’s extension is a set of ideas. In the authors’ terminology, then, a universal term is one that asserts of each idea in that term’s relevant extension that it is identical to (“is put in”) or is not identical to (“is not put in”) the ideas in the relevant extension of its collateral term. A particular term is one that asserts this identity or non-identity only of some. The truth-conditions axiomatized by the authors (II:17–20) can then be easily stated, first in their own terminology (in italics) and then in a modern paraphrase.

every S is P is true	iff	The proposition is affirmative. The subject is universal. The attribute is particular. The extension of the attribute is restricted by that of the subject. The attribute is put in the subject according to the entire extension of the subject.
		The relevant extension of the subject S is its entire extension; the relevant extension of the predicate P is the restriction of its extension of P by that of S. Every element of the relevant extension of S is identical to some element of the relevant extension of P.
no S is P is true	iff	The proposition is negative. The subject and the predicate are universal. The attribute of a negative proposition is always taken generally. Negative propositions separate the attribute from the subject according to the entire extension of the attribute. The attribute is denied of everything contained in the extension of the subject.
		The relevant extension of S is its entire extension. The relevant extension of P is its extension. Every element of the relevant extension of the subject is not identical to every element of the relevant extension of P.

some S is P is true	iff	The proposition is affirmative. The subject and predicate are particular. The extension of the attribute is restricted by that of the subject. The attribute is conceived only in part of the extension of subject.
		The relevant extension of the subject S is the restriction of its extension by that of the predicate P. The relevant extension of P is the restriction of its extension by that of S. Some element of the relevant extension of S is identical to some element in the relevant extension of P.
some S is not P is true	iff	The proposition is negative. The subject is particular. The attribute is universal. The attribute is denied of everything contained in the extension of the subject. Negative propositions separate the attribute from the subject according to the entire extension of the attribute. Negative propositions separate this attribute from the subject, particularly if it is particular.
		The relevant extension of S is its entire extension. The relative extension of P is its extension restricted by that of S. There is some element in the relevant extension of S that is not identical to any element in the extension of P.

e. The Correspondence Theory of Truth

Although these truth-conditions are formulated in terms of extensions, which are composed of ideas, the Logic’s broader intention is to capture a correspondence theory of truth. As explained in Part I, there is a one-one mapping between significance ranges and extensions. Accordingly, although the conditions above refer to the identity or non-identity of ideas in term-extensions, ideas in a term’s extension are proxies for individuals in the term’s significance range. It is true that the Logic’s authors say little about the expressive completeness of mental language. They make no claim that there is an idea in mental language for every individual that actually exists—that, in medieval terms, there is an individual concept for each existing thing. But to insure a genuine correspondence theory, all that the authors need assume is that the ideas in a term’s extension “cover” the individuals in the term’s significance range in the sense that for any individual signified by a term there is some idea in its extension that signifies it. In the trivial case in which an idea has no strict inferiors, the idea itself would “cover” its own significance range.

As they stand, the truth-conditions do not address the issue of existential import of the subjects of affirmative propositions. They do not provide for what happens when an affirmative proposition has a false idea as subject term. The discussion of false ideas in Part I requires that these propositions be false. The issue recurs in Part IV in the discussion of necessary and contingent truth.

3. The Logic of Arguments

a. Summary

(Formater: Insert paragraphs for this section here.)

b. The Syllogistic

Acceptable arguments, including the immediate inferences of the square of opposition and syllogisms, are described in terms of “rules.” An example is the rule for accidental conversion: universal affirmative propositions can be converted by adding a mark of particularity to the attribute which becomes the subject (II:1, KM V 250, B 132). All these rules are laid down without proof. A modern reader, on the other hand, would expect that the authors, having just stated the truth-theory for the categorical propositions in Part II, would have made some effort to argue for the validity of the rules in Part III. They seem to have thought, however, that the rules they cite are too obvious to require justification, and indeed most of the logic of Part III is trivial. They remark, for example, that “there is little value in knowing the rules of the syllogism” (IV:introduction, KM V 354, B 227). Of logical errors they say, “… it is almost impossible for a person of average intelligence who has some insight ever to fall into them” (IV:8, KM V 384-385, B 252). On the other hand, in the later sections of Part III, they attach much importance to the avoidance fallacies, especially various kinds of equivocation.

The rules describing the square of opposition, conversion, and the valid moods are formulated using a series of technical terms: subject and predicate; affirmative and negative proposition, universal and particular term; universal and particular proposition; syllogism; major, middle, and minor term. (A singular proposition is classified as a special case of universal proposition.) These are all understood syntactically with the exception of universal and particular term, and affirmative and negative proposition, which in Part II also have semantic senses.

c. Validity

It is surprising that the authors do not attempt to prove the validity of their rules. It had been common to do so in logic since Aristotle. Nor do they attempt a syntactic account of what counts as a valid mood. In the Logic’s first edition they do discuss the traditional method of reducing the valid moods to Barbara and Celarent and describe a set of traditional mnemonic names for the reductions. (See B, xxxv and 156.) From a modern perspective, that procedure is not without interest because it is an early form of an axiom system even though the set being axiomatized (the valid syllogisms) is trivially finite. The authors, however, dismiss reductions as “useless” and omit the topic in later editions. (III:8, B 156. See B, xxxv and 156.) They may do so because they reject one of the traditional reduction rules, per contradictionem (if A,~B├ ~C, then A,C├ B). The rejection is perhaps due to their more general doubts about indirect proof in Part IV. (See III:9, KM 276, B 157 and IV:2, KM V 367, B 238; IV:9, KM V 388, B 255.)

Although the authors do not prove the validity of their rules or attempt a syntactic characterization of the set of valid moods in general, they do provide what amounts to a syntactic decision procedure for the set of valid moods. They do so by laying down six syntactic rules (III:3), which in various forms have been repeated in textbooks ever since.

Rule 1. The middle term cannot be taken particularly twice, but must be taken universally once.

Rule 2. The terms of the conclusion cannot be taken more universally in the conclusion than in the premises.

Rule 3. No conclusion can be drawn from two negative propositions.

Rule 4. A negative conclusion cannot be proved from two affirmative propositions.

Rule 5. The conclusion always follows the weaker part. That is, if one of the two propositions is negative, the conclusion must be negative; if one of them is particular, it must be particular.

Rule 6. Nothing follows from two particular propositions.

The set of six rules is not new. The four rules that do not mention universal and particular terms were common in medieval logic. Rules 1 and 2, which are today known as “process rules,” are formulated in terms of universal and particular term and are found in contemporary works. The complete list of six rules is given verbatim in Eustache de Saint-Paul. (Summa philosophiae quadripartita, Logia III.2.I. 117, Eustachio-De-S.-Paulo 1648.) Leibniz later used the same rule set in his more formal version of the syllogistic dividing Rule 5 into two. (See Lensen 1990.)

The rules are interesting if understood syntactically. The vocabulary in which they are framed is clearly syntactic except for perhaps universal and particular term, which in Part II had been defined semantically. But as any student knows who has used the rules, universal and particular term also have simple syntactic definitions. A term is universal (or distributive) if and only if it is the subject of a universal proposition or the predicate of a negative. In a number of places in Part III, the authors refer to them syntactically.

Viewed syntactically, the rule set provides a decision procedure for the set of valid moods. By reviewing syntactically each of the 256 syllogisms, it is easy to confirm of each syllogism that if it is not on the list of 24 valid moods, it violates a least one rule. Conversely, it is easy to check, again syntactically, that if a syllogism violates a rule, it is not on the list of 24 valid moods. However, the authors of the Logic are not interested in metatheory. They do not explicitly make the point that the valid rules are exactly those that do not violate a rule, much less prove it.

4. Method

a. Summary

Part IV is about epistemology, both scientific knowledge, which is certain and based on clear and distinct ideas, and lesser sensory knowledge, which is contingent and concerns current events, history, and the future. The goal is to spell out logic’s role in scientific discovery and justification. The introductory sections (IV:1) distinguish genuine knowledge from philosophical and mathematical speculation, which is illustrated by puzzles arising from infinite divisibility. They continue (IV:2–3) with an account of scientific “method,” which consists of reasoning from causes to effects and conversely from effects to causes. The method they describe, which is divided into analysis and synthesis, makes implicit use of syllogistic techniques. Part IV’s central sections (IV:4–12) contain an extended discussion of scientific and sensory knowledge, including “demonstration,” which is another name for logic. The final sections (IV:13–16) warn about the epistemological and moral difficulties connected with faith and contingent beliefs. Remarks here focus on the central sections concerning epistemology, demonstration, and sensory knowledge. They conclude with an explanation of the role of syllogistic logic implicit in the authors’ notion of method.

b. Necessary and Contingent Truth

Certainty in science and the method for achieving it depend on the kind of truth being sought, and in particular, on whether the goal is necessary or contingent truth. The distinction between necessity and contingency had previously been made in Parts I and II. There, the necessity of essential definitions was contrasted with the contingency of accidental predications. The distinction also played a role in the discussion of false ideas. Affirmations with non-referring subjects are false. Some of these are impossible because the subject term has a comprehension that combines modes that are contrary, contradictory, or naturally incompatible (Part II:i). Part IV expands on the distinction between necessary and contingent truth, committing itself to the view that they differ in existential import:

The first reflection is that it is necessary to draw a sharp distinction between two sorts of truths. First are truths that concern merely the nature of things and their immutable essence, independently of their existence. The others concern existing things, especially human and contingent events, which may or may not come to exist when it is a question of the past. I am referring in this context to the proximate causes of things, in abstraction from their immutable order in God’s providence, because on the one hand, God’s providence does not preclude contingency, and on the other, since we know nothing about it [that is, contingent creation], it contributes nothing to our beliefs about things.

For the other kind of truth [viz. of essential natures], since everything [of this sort] is necessary, nothing is true that is not universally true. So we ought to conclude that something is false if it is false in a single case. (IV:13, KM V 398, B 263. See also II:13:iv)

The authors are committing themselves here to one side of a long debate. Earlier logicians were generally agreed that a contingent affirmation with a non-referring subject is false, but they were divided about the case of necessary propositions like essential definitions. Was “Humans are rational animals” true before creation, when there were no humans? Is a chiliagon has 1000 sides true today even though there are no actual chiliagons? Logicians like Aristotle and William of Ockham were clear that all propositions with non-referring subjects are false, even empty affirmations about a species’ nature. Others, like William of Sherwood, John Buridan, and Francisco Suárez, allowed that propositions that affirm of a species its nature (for example, essential definitions) have a timeless status. If true, they are necessarily true. Descartes too held that God can make some affirmations eternally true, like the species definition every triangle has three sides. On the other hand, Descartes appears to be open to inconsistency because he seems to have been the inspiration of the Logic’s doctrine of false ideas. He held that affirmations with non-referring subjects like chimera are false and a major source of error (compare Meditations III.6, Martin 2011). In the passage above, the Logic’s authors commit themselves to the view that propositions that affirm of a species its nature make no existential claim and that if they are true, they are necessarily so. Other affirmations that do not predicate an essence of a species, including propositions concerning worldly matters—for example, reports of sensation or claims about people, history, or geography—are contingent and carry existential import. It follows that the truth-conditions for categorical affirmatives in Part II, which as stated there do not require existential import, must be amended. For affirmations other than those affirming a nature of a species, an additional condition is necessary. Their truth-conditions should contain the requirement that the subject term signifies at least one existing thing. Doing so would also bring the Logic’s truth-theory into agreement with the prevailing opinion in medieval and then contemporary logic (see Ashworth 1973).

The distinction between necessity and contingency is important in epistemology. Though we can know or fail to know both what is necessary and contingent, the degree of certainty attached to each is different. The most important source of certainty is clear and distinct ideas.

c. Certainty, Clear and Distinct Ideas

In the first of two epistemological axioms, the Logic’s authors endorse Descartes’ doctrine that clear and distinct ideas are a source of knowledge:

First Axiom: Everything contained in the clear and distinct ideas of a thing can be truthfully affirmed of that thing (IV:6, KM V 378, B 250).

Examples of clear and distinct ideas include: ourselves as thinking beings, thinking, judging, reasoning, doubting, willing, desiring, sensing, imagining, shape, motion, rest, extended substance, existence, duration, order, number, and God.

Part I makes clear that substantives and adjectives, which are ideas, have intentional content. Sensory perceptions also have content. It consists of the many modes that flood awareness on the occasion of a sensation. This content, according to the Cartesians, may be clear or distinct. In the logical tradition, distinctness has usually been contrasted with generality. To say that an idea is distinct is to say it is a single idea. If it is distinct, it is unambiguous, and its content is internally consistent and possible (II:12, B 112). Clarity is probably to be understood as it is in Aquinas: it is a kind of intellectual light, a gift of God that allows the soul to be aware of an idea’s modal content. (Compare Aquinas, De veritate, q. 13 a. 2 arg. 4.) Thus, if the soul instantiates a clear and distinct idea, it is aware of a consistent and coherent modal content. Axiom I then says that if S is an idea that is conceived by the soul with clarity and distinctness and P is a mode in its content, the soul knows with certainty that every S is P is true. If the proposition is an essential truth, then it is necessary. Moreover, since S’s comprehension is coherent, the proposition S exists is possibly true, even if S has no actual instances. On the other hand, if the proposition is contingent and true, the proposition S exists is actually true.

Examples of clear and distinct ideas are not limited to species, nor is the knowledge they impart limited to essential definitions. An example is the cogito. Several times the Logic endorses Descartes’ argument that because the soul has a clear and distinct idea of itself as a thinking thing, it knows that it exists. The existence of a soul, however, is not necessary, nor is existence part of its nature. Most of the Logic’s examples of clear and distinct ideas, on the other hand, are from Cartesian science or metaphysics, and their contents illuminate essences. Part IV stressed that the bulk of scientific knowledge consists of the knowledge of essences imparted by clear and distinct ideas.

The necessity of essential truths is highlighted by Part IV’s second epistemological axiom, which is about possibility:

Second Axiom: At least possible existence is contained in the idea of everything we conceive clearly and distinctly (IV:6, KM V 378, B 250).

God insures that the soul never has a clear and distinct idea of an impossible being. The second axiom entails that if an essential affirmation every S is P is grounded in a clear and distinct idea, which is the preferred case in science, then possibly there is an S is true. (Arnauld makes clear elsewhere that he does not believe in the existence of possibilia as a category of being distinct from actual things. See “Arnauld to Leibniz,” May 13, 1686; KM VI, pp. 31–32; Stencil 2016). In the Logic’s first edition the authors go so far as to single out possibility as a marker of truth for essential affirmations:

possibility is a sure mark of the truth with respect to what is recognized as possible, whenever it is a question only of the essence of things (IV:13, B 263.)

The authors are making a point familiar from modal logic. An essential truth is either necessary or impossible. Thus, if it is possible, it is necessary. In the case of an essential definition, then, if it is known to be true scientifically by means of a clear and distinct idea, even if its subject term fails of actual reference, it is true and its subject is possible.

In the same text, the authors explain why a geometrical construction is also a source of certainty. Again, the reasoning turns on possibility. The mere construction of a figure with a property shows that the figure possibly possesses that property. But since the properties of a geometrical figure are either necessary or impossible, this possibility alone insures that the property holds of figures of that type necessarily.

While it is true that clear and distinct ideas have the premier role in scientific justification, they are not the only sources of knowledge. Less certain varieties of knowledge are based on demonstration and sensation.

d. Demonstration

Descartes seemed to have explained demonstrations by appeal to clear and distinct ideas. He interpreted the propositions that make up the lines of a logical or mathematical proof as a series of independent epistemological insights, each justified by its own clear and distinct idea. Once an individual line was formulated and appreciated, the thinker is inspired to conjure up an additional clear and distinct idea, and this forms the justification for the next line of the proof, and so on for the proof’s subsequent lines (See Gaukroger 1989.)

The Logic’s authors have a more modern idea of proof. A demonstration, as they understand it, is a series of lines, each of which is either a premise that is either previously proven or certain in itself, or a line that follows logically from earlier lines of the proof. They say:

A true demonstration requires two things: one, that the content includes only what is certain and indubitable; the other that there is nothing defective in the form of the argument. (IV:8, KM V 384, B 251)

Four types of premises are acceptable in a sound proof: propositions that affirm the content of a clear and distinct idea; nominal definitions, which are true by convention; properties of a geometric construction; and previously proven propositions (IV:8, KM V 384, B 251). All other lines in the demonstration must follow formally from earlier lines by rules of logic, presumably the rules of Part III. Perhaps oddly, the authors regard the application of logical rules as relatively trivial. Applying logical rules, they say, is “natural.” How to do so “does not need to be studied” (IV:7, KM V 397, B 252).

e. Sensation and Knowledge of Contingent Truth

A third source of knowledge is sensation. Although sensation is not certain, it is reliable. Its reliability is based on a demonstration. This is the (brief) argument that sensation is reliable because, if not, God would be a deceiver, which he is not. (VFI 28, KM I 355, G 213–214.) Sensory knowledge, moreover, is largely limited to contingent truths about past, present, or future individuals or events.

Although the account of sensation in Part IV is brief, Arnauld explains it more fully in “On True and False Ideas” (VFI 1; KM I, 190, 193, 195–196, 199; G 58, 62–63, 66). There, Arnauld debates Malebranche on whether perception is representational. Arnauld argues fiercely that the soul perceives the world directly, while Malebranche holds that the soul perceives only intermediate representations, which he identifies as ideas in God’s mind. Arnauld maintains that in sensory perception there are only two substances: the soul and the object sensed. As he puts it, the soul perceives the world “by the idea.” The process has two stages. First, the soul is aware that it is having a perception. Second, it is aware of the perception’s content, which consists of modes, some of which are true of the object in the world being perceived and some of which are true of the soul.

At one point he describes perception as a “relation” (VFI 5, KM I 198, G 66. Compare Raconis, De principiis entis a. 3, 827). According to the then-standard analysis of relations, a relational fact between two individuals breaks down into two non-relational substance-mode facts true respectively of the two relata. In other words, the fact that the relation holds breaks down into two nonrelational facts, in each of which the relatum possesses a mode characteristic of its role in the relation. Perception is such a relation. According to Arnauld, when a perception obtains, the soul instantiates a mode, namely an idea which possesses an intentional content that the soul is aware of. Simultaneously, the object sensed instantiates its modes, namely those modes that impact the body’s sense organs. That the soul and the sensed material object possess their respective modes constitutes the relational fact that the one is perceiving the other. It is God, who is not a deceiver, who insures that the material modes in the idea’s content match the modes of the object outside the mind.

Accordingly, veridical sensation consists of a vivid awareness of multiple modes all at once. Some of these are material modes, and as such they are true of the object outside the mind. These material modes consist of various geometrical and mechanical properties that hold to matter according to Cartesian physics. A perception, however, also contains modes of the soul. These are the sensory modes of color, taste, sound, etc. as well as psychological modes like feelings and states of mind. This rich group of material and spiritual modes constitutes the “content” of the perception. Despite the fact that a perception has a content, it is not an idea. Perceptions, for example, do not serve as terms in the propositions of mental language. Its content would be automatically “false” of any subject because it includes a contrary mixture of material and spiritual modes. Rather, the role of perceptual experience is to provide a rich source of modes for abstraction. The modes that the soul is aware of at the time of a veridical sensation are in fact instantiated, some in matter and some in the soul. If on the occasion of a sensation the soul abstracts an idea with a purely material content, the idea is true of the objects in the world impacting the body’s sense organs; if it abstracts an idea with a purely spiritual content, it is true of the soul. Thus, although the Logic’s authors are “rationalist” Cartesians and attach premier importance to clear and distinct ideas, they also allow for empirical knowledge of the material world, albeit of a less certain sort.

f. Method: Analysis and Synthesis

Although medieval logicians had much to say about method, 16^th century figures like Peter Ramus had initiated renewed interest. (See, for example, Edwards 1967.) Earlier in the Logic the authors had made brief methodological remarks on classification and its pitfalls not unlike those of Ramus (IV:2, KM V 243, B 125). Part IV begins with an extended discussion of method.

In the Logic’s account (IV:2, KM V 362-367, B 233–238), method divides into analysis and synthesis. Analysis reasons from effects to causes or from the specific to the general, and synthesis reasons inversely, from causes to effects or from the general to the specific. Both presuppose that science classifies its subject by ideas of increasing generality.

The paradigm the authors seem to have in mind is a chain of syllogisms in the mood Barbara. The chain starts with an affirmative premise that characterizes its subject in terms of a narrow species and finishes with a conclusion that predicates of it a more general idea. The same chain in reverse is a synthesis.

The authors provide an example of analysis. In it, the investigator “discovers” that a subject has St. Louis as a remote ancestor or “cause.” The pattern is a series of syllogisms in Barbara. Each syllogism in the series has two premises, one affirming of a subject that he is the descendent of his father, and a second affirming of his father that he is the descendent of his grandfather. The syllogism’s conclusion then affirms that the subject is the descendent of his grandfather. This pattern is repeated, one syllogism for each subsequent generation, until an ultimate conclusion affirms that the original subject is a descendent of St. Louis. Because increasingly earlier ancestors have increasingly more descendants, each succeeding predicate has a broader extension, and the final predicate is a descendent of St. Louis is the most general of all.

A is a descendant of B, every descendant of B is a descendant of C / ∴ A is a descendant of C

A is a descendant of C, every descendant of C is a descendant of D / ∴ A is a descendant of D

A is a descendant of D, every descendant of D is a descendant of E / ∴ A is a descendant of E

A is a descendant of E, every descendant of E is a descendant of St. Louis / ∴ A is a descendant of St. Louis

Synthesis is the series in reverse order.

Analysis is also called resolution and the method of discovery. It reasons from effect to cause, from a narrower to a broader predicate. Because an effect follows from its cause, it is said to be a posteriori.

Synthesis reasons from cause to effect, and is called the method of composition. Because causes are prior, synthesis is said to be a priori.

Although it is odd to a modern reader to regard a more general class as the cause of its subsets, it was normal in earlier philosophy. Aristotle regarded the genus as the formal cause of the species, and Neoplatonism considered higher nodes in the ontological tree as the more causally productive. The authors retain this paradigm is their understanding of the hierarchy of genera and species represented by the tree of Porphyry. When analysis is applied to the pursuit of the essential truths, it carries the investigator from knowledge of species lower in the tree to knowledge of a genus higher in the tree. As each conclusion is drawn, a new premise would be required that assigns a genus to the species mentioned in the preceding conclusion. An example of the method applied to genera and species is

Socrates is a human, every human is an animal /∴ Socrates is an animal

Socrates is an animal, every animal is a living creature /∴ Socrates is a living creature

Socrates is a living creature, every living creature is a body /∴ Socrates is a body

Socrates is a body, every body is a substance /∴ Socrates is a substance

This chain starts by assigning to Socrates the narrow predicate human, which has the comprehension {rational, self-moving, living, corporeal, being}. It proceeds through species with comprehensions of increasingly fewer modes. It finishes assigning to Socrates the most general genus.

The authors of the Logic were not alone among their contemporaries to have this understanding of cause, or of analysis and synthesis. Spinoza argues for his own version of quasi-Neoplatonic causation in which the order of cause to effect was the same in a sense as the order in logic of predicate to subject. Hobbes defends an account of analysis and synthesis that is almost identical to the Logic’s (Hobbes, De Corpore I.6.1, 66: Hobbes 1992). In various papers, Leibniz explores versions of analysis that are essentially more formal versions of the Logic’s. It was typical of Leibniz to symbolize the predicate of a universal affirmative as a series P₁…P_k of concatenated terms. In his notation, the term letters are intended to stand for modes that are like those that make up species-comprehensions in the Logic. In a typical example, Leibniz lays down an initial premise S is P₁…P_k. The “analysis,” then, is a deduction that proceeds by the application of a simplifying inference rule that deletes terms from the predicate, thus making the new line’s predicate more general. The deduction terminates in a line with the most general predicate of all. The inference rule would be: S is X₁…X_n├ S is X₁…X_n_-1. (See, for example, De arte combinatoria in Parkinson 1966, and Swoyer 1995.)

S is P₁,P_2,P₃,P₄

S is P₁,P_2,P₃

S is P₁,P₂

S is P₁

In sum, the Logic’s notion of cause and its associated methods was a symptom of its time. What is of interest from the perspective of logic is that its details make implicit use of technical ideas from syllogistic logic. It should also be remarked, however, that it is hard to see how these methods actually would be of use in Cartesian physics, about which the Logic says very little.

5. References and Further Reading

a. Primary Sources

Arnauld, Antoine. 1813. Œuvres Philosophiques d’Antoine Arnauld. Paris: Adolphe Delahays. Abbreviated VFI.
Arnauld, Antoine. 1990. On True and False Ideas. Transalated by Stephen Gaukroger. Manchester:, Manchester University Press. Abbreviated G.
Arnauld, Antoine. 2003. Œuvres Philosophiques d’Arnauld. Edited by Elmar Kremer and Denis Moreau. Bristol: Theommes Press. Abbreviated KM.
Arnauld, Antoine and Pierre Nicole. 1996. Logic or the Art of Thinking. Translated by Jill Vance Buroker. Cambridge: Cambridge University Press. Abbreviated B.
Buridan, John. 2001. Summulae de Dialectica. New Haven: Yale University Press.
Eustachio-de-S.-Paulo. 1648. Summa philosophiae quadripartita, de rebus dialecticis, ethicis, physicis et metaphysicis. Cantabrigia [Cambridge]: Rogerus Danielis.
Fonseca S.J., Petrus. 1599. Commentarii in XII libros Metaphysicarum Aristotelis. Frankfurt.
Hobbes, Thomas. 1992. De Corpore. Edited by William Molesworth. London: Routledge-Thoemmes Press.
Raconis, C. F. d’Abra de. 1651. Tertia Pars Philosophiae seu Physicae, Quarta Pars Philosophiae seu Metaphysicae. Totius Philosophiae, hoc est Logicae, Moralis, Physicae et Metaphysicae, brevis et accurata, facilique et clara methodo disposita tractatio. Lugdunum [Lyon]: Irenaeus Barlet.
Suárez, Francisco. 1995. On Beings of Reason (De entibus rationis) Metaphysical Disputation 54. Milwaukee: Marquette University Press.
Toletus S.J., F. 1596. Commentaria una cum quaestionibus in universam Aristotelis logicam. Cologne: Agrippina.
William of Ockham. 1978. Expositio in librum Perihermenias Aristotelis. Edited by A. Gambatese and S. Brown. St Bonaventure, New York: Franciscan Institute.

b. Secondary Sources

Ashworth, E. J. 1973. “Existential Assumptions in Late Medieval Logic.” American Philosophical Quarterly, 10: 141–147.
Auroux, Sylvain. 1982. L’Illuminismo Francese e la Tradizione Logica di Port-Royal. Bologna: CLUEB.
Auroux, Sylvain. 1992. “Port-Royal et l’arbre de Porphyre.” Archives et documents de la Sociéte d’histoire et d’épistémologie des sciences du langage, 6: 109–122.
Auroux, Sylvain. 1993. La Logique des Idées. Montréal, Paris, Bellarmin : Vrin.
Chomsky, Noam. 1966. Cartesian Linguistics. New York: Harper and Row.
Cronin, T. J. 1966. Objective Being in Descartes and Suárez. Rome: Gregorian University Press.
Dominicy, Marc. 1984. La Naissance de la Grammaire Moderne, Bruxelles: Pierre Mardaga.
Edwards, William F. 1967. “Randall on the Development of Scientific Method in the School of Padua—A Continuing Reapraisal.” In Naturalism and Historical Understanding, edited by John P. Anton, 53–69. State University of New York.
Garber, Daniel. 1993. “Descartes and Occasionalism.” In Causation in Early Modern Philosophy, edited by Steven M. Nadler, 9–26. University Park, Pennsylvania: Pennsylvania State University Press.
Gaukroger, Stephen. 1989. Cartesian Logic. Oxford: Oxford University Press.
Lensen, Wolfgang. 1990. “On Leibniz’s Essay Mathesis Rationis.” Topoi, 9, 29–59.
Martin, John N. 2011. “Existential Import in Cartesian Semantics.” History and Philosophy of Logic, 32:2, 1–29.
Martin, John N. 2012. “Existential Commitment and the Cartesian Semantics of the Port Royal Logic.” In New Perspectives on the Square of Opposition, edited by Jean-Yves Beziau. Bern: Peter Lang.
Martin, John N. 2013. “Distributive Terms, Truth, and The Port Royal Logic.” History and Philosophy of Logic, 34:2, 133–154.
Martin, John N. 2016a. “A Note on ’Distributive Terms, Truth, and The Port Royal Logic’.” History and Philosophy of Logic, 37:4, 391–392.
Martin, John N. 2016b. “Privative Negation in The Port Royal Logic.” Review of Symbolic Logic, 9, 23.
Martin, John N. 2016c. “The Structure of Ideas in The Port Royal Logic.” The Journal of Applied Logic, 19, 1–19.
Martin, John N. 2017. “Extension in the Port Royal Logic.” South American Journal of Logic, 3:1, 1-20.
Nadler, Steven. 2011. Occasionalism: Causation among the Cartesians. Oxford: Oxford University Press.
Nadler, Steven M. 1989. Arnauld and the Cartesian Philosophy of Ideas. Manchester: Manchester University Press.
Pariente, Jean-Claude. 1985. L’Analyse du Langage à Port-Royal. Paris: C.N.R.S. Éditions de Minuit.
Parkinson, G. H. R. 1966. Leibniz, Logical Papers. Oxford: Clarendon Press.
Parsons, Terence. 2014. Articulating Medieval Logic. Oxford: Oxford University Press.
Pasnau, Robert. 1997. Theories of Cognition in the Later Middle Ages. Cambridge: Cambridge University Press.
Stencil, Eric. 2016. “Essence and Possibility in the Leibniz-Arnauld Correspondence.” Pacific Philosophical Quarterly, 97, 2–26.
Swoyer, Chris. 1995. “Leibniz on Intension and Extension.” Nous, 29, 96–114.

Author Information

John N. Martin
Email: john.martin@uc.edu
University of Cincinnati
U. S. A.

The Port Royal Logic

Table of Contents

1. The Logic of Terms

a. Summary

b. Ontology

c. Dualism, Ideas

d. Mental Language

e. Intentional Content

f. Kinds of Ideas, Occasionalism

g. Determinative and Explicative Restriction

h. Indeterminate Restriction

i. False Ideas

j. Abstraction

k. The Categories and Predicables

l. Nominalism-Realism

m. Comprehension as a Generalization of Essence

n. Species and Difference

o. Signification and Extension

p. The Structure of Ideas

2. The Logic of Propositions

a. Summary

b. Modality

c. Distributive and Confused Supposition

d. Truth-Conditions for Categorical Propositions

e. The Correspondence Theory of Truth

3. The Logic of Arguments

a. Summary

b. The Syllogistic

c. Validity

4. Method

a. Summary

b. Necessary and Contingent Truth

c. Certainty, Clear and Distinct Ideas

d. Demonstration

e. Sensation and Knowledge of Contingent Truth

f. Method: Analysis and Synthesis

5. References and Further Reading

a. Primary Sources

b. Secondary Sources

Author Information

An encyclopedia of philosophy articles written by professional philosophers.