Special Relativity: Proper Time, Coordinate Systems, and Lorentz Transformations

This supplement to the main Time article explains some of the key concepts of the Special Theory of Relativity (STR). It shows how the predictions of STR differ from classical mechanics in the most fundamental way. Some basic mathematical knowledge is assumed.

Table of Contents

  1. Proper Time
  2. The STR Relationship Between Space, Time, and Proper Time
  3. Coordinate Systems
    1. Coordinates as a Mathematical Language for Time and Space
  4. Cartesian Coordinates for Space
  5. Choice of Inertial Reference Frame
  6. Operational Specification of Coordinate Systems for Classical Space and Time
  7. Operational Specification of Coordinate Systems for STR Space and Time
  8. Operationalism
  9. Coordinate Transformations and Object Transformations
  10. Valid Transformations
  11. Velocity Boosts in STR and Classical Mechanics
  12. Galilean Transformation of Coordinate System
  13. Lorentz Transformation of Coordinate System
  14. Time and Space Dilation
  15. The Full Special Theory of Relativity
  16. References and Further Reading

1. Proper Time

EinsteinThe essence of the Special Theory of Relativity (STR) is that it connects three distinct quantities to each other: space, time, and proper time. ‘Time’ is also called coordinate time or real time, to distinguish it from ‘proper time’. Proper time is also called clock time, or process time, and it is a measure of the amount of physical process that a system undergoes. For example, proper time for an ordinary mechanical clock is recorded by the number of rotations of the hands of the clock. Alternatively, we might take a gyroscope, or a freely spinning wheel, and measure the number of rotations in a given period. We could also take a chemical process with a natural rate, such as the burning of a candle, and measure the proportion of candle that is burnt over a given period.

Note that these processes are measured by ‘absolute quantities’: the number of times a wheel spins on its axis, or the proportion of candle that has burnt. These give absolute physical quantities and do not depend upon assigning any coordinate system, as does a numerical representation of space or real time. The numerical coordinate systems we use firstly require a choice of measuring units (meters and seconds, for example). Even more importantly, the measurement of space and real time in STR is relative to the choice of an inertial frame. This choice is partly arbitrary.

Our numerical representation of proper time also requires a choice of units, and we adopt the same units as we use for real time (seconds). But the choice of a coordinate system, based on an inertial frame, does not affect the measurement of proper time. We will consider the concept of coordinate systems and measuring units shortly.

Proper time can be defined in classical mechanics through cyclic processes that have natural periods – for instance, pendulum clocks are based on counting the number of swings of a pendulum. More generally, any natural process in a classical system runs through a sequence of physical states at a certain absolute rate, and this is the ‘proper time rate’ for the system.

In classical physics, two identical types of systems (with identical types of internal construction, and identical initial states) are predicted to have the same proper time rates. That is, they will run through their physical states in perfect correlation with each other.

This holds even if two identical systems are in relative constant motion with respect to each other. For instance, two identical classical clocks would run at the same rate, even if one is kept stationary in a laboratory, while the other is placed in a spaceship traveling at high speed.

This invariance principle is fundamental to classical physics, and it means that in classical physics we can define: Coordinate time = Proper time for all natural systems. For this reason, the distinction between these two concepts of time was hardly recognized in classical physics (although Newton did distinguish them conceptually, regarding ‘real time’ as an absolute temporal flow, and ‘proper time’ as merely a ‘sensible measure’ of real time; see his Scholium).

However, the distinction only gained real significance in the Special Theory of Relativity, which contradicts classical physics by predicting that the rate of proper time for a system varies with its velocity, or motion through space. The relationship is very simple: the faster a system travels through space, the slower its internal processes go. At the maximum possible speed, the speed of light, c, the internal processes in a physical system would stop completely. Indeed, for light itself, the rate of proper time is zero: there is no ‘internal process’ occurring in light. It is as if light is ‘frozen’ in a specific internal state.

At this point, we should mention that the concept of proper time appears more strongly in quantum mechanics than in classical mechanics, through the intrinsically ‘wave-like’ nature of quantum particles. In classical physics, single point-particles are simple things, and do not have any ‘internal state’ that represents proper time, but in quantum mechanics, the most fundamental particles have an intrinsic proper time, represented by an internal frequency. This is directly related to the wave-like nature of quantum particles. For radioactive systems, the rate of radioactive decay is a measure of proper time. Note that the amount of decay of a substance can be measured in an absolute sense. For light, treated as a quantum mechanical particle (the photon), the rate of proper time is zero, and this is because it has no mass. But for quantum mechanical particles with mass, there is always a finite ‘intrinsic’ proper time rate, represented by the ‘phase’ of the quantum wave. Classical particles do not have any correlate of this feature, which is responsible for quantum interference effects and other non-classical ‘wave-like’ behavior.

2. The STR Relationship Between Space, Time, and Proper Time

STR predicts that motion of a system through space is directly compensated by a decrease in real internal processes, or proper time rates. Thus, a clock will run fastest when it is stationary. If we move it about in space, its rate of internal processes will decrease, and it will run slower than an identical type of stationary clock. The relationship is precisely specified by the most profound equation of STR, usually called the metric equation (or line metric equation). The metric equation is:

(1) coordinate systems 1

This applies to the trajectory of any physical system. The quantities involved are:

D is the difference operator.

Dt is the amount of proper time elapsed between two points on the trajectory.

Dt is the amount of real time elapsed between two points on the trajectory.

Dr is the amount of motion through space between two points on the trajectory.

c is the speed of light, and depends on the units we choose for space and time.

The meaning of this equation is illustrated by considering simple trajectories depicted in a space-time diagram.

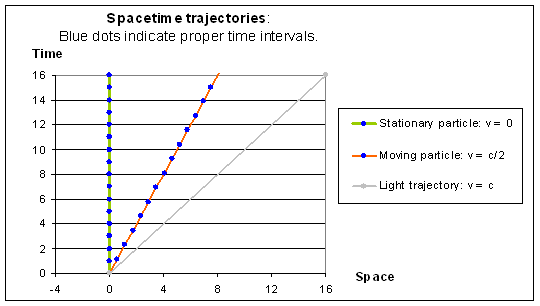
Figure 1. Two simple space-time trajectories.

Figure 1. Two simple space-time trajectories.

If we start at a initial point on the trajectory of a physical system, and follow it to a later point, we find that the system has covered a certain amount of physical space, Dr, over a certain amount of real time, Dt, and has undergone a certain amount of internal process or proper-time, Dt. As long as we use the same units (seconds) to represent proper time and real time, these quantities are connected as described in Equation (1). Proper time intervals are shown in Figure 1 by blue dots along the trajectories. If these were trajectories of clocks, for example, then the blue dots would represent seconds ticked off by the clock mechanism.

In Figure 1, we have chosen to set the speed of light as 1. This is equivalent to using our normal units for time, i.e. seconds, but choosing the units for space as c meters (instead of 1 meter), where c is the speed of light in meters per second. This system of units is often used by physicists for convenience, and it appears to make the quantity c drop out of the equations, since c = 1. However, it is important to note that c is a dimensional constant, and even if its numerical value is set equal to 1 by choosing appropriate units, it is still logically necessary in Equation 1 for the equation to balance dimensionally. For multiplying an interval of time, Dt, by the quantity c converts from a temporal quantity into a spatial quantity. Equations of physics, just like ordinary propositions, can only identify objects or quantities of the same physical kinds with each other, and the role of c as a dimensional constant remains crucial in Equation (1), for the identity it states to make any sense.

Trajectories in Figure 1

  • Trajectory 1 (green) is for a stationary particle, hence Dr = 0 (it has no motion through space), and putting this value in Equation (1), we find that: Dt = Dt. For a stationary particle, the amount of proper time is equal to the amount of coordinate time.
  • Trajectory 2 (red) is for a moving particle, and Dr > 0. We have chosen the velocity in this example to be: v = c/2, half the speed of light. But: v = Dr/Dt (distance traveled in the interval of time). Hence: Dr = ½cDt. Putting this value into Equation (1), we get: c²Dt² = c²Dt²-(½cDt)², or: Dt = Ö(¾)Dt » 0.87Dt. Hence the amount of proper time is only about 87% of coordinate time. Even though this trajectory is very fast, proper time is still only slowed down a little.
  • Trajectory 3 (black) is for a particle moving at the speed of light, with v = c, giving: Dr = cDt. Putting this in Equation (1), we get: c²Dt² = c²Dt²-(cDt)² = 0. Hence for a light-like particle, the amount of proper time is equal to 0.

Now from the classical point of view, Equation (1) is a surprise – indeed, it seems bizarre! For how can mere motion through space directly and precisely affect the rate of physical processes occurring in a system? We are used to the opposite idea, that motion through space, by itself, has no intrinsic effect on processes. This is at the heart of the classical Galilean invariance or symmetry. But STR breaks this rule.

We can compare this situation with classical physics, where (for linear trajectories) we have two independent equations:

(2.a) Dt = Dt

(2.b) Dr = vDt for some coordinate systems 3 (real numbers)

  • Equation (2.a) just means that the rate of proper time in a system is invariant – and we measure it in the same units as coordinate time, t.
  • Equation (2.b) just means that every particle or system has some finite velocity or speed, v, through space, with v defined by: v = Dr/Dt.

There is no connection here between proper time and spatial motion of the system.

The fact that (2) is replaced by (1) in STR is very peculiar indeed. It means that the rate of internal process in a system like a clock (whether it is a mechanical, chemical, or radioactive clock) is automatically connected to the motion of the clock in space. If we speed up a clock in motion through space, the rate of internal process slows down in a precise way to compensate for the motion through space.

The great mystery is that there is no apparent mechanism for this effect, called time dilation. In classical physics, to slow down a clock, we have to apply some force like friction to its internal mechanism. In STR, the physical process of a system is slowed down just by moving it around. This applies equally to all physical processes. For instance, a radioactive isotope decays more slowly at high speed. And even animals, including human beings, should age more slowly if they move around at high speed, giving rise to the Twin Paradox.

In fact, time dilation was already recognized by Lorentz and Poincare, who developed most of the essential mathematical relationships of STR before Einstein. But Einstein formulated a more comprehensive theory, and, with important contributions by Minkowski, he provided an explanation for the effects. The Einstein-Minkowski explanation appeals to the new concept of a space-time manifold, and interprets Equation (1) as a kind of ‘geometric’ feature of space-time. This view has been widely embraced in 20th Century physics. By contrast, Lorentz refused to believe in the ‘geometric’ explanation, and he thought that motion through space has some kind of ‘mechanical’ effect on particles, which causes processes to slow down. While Lorentz’s view is dismissed by most physicists, some writers have persisted with similar ideas, and the issues involved in the explanation of Equation (1) continue to be of deep interest, to philosophers at least.

But before moving on to the explanation, we need to discuss the concepts of coordinate systems for space and time, which we have been assuming so far without explanation.

3. Coordinate Systems

In physics we generally assume that space is a three dimensional manifold and time is a one dimensional continuum. A coordinate system is a way of representing space and time using numbers to represent points. We assign a set of three numbers, (x,y,z), to characterize points in space, and one number, t, to characterize a point in time. Combining these, we have general space-time coordinates: (x,y,z,t). The idea is that every physical event in the universe has a ‘space-time location’, and a coordinate system provides a numerical description of the system of these possible ‘locations’.

Classical coordinate systems were used by Descartes, Galileo, Newton, Leibniz, and other classical physicists to describe space. Classical space is assumed to be a three dimensional Euclidean manifold. Classical physicists added time coordinates, t, as an additional parameter to characterize events. The principles behind coordinate systems seemed very intuitive and natural up until the beginning of the 20th century, but things changed dramatically with the STR. One of Einstein’s first great achievements was to reexamine the concept of a coordinate system, and to propose a new system suited to STR, which differs from the system for classical physics. In doing this, Einstein recognized that the notion of a coordinate system is theory dependent. The classical system depends on adopting certain physical assumptions of classical physics – for instance, that clocks do not alter their rates when they are moved about in space. In STR, some of the laws underpinning these classical assumptions change, and this changes our very assumptions about how we can measure space and time. To formulate STR successfully, Einstein could not simply propose a new set of physical laws within the existing classical framework of ideas about space and time: he had to simultaneously reformulate the representation of space and time. He did this primarily by reformulating the rules for assigning coordinate systems for space and time. He gave a new system of rules suited to the new physical principles of STR, and reexamined the validity of the old rules of classical physics within this new system.

A key feature Einstein focused on is that a coordinate system involves a system of operational principles, which connect the features of space and time with physical processes or ‘operations’ that we can use to measure those features. For instance, the theory of classical space assumes that there is an intrinsic distance (or length) between points of space. We may take distance itself to be an underlying feature of ‘empty space’. Geometric lines can be defined as collections of points in space, and line segments have intrinsic lengths, prior to any physical objects being placed in space. But of course, we only measure (or perceive) the underlying structure of space by using physical objects or physical processes to make measurements. Typically, we use ‘straight rigid rulers’ to measure distances between points of space; or we use ‘uniform, standard clocks’ to measure the time intervals between moments of time. Rulers and clocks are particular physical objects or processes, and for them to perform their measurement functions adequately, they must have appropriate physical properties.

But those physical properties are the subject of the theories of physics themselves. Classical physics, for example, assumes that ordinary rigid rulers maintain the same length (or distance between the end-points) when they are moved around in space. It also assumes that there are certain types of systems (providing ‘idealized clocks’) that produce cyclic physical processes, and maintain the same temporal intervals between cycles through time, even if we move these systems around in space.

These assumptions are internally consistent with principles of measurement in classical physics. But they are contradicted in STR, and Einstein had to reformulate the operational principles for measuring space and time, in a way that is internally consistent with the new physical principles of STR.

We will briefly describe these new operational principles shortly, but there are some features of coordinate systems that are important to appreciate first.

a. Coordinates as a Mathematical Language for Time and Space

The assignment of a numerical coordinate system for time or space is thought of as providing a mathematical language (using numbers as names) for representing physical things (time and space). In a sense, this language could be ‘arbitrarily chosen’: there are no laws about what names can be used to represent things. But naturally there are features that we want a coordinate system to reflect. In particular, we want the assignment of numbers to directly reflect the concepts of distance between points of space, and the size of intervals between moments of time.

We perform mathematical operations on numbers, and we can subtract two numbers to find the ‘numerical distance’ between them. For numbers are really defined as certain structures, with features such as continuity, and we want to use the structures of number systems to represent structural features of space and time.

For instance, we assume in our fundamental physical theory that any two intervals of time have intrinsic magnitudes, which can be compared to each other. The ‘intrinsic temporal distance’ between two moments, t1 and t2, may be the same as that between two quite different moments, t3 and t4. We naturally want to assign numbers to times so that ordinary numerical subtraction corresponds to the ‘intrinsic temporal distance’ between events. We choose a ‘uniform’ coordinate system for time to achieve this.

coordinate systems 4

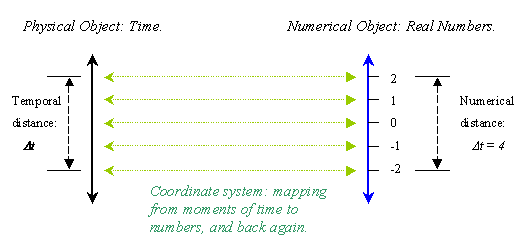
Figure 2. A Coordinate system for time gives a mathematical language for a physical thing.
Numbers are used as names for moments of time.

4. Cartesian Coordinates for Space

Time is simple because it is one-dimensional. Three-dimensional space is much more complex. Because space is three dimensional, we need three separate real numbers to represent a single point. Physicists normally choose a Cartesian coordinate system to represent space. We represent points in this system as: r = (x,y,z), where x, y, and z are separate numerical coordinates, in three orthogonal (perpendicular) directions.

The numerical structure with real-number points is denoted in mathematics as (x,y,z). Three dimensional space itself (a physical thing) is denoted as: coordinate systems 5. A Cartesian coordinate system is a special kind of mapping between points of these two structures. It makes the intrinsic spatial distance between two points in E3 be directly reflected by the ‘numerical distance’ between their numerical coordinates in coordinate systems 5.

The numerical distances in coordinate systems 5are determined by a numerical function for length. A line from the origin: (0,0,0), to the point r = (x,y,z), which is called the vector r, has its length given by the Pythagorean formula:

|r| = √(x²+y²+z²).

More generally, for any two points, r1 = (x1, y1, z1), and: r2 = (x2, y2, z2), the distance function is:

|r2 – r1| = √((x2 – x1)²+ (y2 – y1)²+ (z2 – z1)²)

The special feature of this system is that the lengths of lines in the x, y, or z directions alone are given directly by the values of the coordinates. E.g. if: r = (x,0,0), then the vector to r is a line purely in the x-direction, and its length is simply: |r| = x. If r1 = (x1,0,0), and: r2 = (x2,0,0), then the distance between them is just: |r2 – r1| = (x2 – x1 ). As well, a Cartesian coordinate system treats the three directions, x, y, and z, in a symmetric way: the angles between any pair of these directions is the same, 900. For this reason, a Cartesian system can be rotated, and the same form of the general distance function is maintained in the rotated system.

In fact, there are spatial manifolds which do not have any possible Cartesian coordinate system – e.g. the surface of a sphere, regarded as a two dimensional manifold, cannot be represented by using Cartesian coordinates. Such spaces were first studied as geometric systems in the 19th century, and are called non-classical or non-Euclidean geometries. However, classical space is Euclidean, and by definition:

  • Euclidean space can be represented by Cartesian coordinate systems.

We can define alternative, non-Cartesian, coordinate systems for Euclidean space; for instance, cylindrical and spherical coordinate systems are very useful in physics, and they use mixtures of linear or radial distance, and angles, as the numbers to specify points of space. The numerical formulas for distance in these coordinate systems appear quite different from the Cartesian formula. But they are defined to give the same results for the distances between physical points. This is the most crucial feature of the concept of distance in classical physics:

  • Distance between points in classical space (or between two events that occur at the same moment of time) is a physical invariant. It does not change with the choice of coordinate system.

The form of the numerical equation for distance changes with the choice of coordinate system; but this is done deliberately to preserve the physical concept of distance.

5. Choice of Inertial Reference Frame

A second crucial concept is the idea of a reference frame. A reference frame specifies all the trajectories that are regarded as stationary, or at rest in space. This defines the property of remaining at the same place through time. But the key feature of both classical mechanics and STR is that no unique reference frame is determined. Any object that is not accelerating can be regarded as stationary ‘in its own inertial frame’. It defines a valid reference frame for the whole universe. This is the natural reference frame ‘from the point of view’ of the object, or ‘relative to the object’. But there are many possible choices because given any particular reference frame, any other frame, defined to give everything a constant velocity relative to the first frame is also a valid choice.

The class of possible (physically valid) reference frames is objectively determined, because acceleration is absolutely distinguished from constant motion. Any object that is not accelerating may be regarded as defining a valid reference frame. But the specific choice of a reference frame from the range of possibilities is regarded as arbitrary or conventional. This choice must be made before a coordinate system can be defined to represent distances in space and time. Even after we have chosen a reference frame, there are still innumerable choices of coordinate systems. But the reference frame settles the definition of distances between events, which must be defined as the same in any coordinate system relative to a given reference frame.

The idea of the conventionality of the reference frame is partly evident already in the choice of a Cartesian coordinate system: for it is an arbitrary matter where we choose the origin, or point: 0 = (0,0,0), for such a system. It is also arbitrary which directions we choose for the x, y, and z axes – as long as we make them mutually perpendicular. We are free to rotate a given set of axes, x, y, z, to produce a new set, x’, y’, and z’, and this gives another Cartesian coordinate system. Thus, translations and rotations of Cartesian coordinate systems for space still leave us with Cartesian systems.

But there is a further transformation, which is absolutely central to classical physics, and involves both time and space. This is the Galilean velocity transformation, or velocity boost. The essential point is that we need to apply a spatial coordinate system through time. In pure classical geometry, we do not have to take time into account: we just assign a single coordinate system, at a single moment of time. But in physics we need to apply a coordinate system for space at different moments of time. How do we know whether the coordinate system we apply at one moment of time represents the same coordinate system we use at a later moment of time?

The principles of classical physics mean that we cannot measure ‘absolute location in space’ across time. The reason is the fundamental classical principle that the laws of nature do not distinguish between two inertial frames moving relative to each other at a constant speed. This is the classical Galilean principle of ‘relativity of motion’. Roughly stated, this means that uniform motion through space has no effect on physical processes. And if motion in itself does not affect processes, then we cannot use processes to detect motion.

Newton believed that the classical conception of space requires there to be absolute spatial locations through time nonetheless, and that some special coordinate systems or physical objects will indeed be at ‘absolute rest’ in space. But in the context of classical physics, it is impossible to measure whether any object is at absolute rest, or is in uniform motion in space. Because of this, Leibniz denied that classical physics requires any concept of absolute position in space, and argued that only the notion of ‘relative’ or ‘relational’ space’ is required. In this view, only the relative positions of objects with regards to each other are considered real. For Newton, the impossibility of measuring absolute space does not prevent it from being a viable concept, and even a logically necessary concept. There is still no general agreement about this debate between ‘absolute’ and ‘relative’ or ‘relational’ conceptions of space. It is one of the great historical debates in the philosophy of both classical and relativistic physics. However, it is generally accepted that classical physics makes absolute space undetectable. This means, at least, that in the context of classical physics there is no way of giving an operational procedure for determining absolute position (or absolute rest) through time.

However absolute acceleration is detectable. Accelerations are always accompanied by forces. This means that we can certainly specify the class of coordinate systems which are in uniform motion, or which do not accelerate. These special systems are called inertial systems, or inertial frames, or Galilean frames. The existence of inertial frames is a fundamental assumption of classical physics. It is also fundamental in STR, and the notion of an inertial frame is very similar in both theories.

The laws of classical physics are therefore specified for inertial coordinate systems. They are equally valid in any inertial frame. The same holds for the laws of STR. However, the laws for transforming from one inertial frame to another are different for the two theories. To see how this works, we now consider the operational specification of coordinate systems.

6. Operational Specification of Coordinate Systems for Classical Space and Time

In classical physics, we can define an ‘operational’ measuring system, which allows us to assign coordinates to events in space and time.

Classical Time. We imagine measuring time by making a number of uniform clocks, synchronizing them at some initial moment, checking that they all run at exactly the same rates (proper time rates), and then moving clocks to different points of space, where we keep them ‘stationary’ in a chosen inertial frame. We subsequently measure the times of events that occur at the various places, as recorded by the different clocks at those places.

Of course, we cannot assume that our system of clocks is truly stationary. The entire system of clocks placed in uniform motion would also define a valid inertial frame. But the laws of classical physics mean that clocks in uniform inertial motion run at exactly the same rates, and so the times recoded for specific events turn out to be exactly the same, on the assumptions of the classical theory, for any such system of clocks.

Classical Space. We imagine measuring space by constructing a set of rigid measuring rods or rulers of the same length, which we can (imaginatively at least) set up as a grid across space, in an inertial frame. We keep all the rulers stationary relative to each other, and we use them to measure the distances between various events. Again, the main complication is that we cannot determine any absolutely stationary frame for the grid of rulers, and we can set up an alternative system of rulers which is in relative motion. This results in assigning different ‘absolute velocities’ to objects, as measured in two different frames. However, on the assumptions of the classical theory, the relative distances between any two objects or events, taken at any given moment of time, is measured to be the same in any inertial frame. This is because, in classical physics, uniform motion in itself does not alter the lengths of material objects, or the forces between systems of objects. (Accelerations do alter lengths).

7. Operational Specification of Coordinate Systems for STR Space and Time

In STR, the situation is in many ways very similar to classical physics: there is still a special concept of inertial frames, acceleration is absolutely detectable, and uniform velocity is undetectable. According to STR, the laws of physics still are invariant with regard to uniform motion in space, very much like the classical laws.

We also specify operational definitions of inertial coordinate systems in STR in a similar way to classical physics. However, the system sketched above for assigning classical coordinates fails, because it is inconsistent with the physical principles of STR. Einstein was forced to reconstruct the classical system of measurement to obtain a system which is internally consistent with STR.

STR Time. In STR, we can still make uniform clocks, which run at the same rates when they are held stationary relative to each other. But now there is a problem synchronizing them at different points of space. We can start them off synchronized at a particular common point; but moving them to different points of space already upsets their synchronization, according to Equation (1).

However, while synchronizing distant clocks is a problem, they nonetheless run at the same intrinsic rates as each other when held in the same inertial frame. And we can ensure two clocks are in a common inertial frame as long as we can ensure that they maintain the same distance from each other. We see how to do this next.

Given we have two clocks maintained at the same distance from each other, Einstein showed that there is indeed a simple operational procedure to establish synchronization. We send a light signal from Clock 1 to Clock 2, and reflect it back to Clock 1. We record the time it was sent on Clock 1 as t0, and the time it was received again as a later time, t2. We also record the time it was received at Clock 2 as t1’ on Clock 2. Now symmetry of the situation requires that, in the inertial frame of Clock 1, we must assume that the light signal reached Clock 2 at a moment halfway between t0 and t1, i.e. at the time: t1 = ½(t2 – t0). This is because, by symmetry, the light signal must take equal time traveling in either direction between the clocks, given that they are kept at a constant distance throughout the process, and they do not accelerate. (If the light signal took longer to travel one way than the other, then light would have to move at different speeds in different directions, which contradicts STR).

Hence, we must resynchronize Clock 2 to make: t1’ = t1. We simply set the hands on Clock 2 forwards by: (t1 – t1’), i.e. by: ½(t2 – t0) – t1’. (Hence, the coordinate time on Clock 2 at t1’ is changed to: t1’ + (½(t2 – t0) – t1’) = ½(t2 – t0) = t1.)

This is sometimes called the ‘clock synchronization convention’, and some philosophers have argued about whether it is justified. But there is no real dispute that this successfully defines the only system for assigning simultaneity in time, in the chosen reference frame, which is consistent with STR.

Some deeper issues arise over the notion of simultaneity that it seems to involve. From the point of view of Clock 1, the moment recorded at: t1 = ½(t2 – t0) must be judged as ‘simultaneous’ with the moment recorded at t1’ on Clock 2. But in a different inertial frame, the natural coordinate system will alter the apparent simultaneity of these two events, so that simultaneity itself is not ‘objective’ in STR, except relative to a choice of inertial frame. We will consider this later.

STR Space. In STR, we can measure space in a very similar way as in classical physics. We imagine constructing a set of rigid measuring rods or rulers, which are checked to be the same length in the inertial frame of Clock 1, and we extend this out into a grid across space. We have to move the rulers around to start with, but when we have set up the grid, we keep them all stationary in the chosen inertial frame of Clock 1.

We then use this grid of stationary measuring rods to measure the distances between various events. The main assumption is that identical types of measuring rods (which are the same lengths when we originally compare them at rest with Clock 1), maintain the same lengths after being moved to different places (and being made stationary again with regard to Clock 1). This feature is required by STR.

The main complication, once again, is that we cannot determine any absolutely stationary frame for the grid of rulers. We can set up an alternative system of rulers, which are all in relative motion in a different inertial frame. As in classical physics, this results in assigning different ‘absolute velocities’ to most trajectories in the two different frames. But in this case there is a deeper difference: on the assumptions of STR, the lengths of measuring rods alter according to their velocities. This is called space dilation, and it is the counterpart of time dilation.

Nonetheless, Einstein showed that perfectly sensible operational definitions of coordinate measurements for length, as well as time, are available in STR. But both simultaneity and length become relative to specified inertial frames.

It is this confusing conceptual problem, which involves the theory dependence of measurement, that Einstein first managed to unravel, as the prelude to showing how to radically reconstruct classical physics.

8. Operationalism

Unraveling this problem requires us to specify ‘operational principles’ of measurement, but this does not require us to embrace an operational theory of meaning. The latter is a form of positivism, and it holds that the meaning of ‘time’ or ‘space’ in physics is determined entirely by specifying the procedures for measuring time or space. This theory is generally rejected by philosophers and logicians, and it was rejected by Einstein himself in his mature work. According to operationalism, STR changes the meanings of the concepts of space and time from the classical conception. However, many philosophers would argue that ‘time’ and ‘space’ have a meaning for us which is essentially the same as for Galileo and Newton, because we identify the same kinds of things as time and space; but relativity theory has altered our scientific beliefs about these things – just as the discovery that water is H2O has altered our understanding of the nature of water, without necessarily altering the meaning of the term ‘water’. This semantic dispute is ongoing in the philosophy of science. Having clarified these basic ideas of coordinate systems and inertial frames, we now turn back to the notion of transformations between coordinate systems for different inertial frames.

9. Coordinate Transformations and Object Transformations

Physics uses two different concepts of transformations. It is important to distinguish these carefully.

  • Coordinate transformations: Taking the description of a given process (such as a trajectory), described in one coordinate system, and transforming to its description in an alternative coordinate system.
  • Object transformations: Taking a given process, described in a given coordinate system, and transforming it into a different process, described in the same coordinate system as the original process.

The difference is illustrated in the following diagram for the simplest kind of transformation, translation of space.

coordinate systems 6

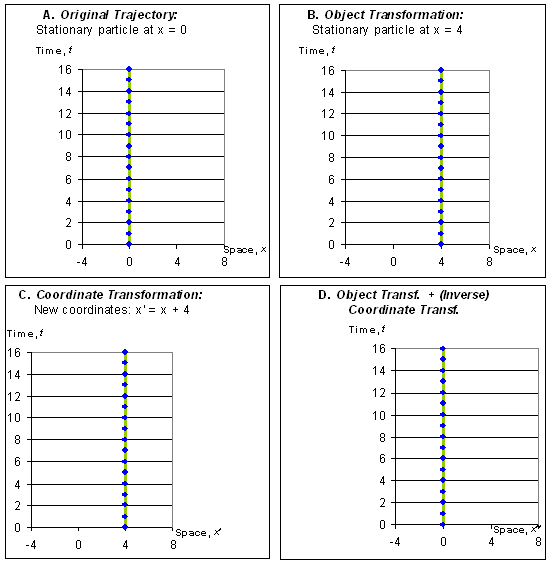
Figure 3. Object, Coordinate, and Combined Transformations.

  • The transformations in Figure 3 are simple space translations.
  • Figure 3 (B) shows an object transformation. The original trajectory (A) is moved in space to the right, by 4 units. The new coordinates are related to the original coordinates by: xnew particle ® xoriginal particle + 4.
  • Figure 3 (C) shows a coordinate transformation: the coordinate system is moved to the left by 4 units. The new coordinate system, x’, is related to the original system, x, by: x’original particle = xoriginal particle + 4. The result ‘looks’ the same as (B).
  • Figure 3 (D) shows a combination of the object transformation (B) and a coordinate transformation, which is the inverse of that in (C), defined by: x’’original particle = xoriginal particle – 4. The result of this looks the same as the original trajectory in (A), because the coordinate transformation appears to ‘undo’ the effect of the object transformation.

10. Valid Transformations

There is an intimate connection between these two kinds of transformations. This connection provides the major conceptual apparatus of modern physics, through the concept of physical symmetries, or invariance principles, and valid transformations.

The deepest features of laws or theories of physics are reflected in their symmetry properties, which are also called invariances under symmetry transformations. Laws or theories can be understood as describing classes of physical processes. Physical processes that conform to a theory are valid physical processes of that theory. Of course, not all (logically) possible processes that we can imagine are valid physical processes of a given theory. Otherwise the theory would encompass all possible processes, and tell us nothing about what is physically possible, as opposed to what is logically conceivable.

Symmetries of a theory are described by transformations that preserve valid processes of the theory. For instance, time translation is a symmetry of almost all theories. This means that if we take a valid process, and transform it, intact, to an earlier or later time, we still have a valid process. This is equivalent to simply setting the ‘temporal origin’ of the process to a later or earlier time.

Other common symmetries are:

  • Rotations in space (if we take a valid process, and rotate it to another direction in space, we end up with another valid process).
  • Translations in space (if we take a valid process, and move it to another position in space, we end up with another valid process).
  • Velocity transformations (if we take a valid process, and give it uniform velocity boost in some direction in space, we end up with another valid process).

These symmetries are valid both in classical physics and in STR. In classical physics, they are called Galilean symmetries or transformations. In STR they are called Lorentz transformations. However, although the symmetries are very similar in both theories, the Lorentz transformations in STR involve features that are not evident in the classical theory. In fact, this difference only emerges for velocity boosts. Translations and rotations are identical in both theories. This is essentially because velocity boosts in STR involve transformations of the connection between proper time and ordinary space and time, which does not appear in classical theory.

The concept of valid coordinate transformations follows directly from that of valid object transformations. The point is that when we make an object transformation, we begin with a description of a process in a coordinate system, and end up with another description, of a different process, given in the same coordinate system. Now instead of transforming the processes involved, we can do the inverse, and make a transformation of the coordinate system, so that we end up with a new coordinate description of the original process, which looks exactly the same as the description of the transformed process in the original coordinate system.

This gives an alternative way of regarding the process, and its transformed image: instead of taking them as two different processes, we can take them as two different coordinate descriptions of the same process.

This is connected to the idea that certain aspects of the coordinate system are arbitrary or conventional. For instance, the choice of a particular origin for time or space is regarded as conventional: we can move the origins in our coordinate description, and we still have a valid system. This is only possible because the corresponding object transformations (time and space translations) are valid physical transformations.

Physicists tend to regard coordinate transformations and valid object transformations interchangeably and somewhat ambiguously, and the distinction between the two is often blurred in applied physics. While this doesn’t cause practical problems, it is important when learning the concepts of the theory to distinguish the two kinds of transformations clearly.

11. Velocity Boosts in STR and Classical Mechanics

STR and classical mechanics have exactly the same symmetries under translations of time and space, and rotations of space. They also both have symmetries under velocity boosts: both theories hold that, if we take a valid physical process, and give it a uniform additional velocity in some direction, we end with another valid physical process. But the transformation of space and time coordinates, and of proper time, are different for the two theories under a velocity boost. In classical physics, it is called a Galilean transformation, while for STR it is called a Lorentz transformation.

To see how the difference appears, we can take a stationary trajectory, and consider what happens when we apply a velocity boost in either theory.

coordinate systems 7

Figure 4. Classical and STR Velocity Boosts give different results.

In both diagrams, the green line is the original trajectory of a stationary particle, and it looks exactly the same in STR and classical mechanics. Proper time events (marked in blue) are equally spaced with the coordinate time intervals in both cases.

If we transform the classical trajectory by giving the particle a velocity (in this example, v = c/2) towards the right, the result (red line) is very simple: the proper time events remain equally spaced with coordinate time intervals. The same sequence of proper time events takes the same amount of coordinate time to complete. The classical particle moves a distance: Dx = v.Dt to the right, where Dt is the coordinate time duration of the original process.

But when we transform the STR particle, a strange thing happens: the proper time events become more widely spaced than the coordinate time intervals, and the same sequence of proper time events takes more coordinate time to complete. The STR particle moves a distance: Dx’ = v.Dt’ to the right, where: Dt’ > Dt, and hence: Dx’ > Dx.

The transformations of the coordinates of the (proper time) points of the original processes are shown in the following table.

coordinate systems 8

Table 1. Example of Velocity Transformation.

We can work out the general formula for the STR transformations of t’ and x’ in this example by using Equation (1). This requires finding a formula for the transformation of time-space coordinates:

(t, 0) ® (t’, x’)

We obtain this by applying Equation (1) in the (t’,x’) coordinate system, giving:

(1’) coordinate systems 9

It is crucial that this equation retains the same form under the Lorentz equation. In this special case, we have the additional facts that:

(i) Dt = Dt, and:(ii) Dx’ = vDt’

We substitute (i) and (ii) in (1’) to get:

coordinate systems 10

This rearranges to give:

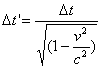coordinate systems 11 and: coordinate systems 12

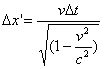
We can see that: Dx’/Dt’ = v. This is a special case of a Lorentz transformation for this simplest kind of trajectory. Note that if we think of this as a coordinate transformation which generates the appearance of this object transformation, we need to move the new coordinate system in the opposite direction to the motion of the object. I.e. if we define a new coordinate system, (x’,t’), moving at –v (i.e. to the left) with regard to the original (x,t) system, then the original trajectory (which appeared stationary in (x,t)) will appear to be moving with velocity +v (to the left) in (x’,t’). In general, object transformations correspond the inverse coordinate transformations.

12. Lorentz Transformations for Velocity Boost V in the x-direction

The previous transformations is only for points on the special line where: x = 0. More generally, we want to work out the formulae for transforming points anywhere in the coordinate system:

(t, x) ® (t’, x’)

The classical formulas are Galilean transformations, and they are very simple.

Galilean Velocity Boost:

(t, x) ® (t, x+vt)t’ = t

x’ = x+vt

The STR formulas are more general Lorentz transformations. The Galilean transformation is simple because time coordinates are unchanged, so that: t = t’. This means that simultaneity in time in classical physics is absolute: it does not depend upon the choice of coordinate system. We also have that distance between two points at a given moment of time is invariant, because if: x2 -x1 = Dx, then: x’2 -x’1 = (x2+vt) – (x1-vt) = Dx. Ordinary distance in space is the crucial invariant quantity in classical physics.

But in STR, we have a complex interdependence of time and space coordinates. This is seen because the transformation formulas for both t’ and x’ are functions of both x and t. I.e. there are functions f and g such that:

t’ = f(x,t) and: x’ = g(x,t)

These functions represent the Lorentz transformations. To give stationary objects a velocity V in the x-direction, these general functions are found to be Lorentz Transformation, and the factor 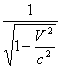coordinate systems 13 is called γ, letting us write these equations more simply as:

Lorentz Transformations: t’ = γ(t+Vx/c2) and: x’ = γ(x+Vt)

We can equally consider the corresponding coordinate transformation, which would generate the appearance of this object transformation in a new coordinate system. It is essentially the same as the object transformation – except it must go in the opposite direction. For the object transformation, which increases the velocity of stationary particles by the speed V in the x direction, corresponds to moving the coordinate system in the opposite direction. I.e. if we define a new coordinate system, and call it (x’,t’), and place this in motion with a speed –V (i.e. V in the negative-x-direction), relative to the (x,t) coordinate system, then the original stationary trajectories in (x,t)-coordinates will appear to have speed V in the new (x’,t’) coordinates.

Because the Lorentz transformation of processes leaves us with valid STR processes, the Lorentz transformation of a STR coordinate system leaves us with a valid coordinate system. In particular, the form of Equation (1) is preserved by the Lorentz transformation, so that we get: coordinate systems 14. This can be checked by substituting the formulas for t’ and x’ back into this equation, and simplifying; the resulting equation turns out to be identical to Equation (1).

13. Galilean Transformation of Coordinate System

One useful way to visualize the effect of a transformation is to make an ordinary space-time diagram, with the space and time axes drawn perpendicular to each other as usual, and then to draw the new set of coordinates on this diagram. In these diagrams, the space axes represent points which are measured to have the same time coordinates, and similarly, the time axes represent points which are measured to have the same space coordinates. When we make a velocity boost, these lines of simultaneity and same-position are altered.

This is shown first for a Galilean velocity boost, where in fact the lines of simultaneity remain the same, but the lines representing position are rotated:

coordinate systems 15

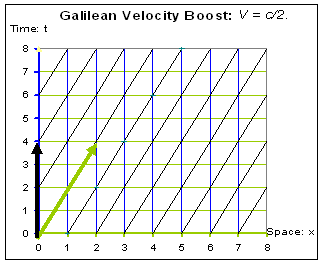
Figure 5. Galilean Velocity Boost.

  • In Figure 5, the (green) horizontal lines are lines of absolute simultaneity. They have the same coordinates in both t and t’.
  • The (blue) vertical lines are lines with the same x-coordinates.
  • The (gray) slanted lines are lines with the same x’-coordinates.
  • The spacing of the x’ coordinates is the same as the x coordinates, which means that relative distances between points are not affected.
  • The solid black arrow represents a stationary trajectory in (x,t).
  • An object transformation of +V moves it onto the green arrow, with velocity: v = c/2 in the (x,t)-system.
  • A coordinate transformation of +V, to a system (x’,t’) moving at +V with regard to (x,t), makes this green arrow appears stationary in the (x’,t’) system.
  • This coordinate transformation makes the black arrow appear to be moving at –V in (x’,t’) coordinates.

14. Lorentz Transformation of Coordinate System

In a Lorentz velocity boost, the time and space axes are both rotated, and the spacing is also changed.

coordinate systems 16

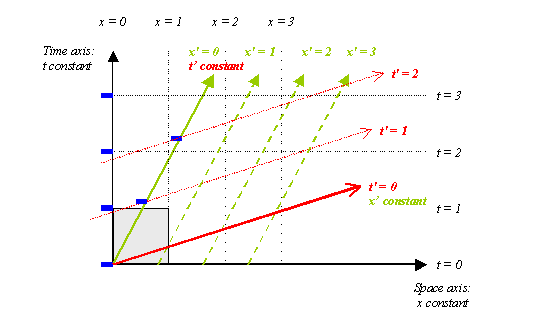
Figure 6. Rotation of Space and Time Coordinate Axes by a Lorentz Velocity Boost. Some proper time events are marked in blue.

To obtain the (x’,t’)-coordinates of a point defined in (x,t)-coordinates, we start at that point, and: (i) move parallel to the green lines, to find the intersection with the (red) t’-axis, which is marked with the x’-coordinates; and: (ii) move parallel to the red lines, to find the intersection with the (green) x’-axis, which is marked with the t’-coordinates. The effects of this transformation on a solid rod or ruler extending from x=0 to x=1, and stationary in (x,t), is shown in more detail below.

coordinate systems 17

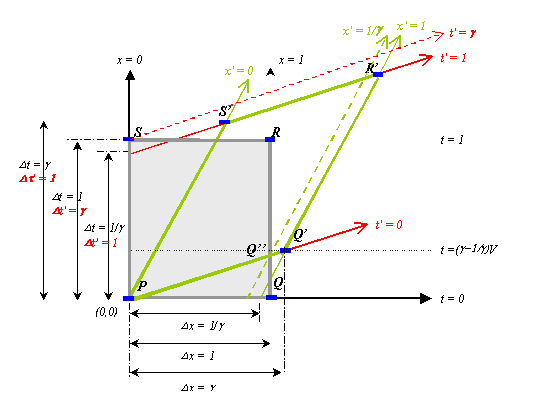
Figure 7. Lorentz Velocity Boost. Magnified view of Figure 6 shows time and space dilation. The gray rectangle represents a unit of the space-time path of a rod (Rod 1) stationary in (x,t). The dark green lines represent a Lorentz (object) transformation of this trajectory, which is a second rod (Rod 2) moving at V in (x,t) coordinates. This is a unit of the space-time path of a stationary rod in (x’,t’).

15. Time and Space Dilation

Figure 7 shows how both time and space dilation effects work. To see this clearly, we need to consider the volumes of space-time that an object like a rod traces out.

  • The (gray) rectangle PQRS represents a space-time volume, for a stationary rod or ruler in the original frame. It is 1-meter long in original coordinates (Dx = 1), and is shown over 1 unit of proper time, which corresponds to one unit of coordinate time (Dt = 1).
  • The rectangle PQ’R’S’ (green edges) represents a second space-time volume, for a rod which appears to be moving in the original frame. This is how the space-time volume of the first rod transforms under a Lorentz transformation.
  • We may interpret the transformation as either: (i) a Lorentz velocity boost of the rod by velocity +V (object transformation), or equally: (ii) a Lorentz transformation to a new coordinate system, (x’,t’), moving at –V with regard to (x,t). Note that:
  • The length of the moving rod measured in x is now shorter than the stationary rod: Dx = 1/γ. This is space dilation.
  • The coordinate time between proper time events on the moving rod measured in t is now longer than for the stationary rod (Dt = γ). This is time dilation.

The need to fix the new coordinate system in this way can be worked out by considering the moving rod from the point of view of its own inertial system.

  • As viewed in its own inertial coordinate system, the green rectangle PQ’R’S’ appears as the space-time boundary for a stationary rod. In this frame:
  • PS’ appears stationary: it is a line where: x’ = 0.
  • PQ’ appears as a line of simultaneity, i.e. it is a line where: t’=0.
  • R’S’ is also a line of simultaneity in t’.
  • Points on R’S’ must have the time coordinate: t’=1, since it is at the time t’ when one unit of proper time has elapsed, and for the stationary object, Dt’ = Dt.
  • The length of PQ’ must be one unit in x’, since the moving rod appears the same length in its own inertial frame as the original stationary rod did.

Time and space dilation are often referred to as ‘perspective effects’ in discussions of STR. Objects and processes are said to ‘look’ shorter or longer when viewed in one inertial frame rather than in another. It is common to regard this effect as a purely ‘conventional’ feature, which merely reflects a conventional choice of reference frame. But this is rather misleading, because time and space dilation are very real physical effects, and they lead to completely different types of physical predictions than classical physics.

However, the symmetrical properties of the Lorentz transformation makes it impossible to use these features to tell whether one frame is ‘really moving’ and another is ‘really stationary’. For instance, if objects get shorter when they are placed in motion, then why do we not simply measure how long objects are, and use this to determine whether they are ‘really stationary’? The details in Figure 7 reveal why this does not work: the space dilation effect is reversed when we change reference frames. That is:

  • Measured in Frame 1, i.e. in (x,t)-coordinates, the stationary object (Rod 1) appears longer than the moving object (Rod 2). But:
  • Measured in Frame 2, using (x’,t’)-coordinates, the moving object (Rod 2) appears stationary, while the originally stationary object (Rod 1) moves. But now the space dilation effect appears reversed, and Rod 2 appears longer than Rod 1!

The reason this is not a real paradox or inconsistency can be seen from the point of view of Frame 2, because now Rod 1 at the moment of time t’ = 0 stretches from the point P to Q’’, rather than from P to Q, as in Frame 1. The line of simultaneity alters in the new frame, so that we measure the distance between a different pair of space-time events. And PQ’’ is now found to be shorter than PQ’, which is the length of Rod 2 in Frame 2.

There is no answer, within STR, as to which rod ‘really gets shorter’. Similarly there is no answer as to which rod ‘really has faster proper time’ – when we switch to Frame 2, we find that Rod 2 has a faster rate of proper time with regard to coordinate time, reversing the time dilation effect apparent in Frame 1. In this sense, we could consider these effects a matter of ‘perspective’ – although it is more accurate to say that in STR, in its usual interpretation, there are simply no facts about absolute length, or absolute time, or absolute simultaneity, at all.

However, this does not mean that time and space dilation are not real effects. They are displayed in other situations where there is no ambiguity. One example is the twins’ paradox, where proper time slows down in an absolute way for a moving twin. And there are equally real physical effects resulting from space dilation. It is just that these effects cannot be used to determine an absolute frame of rest.

16. The Full Special Theory of Relativity

So far, we have only examined the most basic part of STR: the valid STR transformations for space, time, and proper time, and the way these three quantities are connected together. This is the most fundamental part of the theory. It represents relativistic kinematics. It already has very powerful implications. But the fully developed theory is far more extensive: it results from Einstein’s idea that the Lorentz transformations represent a universal invariance, applicable to all physics. Einstein formulated this in 1905: “The laws of physics are invariant under Lorentz transformations (when going from one inertial system to another arbitrarily chosen inertial system)”. Adopting this general principle, he explored the ramifications for the concepts of mass, energy, momentum, and force.

The most famous result is Einstein’s equation for energy: E = mc². This involves the extension of the Lorentz transformation to mass. Einstein found that when we Lorentz transform a stationary particle with original rest-mass m0, to set it in motion with a velocity V, we cannot regard it as maintaining the same total mass. Instead, its mass becomes larger: m = γm0, with γ defined as above. This is another deep contradiction with classical physics.

Einstein showed that this requires us to reformulate our concept of energy. In classical physics, kinetic energy is given by: E = ½ mv². In STR, there is a more general definition of energy, as: E = mc². A stationary particle then has a basic ‘rest mass energy’ of m0c². When it is set in motion, its energy is increased purely by the increase in mass, and this is kinetic energy. So we find in STR that:

Kinetic Energy = mc²-m0c² = (γ-1)m0c²

For low velocities, with: v << c, it is easily shown that: (γ-1)c² is very close to ½v², so this corresponds to the classical result in the classical limit of low energies. But for high energies, the behavior of particles is very different. The discovery that there is an underlying energy of m0c² simply from rest-mass is what made nuclear reactors and nuclear bombs possible: they convert tiny amounts of rest mass into vast amounts of thermal energy.

The main application Einstein explored first was the theory of electromagnetism, and his most famous paper, in which he defined STR in 1905, is called “Electrodynamics of Moving Bodies”. In fact, Lorentz, Poincaré and others already knew that they needed to apply the Lorentz transformation to Maxwell’s theory of classical electromagnetism, and had succeeded a few years earlier in formulating a theory which is extremely similar to Einstein’s in its predictions. Some important experimental verification of this was also available before Einstein’s work (most famously, the Michelson-Morley experiment). But his theory went much further. He radically reformulated the concepts that we use to analyse force, energy, momentum, and so forth. In this sense, his new theory was primarily a philosophical and conceptual achievement, rather than a new experimental discovery of the kind traditionally regarded as the epitome of empirical science.

He also attributed his universal ‘principle of relativity’ to the very nature of space and time itself. With important contributions by Minkowski, this gave rise to the modern view that physics is based on an inseparable combination of space and time, called space-time. Minkowski treated this as a kind of ‘geometric’ entity, based on regarding our Equation (1) as a ‘metric equation’ describing the geometric nature of space-time. This view is called the ‘geometric explanation’ of relativity theory, and this approach led Einstein even deeper into modern physics, when he applied this new conception to the theory of gravity, and discovered a generalised theory of space-time.

The nature of this ‘geometric explanation’ of the connection between space, time, and proper time is one of the most fascinating topics in the philosophy of physics. But it involves the General Theory of Relativity, which goes beyond STR.

17. References and Further Reading

The literature on relativity and its philosophical implications is enormous – and still growing rapidly. The following short selection illustrates some of the range of material available. Original publication dates are in brackets.

  • Bondi, Hermann. 1962. Relativity and Common Sense. Heinemann Educational Books.
    • A clear exposition of basic relativity theory for beginners, with a minimum of equations. Contains useful discussions of the Twins Paradox and other topics.
  • Einstein, Albert. 1956 (1921). The Meaning of Relativity. (The Stafford Little Lectures of Princeton University.) Princeton University Press.
    • Einstein’s account of the principles of his famous theory. Simple in parts, but mainly a fairly technical summary, requiring a good knowledge of physics.
  • Epstein, Lewis Carroll. 1983. Relativity Visualized. Insight Press. San Francisco.
    • A clear, simple, and rather unique introduction to relativity theory for beginners. Epstein illustrates the functional relationships between space, time, and proper time in a clear and direct way, using novel geometric presentations.
  • Grunbaum, Adolf. 1963. Philosophical Problems of Space and Time. Knopf, New York.
    • A collection of original studies by one of the seminal philosophers of relativity theory, this covers an impressive range of issues, and remains an important starting place for many recent philosophical studies.
  • Lorentz, H. A., A. Einstein, H. Minkowski and H. Weyl. 1923. The Principle of Relativity. A Collection of Original Memoirs on the Special and General Theory of Relativity. Trans. W. Perrett and G.B. Jeffery. Methuen. London.
    • These are the major figures in the early development of relativity theory, apart from Poincare, who simultaneously with Lorentz formulated the ‘pre-relativistic’ version of electromagnetic theory, which contains most of the mathematical basis of STR, shortly before Einstein’s paper of 1905. While Einstein deeply admired Lorentz – despite their permanent disagreements about STR – he paid no attention to Poincare.
  • Newton, Isaac. 1686. Mathematical Principles of Natural Philosophy.
    • Every serious student should read Newton’s “Definitions” and “Scholium”, where he introduces his concepts of time and space.
  • Planck, Max. 1998 (1909). Eight Lectures on Theoretical Physics.
    • Planck elegantly summarizes the revolutionary discoveries that characterized the first decade of 20th Century physics. Lecture 8 is one of the earliest accounts of relativity theory. This classic work shows Planck’s penetrating vision of many fundamental themes that soon came to dominate physics.
  • Reichenbach, Hans. 1958 (1928). The Philosophy of Space and Time. Dover, New York.
    • An influential early study of the concepts of space and time, and the relativistic revolution. Although Reichenbach’s approach is underpinned by his positivistic program, which is rejected today by philosophers, the central issues are of continuing interest.
  • Russell, Bertrand. 1977 (1925). ABC of Relativity. Unwin Paperbacks, London.
    • A early popular exposition of the meaning of relativity theory by one of the most influential 20th century philosophers, this presents key philosophical issues with Russell’s characteristic simplicity.
  • Schlipp, P.A. (Ed.) 1949. Albert Einstein: Philosopher-Scientist. The Library of Living Philosophers.
    • A classic collection of papers on Einstein and relativity theory.
  • Spivak, M. 1979. A Comprehensive Introduction to Differential Geometry. Publish or Perish. Berkeley.
    • An advanced mathematical introduction to the modern approach to differentiable manifolds, which developed in the 1960’s. Philosophical interest lies in the detailed semantics for coordinate systems, and the generalizations of concepts of geometry, such as the tangent vector.
  • Tipler, Paul A. 1982. Physics. Worth Publishers Ltd.
    • An extended introductory textbook for undergraduates, Chapter 35, “Relativity Theory”, is a typical modern introduction to relativity theory.
  • Torretti, Roberto. 1983/1996. Relativity and Geometry. Dover, New York.
    • An excellent source for the specialist philosopher, summarizing history and concepts of both the Special and General Theories, with extended bibliography. Combines excellent technical summaries with detailed historical surveys.
  • Wangsness, Roald K. 1979. Electromagnetic Fields. John Wiley & Sons Ltd.
    • This is a typical advanced modern undergraduate textbook on electromagnetism. The final chapter explains how the structure of electrodynamics is derived from the principles of STR.

Back to the main “Time” article.

Author Information

Andrew Holster
Email: ATASA@clear.net.nz
New Zealand