Frequently Asked Questions about Time

This supplement provides background information about many of the topics discussed in both the main Time article and its other companion article What Else Science Requires of Time (That Philosophers Should Know). It is not intended that this article be read in order by section number.

Table of Contents

1. What Are Durations, Instants, Moments, and Points of Time?
2. What Is an Event?
3. What Is a Reference Frame?
4. Curved Space and Cartesian Coordinates
5. What Is an Inertial Frame?
6. What Is Spacetime?
7. What Is a Spacetime Diagram and a Light Cone?
8. What Are Time’s Metric and Spacetime’s Interval?
9. How Does Proper Time Differ from Standard Time and Coordinate Time?
10. Is Time the Fourth Dimension?
11. How Is Time Relative to the Observer?
12. What Is the Relativity of Simultaneity?
13. What Is the Conventionality of Simultaneity?
14. What are the Absolute Past and the Absolute Elsewhere?
15. What Is Time Dilation?
16. How Does Gravity Affect Time?
17. What Happens to Time near a Black Hole?
18. What Is the Solution to the Twins Paradox?
19. What Is the Solution to Zeno’s Paradoxes?
20. How Are Coordinates Assigned to Time?
21. How Do Dates Get Assigned to Actual Events?
22. What Is Essential to Being a Clock?
23. What Does It Mean for a Clock to Be Accurate?
24. What Is Our Standard Clock or Master Clock?
    1. How Does an Atomic Clock Work?
    2. How Do We Find and Report the Standard Time?
25. Why Are Some Standard Clocks Better than Others?
26. What Is a Field?

1. What Are Durations, Instants, Moments, and Points of Time?

A duration is a measure of elapsed time. It is a number with a unit such as seconds or hours. “4” is not a duration, but “4 seconds” is. The second is the agreed-upon standard unit for the measurement of duration in the S.I. system (the International Systems of Units, that is, Le Système International d’Unités). How to carefully define the term second is discussed later in this supplement.

In informal conversation, an instant or moment is a very short duration. In physics, however, an instant is even shorter. It is instantaneous; it has zero duration. This is perhaps what the poet T.S. Eliot was thinking of when he said, “History is a pattern of timeless moments.”

There is another sense of the words instant and moment which means, not a very short duration, but rather a time, as when we say it happened at that instant or at that moment. Now a moment is being considered to be a three-dimensional object, namely a ‘snapshot’ of the universe.  Midnight could be such a moment. This is the sense of the word moment meant by a determinist who says the state of the universe at one point of time determines the state of the universe at any later point or moment. In this sense, a moment is normally considered to be a special three-dimensional object, namely a snapshot of our universe at a moment. This is a Leibnizian notion of what a state is.

It is assumed in all currently accepted fundamental theories of physics that any interval of time is a linear continuum of the points of time that compose it, but it is an interesting philosophical question to ask how physicists know time is a continuum. Nobody could ever measure time that finely, even indirectly.  Points of time cannot be detected. That is, there is no physically possible way to measure that the time is exactly noon even if it is true that the time is noon. Noon is 12 to an infinite number of decimal places, and no measuring apparatus is infinitely precise, and no measurement fails to have a margin of error. But given what we know about points, we should not be trying to detect points of anything. Belief in the existence of points of time is justified holistically by appealing to how they contribute to scientific success, that is, to how the points give our science extra power to explain, describe, predict, and enrich our understanding. In order to justify belief in the existence of points, we need confidence that our science would lose too many of these virtues without the points. Without points, we could not use calculus to describe change in nature.

Consider what a point in time really is. Any interval of time is a real-world model of a segment of the real numbers in their normal order. So, each instant corresponds to just one real number and vice versa. To say this again in other words, time is a line-like structure on sets of point events. Just as the real numbers are an actually infinite set of decimal numbers that can be linearly ordered by the less-than-or-equal relation, so time is an actually infinite set of instants or instantaneous moments that can be linearly ordered by the happens-before-or-at-the-same-time-as relation in a single reference frame. An instant or moment can be thought of as a set of point-events that are simultaneous in a single reference frame.

Although McTaggart disagrees, all physicists would claim that a moment is not able to change because change is something that is detectable only by comparing different moments.

There is a deep philosophical dispute about whether points of time actually exist, just as there is a similar dispute about whether spatial points actually exist. The dispute began when Plato said, “[T]his queer thing, the instant, …occupies no time at all….” (Plato 1961, p. 156d). Some philosophers wish to disallow point-events and point-times. They want to make do with intervals, and want an instant always to have a positive duration. The philosopher Michael Dummett, in (Dummett 2000), said time is not made of point-times but rather is a composition of overlapping intervals, that is, non-zero durations. Dummett required the endpoints of those intervals to be the initiation and termination of actual physical processes. This idea of treating time without instants developed a 1936 proposal of Bertrand Russell and Alfred North Whitehead. The central philosophical issue about Dummett’s treatment of motion is whether its adoption would negatively affect other areas of mathematics and science. It is likely that it would. For the history of the dispute between advocates of point-times and advocates of intervals, see (Øhrstrøm and Hasle 1995). The term interval in the phrase spacetime interval is a different kind of interval.

Even if time is made of points, it does not follow that matter is. It sometimes can be a useful approximation to say an electron or a quark is a point particle, but it remains an approximation. They are really vibrations of quantized fields.

2. What Is an Event?

In the manifest image, the universe is more fundamentally made of objects than events. In the scientific image, the universe is more fundamentally made of events than objects.

But the term event has multiple senses. There is sense 1 and sense 2. In ordinary discourse, one uses sense 1 in which an event is a happening lasting some duration during which some object changes its properties. For example, this morning’s event of buttering the toast is the toast’s changing from having the property of being unbuttered this morning to having the property of being buttered later this morning.

The philosopher Jaegwon Kim, among others, claimed that an event should be defined as an object’s having a property at a time. So, two events are the same if they are both events of the same object having the same property at the same time. This suggestion captures sense 1 of our informal concept of event, but with Kim’s suggestion it is difficult to make sense of the remark, “The vacation could have started an hour earlier.” On Kim’s analysis, the vacation event could not have started earlier because, if it did, it would be a different event. A possible-worlds analysis of events might be the way to solve this problem of change.

Physicists do sometimes use the term event this way, but they also use it differently—in what we here call sense 2—when they say events are point-events or regions of point-events often with no reference to any other properties of those events, such as their having the property of being buttered toast at that time. The simplest point-event in sense 2 is a location in spacetime with zero volume and zero duration. Hopefully, when the term event occurs, the context is there to help disambiguate sense 1 from sense 2. For instance, when an eternalist says our universe is a block of events, the person normally means the universe is the set of all point-events with their actual properties.

To a non-quantum physicist, any physical object is just a series of its point-events plus the values of all their intrinsic properties. For example, the process of a ball’s falling down is a continuous, infinite series of point-events along the path in spacetime of the ball.  One of those events would be this particular point piece of the ball being at a specific spatial location at some specific time. The reason for the qualification about “non-quantum” is discussed at the end of this section.

The physicists’ notion of point-event in real, physical space (rather than in mathematical space) is metaphysically unacceptable to some philosophers, in part because it deviates so much from the way the word event is used in ordinary language and in our manifest image. That is, sense 2 deviates too much from sense 1. For other philosophers, it is unacceptable because of its size, its infinitesimal size. In 1936, in order to avoid point-events altogether in physical space, Bertrand Russell and A. N. Whitehead developed a theory of time that is based on the assumption that every event in spacetime has a finite, non-zero duration. They believed this definition of an event is closer to our common sense beliefs, which it is. Unfortunately, they had to assume that any finite part of an event is also an event, and this assumption indirectly appeals to the concept of the infinitesimal and so is no closer to common sense than the physicist’s assumption that all events are composed of point-events.

McTaggart argued early in the twentieth century that events change. For example, he said the event of Queen Anne’s death is changing because it is receding ever farther into the past as time goes on. Many other philosophers (those of the so-called B-camp) believe it is improper to consider an event to be something that can change, and that the error is in not using the word change properly. This is still an open question in philosophy, but physicists use the term event as the B-theorists do, namely as something that does not change.

In non-quantum physics, specifying the state of a physical system at a time involves specifying the masses, positions and velocities of each of the system’s particles at that time. Not so in quantum mechanics. The simultaneous precise position and velocity of a particle—the key ingredients of a classical particle event—do not exist according to quantum physics. The more precise the position is, the less precise is the velocity, and vice versa. Also, many physicists consider the notion of event in physics to be emergent at a higher scale from a more fundamental lower scale that has no events. The philosopher David Wallace, among others, has emphasized this idea.

The ontology of quantum physics is very different from that of non-quantum physics. The main Time article intentionally downplays this. But, says the physicist Sean Carroll, “at the deepest level, events are not a useful concept,” and one should focus on the wave function.

More than half the physicists in the first quarter of the 21st century believed that a theory of quantum gravity will require (1) quantizing time, (2) having time or spacetime be emergent from a more fundamental entity, (3) having only a finite maximum number of events that can occur in a finite volume. Current relativity theory and quantum theory have none of these three features.

For more discussion of what an event is, see the article on Events.

3. What Is a Reference Frame?

A reference frame is a standard viewpoint or perspective chosen by someone to display quantitative measurements about places of interest in a space plus the phenomena that take place there. It is not an objective feature of nature. To be suited for its quantitative purpose, a reference frame needs to include a coordinate system, that is, is a system of assigning numerical locations or ordered sets of numerical locations to points of the space. If the space is physical spacetime, then each point needs to be assigned at least four numbers, three for its location in space, and one for its location in time. These numbers are called “coordinates.” For every coordinate system, every point-event in spacetime has three spatial coordinate numbers and one time coordinate number. It is a convention that we usually choose the time axis to be straight rather than some other shape, but this is not required, and on the globe we use longitudes as coordinate lines, and these are not straight and not parallel.

Choosing a coordinate system requires selecting some point to be called the system’s “origin” and selecting the appropriate number of coordinate axes that orient the frame in the space. You need at least as many axes as there are dimensions to the space. To add a coordinate system to a reference frame for a space is to add an arrangement of reference lines to the space so that all points of space have unique names. It is often assumed that an observer is located at the origin, but this is not required; it is sufficient to treat the frame “as if” it had an observer. The notion of a reference frame is modern; Newton did not know about reference frames.

The name of a point in a two-dimensional space is an ordered set of two numbers (the coordinates). If a Cartesian coordinate system is assigned to the space, then a point’s coordinate is its signed distance projected along each axis from the origin point, and the axes are straight and mutually perpendicular. The origin is customarily named “(0,0).” For a four-dimensional space, a point is named with a set of four numbers. A coordinate system for n-dimensional space is a mapping from each point to an ordered set of its n coordinate numbers. The most useful numbers to assign as coordinates are real numbers because real numbers enable us to use the techniques of calculus and because their use makes it easy to satisfy the helpful convention that nearby points have nearby coordinates.

Physicists usually suggest that time is like a line. This means time is composed of durationless instants and the set of instants have a linearly-ordered structure under the happens-before-or-at-the-same-time relation, so time is like what mathematicians call “the continuum” and what non-mathematicians call “a line.”

When we speak of the distance between two points in a space, we implicitly mean the distance along the shortest path between them because there might be an infinite number of paths one could take. If a space has a coordinate system, then it has an infinite number of available coordinate systems because there is an unlimited number of choices for an origin, or an orientation of the axes, or the scale.

There are many choices for kinds of reference frames, although the Cartesian coordinate system is the most popular. Its coordinate axes are straight lines and are mutually perpendicular. Assuming Euclidean geometry (and so no curvature of space), the equation of the circle of diameter one centered on the origin of a Cartesian coordinate system is x² + y² = 1. This same circle has a very different equation if a polar coordinate system is used instead.

Reference frames can be created for physical space, or for time, or for spacetime, or for things having nothing to do with real space and time. One might create a two-dimensional (2-D) Cartesian coordinate system, with one coordinate axis for displaying the salaries of a company’s sales persons and a second coordinate axis for displaying their names. Even if the space represented by the coordinate system were to be real physical space, its coordinates would not be physically real. You cannot  add two points. From this fact it can be concluded that not all the mathematical structures in the coordinate system are also reflected in what the system represents. These extraneous mathematical structures are called “mathematical artifacts.”

Below is a picture of a reference frame spanning a space that contains a solid ball. The coordinates are not confined to the surface of the ball but also cover the surrounding space. What we have here is a 3-dimensional Euclidean space that uses a Cartesian coordinate system with three mutually perpendicular axes. The space contains a 3-dimensional (3-D) solid ball:

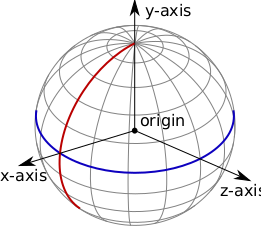
The origin of the coordinate system is at the center of the ball, and the y-axis intersects the north pole and the south pole. Two of the three coordinate axes intersect the blue equator at specified places. The red line represents a typical longitude, but this longitude is not a coordinate axis. The three coordinates of any point in this space form an ordered set (x,y,z) of the x, y, and z coordinates of the point, with commas separating each from the other coordinate labels for the point. Thinking of the ball as the globe, there are points on the Earth, inside the Earth, and outside the Earth. For 3-D space, the individual coordinates normally would be real numbers. For example, we might say a point of interest deep inside the ball (the Earth) has the three coordinates (4.1,π,0), where it is assumed all three numbers have the same units, such as meters. It is customary in a three-dimensional space to label the three axes with the letters x, y, and z, and for (4.1,π,0) to mean that 4.1 meters is the x-coordinate of the point, π meters is the y-coordinate of the same point, and 0 meters is the z-coordinate of the point. The center of the Earth in this graph is located at the origin of the coordinate system; the origin of a frame has the coordinates (0,0,0). Mathematical physicists frequently suppress talk of the units and speak of π being the y-coordinate, although strictly speaking the y-coordinate is π meters. The x-axis is all the points (x,0,0); the y-axis is all the points (0,y,0); the z-axis is all the points (0,0,z), for all possible values of x, y, and z.

In a coordinate system, the axes need not be mutually perpendicular, but in order to be a Cartesian coordinate system, the axes must be mutually perpendicular, and the coordinates of a point in spacetime must be the values along axes of the perpendicular projections of the point onto the axes. All Euclidean spaces can have Cartesian coordinate systems. If the space were the surface of the sphere above, not including its insides or outside, then this two-dimensional space would be a sphere, and it could not have a two-dimensional Cartesian coordinate system because all the axes could not lie within the space. The 2D surface could have a 3D Cartesian coordinate system, though. This coordinate system was used in our diagram above. A more useful coordinate system might be a 3D spherical coordinate system. Space and time in the theory of special relativity are traditionally represented by a frame with four independent, real coordinates (t,x,y,z).

Changing from one reference frame to another does not change any phenomenon in the real world being described with the reference frame, but is merely changing the perspective on the phenomena. If an object has certain coordinates in one reference frame, it usually has different coordinates in a different reference frame, and this is why coordinates are not physically real—they are not frame-free. Durations are not frame-free. Neither are positions, directions, and speeds. An object’s speed is different in different reference frames, with one exception. The upper limit on the speed of any object in space satisfying the principles of special relativity is c, the speed of light in a vacuum. This claim is not relative to a reference frame. This speed c is the upper limit on the speed of transmission from any cause to its effect. This c is the c in the equation E = mc². It is the speed of any particle with zero rest mass such as a photon. The notion of speed of travel through spacetime rather than through space is usually considered by physicists not to be sensible. Whether the notion of speed through time also is not sensible is a controversial topic in the philosophy of physics. See the main Time article’s section “The Passage or Flow of Time” for a discussion of whether it is sensible.

The word reference is often dropped from the phrase reference frame, and the term frame and coordinate system are often used interchangeably. A frame for the physical space in which a particular object always has zero velocity is called the object’s rest frame or proper frame. 

A reference frame is a possible viewpoint. When choosing to place a frame upon a space, there are an infinite number of legitimate choices. Choosing a frame carefully can make a situation much easier to describe. For example, suppose we are interested in events that occur along a highway. We might orient the z-axis by saying it points  up away from the center of Earth, while the x-axis points along the highway, and the y-axis is perpendicular to the other two axes and points across the highway. If events are to be described, then a fourth axis for time would be needed, but its units would be temporal units and not spatial units. It usually is most helpful to make the time axis be perpendicular to the three spatial axes, and to require successive seconds along the axis to be the same duration as seconds of the standard clock. By applying a coordinate system to spacetime, a point of spacetime is specified uniquely by its four independent coordinate numbers, three spatial coordinates and one time coordinate. The word independent implies that knowing one coordinate of a point gives no information about the point’s other coordinates.

Coordinate systems of reference frames have to obey rules to be useful in science. No accepted theory of physics allows a time axis to be shaped like a figure eight. Frames need to honor the laws if they are to be perspectives on real events. For all references frames allowed by relativity theory, if a particle collides with another particle, they must collide in all allowed reference frames. Relativity theory does not allow reference frames in which a particle of light is at rest. Quantum mechanics does. A frame with a time axis in which your shooting a gun is simultaneous with your bullet hitting a distant target is not allowed by relativity theory. Informally, we say it violates the fact that causes occur before their effects in all legitimate reference frames for relativity theory. Formally, we say it violates the light cone structure required by relativity theory.

How is the time axis oriented in the world? This is done by choosing t = 0 to be the time when a specific event occurs such as the Big Bang, or the birth of Jesus. A second along the t-axis usually is required to be congruent to a second of our civilization’s standard clock, especially for clocks not moving with respect to that clock.

A space with a topology defined on it and having any number of dimensions is called a manifold. Newtonian mechanics, special relativity, general relativity, and quantum theory all require the set of all events (in the sense of possible space-time locations) to form a four-dimensional manifold. Informally, what it means to be four-dimensional is that each point cannot be specified with less than four independent numbers. Formally, the definition of dimension is somewhat complicated.

Treating time as a special dimension of spacetime is called spatializing time, and doing this is what makes time precisely describable mathematically in a way that treating time only as becoming does not. It is a major reason why mathematical physics can be mathematical.

One needs to be careful not to confuse the features of time with the features of the mathematics used to describe time. Einstein admitted [see (Einstein 1982) p. 67] that even he often made this mistake of failing to distinguish the representation from the object represented, and it added years to the time it took him to create his general theory of relativity.

Times are not numbers, but time coordinates are. When a time-translation occurs with a magnitude of Δt, this implies the instant I at coordinate t is now associated with another instant I’ at coordinate t’ and this equality holds: t’ = t + Δt. If the laws of physics are time-translation symmetric, which is the normal assumption, then the laws of mathematical physics are invariant relative to the group of transformations of time coordinate t expressed by t ⇒ t + Δt where Δt is an arbitrarily chosen constant real number.

Some features of reality are relative to a reference frame and some are not. Duration is relative. Distance is relative. Spacetime interval is not. The speed of light in a vacuum is not.

4. Curved Space and Cartesian Coordinates

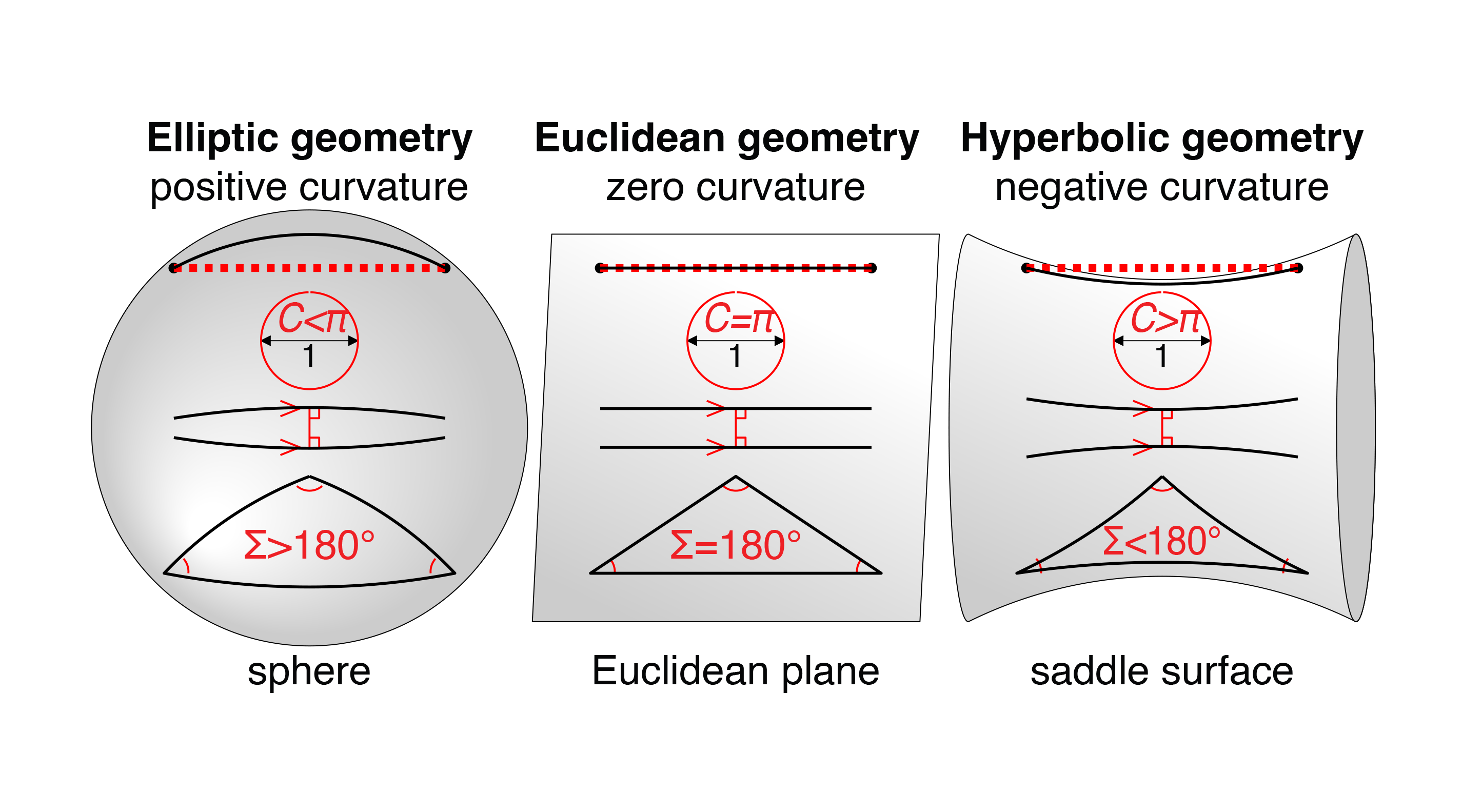
According to general relativity theory, space curves near all masses. Here are the three main types of geometries for representing curvature:

• Euclidean geometry.
• Hyperbolic geometry.
• Elliptical geometry.

The following diagram shows how the three, when viewed from a higher dimension, differ in curvature and in the character of their parallel lines, circles and triangles. Click on the diagram to expand it:

Source: Wikipedia
The geometry of a space exists independently of whatever coordinate system is used to describe it, so one has to take care to distinguish what is a real feature of the geometry from what is merely an artifact of the mathematics used to characterize the geometry.

A Cartesian coordinate system can handle all sorts of curved paths and curved objects, but it fails whenever the space itself curves.  What we just called “the space” could be real physical space or an abstract mathematical space or spacetime or just time.

Any Euclidean space can have a Cartesian coordinate system. A reference frame fixed to the surface of the Earth cannot have a Cartesian coordinate system covering all the surface because the surface curves and the space is therefore not Euclidean. Spaces with a curved geometry require curvilinear coordinate systems in which the axes curve as seen from a higher dimensional Euclidean space in which the lower-dimensional space is embedded. This higher-dimension can be real or unreal.

If the physical world were two-dimensional and curved like the surface of a sphere, then a two-dimensional Cartesian coordinate system for that space must fail to give coordinates to most places in the world. To give all the points of the 2D world their own Cartesian coordinates, one would need a 3D Cartesian system, and each point in the world would be assigned three coordinates, not merely two. For the same reason, if we want an arbitrary point in our real, curving 4D-spacetime to have only four coordinates and not five, then the coordinate system must be curvilinear and not Cartesian.  But what if we are stubborn and say we want to stick with the Cartesian coordinate system and we don’t care that we have to bring in an extra dimension and give our points of spacetime five coordinates instead of four? In that case we cannot trust the coordinate system’s standard metric to give correct answers.

Let’s see why this is so. Although the coordinate system can be chosen arbitrarily for any space or spacetime, different choices usually require different metrics. Suppose the universe is two-dimensional and shaped like the surface of a sphere when seen from a higher dimension.  The 2D sphere has no inside or outside; the extra dimension is merely for our visualization purposes. Then when we use the 3D system’s metric, based on the 3D version of the Pythagorean Theorem, to measure the spatial distance between two points in the space, say, the North Pole and the equator, the value produced is too low. The correct value is higher because it is along a longitude and must stay confined to the surface. The 3D Cartesian metric says the shortest line between the North Pole and a point on the equator cuts through the Earth and so escapes the universe, which indicates the Cartesian metric cannot be correct. The correct metric would compute distance within the space along a geodesic line (a great circle in this case such as a longitude) that is confined to the sphere’s surface.

The orbit of the Earth around the Sun is curved in 3D space, but “straight” in 4D spacetime. The scare quotes are present because the orbit is straight only in the sense that a geodesic is straight. A geodesic path between two points of spacetime is a path of shortest spacetime interval between the points.

One could cover a curved 4D-spacetime with a special Cartesian-like coordinate system by breaking up the spacetime into infinitesimal regions, giving each region its own Cartesian coordinate system, and then stitching the coordinate systems all together where they meet their neighbors. The stitching produces what is customarily called an atlas. Each point would have its own four unique coordinates, but when the flat Cartesian metric is used to compute intervals, lengths, and durations from the coordinate numbers of the atlas, the values will be incorrect.

Instead of considering a universe that is the surface of a sphere, consider a universe that is the surface of a cylinder. This 2D universe is curved when visualized from a 3D Euclidean space in which the cylinder is embedded. Surprisingly, it is not intrinsically curved at all. The measures of the three angles of any triangle sum to 180 degrees. Circumferences of its circles always equal pi times their diameters. We say that, unlike the sphere, the surface of a cylinder is extrinsically curved but intrinsically flat.

For a more sophisticated treatment of reference frames and coordinates, see Coordinate Systems. For an introduction to the notion of curvature of space, see chapter 42 in The Feynman Lectures on Physics by Richard Feynman.

5. What Is an Inertial Frame?

Galileo first had the idea that motion is relative. If you are inside a boat with no windows and are floating on a calm sea, you cannot tell whether the  boat is moving. Even if it is moving, you won’t detect this inside a closed cabin of the boat, say, by seeing a dropped ball curve as it falls or by feeling a push on yourself or seeing all the flies near you being pushed to the back of the room.  Galileo believed steady motion is motion relative to other objects, and there is no such thing as simply motion relative to nothing, or motion relative to fixed, absolute space. Newton disagreed with this. Einstein agreed.

Newton  believed in absolute motion. This is motion of an object that is not dependent upon its relations with any other object. Newton would say an inertial frame is a reference frame moving at constant velocity relative to absolute space.

An inertial observer is someone who feels weightless, as if they are floating. They feel no acceleration and no gravitational field, yet all the laws of physics apply to this observer as they do to anything else.

Einstein described an inertial frame as a reference frame in which Newton’s first law of motion holds. Newton’s first law says an isolated object, that is, an object affected by no total extrinsic force, has a constant velocity over time. It does not accelerate. In any inertial frame, any two separate objects that are moving in parallel and coasting along with no outside forces on them, will remain moving in parallel forever. Einstein described his special theory of relativity in 1905 by saying it requires the laws of physics to have the same form in any inertial frame of reference.

According to the general theory of relativity, there are no global inertial reference frames at all because Newton’s first law is not strictly true globally. It holds to an acceptable degree of approximation in some restricted regions that are sufficiently far away from masses.

Newton’s first law can be thought of as providing a definition of the concept of zero total external force; an object has zero total external force if it is moving with constant velocity. In the real world, no objects behave this way; they cannot be isolated from the force of gravity. Gravity cannot be turned off, and so Newton’s first law fails, and there are no inertial frames. But the first law does hold approximately. That is, it holds well enough for various purposes in many situations. It holds in any infinitesimal region. In larger regions, if spacetime curvature can be ignored for a certain phenomenon of interest, then one can find an inertial frame for the phenomenon. A Cartesian coordinate system fixed to Earth usually will serve adequately as an inertial frame for describing cars on a race track or describing the flight of a tennis ball, but not for describing a rocket’s flight from Paris to Mars. A coordinate frame for space that is fixed on the distant stars and is used by physicists only to describe phenomena far from any of those stars, and far from planets, and far from other massive objects, is very nearly an inertial frame in that region. Given that some frame is inertial, any frame that rotates or otherwise accelerates relative to this first frame is non-inertial.

Newton’s theory requires a flat, Euclidean geometry for space and for spacetime. Special relativity requires a flat Euclidean geometry for space but a flat, non-Euclidean geometry for spacetime. General relativity allows all these but also allows curvature for spacetime as well as space. If we demand that our reference frame’s coordinate system span all of spacetime, then a flat frame does not exist for the real world, just as a plane cannot cover the surface of a sphere. The existence of gravity requires there to be curvature of space around any object that has mass, thereby making a flat frame fail to span some of the space near the object.

Perhaps most importantly, it became generally accepted since the 1920s that Euclid and Kant were mistaken about the geometry of the universe because they failed to distinguish mathematical geometry (which is a priori) from physical geometry (which is empirical). In philosophy, this point was made most strenuously by Hans Reichenbach.

For a deeper philosophical introduction to inertial frames, see chapter 2 of (Maudlin 2012).

6. What Is Spacetime?

Spacetime is a certain combination of space and time. It is the set of locations of events, or it can be considered to be a field where all events are located.

There are actual spacetimes and imaginary spacetimes. Our real four-dimensional spacetime has a single time dimension and at least three space dimensions. It is still an open question whether there are more than three spatial dimensions. But there definitely are imaginary spacetimes with twenty-seven dimensions or three hundred. There could be a three-dimensional  spacetime composed of two spatial dimensions and a time dimension in which points in space indicate the latitude and longitude in Canada for the sale of a company’s widget, and points along the time dimension indicate the date of the sale of the widget. In any spacetime, real or imaginary, the coordinates are the names of locations in space and time. Coordinates are mathematical artifacts.

In 1908, Einstein’s mathematics teacher Hermann Minkowski was the first person to say that real spacetime is fundamental and that space and time are just aspects of spacetime. And he was the first to say different reference frames will divide spacetime differently but correctly into their time part and space part. Einstein was soon convinced by Minkowski’s reasoning.

Later, Einstein discovered that real spacetime is dynamic and not static as in special relativity theory. It is dynamic because its structure, such as its geometry, changes over time. Einstein said it changes as the distribution of matter-energy changes. In special relativity and in Newton’s theory, spacetime is not dynamic; it stays the same regardless of what matter and energy are doing. In any spacetime obeying either the special or the general theory of relativity, the key idea about time is that there is a light-cone structure such that every point in spacetime has both a forward light-cone of future events and a backward light-cone of past events. What this means is explained momentarily.

In his general theory of relativity, Einstein said gravity is a feature of spacetime, namely its curvature. Spacetime curves near gravitational fields, and it curves more the stronger the field strength. The overall, cosmic curvature of space was far from zero at the Big Bang, but it is now about zero, although many cosmologists believe it is evolving toward a positive value. These days the largest curvature of spacetime is in black holes.

In general relativity, spacetime is assumed to be a fundamental feature of reality. It is very interesting to investigate whether this assumption is true. There have been serious attempts to construct theories of physics in which spacetime is not fundamental but instead emerges from something more fundamental such as quantum fields, but none of these attempts have stood up to any empirical observations or experiments that could show the new theories to be superior to the presently accepted theories.

The metaphysical question of whether spacetime is a substantial object or merely a relationship among events, or neither, is considered in the discussion of the relational theory of time in the main Time article. For some other philosophical questions about what spacetime is, see What is a Field?

According  to the physicist George Musser, “Gravity is not a force that propagates through space but a feature of spacetime itself. When you throw a ball high into the air, it arcs back to the ground because Earth distorts the spacetime around it, so that the paths of the ball and the ground intersect again.”

How do we detect that a space is curved if we cannot look down upon it from a higher dimension and see the curvature and must instead make the decision from within the space? The answer is that we can detect deviations from Euclidean geometry, such as (1) initially parallel lines becoming less parallel as they are extended, or (2) failure of the theorem that says the sum of the interior angles of a triangle add to 180 degrees, or (3) the circumference of a circle is not the product of pi and its diameter.

Many physicists who promote string theory believe that spacetime really has many more dimensions of space than three. There are the three common ones, customarily called our “brane” (short for “membrane”), plus others. The higher-dimensional  “hyperspace” in which our brane resides is called the “bulk.” Our 3D brane bends into the bulk. It is believed that light cannot escape our brane but gravity can.

7. What Is a Spacetime Diagram and a Light Cone?

A spacetime diagram is a graphical representation of the coordinates of events in spacetime. Think of the diagram as a picture of a reference frame. In classical spacetime diagrams, one designated coordinate axis is for time. The other axes are for space. A Minkowski spacetime diagram is a special kind of spacetime graph.  It is a particular 4-dimensional generalization of 3-D Cartesian coordinates, one that represents phenomena that obey the laws of special relativity. A Minkowski diagram allows no curvature of spacetime itself, although objects themselves can have curving sides, and they can have curving paths in space.

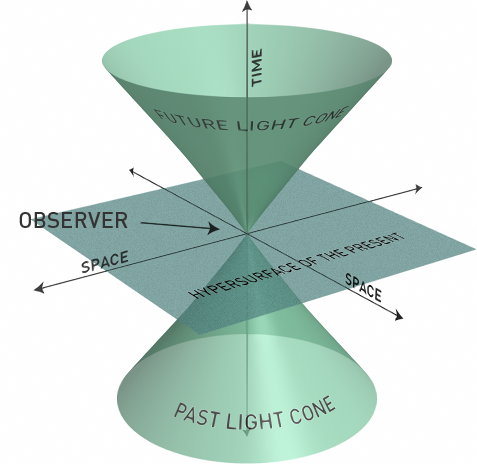
The following diagram is an example of a three-dimensional Minkowski spacetime diagram containing two spatial dimensions (with straight lines for the two axes) and a time dimension (with a vertical straight line for the time axis). If you are located at the origin, then the space part of this spacetime frame constitutes your rest frame; it’s the frame in which you have zero velocity. Two cones emerge upward and downward from the point-event of you, the zero-volume observer being here now at the origin of the reference frame of your spacetime diagram. These cones are your future and past light cones. The two cones are composed of green paths of possible unimpeded light rays emerging from the observer or converging into the observer. The light cone at a point of space exists even if there is no actual light there.

Attribution:Stib at en.wikipedia, CC BY-SA 3.0, Link

By convention, in a Minkowski spacetime diagram, a Cartesian (rectangular) coordinate system is used, the time axis is shown vertically, and one or two of the three spatial dimensions are suppressed (that is, not included).

If the Minkowski diagram has only one spatial dimension, then a flash of light in a vacuum has a perfectly straight-line representation, but it is has a cone-shaped representation if the Minkowski diagram has two spatial dimensions, and it is a sphere if there are three spatial dimensions. Because light travels at such a high speed, it is common to choose the units along the axes so that the path of a light ray is a 45 degree angle and the value of c is 1 light year per year, with light years being the units along each space axis and years being the units along the time axis. Or the value of c could have been chosen to be one light nanosecond per nanosecond. The careful choice of units for the axes in the diagram is important in order to prevent the light cones’ appearing too flat to be informative.

Below is an example of a Minkowski diagram having only one space dimension, so every future light cone has the shape of the letter “V.”

This Minkowski diagram represents a spatially-point-sized Albert Einstein standing still midway between two special places, places where there is an instantaneous flash of light at time t = 0 in coordinate time. At t = 0, Einstein cannot yet see the flashes because they are too far away for the light to reach him yet. The directed arrows represent the path of the four light rays from the flashes. In a Minkowski diagram, a physical point-object of zero volume is represented as occupying a single point at one time and as occupying a line containing all the spacetime points at which it exists. That line is called the  world line of the (point) object. All world lines representing real objects are continuous paths in spacetime. Accelerating objects have curved paths in spacetime. Real objects that are not just points have a world tube rather than merely a world line.

Events on the same horizontal line of the Minkowski diagram are simultaneous in the reference frame. The more tilted an object’s world line is away from the vertical, the faster the object is moving. Given the units chosen for the above diagram, no world line can tilt down more than 45 degrees, or else that object is moving faster than c, the cosmic speed limit according to special relativity.

In the above diagram, Einstein’s world line is straight, indicating no total external force is acting on him. If an object’s world line meets another object’s world line, then the two objects collide.

The set of all possible photon histories or light-speed world lines going through a specific point-event defines the two light cones of that event, namely its past light cone and its future light cone. The future cone or forward cone is called a cone because, if the spacetime diagram were to have two space dimensions, then light emitted from a flash would spread out in the two spatial dimensions in a circle of ever-growing diameter, producing a cone shape over time. In a diagram for three-dimensional space, the light’s wavefront is an expanding sphere and not an expanding cone, but sometimes physicists still will speak informally of its cone.

Every point of spacetime has its own pair of light cones, but the light cone has to do with the structure of spacetime, not its contents, so the light cone of a point exists even if there is no light there.

Whether a member of a pair of events could have had a causal impact upon the other event is an objective feature of the universe and is not relative to a reference frame. A pair of events inside the same light cone are said to be causally-connectible because they could have affected each other by a signal going from one to the other at no faster than the speed of light, assuming there were no obstacles that would interfere. For two causally-connectible events, the relation between the two events is said to be timelike. If you were once located in spacetime at, let’s say, (x₁,y₁,z₁,t₁), then for the rest of your life you cannot affect or participate in any event that occurs outside of the forward light cone whose apex is at (x₁,y₁,z₁,t₁). Light cones are an especially helpful tool because different observers in different rest frames should agree on the light cones of any event, despite their disagreeing on what is simultaneous with what and their disagreeing on the duration between two events. So, the light-cone structure of spacetime is objectively real.

Einstein’s Special Theory does apply to gravitation, but it does so very poorly. It  falsely assumes that gravitational processes have no effect on the structure of spacetime. When attention needs to be given to the real effect of gravitational processes on the structure of spacetime, that is, when general relativity needs to be used, then Minkowski diagrams become inappropriate for spacetime. General relativity assumes that the geometry of spacetime is locally Minkowskian, but not globally Minkowskian. That is, spacetime is locally flat in the sense that in any infinitesimally-sized region one always finds spacetime to be 4D Minkowskian (which is 3D Euclidean for space but not 4D Euclidean for spacetime). When we say spacetime is curved and not flat, we mean it deviates from 4D Minkowskian geometry. In discussions like this, more often the term “Lorentzian” is used in place of “Minkowskian.”

8. What Are Time’s Metric and Spacetime’s Interval?

The metric of a space contains geometric information about the space. It tells the curvature at points, and it tells the distance between any two points along a curve containing the two points. The introduction below discusses distance and duration and spacetime interval. If you change to a different coordinate system, generally you must change the metric. In that sense, the metric is not objective.

In simple situations in a Euclidean space with a Cartesian coordinate system, the metric is a procedure that says that in order to find the duration subtract the event’s starting time from its ending time. More specifically, this metric for a one-dimensional space for time says that, in order to compute the duration between point-event a that occurs at time t(a) and point-event b that occurs at time t(b), one should compute |t(b) – t(a)|, the absolute value of their difference. This is the standard way to compute durations when curvature of spacetime is not involved. When it is involved, such as in general relativity, we need a more exotic metric, and the computations can be extremely complicated.

The metric for spacetime implies the metric for time. The spacetime metric tells the spacetime interval between two point events. The spacetime interval has both space aspects and time aspects. The interval is the measure of the spacetime separation between two point events along a specific spacetime path. Let’s delve into this issue a little more deeply.

There are multiple senses of the word space. A mathematical space is not a physical space. A physicist often represents time as a one-dimensional space, space as a three-dimensional space, and spacetime as a four-dimensional space. More generally, a metric for any sort of space is an equation that says how to compute the distance (or something distance-like, as we shall soon see) between any two points in that space along a curve in the space, given the location coordinates of the two points. Note the coordinate dependence. For ordinary Euclidean space, the usual metric is just the three-dimensional version of the Pythagorean Theorem. In a Euclidean four-dimensional space, the metric is the four-dimensional version of the Pythagorean Theorem.

In a one-dimensional Euclidean space along a straight line from point location x to a point location y, the metric says the distance d between the two points is |y – x|. It is assumed both locations use the same units.

The duration t(a,b) between an event a that occurs at time t(a) and an event b that occurs at time t(b) is given by the equation:

t(a,b) = |t(b) – t(a)|.

This is the standardly-accepted way to compute durations when curvature is not involved. Philosophers have asked whether one could just as well have used half that absolute value, or the square root of the absolute value. More generally, is one definition of the metric the correct one or just the more useful one? That is, philosophers are interested in the underlying issue of whether the choice of a metric is natural in the sense of being objective or whether its choice is a matter of convention.

Let’s bring in more dimensions. In a two-dimensional plane satisfying Euclidean geometry, the formula for the metric is:

d² = (x₂ – x₁)² + (y₂ – y₁)².

It defines what is meant by the distance d between an arbitrary point with the Cartesian coordinates (x₁ , y₁) and another point with the Cartesian coordinates (x₂ , y₂), assuming all the units are the same, such as meters. The x numbers are values in the x dimension, that is, parallel to the x-axis, and the y numbers are values in the y dimension. The above equation is essentially the Pythagorean Theorem of plane geometry. Here is a visual representation of this for the two points:       

If you imagine this graph is showing you what a crow would see flying above a square grid of streets, then the metric equation d² = (x₁ – x₂)²+ (y₁ – y₂)²  gives you the distance d as the crow flies. But if your goal is a metric that gives the distance only for taxicabs that are restricted to travel vertically or horizontally, then a taxicab metric would compute the taxi’s distance this way:

|x₂ – x₁| + |y₂ – y₁|.

So, a space can have more than one metric, and we choose the metric depending on the character of the space and what our purpose is.

Usually for a physical space there is a best or intended or conventionally-assumed metric. If all we want is the shortest distance between two points in a two-dimensional Euclidean space, the conventional metric is:

d² = (x₂ – x₁)² + (y₂ – y₁)²

which is the Pythagorean theorem. But if we are interested in distances along an arbitrary path rather than just the shortest path, then the above metric is correct only infinitesimally, and a more sophisticated metric is required by using the tools of calculus. In this case, the above metric is re-expressed as a difference equation using the delta operator symbol Δ to produce:

(Δs)² = (Δx)²+ (Δy)²

where Δs is the spatial distance between the two points and Δx = x₁ – x₂ and Δy = y₁ – y₂. The delta symbol Δ is not a number but rather is an operator on two numbers that produces their difference. If the differences are extremely small, infinitesimally small, then they are called differentials instead of differences, and then Δs becomes ds, and Δx becomes dx, and Δy becomes dy, and we have entered the realm of differential calculus with:

ds² = dx²+ dy²

The letter d in a differential stands for an infinitesimally small delta operation, and it is not a number.

Let’s generalize this idea from 2D-space to 4D-spacetime. The metric we are now looking for is the space-time interval between two arbitrary point-events, not the distance between them nor the time between them. Although there is neither a duration between New York City and Paris, nor a spatial distance between noon today and midnight later, nevertheless there is a spacetime interval between New York City at noon and Paris at midnight.

Unlike temporal durations and spatial distances, intervals are objective in the sense that the spacetime interval is not relative to a reference frame or coordinate system. All observers measure the same value for an interval, assuming they measure it correctly. The value of an interval between two point events does not change if the reference frame changes. Alternatively, acceptable reference frames are those that preserve the intervals between points.

Any space’s metric says how to compute the value of the separation s between any two points in that space. In special relativity, the four-dimensional abstract space that represents spacetime is indeed special. Its 3-D spatial part is Euclidean and its 1-D temporal part is Euclidean, but the 4D space it is not Euclidean, and its metric is exotic. It is said to be Minkowskian, and it is given a Lorentzian coordinate system. Its metric is defined between two infinitesimally close points of spacetime to be:

ds² = c²dt² – dx²

where ds is an infinitesimal interval (or a so-called differential displacement of the spacetime coordinates) between two nearby point-events in the spacetime; c is the speed of light; the differential dt is the infinitesimal duration between the two time coordinates of the two events; and dx is the infinitesimal spatial distance between the two events. Notice the negative sign. If it were a plus sign, then the metric would be Euclidean.

Because there are three dimensions of space in a four-dimensional spacetime, say dimensions 1, 2, and 3, the differential spatial distance dx is defined to be:

dx² = dx₁² + dx₂² + dx₃²

No negation signs. This equation is obtained in Cartesian coordinates by using the Pythagorean Theorem for three-dimensional space. The differential dx₁ is the displacement along dimension 1 of the three dimensions. Similarly, for 2 and 3. This is the spatial distance between two point-events, not the interval between them.

With these differential equations, the techniques of calculus can then be applied to find the interval between any two point-events along some path s even if they are not nearby in spacetime. Well we can find it if we have the necessary information about the world line s, the path in spacetime, such as its equation in the coordinate system.

In special relativity, the interval between two events that occur at the same place, such as the place where the clock is sitting, is very simple. Since dx = 0, the interval is:

t(a,b) = |t(b) – t(a)|.

This is the absolute value of the difference between the real-valued time coordinates, assuming all times are specified in the same units, say, seconds. We began the discussion of this section by using that metric.

Now let us generalize this notion in order to find out how to use a clock for events that do not occur at the same place. The infinitesimal proper time dτ, rather than the differential coordinate-time dt, is the duration shown by a clock carried along the infinitesimal spacetime interval ds. It is defined in any spacetime obeying special relativity to be:

dτ²= ds²/c².

In general, dτ ≠ dt. They are equal only if the two point-events have the same spatial location so that dx = 0.

As we have seen, the length of a path in spacetime is not calculated the way we calculate the length of a path in space.  In space we use the Euclidean method; in spacetime we use the Minkowski method, which contains a negation sign in its equation ds² = c²dt² – dx². Because spacetime “distances” (intervals) can be negative, and because the spacetime interval between two different events can be zero even when the events are far apart in spatial distance (but reachable by a light ray if intervening material were not an obstacle), the term interval here is not what is normally meant by the term distance.

To get a sense of the oddness of a spacetime interval, note that the spacetime interval between the birth of a photon and its death far away when it is absorbed by an atom is zero even though the two events do not have a zero time interval.

There are three kinds of spacetime intervals: timelike, spacelike, and null. In spacetime, if two events are in principle connectable by a signal moving from one event to the other at less than light speed, the interval between the two events is called timelike. The interval is spacelike if there is no reference frame in which the two events occur at the same place, so they must occur at different places and be some spatial distance apart—thus the choice of the word spacelike. Two events connectable by a signal moving exactly at light speed are separated by a null interval, an interval of magnitude zero.

Here is an equivalent way of describing the three kinds of spacetime intervals. If one of the two events occurs at the origin or apex of a light cone, and the other event is within either the forward light cone or backward light cone, then the two events have a timelike interval. If the other event is outside the light cones, then the two events have a spacelike interval [and are in each other’s so-called absolute elsewhere]. If the two events lie directly on the same light cone, then their interval is null or zero.

The spacetime interval between any two events in a human being’s life must be a timelike interval. No human being can do anything to affect an event outside their future light cone. Such is the human condition according to relativity theory.

The information in the more complicated metric for general relativity enables a computation of the curvature at any point. This more complicated metric is the Riemannian metric tensor field. This is what you know when you know the metric of spacetime.

A space’s metric provides a complete description of the local properties of the space, regardless of whether the space is a physical space or a mathematical space representing spacetime. By contrast, the space’s topology provides a complete description of the global properties of the space such as whether it has external curvature like a cylinder or no external curvature as in a plane; these two spaces are locally the same.

The metric for special relativity is complicated enough, but the metric for general relativity is very complicated.

The discussion of the metric continues in the discussion of time coordinates. For a helpful and more detailed presentation of the spacetime interval and the spacetime metric, see chapter 4 of (Maudlin 2012) and especially the chapter “Geometry” in The Biggest Ideas in the Universe: Space, Time, and Motion by Sean Carroll.

9. How Does Proper Time Differ from Standard Time and Coordinate Time?

Proper time is personal, and standard time is public. Standard time is the proper time reported by the standard clock of our conventionally-chosen standard coordinate system. Coordinate time is the time measured in some conventionally adopted coordinate system. Every properly functioning clock measures its own proper time, the time along its own world tube, no matter how the clock is moving or what forces are acting upon it. Loosely speaking, standard time is the time shown on a designated clock in Paris, France that reports the time in London, England that we agree to be the correct time. The Observatory is assumed to be stationary in the standard coordinate system. Given a coordinate system with a time coordinate and space coordinate, if you sit still, then your proper time is the same as the coordinate time.

But the faster your clock moves compared to the standard clock or the greater the gravitational force on it compared to the standard clock, then the more your clock readings will deviate from standard time as would be very clear if the two clocks were ever to meet. This effect is called time dilation. Under normal circumstances in which you move slowly compared to the speed of light and do not experience unusual gravitational forces, then there is no difference between your proper time and your civilization’s standard time.

Think of any object’s proper time as the time that would be shown on an ideal, small, massless, correct clock that always travels with the object and has no physical effect upon the object and that is not affected if the object is ever frozen. Your cell phone is an exception. Although it has its own proper time, what it reports id not its proper time but instead the proper time of our standard clock adjusted by an hour for each time zone between it and the cell phone. People on Earth normally do not notice that they have different proper times from each other because the time dilation effect is so small for the kind of life they lead.

The proper time interval between two events (on a world line) is the amount of time that elapses according to an ideal clock that is transported between the two events. But there are many paths for the transportation, just as there are many roads between Paris and Berlin. Consider two point-events. Your own proper time between them is the duration between the two events as measured along the world line of your clock that is transported between the two events. Because there are so many physically possible ways to do the clock transporting, for example at slow speed or high speed and near a large mass or far from it, there are so many different possible proper time intervals for the same two events. There is one exception here. The proper time between two points along the worldl ine of a light ray is always zero. So, if you were a photon and traveled across the Milky Way Galaxy, no proper time would elapse  during your journey, although external observers of your journey would measure a large amount of coordinate time.

Here is a way to maximize the difference between proper time and standard time. If you and your clock pass through the event horizon of a black hole and fall toward the hole’s center, you will not notice anything unusual about your proper time, but external observers using Earth’s standard time will measure that you took an extremely long time to enter the horizon.

The actual process by which coordinate time is computed from the proper times of real clocks and the process by which a distant clock is synchronized with a local clock are very complicated, though some of the philosophically most interesting issues here—regarding the relativity of simultaneity and the conventionality of simultaneity—are discussed below.

Authors and speakers who use the word time often do not specify whether they mean proper time or standard time or coordinate time. They assume the context is sufficient for us to know what they mean.

10. Is Time the Fourth Dimension?

Yes and no; it depends on what is meant by the question. It is correct to say time is a dimension but not to say time is a spatial dimension. Time is the fourth dimension of 4D spacetime, but time is not the fourth dimension of physical space because that space has only three dimensions, as far as we know. In 4D spacetime, the time dimension is special and differs in a fundamental way from the other three dimensions.

Mathematicians have a broader notion of the term space than the average person. In their sense, a space need not contain any geographical locations nor any times, and it can have any number of dimensions, even an infinite number. Such a space might be two-dimensional and contain points represented by the ordered pairs in which a pair’s first member is the name of a voter in London and its second member is the average monthly income of that voter. Not paying attention to the two meanings of the term space is the source of all the confusion about whether time is the fourth dimension.

Newton treated space as three dimensional and treated time as a separate one-dimensional space. He could have used Minkowski’s 1908 idea, if he had thought of it, namely the idea of treating spacetime as four-dimensional.

The mathematical space used by mathematical physicists to represent physical spacetime that obeys the laws of relativity is four-dimensional; and in that mathematical space, the space of places is a 3D sub-space, and time is another sub-space, a 1D one. The mathematician Hermann Minkowski was the first person to construct such a 4D mathematical space for spacetime, although in 1895 H. G. Wells treated time informally as the fourth dimension in his novel The Time Machine.

In 1908, Minkowski remarked that “Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.” Many people mistakenly took this to mean that time is partly space, and vice versa. The philosopher C. D. Broad countered that the discovery of spacetime did not break down the distinction between time and space but only their independence or isolation.

The reason why time is not partly space is that, within a single frame, time is always distinct from space. Another way of saying this is to say time always is a distinguished dimension of spacetime, not an arbitrary dimension. What being distinguished amounts to, speaking informally, is that when you set up a rectangular coordinate system on a spacetime with an origin at, say, some important event, you may point the x-axis east or north or up or any of an infinity of other directions, but you may not point it forward in time—you may do that only with the t-axis, the time axis.

For any coordinate system on spacetime, mathematicians of the early twentieth century believed it was necessary to treat a point-event with at least four independent numbers in order to account for the four dimensionality of spacetime. Actually this appeal to the 19th-century definition of dimensionality, which is due to Bernhard Riemann, is not quite adequate because mathematicians have subsequently discovered how to assign each point on the plane to a point on the line without any two points on the plane being assigned to the same point on the line. The idea comes from the work of Georg Cantor. Because of this one-to-one correspondence between the plane’s points and the line’s points, the points on a plane could be specified with just one number instead of two. If so, then the line and plane must have the same dimensions according to the Riemann definition of dimension. To avoid this result, and to keep the plane being a 2D object, the notion of dimensionality of space has been given a new, but rather complex, definition.

There has been much research in string theory regarding whether space has more than three dimensions and whether the dimensionality can differ in different regions of spacetime. If string theory is correct, space might have many more dimensions than three, but string theory is an unconfirmed theory. A space with more dimensions than three for our universe is commonly called “the bulk.”

11. How Is Time Relative to the Observer?

The rate that a clock ticks is relative to the observer. Given one event, the first observer’s clock can measure one value for its duration, but a second clock can measure a different value if it is moving or being affected differently by gravity. Yet, says Einstein, both measurements can be correct. That is what it means to say time is relative to the observer. This relativity is quite a shock to our manifest image of time. According to Newton’s physics, in principle there is no reason why observers cannot agree on what time it is now or how long an event lasts or when some distant event occurred. Einstein’s theory disagrees with Newton’s on all this.

The term “observer” in relativity theory has a technical meaning.  The observer has no effect on the observation. The observer at a point is idealized as a massless point particle having no impact on its environment. Ideally, an observer is a conscious being who can report an observation and who has a certain orientation to what is observed, such as being next to the measured event or being three light years away. If so, the observation is called objective. An observation is the result of the action of observing. It establishes the values of one or more variables as in: “It was noon on my spaceship’s clock when the asteroid impact was detected, so because of the travel time of light I compute that the impact occurred at 11:00.”

Think of an observer as being an omniscient reference frame. Consider what is involved  in being an omniscient reference frame. Information about any desired variable is reported from a point-sized spectator at each spacetime location. A spectator is always accompanied by an ideal, point-sized, massless, perfectly functioning clock that is synchronized with the clocks of other spectators at all other points of spacetime. The observer at a location has all the tools needed for reporting values of variables such as voltage or the presence or absence of grape jelly at that location.

12. What Is the Relativity of Simultaneity?

The relativity of simultaneity is the feature of spacetime in which observers using different reference frames disagree on which events are simultaneous. Simultaneity is relative to the chosen reference frame. A large percentage of both physicists and philosophers of time suggest that this implies simultaneity is not objectively real, and they conclude also that the present is not objectively real, the present being all the events that are simultaneous with being here now.

Why is there disagreement about what is simultaneous with what? It occurs because the two events occur spatially far from each other.

In our ordinary lives, we can neglect all this because we are interested in nearby events. If two events occur near us, we can just look and see whether they occurred simultaneously.  But suppose we are on a spaceship circling Mars when a time signal is received saying it is noon in London, England. Did the event of the sending and receiving occur simultaneously? No. Light takes an hour and twenty minutes to travel from the Earth to the spaceship. If we want to use this time signal to synchronize our clock with the Earth clock, then instead of setting our spaceship clock to noon, we should set it to an hour and twenty minutes before noon.

This scenario conveys the essence of properly synchronizing distant clocks with our nearby clock. There are some assumptions that are ignored for now, namely that we can determine that the spaceship was relatively stationary with respect to Earth and was not in a different gravitational potential field from that of the Earth clock.

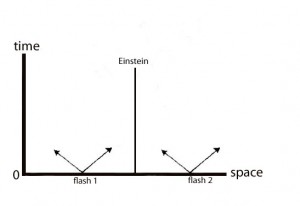
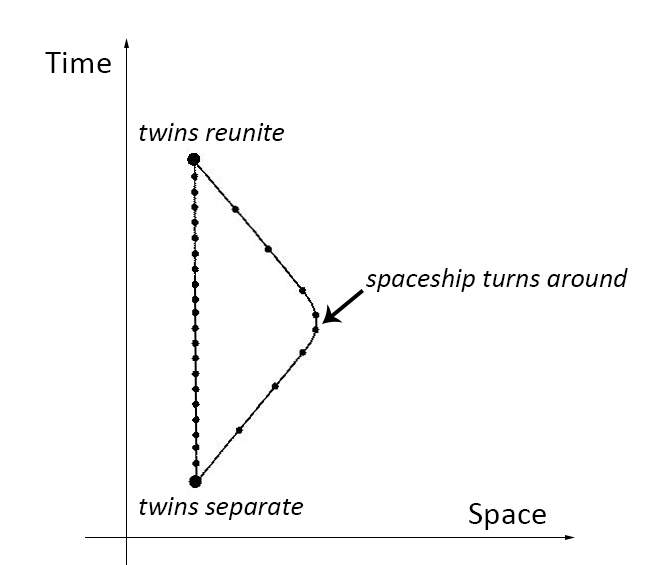
The diagram below illustrates the relativity of simultaneity for the so-called midway method of synchronization. There are two light flashes. Did they occur simultaneously?

The Minkowski diagram represents Einstein sitting still in the reference frame indicated by the coordinate system with the thick black axes. Lorentz is traveling rapidly away from him and toward the source of flash 2. Because Lorentz’s world line is a straight line, we can tell that he is moving at a constant speed. The two flashes of light arrive simultaneously at their midpoint according to Einstein but not according to Lorentz. Lorentz sees flash 2 before flash 1. That is, the event A of Lorentz seeing flash 2 occurs before event C of Lorentz seeing flash 1. So, Einstein will readily say the flashes are simultaneous, but Lorentz will have to do some computing to figure out that the flashes are simultaneous in the Einstein frame because they are not simultaneous to him in a reference frame in which he is at rest.  However, if we’d chosen a different reference frame from the one above, one in which Lorentz is not moving but Einstein is, then it would be correct to say flash 2 occurs before flash 1. So, whether the flashes are or are not simultaneous depends on which reference frame is used in making the judgment. It’s all relative.

There is a related philosophical issue involved with assumptions being made in, say, claiming that Einstein was initially midway between the two flashes. Can the midway determination be made independently of adopting a convention about whether the speed of light is independent of its direction of travel? This is the issue of whether there is a ‘conventionality’ of simultaneity.

13. What Is the Conventionality of Simultaneity?

The relativity of simultaneity is philosophically less controversial than the conventionality of simultaneity. To appreciate the difference, consider what is involved in making a determination regarding simultaneity. The central problem is that you can measure the speed of light only for a roundtrip, not a one-way trip, so you cannot simultaneously check what time it is on your clock and on a distant clock. A related, simpler problem, is to determine whether the speed of light is the same in opposite directions.

Given two events that happen essentially at the same place, physicists assume they can tell by direct observation whether the events happened simultaneously. If they cannot detect that one of them is happening first, then they say they happened simultaneously, and they assign the events the same time coordinate in the reference frame. The determination of simultaneity is very much more difficult if the two events happen very far apart, such as claiming that the two flashes of light reaching Einstein in the scenario of the previous section began at the same time. One way to measure (operationally define) simultaneity at a distance is the midway method. Say that two events are simultaneous in the reference frame in which we are stationary if unobstructed light signals caused by the two events reach us simultaneously when we are midway between the two places where they occurred. This is the operational definition of simultaneity used by Einstein in his theory of special relativity.

This midway method has a significant presumption: that the light beams coming from opposite directions travel at the same speed. Is this a fact or just a convenient convention to adopt? Einstein and the philosophers of time Hans Reichenbach and Adolf Grünbaum have called this a reasonable convention because any attempt to experimentally confirm the equality of speeds, they believed, presupposes that we already know how to determine simultaneity at a distance.

Hilary Putnam, Michael Friedman, and Graham Nerlich object to calling it a convention—on the grounds that to make any other assumption about light’s speed would unnecessarily complicate our description of nature, and we often make choices about how nature is on the basis of simplification of our description of nature.

To understand the dispute from another perspective, notice that the midway method above is not the only way to define simultaneity. Consider a second method, the mirror reflection method. Select an Earth-based frame of reference, and send a flash of light from Earth to Mars where it hits a mirror and is reflected back to its source. The flash occurred at 12:00 according to a correct Earth clock, let’s say, and its reflection arrived back on Earth 20 minutes later. The light traveled the same empty, undisturbed path coming and going. At what time did the light flash hit the mirror? The answer involves the conventionality of simultaneity. All physicists agree one should say the reflection event occurred at 12:10 because they assume it took ten minutes going to Mars, and ten minutes coming back. The difficult philosophical question is whether this way of calculating the ten minutes is really just a convention. Einstein pointed out that there would be no inconsistency in our saying that the flash hit the mirror at 12:17, provided we live with the awkward consequence that light was relatively slow reaching the mirror, but then traveled back to Earth at a faster speed.

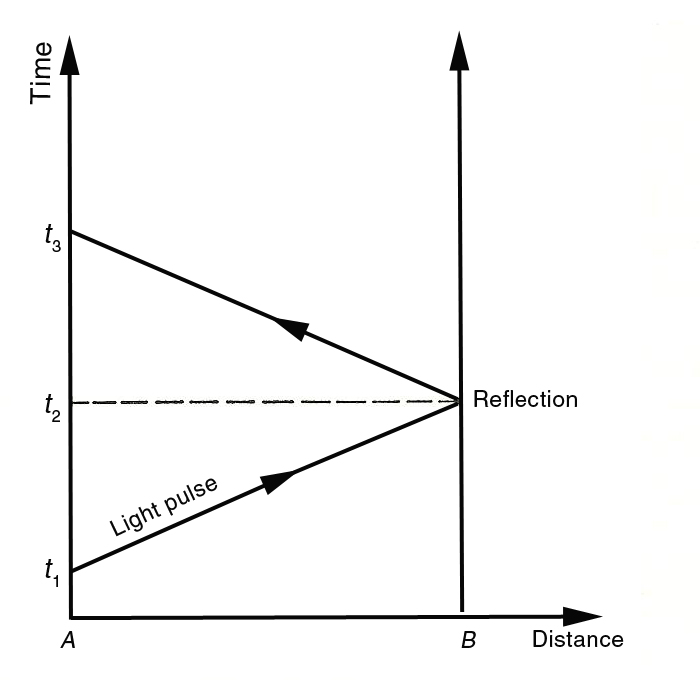
Suppose we want to synchronize a Mars clock with our clock on Earth using the reflection method. Let’s draw a Minkowski diagram of the situation and consider just one spatial dimension in which we are at location A on Earth next to the standard clock used for the time axis of the reference frame. The distant clock on Mars that we want to synchronize with Earth time is at location B. See the diagram.

The fact that the world line of the B-clock is parallel to the time axis shows that the two clocks are assumed to be relatively stationary. (If they are not, and we know their relative speed, we might be able to correct for this.) We send light signals from Earth in order to synchronize the two clocks. Send a light signal from A at time t₁ to B, where it is reflected back to us at A, arriving at time t₃. So, the total travel time for the light signal is t₃ – t₁, as judged by the Earth-based frame of reference. Then the reading t_r on the distant clock at the time of the reflection event should be set to t₂, where:

t₂ = t₁ + (1/2)(t₃ – t₁).

If t_r = t₂, then the two spatially separated clocks are supposedly synchronized.

Einstein noticed that the use of the fraction 1/2 rather than the use of some other fraction implicitly assumes that the light speed to and from B is the same. He said this assumption is a convention, the so-called conventionality of simultaneity, and is not something we could check to see whether it is correct.  Only with the fraction (1/2) are the travel speeds the same going and coming back.

Suppose we try to check whether the two light speeds really are the same. We would send a light signal from A to B, and see if the travel time was the same as when we sent it from B to A. But to trust these durations we would already need to have synchronized the clocks at A and B. But that synchronization process will presuppose some value for the fraction, said Einstein.

Not all philosophers of science agree with Einstein that the choice of (1/2) is a convention, nor with those philosophers such as Putnam who say the messiness of any other choice shows that the choice of 1/2 must be correct. Everyone does agree, though, that any other choice than 1/2 would make for messy physics.

Some researchers suggest that there is a way to check on the light speeds and not simply presume they are the same. Create two duplicate, correct clocks at A. Transport one of the clocks to B at an infinitesimal speed. Going this slow, the clock will arrive at B without having its own time reports deviate from that of the A-clock. That is, the two clocks will be synchronized even though they are distant from each other. Now the two clocks can be used to find the time when a light signal left A and the time when it arrived at B, and similarly for a return trip. The difference of the two time reports on the A and B clocks can be used to compute the light speed in each direction, given the distance of separation. This speed can be compared with the speed computed with the midway method. The experiment has never been performed, but the recommenders are sure that the speeds to and from will turn out to be identical, so they are sure that the (1/2) is correct and not a convention.

Sean Carroll has yet another position on the issue. He says “The right strategy is to give up on the idea of comparing clocks that are far away from each other” (Carroll 2022, 150).

The conventionality of simultaneity is discussed in the encyclopedia article on Eternalism. For additional discussion of the controversies involved in the conventionality of simultaneity, see (Callender 2017, p. 51) and pp. 179-184 of The Blackwell Guide to the Philosophy of Science, edited by Peter Machamer and Michael Silberstein, Blackwell Publishers, Inc., 2002.

14. What are the Absolute Past and the Absolute Elsewhere?

What does it mean to say the human condition is one in which you never will be able to affect an event outside your forward light cone? Here is a visual representation of the human condition according to the special theory of relativity, whose spacetime can always be represented by a Minkowski diagram of the following sort:

The absolutely past events (the green events in the diagram above) are the events in or on the backward light cone of your present event, your here-and-now. The backward light cone of event Q is the imaginary cone-shaped surface of spacetime points formed by the paths of all light rays reaching Q from the past.

The events in your absolute past zone or region are those that could have directly or indirectly affected you, the observer, at the present moment, assuming there were no intervening obstacles. The events in your absolute future zone are those that you could directly or indirectly affect.

An event’s being in another event’s absolute past is a feature of spacetime itself because the event is in the point’s past in all possible reference frames. This feature is frame-independent. For any event in your absolute past, every observer in the universe (who is not making an error) will agree the event happened in your past. Not so for events that are in your past but not in your absolute past. Past events not in your absolute past are in what Eddington called your absolute elsewhere. The absolute elsewhere is the region of spacetime containing events that are not causally connectible to your here-and-now. Your absolute elsewhere is the region of spacetime that is neither in nor on either your forward or backward light cones. No event here and now, can affect any event in your absolute elsewhere; and no event in your absolute elsewhere can affect you here and now.

If you look through a telescope you can see a galaxy that is a million light-years away, and you see it as it was a million years ago. But you cannot see what it looks like now because the present version of that galaxy is outside your light cone, and is in your absolute elsewhere.

A single point’s absolute elsewhere, absolute future, and absolute past form a partition of all spacetime into three disjoint regions. If point-event A is in point-event B’s absolute elsewhere, the two events are said to be spacelike related. If the two are in each other’s forward or backward light cones they are said to be time-like related or to be causally connectible. We can affect or be affected by events that are time-like related to us here and now; we cannot affect or be affected by events that are space-like separated from our here and now. Whether a space-like event occurs before the event of your being here now depends on the chosen frame of reference, but the order of occurrence of a time-like event and our here-and-now is not frame-relative. Another way to make the point is to say that, when choosing a reference frame, we have a free choice about the time order of two events that are space-like related, but we have no freedom when it comes to two events that are time-like related because the causal order determines their time order. That is why the absolute elsewhere is also called the extended present. There is no fact of the matter about whether a point in your absolute elsewhere is in your present, your past, or your future. It is simply a conventional choice of reference frame that fixes what events in your absolute elsewhere are present events.

For any two events in spacetime, they are time-like, space-like, or light-like separated, and this is an objective feature of the pair that cannot change with a change in the reference frame. This is another implication of the fact that the light-cone structure of spacetime is real and objective, unlike features such as durations and lengths.

The past light cone looks like a cone in small regions in a spacetime diagram with one dimension of time and two of space. However, the past light cone is not cone-shaped in a large cosmological region, but rather has a pear-shape because all very ancient light lines must have come from the infinitesimal volume at the Big Bang.

15. What Is Time Dilation?

Time dilation occurs when two synchronized clocks get out of synchrony due either to their relative motion or due to their being in regions of different gravitational field strengths.  An observer always notices that it is the other person’s clock that is behaving oddly, never that their own clock is behaving oddly. When two observers are in relative motion, each can see that the other person’s clock is slowing down relative to their own clock. It’s as if the other person’s time is stretched  or dilated. There is philosophical controversy about whether the dilation is literally a change in time itself or only a change in how  durations are measured using someone else’s clock as opposed to one’s own clock.

The specific amount of time dilation depends on the relative speed of one clock toward or away from the other. If one clock circles the other, their relative speed is zero, so there is no time dilation due to speed, regardless of how fast the rotational speed.

The sister of time dilation is space contraction. The length of an object changes in different reference frames to compensate for time dilation so that the speed of light c in a vacuum is constant in any frame. The object’s length measured perpendicular to the direction of motion is not affected by the motion, but the length measured in the direction of the motion is affected. If you are doing the measuring, then moving sticks get shorter if moving toward you or away from you. The length changes not because of forces, but rather because space itself contracts.  What a shock this is to our manifest image! No one notices that the space around themselves is contracting, only that the space somewhere else seems to be affected.

Here is a picture of the visual distortion of moving objects due to space contraction:

Image: Corvin Zahn, Institute of Physics, Universität Hildesheim,
Space Time Travel (http://www.spacetimetravel.org/)

The picture describes the same wheel in different colors: (green) rotating in place just below the speed of light; (blue) moving left to right just below the speed of light; and (red) remaining still.

To give some idea of the quantitative effect of time dilation:

Among particles in cosmic rays we find protons…that move so fast that their velocities differ infinitesimally from the speed of light: the difference occurs only in the twentieth (sic!) non-zero decimal after the decimal point. Time for them flows more slowly than for us by a factor of ten billion, If, by our clock, such a proton takes a hundred thousand years to cross our stellar system—the Galaxy—then by ‘its own clock’ the proton needs only five minutes to cover the same distance (Novikov 1998, p. 59).

16. How Does Gravity Affect Time?

According to the general theory of relativity, gravitational differences affect time by dilating it—in the sense that observers in a less intense gravitational potential field find that clocks in a more intense gravitational potential field run slow relative to their own clocks. It’s as if the time of the clock in the intense gravitational field is stretched out and not ticking fast enough. For this reason, people in ground floor apartments outlive their twins in penthouses, all other things being equal. Basement flashlights will be shifted toward the red end of the visible spectrum compared to the flashlights in attics. All these phenomena are the effects of gravitational time dilation.

Spacetime in the presence of gravity is curved, according to general relativity. So, time is curved, too. When time curves, clocks do not bend in space as if in a Salvador Dali painting. Instead they undergo gravitational time dilation.

Information from the Global Positioning System (GPS) of satellites orbiting Earth is used by your cell phone to tell you whether you should turn right at the next intersection. The GPS is basically a group of flying atomic clocks that broadcast the time. The curvature of spacetime near Earth is significant enough that gravitational time dilation must be accounted for by these clocks to keep us from making navigation errors. GPS clocks slow down because of gravitational time dilation and speed up because of time dilation due to their high speed. The combined effect is seven seconds for the GPS clocks.  Therefore, these GPS satellites are launched with their clocks adjusted ahead of Earth clocks by about seven seconds and then are periodically readjusted ahead so that they stay synchronized with Earth’s standard time. The smaller the error in the atomic clock in the satellite and in the standard clock the better the GPS system works. That is one reason physicists keep trying to build better clocks. In 2018, gravitational time dilation was measured in Boulder, Colorado, U.S.A. so carefully that it detected the difference in ticking of two initially synchronized atomic clocks that differed in height by only a centimeter. Unfortunately, the actual atomic clocks used in GPS satellites are much less accurate than these atomic clocks.

When a metaphysician asks the question, “What is gravity?” there are three legitimate, but very different, answers. Gravity is (1) a force, (2) intrinsic curvature of spacetime, and (3) exchanges of virtual particles. All three answers are correct and have their uses. When speaking of spilling milk or designing a rocket to visit the moon, the first answer is most appropriate to use. In the context of general relativity, the second answer is most appropriate. For ontology, the third answer is best.

In the context of a future theory of quantum gravity that incorporates gravity into the best features of quantum mechanics and the best features of the standard model of particle physics, the third answer is expected to be best. At this more fundamental level, forces are features of field activity. Those virtual gravity particles are called gravitons, and they are fluctuations within the gravitational field. What is happening with spilled milk is that pairs of virtual entangled particles bubble up out of the relevant fields. Normally one member of the pair has positive momentum, and the other member has negative momentum. Those particles with negative momentum  are exchanged between the milk and the Earth and floor, thereby causing the milk to be attracted to the floor in analogy to how, when someone throws a boomerang beyond you, it can hit you on its way back and push you closer to the thrower.

17. What Happens to Time near a Black Hole?

Time, as measured by an Earth-based clock, slows down for all processes near a black hole. For example, a clock on a spaceship approaching the hole will be slowed down as measured by our standard Earth-based clock. So will people’s actions and thoughts.

What is a black hole? Although Einstein believed a black hole is too strange to actually exist, black holes subsequently have been recognized to be real phenomena existing throughout the universe. Princeton physicist Richard Gott described a black hole as a spherical hotel in which you can check in but cannot check out. Even light sent out from a laser that has fallen in will get dragged back and never escape. That is why the hole is called black. Every massive object has an escape velocity, namely a minimum speed required for a spaceship to fly away directly away from the object and escape into outer space. The escape velocity of any black hole is larger than the velocity of light, which is why it is black.

Black holes are made from material objects getting crushed together, but those material objects get crushed and turned into the energy of spatial curvature making the black hole matter-free and just a strange region of space with no matter in the region. What then keeps the black hole curved after all the matter has vanished? It is the enormous energy of its own warping. That energy is stored within the gravitational field which in turn produces such a high gravitational force that it curves itself until it becomes stable.

A typical black hole is produced by the death of a star whose nuclear fuel has been used up. A healthy star is an explosion. A black hole is an implosion. Matter is a physical object within space and time; a black hole is merely space and time itself. The hole might later contain matter, but this would be due only to new matter falling in after the hole was created, although this matter would soon be sucked toward the center, and it, too, would disappear at the singularity and be converted into pure energy, and the information of this matter would surely be lost when the black hole evaporates—as all black holes do. We on the outside of a black hole know only the mass (including its gravitational activity), rotation, and electric charge. All its other information is hidden from view, as if it has disappeared from the universe. The term “gravitational activity” is referring to the fact that black holes can vibrate at resonant frequencies of its gravitational waves when matter falls into the hole and makes it ring somewhat like a bell having been struck by a hammer.

The center of a black hole is often called its singularity, but strictly speaking the center and the singularity are different. The spatial center is a crushed region of very large spatial curvature. The singularity, on the other hand, is the end of the proper time of any object that plunges into the hole. Nevertheless it is common to casually use the two terms interchangeably.

Most contemporary physicists do not believe there are any singularities of zero volume; they believe those are artifacts of relativity theory, and signs that that relativity theory needs to be improved and reconciled with quantum theory. Instead, they believe the “singularity” is very small but not actually infinitesimal, and the curvature there is extremely high but not infinite. They believe this because relativity theory’s singularity is inconsistent with quantum theory’s requirement that no matter can be confined to a point; the confinement would violate Heisenberg’s Uncertainty Principle of quantum theory. On this issue, contemporary physicists trust quantum mechanics more than relativity theory.

Here is a processed photograph of a black hole surrounded by its colorful but dangerous accretion disk that is radiating electromagnetic radiation (mostly high-energy x-rays) due to particles outside the hole crashing into each other as they are gravitationally pulled toward the hole:

The red and orange area is the accretion disk outside the hole where incoming particles crash into each other. The black region in the center is produced by the black hole’s blocking the light from its own accretion disk that is behind it. The colors in the picture are artifacts added by a computer because the real light (when shifted from x-ray frequencies to optical frequencies) would be white and because humans can detect differences among colors better than differences in the brightness of white light. It is believe that nearly all black holes spin and spin faster the smaller they are, but even if a black hole is not spinning, its surrounding accretion disk beyond its event horizon will surely be spinning. Because of the spinning. the accretion disk is not spherical, but is pizza-shaped. It can have a temperature of from a thousand to many millions of degrees.

The event horizon is a two-dimensional fluid-like surface separating the inside from the outside of the black hole. Think of the event horizon as a two-dimensional spherical envelope. To plunge across the event horizon is to cross a point of no return. Even light generated inside cannot get back out. So, black holes are relatively dark compared to stars. However, because the accretion disk outside the horizon can eject hot, magnetized gas and shine as a quasar, some supermassive black holes are the most luminous objects in all the universe.

If you were unlucky enough to fall through the event horizon, you could see out continually, but you could not send a signal out, nor could you yourself escape even if your spaceship had an extremely powerful thrust. Also, the space around you increasingly collapses, so you would be sucked toward the singularity and squeezed on your way there—a process called “spaghettification.” Despite your soon being crushed to a tiny volume on your way to the end of time at the singularity, you would continue to affect the world outside the black hole via your contribution to its gravity. Spaghettification is not very significant as you cross the horizon of a very large black hole, but it gets very significant as you get near the singularity.

Any macroscopic object can become a black hole if sufficiently compressed. An object made of anti-matter can become a black hole, too. If you bang two rocks together fast enough, they will produce a black hole, and the black hole will begin pulling in nearby particles, including you the experimenter. Luckily even our best particle colliders in Earth’s laboratories are not powerful enough to create black holes, but the creators of those first laboratories were gambling with the future of humanity when they guessed no black hole would be created. High speed black holes the mass of an asteroid could easily pass through our globe regularly without anyone noticing. Their diameter would be nanometer-sized, and they would exit Earth long before any significant amount of mass was absorbed.

All massive stars will become black holes when their fuel runs out and they stop radiating so that the star’s gravity takes over and crushes the star. Our Sun is not quite massive enough to do this, but its future ash will eventually find its way into a black hole.

If an electron were a point particle, then it would have an enormous density and be dense enough to become a black hole. That electrons exist around us and do not become black holes is the best reason to believe electrons are not point particles.

The black hole M87 is pictured above. It has a mass of about 6.5 billion of our suns, so it is too big for it to have originated from the collapse of only a single star. It probably has eaten many nearby stars and much cosmic dust. It is not in the Milky Way but in a distant galaxy 55 million light years from Earth. There is another, smaller yet supermassive black hole at the center of the Milky Way. It, too, is probably made by feeding on neighbor stars and other nearby infalling material. Almost all galaxies have a black hole at their center, but black holes also exist elsewhere. Most black holes are not powerful enough to suck in all the stars around them, just as our sun will never suck in all the planets of our solar system. This is because of the planet’s angular momentum around the Sun. Similarly, most all the electrons and protons in the accretion disk of a black hole have angular momentum that produces enough centrifugal force to resist the black hole’s gravitational pull.

A black hole’s accretion disk also spins if the hole spins, and because of this the Doppler effect shown in the picture above requires the redness at the top to be less bright than at the bottom of the picture. The picture has been altered to remove the blurriness that would otherwise be present due to the refraction from the plasma and dust between the Earth and the black hole. The plasma close to the black hole has a temperature of hundreds of billions of degrees.

The matter orbiting the black hole is a diffuse gas of electrons and protons. …The black hole pulls that matter from the atmospheres of stars orbiting it. Not that it pulls very much. Sagittarius A* is on a starvation diet—less than 1 percent of the stuff captured by the black hole’s gravity ever makes it to the event horizon. (Seth Fletcher. Scientific American, September 2022 p. 53.)

Relativity theory implies an infalling spaceship suffers an infinite time dilation at the event horizon and so does not fall through the horizon in a finite time. Most physicists believe this implication is incorrect and is a reason that relativity theory needs to be revised. When quantum mechanics is taken into account, it seems that the unfortunate spaceship does fall through in a finite time. This is because the gravitational field produced by the spaceship itself acts on the black hole. As the spaceship gets very, very close to the event horizon such as an atom’s width away, the time dilation does radically increase, but the event horizon slightly expands enough to swallow the spaceship in a finite time—a trivially short time as judged from the spaceship, but a very long time as judged from Earth. This occurrence of slight expansion is one sign that the event horizon is fluidlike. After the spaceship is swallowed, the event horizon returns to its original shape, but it is slightly larger now because it is more massive by one spaceship-mass.

By applying quantum theory to black holes, Stephen Hawking discovered that black holes are  not quite black even when the radiation of the accretion disk is not taken into account. Every black hole emits “Hawking radiation” at its horizon. This radiation reduces the mass of the black hole causing it to eventually evaporate. Large black holes take about 10⁶⁷ years to completely evaporate. To appreciate how long a black hole lives, remember that the Big Bang occurred less than twenty billion years ago (2 x 10¹⁰ years ago). Because every black hole absorbs the cosmic background radiation, a black hole will not even start evaporating and losing energy until the hole’s absorption of the cosmic background radiation subsides enough that the hole’s immediate environment is below the temperature of the black hole. Quantum theory suggests black holes get warmer as they shrink. Hawking first realized that they do this by absorbing particles on their event horizon that have negative mass (Yes, “negative”). When a black hole shrinks to the size of a bacterium, its outgoing radiation becomes white-colored, producing a white black-hole. At the very last instant of its life, it evaporates as it explodes in a flash of extremely hot, high-energy particles.

Black holes have many other strange properties. When a pair of particles is produced at the event horizon, one of the pair can fall into the hole while the other flies away from the hole. From the perspective of any particle, it always has positive energy, but from the perspective of a distant, external observer, the infalling particle can have negative energy.

Another odd property is that nearly all physical objects tend to get warmer when you shine a light on them. Think of your ice cream cone in the sunshine. A black hole is an exception. It get colder in the sunshine.

Black holes produce startling visual effects. A light ray can circle outside a black hole once or many times depending upon its angle of incidence to the event horizon. A light ray grazing a black hole can leave at any angle, so a person viewing a black hole from outside can see multiple copies of themselves various angles. Each copy arrives at a different time. We can see the same galaxy more than once because of this. See http://www.spacetimetravel.org/reiseziel/reiseziel1.html for some of these visual effects. An external viewer can also see the part of the accretion disk that is behind the black hole and would be obscured by the hole itself if it were not for gravitational lensing.

Every spherical black hole has the odd geometric feature that its diameter is very much larger than its circumference, which is very unlike the sphere of Euclidean geometry. The diameter “plunges” into the hole.

Additional mass makes a black hole grow. Some black holes have been detected to be 100 billion times more massive than our Sun.

Some popularizers have said that the roles of time and space are reversed within a black hole, but this is not correct. Instead it is only coordinates that reverse their roles. Given a coordinate system whose origin is outside a black hole, its timelike coordinates become spacelike coordinates inside the horizon. If you were to fall into a black hole, your clock would not begin measuring distance. See (Carroll 2022c  251-255) for more explanation of this role reversal.

Black Holes and Information

Do black holes destroy information? Stephen Hawking’s calculation was that information is lost to outsiders as an object hits the singularity; it is an irreversible process. The information is lost before any measurements are made so it is a second kind of information loss for quantum theory. By “information” Hawking meant all the details of an initial state at some time before the object plunges through the event horizon. According to Hawking’s calculation, the details are lost to outsiders because the information is destroyed at the singularity. This loss is inconsistent with standard quantum theory which says information is never lost except during measurements. The leading hypothesis in the first quarter of the 21^st century is that the information is not lost, and it escapes back out through the Hawking radiation during the evaporation process of the black hole. Unfortunately, this hypothesis cannot be experimentally tested because the Hawking radiation is far too weak to be practically measured, and we still do not have a theory of quantum gravity that says whether information is or isn’t lost at the singularity. “In the absence of both theory and data, physicists produced many hypotheses about what might happen in black hole evaporation. Maybe black holes don’t entirely evaporate, but leave behind remnants. Maybe information can’t ever fall in but remain on the event horizon. Maybe it bounces back at the singularity. Maybe it comes out with the Hawking radiation. The latter is the favored hypothesis.

History

In 1783, John Michell speculated that there may be a star with a large enough diameter that the velocity required to escape its gravitational pull would be so great that not even Newton’s particles of light could escape. He called them “dark stars.” Einstein invented the general theory of relativity in 1915, and the next year the German physicist Karl Schwarzschild discovered that Einstein’s equations imply that if a non-rotating, perfectly spherical star, in an  otherwise empty universe were massive enough and its radius were somehow small enough so that it had extremely high density, then it would undergo an unstoppable collapse. Meanwhile, the gravitational force from the object would be so strong that not even light within the hole could escape the inward pull of gravity. In 1935, Arthur Eddington commented upon this discovery that relativity theory allowed a star to collapse this way:

I think there should be a law of nature to stop a star behaving in this absurd way.

Because of Eddington’s prestige, other physicists (with the notable exception of Subrahmanyan Chandrasekhar) agreed. Then in 1939, J. Robert Oppenheimer and his student Hartland Snyder first seriously suggested that some stars would in fact collapse into black holes, and they first clearly described the defining features of a black hole—that “The star thus tends to close itself off from any communication with a distant observer; only its gravitational field persists.” The term “black hole” was first explicitly mentioned by physicist Robert Dicke some time in the early 1960s when he made the casual comparison to a notorious dungeon of the same name in India, the Black Hole of Calcutta. The term was first published in the American magazine Science News Letter in 1964. John Wheeler subsequently promoted use of the term, following a suggestion from one of his students.

Roger Penrose won a Nobel Prize for proving that if you perturb Schwarzchild’s  solution by making the black hole not quite spherical, the new hole still must have a singularity.

It is now known that most of the entropy of the universe is within black holes. Any black hole has more entropy than the material from which it was made.

18. What Is the Solution to the Twins Paradox?

The paradox is an argument that uses the theory of relativity to produce an apparent contradiction. Before giving that argument, let’s set up a typical situation that can be used to display the paradox. Consider two twins at rest on Earth with their correct clocks synchronized. One twin climbs into a spaceship, and flies far away at a high, constant speed, then stops, reverses course, and flies back at the same speed. An application of the equations of special relativity theory shows that the twin on the spaceship will return and be younger than the Earth-based twin. Their clocks disagree about the elapsed time of the trip. Now that the situation has been set up, notice that relativity theory implies that either twin could say they are the stationary twin, so there is a contradiction. Isn’t that an implication of relativity theory?

To recap, the paradoxical argument is that either twin could regard the other as the traveler and thus as the one whose time dilates. If the spaceship were considered to be stationary, then would not relativity theory imply that the Earth-based twin could race off (while attached to the Earth) and return to be the younger of the two twins? If so, then when the twins reunite, each is younger than the other. That result is paradoxical.

Herbert Dingle was the President of London’s Royal Astronomical Society in the early 1950s. He famously argued in the 1960s that this twins paradox reveals an inconsistency in special relativity. All scientists and almost all philosophers disagree with Dingle and say the twin paradox is not a true paradox, in the sense of revealing an inconsistency within relativity theory, but is merely a complex puzzle that can be adequately solved within relativity theory.

The twins paradox is an interesting puzzle that has a solution that depends on the fact that in relativity theory two people who take different paths through spacetime take different amounts of time to do this in analogy to how two hikers take different times in hiking from place A to place B if the two take different paths. The puzzle’s solution depends on noticing that the two situations are not sufficiently similar, and because of this, for reasons to be explained in a moment, the twin who stays home on Earth maximizes his or her own time (that is, proper time) and so is always the older twin when the two reunite. This solution to the paradox involves spacetime geometry, and it has nothing to do with an improper choice of the reference frame. Nor is the puzzle explained by remarking that the two twins feel different accelerations on their body, even though that is true. The resolution of the puzzle has to do with the fact that some paths in spacetime must take more proper time to complete than other paths.

Here is how to understand the paradox. Consider the Minkowski spacetime diagram below.

The principal suggestion for solving the paradox is to note that there must be a difference in the time taken by the twins because their behaviors are different, as shown by the number and spacing of nodes along their two world lines above. The nodes represent ticks of their clocks. Notice how the space traveler’s time is stretched or dilated compared to the coordinate time, which also is the time of the stay-at-home twin. The coordinate time, that is, the time shown by clocks fixed in space in the coordinate system is the same for both travelers. Their personal times are not the same. The traveler’s personal time is less than that of the twin who stays home, and they return home with fewer memories.

For simplicity we are giving the twin in the spaceship an instantaneous initial acceleration and ignoring the enormous  gravitational forces this would produce, and we are ignoring the fact that the Earth is not really stationary but moves slowly through space during the trip.

The key idea for resolving the paradox is not that one twin accelerates and the other does not, although this claim is very popular in the literature in philosophy and physics. The key idea is that, during the trip, the traveling twin experiences less time but more space. That fact is shown by how their world lines in spacetime are different. Relativity theory requires that for two paths that begin and end at the same point, the longer the path in spacetime (and thus the longer the world line in the spacetime diagram) the shorter the elapsed proper time along that path. That difference is why the spacing of nodes or clock ticks is so different for the two travelers. This is counterintuitive (because our intuitions falsely suggest that longer paths take more time even if they are spacetime paths). And nobody’s clock is speeding up or slowing down relative to its own rate a bit earlier.

A free-falling clock ticks faster and more often than any other accurate clock that is used to measure the duration between pairs of events. It is so for the event of the twins leaving each other and reuniting. This is illustrated graphically by the fact that the longer world line in the graph represents a greater distance in space and a greater interval in spacetime but a shorter duration along that world line. The number of dots in the line is a correct measure of the time taken by the traveler. The spacing of the dots represents the durations between ticks of a personal clock along that world line. If the spaceship approached the speed of light, that twin would cover an enormous amount of space before the reunion, but that twin’s clock would hardly have ticked at all before the reunion event.

To repeat this solution in other words, the diagram shows how sitting still on Earth is a way of maximizing the trip time, and it shows how flying near light speed in a spaceship away from Earth and then back again is a way of minimizing the time for the trip, even though if you paid attention only to the shape of the world lines in the diagram and not to the dot spacing within them you might mistakenly think just the reverse. This odd feature of the geometry is one reason why Minkowski geometry is different from Euclidean geometry. So, the conclusion of the analysis of the paradox is that its reasoning makes the mistake of supposing that the situation of the two twins can properly be considered to be essentially the same.

Richard Feynman famously, but mistakenly, argued in 1975 that acceleration is the key to the paradox. As (Maudlin 2012) explains, the acceleration that occurs in the paths of the example above is not essential to the paradox because the paradox could be expressed in a spacetime obeying special relativity in which neither twin accelerates yet the twin in the spaceship always returns younger. The paradox can be described using a situation in which spacetime is compactified in the spacelike direction with no intrinsic spacetime curvature, only extrinsic curvature. To explain that remark, imagine this situation: All of Minkowski spacetime is like a very thin, flat cardboard sheet. It is “intrinsically flat.” Then roll it into a cylinder, like the tube you have after using the last paper towel on the roll. Do not stretch, tear, or otherwise deform the sheet. Let the time axis be parallel to the tube length, and let the one-dimensional space axis be a circular cross-section of the tube. The tube spacetime is still flat intrinsically, as required by special relativity, even though now it is curved extrinsically (which is allowed by special relativity). The travelling twin’s spaceship circles the universe at constant velocity, so its spacetime path is a spiral. The stay-at-home twin sits still, so its spacetime path is a straight line along the tube. The two paths start together, separate, and eventually meet (many times). During the time between separation and the first reunion, the spaceship twin travels in a spiral as viewed from a higher dimensional Euclidean space in which the tube is embedded. That twin experiences more space but less time than the stationary twin. Neither twin accelerates. There need be no Earth nor any mass nearby for either twin. Yet the spaceship twin who circles the universe comes back younger because of the spacetime geometry involved, in particular because the twin travels farther in space and less far in time than the stay-at-home twin.

For more discussion of the paradox, see (Maudlin 2012), pp. 77-83, and, for the travel on the cylinder, see pp. 157-8.

19. What Is the Solution to Zeno’s Paradoxes?

See the article “Zeno’s Paradoxes” in this encyclopedia.

20. How Are Coordinates Assigned to Time?

A single point of time is not a number, but it has a number when a coordinate system is applied to time. When coordinate systems are assigned to spaces, coordinates are assigned to points. The space can be physical space or mathematical space. The coordinates hopefully are assigned in a way that a helpful metric can be defined for computing the distances between any pair of point-places, or, in the case of time, the duration between any pair of point-times. Points, including times, cannot be added, subtracted, or squared, but their coordinates can be. Coordinates applied to the space are not physically real; they are tools used by the analyst, the physicist; and they are invented, not discovered. The coordinate systems gives each instant a unique name.

Technically, the question, “How do time coordinates get assigned to points in spacetime?” presupposes knowing how we coordinatize the four-dimensional manifold that we call spacetime. The manifold is a collection of points (technically, it is a topological space) which behaves as a Euclidean space in neighborhoods around any point. The focus in this section is on its time coordinates.

There is very good reason for believing that time is one-dimensional, and so, given any three different point events, one of them will happen between the other two. This feature is reflected in the fact that when real number time coordinates are assigned to three point events, and one of the three coordinates is between the other two.

Every event on the world-line of the standard clock is assigned a t-coordinate by that special clock. The clock also can be used to provide measures of the duration between two point events that occur along the coordinate line. Each point event along the world-line of the master clock is assigned some t-coordinate by that clock. For example, if some event e along the time-line of the master clock occurs at the spatial location of the clock while the master clock shows, say, t = 4 seconds, then the time coordinate of the event e is declared to be 4 seconds. That is t(e)=4. We assume that e occurs spatially at an infinitesimal distance from the master clock, and that we have no difficulty in telling when this situation occurs. So, even though determinations of distant simultaneity are somewhat difficult to compute, determinations of local simultaneity in the coordinate system are not. In this way, every event along the master clock’s time-line is assigned a time of occurrence in the coordinate system.

In order to extend the t-coordinate to events that do not occur where the standard clock is located, we can imagine having a stationary, calibrated, and synchronized clock at every other point in the space part of spacetime at t = 0, and we can imagine using those clocks to tell the time along their world lines. In practice we do not have so many accurate clocks, so the details for assigning time to these events is fairly complicated, and it is not discussed here. The main philosophical issue is whether simultaneity may be defined for anywhere in the universe. The sub-issues involve the relativity of simultaneity and the conventionality of simultaneity. Both issues are discussed in other sections of this supplement.

Isaac Newton conceived of points of space and time as absolute in the sense that they retained their identity over time. Modern physicists do not have that conception of points; points are identified relative to events, for example, the halfway point in space between this object and that object, and ten seconds after that point-event.

In the late 16th century, the Italian mathematician Rafael Bombelli interpreted real numbers as lengths on a line and interpreted addition, subtraction, multiplication, and division as “movements” along the line. His work eventually led to our assigning real numbers to instants. Subsequently, physicists have found no reason to use complex numbers or other exotic numbers for this purpose, although some physicists believe that the future theory of quantum gravity might show that discrete numbers such as integers will suffice and the exotically structured real numbers will no longer be required.

To assign numbers to instants (the numbers being the time coordinates or dates), we use a system of clocks and some calculations, and the procedure is rather complicated the deeper one probes. For some of the details, the reader is referred to (Maudlin 2012), pp. 87-105. On pp. 88-89, Maudlin says:

Every event on the world-line of the master clock will be assigned a t-coordinate by the clock. Extending the t-coordinate to events off the trajectory of the master clock requires making use of…a collection of co-moving clocks. Intuitively, two clocks are co-moving if they are both on inertial trajectories and are neither approaching each other nor receding from each other. …An observer situated at the master clock can identify a co-moving inertial clock by radar ranging. That is, the observer sends out light rays from the master clock and then notes how long it takes (according to the master clock) for the light rays to be reflected off the target clock and return. …If the target clock is co-moving, the round-trip time for the light will always be the same. …[W]e must calibrate and synchronize the co-moving clocks.

The master clock is the standard clock. Co-moving inertial clocks do not generally exist according to general relativity, so the issue of how to assign time coordinates is complicated in the real world. What follows is a few more interesting comments about the assignment.

The main point of having a time coordinate is to get agreement from others about which values of times to use for which events, namely which time coordinates to use. Relativity theory implies every person and even every object has its own proper time, which is the time of the clock accompanying it. Unfortunately these personal clocks do not usually stay in synchrony with other well-functioning clocks, although Isaac Newton falsely believed they do stay in synchrony. According to relativity theory, if you were to synchronize two perfectly-performing clocks and give one of them a speed relative to the other, then the two clocks readings must differ (as would be obvious if they reunited), so once you’ve moved a clock away from the standard clock you can no longer trust the clock to report the correct coordinate time at its new location.

The process of assigning time coordinates assumes that the structure of the set of instantaneous events is the same as, or is embeddable within, the structure of our time numbers. Showing that this is so is called solving the representation problem for our theory of time measurement. The problem has been solved. This article does not go into detail on how to solve this problem, but the main idea is that the assignment of coordinates should reflect the structure of the space of instantaneous times, namely its geometrical structure, which includes its topological structure, diffeomorphic structure, affine structure, and metrical structure. It turns out that the geometrical structure of our time numbers is well represented by the structure of the real numbers.

The features that a space has without its points being assigned any coordinates whatsoever are its topological features, its differential structures, and its affine structures. The topological features include its dimensionality, whether it goes on forever or has a boundary, and how many points there are. The mathematician will be a bit more precise and say the topological structure tells us which subsets of points form the open sets, the sets that have no boundaries within them. The affine structure is about which lines are straight and which are curved. The diffeomorphic structure distinguishes smooth from bent (having no derivative).

If the space has a certain geometry, then the procedure of assigning numbers to time must reflect this geometry. For example, if event A occurs before event B, then the time coordinate of event A, namely t(A), must be less than t(B). If event B occurs after event A but before event C, then we should assign coordinates so that t(A) < t(B) < t(C).

Consider a space as a class of fundamental entities: points. The class of points has “structure” imposed upon it, constituting it as a geometry—say the full structure of space as described by Euclidean geometry. [By assigning coordinates] we associate another class of entities with the class of points, for example a class of ordered n-tuples of real numbers [for a n-dimensional space], and by means of this “mapping” associate structural features of the space described by the geometry with structural features generated by the relations that may hold among the new class of entities—say functional relations among the reals. We can then study the geometry by studying, instead, the structure of the new associated system [of coordinates]. (Sklar 1976, p. 28)

But we always have to worry that there is structure among the numbers that is not among the entities numbered. Such structures are “mathematical artifacts.”

The goal in assigning coordinates to a space is to create a reference system; this is a reference frame plus (or that includes [the literature is ambiguous on this point]) a coordinate system. For 4D spacetime obeying special relativity with its Lorentzian geometry, a Lorentzian coordinate system is a grid of smooth timelike and spacelike curves on the spacetime that assigns to each point three space-coordinate numbers and one time-coordinate number. No two distinct points of the spacetime can have the same set of four coordinate numbers. Technically, being continuous is a weaker requirement than being smooth, but the difference is not of concern here.

As we get more global, we have to make adjustments. Consider two coordinate systems in adjacent regions. For the adjacent regions, we make sure that the ‘edges’ of the two coordinate systems match up in the sense that each point near the intersection of the two coordinate systems gets a unique set of four coordinates and that nearby points get nearby coordinate numbers. The result is an atlas on spacetime. Inertial frames can have global coordinate systems, but in general, we have to use atlases for other frames. If we are working with general relativity where spacetime can curve and we cannot assume inertial frames, then the best we can do without atlases is to assign a coordinate system to a small region of spacetime where the laws of special relativity hold to a good approximation. General relativity requires special relativity to hold locally, that is, in any infinitesimal region, and thus for space to be Euclidean locally. That means that locally the 3-d space is correctly described by 3-d Euclidean solid geometry. Adding time is a complication. Spacetime is not Euclidean in relativity theory. Infinitesimally, it is Minkowskian or Lorentzian.

Regarding any event in the the atlas, we demand that nearby events get nearby coordinates. When this feature holds everywhere, the coordinate assignment is said to be monotonic or to “obey the continuity requirement.” We satisfy this requirement by using real numbers as time coordinates.

The metric of spacetime in general relativity is not global but varies from place to place due to the presence of matter and gravitation, and it varies over time as the spatial distribution of matter and energy varies with time. So,  spacetime cannot be given its coordinate numbers without our knowing the distribution of matter and energy. That is the principal reason why the assignment of time coordinates to times is so complicated.

To approach the question of the assignment of coordinates to spacetime points more philosophically, consider this challenging remark:

Minkowski, Einstein, and Weyl invite us to take a microscope and look, as it were, for little featureless grains of sand, which, closely packed, make up space-time. But Leibniz and Mach suggest that if we want to get a true idea of what a point of space-time is like we should look outward at the universe, not inward into some supposed amorphous treacle called the space-time manifold. The complete notion of a point of space-time in fact consists of the appearance of the entire universe as seen from that point. Copernicus did not convince people that the Earth was moving by getting them to examine the Earth but rather the heavens. Similarly, the reality of different points of space-time rests ultimately on the existence of different (coherently related) viewpoints of the universe as a whole. Modern theoretical physics will have us believe the points of space are uniform and featureless; in reality, they are incredibly varied, as varied as the universe itself.
—From “Relational Concepts of Space and Time” by Julian B. Barbour, The British Journal for the Philosophy of Science, Vol. 33, No. 3 (Sep., 1982), p. 265.

For a sophisticated and philosophically-oriented approach to assigning time coordinates to times, see Philosophy of Physics: Space and Time by Tim Maudlin, pp. 24-34.

21. How Do Dates Get Assigned to Actual Events?

The following discussion presupposes the discussion in the previous section.

Our purpose in choosing a coordinate system or atlas is to express  time-order relationships (Did this event occur between those two or before them or after them?) and magnitude-duration relationships (How long after A did B occur?) and date-time relationships (When did event A itself occur?). The date of a (point) event is the time coordinate number of the spacetime coordinate of the event. We expect all these assignments of dates to events to satisfy the requirement that event A happens before event B iff t(A) < t(B), where t(A) is the time coordinate of A, namely its date. The assignments of dates to events also must satisfy the demands of our physical theories, and in this case we face serious problems involving inconsistency if a geologist gives one date for the birth of Earth, an astronomer gives a different date, and a theologian gives yet another date.

Ideally for any reference frame, we would like to partition the set of all actual events into simultaneity equivalence classes by some reliable method. All events in one equivalence class happen at the same time in the frame, and every event is in some class or other.

This cannot be done, but it is interesting to know how close we can come to doing it and how we would go about doing it. We would like to be able to say what event near our spaceship circling Mars (or the supergiant star Betelgeuse) is happening now (at the same time as our now where we are located). More generally, how do we determine whether a nearby event and a very distant event occurred simultaneously? Here we face the problem of the relativity of simultaneity and the problem of the conventionality of simultaneity.

How do we calibrate and synchronize our own clock with the standard clock? Let’s design a coordinate system for time. Suppose we have already assigned a date of zero to the event that we choose to be at the origin of our coordinate system. To assign dates (that is, time coordinates) to other events, we must have access to information from the standard clock, our master clock, and be able to use this information to declare correctly that the time intervals between any two consecutive ticks of our own clock are the same. The second is our conventional unit of time measurement, and it is defined to be the duration required for a specific number of ticks of the standard clock.

We then hope to synchronize other clocks with the standard clock so the clocks show equal readings at the same time. We cannot do this. What are the obstacles? The time or date at which a point-event occurs is the number reading on the clock at rest there. If there is no clock there, the assignment process is more complicated. One could transport a synchronized clock to that place, but any clock speed or influence by a gravitational field during the transport will need to be compensated for. If the place is across the galaxy, then any transport is out of the question, and other means must be used.

Because we want to use clocks to assign a time coordinate even to very distant events, not just to events in the immediate vicinity of the clock. As has been emphasized several times throughout this rambling article, the major difficulty is that two nearby synchronized clocks, namely clocks that have been calibrated and set to show the same time when they are next to each other, will not in general stay synchronized if one is transported somewhere else. If they undergo the same motions and gravitational influences, and thus have the same world line or time line, then they will stay synchronized; otherwise, they will not. There is no privileged transportation process that we can appeal to. Einstein offered a solution to this problem.

He suggested the following method. Assume in principle that we have stationary, ideal clocks located anywhere and we have timekeepers there who keep records and adjust clocks. Assume there is an ideal clock infinitesimally near the spaceship. Being stationary in the coordinate system implies it co-moves with respect to the master clock back in London. We need to establish that the two clocks remain the same distance apart, so how could we determine that they are stationary? We determine that, each time we send a light signal from London and bounce it off the distant clock, the roundtrip travel time remains constant. That procedure also can be used to synchronize the two clocks, or at least it can in a world that obeys special relativity, provided we know how far away the distant clock is. For example, the spaceship is known to be a distance d away from London. The roundtrip travel time is, say 2t seconds. When someone at the spaceship receives a signal from London saying it is noon, the person at the spaceship sets their clock to t seconds after noon. This is an ideal method of establishing simultaneity for distant events.

This method has some hidden assumptions that have not been mentioned. For more about this and about how to assign dates to distant events, see the discussions of the relativity of simultaneity and the conventionality of simultaneity.

As a practical matter, dates are assigned to events in a wide variety of ways. The date of the birth of the Sun is assigned very differently from dates assigned to two successive crests of a light wave in a laboratory laser. For example, there are lasers whose successive crests of visible light waves pass by a given location in the laboratory every 10^-15 seconds. This short time is not measured with a stopwatch. It is computed from measurements of the light’s wavelength. We rely on electromagnetic theory for the equation connecting the periodic time of the wave to its wavelength and speed. Dates for other kinds of events, such as the birth of Mohammad or the origin of the Sun, are computed from historical records rather than directly measured with a clock.

22. What Is Essential to Being a Clock?

The definition of “clock” is not a precisely defined term in science, but normally a clock is used for one of three purposes: to tell what time it is, to determine which of two events happened first, and to decide how long an event lasts. In order to do this, the clock needs at least two sub-systems, (1) fairly regular ticking and (2) the counting of those ticks.

Regarding (1), the goal in building the ticking sub-system is to have a tick rate that is stable for a long enough time to be useful. Stability implies it is regular in the sense of not drifting very much over time. The tick rate in clocks that use cyclic processes is called the clock’s “frequency,” and it is measured in cycles per second. So, a clock is intended to have a sufficiently stable frequency for a reasonably continuous period of time. If a clock is stable for only half a second, but you intend to use it to measure events that last about a minute, then it is not stable enough.

Regarding (2), the counting sub-system counts the ticks in order to measure how much time has elapsed between two events of interest, and to calculate what time it is, and to display the result. For one example, in a clock based upon Earth rotations, a tick might be the sun setting below the horizon (as viewed from an agreed upon location), with the count advancing one day for each observed tick.

All other things being equal, the higher the frequency of our best clocks the better. Earth rotations have a low frequency. Pendulums are better. With a quartz clock (used in all our computers and cellphones), a piece of quartz crystal is stimulated with a voltage in order to cause it to vibrate at its characteristic frequency, usually 32,768 cycles per second. So, when 32,768 ticks occur, the quartz clock advances its count by one second. Our civilization’s standard atomic clock ticks at a frequency of 9,192,631,770 ticks per second. After that many ticks, it advances its count by one second.

The longer a clock can tick without gaining or losing a second, the more useful it is for measuring whether universal constants do not vary or drift.

The best atomic clocks are predicted to be off by less than a second in 31 billions years. Nuclear clocks of the future will depend on transitions between energy levels of an atom’s nucleus instead of its electrons.  Nuclear clocks are predicted to be off by only a second in 300 billion years.

Expressed a bit technically in the language of relativity theory, what a clock does is measure its own “proper” time along its trajectory in spacetime. Commenting on this, the philosopher Tim Maudlin said:

An ideal clock is some observable physical device by means of which numbers can be assigned to events on the device’s world-line, such that the ratios of differences in the numbers are proportional to the ratios of interval lengths of segments of the world-line that have those events as endpoints.

So, for example, if an ideal clock somehow assigns the numbers 4, 6, and 10 to events p, q, and r on its world-line, then the ratio of the length of the segment pq to the segment qr is 1:2, and so on. (Maudlin 2012, 108).

An object’s world-line is its trajectory through spacetime.

A clock’s ticking needs to be a regular process but not necessarily a repeatable process. There are two very different ways to achieve a clock’s regular ticking. The most important way is by repetition, namely by cyclic behavior. The most important goal is that any one cycle lasts just as long as any other cycle. This implies the durations between any pair of ticks are congruent. This point is sometimes expressed by saying the clock’s frequency should be constant.

A second way for a clock to contain a regular process or stable ticking is very different, and it does not require there to be any cycles or repeatable process. A burning candle can be the heart of a clock in which duration is directly correlated with, and measured by, how short the candle has become since the burning began. Two ideal candles will regularly burn down the same distance over the same duration. There will be a regular rate of burning, but no cyclic, repeatable burning because, once some part of the candle has burned, it no longer exists to be burned again. This candle timer is analogous to the behavior of sub-atomic ‘clocks’ based on radioactive decay that are used for carbon dating of ancient trees and mammoths.

A daily calendar alone is not a clock unless it is connected to a regular process. It could be part of a clock in which daily progress along the calendar is measured by a process that regularly takes a day per cycle, such as the process of sunrise followed by sunset. A pendulum alone is not a clock because it has no counting mechanism. Your circadian rhythm is often called your biological clock, because it produces a regular cycle of waking and sleeping, but it is not a complete clock because there is no counting of the completed cycles. A stopwatch is not a clock. It is designed to display only the duration between when it is turned on and turned off. But it could easily be converted into a clock by adding a counting and reporting mechanism. Similarly for radioactive decay that measures the time interval between now and when a fossilized organism last absorbed Earth’s air.

Here are some examples of cyclical processes that are useful for clocks: the swings of a pendulum, repeated sunrises, cycles of a shadow on a sundial, revolutions of the Earth around the Sun, bouncing mechanical springs, and vibrations of a quartz crystal. Regularity of the repetitive process is essential because we want a second today to be equal to a second tomorrow, although as a practical matter we have to accept some margin of error or frequency drift. Note that all these repetitive processes for clocks are absolute physical quantities in the sense that they do not depend upon assigning any coordinate system, nor are they dependent on any process occurring in a living being, including any thought.

The larger enterprise of practical time-keeping for our civilization requires that clock readings be available at locations of interest, including onboard our spaceships and inside submarines. This availability can be accomplished in various ways. A standard clock sitting in a room in Paris is a practical standard only if either its times can be broadcast quickly to the desired distant location, or the clock can be copied and calibrated so that the copies stay adequately synchronized even though they are transported to different places. If the copies cannot always stay sufficiently synchronized (calibrated) with the standard clock back in Paris, then we need to know how we can compensate for this deviation from synchrony.

The count of a clock’s ticks is normally converted and displayed in seconds or in some other unit of time such as minutes, nanoseconds, hours, or years. This counting of ticks can be difficult. Our civilization’s 1964 standard clock ticks 9,192,631,770 times per second. Nobody sat down for a second and counted this number. An indirect procedure is required.

It is an arbitrary convention that we design clocks to count up to higher numbers rather than down to lower numbers. It is also a convention that we re-set our clock by one hour as we move across a time-zone on the Earth’s surface in order that the sun be nearly overhead at noons in those zones. In order to prevent noon from ever occurring when the sun is setting, we also add leap years.  However, it is no convention that the duration from instantaneous event A to instantaneous event B plus the duration from B to instantaneous event C is equal to the duration from A to C. It is one of the objective characteristics of time, and failure for this to work out numerically for your clock is a sure sign your clock is faulty.

A clock’s ticking needs to be a practically irreversible process. Any clock must use entropy increase in quantifying time. Some entropy must be created to ensure that the clock ticks forward and does not suffer a fluctuation that causes an occasional tick backward. The more entropy produced the less likely such an unwanted fluctuation will occur.

In addition to our clocks being regular and precise, we also desire our clocks to be accurate. What that means and implies is discussed in the next section.

23. What Does It Mean for a Clock to Be Accurate?

A group of clock readings is very precise if the readings are very close to each other even if they all are wildly inaccurate because they all report that it is 12:38 when actually it is noon.

A clock is accurate if it reports the same time as the standard clock. A properly working clock correctly measures the interval along its own trajectory in spacetime, its so-called proper time. The interval in spacetime is the spatio-temporal length of its trajectory, so a clock is analogous to an odometer for spacetime. Just as a car’s odometer can give a different reading for the distance between two locations if the car takes a different route between two locations, so also a properly working clock can give different measures of the duration of time between two events if the clock takes different spacetime trajectories between them. That is why it is easiest to keep two clocks in synchrony if they are sitting next to each other, and that is why it is easiest to get an accurate measure of the time between two events if they occur at the same place.

Because clocks are intended to be used to measure events external to themselves, a goal in clock building is to ensure there is no difficulty in telling which clock tick is simultaneous with which external event. For most nearby situations and nearby clocks and everyday purposes, the sound made by the ticking helps us make this determination. We hear the tick just as we hear or see the brief event occur that we wish to “time.” Humans actually react faster to what they hear than what they see. Trusting what we see or hear presupposes that we can ignore the difference in time between when a sound reaches our ears and when it is consciously recognized in our brain, and it presupposes that we can safely ignore the difference between the speed of sound and the speed of light.

If a clock is synchronized with the standard clock and works properly and has the same trajectory in spacetime as the standard clock, then it will remain accurate (that is, stay in synchrony) with the standard clock. According to the general theory of relativity, if a clock takes a different trajectory from the standard clock, then its readings will deviate from those of the standard clock, and when the second clock is brought back to be adjacent to the standard clock, the two will give different readings of what time it is. That is, if your well-functioning clock were at rest adjacent to the standard clock, and the two were synchronized, then they would stay synchronized, but if your clock moved away from the standard clock and took some different path through space, then the two would not give the same readings when they were reunited, even though both continued to be correct clocks, so this complicates the question of whether a clock that is distant from the standard clock is telling us standard time. To appreciate the complication, ask yourself the question: When our standard clock shows noon today, what event within a spaceship on Mars occurs simultaneously? Or ask the question: How do you “set” the correct time on the Mars clock?

The best that a designated clock can do while obeying the laws of general relativity is to accurately measure its own proper time. Time dilation will affect the readings of all other clocks and make them drift out of synchrony with the designated clock. It is up to external observers to keep track of these deviations and account for them for the purpose at hand.

There is an underlying philosophical problem and a psychological problem. If we assign a coordinate system to spacetime, and somehow operationally define what it is for a clock at one place to be in synch with a clock at another place, then we can define distant simultaneity in that coordinate system. However, whether spatiotemporally separated clocks are simultaneous is a coordinate-dependent artifact. Even when people understand this philosophical point that arises because of the truth of the general theory of relativity, they still seem unable to resist the temptation to require a correct answer to the question “What event on a spaceship circling Mars is simultaneous with noon today here on Earth” and unable to appreciate that this notion of simultaneity is a convention that exists simply for human convenience.

The quartz clock in your cellphone drifts and loses about a second every day or two, so it frequently needs to be “reset” (that is, restored to synchrony with our society’s standard clock).

Our best atomic clocks need to be reset by one second every 100 million years.

Suppose we ask the question, “Can the time shown on a properly functioning standard clock ever be inaccurate?” The answer is “no” if the target is synchrony with the current standard clock, as the conventionalists believe, but “yes” if there is another target. Objectivists can propose at least three other distinct targets: (1) synchrony with absolute time (as Isaac Newton proposed in the 17th century), (2) synchrony with the best possible clock, and (3) synchrony with the best-known clock. We do not have a way of knowing whether our current standard clock is close to target 1 or target 2. But if the best-known clock is known not yet to have been chosen to be the standard clock, then the current standard clock can be inaccurate in sense 3 and perhaps it is time to call an international convention to discuss adopting a new time standard.

Practically, a reading of ‘the’ standard clock is a report of the average value of the many conventionally-designated standard clocks, hundreds of them distributed around the globe. Any one of these clocks could fail to stay in sync with the average, and when this happens it is re-set (that is, re-calibrated, or re-set to the average reading). The re-setting occurs about once a month to restore accuracy.

There is a physical limit to the shortest duration measurable by a given clock because no clock can measure events whose duration is shorter than the time it takes a signal to travel between the components of that clock, the components in the part that generates the regular ticks. This theoretical limit places a lower limit on the margin of error of any measurement of time made with that clock.

Every physical motion of every clock is subject to disturbances. So, we want to minimize the disturbance, and we want our clock to be adjustable in case it drifts out of synchrony a bit. To achieve this goal, it helps to keep the clock isolated from environmental influences such as heat, dust, unusual electromagnetic fields, physical blows (such as dropping the clock), immersion in liquids, and differences in gravitational force. And it helps to be able to predict how much a specific influence affects the drift out of synchrony so that there can be an adjustment for this influence.

Sailors use clocks to discover the longitude of where they are in the ocean. Finding a sufficiently accurate clock was how 18th and 19th century sailors eventually were able to locate themselves when they could not see land. At sea at night, the numerical angle of the North Star above the horizon is their latitude. Without a clock, they had no way to determine their longitude except by dead reckoning, which is very error-prone. A pendulum clock does not work well when the sea is not smooth. If they had an accurate mechanical clock with them that wasn’t affected by choppy seas, they could use it to find their longitude. First, before setting sail they would synchronize it with the standard clock at zero degrees longitude. Out on the ocean or on some island, this clock would tell them the time back at zero degrees longitude. Then at sea on a particular day, the sailors could wait until the Sun was at its highest point and know the local time is 12 noon. If at that moment their clock read 0900 (that is, 9:00 A.M.), then they would know their clock is off by 3 hours from the time at zero degrees longitude. Because Earth turns on its axis 360 degrees of longitude every day and 15 degrees every hour, the sailors could compute that they were 3 x 15 degrees west of zero degrees, namely at 45 degrees west longitude. Knowing both their latitude and longitude, they could use a map to locate themselves. The first reasonably reliable mechanical clock that could be used for measuring longitude at sea was invented by British clockmaker John Harrison in 1727. It was accurate to one second a month. When mariners adopted similarly accurate mechanical clocks, the number of ships per year that crashed into rocks plummeted.

24. What Is Our Standard Clock or Master Clock?

Our civilization’s standard clock or master clock is the clock that other clocks are synchronized with. It reports ‘the correct time’ because humanity agrees that it does. This standard clock is a designated cesium atomic clock in Paris France. Your cell phone synchronizes its internal clock with this standard clock about once a week.

More specifically, the standard clock reports the proper time for the Royal Observatory Greenwich in London, England which sits at zero degrees longitude (the prime meridian), even though the report is created in a laboratory near Paris. The report is the result of a computational average of reports supplied from a network of many designated atomic clocks situated around the globe.

a. How Does an Atomic Clock Work?

First, a one-paragraph answer to this question. Then a much more detailed answer and explanation.

An atomic clock is a very regular clock that measures the time taken for a fixed number of jumps by electrons between energy levels in atoms. There are many kinds of atomic clocks, but the one adopted worldwide in 1964 for Coordinated Universal Time relied on the very regular behavior of the cesium-133 atom. What is regular is the frequency of the microwave radiation needed for a maser pointed at cesium atoms in a vacuum chamber in order get the cesium to radiate with a specific color—that is, to resonate.  The oscillation of the wave in the maser is analogous to the swing of a pendulum.

Resonance occurs when the cesium isotope’s atoms are stimulated by a special incoming microwave frequency. If the stimulation is not at the proper frequency, the cesium will radiate very little compared to what it can radiate if properly stimulated. The stimulation causes the outer electron to transition from a low-energy ground state to a next higher-energy ground state and then to fall back down again while emitting the same microwave frequency that caused it to bump up in the first place. The oscillation or “waving” of this incoming and outgoing radiation from the maser is the ticking of the clock. Counting those ticks tells us the time. A count of 9,192,631,770 is defined to be one second. Nobody sits there and counts the waves flying by them, but the engineering details of counting them for the time interval from event A to event B are not relevant to any philosophical issues.

Pendulum clocks work by counting swings of the pendulum. Quartz clocks work by counting the shakes of a small piece of quartz crystal set in motion when voltage is applied to it. Astronomical clocks count rotations of the Earth. Atomic clocks work by producing a wave process such as a microwave, and counting a specific number of those waves that pass by a single point in space, then declaring that the time taken is one second on the clock.

The key idea for all objects that deserve to be called “clocks” is that they can be relied upon to produce nearly the same, fixed number of ticks per second. Call that number n. So, for every occurrence of n oscillations, the clock reports that a second has passed. For every 60n oscillations, it reports a minute has passed. For every 60(60n) oscillations it reports an hour, and so forth. The frequency (or, equivalently, the number of oscillations per second) is the clock’s rate of ticking. If the frequency doesn’t drift very much, it is called a “stable” frequency. The more stable the better. The reason why all the above clocks work as clocks is that they can produce relative stable frequencies compared to that of the rest of the universe’s processes such as a president’s heartbeat or the dripping from a goatskin water bag.

The advantage of using an atomic clock that relies on a specific isotope is that (1) for any isotope, all its atoms behave exactly alike, unlike any two quartz crystals or any two rotations of the Earth, (2) the atomic clock’s ticking is very regular compared to any non-atomic clock, (3) it ticks at a very fast rate (high frequency) so it is useful for measurements of events having a very brief duration, (4) the clock can easily be copied and constructed elsewhere, (5) the clock is not easily perturbed,  and (6) there is no deep mystery about why it is a better master clock than other candidates for a master clock.

An atomic clock’s stable frequency is very easy to detect because the isotope “fluoresces” or “shines” or “resonates” in a characteristic, easily-detectable narrow band of frequencies. That is, its frequency distribution has a very, very narrow central peak that clearly differs from the peaks of radiation that can be produced by electron transitions between all other energy levels in the the same atom. It is these transitions from one energy level to another that emit light and produce the resonating. No radioactivity is involved in an atomic clock.

In 1879, James Clerk Maxwell was the first person to suggest using the frequency of atomic radiation as a kind of invariant natural pendulum. This remark showed great foresight, and it was made before the rest of the physics community had yet accepted the existence of atoms. Vibrations in atomic radiation are the most stable periodic events that scientists in the 21^st century have been able to use for clock building.

A cesium atomic clock was adopted in 1967 as the world’s standard clock, and it remains the standard in the 2020s. At the convention, physicists agreed that when 9,192,631,770 cycles of microwave radiation in the clock’s special, characteristic process are counted, then the atomic clock should report that a duration of one atomic second has occurred.

What is this mysterious “special, characteristic process” in cesium clocks that is so stable? This question is answered assuming every cesium atom behaves according to the Bohr model of atoms. The model is easy to visualize, but it provides a less accurate description than does a description in terms of quantum theory. However, quantum theory is more difficult to understand, so mention of it is minimized in this article.

Every atom of a single isotope behaves just like any other, unlike two manufactured pendulums or event two rotations of the Earth. It is not that every atom of an isotope is in the same position or has the same energy or the same velocity, but rather that, besides those properties, they are all alike. Cesium is special because it is the most chemically reactive material in the world, so builders of atomic clocks must be careful to keep  its cesium away from all other kinds of atoms.

An atom’s electrons normally stay in orbit and don’t fly away, nor do they crash into the nucleus. Electrons stay in their orbits until perturbed, and each orbit has a characteristic energy level, a specific value of its energy for any electron in that orbit. When stimulated by incoming electromagnetic radiation, such as from a laser, the electrons can absorb the incoming radiation and transition to higher, more energetic orbits. Which orbit the electron moves to depends  on the energy of the incoming radiation that it absorbs. Higher orbits are orbits are more distant from the nucleus. Also, an electron orbiting in a higher, more energetic orbit is said to be excited because it might emit some radiation spontaneously and transition into one of the lower orbits. There are an infinite number of energy levels and orbits, but they do not differ continuously. They differ by discrete steps. The various energies that can be absorbed and emitted are unique to each isotope of each element. Examining the various frequencies of the emitted radiation of an object gives sufficient information to identify which isotope and element is present. Ditto for the signature of the absorption frequencies. Famously, finding the signature for helium in sunlight was the first evidence that there was helium in the Sun.

A cesium atom’s outer electron shell contains only a single electron, making it chemically reactive to incoming microwave radiation. To take advantage of this feature in a cesium atomic clock, an outer electron in its lowest-energy orbit around the cesium-133 nucleus is targeted by some incoming microwave radiation from the atomic clock’s laser. Doing so makes the electron transition to a higher energy orbit around the cesium nucleus, thus putting the electron into an “excited” state. Properly choosing the frequency of the incoming radiation that hits the target cesium (called successfully “tuning” the laser) can control which orbit the electron transitions to. Tuning the laser is a matter of controlling the laser’s frequency with a feedback loop that keeps it generating the desired, stable frequency. Initially, the cesium is heated to produce a vapor or gas, then the cesium atoms are cooled as a group to reduce their kinetic energy, and then they are magnetically filtered to select only the atoms whose outer electrons are in the lowest possible energy state.

Our Bohr model supposes, following a suggestion from Einstein, that any electromagnetic wave such as a light wave or a microwave or a radio wave can just as well be considered to be composed of small, discrete particle-like objects called photons. The photon’s energy is directly correlated with the wave’s frequency—higher energy photons correspond to higher frequency waves. If a photon of exactly the right energy from the laser arrives and hits a cesium atom’s electron, the electron can totally absorb the photon by taking all its energy and making the electron transition up to a higher energy level. Energy is conserved during absorption and emission.

Later, the electron in a higher, excited state might spontaneously fall back down to one of the various lower energy levels, while emitting a photon of some specific frequency. The value of that frequency is determined by the energy difference in the two energy levelsof the transition. If it is still in an excited state, the (or an) electron might spontaneously fall again to an even lower energy level, and perhaps cascade all the way down to the lowest possible energy level. There is an infinite number of energy levels of any atom, so potentially there is an infinite number of frequencies of photons that can be absorbed and an infinite number of frequencies of photons that can be emitted in the transitions. There are an infinite number, but not just any number, because the frequencies or energies differ in small, discrete steps from each other.

If the electron in a specific energy level were hit with a sufficiently energetic incoming photon, the electron would fly away from the atom altogether, leaving the atom ionized.

For any atom of any isotope of any element with its outer electron in its lowest ground state, there is a characteristic, unique energy value for that state, and there is a characteristic minimum energy for an incoming photon to be able to knock the outer electron up to the very next higher level and no higher, and this is the same energy or frequency that is emitted when that higher-level electron spontaneously transitions back to the lowest level. This ground state behavior of transitioning to the next higher level and back down again is the key behavior of an atom that is exploited in the operation of an atomic clock.

In a cesium atomic clock using the isotope ¹³³Cs, its cesium gas is cooled and manipulated so that nearly all its atoms are in their unexcited, lowest ground state. This manipulation uses the fact that atoms in the two different states have different magnetic properties so they can be separated magnetically. Then the laser’s frequency is tuned until the laser is able to knock the outer electrons from their ground state up to the next higher energy state (but no higher) so that the excited electrons then transition back down spontaneously to the ground level and produce radiation of exactly the same frequency as that of the laser. That is, the target cesium shines or fluoresces with the same frequency it was bombarded with. When this easily-detectable fluorescence occurs, the counting can begin, and the clock can measure elapsed time.

While the definition of a second has stayed the same since 1967, the technology of atomic clocks has not. Scientists in 2020s can make an atomic clock so precise that it would take 30 billion years to drift by a single second. The cesium atomic clock of 1967 drifted quite a bit more. That is why the world’s 1967 time-standard using cesium atomic clocks is likely to be revised in the 21st century.

For more details on how an atomic clock works, see (Gibbs, 2002).

b. How Do We Find and Report the Standard Time?

If we were standing next to the standard clock, we could find the standard time by looking at its display of the time. Almost all countries use a standard time report that is called Coordinated Universal Time. Other names for it are UTC, and Zulu Time. It once was named Greenwich Mean Time (GMT). Some countries prefer their own, different name.

How we find out what time it is when we are not next to the standard click is quite complicated. First, ignoring the problems of time dilation and the relativity of simultaneity raised by Einstein’s theory of relativity that are discussed above, let’s consider the details of how standard time is reported around the world for the vast majority of countries. The international standard time that gets reported is called U.T.C. time, for the initials of the French name for Coordinated Universal Time. The report of U.T.C. time is based on computations and revisions made from the time reports of the Atomic Time (A.T.) of many cesium clocks in many countries.

U.T.C. time is, by agreement, the time at zero degrees longitude. This longitude is an imaginary great circle that runs through the North Pole and South Pole and a certain astronomical observatory in London England, although the report itself is produced near Paris France. This U.T.C. time is used by the Internet and by the aviation industry throughout the world. Different geographical regions of the world have their own time due to the world’s being divided into time zones, approximately by the region’s longitude. Usually a time zone differs by one hour from its neighboring zone.

U.T.C. time is produced from T.A.I. time by adding or subtracting some appropriate integral number of leap years and leap seconds, with leap years added every four years and leap seconds added as needed. T.A.I. time is computed from a variety of reports received of A.T. time (Atomic Time), the time of our standard, conventionally-designated cesium-based atomic clocks. All A.T. times are reported in units called S.I. seconds. A.T. time produces T.A.I. time which produces U.T.C. time.

An S.I. second (that is, a Système International second or a second of Le Système International d’Unités) is defined to be the numerical measure of the time it takes for the motionless (motionless relative to the Greenwich-London observatory), designated, master cesium atomic clock to emit exactly 9,192,631,770 cycles of radiation. The number “9,192,631,770” was chosen rather than some other number by vote at an international convention for the purpose of making the new second be as close as scientists could come to the duration of what was called a “second” back in 1957 when the initial measurements were made on cesium-133 using the best solar-based clocks available then.

The T.A.I. scale from which U.T.C. time is computed is the average of the reports of A.T. time from about 200 designated cesium atomic clocks that are distributed around the world in about fifty selected laboratories, all reporting to Paris. One of those laboratories is the National Institute of Standards and Technology (NIST) in Boulder, Colorado, U.S.A. The calculated average time of the 200 reports is the T.A.I. time, the abbreviation of the French phrase for International Atomic Time. The International Bureau of Weights and Measures (BIPM) near Paris performs the averaging about once a month. If your designated laboratory in the T.A.I. system had sent in your clock’s reading for a certain specified event that occurred in the previous month, then in the present month the BIPM calculates the average answer for all the 200 reported clock readings and sends you a notice of how inaccurate your report was from the average, so you can reset your clock, that is, make adjustments to your atomic clock and hopefully have it be in better agreement with next month’s average for the 200. Time physicists are following the lead over time of their designated clocks because there is nothing better to follow.

A.T. time, T.A.I. time, and U.T.C. time are not kinds of physical time but rather are kinds of reports of physical time.

In the 17th century, Christiaan Huygens recommend dividing a solar day into 24 hours per day and 60 minutes per hour and 60 seconds per minute, making a second be 1/86,400 of a solar day. This is called Universal Time 1 or UT1. This is rotational time. Subsequently, the second was redefined by saying there are 31,556,925.9747 seconds in the tropical year 1900. At the 13th General Conference on Weights and Measures in 1967, the definition of a second was changed again to a specific number of periods of radiation produced by a standard cesium atomic clock (actually, the average of 200 standard atomic clocks). This second is the so-called standard second or the S.I. second. It is defined to be the duration of 9,192,631,770 periods (cycles, oscillations, vibrations) of a certain kind of microwave radiation absorbed in the standard cesium atomic clock. More specifically, the second is defined to be the duration of exactly 9,192,631,770 periods of the microwave radiation required to produce the maximum fluorescence of a small gas cloud of cesium-133 atoms as the single outer-shell electron in these atoms transitions between two specific energy levels of the atom. This is the internationally agreed-upon unit for atomic time in the T.A.I. system. In 1967 the atomic clocks were accurate to one second every 300 years. The accuracy of atomic clocks subsequently have gotten very much better.

All metrologists expect there to be an eventual change in the standard clock by appeal to higher frequency clocks.  The higher ticking rate is important for many reasons, one of which is that the more precise the clock that is used the better physicists can test the time-translation invariance of the fundamental laws of physics, such as checking whether the supposed constants of nature do in fact stay constant over time.

Leap years (with their leap days) are needed as adjustments to the standard clock’s count in order to account for the fact that the number of the Earth’s rotations per Earth revolution does not stay constant from year to year. The Earth is spinning slower every day, but not uniformly. Without an adjustment, the time called “midnight” eventually would drift into the daylight. Leap years are added every four years. The effect on the period is not practically predictable, so, when the irregularity occurs, a leap second is introduced or removed as needed whenever the standard atomic clock gets behind or ahead of the old astronomical clock (Universal Coordinated Time UTC) by more than 0.9 seconds.

The meter depends on the second, so time measurement is more basic than space measurement. It does not follow from this, though, that time itself is more basic than space. In 1983, scientists agreed that the meter is how far light travels in 1/299,792,458 seconds in a vacuum. This conventional number is chosen for four reasons: (i) Choosing the number 299,792,458 made the new meter be very close to the old meter that was once defined to be the distance between two specific marks on a platinum bar kept in the Paris Observatory. (ii) light propagation is very stable or regular; its speed is either constant, or when not constant we know how to compensate for the influence of the medium; (iii) a light wave’s frequency can be made extremely stable (that is, little drift); and (iv) distance cannot be measured more accurately in other ways; using the platinum bar in Paris is a less accurate means of measuring distance.

Time can be measured more accurately and precisely than distance, voltage, temperature, mass, or anything else.

So why bother to improve atomic clocks? The duration of the second can already be measured to 14 or 15 decimal places, a precision 1,000 times that of any other fundamental unit. One reason to do better is that the second is increasingly the fundamental unit. Three of the six other basic units—the meter, lumen and ampere—are defined in terms of the second. (Gibbs, 2002)

One philosophical implication of the standard definition of the second and of the meter is that they fix the numerical value of the speed of light in a vacuum in all inertial frames. The speed is exactly 299,792,458 meters per second. There can no longer be any direct measurement to check whether that is how fast light really moves; it is defined to be moving that fast. Any measurement that produced a different value for the speed of light is presumed to have an error. The error would be in accounting for the influence of gravitation and acceleration, or in its assumption that the light was moving in a vacuum. This initial presumption of where the error lies comes from a deep reliance by scientists on Einstein’s general theory of relativity. However, if it were eventually decided by the community of scientists that the speed of light should not have been fixed as it was, then the scientists would call for a new world convention to re-define the second or the meter.

25. Why Are Some Standard Clocks Better than Others?

Other clocks ideally are calibrated by being synchronized to “the” standard clock, our master clock. It is normally assumed that the standard clock is the most reliable and regular clock. Physicists have chosen the currently-accepted standard clock for two reasons: (1) they believe it will tick very regularly in the sense that all periods between adjacent ticks are sufficiently congruent—they have the same duration. (2) There is no better choice of a standard clock. Choosing a standard clock that is based on the beats of a president’s heart would be a poor choice because clocks everywhere would suddenly and mysteriously get out of synchrony with the standard clock (the heartbeats) when the president goes jogging.

So, some choices of standard clock are better than others. Some philosophers of time believe one choice is better than another because the best choice is closest to a clock that tells what time it really is. Most philosophers of time argue that there is no access to what time it really is except by first having selected the standard clock.

Let’s consider the various goals we want to achieve in choosing one standard clock rather than another. One goal is to choose a clock with a precise tick rate that does not drift very much. That is, we want a clock that has a very regular period—so the durations between ticks are congruent. On many occasions throughout history, scientists have detected that their currently-chosen standard clock seemed to be drifting. In about 1700, scientists discovered that the duration from one day to the next, as determined by the duration between sunrises, varied throughout the year. They did not notice any variation in the duration of a year, so they began to rely on the duration of the year rather than the day.

As more was learned about astronomy, the definition of the second was changed. In the 19th century and before the 1950s, the standard clock was defined astronomically in terms of the mean rotation of the Earth upon its axis (solar time). For a short period in the 1950s and 1960s, the standard clock was defined in terms of the revolution of the Earth about the Sun (ephemeris time), and the second was defined to be 1/86,400 of the mean solar day, which is the average throughout the year of the rotational period of the Earth with respect to the Sun. But all these clocks were soon discovered to drift too much.

To solve these drift problems, physicists chose a certain kind of atomic clock as the standard, and they said it reported atomic time. All atomic clocks measure time in terms of the natural resonant frequencies of electromagnetic radiation absorbed and emitted from the electrons within certain atoms of the clock. The accurate dates of adoption of these standard clocks are omitted in this section because different international organizations adopted different standards in different years. The U.S.A.’s National Institute of Standards and Technology’s F-1 atomic fountain clock is so accurate that it drifts by less than one second every 30 million years. We know there is this drift because it is implied by the laws of physics, not because we have a better clock that measures this drift.

Atomic clocks use the frequency of a specific atomic transition as an extremely stable time standard. While the second is currently defined by caesium-based clocks that operate at microwave frequencies, physicists have built much more accurate clocks that are based on light. These optical clocks tick at much higher frequencies than microwave clocks and can keep time that is accurate to about one part in 10¹⁸, which is about 100 times better than the best caesium clocks.

The international metrology community aims to replace the microwave time standard with an optical clock, but first must choose from one of several clock designs being developed worldwide”—Hamish Johnston, Physics World, 26 March 2021 .

Optical atomic clocks resonate at light frequencies rather than microwave frequencies, and this is why they tick about 100,000 faster than the microwave atomic clocks.

To achieve the goal of restricting drift, and thus stabilizing the clock, any clock chosen to become the standard clock should be maximally isolated from outside effects. A practical goal in selecting a standard clock is to find a clock that can be well insulated from environmental impacts such as convection currents in the Earth’s molten core, comets impacting the Earth, earthquakes, stray electric fields, heavy trucks driving on nearby bumpy roads, the invasion of dust and rust into the clock, extraneous heat, variation in gravitational force, and adulteration of the clock’s gas (for example, the cesium) with other stray elements.

If not insulation, then compensation. If there is some theoretically predictable effect of an environmental influence upon the standard clock, then the clock can be regularly adjusted to compensate for this effect. For example, thanks to knowing the general theory of relativity, we know how to adjust for the difference in gravitational force between being at sea level and being a meter above sea level. Commenting on the insulation problem, Nobel Prize winner Frank Wilczek said that the basic laws of the universe are local, so:

Thankfully, you don’t have to worry about the distant universe, what happened in the past, or what will happen in the future…and it is philosophically important to notice that it is unnecessary to take into account what people,  or hypothetical superhuman beings, are thinking. Our experience with delicate, ultra-precise experiments puts severe pressure on the idea that minds can act directly on matter, through will. There’s an excellent opportunity here for magicians to cast spells, for someone with extrasensory powers to show their stuff, or for an ambitious experimenter to earn everlasting glory by demonstrating the power of prayer or wishful thinking. Even very small effects could be detected. but nobody has ever done this successfully.” Fundamentals: Ten Keys to Reality.

Consider the insulation problem we would have if we were to replace the atomic clock as our standard clock and use instead the mean yearly motion of the Earth around the Sun. Can we compensate for all the relevant disturbing effects on the motion of the Earth around the Sun? Not easily nor precisely. The principal problem is that the Earth’s rate of spin varies in a practically unpredictable manner. This affects the behavior of the solar clock, but not the atomic clock.

Our civilization’s earlier-chosen standard clock once depended on the Earth’s rotations and revolutions, but this Earth-Sun clock is now known to have lost more than three hours in the last 2,000 years. Leap years and leap seconds are added or subtracted occasionally to the standard atomic clock in order to keep our atomic-based calendar in synchrony with the rotations and revolutions of the Earth. We do this because we want to keep atomic-noons occurring on astronomical-noons and ultimately because we want to prevent Northern hemisphere winters from occurring in some future July. These changes do not affect the duration of a second, but they do affect the duration of a year because not all years last the same number of seconds. In this way, we compensate for the Earth-Sun clocks falling out of synchrony with our standard atomic clock.

Another desirable feature of a standard clock is that reproductions of it stay in synchrony with each other when environmental conditions are the same. Otherwise, we may be limited to relying on a specifically-located standard clock that can not be trusted elsewhere and that can be broken, vandalized or stolen.

The principal goal in selecting a standard clock is to reduce mystery in physics. The point is to find a clock process that, if adopted as our standard, makes the resulting system of physical laws simpler and more useful, and allows us to explain phenomena that otherwise would be mysterious. Choosing an atomic clock as standard is much better for this purpose than choosing the periodic revolution of the Earth about the Sun. If scientists were to have retained the Earth-Sun astronomical clock as the standard clock and were to say that by definition the Earth does not slow down in any rotation or in any revolution, then when a comet collides with Earth, tempting the scientists to say the Earth’s period of rotation and revolution changed, the scientists instead would be forced not to say this but to alter, among many other things, their atomic theory and to say the frequency of light emitted from cesium atoms mysteriously increases all over the universe when comets collide with the Earth. By switching to the cesium atomic standard, these alterations are unnecessary, and the mystery vanishes.

To make this point a little more simply, suppose the President’s heartbeats were chosen as our standard clock and so the count of heartbeats always showed the correct time. It would become a mystery why pendulums (and cesium radiation in atomic clocks) changed their frequency whenever the President went jogging, and scientists would have to postulate some new causal influence that joggers have on pendulums and atomic clocks across the globe.

To achieve the goal of choosing a standard clock that maximally reduces mystery, we want the clock’s readings to be consistent with the accepted laws of motion, in the following sense. Newton’s first law of motion says that a body in motion should continue to cover the same distance during the same time interval unless acted upon by an external force. If we used our standard clock to run a series of tests of the time intervals as a body coasted along a carefully measured path, and we found that the law was violated and we could not account for this mysterious violation by finding external forces to blame and we were sure that there was no problem otherwise with Newton’s law or with the measurement of the length of the path, then the problem would be with the clock. Leonhard Euler (1707-1783) was the first person to suggest this consistency requirement on our choice of a standard clock. A similar argument holds today but with using the laws of motion from Einstein’s general theory of relativity, one of the two fundamental theories of physics.

When we want to know how long a basketball game lasts, why do we subtract the start time from the end time? The answer is that we accept a metric for duration in which we subtract the two time numbers. Why do not we choose another metric and, let’s say, subtract the square root of the start time from the square root of the end time? This question is implicitly asking whether our choice of metric can be incorrect or merely inconvenient.

When we choose a standard clock, we are choosing a metric. By agreeing to read the clock so that a duration from 3:00 to 5:00 is 5-3 hours, and so 2 hours, we are making a choice about how to compare two durations in order to decide whether they are equal, that is, congruent. We suppose the duration from 3:00 to 5:00 as shown by yesterday’s reading of the standard clock was the same as the duration from 3:00 to 5:00 on the readings from two days ago and will be the same for today’s readings and tomorrow’s readings.

Philosophers of time continue to dispute the extent to which the choice of metric is conventional rather than objective in the sense of being forced on us by nature. The objectivist says the choice is forced and that the success of the standard atomic clock over the standard solar clock shows that we were more accurate in our choice of the standard clock. An objectivist says it is just as forced on us as our choosing to say the Earth is round rather than flat. It would be ridiculous to insist the Earth is flat. Taking the conventional side on this issue, Adolf Grünbaum argued that time is metrically amorphous. It has no intrinsic metric. Instead, we choose the metric we do in order only to achieve the goals of reducing mystery in science, but satisfying those goals is no sign of being correct.

The conventionalist, as opposed to the objectivist, would say that if we were to require by convention that the instant at which Jesus was born and the instant at which Abraham Lincoln was assassinated are to be only 24 seconds apart, whereas the duration between Lincoln’s assassination and his burial is to be 24 billion seconds, then we could not be mistaken. It is up to us as a civilization to say what is correct when we first create our conventions about measuring duration. We can consistently assign any numerical time coordinates we wish, subject only to the condition that the assignment properly reflects the betweenness relations of the events that occur at those instants. That is, if event J (birth of Jesus) occurs before event L (Lincoln’s assassination) and this, in turn, occurs before event B (burial of Lincoln), then the time assigned to J must be numerically less than the time assigned to L, and both must be less than the time assigned to B so that t(J) < t(L) < t(B). A simple requirement. Yes, but the implication is that this relationship among J, L, and B must hold for events simultaneous with J, and for all events simultaneous with K, and so forth.

It is other features of nature that lead us to reject the above convention about 24 seconds and 24 billion seconds. What features? There are many periodic processes in nature that have a special relationship to each other; their periods are very nearly constant multiples of each other, and this constant stays the same over a long time. For example, the period of the rotation of the Earth is a fairly constant multiple of the period of the revolution of the Earth around the Sun, and both these periods are a constant multiple of the periods of a swinging pendulum and of vibrations of quartz crystals. The class of these periodic processes is very large, so the world will be easier to describe if we choose our standard clock from one of these periodic processes. A good convention for what is regular will make it easier for scientists to find simple laws of nature and to explain what causes other events to be irregular. It is the search for regularity and simplicity and removal of mystery that leads us to adopt the conventions we do for the numerical time coordinate assignments and thus leads us to choose the standard clock we do choose. Objectivists disagree and say this search for regularity and simplicity and removal of mystery is all fine, but it is directing us toward the correct metric, not simply the useful metric.

For additional discussion of some of the points made in this section, including the issue of how to distinguish an accurate clock from an inaccurate one, see chapter 8 of (Carnap 1966).

26. What Is a Field?

The technical word “field” means something that extends throughout space and that exerts a force on various things it encounters. The most familiar field is the temperature field for a single time; it is displayed on the screen during a weather report. It shows the temperature at each place represented on the map such as 70 degrees Fahrenheit now in New York, and 71 degrees now in Washington, DC. The field is a special kind of extended object having three or more dimensions with each place having a value for some physical variable—temperature in this example.

Suppose your system of interest is a room instead of the cosmos, and you wish to understand sound in the room. This means you want to know about its air density field. Sound waves in the room are oscillations of this field due to changing air density in different places at different times.

Unlike a temperature field or an air density field, some fields always have directions at their points. A wind field has a speed and a direction at each place. A magnetic field has a strength and a direction at each place.

What is the advantage of treating the world in terms of fields? Here is a brief answer. In any field theory with the property called “locality,” any change in a field’s value at a place can directly induce changes only in infinitesimally-nearby places. Think of points in the field as interacting only with their nearest neighbors, which in turn interact with their own neighbors, and so forth. So, field theory with locality has the advantage that, if you want to know what will happen next at a place, you do not have to consider the influence of everything everywhere in the universe but only the field values at the place of interest and the rates of change of those values. Computing the effect of a change can be much simpler this way.

In Newton’s mechanics, two distant objects act on each other directly and instantaneously. In contemporary mechanics, the two distant objects act on each other only indirectly via the field between them. However, Newton’s theory of gravity without fields is sometimes more practical to use because gravitational forces get weaker with distance, and the gravitational influence of all the distant particles can be ignored for some practical purposes.

The universe at a time is approximately a system of particles in spacetime, but, more fundamentally, the best, educated guess of physicists is that it is a system of co-existing quantized fields acting on the vacuum or being the vacuum. We know this is so for all non-gravitational phenomena, but do not have a definitive theory of the gravitational field that involves quantum phenomena. In the early years of using the concept of fields, the fields were considered something added to systems of particles, but the modern viewpoint (influenced by quantum mechanics) is that particles themselves are only local vibrations or excitations of fields; the particles are the vibrations that are fairly stable in the sense of persisting (for the particle’s lifetime) and not occupying a large spatial region as the field itself does.

The classical concept of there being a particle at a point does not quite hold in quantum field theory. The key ontological idea is that the particles supervene on the fields. Particles are epiphenomena. Also, the particles of quantum fields do not change their values continuously as do particles in classical fields. A particle in a quantum field is able to change its energy only in discrete jumps.

The concept of a field originated with Pierre-Simon Laplace in about 1800. He suggested Newton’s theory of gravity could be treated as being a field theory. In Laplace’s field theory of gravity, the notion of action at a distance was eliminated. Newton would have been happy with this idea of a field because he always doubted that gravity worked by one object’s mass acting directly on another distant object instantaneously. In a letter to Richard Bentley, he said:

It is inconceivable that inanimate brute matter should, without the intervention of something else which is not material, operate upon and affect other matter, and have an effect upon it, without mutual contact.

Michael Faraday was the first physicist to assert that fields in this sense are real, not just mathematical artifacts.

Instantaneous actions were removed from the treatment of electricity and magnetism by Maxwell in the 1860s when he created his theory of electromagnetism as a field theory. Changes in electromagnetic forces were propagated, not instantaneously, but at the speed c of light. Instantaneous actions were eventually removed from gravitational theory in Einstein’s general theory of relativity of 1915. It was Einstein who first claimed that spacetime itself is the field associated with gravity. According to Einstein,

As the Earth moves, the direction of its gravitational pull does not change instantly throughout the universe. Rather, it changes right where the Earth is located, and then the field at that point tugs on the field nearby, which tugs on the field a little farther away, and so on in a wave moving outward at the speed of light. (Carroll 2019, p. 249)

Gravitational force, according to Einstein’s theory, is not really a force in the usual sense of the term, but is the curvature of spacetime.

Depending upon the field, a field’s value at a point in space might be a simple number (as in the Higgs field), or a vector (as in the classical electromagnetic field), or a tensor (as in Einstein’s gravitational potential field), or even a matrix. Fields obey laws, and these laws usually are systems of partial differential equations that hold at each point.

As mentioned briefly above, with the rise of quantum field theory, instead of a particle being treated as a definite-size object within spacetime it is treated as a special kind of disturbance of the field itself, a little “hill” or deviation above its average value nearby. For example, an electron is a localized disturbance in the electromagnetic field. The anti-electron is a localized disturbance in the same field, and so is a photon. The disturbance is a fuzzy bundle of quantized energy occupying a region of space bigger than a single point, but having a maximum at a place that would classically have been called the “particle’s location.” A particle is a little hill in the field. These hills can be stationary or moving. The hills can pass by each other or pass through other hills or bounce off them, depending on the kinds of hills. Moving hills carry information and energy from one place to another. New energy inputted into the field can increase the size of the hill, but only in discrete sizes. Any hill has a next bigger possible size (or energy).

So, the manifest image of a particle cannot easily be reconciled with the quantum mechanical image of a particle. Although fields, not particles, are ontologically basic, it does not follow from this that particles are not real. They are real but odd because they are emergent and epiphenomenal entities having no sharply defined diameter and not being able to change their sizes gradually. Although an electron does have a greater probability of being detected more at some places than at others, in any single detection at a single time the electron is detected only at a point, not a region. The electron is a disturbance that spreads throughout space, although the high-amplitude parts are in a very small region.  Despite its having no sharp boundary, the electron is physically basic in the sense that it has no sub-structure particle. The proton is not basic because it is made of quarks and gluons. Particles with no sub-structure are called elementary particles.

Relativity theory’s biggest ontological impact is that whether a particle is present depends on the observer. An accelerating observer might observe (that is, detect) particles being present in a specific region while a non-accelerating observer can see no particles there. For a single region of spacetime, there can be particles in the region in one reference frame and no particles in that region for another frame, yet both frames are correct descriptions of reality!

One unusual feature of quantum mechanics is the Heisenberg Uncertainty Principle. It implies that any object, such as an electron, has complementary features. For example, it has values for its position and for the rate of change of its position, but the values are complementary in the sense that the more precisely one value is measured the less precisely the other value can be measured. Fields are objects, too, and so Heisenberg’s Uncertainty Principle applies also to fields. Fields have complementary features. The more certain you are of the value of a field at one location in space, the less certain you can be of its rate of change at that location. Thus the word “uncertainty” in the name Heisenberg Uncertainty Principle.

There are many basic quantum fields that exist together. There are four fundamental matter fields, two of which are the electron field and the quark field. There are five fundamental force-carrying fields, such as the electromagnetic field and the Higgs field. All physicists believe there are more, as yet unknown, fields, such as a dark matter field, a dark energy field, and a quantum-gravity field.

Fields often interact with other fields. The electron has the property of having an electric charge. What this means in quantum field theory is that the property of having a certain electric charge is a short description of how the electron field interacts with the electromagnetic field. The electromagnetic field interacts with the electron field whenever an energetic photon transitions into an electron and a positron (that is, an anti-electron). What it is for an electron to have a mass is that the electron field interacts with the Higgs field. Physicists presuppose that two fields can interact with each other only when they are at the same point. If this presupposition were not true, our world would be a very spooky place.

According to quantum field theory, once one of these basic fields comes into existence it does not disappear; the field exists everywhere from then on. Magnets create magnetic fields, but if you were to remove all the magnets, there would still be a magnetic field, although it would be at its minimum strength. Sources of fields are not essential for the existence of fields.

Because of the Heisenberg Uncertainty Principle, even when a field’s value is the lowest possible (called the vacuum state or unexcited state) in a region, there is always a non-zero probability that its value will spontaneously deviate from that value in the region. The most common way this happens is via virtual-pair production. This occurs when a particle and its anti-particle spontaneously come into existence in the region, then rapidly annihilate each other in a small burst of energy. You can think of space in its smallest regions as being a churning sea, a sea of pairs of these particles and their anti-particles that are continually coming into existence and then rapidly being annihilated. These virtual particles are certain compact quantum vacuum fluctuations. So, even if all universe’s fields were to be at their lowest state, empty space always would have some activity and energy. This energy of the vacuum state is inaccessible to us; we can never use it to do work. Nevertheless, the energy of these virtual particles does contribute to the energy density of so-called “empty space.” The claim has been carefully verified experimentally.

This story or description of virtual particles is helpful but can be misleading when it is interpreted as suggesting that something is created from nothing in violation of energy conservation. However, it is correct to draw the conclusion from the story that the empty space of physics is not the metaphysician’s nothingness. So, there is no region of empty space where there could be empty time or changeless time in the sense meant by a Leibnizian relationist.

Because all these fields are quantum fields, their disturbances or excitations can occur only in quantized chunks, namely integer multiples of some baseline energy, the so-called zero-point energy, which is the lowest possible positive energy. It is these chunks, called “quanta,” that make the theory be a quantum theory.

Although fields that exist cannot go out of existence, they can wake up from their slumbers and turn on. Soon after the Big Bang, the Higgs field, which had a value of zero everywhere, began to increase in value as the universe started cooling. When the universe’s temperature fell below a certain critical value, the field grew spontaneously. From then on, any particle that interacted with the Higgs field acquired a mass. Before that, all particles were massless. The more a particle interacts with the Higgs field, the heavier it is. The photon does not interact at all with the Higgs field. The neutrino interacts the least.

What is the relationship between spacetime and all these fields? Are the fields in space or, as Einstein once asked, are they properties of space, or is there a different relationship? Some physicists believe the gravitational field does reside within spacetime, but others believe it does not.

Many physicists believe that the universe is not composed of many fields; it is composed of a single field, the quantum field, which has a character such that it appears as if it is composed of various different fields. This one field is the vacuum, and all particles are really just fluctuations in the vacuum.

There is also serious speculation that fields are not the ontologically basic entities; information is the universe’s basic entity.

For an elementary introduction to quantum fields, see the video https://www.youtube.com/watch?v=X5rAGfjPSWE.

Back to the main “Time” article for references.

 

Author Information

Bradley Dowden
Email: dowden@csus.edu
California State University Sacramento
U. S. A.