Jerry A. Fodor (1935—2017)
 Jerry Fodor was one of the most important philosophers of mind of the late twentieth and early twenty-first centuries. In addition to exerting an enormous influence on virtually all parts of the literature in the philosophy of mind since 1960, Fodor’s work had a significant impact on the development of the cognitive sciences. In the 1960s, along with Hilary Putnam, Noam Chomsky, and others, Fodor presented influential criticisms of the behaviorism that dominated much philosophy and psychology at the time. Fodor went on to articulate and defend an alternative conception of intentional states and their content that he argues vindicates the core elements of folk psychology within a physicalist framework.
Jerry Fodor was one of the most important philosophers of mind of the late twentieth and early twenty-first centuries. In addition to exerting an enormous influence on virtually all parts of the literature in the philosophy of mind since 1960, Fodor’s work had a significant impact on the development of the cognitive sciences. In the 1960s, along with Hilary Putnam, Noam Chomsky, and others, Fodor presented influential criticisms of the behaviorism that dominated much philosophy and psychology at the time. Fodor went on to articulate and defend an alternative conception of intentional states and their content that he argues vindicates the core elements of folk psychology within a physicalist framework.
Fodor developed two theories that have been particularly influential across disciplinary boundaries. He defended a “Representational Theory of Mind,” according to which thinking is a computational process defined over mental representations that are physically realized in the brain. On Fodor’s view, these mental representations are internally structured much like sentences in a natural language, in that they have both a syntax and a compositional semantics. Fodor also defends an influential hypothesis about mental architecture, namely, that low-level sensory systems (and language) are “modular,” in the sense that they’re “informationally encapsulated” from the higher-level “central” systems responsible for belief formation, decision-making, and the like. Fodor’s work on modularity has been especially influential among evolutionary psychologists, who go much further than Fodor in claiming that the systems underlying even high-level cognition are modular, a view that Fodor himself vehemently resists.
Fodor has defended a number of other well-known views. He was an early proponent of the claim that mental states are functional states, defined by their role in a cognitive system and not by the physical material that constitutes them. Alongside functionalism, Fodor articulated an early and influential version of non-reductive physicalism, according to which mental states are realized by, but not reducible to, physical states of the brain. Fodor was also a staunch defender of nativism about the structure and contents of the human mind, arguing against a variety of empiricist theories and famously arguing that all lexical concepts are innate. Fodor vigorously argued against all versions of conceptual role semantics in philosophy and psychology, and articulated an alternative view he calls “informational atomism,” according to which lexical concepts are unstructured “atoms” that have their content in virtue of standing in certain external, “informational” relations to entities in the environment.
Table of Contents
- Biography
- Physicalism, Functionalism, and the Special
Sciences
- Intentional Realism
- The Representational Theory of Mind
- Content and Concepts
- Nativism
- Modularity
- References and Further Reading
1. Biography
Jerry Fodor was born in New York City on April 22, 1935. He received his A.B. degree from Columbia University in 1956 and his Ph.D. from Princeton University in 1960. His first academic position was at MIT, where he taught in the Departments of Philosophy and Psychology until 1986. He was Distinguished Professor at CUNY Graduate Center from 1986 to 1988, when he moved to Rutgers University, where he was State of New Jersey Professor of Philosophy and Cognitive Science until his retirement in 2016. Fodor died on November 29, 2017.
2. Physicalism, Functionalism, and the
Special Sciences
Throughout his career Fodor endorsed physicalism, the claim that all the genuine particulars and properties in the world are either identical to or in some sense determined by and dependent upon physical particulars and properties. Although there are contested questions about how physicalism should be formulated and understood (Melnyk 2003, Stoljar 2010), there is nevertheless widespread acceptance of some or other version of physicalism among philosophers of mind. To accept physicalism is to deny that psychological and other non-basic properties of the world “float free” from fundamental physical properties. Accepting physicalism thus goes hand in hand with rejecting mind-body dualism.
Some of Fodor’s early work (1968, 1975) aimed (i) to show that “mentalism” was a genuine alternative to dualism and behaviorism, (ii) to show that behaviorism had a number of serious shortcomings, (iii) to defend functionalism as the appropriate physicalist metaphysics underlying mentalism, and (iv) to defend a conception of psychology and other special sciences according to which higher-level laws and the properties that figure in them are irreducible to lower-level laws and properties. Let’s consider each of these in turn.
For much of the twentieth century, behaviorism was widely regarded as the only viable physicalist alternative to dualism. Fodor helped to change that, in part by drawing a clear distinction between mere mentalism, which posits the existence of internal, causally efficacious mental states, and dualism, which is mentalism plus the view that mental states are states of a non-physical substance. Here’s Fodor in his classic book Psychological Explanation:
[P]hilosophers who have wanted to banish the ghost from the machine have usually sought to do so by showing that truths about behavior can sometimes, and in some sense, logically implicate truths about mental states. In so doing, they have rather strongly suggested that the exorcism can be carried through only if such a logical connection can be made out. … [O]nce it has been made clear that the choice between dualism and behaviorism is not exhaustive, a major motivation for the defense of behaviorism is removed: we are not required to be behaviorists simply in order to avoid being dualists (1968, pp. 58-59).
Fodor thus argues that there’s a middle road between dualism and behaviorism. Attributing mental states to organisms in explaining how they get around in and manipulate their environments need not involve the postulation of a mental substance different in kind from physical bodies and brains. In Fodor’s view, behaviorists influenced by Wittgenstein and Ryle ignored the distinction between mentalism and dualism. As Fodor puts it, “confusing mentalism with dualism is the original sin of the Wittgensteinian tradition” (1975, p. 4).
In addition to clearly distinguishing mentalism from dualism, Fodor put forward a number of trenchant objections to behaviorism and the various arguments for it. He argued that neither knowing about the mental states of others nor learning a language with mental terms requires that there be a logical connection between mental and behavioral terms, thus undermining a number of epistemological and linguistic arguments for behaviorism (Fodor and Chihara 1965, Fodor 1968). Perhaps more importantly, Fodor argued that empirical theories in cognitive psychology and linguistics provide a powerful argument against behaviorism, since they posit the existence of various mental states that are not definable in terms of overt behavior (Fodor 1968, 1975). Along with the arguments of Putnam (1963, 1967) and Chomsky (1959), among others, Fodor’s early arguments against behaviorism were an important step in the development of the then emerging cognitive sciences.
Central to this development was the rise of functionalism as a genuine alternative to behaviorism, and Fodor’s Psychological Explanation (1968) was one of the first in-depth treatments and defenses of this view (see also Putnam 1963, 1967). Unlike behaviorism, which attempts to explain behavior in terms of law-like relationships between stimulus inputs and behavioral outputs, functionalism explains behavior in terms of internal properties that mediate between inputs and outputs. Indeed, the main claim of functionalism is that mental properties are individuated in terms of the various causal relations they enter into, where such relations are not restricted to mere input-output relations, but also include their relations to a host of other properties that figure in the relevant empirical theories. Although, at the time, the distinctions between various forms of functionalism weren’t as clear as they are now, Fodor’s brand of functionalism is a version of what is now known as “psycho-functionalism”. On this view, the causal roles that define mental properties are provided by empirical psychology, and not, say, the platitudes of commonsense psychology, or the analyticities expressive of the meanings of mental terms; see Rey (1997, ch.7) and Shoemaker (2003) for discussion.
By defining mental properties in terms of their causal roles, functionalists allow that the same mental property can be instantiated by different kinds of physical systems. Functionalism thus goes hand in hand with the multiple realizability of mental properties. If a given mental property, M, is a functional property that’s defined by a specific causal condition, C, then any number of distinct physical properties, P1, P2, P3… Pn, may each “realize” M in virtue of meeting condition C. Functionalism thereby characterizes mental properties at a level of abstraction that ignores differences in the physical structure of the systems that have these properties. Early functionalists, like Fodor and Putnam, thus took themselves to be articulating a position that was distinct not only from behaviorism, but also from type-identity theory, which identifies mental properties with neurophysiological properties of the brain. If functionalism implies that mental properties can be realized by different physical properties in different kinds of systems (or the same system over time), then functionalism apparently precludes identifying mental properties with physical properties.
Fodor, in particular, articulated his functionalism so that it was seen to have sweeping consequences for debates concerning reductionism and the unity of science. In his seminal essay “Special Sciences” (1974), and also in the introductory chapter of his classic book The Language of Thought (1975), Fodor spells out a metaphysical picture of the special sciences that eventually came to be called “non-reductive physicalism”. This picture is physicalist in that it accepts what Fodor calls the “generality of physics,” which is the claim that every event that falls under a special science predicate also falls under a physical predicate, but not vice versa. It’s non-reductionist in that it denies that “the special sciences should reduce to physical theories in the long run” (1974, p. 97). Traditionally, reductionists sought to articulate bridge laws that link special science predicates with physical predicates, either in the form of bi-conditionals or identity statements. Fodor argues not only that the generality of physics does not require the existence of bridge laws, but that such laws will in general be unavailable given that the events picked out by special science predicates will be “wildly disjunctive” from the perspective of physics (1974, p. 103). Multiple realizability thus guarantees that special science predicates will cross-classify phenomena picked out by physical predicates. This, in turn, undermines the reductionist hope of a unified science whereby the higher-level theories of the special sciences reduce to lower-level theories and ultimately to fundamental physics. On Fodor’s picture, then, the special sciences are “autonomous” in that they articulate irreducible generalizations that quantify over irreducible and casually efficacious higher-level properties (1974, 1975; see also 1998b, ch.2).
Functionalism and non-reductive physicalism are now commonplace in philosophy of mind, and provide the backdrop for many contemporary debates about psychological explanation, laws, multiple realizability, mental causation, and more. This is something for which Fodor surely deserves much of the credit (or blame, depending on one’s view; see Kim 2005 and Heil 2003 for criticisms of the metaphysical underpinnings of non-reductive physicalism).
3. Intentional Realism
A central aim of Fodor’s work is to defend the core elements of folk psychology as at least the starting point for a serious scientific psychology. At a minimum, folk psychology is committed to two kinds of states: belief-like states, which represent the world and guide one’s behavior, and desire-like states, which represent one’s goals and motivate behavior. We routinely appeal to such states in our common-sense explanations of people’s behavior. For example, we explain why John went to the store in terms of his desire for milk and his belief that there’s milk for sale at the store. Fodor is impressed by the remarkable predictive power of such belief-desire explanations. The following passage is typical:
Common sense psychology works so well it disappears. It’s like those mythical Rolls Royce cars whose engines are sealed when they leave the factory; only it’s better because they aren’t mythical. Someone I don’t know phones me at my office in New York from—as it might be—Arizona. ‘Would you like to lecture here next Tuesday?’ are the words he utters. ‘Yes thank you. I’ll be at your airport on the 3 p.m. flight’ are the words that I reply. That’s all that happens, but it’s more than enough; the rest of the burden of predicting behavior—of bridging the gap between utterances and actions—is routinely taken up by the theory. And the theory works so well that several days later (or weeks later, or months later, or years later; you can vary the example to taste) and several thousand miles away, there I am at the airport and there he is to meet me. Or if I don’t turn up, it’s less likely that the theory failed than that something went wrong with the airline. … The theory from which we get this extraordinary predictive power is just good old common sense belief/desire psychology. … If we could do that well with predicting the weather, no one would ever get his feet wet; and yet the etiology of the weather must surely be child’s play compared with the causes of behavior. (1987, pp. 3-4)
Passages like this may suggest that Fodor’s intentional realism is wedded to the folk-psychological categories of “belief” and “desire”. But this isn’t so. Rather, Fodor’s claim is that there are certain core elements of folk psychology that will be shared by a mature scientific psychology. In particular, Fodor’s view is that a mature psychology will posit states with the following features:@
(1) They will be intentional: they will be “about” things and they will be semantically evaluable. (John’s belief that there’s milk at the store is about the milk at the store, and can be semantically evaluated as true or false.)
(2) They will be causal: they will figure in genuine causal explanations and laws. (John’s belief that there’s milk at the store and his desire for milk figure in a law-like causal explanation of John’s behavior.)
Fodor’s intentional realism thus doesn’t require that folk-psychological categories themselves find a place in a mature psychology. Indeed, Fodor has suggested that the individuation conditions for beliefs are “so vague and pragmatic” that they may not be fit for empirical psychology (1990, p. 175). What Fodor is committed to is the claim that a mature psychology will be intentional through and through, and that the intentional states it posits will be causally implicated in law-like explanations of human behavior. Exactly which intentional states will figure in a mature psychology is a matter to be decided by empirical inquiry, not by a priori reflection on our common sense understanding.
Fodor’s defense of intentional realism is usefully viewed as part of a rationalist tradition that stresses the human mind’s striking ability to think about indefinitely many arbitrary properties of the world. Our minds are apparently sensitive not only to abstract properties such as being a democracy and being virtuous, but also to abstract grammatical properties such as being a noun phrase and being a verb phrase, as well as to such arbitrary properties as being a tiny folded piece of paper, being an oddly-shaped canteen, being a crumpled shirt, and being to the left of my favorite mug. On Fodor’s (1986) view, a system can selectively respond to such non-sensory properties (or properties that are not “transducer detectable”) only if it’s an intentional system capable of manipulating representations of these properties. More specifically, Fodor claims that the distinguishing feature of intentional systems is that they’re sensitive to “non-nomic” properties, that is, properties of objects that do not determine that they fall under laws of nature. Consider Fodor’s (1986) example being a crumpled shirt. Although laws of nature govern crumpled shirts, no object is subsumed under a law in virtue of being a crumpled shirt. Nevertheless, the property of being a crumpled shirt is one that we can represent an object as having, and such representations do enter into laws. For instance, there’s presumably a law-like relationship between my noticing the crumpled shirt, my desire to remark upon it, and my saying “there’s a crumpled shirt”. On Fodor’s view, the job of intentional psychology is to articulate laws governing mental representations that figure in genuine causal explanations of people’s behavior (Fodor 1987, 1998a).
Although positing mental representations that have semantic and causal properties—states that satisfy (1) and (2) above—may not seem particularly controversial, the existence of causally efficacious intentional states has been denied by all manner of behaviorists, epiphenomenalists, Wittgensteinians, interpretationists, instrumentalists, and (at least some) connectionists. Much of Fodor’s work is devoted to defending intentional realism against such views as they have arisen in both philosophy and psychology. In addition to defending intentional realism against the behaviorism of Skinner and Ryle (Fodor 1968, 1975, Fodor et al. 1974), Fodor defends it against the threat of epiphenomenalism (Fodor 1989), against Wittgenstein and other defenders of the “private language argument” (Fodor and Chihara 1965, Fodor 1975), against the eliminativism of the Churchlands (Fodor 1987, 1990), against the instrumentalism of Dennett (Fodor 1981a, Fodor and Lepore 1992), against the interpretationism of Davidson (Fodor 1990, Fodor and Lepore 1992, Fodor 2004), and against certain versions of connectionism (Fodor and Pylyshyn 1988, Fodor 1998b, chs. 9 and 10).
4. The Representational Theory of Mind
For physicalists, accepting that there are mental states that are both intentional and causal raises the question of how such states can exist in a physical world. Intentional realists must explain, for instance, how lawful relations between intentional states can be understood physicalistically. Of particular concern is the fact that at least some intentional laws describe rational relations between the states they quantify over, and, at least since Descartes, philosophers have worried about how a purely physical system could be rational (see Lowe 2008 for skepticism from a non-Cartesian dualist). Fodor’s Representational Theory of Mind (RTM) is his attempt to answer such worries.
As Fodor points out, RTM is “really a loose confederation of theses” that “lacks, to put it mildly, a canonical formulation” (1998a, p. 6). At its core, though, RTM is an attempt to combine Alan Turing’s work on computation with intentional realism (as outlined above). Broadly speaking, RTM claims that mental processes are computational processes, and that intentional states are relations to mental representations that serve as the domain of such processes. On Fodor’s version of RTM, these mental representations have both syntactic structure and a compositional semantics. Thinking thus takes place in an internal language of thought.
Turing demonstrated how to construct a purely mechanical device that could transform syntactically–individuated symbols in a way that respects the semantic relations that exist between the meanings, or contents, of the symbols. Formally valid inferences are the paradigm. For instance, modus ponens can be realized on a machine that’s sensitive only to syntactic properties of symbols. The device thus doesn’t have “access” to the symbols’ semantic properties, but can nevertheless transform the symbols in a truth-preserving way. What’s interesting about this, from Fodor’s perspective, is that mental processes also involve chains of thoughts that are truth-preserving. As Fodor puts it:
[I]f you start out with a true thought, and you proceed to do some thinking, it is very often the case that the thoughts that thinking leads you to will also be true. This is, in my view, the most important fact we know about minds; no doubt it’s why God bothered to give us any. (1994, p. 9)
In order to account for this “most important” fact, RTM claims that thoughts themselves are syntactically-structured representations, and that mental processes are computational processes defined over them. Given that the syntax of a representation is what determines its causal role in thought, RTM thereby serves to connect the fact that mental processes are truth-preserving with the fact that they’re causal. On Fodor’s view, “this bringing of logic and logical syntax together with a theory of mental processes is the foundation of our cognitive science” (2008, p. 21).
Suppose a thinker believes that if John ran, then Mary swam. According to RTM, for a thinker to hold such a belief is for the thinker to stand in a certain computational relation to a mental representation that means if John ran, then Mary swam. Now suppose the thinker comes to believe that John ran, and as a result comes to believe that Mary swam. RTM has it that the causal relations between these thoughts hold in virtue of the syntactic form of the underlying mental representations. By picturing the mind as a “syntax-driven machine” (Fodor, 1987, p. 20), RTM thus promises to explain how the causal relations among thoughts can respect rational relations among their contents. It thereby provides a potentially promising reply to Descartes’ worry about how rationality could be exhibited by a mere machine. As Fodor puts it:
So we can now (maybe) explain how thinking could be both rational and mechanical. Thinking can be rational because syntactically specified operations can be truth preserving insofar as they reconstruct relations of logical form; thinking can be mechanical because Turing machines are machines. … [T]his really is a lovely idea and we should pause for a moment to admire it. Rationality is a normative property; that is, it’s one that a mental process ought to have. This is the first time that there has ever been a remotely plausible mechanical theory of the causal powers of a normative property. The first time ever. (2000, p. 19)
In Fodor’s view, it’s a major argument in favor of RTM that it promises an explanation of how mental processes can be truth-preserving, and a major strike against traditional empiricist and associationist theories that, in his view, they offer no plausible competing explanation (2000, pp. 15-18; 2003, pp. 90-94; Fodor and Pylyshyn 1998). (Note that Fodor does not think that RTM offers a satisfying explanation of all aspects of human rationality, as discussed below in the section on modularity.)
In addition to explaining how truth-preserving mental processes could be realized causally, Fodor argues, RTM provides the only hope of explaining the so-called “productivity” and “systematicity” of thought (Fodor 1987, 1998a, 2008). Roughly, productivity is the feature of our minds whereby there is no upper bound to the number of thoughts we can entertain. We can think that the dog is on the deck; that the dog, which chased the squirrel, is on the deck; that the dog, which chased the squirrel, which foraged for nuts, is on the deck; and so on, indefinitely.
Of course, there are thoughts whose contents are so long or complex that other factors prevent us from entertaining them. But abstracting away from such performance limitations, it seems that a theory of our conceptual competence must account for such productivity. Thought also appears to be systematic, in the following sense: a mind that is capable of entertaining a certain thought, p, is also capable of entertaining logical permutations of p. For example, minds that can entertain the thought that the book is to the left of the cup can also entertain the thought that the cup is to the left of the book. Although it’s perhaps possible that there could be minds that do not exhibit such systematicity—a possibility denied by some, for example, Evans (1982) and Peacocke (1992)—it at least appears to be an empirical fact that all minds do.
In Fodor’s view, RTM is the only theory of mind that can explain productivity and systematicity. According to RTM, mental states have internal, constituent structure, and the content of mental states is determined by the content of their constituents and how those constituents are put together. Given a finite base of primitive representations, our capacity to entertain endlessly many thoughts can be explained by positing a finite number of rules for combining representations, which can be applied endlessly many times in the course of constructing complex thoughts. RTM offers a similar explanation of systematicity. The reason that a mind that can entertain the thought that the book is to the left of the cup can also entertain the thought that the cup is to the left of the book is that these thoughts are built up out of the same constituents, using the same rules of combination. RTM thus explains productivity and systematicity because it claims that mental states are representations that have syntactic structure and a compositional semantics. One of Fodor’s main arguments against alternative, connectionist theories is that they fail to account for such features (Fodor and Pylyshyn 1988, Fodor 1998b, chs. 9 and 10).
A further argument Fodor offers in favor of RTM is that successful empirical theories of various non-demonstrative inferences presuppose a system of internal representations in which such inferences are carried out. For instance, standard theories of visual perception attempt to explain how a percept is constructed on the basis of the physical information available and the visual system’s built-in assumptions about the environment, or “natural constraints” (Pylyshyn 2003). Similarly, theories of sentence perception and comprehension require that the language system be able to represent distinct properties (for instance, acoustic, phonological, and syntactic properties) of a single utterance (Fodor et al. 1974). Both sorts of theories require that there be a system of representations capable of representing various properties and serving as the medium in which such inferences are carried out. Indeed, Fodor claims that the best argument in favor of RTM is that “some version or other of RTM underlies practically all current psychological research on mentation, and our best science is ipso facto our best estimate of what there is and what it’s made of” (Fodor 1987, p. 17). Fodor’s The Language of Thought (1975) is the locus classicus of this style of argument.
5. Content and Concepts
Suppose, as RTM suggests, that mental processes are computational processes, and that this explains how rational relations between thoughts can be realized by purely casual relations among symbols in the brain. This leaves open the question of how such symbols come to have their meaning, or content. At least since Brentano, philosophers have worried about how to integrate intentionality into the physical world, a worry that has famously led some to accept the “baselessness of intentional idioms and the emptiness of a science of intention” (Quine 1960, p. 221). Much of Fodor’s work from the 1980s onward was focused on this representational (as opposed to the computational) component of RTM. Although Fodor’s views changed in various ways over the years, some of which are documented below, a unifying theme throughout this work is that it’s at least possible to provide a naturalistic account of intentionality (Fodor 1987, 1990, 1991, 1994, 1998a, 2004, 2008; Fodor and Lepore 1992, 2002; Fodor and Pylyshyn 2014).
In the 1960s and early 1970s, Fodor endorsed a version of so-called “conceptual role semantics” (CRS), according to which the content of a representation is (partially) determined by the conceptual connections it bears to other representations. To take two hoary examples, CRS has it that “bachelor” gets its meaning, in part, by bearing an inferential connection to “unmarried,” and “kill” gets its meaning, in part, by bearing an inferential connection to “die”. Such inferential connections hold, on Fodor’s early view, because “bachelor” and “kill” have complex structure at the level at which they’re semantically interpreted—that is, they have the structure exhibited by the phrases “unmarried adult male” and “cause to die” (Katz and Fodor 1963). In terms of concepts, the claim is that the concept BACHELOR has the internal structure exhibited by ‘UNMARRIED ADULT MALE’, and the concept KILL has the internal structure exhibited by ‘CAUSE TO DIE’. (This article follows the convention of writing the names of concepts in capitals.)
However, Fodor soon came to think that there are serious objections to CRS. Some of these objections were based on his own experimental work in psycholinguistics, which he took to provide evidence against the existence of complex lexical structure. In particular, experimental evidence suggested that understanding a sentence does not involve recovering the (putative) decompositions of the lexical items it contains (Fodor et al. 1975, Fodor et al. 1980). For example, if “bachelor” has the semantic structure exhibited by “unmarried adult male,” then there is an implicit negation in the sentence “If practically all the men in the room are bachelors, then few men in the room have spouses.” But the evidence suggested that it’s easier to understand that sentence than similar sentences containing either an explicit negative (“not married”) or a morphological negative (“unmarried”), as in “If practically all the men in the room are not married/unmarried, then few men in the room have spouses”. This shouldn’t be the case, Fodor reasoned, if “bachelor” includes the negation at the level at which it is semantically interpreted (Fodor et al. 1975, Fodor et al. 1980). (For alternative explanations see Jackendoff (1983, pp. 125-127; 1992, p. 49; 2002, ch. 11), Katz (1977, 1981) and Miller and Johnson-Laird (1976, p. 328).)
In part because of the evidence against decompositional structure, Fodor at one point seriously considered the view that inferential connections among lexical items hold in virtue of inference rules, or “meaning postulates,” which renders CRS consistent with a denial of the claim that lexical items are semantically structured (1975, pp. 148-152). However, Fodor ultimately became convinced that Quine’s doctrine of “confirmation holism” undermines the appeal to meaning postulates, and more generally, any view that implies a principled distinction between those conceptual connections that are “constitutive” of a concept and those that are “merely collateral”. According to confirmation holism, our beliefs don’t have implications for experience when taken in isolation. As Quine famously puts it, “our statements about the external world face the tribunal of sense experience not individually but only as a corporate body” (1953, p. 41). This implies that disconfirming a belief is never simply a matter of testing it against experience. For one could continue to hold a belief in the face of recalcitrant data by revising other beliefs that form part of one’s overall theory. As Quine says, “any statement can be held true come what may, if we make drastic enough adjustments elsewhere in the system” (1953, p. 43). Such Quinean considerations motivate Fodor’s claim that CRS theorists should not appeal to meaning postulates:
Exactly because meaning postulates break the ‘formal’ relation between belonging to the structure of a concept and being among its constitutive inferences, it’s unclear why it matters … whether a given inference is treated as meaning-constitutive. Imagine two minds that differ in that ‘whale → mammal’ is a meaning postulate for one but is ‘general knowledge’ for the other. Are any further differences between these minds entailed? If so, which ones? Is this wheel attached to anything at all? It’s a point that Quine made against Carnap that the answer to ‘When is an inference analytic?’ can’t be just ‘Whenever I feel like saying that it is’. (1998a, p. 111)
Moreover, confirmation holism suggests that the epistemic properties of a concept are potentially connected to the epistemic properties of every other concept, which, according to Fodor, suggests that CRS inevitably leads to semantic holism, the claim that all of a concept’s inferential connections are constitutive. But Fodor argues that semantic holism is unacceptable, since it’s incompatible with the claim that concepts are shareable: “since practically everybody has some eccentric beliefs about practically everything, holism has it that nobody shares any concepts with anybody else” (2004, p. 35; see also Fodor and Lepore 1992, Fodor 1998a). This implication would undermine the possibility of genuine intentional generalizations, which require that type-identical contents are shared across both individuals and different time-slices of the same individual. (Fodor rejects appeals to a weaker notion of “content similarity”; see Fodor and Lepore 1992, pp. 17-22; Fodor 1998a, pp. 28-34.)
Proponents of CRS might reply to these concerns about semantic holism by accepting the ‘molecularist’ claim that only some inferential connections are concept-constitutive. But Fodor suggests that the only way to distinguish the constitutive connections from the rest is to endorse an analytic/synthetic distinction, which, again, confirmation holism gives us reason to reject (for example, 1990, p. x, 1998a, p. 71, 1998b, pp. 32-33, 2008). Fodor’s Quinean point, ultimately, is that theorists should be reluctant to claim that there are certain beliefs people must hold, or inferences they must accept, in order to possess a concept. For thinkers can apparently have any number of arbitrarily strange beliefs involving some concept, consistent with them sharing that concept with others. As Fodor puts it:
[P]eople can have radically false theories and really crazy views, consonant with our understanding perfectly well, thank you, which false views they have and what radically crazy things it is that they believe. Berkeley thought that chairs are mental, for Heaven’s sake! Which are we to say he lacked, the concept MENTAL or the concept CHAIR? (1987, p. 125) (For further reflections along similar lines, see Williamson 2007.)
On Fodor’s view, proponents of CRS are faced with two equally unsatisfying options: they can agree with Quine about the analytic/synthetic distinction, but at the cost of endorsing semantic holism and its unpalatable consequences for the viability of intentionality psychology; or they can deny holism and accept molecularism but at the cost of endorsing an analytic/synthetic distinction, which Fodor thinks nobody knows how to draw.
It bears emphasis that Fodor doesn’t claim that confirmation holism, all by itself, rules out the existence of certain “local” semantic connections that hold as a matter of empirical fact. Indeed, contemporary discussions of possible explanatory roles for analyticity involve delicate psychological and linguistic considerations that are far removed from the epistemological considerations that motivated the positivists. For instance, there are the standard convergences in people’s semantic-cum-conceptual intuitions, which cry out for an empirical explanation. Although some argue that such convergences are best explained by positing analyticities (Grice and Strawson 1956, Rey 2005, Rives 2016), Fodor argues that all such intuitions can be accounted for by an appeal to Quinean “centrality” or “one-criterion” concepts (Fodor 1998a, pp. 80-86). Considerations in linguistics that bear on the existence of an empirically grounded analytic/synthetic distinction include the syntactic and semantic analyses of ‘causative’ verbs, the ‘generativity’ of the lexicon, and the acquisition of certain elements of syntax. Fodor has engaged linguists on a number of such fronts, arguing against proposals of Jackendoff (1992), Pustejovsky (1995), Pinker (1989), Hale and Keyser (1993), and others, defending the Quinean line (see Fodor 1998a, pp. 49-56, and Fodor and Lepore 2002, chs. 5-6; see Pustejovsky 1998 and Hale and Keyser 1999 for rejoinders). Fodor’s view is that all of the relevant empirical facts about minds and language can be explained without any analytic connections, but merely deeply believed ones, precisely as Quine argued.
On Fodor’s view, the problems plaguing CRS ultimately arise as a result of its attempt to connect a theory of meaning with certain epistemic conditions of thinkers. A further argument against such views, Fodor claims, is that such epistemic conditions violate the compositionality constraint that is required for an explanation of productivity and systematicity (see above). For instance, if one believes that brown cows are dangerous, then the concept BROWN COW will license the inference ‘BROWN COW → DANGEROUS’; but this inference is not determined by the inferential roles of BROWN and COW, which it ought to be if meaning-constituting inferences are compositional (Fodor and Lepore 2002, ch.1; for discussion and criticism, see, for example, Block 1993, Boghossian 1993, and Rey 1993).
Another epistemic approach, favored by many psychologists, takes concepts to have “prototype” structure. According to these theories, the structure of a lexical concept specifies the prototypical features of its instances, that is, the features that its instances tend to (but need not) have (Rosch and Mervis 1975). Prototype theories are epistemic accounts because, on these views, having a concept is a matter of knowing the features of its prototypical instances. Given this, Fodor argues that prototype theories are also in danger of violating compositionality. For example, knowing what prototypical pets (dogs) are like and what prototypical fish (trout) are like does not guarantee that you know what prototypical pet fish (goldfish) are like (Fodor 1998a, pp. 102-108, Fodor and Lepore 2002, ch. 2). Since compositionality is required in order to explain the productivity and systematicity of thought, and prototype structures do not compose, it follows that concepts don’t have prototype structure. Fodor (1998b, ch. 4) extends this kind of argument to epistemic accounts that posit so-called “recognitional concepts,” that is, concepts that are individuated by certain recognitional capacities. (For discussion and criticism, see, for example, Horgan 1998, Recanati 2002, and Prinz 2002.)
Fodor thus rejects all theories that individuate concepts in terms of their epistemic properties and their internal structure, and ultimately defends what he calls “informational atomism,” according to which lexical concepts are unstructured atoms whose content is determined by certain informational relations they bear to phenomena in the environment. In claiming that lexical concepts are internally unstructured, Fodor’s informational atomism is meant to respect the evidence and arguments against decomposition, definitions, prototypes, and the like. In claiming that none of the epistemic properties of concepts are constitutive, Fodor is endorsing what he sees as the only alternative to molecularist and holistic theories of content, neither of which, as we’ve seen, he takes to be viable. By separating epistemology from semantics in this way, Fodor’s theory places virtually no constraints on what a thinker must believe or infer in order to possess a particular concept. For instance, what determines whether a mind possesses DOG isn’t whether it has certain beliefs about dogs, but rather whether it possess an internal symbol that stands in the appropriate mind-world relation to the property of being a dog. Rather than talking about concepts as they figure in beliefs, inferences, or other mental states, Fodor instead talks of mere “tokenings” of concepts, where for him these are internal symbols that need not play any specific role in cognition. In his view, this is the only way for a theory of concepts to respect Quinean strictures on analyticity and constitutive conceptual connections. Indeed, Fodor claims that by denying that “the grasp of any interconceptual relations is constitutive of concept possession,” informational atomism allows us to “see why Quine was right about there not being an analytic/synthetic distinction” (Fodor 1998a, p. 71).
Fodor’s most explicit characterization of the mind-world relation that determines content is his “asymmetry dependency” theory (1987, 1990). According to this theory, the concept DOG means dog because dogs cause tokenings of DOG, and non-dogs causing tokenings of DOG is asymmetrically dependent upon dogs causing DOG. In other words, non-dogs wouldn’t cause tokenings of DOG unless dogs cause tokenings of DOG, but not vice versa. This is Fodor’s attempt to meet Brentano’s challenge of providing a naturalistic sufficient condition for a symbol to have a meaning. Not surprisingly, many objections have been raised to Fodor’s asymmetric dependency theory; for an overview see Loewer and Rey 1991.
It’s important to see that in rejecting epistemic accounts of concepts Fodor is not claiming that epistemic properties are irrelevant from the perspective of a theory of concepts. For such properties are what sustain the laws that “lock” concepts onto phenomena in the environment. For instance, it is only because thinkers know a range of facts about dogs—what they look like, that they bark, and so forth—that the concept DOG is lawfully connected to dogs. Knowledge of such facts thus plays a causal role in fixing the content of DOG. But on Fodor’s view, this knowledge doesn’t play a constitutive role. While such epistemic properties mediate the connection between tokens of DOG and dogs, this a mere “engineering” fact about us, which has no implications for the metaphysics of concepts or concept possession (1998a, p. 78). As Fodor puts it, “it’s that your mental structures contrive to resonate to doghood, not how your mental structures contrive to resonate to doghood, that is constitutive of concept possession” (1998a, p. 76). Although the internal relations that DOG bears to other concepts and to percepts are what mediate the connection between DOG and dogs, on Fodor’s view such relations do not determine the content of DOG.
Fodor’s theory is a version of semantic externalism, according to which the meaning of a concept is exhausted by its reference. There are two well-known problems with any such referentialist theory: Frege cases, which putatively show that concepts that have different meanings can nevertheless be referentially identical; and Twin cases, which putatively show that concepts that are referentially distinct can nevertheless have the same meaning. Together, Frege cases and Twin cases suggest that meaning and reference are independent in both directions. Fodor has had much to say about each kind of case, and his views on both have changed over the years.
If conceptual content is exhausted by reference, then two concepts with the same referent ought to be identical in content. As Fodor says, “if meaning is information, then coreferential representations must be synonyms” (1998a, p. 12). But, prima facie, this is false. For as Frege pointed out, it’s easy to generate substitution failures involving coreferential concepts: “John believes that Hesperus is beautiful” may be true while “John believes that Phosphorus is beautiful” is false; “Thales believes that there’s water in the cup” may be true while “Thales believes that there’s H2O in the cup” is false; and so on. Since it’s widely believed that substitution tests are tests for synonymy, such cases suggest that coreferential concepts aren’t synonyms. In light of this, Fregeans introduce a layer of meaning in addition to reference that allows for a semantic distinction between coreferential but distinct concepts. On their view, coreferential concepts are distinct because they have different senses, or “modes of presentation” of a referent, which Fregeans typically individuate in terms of conceptual role (Peacocke 1992).
In one of Fodor’s important early articles on the topic, “Methodological Solipsism Considered as a Research Strategy in Cognitive Psychology” (1980), he argued that psychological explanations depend upon opaque taxonomies of mental states, and that we must distinguish the content of coreferential terms for the purposes of psychological explanation. At that time Fodor thus allowed for a kind of content that’s determined by the internal roles of symbols, which he speculated might be “reconstructed as aspects of form, at least insofar as appeals to content figure in accounts of the mental causation of behavior” (1980, p. 240). However, once he adopted a purely externalist semantics (Fodor 1994), Fodor could no longer allow for a notion of content determined by such internal relations. If conceptual content is exhausted by reference, as informational semantics has it, then there cannot be a semantic distinction between distinct but coreferential concepts.
In later work Fodor thus proposes to distinguish coreferential concepts purely syntactically, and defends the view that modes of presentation (MOPs) are the representational vehicles of thoughts (Fodor 1994, 1998a, 2008, Fodor and Pylyshyn 2014). Taking MOPs to be the syntactically-individuated vehicles of thought serves to connect the theory of concepts to RTM. As Fodor and Pylyshyn put it:
Frege just took for granted that, since coextensive thoughts (concepts) can be distinct, it must be difference in their intensions that distinguish them. But RTM, in whatever form, suggests another possibility: Thoughts and concepts are individuated by their extensions together with their vehicles. The concepts THE MORNING STAR and THE EVENING STAR are distinct because the corresponding mental representations are distinct. That must be so because the mental representation that expresses the concept THE MORNING STAR has a constituent that expresses the concept MORNING, but the mental representation that expresses the concept THE EVENING STAR does not. That’s why nobody can have the concept THE MORNING STAR who doesn’t have the concept MORNING and nobody can have the concept THE EVENING STAR who doesn’t have the concept EVENING. … The result of Frege’s missing this was a century during which philosophers, psychologists, and cognitive scientists in general spent wringing their hands about what meanings could possibly be. (2014, pp. 74-75)
An interesting consequence of this syntactic treatment is that people’s behavior in Frege cases can no longer be given an intentional explanation. Instead, such behavior is explained at the level of syntactically-individuated representations. If, as Fodor suggested in his earlier work (1981), psychological explanations standardly depend upon opaque taxonomies of mental states, then this treatment of Frege cases would threaten the need for intentional explanations in psychology. In an attempt to block this threat, Fodor (1994) argues that Frege cases are in fact quite rare, and can be understood as exceptions rather than counterexamples to psychological laws couched in terms of broad content. The viability of a view that combines a syntactic treatment of Frege cases with RTM has been the focus of a fair amount of literature; see Arjo 1997, Aydede 1998, Aydede and Robins 2001, Brook and Stainton 1997, Rives 2009, Segal 1997, and Schneider 2005.
Let us now turn to Fodor’s treatment of Twin cases. Putnam (1975) asks us to imagine a place, Twin Earth, which is just like earth except the stuff Twin Earthians pick out with the concept WATER is not H2O but some other chemical compound XYZ. Consider Oscar and Twin Oscar, who are both entertaining the thought THERE’S WATER IN THE GLASS. Since they’re physical duplicates, they’re type-identical with respect to everything mental inside their heads. However, Oscar’s thought is true just in case there’s H2O in the glass, whereas Twin Oscar’s thought is true just in case there’s XYZ in the glass. A purely externalist semantics thus seems to imply that Oscar and Twin Oscar’s WATER concepts are of distinct types, despite the fact that Oscar and Twin Oscar are type-identical with respect to everything mental inside their heads. Supposing that intentional laws are couched in terms of broad content, it would follow that Oscar’s and Twin Oscar’s water-directed behavior don’t fall under the same intentional laws.
Such consequences have seemed unacceptable to many, including Fodor, who in his book Psychosemantics (1987) argues that we need a notion of “narrow” content that allows us to account for the fact that Oscar’s and Twin-Oscar’s mental states will have the same causal powers despite differences in their environments. Fodor there defends a “mapping” notion of narrow content, inspired by David Kaplan’s work on demonstratives, according to which the narrow content of a concept is a function from contexts to broad contents (1987, ch. 2). The narrow content of Oscar’s and Twin Oscar’s concept WATER is thus a function that maps Oscar’s context onto the broad content H2O and Twin Oscar’s context onto the broad content XYZ. Such narrow content is shared because Oscar and Twin Oscar are computing the same function. It was Fodor’s hope that this notion of narrow content would allow him to respect the standard Twin-Earth intuitions, while at the same time claim that the intentional properties relevant for psychological explanation supervene on facts internal to thinkers.
However, in The Elm and the Expert (1994) Fodor gives up on the notion of narrow content altogether, and argues that intentional psychology need not worry about Twin cases. Such cases, Fodor claims, only show that it’s conceptually (not nomologically) possible that broad content doesn’t supervene on facts internal to thinkers. One thus cannot appeal to such cases to “argue against the nomological supervenience of broad content on computation since, as far as anybody knows … chemistry allows nothing that is as much like water as XYZ is supposed to be except water” (1994, p. 28). So since Putnam’s Twin Earth is nomologically impossible, and “empirical theories are responsible only to generalizations that hold in nomologically possible worlds,” Twin cases pose no threat to a broad content psychology (1994, p. 29). If it turned out that such cases did occur, then, according to Fodor, the generalizations missed by a broad content psychology would be purely accidental (1994, pp. 30-33). Fodor’s view is thus that Twin cases, like Frege cases, are fully compatible with an intentional psychology that posits only two dimensions to concepts: syntactically-individuated representations and broad contents. Much of Fodor’s work on concepts and content after The Elm and the Expert consisted of further articulation and defense of this view (Fodor 1998a, 2008, Fodor and Pylyshyn 2014).
6. Nativism
In The Language of Thought (1975), Fodor argued not only in favor of RTM but also in favor of the much more controversial view that all lexical concepts are innate. Fodor’s argument starts with the noncontroversial claim that in order to learn a concept one must learn its meaning, or content. But Fodor argues that any such account requires that learnable concepts have meanings that are semantically complex. For instance, if the meaning of BACHELOR is unmarried adult male, then a thinker can learn BACHELOR by confirming the hypothesis that it applies to things that are unmarried adult males. Of course, in order to formulate this hypothesis one must already possess the concepts UNMARRIED, ADULT, and MALE. Standard models of concept learning thus do not apply to primitive concepts that lack internal structure. For instance, one cannot formulate the hypothesis that red things fall under RED unless one already has RED, for the concept RED is a constituent of that very hypothesis. Therefore, primitive concepts like RED cannot be learned, that is, they must be innate. If, as Fodor argues, all lexical concepts are primitive, then it follows that all lexical concepts are innate (1975, ch. 2).
It bears emphasis that Fodor’s claim is not that experience plays no role in the acquisition of lexical concepts. Experience must play a role on any account of concept acquisition, just as it does on any account of language acquisition. Rather, Fodor’s claim is that lexical concepts are not learned on the basis of experience but triggered by it. As Fodor puts it in his most well-known article on the topic, “The Present Status of the Innateness Controversy,” his nativist claim is that the relation between experience and concept acquisition is brute-causal, not rational or evidential:
Nativists and Empiricists disagree on the extent to which the acquisition of lexical concepts is a rational process. In respect of this disagreement, the traditional nomenclature of “Rationalism vs. Empiricism” could hardly be more misleading. It is the Empiricist view that the relation between a lexical concept and the experiences which occasion its acquisition is normally rational—in particular, that the normal relation is that such experiences bestow inductive warrant upon hypotheses which articulate the internal structure of the concepts. Whereas, it’s the Rationalist view that the normal relation between lexical concepts and their occasioning experiences is brute-causal, i.e. “merely” empirical: such experiences function as the innately specified triggers of the concepts which they—to borrow the ethological jargon—“release”. (1981b, pp. 279-280)
Most theories of concepts—such as conceptual role and prototype theories, discussed above—assume that many lexical concepts have some kind of internal structure. In fact, theorists are sometimes explicit that their motivation for positing complex lexical structure is to reduce the number of primitives in the lexicon. As Ray Jackendoff puts it:
Nearly everyone thinks that learning anything consists of constructing it from previously known parts, using previously known means of combination. If we trace the learning process back and ask where the previously known parts came from, and their previously know parts came from, eventually we have to arrive at a point where the most basic parts are not learned: they are given to the learner genetically, by virtue of the character of brain development. … Applying this view to lexical learning, we conclude that lexical concepts must have a compositional structure, and that the word learner’s [mind] is putting meanings together from smaller parts (2002, 334). (See also Levin and Pinker 1991, p. 4.)
It’s worth stressing that while those in the empiricist tradition typically assume that the primitives are sensory concepts, those who posit complex lexical structure need not commit themselves to any such empiricist claim. Rather, they may simply assume that very few lexical items not decomposable, and deal with the issue of primitives on a case by case basis, as Jackendoff (2002) does. In fact, many of the (apparent) primitives appealed to in the literature—for example, EVENT, THING, STATE, CAUSE, and so forth—are quite abstract and thus not ripe for an empiricist treatment. In any case, as we noted above, Fodor is led to adopt informational atomism, in part, because he is persuaded by the evidence that lexical concepts do not have any structure, decompositional or otherwise. He thus denies that appealing to lexical structure provides an adequate reply to his argument for concept nativism (Fodor 1981b, 1998a, 2008, Fodor and Lepore 2002).
In Concepts: Where Cognitive Science Went Wrong (1998a), Fodor worries about whether his earlier view is adequate. In particular, he’s concerned about whether it has the resources to explain questions such as why it is experiences with doorknobs that trigger the concept DOORKNOB:
[T]here’s a further constraint that whatever theory of concepts we settle on should satisfy: it must explain why there is so generally a content relation between the experience that eventuates in concept attainment and the concept that the experience eventuates in attaining. … [A]ssuming that primitive concepts are triggered, or that they’re ‘caught’, won’t account for their content relation to their causes; apparently only induction will. But primitive concepts can’t be induced; to suppose that they are is circular. (1998a, p. 132)
Fodor’s answer to this worry involves a metaphysical claim about the nature of the properties picked out by most of our lexical concepts. In particular, he claims that it’s constitutive of these properties that our minds “lock” to them as a result of experience with their prototypical (stereotypical) instances. As Fodor puts it, being a doorknob is just “being the kind of thing that our kinds of minds (do or would) lock to from experience with instances of the doorknob stereotype” (1998a, p. 137; see also 2008). By construing such properties as mind-dependent in this way, Fodor thus provides a metaphysical reply to his worry above: there need not be a cognitive or evidential relation between our experiences with doorknobs and our acquisition of DOORKNOB, for being a doorknob just is the property that our minds lock to as a result of experiencing stereotypical instances of doorknobs. Fodor sums up his view as follows:
[I]f the locking story about concept possession and the mind-dependence story about the metaphysics of doorknobhood are both true, then the kind of nativism about DOORKNOB that an informational atomist has to put up with is perhaps not one of concepts but of mechanisms. That consequence may be some consolation to otherwise disconsolate Empiricists. (1998a, p. 142)
In LOT 2: The Language of Thought Revisited (2008), Fodor extends his earlier discussions of concept nativism. Whereas his previous argument turned on the empirical claim that lexical concepts are internally unstructured, Fodor here says that this claim is “superfluous”: “What I should have said is that it’s true and a priori that the whole notion of concept learning is per se confused” (2008, p. 130). Consider a patently complex concept such as GREEN OR TRIANGULAR. Learning this concept would require confirming the hypothesis that the things that fall under it are either green or triangular. However, Fodor says:
[T]he inductive evaluation of that hypothesis itself requires (inter alia) bringing the property green or triangular before the mind as such. You can’t represent something as green or triangular unless you have the concepts GREEN, OR, and TRIANGULAR. Quite generally, you can’t represent anything as such and such unless you already have the concept such and such. … This conclusion is entirely general; it doesn’t matter whether the target concept is primitive (like GREEN) or complex (like GREEN OR TRIANGULAR). (2008, p. 139)
Fodor’s diagnosis of this problem is that standard learning models wrongly assume that acquiring a concept is a matter of acquiring beliefs. Instead, Fodor suggests that “beliefs are constructs out of concepts, not the other way around,” and that the failure to recognize this is what leads to the above circularity (2008, pp. 139-140; see also Fodor’s contribution to Piattelli-Palmarini, 1980).
Fodor’s story about concept nativism in LOT 2 runs as follows: although no concepts—not even complex ones—are learned, concept acquisition nevertheless involves inductive generalizations. We acquire concepts as a result of experiencing their prototypical instances, and learning a prototype is an inductive process. Of course, if concepts were prototypes then it would follow that concept acquisition would be an inductive process. But, as we saw above, Fodor claims that concepts can’t be prototypes since prototypes violate compositionality. Instead, Fodor suggests that learning a prototype is a stage in the acquisition of a concept. His picture thus looks like this (2008, p. 151):
Initial state → (P1) → stereotype/prototype formation → (P2) → locking (= concept attainment).
Why think that P1 is an inductive process? Fodor here appeals to “well-known empirical results suggesting that even very young infants are able to recognize and respond to statistical regularities in their environments,” and claims that “a genetically endowed capacity for statistical induction would make sense if stereotype formation is something that minds are frequently employed to do” (2008, p. 153). What renders this picture consistent with Fodor’s claim that “there can’t be any such thing as concept learning” (p. 139) is that he does not take P2 to be an inferential or intentional process (pp. 154-155). What kind of process is it? Here, Fodor doesn’t have much to say, other than it’s the “kind of thing that our sort of brain tissue just does”: “Psychology gets you from the initial state to P2; then neurology takes over and gets you the rest of the way to concept attainment” (p. 152). So, again, Fodor’s ultimate story about concept nativism is consistent with the view, as he puts it in Concepts, that “maybe there aren’t any innate ideas after all” (1998a, p. 143). Instead, there are innate mechanisms, which take us from the acquisition of prototypes to the acquisition of concepts.
7. Modularity
In his influential book, The Modularity of Mind (1983), Fodor argues that the mind contains a number of highly specialized, “modular” systems, whose operations are largely independent from each other and from the “central” system devoted to reasoning, belief fixation, decision making, and the like. In that book, Fodor was particularly interested in defending a modular view of perception against so-called “New Look” psychologists and philosophers (for example, Bruner, Kuhn, Goodman), who took cognition to be more or less continuous with perception. Whereas New Look theorists focused on evidence suggesting various top-down effects in perceptual processing (for example, ways in which what people believe and expect can affect what they see), Fodor was impressed by evidence from the other direction suggesting that perceptual processes lack access to such “background” information. Perceptual illusions provide a nice illustration. In the famous Müller-Lyer illusion (Figure 1), the top line looks longer than the bottom line even though they’re identical in length.
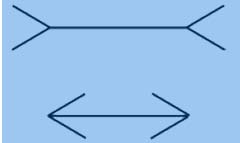 Figure 1. The Müller-Lyer
Figure 1. The Müller-Lyer
Illusion
As Fodor points out, if knowing that the two lines are identical in length does not change the fact that one looks longer than the other, then clearly perceptual processes don’t have access to all of the information available to the perceiver. Thus, there must be limits on how much information is available to the visual system for use in perceptual inferences. In other words, vision must be in some interesting sense modular. The same goes for other sensory/input systems, and, on Fodor’s view, certain aspects of language processing.
Fodor spells out a number of characteristic features of modules. That knowledge of an illusion doesn’t make the illusion go away illustrates one of their central features, namely, that they are informationally encapsulated. Fodor says:
[T]he claim that input systems are informationally encapsulated is equivalent to the claim that the data that can bear on the confirmation of perceptual hypotheses includes, in the general case, considerably less that the organism may know. That is, the confirmation function for input systems does not have access to all the information that the organism internally represents. (1983, p. 69)
In addition, modules are supposed to be domain specific, in the sense that they’re restricted in the sorts of representations (such as visual, auditory, or linguistic) that can serve as their inputs (1983, pp. 47-52). They’re also mandatory. For instance, native English speakers cannot hear utterances of English as mere noise (“You all know what Swedish and Chinese sound like; what does English sound like?” 1983, p. 54), and people with normal vision and their eyes open cannot help but see the 3-D objects in front of them. In general, modules “approximate the condition so often ascribed to reflexes: they are automatically triggered by the stimuli that they apply to” (1983, pp. 54-55). Not only are modular processes domain-specific and out of our voluntary control, they’re also exceedingly fast. For instance, subjects can “shadow” speech (repeat what is heard when it’s heard) with a latency of about 250 milliseconds, and match a description to a picture with 96% accuracy when exposed for a mere 167 milliseconds (1983, pp. 61-64). In addition, modules have shallow outputs, in the sense that the information they carry is simple, or constrained in some way, which is required because otherwise the processing required to generate them couldn’t be encapsulated. As Fodor says, “if the visual system can deliver news about protons, then the likelihood that visual analysis is informationally encapsulated is negligible” (1983, p. 87). Fodor tentatively suggests that the visual system delivers as outputs “basic” perceptual categories (Rosch et al. 1976) such as dog or chair, although others take shallow outputs to be altogether non-conceptual (Carruthers 2006, p. 4). In addition to these features, Fodor also suggests that modules are associated with fixed neural architecture, exhibit characteristic and specific breakdown patterns, and have an ontogeny that exhibits a characteristic pace and sequencing (1983, pp. 98-101).
On Fodor’s view, although sensory systems are modular, the “central” systems underlying belief fixation, planning, decision-making, and the like, are not. The latter exhibit none of the characteristic features associated with modules since they are domain-general, unencapsulated, under our voluntary control, slow, and not associated with fixed neural structures. Fodor draws attention, in particular, to two distinguishing features of central systems: they’re isotropic, in the sense that “in principle, any of one’s cognitive commitments (including, of course, the available experiential data) is relevant to the (dis)confirmation of any new belief” (2008, p. 115); and they’re Quinean, in the sense that they compute over the entirety of one’s belief system, as when one settles on the simplest, most conservative overall belief—as Fodor puts it, “the degree of confirmation assigned to any given hypothesis is sensitive to properties of the entire belief system” (1983, p. 107). Fodor’s picture of mental architecture is one in which there are a number of informationally encapsulated modules that process the outputs of transducer systems, and then generate representations that are integrated in a non-modular central system. The Fodorean mind is thus essentially a big general-purpose computer, with a number of domain-specific computers out near the edges that feed into it.
Fodor’s work on modularity has been criticized on a number of fronts. Empiricist philosophers and psychologists are typically quite happy with the claim that the central system is domain-general, but have criticized Fodor’s claim that input systems are modular (see Prinz 2006 for an overview). Fodor’s work has also been attacked by those who share his rationalist and nativist sympathies. Most notably, evolutionary psychologists reject Fodor’s claim that there must be a non-modular system responsible for integrating modular outputs, and argue instead that the mind is nothing but a collection of modular systems (see Barkow, Cosmides, and Tooby 1992, Carruthers 2006, Pinker 1997, and Sperber 2002). According to such “massive modularity” theorists, what Fodor calls the “central” system is in fact built up out of a number of domain-specific modules, for example, modules devoted to common-sense reasoning about physics, biology, psychology, and the detection of cheaters, to name a few prominent examples from the literature. (The notion of “module” used by such theorists is different in various ways from the notion as introduced by Fodor; see Carruthers 2006 and Barrett 2015.) In addition, evolutionary psychologists claim that these central modules are adaptations, that is, products of selection pressures that faced our hominid ancestors.
That Fodor is a staunch nativist might lead one to believe that he is sympathetic to applying adaptationist reasoning to the human mind. This would be a mistake. Fodor has long been skeptical of the idea that the mind is a product of natural selection, and in his book The Mind Doesn’t Work That Way (2001) he replies to a number of arguments purporting to show that it must be. For instance, evolutionary psychologists claim that the mind must be “reverse engineered”: in order to figure out how it works, we must know what its function is; and in order to know what its function is we must know what it was selected for. Fodor rejects this latter inference, and claims that natural selection is not required in order to underwrite claims about the teleology of the mind. For the notion of function relevant for psychology might be synchronic, not diachronic: “You might think, after all, that what matters in understanding the mind is what ours do now, not what our ancestors’ did some millions of years ago” (1998b, p. 209). Indeed, in general, one does not need to know about the evolutionary history of a system in order to make inferences about its function:
[O]ne can often make a pretty shrewd guess what an organ is for on the basis of entirely synchronic considerations. One might thus guess that hands are for grasping, eyes for seeing, or even that minds are for thinking, without knowing or caring much about their history of selection. Compare Pinker (1997, p. 38): “psychologists have to look outside psychology if they want to explain what the parts of the mind are for.” Is this true? Harvey didn’t have to look outside physiology to explain what the heart is for. It is, in particular, morally certain that Harvey never read Darwin. Likewise, the phylogeny of bird flight is still a live issue in evolutionary theory. But, I suppose, the first guy to figure out what birds use their wings for lived in a cave. (2000, p. 86)
Fodor’s point is that even if one grants that natural selection underwrites teleological claims about the mind, it doesn’t follow that in order to understand a psychological mechanism one must understand the selection pressures that led to it.
Evolutionary psychologists also argue that the adaptive complexity of the mind is best explained by the hypothesis that it is a collection of adaptations. For natural selection is the only known explanation for adaptive complexity in the living world. In response, Fodor claims that the complexity of our minds is irrelevant to the question of whether they’re the products of natural selection:
[W]hat matters to the plausibility that the architecture of our minds is an adaptation is how much genotypic alternation would have been required for it to evolve from the mind of the nearest ancestral ape whose cognitive architecture was different from ours. About that, however, nothing is known. … [I]t’s entirely possible that quite small neurological reorganizations could have effected wild psychological discontinuities between our minds and the ancestral ape’s. … If that’s right, then there is no reason at all to believe that our cognition was shaped by the gradual action of Darwinian selection on prehuman behavioral phenotypes. (2000, pp. 87-88)
Fodor thus argues that adaptive complexity does not warrant the claim that our minds are products of natural selection. In a co-authored book with Massimo Piattelli-Palmarini, What Darwin Got Wrong (2010), Fodor goes much further, arguing that adaptationist explanations in general are both decreasingly of interest in biology and, on further reflection, actually incoherent. Perhaps needless to say, the book has occasioned considerable controversy (see Sober 2010, Pigliucci 2010, Block and Kitcher 2010, and Godfrey-Smith 2010; Fodor and Piattelli-Palmarini reply to their critics in an afterword in the paperback edition of the book).
In The Mind Doesn’t Work That Way (2000), and also in LOT 2 (2008), Fodor reiterates and defends his claim that the central systems are non-modular, and connects this view to more general doubts about the adequacy of RTM as a comprehensive theory of the human mind, doubts that he first voiced in his classic The Modularity of Mind (1983). One of the main jobs of the central system is the fixation of belief via abductive inferences, and Fodor argues that the fact that such inferences are holistic, global, and context-dependent implies that they cannot be realized in a modular system. Given RTM’s commitment to the claim that computational processes are sensitive only to local properties of mental representations, these features of central cognition thus appear to fall outside of RTM’s scope (2000, chs. 2-3; 2008, ch. 4).
Consider, for instance, the simplicity of a belief. As Fodor says: “The thought that there will be no wind tomorrow significantly complicates your arrangements if you had intended to sail to Chicago, but not if your plan was to fly, drive, or walk there” (2000, p. 26). Whether or not a belief complicates a plan thus depends upon the beliefs involved in the plan—that is, the simplicity of a belief is one of its global, context-dependent properties. However, the syntactic properties of representations are local, in the sense that they depend on their intrinsic, context-independent properties. Fodor concludes that to the extent that cognition involves global properties of representations, RTM cannot provide a model of how cognition works:
[A] cognitive science that provides some insight into the part of the mind that isn’t modular may well have to be different, root and branch, from the kind of syntactical account that Turing’s insights inspired. It is, to return to Chomsky’s way of talking, a mystery, not just a problem, how mental processes could be simultaneously feasible and abductive and mechanical. Indeed, I think that, as things now stand, this and consciousness look to be the ultimate mysteries about the mind. (2000, p. 99).
Thus, although Fodor has long championed RTM as the best theory of cognition available, he claims that its application is limited to those portions of the mind that are modular. Needless to say, some disagree with Fodor’s assessment of the limits of RTM (see Carruthers 2006, Ludwig and Schneider 2008, Pinker 2005, and Barrett 2015).
8. References and Further Reading
- Arjo, Dennis (1996) “Sticking Up for Oedipus: Fodor on Intentional Generalizations and Broad Content,” Mind & Language 11: 231-235.
- Aydede, Murat (1998) “Fodor on Concepts and Frege Puzzles,” Pacific Philosophical Quarterly 79: 289-294.
- Aydede, Murat & Philip Robbins (2001) “Are Frege Cases Exceptions to Intentional Generalizations?” Canadian Journal of Philosophy 31: 1-22.
- Barkow, Jerome, Cosmides, Leda, and Tooby, John (Eds.) The Adapted Mind. Oxford: Oxford University Press.
- Barrett, H. Clark (2015) The Shape of Thought: How Mental Adaptations Evolve. Oxford: Oxford University Press.
- Block, Ned (1993). “Holism, Hyper-Analyticity, and Hyper-Compositionality,” Philosophical Issues 3: 37-72.
- Block, Ned and Philip Kitcher (2010) “Misunderstanding Darwin: Natural Selection’s Secular Critics Get it Wrong,” Boston Review (March/April).
- Boghossian, Paul (1993). “Does Inferential Role Semantics Rest on a Mistake?” Philosophical Issues 3: 73-88.
- Brook, Andrew and Robert Stainton (1997) “Fodor’s New Theory of Content and Computation,” Mind & Language 12: 459-474.
- Carruthers, Peter (2003) “On Fodor’s Problem,” Mind & Language 18: 502-523.
- Carruthers, Peter (2006) The Architecture of the Mind: Massive Modularity and the Flexibility of Thought. Oxford: Oxford University Press.
- Chomsky, Noam (1959) “A Review of B.F. Skinner’s Verbal Behavior,” Language 35: 26-58.
- Evans, Gareth (1982) Varieties of Reference. Oxford: Oxford University Press.
- Fodor, Janet, Jerry Fodor, and Merril Garrett (1975) “The Psychological Unreality of Semantic Representations,” Linguistic Inquiry 4: 515-531.
- Fodor, Jerry (1974) “Special Sciences (Or: The Disunity of Science as a Working Hypothesis)” Synthese 28:97-115.
- Fodor, Jerry (1975) The Language of Thought. New York: Crowell.
- Fodor, Jerry (1980) “Methodological Solipsism Considered as a Research Strategy in Cognitive Psychology,” Behavioral and Brain Sciences 3: 63-109. Reprinted in Fodor (1981a).
- Fodor, Jerry (1981a) RePresentations: Philosophical Essays on the Foundations of Cognitive Science. Cambridge, MA: MIT Press.
- Fodor, Jerry (1981b) “The Present Status of the Innateness Controversy,” In Fodor (1981a).
- Fodor, Jerry (1983) The Modularity of Mind. Cambridge, MA: MIT Press.
- Fodor, Jerry (1986) “Why Paramecia Don’t Have Mental Representations,” Midwest Studies in Philosophy 10: 3-23.
- Fodor, Jerry (1987) Psychosemantics: The Problem of Meaning in the Philosophy of Mind. Cambridge, MA: MIT Press.
- Fodor, Jerry (1989) “Making mind matter more,” Philosophical Topics 67: 59-79.
- Fodor, Jerry (1990) A Theory of Content and Other Essays. Cambridge, MA: MIT Press.
- Fodor, Jerry (1991) “Replies,” In Loewer and Rey (Eds.) Meaning in Mind: Fodor and His Critics. Oxford: Blackwell.
- Fodor, Jerry (1994) The Elm and the Expert: Mentalese and Its Semantics. Cambridge, MA: MIT Press.
- Fodor, Jerry (1998a) Concepts: Where Cognitive Science Went Wrong. New York: Oxford University Press.
- Fodor, Jerry (1998b) In Critical Condition: Polemical Essays on Cognitive Science and the Philosophy of Mind. Cambridge, MA: MIT Press.
- Fodor, Jerry (2000) The Mind Doesn’t Work That Way: The Scope and Limits of Computational Psychology. Cambridge, MA: MIT Press.
- Fodor, Jerry (2003) Hume Variations. Oxford: Oxford University Press.
- Fodor, Jerry (2004) “Having Concepts: A Brief Refutation of the 20th Century,” Mind & Language 19: 29-47.
- Fodor, Jerry, and Charles Chihara (1965) “Operationalism and Ordinary Language,” American Philosophical Quarterly 2: 281-295.
- Fodor, Jerry, Thomas Bever, and Merrill Garrett (1974) The Psychology of Language: An Introduction to Psycholinguistics and Generative Grammar. New York: McGraw Hill.
- Fodor, Jerry, Merril Garrett, Edward Walker, and Cornelia Parkes (1980) “Against Definitions,” Reprinted in Margolis and Laurence (1999).
- Fodor, Jerry, and Zenon Pylyshyn (1988) “Connectionism and Cognitive Architecture: A Critical Analysis,” Cognition 28: 3-71.
- Fodor, Jerry, and Ernest Lepore (1992) Holism: A Shopper’s Guide. Oxford: Blackwell.
- Fodor, Jerry, and Ernest Lepore (2002) The Compositionality Papers. New York: Oxford University Press.
- Fodor, Jerry, and Massimo Piattelli-Palmarini (2010) What Darwin Got Wrong. Farrar, Straus and Giroux.
- Fodor, Jerry, and Zenon Pylyshyn (2014) Minds without Meanings. Cambridge, MA: MIT Press.
- Godfrey-Smith, Peter (2010) “It Got Eaten,” London Review of Books, 32 (13): 29-30.
- Hale, Kenneth, and Samuel Jay Keyser (1993) “On Argument Structure and Lexical Expression of Syntactic Relations,” in K. Hale and S.J. Keyser (Eds.) The View From Building 20 Cambridge, MA: MIT Press.
- Hale, Kenneth, & Samuel Jay Keyser (1999) “A Response to Fodor and Lepore “Impossible Words?”” Linguistic Inquiry 30: 453–466.
- Heil, John (2003). From An Ontological Point of View. Oxford: Oxford University Press.
- Horgan, Terrence (1998). “Recognitional Concepts and the Compositionality of Concept Possession,” Philosophical Issues 9: 27-33.
- Jackendoff, Ray (1983). Semantics and Cognition. Cambridge, MA: MIT Press.
- Jackendoff, Ray (1992). Languages of the Mind. Cambridge, MA: MIT Press.
- Katz, Jerrold (1977) “The Real Status of Semantic Representations,” Linguistic Inquiry 8: 559-84.
- Katz, Jerrold (1981) Language and Other Abstract Objects. Oxford: Blackwell.
- Katz, Jerrold, and J.A. Fodor (1963) “The Structure of a Semantic Theory,” Language 39:170-210.
- Kim, Jaegwon (2005) Physicalism, or Something Near Enough. Princeton, NJ: Princeton University Press.
- Loewer, Barry, and Georges Rey (Eds.) (1991). Meaning in Mind: Fodor and His Critics. Oxford: Blackwell.
- Lowe, E.J. (2008) Personal Agency: The Metaphysics of Mind and Action. Oxford: Oxford University Press.
- Ludwig, Kirk, and Susan Schneider (2008) “Fodor’s Challenge to the Classical Computational Theory of Mind,” Mind & Language, 23, 123-143.
- Melnyk, Andrew (2003) A Physicalist Manifesto: Thoroughly Modern Materialism. Cambridge: Cambridge University Press.
- Miller, George, and Johnson-Laird, Philip (1976). Language and Perception. Cambridge, MA: Harvard University Press.
- Peacocke, Christopher (1992) A Study of Concepts. Cambridge, MA: MIT Press.
- Piattelli-Palmarini, Massimo (1980) Language and Learning. Cambridge, MA: Harvard University Press.
- Pigliucci, Massimo (2010) “A Misguided Attack on Evolution” Nature 464: 353–354.
- Pinker, Steven (1989) Learnability and Cognition. Cambridge, MA: MIT Press.
- Pinker, Steven (1997) How the Mind Works. New York: W. W. Norton & Company.
- Pinker, Steven (2005) “So How Does the Mind Work?” Mind & Language 20: 1-24.
- Prinz, Jesse (2002) Furnishing the Mind. Cambridge, MA: MIT Press.
- Prinz, Jesse (2006) “Is the Mind Really Modular?” In Stainton (Ed.) Contemporary Debates in Cognitive Science. Oxford: Blackwell.
- Pustejovsky, James (1995) The Generative Lexicon. Cambridge, MA: MIT Press.
- Pustejovsky, James (1998) “Generativity and Explanation in Semantics: A Reply to Fodor and Lepore” Linguistic Inquiry 29: 289-311.
- Putnam, Hilary (1963) “Brains and Behavior”, reprinted in Putnam 1975b, pp. 325–341.
- Putnam, Hilary (1967) “The Nature of Mental States”, reprinted in Putnam 1975b, 429–440.
- Putnam, Hilary (1975) “The Meaning of ‘Meaning’,” Minnesota Studies in the Philosophy of Science 7: 131-193.
- Putnam, Hilary (1975b) Mind, Language, and Reality, vol. 2. Cambridge: Cambridge University Press.
- Pylyshyn, Zenon (2003) Seeing and Visualizing. Cambridge, MA: MIT Press.
- Quine, W.V. O. (1953) “Two Dogmas of Empiricism,” In From a Logical Point of View, Cambridge, MA: Harvard University Press.
- Quine, W.V. O. (1960) Word and Object. Cambridge, MA: MIT Press.
- Recanati, François (2002) “The Fodorian Fallacy,” Analysis 62: 285-289.
- Rey, Georges (1993) “Idealized Conceptual Roles,” Philosophy and Phenomenological Research 53: 47-52.
- Rey, Georges (2005) “Philosophical analysis as cognitive psychology,” In H. Cohen and C. Lefebvre (Eds.) Handbook of Categorization in Cognitive Science. Dordrecht: Elsevier.
- Rives, Bradley (2009) “Concept Cartesianism, Concept Pragmatism, and Frege Cases,” Philosophical Studies 144: 211-238.
- Rives, Bradley (2016) “Concepts and Analytic Intuitions,” Analytic Philosophy 57(4): 285-314.
- Rosch, Eleanor and Carolyn Mervis (1975) “Family Resemblances: Studies in the Internal Structure of Categories,” Cognitive Psychology 7: 573-605.
- Rosch, Eleanor, Mervis, C., Gray, W., Johnson, D., and Boyes-Braem, P. (1976). “Basic Objects in Natural Categories,” Cognitive Psychology 8: 382–439.
- Schneider, Susan (2005) “Direct Reference, Psychological Explanation, and Frege Cases,” Mind & Language 20: 423-447.
- Segal, Gabriel (1997) “Content and Computation: Chasing the Arrows,” Mind & Language 12: 490-501.
- Shoemaker, Sydney (2003) “Some Varieties of Functionalism,” In Shoemaker, Identity, Cause, and Mind, Oxford: Oxford University Press.
- Sober, Eliot (2010) “Natural Selection, Causality, and Laws: What Fodor and Piattelli-Palmarini Got Wrong,” Philosophy of Science 77(4): 594-607.
- Sperber, Daniel (2002) “In defense of massive modularity,” In Dupoux (Ed.) Language, Brain, and Cognitive Development. Cambridge, MA: MIT Press.
- Stoljar, Daniel (2010 Physicalism. New York: Routledge.
- Williamson, Timothy (2007) The Philosophy of Philosophy. Oxford: Blackwell.
Author Information
Bradley Rives
Email: rives@iup.edu
Indiana University of Pennsylvania
U. S. A.

 Jerry Fodor was one of the most important philosophers of mind of the late twentieth and early twenty-first centuries. In addition to exerting an enormous influence on virtually all parts of the literature in the philosophy of mind since 1960, Fodor’s work had a significant impact on the development of the cognitive sciences. In the 1960s, along with Hilary Putnam, Noam Chomsky, and others, Fodor presented influential criticisms of the
Jerry Fodor was one of the most important philosophers of mind of the late twentieth and early twenty-first centuries. In addition to exerting an enormous influence on virtually all parts of the literature in the philosophy of mind since 1960, Fodor’s work had a significant impact on the development of the cognitive sciences. In the 1960s, along with Hilary Putnam, Noam Chomsky, and others, Fodor presented influential criticisms of the 
 Organicism is the position that the universe is orderly and alive, much like an organism. According to
Organicism is the position that the universe is orderly and alive, much like an organism. According to