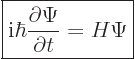What Else Science Requires of Time (That Philosophers Should Know)
This article is one of the three supplements of the main Time article. The other two are Frequently Asked Questions about Time and Special Relativity: Proper Times, Coordinate Systems, and Lorentz Transformations (by Andrew Holster).
Table of Contents
1. What are Theories of Physics?
The term theory has many senses, even in physics. In the main article “Time” and in these supplements, it is used in a special, technical sense, not in the sense of an explanation as in the remark, “My theory is that the mouse stole the cheese,” nor in the sense of a prediction as in the remark, “My theory is that the mouse will steal the cheese.” The general theory of relativity is an example of our intended sense. The key feature is that the theory contain laws that are not vague. Philosophical theories tend to be vague. Think of the philosophical theories of mind, meaning, history, free will, and so forth. They are often mere slogans or a few sentences that sketch an idea intended to resolve something that is puzzling, even if the sketch fills an entire book.
Ideally the confirmed theories of physics do three things: explain what we already know, predict what we don’t, and help us understand what we can. Theories themselves do not do the explaining; we humans use them in order to explain. However, the idiom is commonly used.
Whether to add a fourth thing—that the fundamental theories are true or at least approximately true—has caused considerable controversy among philosophers of science. The Harvard philosopher Hilary Putnam is noted for arguing that the success of precise theories in physics would be miraculous if they were not at least approximately true.
Averaging over the history of physics, more and more phenomena are being explained with fewer and fewer laws. This led to the hope that there would be a fundamental set of laws explaining all phenomena, one in which it would be clear how the laws of relativity theory and the laws of quantum theory are approximately true. This hope is the hope for a “theory of everything.” However, one cannot know a priori that there is such a theory to be found.
Regarding the term “fundamental,” if law A and law B can be explained by law C, and C is logically consistent, then law C is considered to be more fundamental than A and B, presuming that C is not simply equivalent to the conjunction “A and B.” The word “basic” is often used synonymously with “fundamental.”
The field of physics contains many philosophical presuppositions: that nature is understandable, that nature is lawful, that those laws are best represented in the language of mathematics, that the laws tell us how nature changes from time to time, that the fundamental laws do not change with time, that there is only one correct fundamental theory of everything physical, that a scientific law is not really a law if it holds only when a supernatural being decides not to intervene and allow a miracle to be performed, and that we are not brains in a vat nor characters in someone’s computer game. But these philosophical presuppositions are not held dogmatically. Ideally, they would be rejected if scientists were to find new evidence that they should be changed.
Here is the opinion of the cosmologist Stephen Hawking on the nature of scientific laws:
I believe that the discovery of these laws has been humankind’s greatest achievement…. The laws of nature are a description of how things actually work in the past, present and future…. But what’s really important is that these physical laws, as well as being unchangeable, are universal [so they apply to everything everywhere all the time]. (Brief Answers to the Big Questions, 2018).
We humans are lucky that we happen to live in a universe that is so explainable, predictable and understandable, and that is governed by so few laws. The philosophical position called “scientific realism” implies that entities we do not directly observe but only infer theoretically from the laws (such as spacetime) really do exist. Scientific realism is controversial among philosophers, despite its popularity among physicists.
A popular version of scientific realism that accounts for the fact that scientific theories eventually are falsified and need to be revised but not totally rejected is called “structural scientific realism.” For example, much of the structure of early 20th century atomic theory is retained even though that theory was replaced by a more sophisticated version of atomic theory later in the 20th century and an even more sophisticated version in the 21st century. Atoms are not what they used to be.
Most importantly for the “Time” article, the theories of physics help us understand the nature of time. They do this primarily by their laws. Much has been said in the literature of the philosophy of science about what a scientific law is. The philosopher David Lewis claimed that a scientific law is whatever provides a lot of information in a compact and simple expression. This is a justification for saying a law must be a general claim. The claim that Mars is farther from the Sun than is the Earth is true, but it does not qualify as being a law because it is not general enough. The Second Law of Thermodynamics is general enough.
It is because theories in science are designed for producing interesting explanations, not for encompassing all the specific facts, that there is no scientific law that specifies your age and phone number. Some theories are expressed fairly precisely, and some are expressed less precisely. All other things being equal, the more precise the better. If they have important simplifying assumptions but still give helpful explanations of interesting phenomena, then they are often said to be models. Very simple models are said to be toy models (“Let’s consider a cow to be a perfect cube, and assume 4.2 is ten.”) However, physicists do not always use the terms this way. Very often they use the terms “theory” and “model” interchangeably. For example, the Standard Model of Particle Physics is a theory in the sense used in this section, but for continuity with historical usage of the term physicists have never bothered to replace the word “model” with “theory.”
In physics, the fundamental laws in the theories are equations. The equations of the laws are meant to be solved for different environments, with the environment providing different initial values for the variables within the equations. Solutions to the equations are used to provide predictions about what will happen. For example, Karl Schwarzschild found the first exact solution to Einstein’s equations of general relativity. The environment (the set of initial conditions) he chose was a large sphere of gas in an otherwise empty universe, and the solution was what is now called a black hole. At the time, Einstein said he believed this solution was not predicting the existence of anything that is physically real, though now we know Einstein was mistaken. Roger Penrose won a Nobel Prize for proving that under a variety of normal conditions and their perturbations in our spacetime, the general theory of relativity implies that there will be black holes containing singularities within an event horizon that can be passed through.
According to a great many physicists, predictions made by using the theories of physics should be as accurate as possible and not merely precise. In addition, most researchers say a theory ideally should tell us how the system being studied would behave if certain conditions were to be changed in a specified way, for example, if the density of water were doubled or more moons were orbiting the planet. Knowing how the system would behave under different conditions helps us understand the causal structure of the system.
Physicists want their theories to help make accurate and precise predictions, but when the predications in a test are not accurate and precise, the first thought is that perhaps there was a sloppy test of the prediction. If the physicists become satisfied that the test is well run, then their thoughts turn to whether the test might be a sign that there exists some as yet unknown particle or force at work causing the mismatch between theory and experiment. That is why physicists love anomalies.
Theories of physics are, among other things, a set of laws and a set of ways to link its statements to the real, physical world. A theory might link the variable “t” to time as measured with a standard clock, and link the constant “M” to the known mass of the Earth. In general, the mathematics in mathematical physics is used to create mathematical representations of real entities and their states and behaviors. That is what makes it be an empirical science, unlike pure mathematics.
Do the laws of physics actually govern us? In Medieval Christian theology, the laws of nature were considered to be God’s commands, but today saying nature “obeys” scientific laws or that nature is “governed” by laws is considered by scientists to be a harmless metaphor. Scientific laws are called “laws” because they constrain what can happen; they imply this will happen and that will not. It was Pierre Laplace who first declared that fundamental scientific laws are hard and fast rules with no exceptions.
Philosophers’ positions on laws divide into two camps, Humean and anti-Humean. Anti-Humeans consider scientific laws to be bringing nature forward into existence. It is as if laws are causal agents. Some anti-Humeans side with Aristotle that whatever happens is because parts of the world have essences and natures, and the laws are describing these essences and natures. This position is commonly accepted in the manifest image. Humeans, on the other hand, consider scientific laws simply to be patterns of nature that very probably will hold in the future. The patterns summarize the behavior of nature. The patterns do not “lay down the law for what must be.” In response to the question of why these patterns and not other patterns, some Humeans say they are patterns described with the most useful concepts for creatures with brains like ours (and other patterns might be more useful for extraterrestrials). More physicists are Humean than anti-Humean. More philosophers are anti-Humean than Humean.
In our fundamental theories of physics, the standard philosophical presupposition is that a state of a physical system describes what there is at some time, and a law of the theory—an “evolution law” or “dynamical law”—describes how the system evolves from a state at one time into a state at another time. All evolution laws in our fundamental theories are differential equations.
All fundamental laws of relativity theory are time-reversible. Time-reversibility implies the fundamental laws do not notice the future direction from the past direction. The second law of thermodynamics does notice this; it says entropy tends to increase toward the future; so the theory of thermodynamics is not time-reversible (but it is also not a fundamental theory). And time-reversibility fails for quantum measurements (for a single universe).
Time-translation invariance is a meta-law that implies the laws of physics we have now are the same laws that held in the past and will hold in the future, and it implies that all instants are equivalent. This is not implying that if you bought an ice cream cone yesterday, you will buy one tomorrow. Unfortunately there are difficulties with time-translation invariance. For example, a translation in time to a first moment would be to a special moment with no earlier moment, so there is at least one exception to the claim that all moments are indistinguishable. A deeper question is whether any of the laws we have now might change in the future. The default answer is “no,” but this is just an educated guess. And any evidence that a fundamental can fail will be treated by some physicists as evidence that it was never a law to begin with, while it will be treated by others as proof that time-translation invariance fails. Hopefully a future consensus will be reached one way or the other.
Epistemologically, the laws of physics are hypotheses that are helpful to hold and that have not been refuted. However, some laws are believed less strongly than others, and so are more likely to be changed than others if future observations indicate a change is needed. The laws held most strongly in this sense are the Second Law of thermodynamics and the laws of general relativity and quantum mechanics.
Physical constants are parameters in a physical theory that cannot be explained by that theory. The laws of our fundamental theories contain many constants such as the fine-structure constant, the value for the speed of light in a vacuum, Planck’s constant, and the rest mass of a proton. For some of these constants (a.k.a. parameters), the Standard Model of Particle Physics indicates that we should be able to compute the value exactly, but practical considerations of solving the equations in order to obtain this exact value have been insurmountable, so we have had to make do with a good measurement. That is, we measure the constant carefully and precisely, and then select this measurement outcome as a best, specific value for the constant to be placed into the theories containing the constant. A virtue of a theory is to not have too many such constants. If there were too many, then the theory could never be disproved by data because the constants always could be adjusted to account for any new data, and so the theory would be pseudoscientific. Unfortunately, the constants in quantum field theory look remarkably arbitrary.
Regarding the divide between science and pseudoscience, the leading answer is that:
what is really essential in order for a theory to be scientific is that some future information, such as observations or measurements, could plausibly cause a reasonable person to become either more or less confident of its validity. This is similar to Popper‘s criteria of falsifiability, while being less restrictive and more flexible (Dan Hooper).
a. The Core Theory
Some physical theories are fundamental, and some are not. Fundamental theories are foundational in the sense that their laws cannot be derived from the laws of other physical theories even in principle. For example, the second law of thermodynamics is not fundamental, nor are the laws of plate tectonics in geophysics despite their being critically important to their respective sciences. The following two theories are fundamental: (i) the general theory of relativity, and (ii) quantum mechanics. Their amalgamation is what Nobel Prize winner Frank Wilczek called the Core Theory, the theory of almost everything physical. It is a version of quantum field theory.
Nearly all scientists believe this Core Theory holds not just in our solar system, but all across the universe, and it held yesterday and will hold tomorrow. Wilczek claimed:
[T]he Core has such a proven record of success over an enormous range of applications that I can’t imagine people will ever want to junk it. I’ll go further: I think the Core provides a complete foundation for biology, chemistry, and stellar astrophysics that will never require modification. (Well, “never” is a long time. Let’s say for a few billion years.)
This implies one could think of biology as applied quantum theory.
The Core Theory does not include the big bang theory, which is the standard model of cosmology. The Core Theory does not use the terms time’s arrow or now. The concept of time in the Core Theory is primitive or “brute.” It is not definable, but rather it is used to define other concepts such as length.
It is believed by most physicists that the Core Theory can be used in principle to adequately explain the behavior of a leaf, a galaxy, and a brain. The hedge phrase “in principle” is important. One cannot replace it with “in practice” or “practically.” Practically there are many limitations on the use of the Core Theory. Here are some of the limitations. Leaves are too complicated. There are too many layers of emergence needed from the Core Theory to leaf behavior. Also, there is a margin of error in any measurement of anything. There is no way to acquire the leaf data precisely enough to deduce the exact path of a leaf falling from a certain tree 300 years ago. Even if this data were available, the complexity of the needed calculations would be prohibitive. Commenting on these various practical limitations for the study of galaxies, the cosmologist Andrew Ponzen said “Ultimately, galaxies are less like machines and more like animals—loosely understandable, rewarding to study, but only partially predictable.”
The Core has been tested in many extreme circumstances and with great sensitivity, so physicists have high confidence in it. There is no doubt that for the purposes of doing physics the Core Theory provides a demonstrably superior representation of reality to that provided by its alternatives. But all physicists know the Core is not strictly true and complete, and they know that some features will need revision—revision in the sense of being modified or extended. Physicists are motivated to discover how to revise it because such a discovery can lead to great praise from the rest of the physics community. Wilczek says the Core will never need modification for understanding (in principle) the special sciences of biology, chemistry, stellar astrophysics, computer science and engineering, but he would agree that the Core needs revision in order to adequately explain why 95 percent of the universe consists of dark energy and dark matter, why the universe has more matter than antimatter, why neutrinos change their identity over time, and why the energy of empty space is as small as it is. One philosophical presupposition here is that the new Core Theory will be a single, logically consistent theory.
The Core Theory presupposes that time exists, that it is a feature of spacetime, and that spacetime is more fundamental than time. Within the Core Theory, relativity theory allows space to curve, ripple, and expand; and curving, rippling, and expanding can vary over time. Quantum theory alone does not allow any of these, although a future revision of quantum theory within the Core Theory is expected to allow them.
In the Core Theory, the word time is a theoretical term, and the dimension of time is treated somewhat like a single dimension of space. Space is informally considered to be a set of all possible point-locations. Time is a set of all possible point-times. Spacetime is a set of all possible point-events. Spacetime is presumed to be at least four-dimensional and also to be a continuum of points and thus to be continuous, with time being a distinguished, one-dimensional sub-space of spacetime. Because the time dimension is so different from a space dimension, physicists very often speak of (3+1)-dimensional spacetime rather than 4-dimensional spacetime. Both relativity theory and quantum theory assume that three-dimensional space is isotropic (rotation symmetric) and homogeneous (translation symmetric) and that there is translation symmetry in time (but other considerations in cosmology cast doubt on this symmetry). Regarding all these symmetries, all the physical laws do need to obey them, but specific physical systems within space-time need not. For example, your body could become very different if you walk across the road at noon on Tuesday instead of Friday, even though the Tuesday laws are also the Friday laws.
The Core Theory also presupposes reductionism throughout science in the sense that large-scale laws are based on the small-scale laws. For example, the laws of geology are based on the fundamental laws of physics. The only exception to reductionism seems to be due to quantum coherence in which the behavior of any group of particles is not fully describable by complete knowledge of the behavior of all its individual particles. This is a very important exception to reductionism.
The Core Theory presupposes an idea Laplace had in 1800 that is now called the Laplacian Paradigm—that all dynamical laws should have the form of describing how a state of a system at one time turns into a different state at another time. This implies that a future state is entailed by a single past state rather does not demand more information such as the entire history of the system. This latter implication is often described by saying the laws are Markovian.
The Core Theory does not presuppose or explicitly mention consciousness. The typical physicist believes consciousness is contingent; it happens to exist but it is not a necessary feature of the universe. That is, consciousness happened to evolve because of fortuitous circumstances, but it might not have. Many philosophers throughout history have disagreed with this treatment of consciousness, especially the idealist philosophers of the 19th century.
[For the experts: More technically, the Core Theory is the renormalized, effective quantum field theory that includes both the Standard Model of Particle Physics and the weak field limit of Einstein’s General Theory of Relativity in which gravity is very weak and spacetime is almost flat, and no assumption is made about the character or even the existence of space and time below the Planck length and Planck time.]
2. Relativity Theory
 Of all the theories of science, relativity theory has had the greatest impact upon our understanding of the nature of time. Relativity theory implies time is one component of four-dimensional spacetime, and time can curve and dilate.
Of all the theories of science, relativity theory has had the greatest impact upon our understanding of the nature of time. Relativity theory implies time is one component of four-dimensional spacetime, and time can curve and dilate.
When the term relativity theory is used, it usually refers to the general theory of relativity of 1915 with the addition of a cosmological constant, but sometimes it refers to the special theory of relativity of 1905. Both are theories of time. Both have been well-tested; and they are almost universally accepted among physicists. Today’s physicists understand them better than Einstein himself did. “Einstein’s twentieth-century laws, which—in the realm of strong gravity—began as speculation, became an educated guess when observational data started rolling in, and by 1980, with ever-improving observations, evolved into truth” (Kip Thorne).
Although the Einstein field equations in his general theory:
are exceedingly difficult to manipulate, they are conceptually fairly simple. At their heart, they relate two things: the distribution of energy in space, and the geometry of space and time. From either one of these two things, you can—at least in principle—work out what the other has to be. So, from the way that mass and other energy is distributed in space, one can use Einstein’s equations to determine the geometry of that space, And from that geometry, we can calculate how objects will move through it (Dan Hooper).
The main assumption of GR, general relativity theory, is the principle of equivalence: gravity is basically acceleration. That is, for small objects and for a short duration, gravitational forces cannot be distinguished from forces produced by acceleration.
GR has many assumptions and implications that are usually never mentioned so explicitly. One is that gravity did not turn off for three seconds during the year 1777 in Australia. A more general one is that the theory’s fundamental laws are the same regardless of what time it is. This feature is called time-translation invariance.
The relationship between the special and general theories is slightly complicated. Both theories are about the motion of objects and both approach agreement with Newton’s theory the slower the speed of those objects, and the weaker the gravitational forces involved, and the lower the energy of those objects. General relativity implies the truth of special relativity in all infinitesimal regions of spacetime, but not vice versa.
General relativity holds in all reference frames, but special relativity holds only for inertial reference frames, namely non-accelerating frames. Special relativity implies the laws of physics are the same for all inertial observers, that is, observers who are moving at a constant velocity relative to each other. ‘Observers’ in this sense are also the frames of reference themselves, or they are persons of zero mass and volume making measurements from a stationary position in a coordinate system. These observers need not be conscious beings.
Special relativity allows objects to have mass but not gravity. Also, it always requires a flat geometry—that is, a Euclidean geometry for space and a Minkowskian geometry for spacetime. General relativity does not have those restrictions. General relativity is a very specific theory of gravity, assuming the theory is supplemented by a specification of the distribution of matter-energy at some time. Both the special and general theory imply that Newton’s two main laws of F = ma and F = GmM/r2 hold only approximately.
Special relativity is not a specific theory but rather is a general framework for theories, and it is not a specific version of general relativity. Nor is general relativity a generalization of special relativity. The main difference between the two is that, in general relativity, spacetime does not simply exist passively as a background arena for events. Instead, spacetime is dynamical in the sense that changes in the distribution of matter and energy in any region of spacetime are directly related to changes in the curvature of spacetime in that region (though not necessarily vice versa).
Unlike classical theories, general relativity is geometric. What this means is that when an artillery shell flies through the air and takes a curved path in space relative to the ground because of a gravitational force acting upon it, what is really going on is that the artillery shell is taking a geodesic or the straightest path of least energy in spacetime, which is a curved path as viewed from a higher space dimension. That is why gravity or gravitational attraction is not a force but rather a curvature, a curvature of spacetime.
The theory of relativity is generally considered to be a theory based on causality:
One can take general relativity, and if you ask what in that sophisticated mathematics is it really asserting about the nature of space and time, what it is asserting about space and time is that the most fundamental relationships are relationships of causality. This is the modern way of understanding Einstein’s theory of general relativity….If you write down a list of all the causal relations between all the events in the universe, you describe the geometry of spacetime almost completely. There is still a little bit of information that you have to put in, which is counting, which is how many events take place…. Causality is the fundamental aspect of time. (Lee Smolin).
(An aside for the experts: The theory of relativity requires spacetime to have at least four dimensions, not exactly four dimensions. Technically, any spacetime, no matter how many dimensions it has, is required to be a differentiable manifold with a metric tensor field defined on it that tells what geometry it has at each point. General relativistic spacetimes are manifolds built from charts involving open subsets of R4. General relativity does not consider a time to be a set of simultaneous events that do or could occur at that time; that is a Leibnizian conception. Instead, general relativity specifies a time in terms of the light cone structures at each place. A light cone at a spacetime point specifies what events could be causally related to that point, not what events are causally related to it.)
Relativity theory implies time is a continuum of instantaneous times that is free of gaps just like a mathematical line. This continuity of time was first emphasized by the philosopher John Locke in the late seventeenth century, but it is meant here in a more detailed, technical sense that was developed for calculus only toward the end of the 19th century.
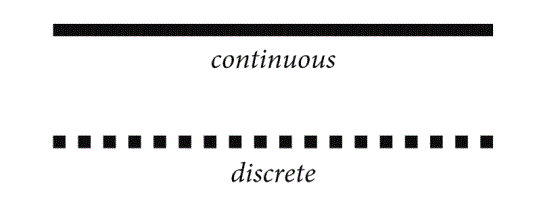
According to both relativity theory and quantum theory, time is not discrete or quantized or atomistic. Instead, the structure of point-times is a linear continuum with the same structure as the mathematical line or the real numbers in their natural order. For any point of time, there is no next time because the times are packed together so tightly. Time’s being a continuum implies that there is a non-denumerably infinite number of point-times between any two non-simultaneous point-times. Some philosophers of science have objected that this number is too large, and we should use Aristotle’s notion of potential infinity and not the late 19th century notion of a completed infinity. Nevertheless, accepting the notion of an actual nondenumerable infinity is the key idea used to solve Zeno’s Paradoxes and to remove inconsistencies in calculus.
The fundamental laws of physics assume the universe is a collection of point events that form a four-dimensional continuum, and the laws tell us what happens after something else happens or because it happens. These laws describe change but do not themselves change. At least that is what laws are in the first quarter of the twenty-first century, but one cannot know a priori that this is always how laws must be. Even though the continuum assumption is not absolutely necessary to describe what we observe, so far it has proved to be too difficult to revise our theories in order to remove the assumption and retain consistency with all our experimental data. Calculus has proven its worth.
No experiment is so fine-grained that it could show times to be infinitesimally close together, although there are possible experiments that could show the assumption to be false if the graininess of time were to be large enough.
Not only is there much doubt about the correctness of relativity in the tiniest realms, there is also uncertainty about whether it works differently on cosmological scales than it does at the scale of atoms, houses, and solar systems, but so far there are no rival theories that have been confirmed. A rival theory intended to incorporate what is correct about the quantum realm is often called a theory of quantum gravity.
Einstein claimed in 1916 that his general theory of relativity needed to be replaced by a theory of quantum gravity. Subsequent physicists generally agree with him, but that theory has not been found so far. A great many physicists of the 21st century believe a successful theory of quantum gravity will require quantizing time so that there are atoms of time. But this is just an educated guess.
If there is such a thing as an atom of time and thus such a thing as an actual next instant and a previous instant, then an interval of time cannot be like an interval of the real number line because no real number has a next number or a previous number. It is conjectured that, if time were discrete, then a good estimate for the duration of an atom of time is 10-44 seconds, the so-called Planck time. No physicist can yet suggest a practical experiment that is sensitive to this tiny scale of phenomena. For more discussion, see (Tegmark 2017).
The special and general theories of relativity imply that to place a reference frame upon spacetime is to make a choice about which part of spacetime is the space part and which is the time part. No choice is objectively correct, although some choices are very much more convenient for some purposes. This relativity of time, namely the dependency of time upon a choice of reference frame, is one of the most significant philosophical implications of both the special and general theories of relativity.
Since the discovery of relativity theory, scientists have come to believe that any objective description of the world can be made only with statements that are invariant under changes in the reference frame. Saying, “It is 8:00” does not have a truth value unless a specific reference frame is implied, such as one fixed to Earth with time being the time that is measured by our civilization’s standard clock. This relativity of time to reference frames is behind the remark that Einstein’s theories of relativity imply time itself is not objectively real whereas spacetime is.
Regarding relativity to frame, Newton would say that if you are seated in a vehicle moving along a road, then your speed relative to the vehicle is zero, but your speed relative to the road is not zero. Einstein would agree. However, he would surprise Newton by saying the length of your vehicle is slightly different in the two reference frames, the one in which the vehicle is stationary and the one in which the road is stationary. Equally surprising to Newton, the duration of the event of your drinking a cup of coffee while in the vehicle is slightly different in those two reference frames. These relativistic effects are called space contraction and time dilation, respectively. So, both length and duration are frame dependent and, for that reason, say physicists, they are not objectively real characteristics of objects. Speeds also are relative to reference frame, with one exception. The speed of light in a vacuum has the same value c in all frames that are allowed by relativity theory. Space contraction and time dilation change in tandem so that the speed of light in a vacuum is always the same number.
Relativity theory allows great latitude in selecting the classes of simultaneous events, as shown in this diagram. Because there is no single objectively-correct frame to use for specifying which events are present and which are past—but only more or less convenient ones—one philosophical implication of the relativity of time is that it seems to be easier to defend McTaggart’s B theory of time and more difficult to defend McTaggart’s A-theory that implies the temporal properties of events such as “is happening now” or “happened in the past” are intrinsic to the events and are objective, frame-free properties of those events. In brief, the relativity to frame makes it difficult to defend absolute time.
Relativity theory challenges other ingredients of the manifest image of time. For two point-events A and B common sense says they either are simultaneous or not, but according to relativity theory, if A and B are distant from each other and occur close enough in time to be within each other’s absolute elsewhere, then event A can occur before event B in one reference frame, but after B in another frame, and simultaneously with B in yet another frame. No person before Einstein ever imagined time has such a strange feature.
The special and general theories of relativity provide accurate descriptions of the world when their assumptions are satisfied. Both have been carefully tested. One of the simplest tests of special relativity is to show that the characteristic half-life of a specific radioactive material is longer when it is moving fast.
The special theory does not mention gravity, and it assumes there is no curvature to spacetime, but the general theory requires curvature in the presence of mass and energy, and it requires the curvature to change as their distribution changes. The presence of gravity in the general theory has enabled the theory to be used to explain phenomena that cannot be explained with either special relativity or Newton’s theory of gravity or Maxwell’s theory of electromagnetism.
Because of the relationship between spacetime and gravity, the equations of general relativity are much more complicated than are those of special relativity. But general relativity assumes the equations of special relativity hold at least in all infinitesimal regions of spacetime.
To give one example of the complexity just mentioned, the special theory clearly implies there is no time travel to events in one’s own past. Experts do not agree on whether the general theory has this same implication because the equations involving the phenomena are too complex for them to solve directly. Because of the complexity of Einstein’s equations, all kinds of tricks of simplification and approximation are needed in order to use the laws of the theory on a computer for all but the simplest situations. Approximate solutions are a practical necessity.
Regarding curvature of time and of space, the presence of mass at a point implies intrinsic spacetime curvature at that point, but not all spacetime curvature implies the presence of mass. Empty spacetime can still have curvature, according to general relativity theory. This unintuitive point has been interpreted by many philosophers as a good reason to reject Leibniz’s classical relationism. The point was first mentioned by Arthur Eddington.
Two accurate, synchronized clocks do not stay synchronized if they undergo different gravitational forces. This is a second kind of time dilation, in addition to dilation due to speed. So, a correct clock’s time depends on the clock’s history of both speed and gravitational influence. Gravitational time dilation would be especially apparent if a clock were to approach a black hole. The rate of ticking of a clock approaching the black hole slows radically upon approach to the horizon of the hole as judged by the rate of a clock that remains safely back on Earth. This slowing is sometimes misleadingly described as “time slowing down.” After a clock falls through the event horizon, it can still report its values to Earth, and when it reaches the center of the hole not only does it stop ticking, but it also reaches the end of time, the end of its proper time.
The general theory of relativity theory has additional implications for time. It implies that spacetime can curve or warp. Whether it curves into a fifth dimension is unknown, but it definitely curves as if it were curving into a fifth dimension. In 1948-9, the logician Kurt Gödel discovered radical solutions to Einstein’s equations, solutions in which there are what are called “closed time-like curves” in graphical representations of spacetime. The unusual curvature is due to the rotation of all the matter throughout Gödel’s universe. As one progresses forward in time along one of these curves, one arrives back at one’s starting point—thus, backward time travel! There is no empirical evidence that our own universe has this rotation. Some experts in relativity theory are not convinced by Gödel’s work that time travel is possible in any universe.
Here is Einstein’s reaction to Gödel’s work on time travel:
Kurt Gödel’s essay constitutes, in my opinion, an important contribution to the general theory of relativity, especially to the analysis of the concept of time. The problem involved here disturbed me already at the time of the building of the general theory of relativity, without my having succeeded in clarifying it.
Let’s explore the microstructure of time in more detail while repeating a few points that have already been made within the article. In mathematical physics that is used in both relativity theory and quantum theory, the ordering of instants by the happens-before relation of temporal precedence is complete in the sense that there are no gaps in the sequence of instants. Any interval of time is a continuum, so the points of time form a linear continuum. Unlike physical objects, physical time and physical space are believed to be infinitely divisible—that is, divisible in the sense of the actually infinite, not merely in Aristotle’s sense of potentially infinite. Regarding the density of instants, the ordered instants are so densely packed that between any two there is a third so that no instant has a very next instant. Regarding continuity, time’s being a linear continuum implies that there is a nondenumerable infinity of instants between any two non-simultaneous instants. The rational number line does not have so many points between any pair of different points; it is not continuous the way the real number line is, but rather contains many gaps. The real numbers such as pi and the square root of two help to fill the gaps.
The actual temporal structure of events can be embedded in the real numbers, at least locally, but how about the converse? That is, to what extent is it known that the real numbers can be adequately embedded into the structure of the instants, at least locally? This question is asking for the justification of saying time is not discrete, that is, not atomistic. The problem here is that the shortest duration ever measured is about 250 zeptoseconds. A zeptosecond is 10-21 second. For times shorter than about 10-43 second, which is the physicists’ favored candidate for the duration of an atom of time, science has no experimental grounds for the claim that between any two events there is a third. Instead, the justification of saying the reals can be embedded into the structure of the instants is that (i) the assumption of continuity is very useful because it allows the mathematical methods of calculus to be used in the physics of time; (ii) there are no known inconsistencies due to making this assumption; and (iii) there are no better theories available. The qualification earlier in this paragraph about “at least locally” is there in case there is time travel to the past. A circle is continuous, and one-dimensional, but it is like the real numbers only locally.
One can imagine two empirical tests that would reveal time’s discreteness if it were discrete—(1) being unable to measure a duration shorter than some experimental minimum despite repeated tries, yet expecting that a smaller duration should be detectable with current equipment if there really is a smaller duration, and (2) detecting a small breakdown of Lorentz invariance. But if any experimental result that purportedly shows discreteness is going to resist being treated as a mere anomaly, perhaps due to error in the measurement apparatus, then it should be backed up with a confirmed theory that implies the value for the duration of the atom of time. This situation is an instance of the kernel of truth in the physics joke that no observation is to be trusted until it is backed up by theory.
It is commonly remarked that, according to relativity theory, nothing can go faster than c, the speed of light, not even the influence of gravity. The remark needs some clarification, else it is incorrect. Here are three ways to go faster than the speed c. (1) First, the medium needs to be specified. c is the speed of light in a vacuum. The speed of light in certain crystals can be much less than c, say 40 miles per hour, and if so, then a horse outside the crystal could outrun the light beam. (2) Second, the limit c applies only to objects within space relative to other objects within space, and it requires that no object pass another object locally at faster than c. However, the general theory of relativity places no restrictions on how fast space itself can expand. So, two galaxies can fly apart from each other at faster than the speed c of light if the intervening space expands sufficiently rapidly. (3) Imagine standing still outside on the flat ground and aiming your (ideal, perfectly narrow beam) laser pointer forward and parallel to the ground. Now change the angle in order to aim the pointer down at your feet. During that process of changing the angle, the point of intersection of the pointer and the tangent plane of the ground will move toward your feet faster than the speed c. This does not violate relativity theory because the point of intersection is merely a geometrical object, not a physical object, so its speed is not restricted by relativity theory.
In 1916, Einstein claimed that his theory implies gravitational waves would be produced by any acceleration of matter. Drop a ball from the Leaning Tower of Pisa, and this will shake space-time and produce ripples that will emanate in all directions from the Tower. The existence of these ripples was confirmed in 2015 by the LIGO observatory (Laser Interferometer Gravitational-Wave Observatory) when it detected ripples caused by the merger of two black holes.
This sub-section has emphasized time and space, but according to relativity theory it is not just time and space that are relative. So are energy and mass. The energy you measure for some phenomenon differs depending on how fast you move and in what direction.
For more about special relativity, see Special Relativity: Proper Times, Coordinate Systems, and Lorentz Transformations.
3. Quantum Mechanics
In addition to relativity theory, the other fundamental theory of physics is quantum mechanics. According to the theory, the universe is fundamentally quantum. What this means is that everything fluctuates randomly. Kip Thorne gives this helpful example:
When we use high-precision instruments to look at tiny things, we see big fluctuations. The location of an electron inside an atom fluctuates so rapidly and so randomly, that we can’t know where the electron is at any moment of time. The fluctuations are as big as the atom itself. That’s why the quantum laws of physics deal with probabilities for where the electron is….
Quantum mechanics was developed in the late 1920s. At that time, it was applied to particles and not to fields. In the 1970s, it was successfully applied to quantum fields via the new theory called “quantum field theory.” There is considerable agreement among the experts that quantum mechanics and quantum field theory have deep implications about the nature of time, but there is little agreement on what those implications are.
Time is a continuum in quantum mechanics, just as it is in all fundamental classical theories of physics, but change over time is treated in quantum mechanics very differently than in all previous theories—because of quantum discreteness and because of discontinuous wave function collapse during measurement with a consequent loss of information.
First, let’s consider the discreteness. This discreteness is not shown directly in the equations, but rather in two other ways. (1) For any wave, according to quantum mechanics, there is a smallest possible amplitude it can have, called a “quantum.” Smaller amplitudes simply do not occur. As Hawking quipped: “It is a bit like saying that you can’t buy sugar loose in the supermarket, it has to be in kilogram bags.” (2) The possible solutions to the equations of quantum mechanics form a discrete set, not a continuous set. For example, the possible values of certain variables such as energy states of an electron within an atom are allowed by the equations to have values that change to another value only in multiples of minimum discrete steps in a shortest time. A single step is sometimes called a “quantum leap.” For example, when applying the quantum equation to a world containing only a single electron in a hydrogen atom, the solutions imply the electron can have -13.6 electron volts of energy or -3.4 electron volts of energy, but no value between those two. This illustrates how energy levels are quantized. However, in the equation, the time variable can change continuously and thus have any of a continuous range of real-number values.
Quantum mechanics is our most successful theory in all of science. One success is that the theory has been used to predict the measured value of the anomalous magnetic moment of the electron extremely precisely and accurately. The predicted value, expressed in terms of a certain number g, is the real number:
g/2 = 1.001 159 652 180 73…
Experiments have confirmed this predicted value to this many decimal places. This accuracy of one part in a trillion is analogous to measuring the distance to a footprint on the moon to within a hair’s width. No similar feat of precision and accuracy can be accomplished by any other theory of science.
The variety of phenomena that quantum mechanics can be used to successfully explain is remarkable. For four examples, it explains (1) why you can see through a glass window but not a potato, (2) why the Sun has lived so long without burning out, (3) why atoms are stable so that the negatively-charged electrons do not spiral into the positively-charged nucleus, and (4) why the periodic table of elements has the structure and numerical values it has. Without quantum mechanics, these four facts (and many others) must be taken to be brute facts of nature.
Regarding the effect of quantum theory on ontology, the world’s potatoes, galaxies and brains have been considered by a number of twentieth-century philosophers to be just different mereological sums of particles, but the majority viewpoint among philosophers of physics in the twenty-first century is that potatoes, galaxies and brains are, instead, fairly stable patterns over time of interacting quantized fields. Also, the 20th century debate about whether an electron is a point object or an object with a small, finite width has been settled by quantum field theory. It is neither. An electron takes up all of space; it is a “bump” or “packet of waves” with a narrow peak but that actually that trails off to trivially lower and lower amplitude throughout the electron field. The electron field itself fills all of space. A sudden disturbance in a field will cause wave packets to form, thus permitting particle creation. In short, a particle is an epiphenomenon of fields.
Scientists sometimes say “Almost everything is made of quantum fields.” They mean everything physical is made of quantum fields except gravity. Cows and electrons are made of quantum fields. But this is not claiming that the physicists have a solution to the notorious ontological problems of philosophy such as what songs, numbers, and chess games are made of.
Quantum mechanics is well tested and very well understand mathematically, yet it is not well understood intuitively or informally or philosophically or conceptually. One of the founders of quantum field theory, Richard Feynman, said he did not really understand his own theory. Surprisingly, physicists still do not agree on the exact formulation of the theory and how it should be applied to the world.
Three, among many, popular attempts to explain quantum mechanics are the Copenhagen interpretation, the hidden variables interpretation, and the many-worlds interpretation. The three are described below. They are proposed answers to the question, “What is really going on?” Because these interpretations have different physical principles and can make different experimental predictions, they are actually competing theories. That is also why there is no agreement on what the axioms of quantum mechanics are if it were ever to be formalized and axiomatized. For much of the history of the 20th century, many physicists resisted the need to address the question “What is really going on?” Their mantra was “Shut up and calculate” and do not explore the philosophical questions involving quantum mechanics. Turning away from a head-in-the-sand approach to quantum mechanics, Andrei Linde, co-discoverer of the theory of inflationary cosmology, said, “We [theoretical physicists] need to learn how to ask correct questions, and the very fact that we are forced right now to ask…questions that were previously considered to be metaphysical, I think, is to the great benefit of all of us.”
Quantum mechanics began as a non-relativistic particle theory in the 1920s. It now includes quantum field theory, which is quantum mechanics applied to quantum fields and obeying the laws of special relativity, but not general relativity. There reason for the change is that most physicists believe what had once been called a “particle” is really a group of vibrations in a quantum field, with any single vibration filling all of space. A particle is understood to be a wave packet of a wave that vibrates a million billion times every second and has a localized peak in amplitude but is nearly zero amplitude throughout the rest of space. If we use a definition that requires a fundamental particle to be an object with a precise, finite location, then quantum mechanics now implies there are no fundamental particles. For continuity with the past usage, particle physicists do still call themselves “particle physicists” and say they study “particles” and “the particles’ positions,” and other “particle behavior”; but they know this is not what is really going on. These terms are not intended to be taken literally, nor used in the informal sense of ordinary language. The particle language, though, is very often useful pretense because it is good enough for many scientific purposes such as in Feynman diagrams of quantum field theory to simplify what would otherwise be an enormously complex description requiring solutions of thousands of integrals.
Max Born, one of the fathers of quantum mechanics, first suggested interpreting quantum waves as being waves of probability. As Stephen Hawking explains it:
In quantum mechanics, particles don’t have well-defined positions and speeds. Instead, they are represented by what is called a wave function. This is a number at each point of space. The size of the wave function gives the probability that the particle will be found in that position. The rate at which the wave function varies from point to point gives the speed of the particle. One can have a wave function that is very strongly peaked in a small region. This will mean that the uncertainty in position is small. But the wave function will vary very rapidly near the peak, up on one side and down on the other. Thus the uncertainty in the speed will be large. Similarly, one can have wave functions where the uncertainty in the speed is small but the uncertainty in the position is large.
The wave function contains all that one can know of the particle, both its position and its speed. If you know the wave function at one time, then its values at other times are determined by what is called the Schrödinger equation. Thus one still has a kind of determinism, but it is not the sort that Laplace envisaged (Hawking 2018, 95-96).
As quantum mechanics is typically understood, if we want to describe the behavior of a system over time, then we start with its initial state, namely the wave function Ψ(x,t0) for places x and particular times t, and we insert this wave function into the Schrödinger wave equation that says how the wave function (that is, the state) changes over time. That equation is the partial differential equation:
i is the square root of negative one. h-bar is Planck’s constant divided by 2π, and H is the Hamiltonian operator. The state Ψ can be used (with some manipulation) to show the probability p(x,t) that a certain particle will be measured to be at place x at a future time t, if a measurement were made, where
p(x,t) = Ψ*(x,t)Ψ(x,t).
The asterisk is the complex conjugate operator, but let’s not delve any more into the mathematical details.
On most interpretations of quantum mechanics (but not for the Bohm interpretation) fundamental particles are considered to be waves, or, to speak more accurately, they are considered to be “wavicles,” namely entities that have both a wave and a particle nature, but which are never truly either. The electron that once was conceived to be a tiny particle orbiting an atomic nucleus is now better conceived as something larger and not precisely defined spatially, a cloud that completely surrounds the nucleus, a cloud of possible places where the electron could be found if it were to be measured. The electron or any other particle is no longer well-conceived as having a sharply defined trajectory. A wave cannot have a single, sharp, well-defined trajectory. The location and density distribution of the electron cloud around an atom is the product of two opposite tendencies: the electron-qua-wave “wants” to spread out away from the nucleus just as waves in a pond spread out away from the point where the rock fell into the pond, and the electron-qua-particle is a negatively-charged particle moving at high speed around the nucleus and that “wants” to reach the positive electric charge of the nucleus because opposite charges attract.
As goes the electron, so goes the human body. Ontologically, we humans are made of wavicles in quantum fields.
Indeterminism
An especially interesting philosophical question is whether quantum theory implies indeterminism, namely, that the state of the universe at one time does not determine all future states. This is still an open question, but the majority position is that it does imply indeterminism in our universe, and information is not conserved in our universe if measurement processes are included because measurements lose information.
The scientific ideal since Newton’s time has been that information is always conserved. If so, then physical determinism is true. That is, prediction of both all past states and all future states from one present state is theoretically possible, at least for Laplace’s Demon who knows all the laws and has no limits on its computational abilities. But in quantum mechanics, because it includes measurements, there could not be a Laplace’s Demon. Another way of expressing this same point is to point out that all possible available quantum information would not be enough for the Demon.
Let’s explain this a bit more. Consider the difference between practical predictions and theoretically possible predictions. There are three kinds of reasons why physicists cannot practically predict what will happen in the future: (1) It is too tedious of a job to acquire knowledge of the microstate of a system; the microstate is fixed by the locations and momenta of each of its zillions of molecules at the same time. (2) The equations to be used are just too complicated for us to solve even with the aid of computers and even if we were to completely know an initial state at a time. (3) Physical systems are often chaotic. For example, not accounting for a flap of a single butterfly’s wings at some instant in China last month can radically affect the predicted weather next month in France.
These practical obstacles are not obstacles for Laplace’s Demon who has unlimited knowledge of all that can be known, and who has unlimited computational power. Information about forces is not needed because in principle the Newtonian force equation F = ma allows the acceleration a to be computed from the information about velocity. But Laplace’s Demon has new problems. With the rise of quantum mechanics, scientists have had to revise their ideal of scientific determinism, for two reasons that set obstacles in principle and not just in practice: (1) The theory of quantum mechanics implies the wave function evolves deterministically, except during measurements. (2) Heisenberg’s Uncertainty Principle sets limits on the precise values of pairs of variables. For example, the more precise the position of a particle is fixed the less precisely is its velocity fixed.
According to the Copenhagen interpretation of quantum mechanics, which became the orthodox interpretation of the twentieth century, given how things are at some initial time, the Schrödinger equation describes not what will happen at later times, but only the probabilities of what will happen at later times. The probabilities imply indeterminism. The probabilities are not a product of the practical limitations on the human being’s ability to gather all the information about the initial state nor are the probabilities a product of the limits of the computers being used to help make predictions.
The presence of these irremovable probabilities indicates a characteristic randomness at the heart of nature. The probabilities rarely reveal themselves to us in our everyday, macroscopic experience because, at our scale, every value of the relevant probabilities is extremely close to one. Nevertheless, everything fluctuates randomly, even cows and moons.
According to quantum mechanics, a state of a system is described very differently from all earlier theories of physics. It is described using the Schrödinger wave function. The wave is not a wave similar to the electromagnetic wave that exists in our physical space; the wave is a mathematical tool. The state is represented as a vector in an infinite dimensional Hilbert space that is smooth and so continuous. Schrödinger’s wave function describes the state, and Schrödinger’s wave equation describes how the state changes deterministically from one time to another (except for measurements).
The theory of quantum mechanics is tied to physical reality by the Born Rule. This rule says the square of the amplitude of the wave function is proportional to the probability density function. To oversimplify a bit, what this means is that the Born Rule specifies for a time and place not what exactly will happen there then but only the probabilities of this or that happening there then, such as it being 5% probable an electron will be detected in this spatial region when a certain electron-detecting measurement is made at a certain time. So, probability is apparently at the heart of quantum mechanics and thus of Nature itself. For this reason, Max Born and then many other experts recommended thinking of the wave function as a wave of probabilities. Because of these probabilities, if you were to repeat a measurement, then the outcome the second time might be different even if the both initial states are the same. So, the key principle of causal determinism, namely “same cause, same effect,” fails.
The Copenhagen Interpretation
 The Copenhagen interpretation is a vague, anti-realist theory containing a collection of beliefs about what physicists are supposed to do with the mathematical formalism of quantum mechanics. This classical interpretation of quantum mechanics was created by Niels Bohr and his colleagues in the 1920s. It is called the Copenhagen interpretation because Bohr taught at the University of Copenhagen. According to many of its advocates, it has implications about time reversibility, determinism, the conservation of information, locality, the principle that causes affect the future and not the past, and the reality of the world independently of its being observed—namely, that they all fail.
The Copenhagen interpretation is a vague, anti-realist theory containing a collection of beliefs about what physicists are supposed to do with the mathematical formalism of quantum mechanics. This classical interpretation of quantum mechanics was created by Niels Bohr and his colleagues in the 1920s. It is called the Copenhagen interpretation because Bohr taught at the University of Copenhagen. According to many of its advocates, it has implications about time reversibility, determinism, the conservation of information, locality, the principle that causes affect the future and not the past, and the reality of the world independently of its being observed—namely, that they all fail.
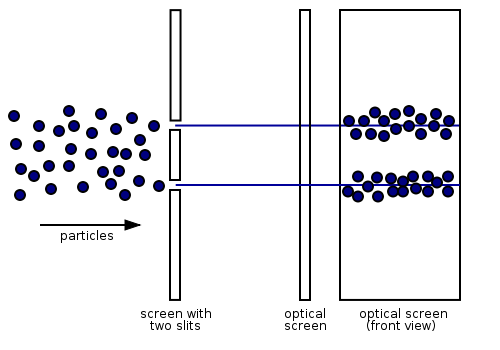
Let’s consider how a simple experiment can reveal quantum mechanics’ implications for how we should understand the world in a new way. In the famous double-slit experiment, which is a modern variant on Thomas Young’s double slit experiment that convinced physicists to believe that light was a wave, electrons all having the same energy are repeatedly ‘shot’ toward two parallel slits or openings in an otherwise impenetrable metal plate. Here is a diagram of the experimental set up when the electrons are observed passing through the slits:
The target shows two fuzzy rows where the electrons collide with the optical screen The optical screen that displays the dots behind the plate is similar to a computer monitor that displays a pixel-dot when and where an electron collides with it. The diagram is an aerial view or bird’s eye view of electrons passing through two slits in a plate (such as a piece of steel containing two narrow, parallel slits) and then hitting an optical screen that is behind two slits. The screen is shown twice, once in an aerial view and also in a full frontal view as seen from the left. The electrons can pass through the plate by entering through the plate’s left (upper) slit or right (lower) slit and can ricochet off the edges and each other. The slits are very narrow and are closely spaced apart. Bullets, pellets, BBs, grains of sand, and other macroscopic objects would produce an analogous pattern.
What is especially interesting is that the electrons behave differently depending upon whether they are being observed going through the slits. When observed, the electrons leave a pattern of only two parallel bands (thick, fuzzy lines) on the screen behind the plate as shown in the above diagram, but they behave differently when not observed at the slits.
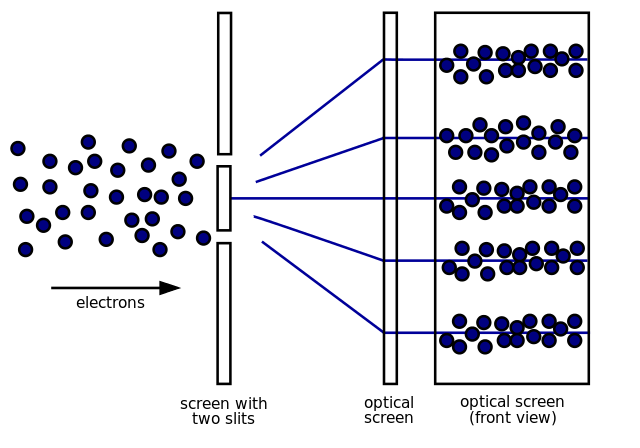
Here is a diagram of the experimental situation when the electrons are not observed at the slits:
When unobserved, the electrons leave a pattern of many alternating dark and bright bands on the screen as shown in the diagram above. This pattern is very similar to the pattern obtained by diffraction of classical waves such as water waves when they interfere with themselves either constructively or destructively after passing through two nearby openings in a wall at the water’s surface. When a wave’s trough meets a peak at the screen, no dot is produced. When two troughs meet at the screen, the result is a dot. Ditto for two peaks. There are multiple, parallel stripes produced along the screen, but only five are shown in the diagram. Stripes farther from the center of the screen are slightly dimmer. Waves have no problem going through two or more slits simultaneously. Because the collective electron behavior over time looks so much like optical wave diffraction, this is considered to be definitive evidence of electrons behaving as waves. The same pattern of results occurs if neutrons or photons are used in place of electrons.
The other remarkable feature of this experiment is that the pattern of interference is produced even when the electrons are shot one at a time at the plate over several minutes. One would not expect this result because presumably the phenomenon seems to depend on two electrons simultaneously travelling through separate slits and interacting with each other on the other side of the plate. But can an electron interact with itself from a few seconds earlier? The Princeton University physicist John Wheeler answered this question with a “yes,” which astounded his colleagues because this answer implies the present affects the past. But in his 1983 book Quantum Theory and Measurement, Wheeler declared: “Equipment operating in the here and now has an undeniable part in bringing about that which appears to have happened.”
The favored explanation of the double-slit experiment is to assume so-called “wave-particle duality,” namely that a single electron or neutron has both wave and particle properties. When an electron is unobserved, it is a wave that can be in many places at once, but when it is observed it is a particle having a specific location. This mix of two apparently incompatible properties (wave properties and particle properties) is called a “duality,” and the electron is said to behave as a “wavicle.”
Advocates of the Copenhagen Interpretation of quantum mechanics conclude that, when an electron is not observed at the moment of passing through the slits, it passes through both of the two slits, but not in the sense that a tiny bullet-like object is in two places at once but rather in the sense that the experiment’s state is a superposition of two states, one in which the electron goes through the left slit and one in which it goes through the right slit. Any measurement of which slit the electron goes through will “collapse” this superposition and force there to be a state in which the electron acts like a bullet and hits the region expected to be hit by a bullet-like object. The wave function Ψ suddenly becomes shaped like a spike. The term “collapse” means that the physical system abruptly stops being correctly described as having a deterministic evolution according to the Schrödinger equation, the equation of quantum mechanics that describes the evolution of quantum states. As David Alpert describes superposition, the wave function corresponding to a particle at slit A will have a bump near A and be zero everywhere else. The wave function for a particle located at slit B will have a bump near B and be zero everywhere else. The wave function that represents a particle in a superposition of being located at A and being located at B will have a bump at point A and a bump at point B and be zero everywhere else.
Advocates of superposition as a means of explaining the two slit experiment assume that, if it is not known what path is taken by the electron, then it is allowed to do everything possible simultaneously.
This positing of superposition is the most popular assumption, but, as will be explained below, many physicists object to the assumption and prefer to explain the double-slit experiment by positing that during the experiment physical time will “branch” into multiple times as the universe splits into many worlds or universes. In one world, an electron goes through the left slit; but in another world it goes through the right slit. This many-worlds interpretation is described below.
Influenced by Logical Positivism, which was dominant in analytic philosophy in the first half of the twentieth century, some advocates of the Copenhagen interpretation say that our belief that there is something a physical system is doing when it is not being measured is meaningless. In other words, a fully third-person perspective is impossible.
To explain the double-slit experiment, Niels Bohr proposed an instrumentalist interpretation of the world by saying there is no determinate, unfuzzy way the world is when it is not being observed. There is only a cloud of possible values for each property of the system that might be measured. Eugene Wigner, a Nobel Prize winning physicist, promoted the more extreme claim that there exists a determinate, unfuzzy reality only when a conscious being is observing it. This is an anti-realist interpretation that many have claimed was foreshadowed by the writing of Eastern mysticism. The interpretation prompted Einstein, an opponent of mysticism and anti-realism, to ask a supporter of Bohr whether he really believed that the moon exists only when it is being looked at.
Sympathetic to this attitude of Einstein’s, Erwin Schrödinger created his thought experiment about a cat in a windowless box. A vial of poison gas in the box has a 50% probability of being broken during the next minute depending on the result of a quantum event such as the fission of a radioactive uranium atom. If the vial is broken during the next minute, the cat is poisoned and dies. Otherwise it is not poisoned. According to Wigner’s version of the Copenhagen Interpretation, argued Schrödinger, if the box is not observed by a conscious being at the end of the minute, the cat remains in a superposition of two states, the cat being alive and the cat being dead, and this situation can continue for days until someone finally looks into the box. Schrödinger believed this Copenhagen interpretation of the cat in the box is absurd, so the Copenhagen interpretation is therefore false.
The double-slit experiment and the Schrödinger’s cat thought experiment have caused philosophers of physics to disagree about what an object is, what it means for an object to have a location, how an object maintains its identity over time, and whether consciousness of the measurer is required in order to make reality become determinate and “not fuzzy” or “not blurry.” There was speculation that perhaps a device that collapses the wave function could be used as a consciousness detector that would detect whether an insect or a computer has consciousness. Eugene Wigner and John von Neumann were the most influential physicists to suggest that perhaps consciousness collapses the wave function.
Einstein was unhappy with another implication of quantum theory, that one could know in principle everything there is to know about a system of particles, yet know nothing for sure about any part of the system such as the behavior of a single particle.
Reacting to the incompleteness demanded by the Copenhagen interpretation, Einstein proposed that there would be a future discovery of as yet unknown “hidden” variables. These are extra variables or properties that, when taken into account by a revised Schrödinger wave function, would make quantum mechanics be deterministic and thus representationally complete. Einstein believed you would not need probabilities if you had access to the precise values of all the variables affecting a system, including the variables that are currently hidden. In the 1950s, David Bohm agreed with Einstein and went some way in this direction by building a revision of quantum mechanics that has hidden variables and, unlike the Copenhagen Interpretation, has no instantaneous collapse of the wave function during measurement, but his interpretation has not succeeded in moving the needle of scientific opinion because of the difficulty of accounting for quantum field theory.
The quantum measurement problem is the problem of how to understand the process of measurement. It is quite a difficult problem, and it has occupied the very best minds among the community of physicists and philosophers of physics for many years. There has been controversy about whether it is merely a philosophical problem or also a scientific problem.
A measurement is often done by a conscious being, but a measurement in the most general sense of the term includes any interaction with anything external to the system that causes the system’s wave function to collapse into a single state rather than a state of superposition of the states with each indicating a different value for the measurement outcome. During measurement the system collapses into a definite state of whatever observable is being measured. The equations of quantum theory tell the probability for the collapse to a particular state. During the collapse, no laws of physics are changed, but important information is lost. What this means is that from a knowledge of the state of the situation after the measurement (in any single universe), one cannot compute the state before the measurement.
Wouldn’t you like to know the mechanism that produced the value of 4 when your measurement could have had the values of 1, 2, 3, 4, or 5? Quantum theory cannot give you an answer.
Classically, an ideal measurement need not disturb the system being measured. As first suggested by Werner Heisenberg, according to quantum mechanics this classical ideal of measurement is unachievable in principle; experimenters always disturb the system they are measuring, and the measurement causes loss of information. This disturbance happens locally and instantaneously. Also, because of the information loss, there is a fundamental time asymmetry in the measurement process so reversing the process in time need not take you back to the situation before the measurement began.
However, different quantum mechanical interpretations solve the measurement problem differently. According to the Copenhagen interpretation and many other interpretations, any measurement triggers the instantaneous collapse of the system’s quantum state from being a superposition of possible measurement outcomes to a single state with a definite measured outcome. This notion of instantaneous collapse conflicts with the theory of relativity which requires effects to move no faster than the speed of light in a vacuum. Unfortunately, creating an experiment to confirm any claim about the speed of the collapse of the wave function faces the obstacle that no practical measurement can detect such a short interval of time:
Yet what we do already know from experiments is that the apparent speed at which the collapse process sweeps through space, cleaning the fuzz away, is faster than light. This cuts against the grain of relativity in which light sets an absolute limit for speed (Andrew Pontzen).
The Copenhagen interpretation implies that, during the measurement process, the continuous evolution of the wave function halts abruptly, and the wave function “collapses” from a superposition of multiple possible states of the system under investigation to a single state with a single, definite value for whatever is being measured. Using a detector to measure which slit the electron went through in the double-slit experiment is the paradigm example. Before the measurement, the system’s state is a superposition of two states: the electron going through the left slit and the same electron going through the right slit simultaneously. But during the measurement the superposition collapses. If an observer determines which slit the electron goes through, then this interferes with what is being measured, and the interference pattern beyond the slits collapses or disappears and the electrons act like small, discrete particles.
Here is a simple, crude analogy that has been pedagogically helpful. Think of electrons as if they are spinning coins on a table top. They are neither heads up nor tails up until your hand pushes down on the coin, forcing it to have just one of the two possibilities. Your hand activity is the measurement process.
The Copenhagen interpretation implies that a measurement apparatus itself cannot be in a superposition, nor can an observer, nor can a universe. Quantum theory on the Copenhagen interpretation cannot apply to everything because it necessarily must split the universe into a measured part and an unmeasured part, and it can describe only the measured part but not the process of measurement itself nor what is happening when there is no measurement. So, in that sense, this quantum theory is an incomplete theory of nature, as Einstein so often emphasized. Einstein was very dissatisfied with the Copenhagen interpretation’s requirement that, during any measurement, the usual principles of quantum mechanics stop applying. Einstein wanted a quantum theory that describes the world without mentioning measuring instruments or the terms “measurement” and “collapse.” He wanted what is called “completeness.”
In response to this understanding of quantum measurement, the influential physicist John Bell said, “Bohr was inconsistent, unclear, willfully obscure, and right. Einstein was consistent, clear, down-to-earth, and wrong.” Bohr’s style of writing was very Hegelian. He is noted for saying, “Clarity crowds out depth!”
According to the Copenhagen Interpretation, during any measurement the wave function expressing the possible values of the measurement collapses to one with the actual value. The other possibilities are deleted. And quantum information is quickly lost. The measurement process is irreversible. So, during any measurement, from full knowledge of the new state after the measurement, the prior state cannot be deduced, even by Laplace’s Demon. Different initial states may transition into the same final state. So, the following classical principles fail: time reversibility, conservation of information, and determinism.
When a measurement occurs, it is almost correct to explain this as follows: At the beginning of the measurement, the system “could be in any one of various possibilities, we’re not sure which.” Strictly speaking, this is not quite correct. Before the measurement is made, the system is actually in a superposition of multiple states, one for each possible outcome of the measurement, with each outcome having a fixed probability of occurring as determined by the formalism of quantum mechanics; and the measurement itself is a procedure that removes the superposition and realizes just one of those states. Informally, this is sometimes summarized in the remark that measurement turns the situation from fuzzy to definite.
For an instant, a measurement on an electron can say it is there at this specific place, but immediately afterward, due to some new interaction, the electron becomes fuzzy again, and once again there is no single truth about precisely where an electron is, but only a single truth about the probabilities for finding the electron in various places if certain kinds of measurements were to be made.
The measurement problem is really an unsolved scientific problem, not merely a problem of interpretation. Following the lead of Einstein’s complaints in the 1930s, there has been growing dissatisfaction with the Copenhagen’s requirement that, during a measurement of quantum properties, quantum mechanics fails to apply to the measurement situation because of a collapse. Many opponents of the Copenhagen Interpretation have reacted in this way:
In the wake of the Solvay Conference (in 1927), popular opinion within the physics community swung Bohr’s way, and the Copenhagen approach to quantum mechanics settled in as entrenched dogma. It’s proven to be an amazingly successful tool at making predictions for experiments and designing new technologies. But as a fundamental theory of the world, it falls woefully short (Sean Carroll).
George Ellis, co-author with Stephen Hawking of the influential book The Large-Scale Structure of Space-Time, identifies what he believes is a key difficulty with our understanding of collapse during measurement: “Usually, it is assumed that the measurement apparatus does not obey the rules of quantum mechanics, but this [assumption] contradicts the presupposition that all matter is at its foundation quantum mechanical in nature.”
Those who want to avoid having to bring consciousness of the measurer into quantum physics and who want to restore time-reversibility and determinism and conservation of quantum information typically recommend adopting a different interpretation of quantum mechanics that changes how measurement is treated. Einstein had a proposal for an original theory of quantum mechanics, the Hidden Variables interpretation. He hoped that by adding new laws specifying the behavior of so-called “underlying variables” affecting the system, the consequence would be that determinism, time-reversibility, and information conservation would be restored, and there would be no need to speak of a discontinuous collapse of the wave function during measurement. Also, quantum probabilities would be epistemological; they would be caused by our lack of knowledge of the extra variables. Nature herself wouldn’t have any imprecision. Challenging Einstein’s proposal, John Bell showed that any hidden variable assumption designed to make quantum mechanics deterministic would produce the so-called “Bell inequalities.” Later experiments in the 21st century showed that the inequalities fail. So, Einstein’s proposal never gathered much support.
During the twentieth century, the Copenhagen interpretation continued to be accepted as the principal way to understand quantum mechanics, but it has been in decline in the 21st century among experts, if not in all the graduate school textbooks. The main problem is to give a better explanation of the Copenhagen “collapse.” Nevertheless, either the wave function actually does collapse, or else something is happening that makes it look very much as if the wave function collapses. What is this “something”?
The philosophical background of the measurement problem began with the 18th century dispute between rationalists and empiricists. Speaking very loosely, the empiricist wanted to get the observer out of the system being measured, and the rationalist said that the observer is inextricably bound to the system being observed. So, quantum mechanics according to the Copenhagen Interpretation has an original notion of what it is to control an experiment.
The Many-Worlds Interpretation and Branching Time
According to the Many-Worlds interpretation of quantum mechanics, there are no collapses, and anything that can happen according to quantum mechanics in our universe does happen in some universe or other. If at noon you could go to lunch or stay working in your office, then at noon the universe branches into two universes, one in which you go to lunch at noon, and one in which you stay working in your office at noon. This interpretation requires a revision in the meaning of the terms “universe,” “world” and “you.”
That is the maximalist interpretation of the Many-World interpretation and the one that has attracted the most attention from philosophers of physics.
The universe according to the Many-Worlds interpretation is deterministic, and information is always conserved; but a single world is not deterministic nor is information conserved there. The Many-Worlds interpretation produces the same probabilities for a prediction in our actual world as does the Copenhagen interpretation. But if Laplace’s Demon were to have access to all the quantum information in the multiverse at one instant, it could tell you the outcome of any measurement made in our world or any other world at any time in the future or past. In short, quantum information is conserved in the sum of all worlds, though not in our actual world.
Saying the universe splits into many worlds is a higher-level emergent claim that helps humans understand what happens during certain changes, but actually the universe’s wave function evolves smoothly and continuously over time. Over time there is more branching, more entanglement, and more entropy.
The Many-Worlds proposal is attractive to many philosophers of physics because it has the virtue that it removes the radical distinction between the measurer and what is measured and replaces it with a continuously evolving wave function for the combined system of measurement instruments plus measurer (for the entire collection of worlds). During a measurement, it will appear to a person within a single world as if there is a collapse of the world’s wave function, but the wave function for the totality of worlds does not actually collapse. The laws of the Many-Worlds interpretation are time-reversible symmetric and deterministic in the sense described above, they conserve quantum information, and there is no need for the anti-realist stance taken by Bohr.
The worlds of the Many-Worlds Interpretation are not sprinkled throughout space with some existing before or after others. Instead, space and time exist only within single worlds. The Many-Universe Interpretation to be discussed below does not treat space and time this way.
It is an open question for the Many-World interpretation whether the same fundamental scientific laws hold in all universes. And it is an open question whether to take the universes literally or, instead, to say they are helpful “bookkeeping devices.”
The Many-Worlds interpretation is frequently called the Everettian interpretation for its founder Hugh Everett III. It implies that, during any measurement (or possible measurement) having some integer number n of possible outcomes, our world splits instantaneously into n copies of itself, each with a different outcome for the measurement. If a measurement can produce any value from 0 to 10, and we measure the value to be “8,” then the counterparts of us who live in the other worlds and who have the same memories as us see an outcome other than “8”. Clearly, the weirdness of the Copenhagen theory has been traded for a new kind of weirdness.
In the Many-Worlds interpretation, there is no access from one world to another. They exist “in parallel” and not within the same physical space, so any two are neither far from nor close to each other. Instead, space exists within a world, each world having its own space. Information is conserved across the worlds, but not within any single world. If we had access to all information about all the many worlds (the collective wave function) and had unlimited computational capacity like Laplace’s Demon, then we could see that the many worlds evolve deterministically and time-reversibly and see that the collective wave function never collapses discontinuously. Unfortunately, nobody can know the exact wave function for the entire multiplicity of worlds. In a single world, the ideally best available information implies only the probability of a measurement outcome, not an exact value of the measurement. So, in this sense, probability and randomness remain at the heart of our own world.
As we have seen above, the Many-Worlds theory does not accept the Copenhagen version of measurement collapse. Instead, it implies that, when a system is measured, all that is required is that the system interact with and become entangled with its environment during the measurement, thereby producing a single value for the measurement. This interaction process is called “decoherence.” So, in the two-slit experiment, the electron does not go into a superposition state but rather the universe splits into two universes, one in which the electron goes through the left slit and a completely separate universe in which the electron goes through the right slit. The many-worlds theory implies measurement is a reversible process, as are all other processes.
Most interactions are strong enough to produce decoherence; so, it takes very careful work to create the kind of interaction that preserves coherence. Preserving coherence is the most difficult goal to achieve in the construction of a quantum computer, and cooling is one of the main techniques used to achieve the goal. Interactions that cause decoherence are called “noise” in a quantum computer.
According to the Many-Worlds theory, the moon is there when it is not being looked at because the moon is always interacting with some particle or other and thereby decohering and, in that sense, getting measured. Decoherence is also why the moon’s quantum properties are not visible to us at our macroscale. Nevertheless, the moon is a quantum object (an object obeying the rules of quantum theory), as are all other objects.
The multiverse of the Many-Worlds theory is a different multiverse from the multiverse of chaotic inflation that is described below in the section about extending the big bang theory. Those universes produced by inflation exist within a single background physical space, unlike in the multiverse of the Many-Worlds theory of quantum mechanics where space exists only within a single world. However, in both kinds of multiverse time is better envisioned, not as linear, but rather as increasingly branching into the times of the new universes. It is extremely likely that there will be no un-branching nor branch removal nor branch fusing. At any time in any universe, that universe had relatively fewer branches in the past, and this feature will continue forever. The future is “a garden of forking paths,” said Jorge Luis Borges. If Leibniz were alive, he might say we live in the best of all possible branches.
Even though every expert agrees on what the wave function is doing mathematically and that it gets new parts when there is an interaction, including a measurement, not every expert wants to say a new part is literally describing a new world; some experts consider this to be ontological overreach. But Carroll’s book Something Deeply Hidden defends the claim that the multiverse theory satisfies Occam’s Razor better than all competitors.
What the Copenhagen theory calls quantum fuzziness or a superposition of states, Everett calls a superposition of many alternate, unfuzzy universes. The reason that there is no problem with energy conservation is that, if a world splits into seven new worlds, then each new world has one-seventh the energy of its parent world.
A principal problem for the many-worlds interpretation is the difficulty of explaining how the concept of a probability measure works across many worlds. For example, it is unclear what it means to say the electron went through the left slit in 50% of the worlds.
Some researchers have suggested there is a problem with showing that the Many-Worlds interpretation is logically consistent with what else we know. Other problems exist such as the fact that experts do not agree on whether the quantum wave function is a representation of reality, or only of our possible knowledge of reality. And there is no consensus on whether we currently possess the fundamental laws of quantum theory, as Everett believed, or instead only an incomplete version of the fundamental laws, as Einstein believed.
Heisenberg’s Uncertainty Principle
In quantum mechanics, various Heisenberg Uncertainty Principles restrict the simultaneous values of pairs of variables, for example, a particle’s position and momentum. The values cannot both be zero at the same time. Another Heisenberg uncertainty principle places the same restriction on time and energy, such as during particle emission or absorption.
The Copenhagen Interpretation presented the uncertainty principle as being about measurement restrictions and about disturbing a system by measuring it. As Sean Carroll emphasizes, this misunderstands the principle. He argues that the Uncertainty Principle is not about measurements, although it has implications about measurements. It is about what states exist, and it says there exists no state in which a particle has a precise position and momentum at the same time. It is not about a limitation on our knowledge of the state; it is not implying there is a precise position and momentum, but we measurers are limited in what we can know about this. The Heisenberg Uncertainty Principle has nothing to do with whether a measurement does or does not disturb a system (by, for example, bombarding it with a photon). The principle is a claim about nature independent of whether a measurement is ever made, says Carroll, and it describes the inherent fuzziness of nature.
Epistemological uncertainty differs from ontological uncertainty. We are referring to epistemological uncertainty when we say, “I am uncertain. I just don’t know.” We are referring to ontological uncertainty when we say, “Things are inherently fuzzy. They are not determinate.” Most theoretical physicists believe the Heisenberg Uncertainty Principle of quantum mechanics is about ontological uncertainty.
Those who prefer epistemological uncertainty often recommend thinking about having a very sharp photograph of a moving ball, such as a tennis ball taken during a tennis match. The photograph provides precise information about where the ball is, but not where it is going or how fast it is moving. On the other hand, think about having a time-lapse photograph showing the ball as a blurry streak. This photograph gives you considerable information about where the ball is going and how fast it is moving, but provides little information about where the ball is at a specific time. On its epistemological interpretation, Heisenberg’s Uncertainty Principle is a constraint saying you can have one of the two photographs but not both. Nature herself “has” both photographs, but your knowledge is restricted to at best one photograph.
Experts are still unsure how well they understand quantum measurement, and they worry they may have to alter the story if quantum measurement becomes better understood.
Quantum uncertainties of measurement do not appear in a single measurement. They are detected over a collection of measurements because any single measurement has (in principle and not counting practical measurement error) a precise value and is not “fuzzy” or uncertain or indeterminate. Repeated measurements necessarily produce a spread in values that reveal the fuzzy, wavelike characteristics of the phenomenon being measured, and these measurements collectively obey the Heisenberg inequality. Heisenberg himself thought of his uncertainty principle as being about how the measurer necessarily disturbs the measurement and not about how nature itself does not have definite values.
The Heisenberg Uncertainty Principle about energy is commonly said to be a loan agreement with nature in which borrowed energy must be paid back. There can be temporary violations in the classical law of the conservation of energy as the borrowing takes place. The classical law of conservation says the total energy of a closed and isolated system is always conserved and can only change its form but not disappear or increase. For example, a falling rock has kinetic energy of motion during its fall to the ground, but when it collides with the ground, the kinetic energy changes its form to extra heat in the ground, extra heat in the rock, and the sound energy of the collision. No energy is lost in the process. This classical law can be violated in two ways: (1) if the universe (or the isolated system being studied) expands in volume, and (2) by being violated by an amount –E for a time –t, as described by Heisenberg’s Uncertainty Principle. The classical law is often violated for very short time intervals and is less likely to be violated as the time interval increases. Some philosophers of physics have described this violation as something coming from nothing and as something disappearing into nothing, which is misleading to people who use these terms in their informal sense instead of the sense intended by quantum field theory. The quantum “nothing” or quantum vacuum, however, is not really what many philosophers call “nothing.” Quantum field theory (rather than quantum mechanics) does contain a more sophisticated law of conservation of energy that has no violations and that accounts for the deviations from the classical law.
Virtual Particles, Wormholes, and Quantum Foam
Quantum theory and relativity theory treat the vacuum radically differently from each other. Quantum theory’s vacuum contains virtual particles and probably a “foam” of them. Quantum theory requires virtual particles to be created out of the quantum vacuum via spontaneous, random quantum fluctuations—due to Heisenberg’s Uncertainty Principles. Because of this behavior, no quantum field can have a zero value at any place for very long.
Despite their name, virtual particles are real, but they are unusual, because they borrow energy from the vacuum and pay it back very quickly, so quickly that they cannot be detected with our instruments. What happens is that, when a pair of energetic virtual particles—say, an electron and anti-electron—form from “borrowed” energy in the vacuum, the two exist for a short time before being annihilated or reabsorbed, thereby giving back their borrowed energy. The greater the energy of the virtual pair, the shorter the duration of their existence before being reabsorbed. The more energy that is borrowed, the quicker it is paid back.
There are never any isolated particles because elementary particles are surrounded by a cloud of virtual particles. Many precise experiments can be explained only by assuming there is this cloud. Without assuming the existence of virtual particles, quantum theory would not be able to predict this precise value of the electron’s magnetic moment
g/2 = 1.001 159 652 180 73…
that agrees to this many significant digits with our most careful measurements. So, physicists are confident in the existence of virtual particles.
An electron is continually surrounded by virtual photons of temporarily borrowed energy. Some virtual photons exist long enough to produce electron-positron pairs, and these buffet the electron they came from. This buffeting produces the so-called “Lamb shift” of energy levels within an atom.
Virtual particles are not exactly particles like the other particles of the quantum fields. Both are excitations of these fields, and they both have gravitational effects and thus effects on time, but virtual particles are not equivalent to ordinary quantum particles, although the longer lived ones are more like ordinary particle excitations than the short lived ones.
Virtual particles are just a way to calculate the behavior of quantum fields, by pretending that ordinary particles are changing into weird particles with impossible energies, and tossing such particles back and forth between themselves. A real photon has exactly zero mass, but the mass of a virtual photon can be absolutely anything. What we mean by “virtual particles” are subtle distortions in the wave function of a collection of quantum fields…but everyone calls them particles [in order to keep their names simple] (Carroll 2019, p. 316).
The physicist John Wheeler suggested that the ultramicroscopic structure of spacetime for periods on the order of the Planck time (about 5.4 x 10-44 seconds) or less in regions about the size of the Planck length (about 1.6 x 10-35 meters) is a quantum foam of rapidly changing curvature of spacetime, with micro-black-holes and virtual particle-pairs and perhaps wormholes rapidly forming and dissolving. There is chaos in the tiniest realms if Wheeler is correct.
The Planck time is the time it takes light to travel a Plank length in a vacuum. The terms Planck length and Planck time were inventions of Max Planck in the early twentieth-century during his quest to find basic units of length and time that could be expressed in terms only of universal constants. He defined the Planck unit of time algebraically as √(ħG/c5). √ is the square root symbol. ħ is Planck’s constant in quantum theory divided by 2π; G is the gravitational constant in Newtonian mechanics; c is the speed of light in a vacuum in relativity theory. Three different theories of physics are tied together in this one expression. The Planck time is a theoretically interesting unit of time, but not a practical one. No known experimental procedure can detect events that are this brief.
Positive but indirect evidence for the existence of quantum foam comes from careful measurements of the Casimir Effect between two mirrors or conducting plates, in which as they get very near to each other there is a new force that starts pushing them even closer. But Kip Thorne warned us in 2014: “Back in the 1950s John Wheeler gave persuasive arguments for quantum foam, but there is now evidence that the laws of quantum gravity might suppress the foam and might even prevent it from arising.”
Another remarkable, but speculative, implication about virtual particles is that it seems to many physicists that it is possible in principle to connect two black holes into a wormhole and then use the hole for time travel to the past. “Vacuum fluctuations can create negative mass and negative energy and a network of wormholes that is continually fluctuating in and out of existence…. The foam is probabilistic in the sense that, at any moment, there is a certain probability the foam has one form and also a probability that it has another form, and these probabilities are continually changing” (Kip Thorne). The foam process can create a negative energy density and thus create exotic matter whose gravity repels rather than attracts, which is the key ingredient needed to widen a wormhole and turn it into a time machine for backward time travel that would be usable by human beings. A wormhole is a tunnel through space and time from one place to another in which your travel through the hole could allow you to reach a place before anyone moving at the speed of light or less, but not through the hole, had time to get there. Without sufficient negative gravitational force in its neck connecting its two opening holes, it has a natural tendency to close its neck, that is, “pinch off” to a width with zero diameter. For a popular-level discussion of how to create this real time machine as opposed to a science fiction time machine, see the book The Warped Side of Our Universe: An Odyssey Through Black Holes, Wormholes, Time Travel, and Gravitational Waves by Kip Thorne and Lia Halloran, 2023. Thorne says: “One way to make a wormhole, where previously there was none, is to extract it from the quantum foam…, enlarge it to human size or larger, and thread it with exotic matter to hold it open.” Later in the present article, there is more explanation of the negative gravitational energy of this exotic matter.
Another controversial implication about virtual particles is that there is a finite but vanishingly small probability that a short-lived potato or brain will spontaneously fluctuate out of the vacuum in your closet tomorrow. If such an improbable event were to happen, many persons would be apt to say that a miracle had happened, and God had temporarily intervened and suspended the laws of science.
Entanglement and Non-Locality
Schrodinger introduced the term “entanglement” in 1935 to describe what is perhaps the strangest feature of quantum mechanics. Yet it is an experimentally well-confirmed feature of reality.
When two particles become entangled, they can no longer be treated independently of each other because their properties are tied together even if they move a great distance away from each other. Normally we can fully describe an object without referring to objects elsewhere, but this feature called “locality” fails in the case of entanglement. Locality is the feature that implies an object is influenced directly only by its immediate surroundings. The distant sun influences our skin on Earth, but not directly—only indirectly by sending photons that eventually collide with our skin. Most versions of quantum theory imply that locality fails to be a universal feature of our universe. Einstein was bothered more by quantum mechanics’ non-local entanglement than by either its indeterminism or its uncertainty principles or the breakdown of the idea that knowing a whole you still do not know any part for sure. He was the first person to clearly see that quantum mechanics is local but incomplete or else complete but non-local. He hoped for the incompleteness.
If two particles somehow become entangled, this does not mean that, if you move one of them, then the other one moves, too. It is not that kind of entanglement. If you act on one member of an entangled pair, nothing happens to the other member. So, entanglement cannot be used as a means of message transfer. Entanglement is only a correlation. Normally, when an entangled pair is created in a laboratory, the two are very close in space to each other, but they can stay entangled as they move far from each other. A quantum measurement by Alice of a certain property of one member of an entangled pair of particles will instantaneously or nearly instantaneously determine the value of that property that would be found by Bob if he were to make a similar measurement on the other member of the pair, no matter how far away the two particles are from each other and no matter the duration between the two acts of measuring. So, Alice and Bob’s measurement processes can be space-like separated from each other.
In a letter to Max Born in 1947, Einstein referred to non-locality pejoratively as “spooky action at a distance.” Most physicists still use the term, but actually it is not a causal action. It is a spooky correlation over a distance. It is a way of propagating definiteness, not information. Non-locality is very unintuitive, but the most favored explanation of the experimental data (involving measuring one particle in a pair of entangled particles and thereby fixing the measured value of the other particle) is that neither particle has a definite value for the property to be measured until after the first particle is measured, after which the second one’s value is fixed instantaneously. This implies that quantum theory does not allow Alice to know the specific value of her measurement before it is made, so she cannot know in advance what value Bob will measure. Thus she cannot send information to Bob instantaneously.
In 1935, Erwin Schrödinger said:
Measurements on (spatially) separated systems cannot directly influence each other—that would be magic.
Einstein agreed. Yet the magic seems to exist. “I think we’re stuck with non-locality,” said John Bell.
Entanglement comes in degrees. Ontologically, the key idea about quantum entanglement is that if a particle becomes entangled with one or more other particles within the system, then it loses some of its individuality. The whole system becomes more than the sum of its parts. The state of an entangled group of particles is not determined by the sum of the states of each separate particle. In that sense, quantum mechanics has led to the downfall of classical reductionism.
Failure of locality of a system arises only during measurement. When measurement is not involved, quantum theory is a local theory. When you measure one of two entangled particles, that breaks the entanglement. The breaking is called decohering.
Many physicists believe entanglement is linked to the emergence of space in the sense that if we were to know the degree of entanglement between two quantum particles, then we could derive the distance between them. Some of them speculate that time also is a product of quantum entanglement. To settle that issue, entanglement needs to be better understood.
The philosopher David Albert has commented that “In order to make sense of this ‘instaneity’ of the quantum correlation, it looks as if there is a danger that one may require an absolute notion of simultaneity of exactly the kind that the special theory of relativity denied.” The philosopher Huw Price speculated in (Price 1996) that nonlocal processes are really backwards causal processes with effects occurring before their causes. Juan Maldacena has conjectured that entanglement of two objects is really a wormhole connecting the two. Leonard Susskind has emphasized that it is not just particles that can become entangled. Parts of space can be entangled with each other, and he conjectures that it is this entanglement that “holds space together.”
Quantum tunneling
Quantum mechanics allows tunneling in the sense that a particle can penetrate through a potential energy barrier that is higher in energy than the particle should be able to penetrate according to classical theory. For example, according to quantum mechanics, there is a chance that, if a rock is sitting quietly in a valley next to Mt. Everest, it will leave the valley spontaneously and pass through the mountain and appear intact on the other side. The probability is insignificant but not zero. It is an open question in physics as to how long it takes the object to do the tunneling. Some argue that the speed of the tunneling is faster than light speed. The existence of quantum tunneling is accepted because it seems to be needed to explain some radioactive decays, and some chemical bonds, and how sunlight is produced by protons in our sun overcoming their mutual repulsion and fusing.
Approximate Solutions
Like the equations of the theory of relativity, the equations of quantum mechanics are very difficult to solve and use except in very simple situations. The equations cannot be used directly in digital computers. There have been many Nobel-Prize winning advances in chemistry by finding methods of approximating quantum theory in order to simulate the results of chemical activity within a computer. For one example, Martin Karplus won the Nobel Prize for chemistry in 2013 for creating approximation methods for computer programs that describe the behavior of the retinal molecule in our eye’s retina. The molecule has almost 160 electrons, but he showed that, for describing how light strikes the molecule and begins the chain reaction that produces the electrical signals that our brain interprets during vision, chemists can successfully use an approximation; they need to pay attention only to the molecule’s outer electrons.
Emergent Time and Quantum Gravity
There has been much speculation about the role of time in a theory of quantum gravity, a theory of quantum mechanics that reconciles its differences with general relativity. Perhaps the new theory will need to make use of special solutions to the Schrödinger equation that normally are not discussed—solutions describing universes that don’t evolve at all. For these solutions, there is no time, and the quantum state is a superposition of many different classical possibilities:
In any one part of the state, it looks like one moment of time in a universe that is evolving. Every element in the quantum superposition looks like a classical universe that came from somewhere, and is going somewhere else. If there were people in that universe, at every part of the superposition they would all think that time was passing, exactly as we actually do think. That’s the sense in which time can be emergent in quantum mechanics…. This kind of scenario is exactly what was contemplated by physicists Stephen Hawking and James Hartle back in the early 1980s (Carroll 2016, 197-9).
a. Standard Model
The Standard Model of particle physics was proposed in the 1970s, and subsequently it has been revised and well tested. The Model is designed to describe elementary particles and the physical laws that govern them. The Standard Model is really a loose collection of theories describing seventeen different particle fields except for gravitational fields. It is our civilization’s most precise and powerful theory of physics. It originally was called a model, but now has the status of a confirmed theory. Because of this it probably should not be called a “model” because it does not contain simplifications as do other models, but its name has not changed over time.
The theory sets severe limits of what exists and what can possibly happen. The Standard Model implies that a particle can be affected by some forces but not others. It implies that a photon cannot decay into two photons. It implies that protons attract electrons and never repel them. It also implies that every proton consists in part of two up quarks and one down quark that interact with each other by exchanging gluons. The gluons “glue” the particles together via the strong nuclear force just as photons glue electrons to protons via the electromagnetic force. Unlike how Isaac Newton envisioned forces, all forces are transmitted by particles. That is, all forces have carrier particles that “carry” the force from one place to another.
For example, consider how the photon is treated in the Standard Model. The exchange of gluons within the proton “glues” its constituent quarks together and keeps them from escaping. More than 90% of the mass of the proton is not due to the mass of its quarks. It is due to a combination of virtual quarks, virtual antiquarks and virtual gluons. Because the virtual particles exist over only very short time scales, they are too difficult to detect by any practical experiment, and so they are called “virtual particles.” However, this word “virtual” does not imply “not real.”
The properties of spacetime points that serve to distinguish any particle from any other are a spacetime point’s values for mass, spin, and charge at that point. Nothing else. There are no other differences among what is at a point, according to the Standard Model, so in that sense fundamental physics is very simple. If we are talking about a point inside a pineapple, what about the value of its pineapple-ness? In principle, according to the Standard Model, the pineapple’s characteristics depend only on these other, more fundamental characteristics. Charge, though, is not simply electromagnetic charge. There are three kinds of color charge for the strong nuclear force, and two kinds of charge for the weak nuclear force. In the atom’s nucleus, the strong force holds two protons together tightly enough that their positive electric charges do not push them away from each other. The strong force also holds the three quarks together inside a proton. The weak force turns neutrons into protons and spits out electrons. It is the strangest of all the forces because it allows some rare exceptions to symmetry under T, the operation of time transformation. (T is the transformation that reverses all processes).
Except for gravity, the Standard Model describes all the universe’s forces. Strictly speaking however, these theories are about interactions rather than forces. A force is just one kind of interaction. Another kind of interaction does not involve forces but rather changes one kind of particle into another kind. The neutron, for example, changes its appearance depending on how it is probed. The weak interaction can transform a neutron into a proton. It is because of transformations like this that the concepts of something being made of something else and of one thing being a part of a whole become imprecise for very short durations and short distances. So, classical mereology—the formal study of parts and the wholes they form—fails at this scale.
The concept of interaction is very exotic. When a particle interacts with another particle, the two particles exchange other particles, the so-called carriers of the interactions. So, when milk is spilled onto the floor, what is going on is that the particles of the milk and the particles in the floor and the particles in the surrounding air exchange a great many carrier particles with each other, and the exchange is what is called “spilling milk onto the floor.” Yet all these varied particles are just tiny fluctuations of fields. This scenario indicates one important way in which the scientific image has moved very far away from the manifest image.
According to the Standard Model, but not according to general relativity theory, all particles must move at light speed c unless they interact with other fields. All the particles in your body such as its protons and electrons would move at the speed c if they were not continually interacting with the Higgs Field. The Higgs Field can be thought as being like a “sea of molasses” that slows down all protons and electrons and gives them the mass and inertia they have. “All mass is interaction,” said Richard Feynman. Neutrinos are not affected by the Higgs Field, but they move slightly less than c because they are slightly affected by the field of the weak interaction. Of all the particles described by the Standard Model of Particle Physics, the Higgs boson is the strangest.
The Standard Model helps explain what is happening in an atomic clock when an electron in a cesium atom changes energy levels and radiates some light indicating the clock is properly tuned. The Standard Model implies that the electron, being a localized vibration in the electron field suddenly vibrates less, thereby loses energy, and the lost energy is transferred to the electromagnetic field, creating a localized vibration there is a new photon.
As of the first quarter of the twenty-first century, the Standard Model is incomplete because it cannot account for gravity or dark matter or dark energy or the fact that there is more matter than anti-matter. When a new version of the Standard Model does all this, then it will perhaps become the long-sought “theory of everything.”
4. Big Bang
The big bang theory in some form or other (with or without inflation) is accepted by nearly all cosmologists, astronomers, astrophysicists, and philosophers of physics, but it is not as firmly accepted as is the theory of relativity and is not part of the Core Theory of Physics.
The big bang theory is our civilization’s standard model for cosmology. The classical version of the big bang theory implies that the universe once was extremely small, extremely dense, extremely hot, nearly uniform, at minimal entropy, expanding; and it had extremely high energy density and severe curvature of its spacetime at all scales. Now the universe has lost all these properties except one: it is still expanding.
Some cosmologists believe time began with the big bang 13.8 billion years ago, at the famous cosmic time of t = 0, but the classical big bang theory itself does not imply anything about when time began, nor whether anything was happening before the big bang, although those features could be added into a revised theory of the big bang.
As far as is known, the big bang explosion was a rapid expansion of space itself, not an expansion of something into a pre-existing void. Think of the expansion as being due to the creation of new space everywhere very quickly. Space has no center around which it expanded. As the universe expanded, it diluted. It probably expanded in all directions almost evenly, and it probably did not produce any destruction. As it expanded, some of the energy was converted into matter (via E=mc2) until finally the first electrons were created; and later, the first atoms.
The big bang theory is only a theory of the observable universe, not of the whole universe. The observable universe is the part of the universe that in principle could be observed by creatures on Earth or that could have interacted with us observers via actions that move at the speed of light.
The unobservable universe may have no edge, but the observable universe definitely does. Its diameter is about 93 billion light years, and it is rapidly growing more every day. The observable universe is a sphere containing from 350 billion to one trillion large galaxies; it is also called “our Hubble Bubble” and “our pocket universe.” It is still producing new stars, but the production rate is ebbing. 95% of the stars that will ever exist have already been born. The very first stars came into existence about 200-400 million years after the big bang. Every galaxy, including the Milky Way, has about a trillion stars with planets orbiting them.
Scientists have no well-confirmed idea about the universe as a whole; the universe might or might not be very similar to the observable universe, but the default assumption is that the unobservable universe is like the observable universe. It is unknown whether the unobservable universe’s volume is infinite, but many cosmologists believe the actual universe is not infinite and is about 250 times the volume of our observable universe.
Each day, more stars become inaccessible to us here on Earth. Because of their high speed of recession from Earth, we could never send observers or signals to affect those stars. “Of the 2 trillion galaxies contained within our observable Universe, only 3% of them are presently reachable, even at the speed of light” (Ethan Siegel). That percentage will slowly reduce to zero.
The big bang explosion began approximately 13.8 billion years ago. At that time, the observable universe would have had an ultramicroscopic volume. The explosion created new space and new matter, and this explosive process of particles flying away from each other continues to create new space today. Four and a half billion years ago, our solar system was formed from products of this big bang that condensed .
The classical theory of the big bang was revised in 1988 to say the expansion rate has been accelerating slightly for the last five billion years due to the pervasive presence of a “dark” energy, and this rate will continue to increase forever. Dark energy is whatever it is that speeds up the expansion of the universe at the cosmic level. It has its name because so little is known about it. It is also sometimes called “the energy of the vacuum,” but many physicists believe this is a bad name because, if it were the energy of the vacuum, then the universe would have pulled itself apart very soon after the big bang and there would be no stars. Those who suspect that this energy density of empty space cannot dilute and so stays constant or only very slightly decreases as space expands also refer to it as “Einstein’s cosmological constant.” Because of this energy, the term “empty space” does not mean to physicists what it means in ordinary language such as when we say the space in his closet is now empty of all his belongings, so it is ready for re-painting. Nor does it mean the same thing to philosophers who believe empty space contains absolutely nothing. A physicist who uses the term “empty space” usually means a space with no significant overall curvature but one that is still full of quantum fields.
The discovery of dark energy helped explain the problem that some stars seemed to be slightly older than the previously predicted lower age of the universe. The presence of dark energy indicates that the universe is older than this predicted age, so the problem was solved.
Currently, space is expanding as time increases because most clusters of galaxies are flying farther away from each other, even though galaxies, planets, and molecules themselves are not now expanding. Eventually though, according to the most popular version of the big bang theory, in the very distant future, even these objects will expand away from each other and all structures of particles eventually will be annihilated as will all non-elementary particles themselves, leaving only an expanding soup of elementary particles as the universe chills and asymptotically approaches thermodynamic equilibrium. This is the universe’s so-called heat death or big chill.
The big bang theory presupposes that the ultramicroscopic-sized observable universe at a very early time had an extremely large curvature, but most cosmologists believe that the universe has flattened out and now no longer has any significant spatial curvature on the largest scale of billions of light years. Also, astronomical observations reveal that the current distribution of matter in the universe tends towards uniformity as the scale increases, so its initial curvature is fading away. At these very large scales, the material in our space is homogeneous and isotropic. That is, wherever in the observable universe you are located and what direction you are looking, you will see at large distances about the same overall temperature, the same overall density, and the same lumpy structure of dense super-clustered galaxies separated by hollow voids. Technically, the concept of curvature is complex; it is Riemannian curvature. In the voids the curvature is negative.
Here is a picture that displays the evolution of the observable universe since the big bang—although the picture displays only two of our three spatial dimensions. Time is increasing to the right while space increases both up and down and in and out of the picture:
Attribution: NASA/WMAP Science Team
Clicking on the picture will produce an expanded picture with more detail.
The term big bang does not have a precise definition. It does not always refer to a single, first event; rather, it more often refers to a brief duration of early events as the universe underwent a rapid expansion. In fact, the idea of a first event is primarily a product of accepting the theory of relativity, which is known to fail in the limit as the universe’s volume approaches zero. Actually, the big bang theory itself is not a specific theory, but rather a framework for more specific big bang theories.
Astronomers on Earth detect microwave radiation arriving in all directions. It is a fossil record of the cooled down heat from the big bang. More specifically, it is electromagnetic radiation produced about 380,000 years after the big bang when the universe suddenly turned transparent for the first time. At the time of first transparency the universe was about one hundredth of its current age and one millionth of its present size and had cooled down to 3,000 degrees Kelvin, which was finally cool enough to form atoms and to allow photons for the first time to move freely without being immediately reabsorbed by neighboring particles. This primordial electromagnetic radiation has now reached Earth as the universe’s most ancient light. Because of space’s expansion during the light’s travel to Earth, the ancient light has cooled and dimmed, and its wavelength has increased and become microwave radiation with a corresponding temperature of only 2.73 degrees Celsius above absolute zero. The microwave’s wavelength is about two millimeters and is small compared to the 100-millimeter wavelength of the microwaves in kitchen ovens. Measuring this incoming Cosmic Microwave Background (CMB) radiation reveals it to be extremely uniform in all directions in the sky (provided you are not moving relative to it).
Extremely uniform, but not perfectly uniform. CMB radiation varies very slightly with the angle it is viewed from. Any two directions differ by about one part in 100,000 or about ten thousandth of a degree of temperature. These small temperature fluctuations of the currently arriving microwave radiation are caused by fluctuations in the density of the matter of the early plasma and so are probably the origin of what later would become today’s galaxies with the dark voids between them because the high density regions will contract under the pull of gravity and can eventually cause a collapse of its matter into stars and galaxies and clusters of galaxies, and the low density regions will thereby become less dense. So, the inflation theory is one way to explain the pattern of galaxies and clusters of galaxies that we see today.
After the early rapid expansion ended, the universe’s expansion rate became constant and comparatively low for billions of years. This rate is now accelerating slightly because there is a another source of expansion—the repulsion of dark energy. The influence of dark energy was initially insignificant for billions of years, but its key feature is that it does not dilute as the space undergoes expansion. So, finally, after about seven or eight billion years of space’s expanding after the big bang, the dark energy became an influential factor and started to significantly accelerate the expansion. Today the expansion rate is becoming more and more significant. For example, the diameter of today’s observable universe will double in about 10 billion years. This influence from dark energy is shown in the above diagram by the presence of the curvature that occurs just below and before the abbreviation “etc.” Future curvature will be much greater. Most cosmologists believe this dark energy is the energy of space itself, and they call it “vacuum energy.”
The initial evidence for dark energy came from observations in 1998 of Doppler shifts of supernovas. These observations are called “redshifts,” and they are best explained by the assumption that the average distance between supernovas are increasing at an accelerating rate. Because of this rate increase, any receding galaxy cluster will eventually recede from us faster than the speed of light and thus become causally disconnected from us. In 100 billion years, the Milky Way will be the only galaxy left in the observable universe.
Seen from a distance, the collection of galaxy clusters look somewhat like a spider web. But the voids are eating the spider web. Observations by astronomers indicate the dark voids are pushing the nearby normal matter away and are growing and now are beginning to rip apart the filaments in the web.
The universe is currently expanding, so every galaxy cluster is, on average, moving a bit away from the others. The influence of the expansion is not currently significant except at the level of galaxy clusters, but the influence is accelerating, and in a few billion years it will rip apart all galaxy superclusters, then later the individual clusters, then galaxies, and someday all solar systems, and ultimately even all configurations of elementary particles, as the universe approaches its “heat death” or “big chill.”
The term “our observable universe” and the synonymous term “our Hubble bubble,” refer to everything that some person on Earth could in principle observe. Cosmologists presume there is no good reason to suppose that distant observers elsewhere couldn’t see more things than are observable from here on Earth. Physicists are agreed that, because of this reasoning, there exist objects that are in the universe but not in our observable universe. Because those unobservable objects are also the product of our big bang, cosmologists assume that they are similar to the objects we on Earth can observe—that those objects form atoms and galaxies, and that time behaves there as it does here. But there is no guarantee that this convenient assumption is correct. Occam’s Razor suggests it is correct, but that is the sole basis for such a claim. So, it is more accurate to say the classical big bang theory implies that the observable universe once was extremely small, dense, hot, and so forth, and not that the entire universe was this way.
Occasionally, someone remarks that the big bang is like a time-reversed black hole. The big bang is not like this because the entropy in a black hole is extremely high, but the entropy of the big bang was extremely low.
Because the big bang happened about 13.8 billion years ago, you might think that no observable object can be more than 13.8 billion light-years from Earth, but this would be a mistake that does not take into account the fact that the universe has been expanding all that time. The relative distance between galaxies is increasing over time. That is why astronomers can see about 45 billion light-years in any direction and not merely 13.8 billion light-years.
When contemporary physicists speak of the age of our universe and of the time since our big bang, they are implicitly referring to cosmic time measured in the cosmological rest frame. This is time measured in a unique reference frame in which the average motion of all the galaxies is stationary and the Cosmic Microwave Background radiation is as close as possible to being the same in all directions. This frame is not one in which the Earth is stationary. Cosmic time is time measured by a clock that would be sitting as still as possible while the universe expands around it. In cosmic time, the time of t = 0 years is when the time that the big bang began, and t = 13.8 billion years is our present. If you were at rest at the spatial origin in this frame, then the Cosmic Microwave Background radiation on a very large scale would have about the same average temperature in any direction.
The cosmic rest frame is a unique, privileged reference frame for astronomical convenience, but there is no reason to suppose it is otherwise privileged. It is not the frame sought by the A-theorist who believes in a unique present, nor by Isaac Newton who believed in absolute rest, nor by James Clerk Maxwell who believed in an aether at rest and that waved whenever a light wave passed through.
The cosmic frame’s spatial origin point is described as follows:
In fact, it isn’t quite true that the cosmic background heat radiation is completely uniform across the sky. It is very slightly hotter (i.e., more intense) in the direction of the constellation of Leo than at right angles to it…. Although the view from Earth is of a slightly skewed cosmic heat bath, there must exist a motion, a frame of reference, which would make the bath appear exactly the same in every direction. It would in fact seem perfectly uniform from an imaginary spacecraft traveling at 350 km per second in a direction away from Leo (towards Pisces, as it happens)…. We can use this special clock to define a cosmic time…. Fortunately, the Earth is moving at only 350 km per second relative to this hypothetical special clock. This is about 0.1 percent of the speed of light, and the time-dilation factor is only about one part in a million. Thus to an excellent approximation, Earth’s historical time coincides with cosmic time, so we can recount the history of the universe contemporaneously with the history of the Earth, in spite of the relativity of time.
Similar hypothetical clocks could be located everywhere in the universe, in each case in a reference frame where the cosmic background heat radiation looks uniform. Notice I say “hypothetical”; we can imagine the clocks out there, and legions of sentient beings dutifully inspecting them. This set of imaginary observers will agree on a common time scale and a common set of dates for major events in the universe, even though they are moving relative to each other as a result of the general expansion of the universe…. So, cosmic time as measured by this special set of observers constitutes a type of universal time… (Davies 1995, pp. 128-9).
It is a convention that cosmologists agree to use the cosmic time of this special reference frame, but it is an interesting fact and not a convention that our universe is so organized that there is such a useful cosmic time available to be adopted by the cosmologists. Not all physically possible spacetimes obeying the laws of general relativity can have this sort of cosmic time.
History of the Theory
The big bang theory originated with several people, although Edwin Hubble’s very careful observations in 1929 of galaxy recession from Earth were the most influential pieces of evidence in its favor. Noticing that the more distant galaxies are redder than nearby ones, he showed that on average the farther a galaxy is from Earth, the faster is recedes from Earth. (But neither he nor anyone else noticed until the end of the twentieth century that far away galaxies were actually accelerating away from nearby galaxies.) In 1922, the Russian physicist Alexander Friedmann discovered that the general theory of relativity allows an expanding universe. Unfortunately, Einstein reacted to this discovery by saying this is a mere physical possibility and not a feature of the actual universe. He later retracted this claim, thanks in large part to the influence of Hubble’s data. The Belgian physicist Georges Lemaître is another father of the big bang theory. He suggested in 1927 that there is some evidence the universe is expanding, and he defended his claim using previously published measurements of galaxy speeds. He calculated these speeds from the Doppler shifts in their light frequency, as did Hubble.
The big bang theory was very controversial when it was created in the 1920s. At the time and until the 1960s, physicists were unsure whether proposals about cosmic origins were pseudoscientific and so should not be discussed in a well-respected physics journal. In the late 1960s, Stephen Hawking and Roger Penrose convinced the professional cosmologists that there must have been a big bang. The theory’s primary competitor during the preceding time was the steady state theory. That theory allows space to expand in volume but only if this expansion is compensated for by providing spontaneous creation of matter in order to keep the universe’s overall density constant over time.
In the 2020s, the standard model of the big bang is known as the lambda-CDM model. Lambda is the force accelerating the expansion, and CDM is cold dark matter.
a. Cosmic Inflation
According to one very popular revision of the classical big bang theory, the cosmic inflation theory, the universe was created from quantum fluctuations in a scalar inflaton field, then the field underwent a cosmological phase transition for some unknown reason causing an exponentially accelerating expansion of space (thereby putting the “bang” in the big bang), and, then for some unknown reason it stopped inflating very soon after it began. When the inflation ended, the universe continued expanding at a slower, and almost constant, rate. In the earliest period of this inflation, the universe’s temperature was zero and it was empty of particles, but at the end it was extremely hot and flooded with particles that were created from the potential energy of the inflaton field.
By the time that inflation was over, every particle was left in isolation, surrounded by a vast expanse of empty space extending in every direction. And then—only a fraction of a fraction of an instant later—space was once again filled with matter and energy. Our universe got a new start and a second beginning. After a trillionth of a second, all four of the known forces were in place, and behaving much as they do in our world today. And although the temperature and density of our universe were both dropping rapidly during this era, they remained mind-boggingly high—all of space was at a temperature of 1015 degrees. Exotic particles like Higgs bosons and top quarks were as common as electrons and photons. Every last corner of space teemed with a dense plasma of quarks and gluons, alongside many other forms of matter and energy. After expanding for another millionth of a second, our universe had cooled down enough to enable quarks and gluons to bind together forming the first protons and neutrons (Dan Hooper, At the Edge of Time, p. 2).
Cosmic inflation is not a single, specific theory but is a category of theories that might explain a wide variety of otherwise inexplicable phenomena. Still, it is an informed guess. Many cosmologists do not believe in cosmic inflation, and they hope there is another explanation of the phenomena that inflation theory explains. But that other explanation has not been found, so inflationary cosmology is the dominant paradigm, that is, the most favored explanation of our universe’s origins.
The virtue of the inflation theory is that it provides an explanation for (i) why there is currently so little curvature of space on large scales (the flatness problem), (ii) why the microwave radiation that arrives on Earth from all directions is so uniform (the cosmic horizon problem), (iii) why there are not point-like magnetic monopoles most everywhere (called the monopole problem), and (iv) why we have been unable to detect proton decay that has been predicted (the proton decay problem). It is difficult to solve these problems in some other way than by assuming cosmic inflation.
According to the theory of inflation, assuming the big bang began at time t = 0, then the epoch of inflation (the epoch of radically repulsive gravity) began at about t = 10-36 seconds and lasted until about t = 10-33 seconds, during which time the volume of space increased by a factor of a billion billion billion times or 1026, and any initial unevenness in the distribution of energy was almost all smoothed out, that is, smoothed out from the large-scale perspective, somewhat in analogy to how blowing up a balloon removes its initial folds and creases so that it looks flat when a small section of it is viewed close up.
Although the universe at the beginning of the inflation was actually much smaller than the size of a proton, to help with understanding the rate of inflation you can think of the universe instead as having been the size of a marble. Then during the inflation period this marble-sized object expanded abruptly to a gigantic sphere whose radius is the distance that now would reach from Earth to the nearest supercluster of galaxies. This would be a spectacular change in something marble-sized.
The speed of this inflationary expansion was much faster than light speed. However, this fast expansion speed does not violate Einstein’s general theory of relativity because that theory places no limits on the speed of expansion of space itself.
At the end of that inflationary epoch at about t = 10-33 seconds or so, the inflation stopped. In more detail, what this means is that the exploding material decayed for some unknown reason and left only normal matter with attractive gravity. Meanwhile, our universe continued to expand, although now at a slow, nearly constant, rate. It went into its “coasting” phase. Regardless of any previous curvature in our universe, by the time the inflationary period ended, the overall structure of space on the largest scales was nearly flat in the sense that it had very little spatial curvature, and its space was extremely homogeneous. Today, we see evidence from the Cosmic Microwave Background radiation arriving to Earth’s telescopes that the universe is homogeneous on its largest scale.
But at the very beginning of the inflationary period, there surely were some very tiny imperfections due to the earliest quantum fluctuations in the inflaton field. These quantum imperfections inflated at the end of the inflationary period into small perturbations or slightly bumpy regions . Subsequently, the denser regions attracted more material than the less dense regions, and these dense regions would eventually turn into future galaxies. The less dense regions would eventually evolve into the current dark voids between the galaxies. Those early quantum fluctuations have now left their traces in the very slight hundred-thousandth of a degree differences in the temperature of the cosmic microwave background radiation at different angles as one now looks out into space from Earth with microwave telescopes. In this way, the inflation theory predicts the CMB values that astronomers on Earth see with their microwave telescopes, thereby solving the cosmic horizon problem.
Let’s re-describe the process of inflation. Before inflation began, for some as yet unknown reason the universe contained an unstable inflaton field or false vacuum field. For some other, as yet unknown reason, this energetic field expanded and cooled and underwent a spontaneous phase transition (somewhat analogous to what happens when water that is cooled spontaneously freezes into ice). That phase transition caused the highly repulsive primordial material to hyper-inflate exponentially in volume for a very short time. To re-describe this yet again, during the primeval inflationary epoch, the gravitational field’s stored, negative, repulsive, gravitational energy was rapidly released, and all space wildly expanded. At the end of this early inflationary epoch at about t = 10-33 seconds, the highly repulsive material decayed for some as yet unknown reason into ordinary matter and energy, and the universe’s expansion rate stopped increasing exponentially, and the expansion rate dropped precipitously and became nearly constant. During the inflationary epoch, the entropy continually increased, so the second law of thermodynamics was not violated.
Alan Guth described the inflationary period this way:
There was a period of inflation driven by the repulsive gravity of a peculiar kind of material that filled the early universe. Sometimes I call this material a “false vacuum,” but, in any case, it was a material which in fact had a negative pressure, which is what allows it to behave this way. Negative pressure causes repulsive gravity. Our particle physics tells us that we expect states of negative pressure to exist at very high energies, so we hypothesize that at least a small patch of the early universe contained this peculiar repulsive gravity material which then drove exponential expansion. Eventually, at least locally where we live, that expansion stopped because this peculiar repulsive gravity material is unstable; and it decayed, becoming normal matter with normal attractive gravity. At that time, the dark energy was there, the experts think. It has always been there, but it’s not dominant. It’s a tiny, tiny fraction of the total energy density, so at that stage at the end of inflation the universe just starts coasting outward. It has a tremendous outward thrust from the inflation, which carries it on. So, the expansion continues, and as the expansion happens the ordinary matter thins out. The dark energy, we think, remains approximately constant. If it’s vacuum energy, it remains exactly constant. So, there comes a time later where the energy density of everything else drops to the level of the dark energy, and we think that happened about five or six billion years ago. After that, as the energy density of normal matter continues to thin out, the dark energy [density] remains constant [and] the dark energy starts to dominate; and that’s the phase we are in now. We think about seventy percent or so of the total energy of our universe is dark energy, and that number will continue to increase with time as the normal matter continues to thin out. (World Science U Live Session: Alan Guth, published November 30, 2016 at https://www.youtube.com/watch?v=IWL-sd6PVtM.)
Before about t = 10-46 seconds, there was a single basic force rather than the four we have now. The four basic forces (or basic interactions) are: the force of gravity, the strong nuclear force, the weak force, and the electromagnetic force. At about t = 10-46 seconds, the energy density of the primordial field was down to about 1015 GEV, which allowed spontaneous symmetry breaking (analogous to the spontaneous phase change in which water cools enough to spontaneously change to ice); this phase change created the gravitational force as a separate basic force. The other three forces had not yet appeared as separate forces.
Later, at t = 10-12 seconds, there was even more spontaneous symmetry breaking. First the strong nuclear force, then the weak nuclear force and finally the electromagnetic force became separate forces. For the first time, the universe now had exactly four separate forces. At t = 10-10 seconds, the Higgs field turned on. This slowed down many kinds of particles by giving them mass so they no longer moved at light speed.
Much of the considerable energy left over at the end of the inflationary period was converted into matter, antimatter, and radiation, such as quarks, antiquarks, and photons. The universe’s temperature escalated with this new radiation; this period is called the period of cosmic reheating. Matter-antimatter pairs of particles combined and annihilated, removing from the universe all the antimatter and almost all the matter. At t = 10-6 seconds, this matter and radiation had cooled enough that quarks combined together and created protons and neutrons. After t = 3 minutes, the universe had cooled sufficiently to allow these protons and neutrons to start combining strongly to produce hydrogen, deuterium, and helium nuclei. At about t = 379,000 years, the temperature was low enough (around 2,700 degrees C) for these nuclei to capture electrons and to form the initial hydrogen, deuterium, and helium atoms of the universe. With these first atoms coming into existence, the universe became transparent in the sense that short wavelength light (about a millionth of a meter) was now able to travel freely without always being absorbed very soon by surrounding particles. Due to the expansion of the universe since then, this early light’s wavelength expanded and is today invisible on Earth because it is at much longer wavelength than it was 379,000 years ago. That radiation is now detected on Earth as having a wavelength of 1.9 millimeters, and it is called the cosmic microwave background radiation or CMB. That energy is continually arriving at the Earth’s surface from all directions. It is almost homogenous and almost isotropic.
As the universe expands, the CMB radiation loses energy; but this energy is not lost from the universe, nor is the law of conservation of energy violated. There is conservation because the same amount of energy is gained by going into expanding the space.
In the literature in both physics and philosophy, descriptions of the big bang often speak of it as if it were the first event, but the big bang theory does not require there to be a first event, an event that had no prior event. Any description mentioning the first event is a philosophical position, not something demanded by the scientific evidence. Physicists James Hartle and Stephen Hawking once suggested that looking back to the big bang is just like following the positive real numbers back to ever-smaller positive numbers without ever reaching the smallest positive one. There isn’t a smallest positive number. If Hartle and Hawking are correct that time is strictly analogous to this, then the big bang had no beginning point event, no initial time.
The classical big bang theory is based on the assumption that the universal expansion of clusters of galaxies can be projected all the way back to a singularity, to a zero volume at t = 0. The assumption is faulty. Physicists now agree that the projection to a smaller volume must become untrustworthy for any times less than the Planck time. If a theory of quantum gravity ever gets confirmed, it is expected to provide more reliable information about the Planck epoch from t=0 to the Planck time, and it may even allow physicists to answer the questions, “What caused the big bang?” and “Did anything happen before then?”
History of the Theory
The original theory of inflationary expansion (without eternal inflation and many universes) was created by Alan Guth, along with Andrei Linde, Paul Steinhardt, Alexei Sterobinsky and others in the period 1979-1982. It saved the big bang theory from refutation because it explained so many facts that the classical big bang theory conflicts with.
The theory of primordial cosmic strings has been the major competitor to the theory of cosmic inflation, but the above problems labeled (i), (ii), (iii), and (iv) are more difficult to solve with strings and without inflation. The theory of inflation is accepted by a great many members of the community of professional cosmologists, but it is not as firmly accepted as is the big bang theory. Princeton cosmologist Paul Steinhardt and Neil Turok of the Perimeter Institute are two of inflation’s noteworthy opponents, although Steinhardt once made important contributions to the creation of inflation theory. One of their major complaints is that at the time of the big bang, there should have been a great many long wavelength gravitational waves created, and today we have the technology that should have detected these waves, but we find no evidence for them. Steinhardt recommends replacing inflation theory with a revised big bounce theory.
For a short lecture by Guth on these topics that is designed for students, see https://www.youtube.com/watch?v=ANCN7vr9FVk.
b. Eternal Inflation and Many Universes
Although there is no consensus among physicists about whether there is more than one universe, many of the big bang inflationary theories are theories of eternal inflation, of the eternal creation of more big bangs and thus more universes. The theory is called the theory of chaotic inflation, the theory of the inflationary multiverse, the Multiverse Theory, and the Many-Worlds theory (although these worlds are different from the worlds of Hugh Everett’s theory). The key idea is that once inflation gets started it cannot easily be turned off.
The inflaton field is the fuel of our big bang and of all of the other big bangs. Advocates of eternal inflation say that not all the inflaton fuel is used up in producing just one big bang, so the remaining fuel is available to create other big bangs, at an exponentially increasing rate because the inflaton fuel increases exponentially faster than it gets used. Presumably, there is no reason why this process should ever end, so there will be a potentially infinite number of universes in the multiverse. Also, there is no good reason to suppose our actual universe was the first one, although technically whether one big bang occurred before or after another is not well defined.
A helpful mental image here is to think of the multiverse as a large, expanding space filled with bubbles of all sizes, all of which are growing. Each bubble is its own universe, and each might have its own physical constants, its own number of dimensions, even some laws of physics different from ours. In some of these universes, there may be no time at all. Regardless of whether a single bubble universe is inflating or no longer inflating, the space between the bubbles is inflating and more bubbles are being born at an exponentially increasing rate. Because the space between bubbles is inflating, nearby bubbles are quickly hurled apart. That implies there is a low probability that our bubble universe contains any empirical evidence of having interacted with a nearby bubble.
After any single big bang, eventually the hyper-inflation ends within that universe. We say its bit of inflaton fuel has been used up. However, after the hyper-inflation ends, the expansion within that universe does not. Our own expanding bubble was produced by our big bang 13.8 billion years ago. It is called the Hubble Bubble.
Even if our Hubble Bubble has a finite volume, unobservable space in our universe might be infinite, and if so then there probably are an infinite number of infinite universes among all the bubbles.
The inflationary multiverse is not the quantum multiverse predicted by the many-worlds theory. The many-worlds theory says every possible outcome of a quantum measurement persists in a newly created world, a parallel universe. If you turn left when you could have turned right, then two universes are instantly created, one in which you turned left, and a different one in which you turned right. A key feature of both the inflationary multiverse and the quantum multiverse is that the wave function does not collapse when a measurement occurs. Unfortunately both theories are called the multiverse theory as well as the many-worlds theory, so a reader needs to be alert to the use of the term. The Everettian Theory is the theory of the quantum multiverse but not of the inflationary multiverse.
The theory of eternal inflation with a multiverse was created by Linde in 1983 by building on some influential work by Gott and Vilenkin. The multiplicity of universes of the inflationary multiverse also is called parallel worlds, many worlds, alternative universes, alternate worlds, and branching universes—many names denoting the same thing. Each universe of the multiverse normally is required to use some of the same physics (there is no agreement on how much) and all the same mathematics. This restriction is not required by a logically possible universe of the sort proposed by the philosopher David Lewis.
Normally, philosophers of science say that what makes a theory scientific is not that it can be falsified (as the philosopher Karl Popper proposed), but rather is that there can be experimental evidence for it or against it. Because it is so difficult to design experiments that would provide evidence for or against the multiverse theories, many physicists complain that their fellow physicists who are developing these theories are doing technical metaphysical conjecture, not physics. However, the response from defenders of multiverse research is usually that they can imagine someday, perhaps in future centuries, running crucial experiments, and, besides, the term physics is best defined as being whatever physicists do professionally.
5. Infinite Time
Is time infinitely divisible? Yes, because general relativity theory and quantum theory require time to be a continuum. But this answer will change to “no” if these theories are eventually replaced by a Core Theory that quantizes time. “Although there have been suggestions by some of the best physicists that spacetime may have a discrete structure,” Stephen Hawking said in 1996, “I see no reason to abandon the continuum theories that have been so successful.” Twenty-five years later, the physics community became much less sure that Hawking is correct.
Did time begin at the big bang, or was there a finite or infinite time period before our big bang? The answer is unknown. There are many theories that imply an answer to the question, but the major obstacle in choosing among them is that the theories cannot be tested practically.
Will time exist infinitely many years from now? The most popular answer is “yes,” but physicists are not sure. Stephen Hawking and James Hartle said the difficulty of knowing whether the past and future are infinite in duration turns on our ignorance of whether the universe’s positive energy is exactly canceled out by its negative energy. All the energy of gravitation and spacetime curvature is negative energy. Hawking said in 2018:
When the Big Bang produced a massive amount of positive energy, it simultaneously produced the same amount of negative energy. In this way, the positive and the negative add up to zero, always. It’s another law of nature. So, where is all this negative energy today? It’s … in space. This may sound odd, …space itself is a vast store of negative energy. Enough to ensure that everything adds up to zero.
A short answer to the question “Why is the energy of gravitation negative and not positive?” is that this negative energy is needed if the law of conservation of energy is going to be true or approximately true. The long answer says to consider a universe containing only a ball above the surface of Earth. It has gravitational potential energy because of its position in the Earth’s gravitational field—the higher, the more energy. The quantitative value of this gravitational potential energy depends on where you set your zero point in the coordinate system you choose, that is, the point where the potential energy is zero. Customarily this is chosen to be at an infinite distance away from Earth (and away from any other objects if they were to be added into our toy universe). Let go of the ball, and it will fall toward the Earth. As gravitational potential energy of position is converted to kinetic energy of motion during the fall of the ball toward Earth, the sum of the two energies remains constant. When the ball reaches Earth, it will have much less than zero potential energy. Its potential energy will be even more negative. An analogous but more complicated argument applies to a large system, such as all the objects of the universe. We would not want to make the zero point for potential energy have anything to do with the Earth if we are making the calculations for all the universe, thus the choice of zero at an infinite distance away from Earth. One assumption in this argument is that what is physically real is not the numerical value of energy but of energy differences.
If total of the universe’s energy is either negative or positive and never zero (and if quantum mechanics is to be trusted, including its law of conservation of energy), then time is infinite in the past and future. Here is the argument for this conclusion. The law of conservation of energy implies energy can change forms, but if the total were ever to be non-zero, then the total energy could never become exactly zero (nor ever have been exactly zero) because that would violate the law of conservation of energy. So, if the total of the universe’s energy is non-zero, then there always have been states whose total energy is non-zero, and there always will be states of non-zero energy. That implies there can be no first instant or last instant and thus that time is eternal.
There is no solid evidence that the total energy of the universe is non-zero, but a slim majority of the experts favor a non-zero total, although their confidence in this is not strong. Assuming there is a non-zero total, there is no favored theory of the universe’s past, but there is a favored theory of the future—the big chill theory. The big chill theory implies the universe just keeps getting chillier forever as space expands and gets more dilute, and so there always will be changes and thus new events produced from old events and time is potentially infinite in the future.
Here are more details of the big chill theory. 95% of all stars that ever will be born have already been born. The last star will burn out in 1015 years. Then all the stars and dust within each galaxy will fall into black holes. Then the material between galaxies will fall into black holes as well, and finally in about 10100 years all the black holes will evaporate, leaving only a soup of elementary particles that gets less dense and therefore “chillier” as the universe’s expansion continues. The microwave background radiation will continue to red shift more and more into longer wavelength radio waves. Future space will expand toward thermodynamic equilibrium. But because of vacuum energy, the temperature will only approach, but never quite reach, zero on the Kelvin scale. Thus the universe descends into a “big chill,” having the same amount of total energy it always has had.
Here is some final commentary about the end of time:
In classical general relativity, the big bang is the beginning of spacetime; in quantum general relativity—whatever that may be, since nobody has a complete formulation of such a theory as yet—we don’t know whether the universe has a beginning or not.
There are two possibilities: one where the universe is eternal, one where it had a beginning. That’s because the Schrödinger equation of quantum mechanics turns out to have two very different kinds of solutions, corresponding to two different kinds of universe.
One possibility is that time is fundamental, and the universe changes as time passes. In that case, the Schrödinger equation is unequivocal: time is infinite. If the universe truly evolves, it always has been evolving and always will evolve. There is no starting and stopping. There may have been a moment that looks like our big bang, but it would have only been a temporary phase, and there would be more universe that was there even before the event.
The other possibility is that time is not truly fundamental, but rather emergent. Then, the universe can have a beginning. …And if that’s true, then there’s no problem at all with there being a first moment in time. The whole idea of “time” is just an approximation anyway (Carroll 2016, 197-8).
Back to the main “Time” article for references and citations.
Author Information
Bradley Dowden
Email: dowden@csus.edu
California State University, Sacramento
U. S. A.