Kit Fine (1946—)
 Kit Fine is an English philosopher who is among the most important philosophers of the turn of the millennium. He is perhaps most influential for reinvigorating a neo-Aristotelian turn within contemporary analytic philosophy. Fine’s prolific work is characterized by a unique blend of logical acumen, respect for appearances, ingenious creativity, and originality. His vast corpus is filled with numerous significant contributions to metaphysics, philosophy of language, logic, philosophy of mathematics, and the history of philosophy.
Kit Fine is an English philosopher who is among the most important philosophers of the turn of the millennium. He is perhaps most influential for reinvigorating a neo-Aristotelian turn within contemporary analytic philosophy. Fine’s prolific work is characterized by a unique blend of logical acumen, respect for appearances, ingenious creativity, and originality. His vast corpus is filled with numerous significant contributions to metaphysics, philosophy of language, logic, philosophy of mathematics, and the history of philosophy.
Although Fine is well-known for favoring ideas familiar from the neo-Aristotelian tradition (such as dependence, essence, and hylomorphism), his work is most distinctive for its methodology. Fine’s general view is that metaphysics is not best approached through the study of language Roughly put, Fine’s approach focuses on providing a rigorous account of the apparent phenomena themselves, and not just how we represent them in language or thought, prior to any attempt to discern the reality underlying them. Furthermore, a strong and ecumenical respect for the intelligible options, demands patience for the messy details, even when they resist tidying or systematization. All this leads to a steadfastness in refusing to allow epistemic qualms about how we know what we seem to know to interfere with our attempts to clarify just what it is that we seem to know.
This article surveys the wide variety of Fine’s contributions to philosophy, and it conveys what Fine’s distinctive methodology is and how it informs his contributions to philosophy.
Table of Contents
- Biography
- Fine Philosophy
- Metaphysics
- Philosophy of Language
- Logics and Mathematics
- History
- References and Further Reading
1. Biography
Fine was born in England on March 26, 1946. He earned a B.A. in Philosophy, Politics, and Economics at the University of Oxford in 1967. He was then appointed to a position at the University of Warwick. There he was mentored by Arthur Prior. Although Fine was never enrolled in a graduate program, his Ph.D. thesis For Some Proposition and So Many Possible Worlds was examined and accepted by William Kneale and Dana Scott just two years later.
Since then, Fine has held numerous academic appointments, including at: University of Warwick; St John’s College, University of Oxford; University of Edinburgh; University of California, Irvine; University of Michigan, Ann Arbor; and University of California, Los Angeles. Fine joined New York University’s philosophy department in 1997, where he is now Silver Professor and University Professor of Philosophy and Mathematics. He is currently also a Distinguished Research Professor at the University of Birmingham. Fine also held visiting positions at: Stanford University; University of Toronto; University of Arizona; Australian National University; University of Melbourne; Princeton University; Harvard University; New York University at Abu Dhabi; University of Aberdeen; and All Souls College, University of Oxford.
He has served the profession as an editor or an editorial board member of Synthese; The Journal of Symbolic Logic; Notre Dame Journal of Formal Logic; and Philosophers’ Imprint.
Fine’s contributions to philosophy have been recognized by numerous awards, including a Guggenheim Foundation Fellowship, American Council of Learned Societies Fellowship, Fellow of the American Academy of Arts and Sciences, Fellow at the National Center for the Humanities, Corresponding Fellow at the British Academy, an Anneliese Maier Research Award from the Alexander von Humboldt Foundation, and a Leibowitz Award (with Stephen Yablo).
Fine’s corpus is enormous. By mid-2020 he had published over 130 journal articles, 5 books. At least half a dozen articles and 8 monographs are forthcoming. His work is at once of both great breadth and depth, spanning many core areas of philosophy and engaging its topics with great erudition and technical sophistication. His trailblazing work is highly original, rarely concerned with wedging into topical or parochial debates but rather with making novel advances to the field in creative and unexpected ways. This article de-emphasizes his technical contributions, and it focuses upon his more distinctive or influential work.
2. Fine Philosophy
When engaging with the work of any prolific philosopher exhibiting great breadth and originality, it is tempting to look for some core “philosophical attractors” that animate, unify, or systematize their work. These attractors may then serve as useful aids to understanding their work and highlighting its most distinctive features.
Perhaps the most familiar form a philosophical attractor might take is that of a doctrine. These “doctrinal attractors” are polarized, pulling in some views while repelling others. Their “magnetic” tendencies are what systematize a thinkers’ thought. In the history of modern philosophy, two obvious examples are Spinoza and Leibniz. Their commitment to the principle of sufficient reason, the doctrine that everything has a reason or cause, underwrites vast swaths of their respective philosophies (Spinoza 1677; Leibniz 1714). A good example in the twentieth century is David Lewis. One can scarcely imagine understanding Lewis’s philosophy without placing at its core the doctrines of Humean supervenience and modal realism (Lewis 1986).
Another form a philosophical attractor might take is that of a methodology. These methodological attractors are also polarized, but they exert their force less on views and more on which data to respect and which to discard, which distinctions to draw and which to ignore, how weighty certain considerations should be or not, and the like. Hume is an example in the history of modern philosophy. His commitment to respecting only that which makes an observable difference guides much of his philosophy (Hume 1739). Saul Kripke is an example in the twentieth century. One can scarcely imagine understanding his philosophy without placing at its core a respect for common sense and intuitions about what we should say of actual and counterfactual situations (Kripke 1972).
There is no question that Fine is well-known for his association with certain doctrines or topics. These include: actualism, arbitrary objects, essentialism, ground, hylomorphism, modalism, procedural postulationism, semantic relationism, (formerly) supervaluationism, three-dimensionalism, and truthmaker semantics. But as important as these may be to understanding Fine’s work, they do not serve individually or jointly as doctrinal attractors in the way that, for example, Humean supervenience or modal realism did so vividly for Lewis.
Instead, Fine’s work is better understood in terms of a distinctive “Finean” cluster of methodological attractors. Fine himself has not spelled out the details of the cluster explicitly. But some explicit discussion of it can be found in his early work (1982c: §A2). There are also discussions suggestive of the cluster scattered across many of his later works. But perhaps the strongest impression emerges by osmosis from sustained engagement with a range of his work.
The Finean cluster may be roughly summarized by the following methodological “directives”:
-
- Provide a rigorous account of the appearances first before trying to discern the reality underlying them.
- Focus on the phenomenon itself and not just how we represent or express it in language or thought.
- Respect what’s at issue by not allowing worries about what we can mean from preventing us from accepting the intelligibility of notions that strike us as intelligible.
- Be patient with the messy details even when they resist tidying or systematization.
- Don’t allow epistemic worries about how we know what we seem to know interfere with or distract us from clarifying what it is that we seem to know.
Some of these directives interact or overlap. Even so, separating them helps highlight their different emphases. Bearing them in mind both individually and jointly is crucial to understanding Fine’s distinctive approach to the vast array of topics covered in his work.
Sometimes the influence of the directives is rather explicit. For example, the first directive clearly influences Fine’s views on realism and the nature of metaphysics. Implicit in this directive is a distinction between appearance and reality. Fine suggests that each is the focus of its own branch of metaphysics. Naïve metaphysics studies the appearances whereas foundational metaphysics studies their underlying reality. Because we have not yet achieved rigorous clarification of the appearances, Fine believes it would be premature to investigate the reality underlying them.
Other times, however, the directives exert their influence in more implicit ways. To illustrate, consider the first directive’s emphasis on providing a rigorous account of the appearances. Although Fine’s tremendous technical skill is clear in his work in formal logic, it also suffuses his philosophical work. Claims or ideas are often rigorously formalized in appendices or sometimes in the main text. Even when Fine’s prose is informal at the surface, it is evident that his technical acuity and logical rigor support it from beneath.
The second directive is perhaps most evident in Fine’s focus on the phenomena. Even in our post-positivistic times, some philosophers still lose their nerve when attempting to do metaphysics and, instead, retreat to our language or thought about it. An aversion to this is implicit throughout Fine’s work. Sometimes Fine makes his aversion explicit (2003a: 197):
…in this paper…I have been concerned, not with material things themselves, but with our language for talking about material things. I feel somewhat embarrassed about writing such a strongly oriented linguistic paper in connection with a metaphysical topic, since it is my general view that metaphysics is not best approached through the study of language.
Behind Fine’s remarks is a view that the considerations relevant to language often differ from those relevant to its subject matter. Only confusion can result from this sort of mismatch. So Fine’s apology is perhaps best explained by his unapologetic insistence that our interest is in the phenomena. However esoteric or unruly they may be, we should boldly resist swapping them out for the pale shadows they cast in language or thought.
The third directive is implicit in Fine’s frequent objections to various doctrines for not properly respecting the substantiveness, or even intelligibility, of certain positions. To illustrate, Fine defends his famous counterexamples against modal conceptions of essence by applying the third directive (1994b: 5):
Nor is it critical to the example that the reader actually endorse the particular modal and essentialist claims to which I have made appeal. All that is necessary is that he should recognize the intelligibility of a position which makes such claims.
Even if the claims are incorrect, their intelligibility is still enough to establish that there is a genuine non-modal conception of essence. Considerations like these illustrate Fine’s ecumenical approach. But this ecumenicity does not imply that anything goes, as Fine makes clear elsewhere when discussing fundamentality (2013a: 728):
Of course, we do not want to be able to accommodate any old position on what is and is not fundamental. The position should be coherent and it should perhaps have some plausibility. It is hard to say what else might be involved, but what seems clear is that we should not exclude a position simply on the grounds that it does not conform to our theory…
There appears to be a sort of humility driving Fine’s applications of the fourth directive. Philosophy aspires to the highest standards of clarity, precision, and rigor. This is why philosophical progress is so hard to achieve, and so modest when it is achieved. Thus, at least at this early stage of inquiry, there is a sort of arrogance in justifying one’s disregard for certain positions by appealing to one’s doctrinal commitments. Perhaps this also explains the scarcity of doctrinal attractors in Fine’s work.
The fourth directive often manifests in Fine’s work as an openness—perhaps even a fondness—for drawing many subtle distinctions. To some extent, this is explained by Fine’s keen eye for detail and his respect for nuance. But a deeper rationale derives from an interaction between the first two directives. For if these subtle distinctions belong to the appearances, then we must ultimately expect a rigorous account of the latter to include the former. This helps explain Fine’s patient and sustained interest in these distinctions, even when they resist analysis, raise difficulties of their own, or are just unpopular.
The fifth directive helps explain what might otherwise seem like a curious gap in Fine’s otherwise broad corpus. With only a few exceptions (2005d; 2018a), Fine has written little directly on epistemology. When Fine’s work indirectly engages epistemology, it is often with ambivalence. And epistemic considerations rarely play any serious argumentative role. For example, one scarcely finds him ever justifying a claim by arguing that it would be easier to know than its competitors. Fine’s distance from epistemic concerns does not stem from any disdain for them. It rather stems from the influence of the other directives. It would be premature to attempt to account for our knowledge of the appearances prior to providing a rigorous account of what they are. As Fine has sometimes quipped in conversation, “Metaphysics first, epistemology last”.
3. Metaphysics
Fine is widely regarded as having played a pivotal role in the recent surge of interest in broadly neo-Aristotelian metaphysics. It is, however, not easy to say just what neo-Aristotelian metaphysics is. One might characterize it as a kind of resistance to the “naturalistic” approaches familiar in much of late 20th century metaphysics. Granted, it is not straightforward how those approaches fit within the Aristotelian tradition. But the complexities of Aristotle’s own approach to metaphysics and the natural world suggest that any such characterization is, at best, clumsy and oversimplified. Another characterization of neo-Aristotelian might associate it with certain distinctive topics, including essence, substance, change, priority, hylomorphism, and the like. Granted, these topics do animate typical examples of neo-Aristotelian metaphysics. But it is also clear that these topics are not its exclusive property. Perhaps the best way to characterize neo-Aristotelian metaphysics is to engage with the metaphysics of one of its most influential popularizers and practitioners in contemporary times: Kit Fine.
What is metaphysics? Fine believes it is the confluence of five features (2011b). First, the subject of metaphysics is the nature of reality. But physics, mathematics, aesthetics, epistemology, and many other areas of inquiry are also concerned with the nature of reality. What distinguishes metaphysics from them is its aim, its methods, its scope, and its concepts. The aim of metaphysics is to provide a foundation for what there is. The method of metaphysics is characteristically apriori. The scope of metaphysics is as general as can be. And the concepts of metaphysics are transparent in the sense that there is no “gap” between the concept itself and what it is about.
The distinction between appearance and reality plays a prominent role in Fine’s conception of metaphysics (1982c: §A2; 2017b). Given such a distinction, one aim of metaphysics is to characterize how things are in reality. In Aristotelian fashion, this begins with the appearances. We start with how things appear, and the task is then to vindicate the appearances as revelatory of the underlying reality, or else to explain away the appearances in terms of some altogether different underlying reality. Both the revelatory and the reductionist projects presuppose the appearances, and so it is vital to get straight on what they are first. Fine calls this project naïve metaphysics. Only once adequate progress has been made on the naïve metaphysics of a subject will we be in a position to consider how it relates to fundamental reality. Fine calls this second project foundational metaphysics. Much of Fine’s work in metaphysics is best regarded as contributing to the naïve metaphysics of various topics (modality, part/whole, persistence) or to clarifying what conceptual tools (essence, reality, ground) will be needed to relate naïve metaphysics to foundational metaphysics. As Fine puts it (2017b: 108):
In my own view, the deliverances of foundational metaphysics should represent the terminus of philosophical enquiry; and it is only once we have a good handle on the corresponding questions within naïve metaphysics, with how things appear, that we are in any position to form an opinion on their reality.
Fine often suggests doubts about our having made anywhere near enough progress in naïve metaphysics to embark yet on foundational metaphysics. Because Fine suspects it would be premature to pursue foundational metaphysics at this early (for philosophy!) stage of inquiry, one should resist interpreting his work as pronouncing upon the ultimate nature of reality or the like. These sentiments are microcosmic embodiments of the five directives characterizing Fine’s philosophical approach.
a. Modality
Much of Fine’s earliest work focused on technical questions within formal logic, especially modal logic. But in the late 1970’s, Fine’s work began increasingly to consider applications of formal methods—especially the tools of modal logic—to the philosophy of modality. This shift produced a variety of influential contributions.
One of Fine’s earliest contributions to modality was to develop an ontological theory of extensional and intensional entities (1977b). The theory assumes a familiar possible worlds account of its intensional entities: properties are sets of world-individual pairs, propositions are sets of worlds, and so on. This approach is often taken to disregard any internal “structure” in the entities for which it accounts. But Fine resourcefully argues that a great deal of “structure” may still be discerned, including existence, being qualitative, being logical, having individual constituents, and being essentially modal. This work, together with Fine’s developments of Prior’s form of actualism (1977a), prefigured the recent debate between necessitists who assert that necessarily everything is necessarily something and contingentists who deny this (Williamson 2013b).
Fine continued exploring the applications of modal logic in the work that followed. The technical development of first-order modal theories is explored in one trio of papers (1978a; 1978b; 1981b). A second trio of papers explores applications of first-order modal theories to the formalization of various metaphysical theories of sets (1981a), propositions (1980), and facts (1982b). The second trio contains a wealth of distinctions and arguments. Some of them, with the benefit of hindsight, prefigure what would later become some of Fine’s more influential ideas.
For one example, the formalizations in 1981a are explicitly intended to capture plausible essentialist views about the identity or nature of sets. It is not difficult to view some of Fine’s remarks in this paper as anticipating his later celebrated set-theoretic counterexamples to the modal theory of essence (1994b).
For another example, 1982b argues against the still-common view that identifies facts with true propositions. The proposition that dogs bark exists regardless of whether dogs bark, whereas the fact that dogs bark exists only if they do.
In discussing these and related topics, Fine also introduced a general argumentative strategy against a variety of controversial metaphysical views. To illustrate, consider a modal variant of the preceding view that identifies possible facts with possibly true propositions. Suppose possible objects are abstracta. If a possible object is thus-and-so, then possibly it is actually thus-and-so. In particular, a possible donkey is possibly an actual donkey. Now, an actual donkey is a concrete object. So, we then have an abstract object—a possible donkey—that is possibly concrete. But no abstracta is possibly concrete. And so not all possible objects are abstracta. This sort of argument can also be used to show that possible facts are not propositions and that possible worlds are not abstract.
Fine’s work on modality is animated by a commitment to modal actualism (see his introduction to 2005b). This combines two theses. The first, modalism, is that modal notions are intelligible and irreducible to non-modal notions. The second, actualism, is that actuality is prior to mere possibility.
One of modalism’s most infamous detractors was Quine. Fine provides detailed reconstructions of Quine’s arguments against the intelligibility of de re modality and equally detailed criticisms of them (1989c; 1990). Quine’s arguments and Fine’s criticisms involve disentangling delicate issues concerning the modal question of de re modality, the semantic question of singular (or direct) reference, and the metaphysical question of transworld identity. These issues, according to Fine, have often been conflated in the literature (2005e).
One of the main problems facing actualism is to explain how to make sense of discourse about the merely possible, or “possibilist discourse”, given that mere possibilia are ultimately unreal. Fine takes up the challenge of reducing possibilist discourse to actualist discourse in a series of articles (1977a; 1985c; 2002b). A notable theme of Fine’s reductive strategy is a resistance to “proxy reduction”. Roughly, a proxy reduction attempts to reduce items of a target domain by associating them one-by-one with items from a more basic domain. In this case, a proxy reduction of possibilist discourse would reduce a merely possible object by associating it with an actual object. Although it is often assumed that reduction must proceed in this way by “proxy”, Fine argues that it needn’t. Instead, Fine pursues a different approach. The idea is to reduce the claim that a possible object has a feature to the claim that possibly some object (actually) has that feature. Thus, the claim that Wittgenstein’s possible daughter loathed philosophy is reduced to the claim that possibly Wittgenstein’s daughter (actually) loathed philosophy. This is not a proxy reduction because it does not associate Wittgenstein’s possible daughter with any actual object. Criticisms of the approach from Williamson 2013b and others recently prompted Fine to develop a new “suppositional” approach (2016c).
Although modalists often distinguish between various kinds of modality, they have often thought that the varieties can ultimately be understood in terms of a single kind of modality. Fine, however, argues against this sort of “monism” about modality (2002c). Modality is, instead, fundamentally diverse. There are, argues Fine, at least three diverse and irreducible modal domains: the metaphysical, the normative, and the nomological.
In addition to this diversity in the modal domains, Fine also argues that there is diversity within a given modal domain (2005c). This emerges in considering a puzzle of how it is possible that Socrates is a man but does not exist, given that it is necessary that Socrates is a man but possible that Socrates does not exist. Just as there is a distinction between sempiternal truths that hold at each time (for example, ‘Trump lies or not’) and eternal truths that hold regardless of the time (for example, ‘2+2=4’), so too there are worldly necessities that hold at each world (for example, ‘Trump lies or not’) and unworldly or transcendent necessities that hold regardless of the world (for example, ‘2+2=4’). The puzzle can then be resolved by taking ‘Socrates is a man’ to be an unworldly necessity while taking ‘Socrates does not exist’ to be a worldly (contingent) possibility. The distinction between worldly and unworldly necessities provides for three grades of modality. The unextended grade concerns the purely worldly necessities, the extended grade concerns the purely worldly necessities and the purely unworldly necessities, and the superextended grade concerns “hybrids” of the first two grades. Fine argues that the puzzle’s initial appeal depends upon confusing these three grades of modality.
b. Essence
Perhaps one of Fine’s most well-known contributions to metaphysics is to rehabilitate the notion of essence. A notable antecedent was Kripke 1972. Positivism’s antipathy to metaphysics was still exerting much influence on philosophy when Kripke powerfully advocated for the legitimacy of a distinctively metaphysical notion of modality. Kripke used this notion to suggest various essentialist theses. Among them were that a person’s procreative origin was essential to them and that an artifact’s material origin was essential it. These essentialist theses, however, were usually taken to be theses of metaphysical necessity. The implicit background conception of essence was accordingly modal. On one formulation of it, an item has some feature essentially just in case it is necessary that it has that feature. Thus, Queen Elizabeth’s procreative origin is essential to her just in case it is necessary that she have that origin.
One of Fine’s distinctive contributions to rehabilitating essence was to argue against the modal conception of it (1994b). To do so, Fine introduced what is now a famous example. Consider the singleton set {Socrates} (the set whose sole member is Socrates). It is necessary that, if this set exists, then it has Socrates as a member. And so, by the modal conception, the set essentially has Socrates as a member. But, Fine argues, on plausible assumptions, it is also necessary that Socrates is a member of {Socrates}. And so, by the modal conception, it follows that Socrates is essentially a member of {Socrates}. This, however, is highly implausible: it is no part of what Socrates is that he should be a member of any set whatsoever. Fine raises a battery of similar counterexamples to the modal conception. His diagnosis of where it goes awry is that it is insensitive to the source of necessity. It lies in the nature of the singleton {Socrates}, not Socrates, that it has Socrates as a member. This induces an asymmetry in essentialist claims: {Socrates} essentially contains Socrates, but it is not the case that Socrates is essentially contained by {Socrates}. No modal conception of essence can capture this asymmetry because the two claims are both equally necessary.
Even if the modal conception of essence fails, it is not as if essence and modality are unconnected. Indeed, Fine provocatively suggests a reversal of the traditional connection. Whereas the modal approach attempted to characterize essence in terms of modality, Fine suggests instead that metaphysical necessities hold in virtue of the essences of things (1994b).
Whether or not this suggestion is correct, separating essence from modality already implies that the study of essence cannot be subsumed under the study of modality. Instead, it would seem essence must be studied as a subject in its own right. Toward this end, Fine discusses a wealth of distinctions involving essence including the distinctions between constitutive and consequential essence, immediate and mediate essence, and more (1994d).
An especially important application of essence is to the notion of ontological dependence. What something is may depend upon what another thing is. In this ontological sense of dependence, a set may depend on its members, or an instance of a feature may depend upon the individual bearing it. Fine has explored this notion of ontological dependence in detail and used to provide a characterization of substance (1995b). Additionally, he has also developed the formal logic and semantics of essence (1995a; 2000c).
c. Ontology
Ontology is often taken to concern what there is, or what exists. Some, however, have argued that there is a significant difference between being (what there is) and what exists. When being and existence are distinguished, it is often to claim that some things that have being nevertheless do not exist.
A recurring theme in Fine’s work is an openness to consider the being or nature of items regardless of whether they exist (1982b: §1; 1982c: §E1). This is most evident in the case of items that we are convinced do not exist. Like many others, Fine believes that, ultimately, there are no non-existents. But, perhaps unlike many others, Fine also believes that this is no obstacle to exploring their status or their nature (1982c). Fine’s explorations of this are rich in distinctions. The three most prominent are between Platonism and empiricism, literalism and contextualism, and internalism and externalism. The Platonist says non-existents do not depend on us or our activities, whereas the empiricist says they do. The literalist says non-existents literally have the properties they are said to have (for example, Sherlock Holmes literally lives in London), whereas the contextualist says instead that these properties are at most only had in a relevant context (namely, the Holmes stories). The internalist individuates non-existents solely in terms of the properties they have “internally” to the contexts in which they occur, whereas the externalist does not. Fine believes that all eight combinations of views are possible. But he focuses on developing and arguing against the four internalist views. A notable counterexample Fine gives to internalism is a story in which we imagine twins Dum and Dee who are indiscernible internally to the story but are nevertheless distinct. Two follow-up papers developing and defending externalism (Fine’s own favored combination conjoins empiricism, contextualism, and externalism) and comparing it to alternatives were planned but have not yet appeared (although 1984a further discusses related issues in the context of a critical review).
Behind Fine’s openness to considering the being or nature of items regardless of whether they exist is a general conception of ontology (2009). At least since Quine 1948, the dominant view has been that ontology’s central question, “What exists?”, should be understood as the question “What is there?”, and that this in turn should be understood as a quantificational question. Thus, to ask “Do numbers exist?” is to ask “Is there an x such that x is a number?”. Fine argues against this approach. One difficulty is that it seems to mischaracterize the logical form of ontological claims. Suppose we wish to answer “Yes, numbers exist”. It does not seem adequate to the answer that merely some number, say 13, exists. But that is all that is required for the quantificational answer to be correct. Instead, it seems our answer must be that all the numbers exist. This answer has the form “For every x, if x is a number, then x exists”. If ‘x exists’ is understood in the Quinean way in terms of a quantifier (namely: x exists =df. ∃y(x = y)), then it expresses a triviality that fails to capture the intended significance of the ontological question. Fine suggests that the intended significance can be restored by appealing to the notion of reality. The ontological, as opposed to quantificational question “Do numbers exist?” asks whether it is true that “For every x, if x is a number, then there is some feature that, in reality, x has”. This question is not answered by basic mathematical facts, but instead by whether numbers are part of the facts constituting reality.
Many ontologies are “constructional”. Some of their objects are accepted for being constructs of other accepted objects (perhaps with some objects as “given”: accepted but not on the basis of anything else). For example, we may accept subatomic particles into our ontology because they “construct” atoms, and we may also accept forests into our ontology because they are “constructed by” trees. Fine pursues an abstract study of constructional ontologies (1994e). The theory Fine develops can distinguish between actual and possible ontologies, as well as between absolute and relativist ontologies.
Relations have long puzzled philosophers. An especially difficult class of relations are those that appear to be non-symmetric. Unrequited love provides an example: although Scarlett loves Rhett, Rhett does not love Scarlett. It may seem that the relation loves is “biased” in that its first relatum is the lover and the second relatum the beloved. But it seems we must also recognize a converse is loved by relation “biased” in that its first relatum is the beloved and the second relatum the lover. Now, when Scarlett loves Rhett, is this because Scarlett and Rhett in this order stand in the loves relation, or because Rhett and Scarlett in that order stand in the is loved by relation? It seems we must say at least one, but either alone is arbitrary and both together is profligate. Fine develops a solution in terms of unbiased or “neutral” relations (2000b).
d. Mereology
Fine has made a variety of important contributions to abstract mereology (the theory of part and whole) as well as to its applications to various sorts of objects. Sometimes the term ‘mereology’ is used for a specific theory of mereology, namely classical extensional mereology. But an important theme in Fine’s work on mereology is to argue that this theory, and indeed much other thinking on mereology, is unduly narrow. Instead, Fine believes there is a highly general mereological framework that may accommodate a plurality of notions of part-whole (2010c). Different notions of part-whole correspond to different operations that may compose wholes from their parts. The notion of fusion from classical extensional mereological is but one of these compositional operations (and not a uniquely interesting one, he thinks). But there are other compositional operations that may apply even to abstract objects outside space and time. For example, the set-builder operation may be regarded as building a whole (the set) from its parts (its members). (Unlike Lewis 1991’s similar suggestion, Fine does not take the set-builder operation to be the fusion operation.) Fine contends that the general mereological framework for the plurality can be developed in abstraction from any of these particular applications of it.
Much of Fine’s work on mereology, however, has concerned its application to the objects of ordinary life and, in particular, to material things. Many have wanted to regard a material thing as identical with its matter. Perhaps the main objection to this view is the sheer wealth of counterexamples. A statue may be well-made although its matter is not. Fine has defended counterexamples like these at length (2003a). Even if a material thing and its matter are not identical, it may still seem as if they can occupy the same place at the same time. After all, the statue is now where its matter is. And some, including Locke, in 1689, have claimed that it is impossible for any two things (at least of the same sort) to occupy the same place at the same time. But Fine presents counterexamples even to this Lockean thesis (2000a). One can imagine, for instance, two letters being written on two sides of the same sheet of paper (or even written using the same words but which have dual meanings). The two letters then coincide but are distinct.
Even if material things are not identical to their matter, it may still be maintained that they are somehow aggregates of their matter. An aggregate of objects exists at a place or at a time exactly whenever or wherever some of those objects do too. If a quantity of gold, for example, is an aggregate of its left and right parts, then the quantity will exist whenever its left or right parts exist and wherever its left or right parts exist. But, Fine argues, if the left part is destroyed, the quantity will cease to exist although the aggregate will not. In general, then, ordinary material things are not aggregates but are instead compounds (1994a).
These considerations extend to how material things persist through time. A common view is that they persist by having (material) temporal parts. This view takes the existence of objects in time to be essentially like their extension in space: aggregative. Objects persist through time in much the same way as events unfold. But Fine argues, partly on the basis of mereological considerations, that this delivers highly implausible results, and suggests that instead we must recognize that the existence of objects in time is fundamentally different than their extension in space (Fine [1994a]; 2006a).
The lesson Fine draws from the preceding considerations is that a material thing neither is identical with, nor a mere aggregation of, its matter. Instead, Fine believes that the correct mereology of material things will be a version of hylomorphism: a material thing will be a compound of matter and form (2008a). Fine’s first applications of hylomorphism to acts, objects, and events provides an early glimpse of its broad scope (1982a). But the full breadth of its scope only emerged with Fine’s development of a general hylomorphic theory (1999). Its key notion is that of an embodiment. An embodiment may be either timeless (rigid) or temporal (variable). A rigid embodiment r = a,b,c,…/R is the object resulting from the objects a,b,c,… being in the relation R. A rigid embodiment is a hylomorphic compound that exists timelessly just in case its “matter” (the objects a,b,c,…) is in the requisite “form” (the relation R). So, for example, the statue (r) is identical with the hylomorphic compound of its clay parts (a,b,c,…) in the form of a statue (R). By contrast, a variable embodiment corresponds to a principle uniting its manifestations across times. Thus, a variable embodiment v = /V/ is a function V from times to things (which may themselves be rigid embodiments). Thus, for example, the statue over time (v) is a series of states at a time.
e. Realism
Fine has made influential contributions to debates about realism (2001). In general, the realist claims that some domain (for example, the mental or the moral) is real, whereas the antirealist claims that it is unreal. Although debates between realists and antirealists are common throughout philosophy, a precise and general characterization of their debate has been elusive. Fine argues against a variety of approaches familiar from the literature before settling on a distinctively metaphysical approach. What makes it distinctively metaphysical is its essential appeal to a metaphysical (as opposed to epistemic, conceptual, or semantic) notion of reality as well as to relatedly metaphysical notions of factuality and ground.
We may illustrate Fine’s approach by example. Set aside the moral error-theorist who believes that there are no moral facts whatsoever. Suppose, instead, that there are moral facts. One of them might be, we may suppose, that pointless torture is morally wrong. Moral realists and antirealists alike may agree that this fact is moral for containing some moral constituents (such as the property moral wrongness). And, unlike the error-theorist, they may agree that this fact obtains. What they dispute, however, is the fact’s status as real or unreal. Antirealism may come in either of two forms. The antirealist reductionist may, for example, accept the moral fact but insist that it is grounded in non-moral, naturalist facts that do not contain any moral constituents. The moral fact is unreal because it is grounded in non-moral facts. And the antirealist nonfactualist may, for example, accept the moral fact but insist that it is “nonfactual” in the sense that it does not represent reality but is rather a sort of “projection” of our attitudes, expressions, activities, or practices. The moral fact is unreal because it is neither real nor grounded in what is real. By contrast, the realist position consists in taking the moral fact as neither reducible nor nonfactual. The dispute between the realist, the antirealist reductionist, and the antirealist nonfactualist therefore turns on considerations of what grounds the moral facts. And, in general, debates over realism are, in effect, debates over what grounds what and therefore may be settled by determining what grounds what.
The framework Fine devised for debates over realism has proven rich in its implications. For one illustration, the metaphysical notion of reality figures prominently in other parts of Fine’s philosophy. Fine believes that the notion of reality plays a prominent role in ontological questions. And Fine uses the notion of reality to characterize the debate in the philosophy of time over the reality or unreality of tense. But the notion of ground provides an even more vivid illustration. In addition to ground’s central role in realist debates, it has itself become a topic of intense interest of its own.
f. Ground
Ground, as Fine conceives of it, is a determinatively explanatory notion. To say that Aristotle’s being rational and his being animal grounds his being a rational animal is to say that Aristotle is a rational animal because of, or in virtue of, his being rational and his being animal. Not only do questions of ground enjoy a prominent place in realist debates, but also within philosophy as a whole. Are moral facts grounded in naturalist facts? Are mental facts grounded in physical facts? Are facts of personal identity grounded in facts of psychological continuity? These and other questions of ground are among the biggest and most venerable questions in philosophy.
It is therefore a curiosity of recent times that ground has become a “hot topic” with a rapidly-expanding literature (Raven 2020). This is perhaps partly explained by the anti-metaphysical sentiments that swept over 20th century analytic philosophy. Although philosophers did not entirely turn their backs on questions of ground, the anti-metaphysical sentiments created a climate in which many felt the need to reinterpret them as questions of another sort (such as conceptual analysis, supervenience, or truthmaking). Fine, however, played a highly influential role in changing this climate. This is partly because Fine’s work not only discussed ground in its application to other topics (such as realism), but also treated ground as a topic worthy of study in its own right (see Raven 2019 for further discussion). Fine provided a detailed exploration of ground, introducing many now familiar distinctions of ground and its connections to related topics, such as essence (2012c). Additionally, Fine has developed the so-called “pure logic” of ground (2012d). He also problematized ground by discovering some puzzles involving ground and its relation to classical logic (2010b).
Although Fine had recognized certain similarities between essence and ground, he was initially inclined to separate them (2012c: 80):
The two concepts [essence and ground] work together in holding up the edifice of metaphysics; and it is only by keeping them separate that we can properly appreciate what each is on its own and what they are capable of doing together.
But not long after, Fine changed his view (2015b: 297):
I had previously referred to essence and ground as the pillars upon which the edifice of metaphysics rests…, but we can now see more clearly how the two notions complement one another in providing support for the very same structure.
The unification appeals to a conception of constitutively necessary and sufficient conditions on arbitrary objects (1985d). For example, for true belief to be essential to knowledge is for it to be a constitutively necessary condition on an arbitrary person’s knowing something that they truly believe it. And, for another example, for a set’s having no members to ground its being identical with the null set is for it to be a constitutively sufficient condition on an arbitrary set’s having no members that it is identical with the null set.
This previous example illustrates an identity criterion: a statement of the conditions in virtue of which two items are the same. Many philosophers have been tempted to reject identity criteria for being pointless, trivial, or unintelligible. But Fine argues against such rejections and, instead, defends the intelligibility and, indeed, the potential substantivity of identity criteria by appealing to ground and arbitrary objects (2016b). Roughly, an identity criterion states that, given two arbitrary objects, they are the same when the fact that they are identical is grounded in the fact that they satisfy a specified condition. For example, given two arbitrary sets, they are the same when their identity is grounded in their having the same members.
g. Tense
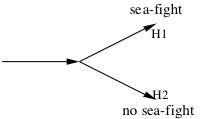
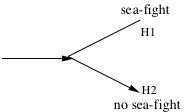
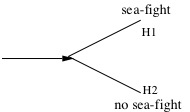
One striking application of Fine’s work on realism and ground is to the philosophy of time. McTaggart 1908 notoriously argued for the unreality of time. Although McTaggart’s argument generated considerable discussion, the general impression has been that whatever challenge it posed to the reality of time can somehow be met. Fine argues that the challenge lurking within McTaggart’s argument is more formidable than usually thought (2005f, of which 2006b is an abridgement). Taking inspiration from McTaggart, Fine formulates his own argument against the reality of tense. The argument relies on four assumptions that each make essential appeal to the notion of reality:
| Realism | Reality is constituted (at least, in part) by tensed facts. |
| Neutrality | No time is privileged, the tensed facts that constitute reality are not oriented towards one time as opposed to another. |
| Absolutism | The constitution of reality is an absolute matter, not relative to a time or other form of temporal standpoint. |
| Coherence | Reality is not contradictory; it is not constituted by facts with incompatible content. |
Reality contains some tensed facts (Realism). Because things change, these will be diverse. Although you are reading, you aren’t always reading. So, one of these tensed facts is that you are reading whereas another of them is that you are not reading. None of these tensed facts are oriented toward any particular time (Neutrality). Nor do they obtain relative to any particular time (Absolutism). So reality is constituted by incompatible facts. But reality cannot be incoherent like that (Coherence). And so the four assumptions conflict. The antirealist reaction is to reject Realism, and so the reality of time. The realist accepts Realism, and so must reject another assumption. The challenge is to explain which. The “standard” realist denies Neutrality by privileging the present time. But Fine argues that there are two overlooked “nonstandard” responses. The relativist denies Absolutism, and so takes the constitution of reality to be irreducibly relative to a time. The fragmentalist denies Coherence, and so takes reality to divide into incompatible temporal “fragments”. Fine argues that the nonstandard realisms (and, in particular, fragmentalism) are, despite their obscurity, more defensible than standard realism.
Fine relates these considerations to the vexing case of first-personal realism. Standard realism about first-personal facts implausibly privileges a first-personal perspective. Overlooking nonstandard realisms, one may then draw the antirealist conclusion that there are no first-personal facts. But Fine’s apparatus reveals two nonstandard realist options: relativism and fragmentalism. According to Fine, these options (and, in particular, fragmentalism) are especially intuitive in the first-personal case. Indeed, Fine suggests that the question of the reality of tense might have more in common with the question of the reality of the first-personal, despite its more familiar association with the question of the reality of the modal.
4. Philosophy of Language
Fine has made four main contributions to the philosophy of language. The first two are in support of the referentialist tradition. One is to bolster arguments against the competing Fregean tradition. The other is to develop a novel version of referentialism, semantic relationism, that is superior to its referentialist competitors. The third contribution is to the nature of vagueness. And the fourth contribution is the development of an original approach to semantics, truthmaker semantics.
a. Referentialism
The referentialist tradition takes certain terms, especially names, to refer without the mediation of any Fregean sense or other descriptive information. Fine has made two main contributions in support of referentialism.
Fine’s first contribution to referentialism is to bolster arguments against Fregeanism. This includes a variety of supporting arguments scattered throughout his book Semantic Relationism (2007b). Perhaps the most notable of these is a thought experiment against the existence of the senses the Fregean posits (2007b: 36). The scenario involves a person in a universe that is perfectly symmetrically arranged around her center of vision. Her visual field therefore perfectly duplicates whatever is visible on the left to the right, and on the right to the left. When she is approached by two identical twins, she may name each ‘Bruce’. It seems she may refer by name to each. The Fregean can agree only if there is a pair of senses, one for the left ‘Bruce’ and the other for the right ‘Bruce’. But given the symmetry of the scenario, it seems there is no possible basis for thinking that the pair exists.
b. Semantic Relationism
Fine’s second contribution to referentialism is to introduce and develop what he argues is its most viable form: semantic relationism. The view is developed in his book Semantic Relationism which expands on his John Locke Lectures delivered at University of Oxford in 2003 (2007b).
Semantic relationism is representational in that it aims to account for the meanings of expressions in terms of what they represent (objects, properties, states of affairs, and so on). But it differs significantly from other representational approaches. These have typically (and implicitly) assumed that the meaning of an expression is intrinsic to it and so one is never required to consider any other expressions in accounting for the meaning of a given expression. Semantic relationism denies this. Instead, the meaning of (at least some) expressions at least partly consists in its “coordinative” relations to other meaningful expressions. This is different from typical kinds of semantic holism which usually characterize an expression’s meaning in non-representational terms and, instead, in terms of its inferential role.
One of the main benefits of semantic relationism is that it provides solutions to a variety of vexing puzzles, including the antinomy of the variable (2003b), Frege’s puzzle (Frege 1892), and Kripke’s puzzle about belief (Kripke 2011). To illustrate, Frege observed that an identity statement, like ‘Cicero is Cicero’, could be uninformative whereas another, like ‘Cicero is Tully’, could be informative despite the names ‘Cicero’ and ‘Tully’ being coreferential. Frege’s own solution was to bifurcate semantics into a level of sense and a level of reference. This enabled him to claim that the names ‘Cicero’ and ‘Tully’ differ in sense but not in reference. But powerful arguments from Kripke 1972 and others convinced many that the semantics of names only involve reference, not sense. How could one reconcile this referentialism about the semantics of names with Frege’s observation? Semantic relationism offers a novel answer. The pair ‘Cicero’,’Cicero’ in ‘Cicero is Cicero’ are coordinated: it is a semantic requirement that they co-refer. By contrast, the pair ‘Cicero’,‘Tully’ in ‘Cicero is Tully’ are uncoordinated: it is not a semantic requirement that they co-refer. This difference in coordination among the pairs of expressions explains the difference in their informativeness. But it is only by considering the pairs in relation to one another that this difference can even be recognized. The notion of semantic requirement involves a distinctive kind of semantic modality that Fine argues should play a significant role in semantic theorizing (2010a).
c. Vagueness
Fine provided what is widely considered to be the locus classicus for the so-called supervaluationist approach to vagueness (1975d). On this approach, vagueness is a kind of deficiency in meaning. What makes the deficiency specific to vagueness is that it gives rise to “borderline cases”. For example, the vague predicate ‘is bald’ admits of borderline cases. These are cases in which the predicate’s meaning does not settle whether it applies or does not apply to, say, a man with a receding hairline and thinning hair. Borderline cases pose an initial problem for classical logic. For if the predicate ‘is bald’ neither truly applies nor falsely applies in such cases, how could it be true to say ‘That man is bald or is not bald’? Supervaluationism answers by considering the admissible ways in which a vague predicate can be completed or made more precise. The sentence ‘That man is bald’ is “super-true” if true under every such “precisification”, “super-false” if false under every “precisification”, and neither otherwise. It can then be argued that ‘That man is bald or is not bald’ will be super-true because it will be true under every precisification, despite neither disjunct being super-true. This in turn helps supervaluationism provide a response to the Sorites Paradox.
In more recent work, Fine has given up on supervaluationism and instead developed an alternative approach. Fine’s reasons for rejecting supervaluationism are not specific to it but rather derive from a more far-reaching argument. Fine presents an apparent proof of the impossibility of vagueness (2008b). The challenge is to explain where the proof goes awry, since there is no question that vagueness is possible. But, Fine argues, standard accounts of vagueness, including especially supervaluationism, cannot satisfactorily meet this challenge. So, an alternative account is needed.
Fine develops such an alternative account that relies on a distinction between global and local vagueness (2015a). Global vagueness is vagueness over a range of cases, such as a series of indiscernible but distinct color tiles arranged incrementally from orange to red. Local vagueness is vagueness in a single case, such as in a single vermilion tile midway between the orange and red tiles. Given the distinction, there is a strong temptation to reduce global vagueness to local vagueness. But Fine argues against this. His own “globalist” approach, he argues, not only is able to meet the challenge of explaining the possibility of vagueness, but also why it does not succumb to the Sorites Paradox.
d. Truthmaker Semantics
In a series of articles, Fine develops a novel semantic approach he calls truthmaker semantics. The approach is in some ways like the more familiar possible-worlds semantics and, especially, situation semantics. But truthmaker semantics diverges from both. The contrast with possible-worlds semantics is especially vivid. On the latter approach, the truth-value of a sentence is evaluated with respect to a possible world in its entirety, no matter how irrelevant parts of that world might be to making the sentence true. Thus, ‘Fido barks’ will be true with respect to an entire possible world just in case it is a world in which Fido barks. Such a world includes much that is irrelevant to Fido’s barking, including sea turtle migration, weather patterns in sub-Saharan Africa, and distant galaxies. Truthmaker semantics departs in two ways from this. First, and like situation semantics, it replaces worlds with states which may, to a first approximation, be regarded as parts of worlds. So, for example, it is not the entire world—sea turtle migration, sub-Saharan weather, and distant galaxies included—that verifies or makes ‘Fido barks’ true, but rather instead just the state of Fido’s barking. What’s more, this state, unlike the entire world itself, does not verify any truths about sea turtles, sub-Saharan weather, and distant galaxies. Second, and unlike situation semantics, it is required that a state verifying a sentence must be wholly or exactly relevant to its truth. So, for example, the state that Fido barks and it’s raining in Djibouti will not verify ‘Fido barks’ because it includes an irrelevant part about Djibouti’s weather.
The general framework of truthmaker semantics is developed over the course of numerous articles (but see 2017c for an overview). An important feature of it is its abstractness. The semantics is specified in terms of a space of states, or a state space. The state space is assumed to have some mereological structure. But the assumptions are minimal and, in particular, no assumptions are made about the nature of the states themselves. This makes the framework highly abstract. This in turn grants the framework enormous flexibility in its potential range of applications. Indeed, Fine believes the main benefits of the general framework emerge from its wealth of applications to a wide variety of topics. These include: analytic entailment (2016a), counterfactuals (2012a; 2012b), ground (2020a), intuitionistic logic (2014b), semantic content (Fine [2017a,2017b]), the is-ought gap (2018b), verisimilitude (2019d; 2020b), impossible worlds (2019c), deontic and imperative and imperative statements (2014a; 2019a; 2019b), and more. This is not the place for a comprehensive survey of these applications. Still, one may get a sense of them by considering three applications in more detail.
First, consider counterfactuals. The standard semantics for counterfactuals derives from Stalnaker 1968 and Lewis 1973. According to Lewis’ version of it, the counterfactual ‘If A then it would be that C’ is true just in case no possible world in which A but not C is true is closer to actuality than any in which both A and C are true. Fine’s opposition to this semantics is evident from his critical notice (1975a) of Lewis’s book. There Fine introduced the so-called “future similarity objection”. It takes the form of a counterexample showing that small changes can make for great dissimilarities. Fine’s celebrated case was the counterfactual ‘If Nixon had pressed the button, then there would have been a nuclear holocaust’. Although it seems true, the standard semantics struggles to validate it. The great dissimilarities of a world where Nixon pressed the button causing nuclear holocaust ensure it is further from actuality than a world where Nixon pressed the button without nuclear holocaust. Fine’s critical notice also contained the seeds of ideas that later emerged in his work on truthmaker semantics. There he also objects that the standard semantics is committed to unsound implications because it permits the substitution of tautologically equivalent statements. This objection was prescient for anticipating a similar difficulty later developed in greater detail against the standard semantics (2012a; 2012b). Fine argues that the difficulty can be avoided by providing a truthmaker semantics for counterfactuals. Roughly, ‘If A then it would be that C’ is true just in case any possible outcome of a state verifying A also contains a state verifying C.
Second, consider intuitionistic logic. Realists and antirealists alike tend to agree that certain technical aspects of intuitionistic logic provide a natural home for antirealism. This would be a mistake, however, if intuitionistic logic could be given a realist semantic foundation. Fine shows how truthmaker semantics can be used to provide just such a realist semantics for intuitionistic logic (2014b).
Third, consider the is-ought gap. Hume 1739 famously argued for a gap between ‘is’ and ‘ought’ statements: one cannot validly derive any statement about what ought to be from any statements about what is. Despite the appeal of such a gap, it has not been easy to formulate it clearly. What’s more, standard formulations are vulnerable to superficial but resilient counterexamples (Prior 1960). Fine shows how truthmaker semantics can be used to formulate the gap in a way that avoids such superficial counterexamples (2018b).
5. Logics and Mathematics
Fine has made a variety of seminal technical contributions to formal logic as well as to philosophical logic and the philosophy of mathematics. These contributions may be organized, respectively, into three major groups: formal logic (especially modal logics), arbitrary objects, and the foundations of mathematics (broadly construed so as to include the theory of sets and classes).
a. Logics
Most of Fine’s earliest work focused on technical questions within formal logic, especially on modal logics. A detailed synopsis of Fine’s technical work is beyond the scope of this article. But a very brief summary of them can be given here:
- various results about modal logics with propositional quantifiers (1970 which presents results from Fine’s Ph.D. dissertation 1969);
- a completeness proof for a predicate logic without identity but with primitive numerical quantifiers (1972a);
- early developments of graded modal logic (1972b);
- various results about S4 logics (those with reflexive and transitive Kripke frames) and certain extensions of them (1971; 1972c; 1974a; 1974b);
- the application of normal forms to a general completeness proof for “uniform” modal logics (1975b);
- a seminal “canonicity theorem” for modal logics (1975c);
- completeness results for logics containing K4 (those with transitive Kripke frames) (1974c; 1985a);
- failure of Craig’s interpolation lemma for various quantified modal logics (1979);
- the underivability of a quantifier permutation principle in certain modal systems without identity (1983b);
- an exploration into whether truth can be defined without the notion of satisfaction (joint work with McCarthy 1984b);
- incompleteness results for standard semantics for quantified relevance logic and an alternative semantics for it that is complete (1988; 1989a);
- the development of stability (or “felicitous”) semantics for the conception of “negation as failure” in logic programming and computer science (1989b); and
- general results about how properties of “monomodal” logics containing a single modal operator may transfer to a “multimodal” logic joining them (joint work with Schurz 1996).
In addition, Fine also wrote several articles in economic theory (1973a; 1972d), including two with his brother, economist Ben Fine (1974d; 1974e).
b. Arbitrary Objects
We often speak of arbitrary objects—an arbitrary integer, an arbitrary American, and so on. But at least since Berkeley 1710, the notion of an arbitrary object has been thought to be dispensable, if not outright incoherent. But in Fine’s book Reasoning with Arbitrary Objects, he argued that familiar opposition to arbitrary objects is misplaced and that they can, contrary to received wisdom, be given a rigorous theoretical foundation (1985d and its abridgements 1983a; 1985b).
The matter is not a mere intellectual curiosity. For it turns out, according to Fine, that arbitrary objects have various important applications. One salient application is to natural deduction and, especially, the logic of generality (1985d; 1985b). To illustrate, consider how one might explain the rule of universal generalization to students of a first formal logic course. One might say that if one can show that an arbitrary item a satisfies some condition f, then one may deduce that every item whatsoever satisfies that condition: “xf(x). Standard glosses on the rule ultimately attempt to avoid any appeal to the arbitrary item in favor of some alternative construal. But given Fine’s defense of arbitrary objects, there is no need to avoid appealing to them, and, in fact, it may be argued that they provide a more direct and satisfying account of the rule than alternative accounts do. Fine has also explored other applications to mathematical logic, the philosophy of language, and the history of ideas are also explored (1985d).
More recently, Fine has found new applications for arbitrary objects. One is to Cantor’s abstractionist constructions of cardinal numbers and order types. The constructions have faced formidable objections. But, according to Fine, the objections can be overcome by appealing to the theory of arbitrary objects (1998). In a belated companion article, Fine argues that his theory of arbitrary objects combined with the Cantorian approach can be extended to provide a general theory of types or forms, of which structural universals end up being a special case (2017a). And Fine also puts arbitrary objects to use when attempting to provide a paradox-free construction of sets or classes that allows for the existence of a universal class and for the Frege-Russell cardinal numbers (2005a), characterizing identity criteria (2016b) as well as unified foundations for essence and ground (2015b). Fine is currently preparing a revised version of Reasoning with Arbitrary Objects.
c. Philosophy of Mathematics
Most of Fine’s contributions to the philosophy of mathematics concern various foundational issues. Much recent interest in these issues derives from Frege’s infamous attempt to secure the foundations of mathematics by deriving it from logic alone. Frege’s attempt foundered in the early 1900s with the discovery of the set-theoretic paradoxes. Much of Fine’s work in the philosophy of mathematics concern the prospects for reviving Frege’s project without paradox.
At the heart of Frege’s own attempt was the notion of abstraction. Just as we may abstract the direction of two lines from their being parallel, so too we may abstract the number of two classes from their equinumerosity. Frege’s own use of abstraction ultimately led to paradox. But since then, neo-Fregeans (such as Fine’s colleague Crispin Wright and Bob Hale) have attempted to salvage much of Frege’s project by refining the use of abstraction in various ways. Fine has provided a detailed exploration of a general theory of abstraction as well as its prospects for sustaining neo-Fregean ambitions (2002a).
The discovery of the set-theoretic paradoxes generated turmoil within the foundations of mathematics and for associated philosophical programs. Since then, there have been a variety of attempts to provide a paradox-free construction of sets or classes. These attempts usually assume a notion of membership in their construction of the ontology. But Fine reverses the direction and constructs notions of membership in terms of the assumed ontology. This, Fine argues, has various advantages over standard constructions (2005a).
Many have thought that a central lesson of the aforementioned set-theoretic paradoxes is that quantification is inevitably restricted. Were it possible to quantify unrestrictedly over absolutely everything, then paradox would result. Instead, we may indefinitely extend the range of quantification without ever paradoxically quantifying over absolutely everything. So, it seems, quantification is always restricted, albeit indefinitely extendible. A persistent difficulty in sustaining this point of view, however, is the apparent arbitrariness of any restriction. Fine argues that the difficulty can be avoided (2006c). Quantification’s being absolute and its being unrestricted are often conflated. But Fine argues that they are distinct. Distinguishing them allows us to conceive of the possibility of quantification that is unrestricted but not absolute.
A recurring theme in some of the preceding papers is an approach to mathematics that Fine calls procedural postulationism. Traditional versions of postulationism take the existence of mathematical items and the truths about them to derive from certain propositions we postulate. But Fine’s procedural postulationism takes these postulates to be imperatival instead (e.g. “For each item in the domain that is a number, introduce another number that is its successor”). Fine believes this one difference helps postulationism provide a more satisfactory metaphysics, semantics, and epistemology of mathematics. Although procedural postulationism is hinted at in the previous articles, it is discussed in more detail in the context of discussing knowledge of mathematical items (2005d). Fine has indicated that he believes the core ideas of procedural postulationism may extend more generally, and briefly discusses their application to the metaphysics of material things (2007a).
6. History
It is not hard to find Aristotle’s influence in much of Fine’s work. But in addition to developing various Aristotelian themes, Fine has also directly contributed to more exegetical scholarship on Aristotle’s own work. These contributions have primarily focused on developing an account of Aristotle’s views on substance and what we may still learn from them. This begins with an attempt to formalize Aristotle’s views on matter (1992). Fine later raises a puzzle for Aristotle (and other neo-Aristotelians) concerning how the matter now composing one hylomorphic compound, say Callias, could later come to compose another hylomorphic compound, say Socrates (1994c). According to Aristotle, the world contains elements that may compose mixtures, and these mixtures in turn compose substances. Fine argues against conceptions of mixtures that take them to be at the same level as the elements composing them and, instead, defends a conception on which they are at a higher level (1995d). Finally, Fine argues that the best interpretation of a vexing discussion in Metaphysics Theta.4 is that Aristotle was attempting to introduce a novel conception of modality (2011a).
Additionally, Fine has written on Husserl’s discussions from the Logical Investigations on part and whole and the related topics of dependence, necessity, and unity (1995c). Fine also has work in preparation on Bolzano’s conception of ground.
7. References and Further Reading
- Berkeley, George. 1710. A Treatise Concerning the Principles of Human Knowledge.
- Fine, Kit. 1969. For Some Proposition and So Many Possible Worlds. University of Warwick.
- Fine, Kit. 1970. “Propositional Quantifiers in Modal Logic.” Theoria 36 (3): 336-46.
- Fine, Kit. 1971. “The Logics Containing S4.3.” Zeitschrift für Mathematische Logik und Grundlagen der Mathematik 17 (1): 371-76.
- Fine, Kit. 1972a. “For So Many Individuals.” Notre Dame Journal of Formal Logic 13 (4): 569-72.
- Fine, Kit. 1972b. “In So Many Possible Worlds.” Notre Dame Journal of Formal Logic 13 (4): 516-20.
- Fine, Kit. 1972c “Logics Containing S4 without the Finite Model Property.” In Conference in Mathematical Logic–London ’70, edited by W. Hodges. New York: Springer-Verlag.
- Fine, Kit. 1972d. “Some Necessary and Sufficient Conditions for Representative Decision on Two Alternatives.” Econometrica 40 (6): 1083-90.
- Fine, Kit. 1973a. “Conditions for the Existence of Cycles under Majority and Non-minority Rules.” Econometrica 41 (5): 889-99.
- Fine, Kit. 1974a. “An Ascending Chain of S4 Logics.” Theoria 40 (2): 110-16.
- Fine, Kit. 1974b. “An Incomplete Logic Containing S4.” Theoria 40 (1): 23-29.
- Fine, Kit. 1974c. “Logics Containing K4 – Part I.” The Journal of Symbolic Logic 39 (1): 31-42.
- Fine, Kit. 1975a. “Critical Notice: Counterfactuals, by David Lewis.” Mind 84 (335): 451-58. Reprinted in Modality and Tense: Philosophical Papers.
- Fine, Kit. 1975b. “Normal Forms in Modal Logic.” Notre Dame Journal of Formal Logic 16 (2): 229-34.
- Fine, Kit. 1975c. “Some Connections Between Elementary and Modal Logic.” In Proceedings of the Third Scandinavian Logic Symposium, edited by S. Kanger. Amsterdam: North-Holland.
- Fine, Kit. 1975d. “Vagueness, Truth and Logic.” Synthese 30: 265-300.
- Fine, Kit. 1977a “Prior on the Construction of Possible Worlds and Instants.” In Worlds, Times and Selves, edited by A. N. Prior and K. Fine. London: Duckworth. Reprinted in Modality and Tense: Philosophical Papers.
- Fine, Kit. 1977b. “Properties, Propositions and Sets.” Journal of Philosophical Logic 6: 135-91.
- Fine, Kit. 1978a. “Model Theory for Modal Logic – Part I: The De Re/De Dicto Distinction.” Journal of Philosophical Logic 7 (1): 125-56.
- Fine, Kit. 1978b. “Model Theory for Modal Logic – Part II: The Elimination of De Re Modality.” Journal of Philosophical Logic 7 (1): 277-306.
- Fine, Kit. 1979. “Failures of the Interpolation Lemma in Quantified Modal Logic.” The Journal of Symbolic Logic 44 (2): 201-06.
- Fine, Kit. 1980. “First-order Modal Theories II – Propositions.” Studia Logica 39 (2/3): 159-202.
- Fine, Kit. 1981a. “First-order Modal Theories I – Sets.” Noûs 15 (2): 177-205.
- Fine, Kit. 1981b. “Model Theory for Modal Logic – Part III: Existence and Predication.” Journal of Philosophical Logic 10 (3): 293-307.
- Fine, Kit. 1982a. “Acts, Events and Things.” In Language and Ontology, edited by W. Leinfellner, E. Kraemer and J. Schank. Wien: Hölder-Pichler-Tempsky, as part of the proceedings of the Sixth International Wittgenstein Symposium 23rd to 30th August 1981, Kirchberg/Wechsel (Austria).
- Fine, Kit. 1982b. “First-order Modal Theories III – Facts.” Synthese 53: 43-122.
- Fine, Kit. 1982c. “The Problem of Non-existents.” Topoi 1: 97-140.
- Fine, Kit. 1983a. “A Defence of Arbitrary Objects.” Proceedings of the Aristotelian Society, Supplementary Volume 57: 55-77.
- Fine, Kit. 1983b. “The Permutation Principle in Quantificational Logic.” Journal of Philosophical Logic 12 (1): 33-37.
- Fine, Kit. 1984a. “Critical Review of Parsons’ Non-Existent Objects.” Philosophical Studies 45 (1): 95-142.
- Fine, Kit. 1985a. “Logics Containing K4 – Part II.” The Journal of Symbolic Logic 50 (3): 619-51.
- Fine, Kit. 1985b. “Natural Deduction and Arbitrary Objects.” Journal of Philosophical Logic 14: 57-107.
- Fine, Kit. 1985c “Plantinga on the Reduction of Possibilist Discourse.” In Alvin Plantinga, edited by J. E. Tomberlin and P. van Inwagen. Dordrecht: Reidel. Reprinted in Modality and Tense: Philosophical Papers.
- Fine, Kit. 1985d. Reasoning with Arbitrary Objects. Oxford: Blackwell.
- Fine, Kit. 1988. “Semantics for Quantified Relevance Logic.” Journal of Philosophical Logic 17 (1): 27-59.
- Fine, Kit. 1989a “Incompleteness for Quantified Relevance Logics.” In Directions in Relevant Logics, edited by R. Sylvan and J. Norman. Dordrecht: Kluwer.
- Fine, Kit. 1989b “The Justification of Negation as Failure.” In Proceedings of the Congress on Logic, Methodology and the Philosophy of Science VIII, edited by J. Fenstad, T. Frolov and R. Hilpinen. Amsterdam: Elsner Science Publishers B. V.
- Fine, Kit. 1989c. “The Problem of De Re Modality.” In Themes from Kaplan, edited by J. Almog, J. Perry and H. Wettstein. Oxford: Oxford University Press. Reprinted in Modality and Tense: Philosophical Papers.
- Fine, Kit. 1990. “Quine on Quantifying In.” In Proceedings of the Conference on Propositional Attitudes, edited by C. A. Anderson and J. Owens. Stanford: CSLI. Reprinted in Modality and Tense: Philosophical Papers.
- Fine, Kit. 1992. “Aristotle on Matter.” Mind 101 (401): 35-57.
- Fine, Kit. 1994a. “Compounds and Aggregates.” Noûs 28 (2): 137-58.
- Fine, Kit. 1994b. “Essence and Modality.” Philosophical Perspectives 8: 1-16.
- Fine, Kit. 1994c “A Puzzle Concerning Matter and Form.” In Unity, Identity, and Explanation in Aristotle’s Metaphysics, edited by T. Scaltsas, D. Charles and M. L. Gill. Oxford: Oxford University Press.
- Fine, Kit. 1994d “Senses of Essence.” In Modality, Morality and Belief: Essays in Honor of Ruth Barcan Marcus, edited by W. Sinnott-Armstrong. Cambridge: Cambridge University Press.
- Fine, Kit. 1994e. “The Study of Ontology.” Noûs 25 (3): 263-94.
- Fine, Kit. 1995a. “The Logic of Essence.” Journal of Philosophical Logic 24: 241-73.
- Fine, Kit. 1995b. “Ontological Dependence.” Proceedings of the Aristotelian Society 95: 269-90.
- Fine, Kit. 1995c. “Part-Whole.” In The Cambridge Companion to Husserl, edited by B. Smith and D. Woodruff. Cambridge: Cambridge University Press.
- Fine, Kit. 1995d. “The Problem of Mixture.” Pacific Philosophical Quarterly 76 (3-4): 266-369.
- Fine, Kit. 1998. “Cantorian Abstraction: A Reconstruction and Defense.” The Journal of Philosophy 95 (12): 599-634.
- Fine, Kit. 1999. “Things and Their Parts.” Midwest Studies in Philosophy 23: 61-74.
- Fine, Kit. 2000a. “A Counter-example to Locke’s Thesis.” The Monist 83 (3): 357-61.
- Fine, Kit. 2000b. “Neutral Relations.” The Philosophical Review 109 (1): 1-33.
- Fine, Kit. 2000c. “Semantics for the Logic of Essence.” Journal of Philosophical Logic 29 (6): 543-84.
- Fine, Kit. 2001. “The Question of Realism.” Philosophers’ Imprint 1 (2): 1-30.
- Fine, Kit. 2002a. The Limits of Abstraction. Oxford: Clarendon Press.
- Fine, Kit. 2002b. “The Problem of Possibilia.” In Handbook of Metaphysics, edited by D. Zimmerman. Oxford: Oxford University Press. Reprinted in Modality and Tense: Philosophical Papers.
- Fine, Kit. 2002c. “The Varieties of Necessity.” In Conceivability and Possibility, edited by T. S. Gendler and J. Hawthorne. Oxford: Oxford University Press. Reprinted in Modality and Tense: Philosophical Papers.
- Fine, Kit. 2003a. “The Non-Identity of a Material Thing and Its Matter.” Mind 112 (446): 195-234.
- Fine, Kit. 2003b. “The Role of Variables.” The Journal of Philosophy 50 (12): 605-31.
- Fine, Kit. 2005a. “Class and Membership.” The Journal of Philosophy 102 (11): 547-72.
- Fine, Kit. 2005b. Modality and Tense: Philosophical Papers. Oxford: Clarendon Press.
- Fine, Kit. 2005c. “Necessity and Non-existence.” In Modality and Tense: Philosophical Papers.
- Fine, Kit. 2005d. “Our Knowledge of Mathematical Objects.” In Oxford Studies in Epistemology, edited by T. S. Gendler and J. Hawthorne. Oxford: Clarendon Press.
- Fine, Kit. 2005e. “Reference, Essence, and Identity.” In Modality and Tense: Philosophical Papers. Oxford: Clarendon Press.
- Fine, Kit. 2005f. “Tense and Reality.” In Modality and Tense: Philosophical Papers. Oxford: Clarendon Press.
- Fine, Kit. 2006a. “In Defense of Three-Dimensionalism.” The Journal of Philosophy 103 (12): 699-714.
- Fine, Kit. 2006b. “The Reality of Tense.” Synthese 150 (3): 399-414.
- Fine, Kit. 2006c “Relatively Unrestricted Quantification.” In Absolute Generality, edited by A. Rayo and G. Uzquiano. Oxford: Clarendon Press.
- Fine, Kit. 2007a. “Response to Kathrin Koslicki.” dialectica 61 (1): 161-66.
- Fine, Kit. 2007b. Semantic Relationism. Oxford: Blackwell Publishing.
- Fine, Kit. 2008a. “Coincidence and Form.” Proceedings of the Aristotelian Society, Supplementary Volume 82 (1): 101-18.
- Fine, Kit. 2008b. “The Impossibility of Vagueness.” Philosophical Perspectives 22 (Philosophy of Language): 111-36.
- Fine, Kit. 2009. “The Question of Ontology.” In Metametaphysics: New Essays on the Foundations of Ontology, edited by D. Chalmers, D. Manley and R. and Wasserman. Oxford: Oxford University Press.
- Fine, Kit. 2010a. “Semantic Necessity.” In Modality: Metaphysics, Logic, and Epistemology, edited by B. Hale and A. Hoffmann. Oxford: Oxford University Press.
- Fine, Kit. 2010b. “Some Puzzles of Ground.” Notre Dame Journal of Formal Logic 51 (1): 97-118.
- Fine, Kit. 2010c. “Towards a Theory of Part.” The Journal of Philosophy 107.
- Fine, Kit. 2011a. “Aristotle’s Megarian Manoeuvres.” Mind 120 (480): 993-1034.
- Fine, Kit. 2011b. “What is Metaphysics?” In Contemporary Aristotelian Metaphysics, edited by T. E. Tahko. Cambridge: Cambridge University Press.
- Fine, Kit. 2012a. “Counterfactuals without Possible Worlds.” The Journal of Philosophy 59 (3): 221-46.
- Fine, Kit. 2012b. “A Difficulty for the Possible Worlds Analysis of Counterfactuals.” Synthese 189 (1): 29-57.
- Fine, Kit. 2012c “Guide to Ground.” In Metaphysical Grounding: Understanding the Structure of Reality, edited by F. Correia and B. Schnieder. Cambridge: Cambridge University Press.
- Fine, Kit. 2012d. “The Pure Logic of Ground.” The Review of Symbolic Logic 25 (1): 1-25.
- Fine, Kit. 2013a. “Fundamental Truths and Fundamental Terms.” Philosophy and Phenomenological Research 87 (3): 725-32.
- Fine, Kit. 2014a. “Permission and Possible Worlds.” dialectica 68 (3): 317-36.
- Fine, Kit. 2014b. “Truth-Maker Semantics for Intuitionistic Logic.” Journal of Philosophical Logic 43: 549-77.
- Fine, Kit. 2015a. “The Possibility of Vagueness.” Synthese 194 (10): 3699-725.
- Fine, Kit. 2015b. “Unified Foundations for Essence and Ground.” Journal of the American Philosophical Association 1 (2): 296-311.
- Fine, Kit. 2016a. “Angellic Content.” Journal of Philosophical Logic 45 (2): 199-226.
- Fine, Kit. 2016b. “Identity Criteria and Ground.” Philosophical Studies 173 (1): 1-19.
- Fine, Kit. 2016c. “Williamson on Fine on Prior on the Reduction of Possibilist Discourse.” Canadian Journal of Philosophy 46 (4-5): 548-70.
- Fine, Kit. 2017a. “Form.” The Journal of Philosophy CXIV (10): 509-35.
- Fine, Kit. 2017b. “Naive Metaphysics.” Philosophical Issues 27: 98-113.
- Fine, Kit. 2017c. “Truthmaker Semantics.” In A Companion to the Philosophy of Language, edited by B. Hale, C. Wright and A. Miller. West Sussex: Wiley-Blackwell.
- Fine, Kit. 2018a. “Ignorance of Ignorance.” Synthese 195 (9): 4031-45.
- Fine, Kit. 2019c. “Constructing the Impossible.” In to appear in a collection of papers for Dorothy Edgington.
- Fine, Kit. 2020a. “Semantics.” In The Routledge Handbook of Metaphysical Grounding, edited by M. J. Raven. New York: Routledge.
- Fine, Kit, and Ben Fine. 1974d. “Social Choice and Individual Rankings I.” Review of Economic Studies 41: 303-22.
- Fine, Kit, and Ben Fine. 1974e. “Social Choice and Individual Rankings II.” Review of Economic Studies 41: 459-75.
- Fine, Kit, and Timothy McCarthy. 1984b. “Truth without Satisfaction.” Journal of Philosophical Logic 13 (4): 397-421.
- Fine, Kit, and Gerhard Schurz. 1996. “Transfer Theorems for Multimodal Logics.” In Logic and Reality: Essays on the Legacy of Arthur Prior, edited by J. Copeland. Oxford: Clarendon.
- Frege, Gottlob. 1892. “On Sense and Reference.” In Translations from the Philosophical Writings of Gottlob Frege, edited by P. T. Geach and M. Black. Oxford: Blackweel.
- Hume, David. 1739. “A Treatise of Human Nature”, edited by L. A. Selby-Bigge and P. H. Nidditch. Oxford: Clarendon Press.
- Kripke, Saul. 1972. Naming and Necessity. Cambridge, MA: Harvard University Press.
- Kripke, Saul. 2011. “A Puzzle about Belief.” In Philosophical Troubles: Collected Papers, Volume I. Oxford: Oxford University Press.
- Leibniz, Gottried Wilhelm. 1714. Monadology.
- Lewis, David. 1973. Counterfactuals. Oxford: Blackwell Publishers.
- Lewis, David. 1986. On the Plurality of Worlds. Oxford: Blackwell Publishers.
- Lewis, David. 1991. Parts of Classes. Oxford: Blackwell.
- Locke, John. 1689. An Essay Concerning Human Understanding.
- McTaggart, J. M. E. 1908. “The Unreality of Time.” Mind 17: 457-74.
- Prior, A. N. 1960. “The Autonomy of Ethics.” Australasian Journal of Philosophy 38 (3): 199-206.
- Quine, Willard Van Orman. 1948. “On What There is.” Review of Metaphysics 2: 21-38. Reprinted in From a Logical Point of View, 2nd ed., Harvard: Harvard University Press, 1980, 1-19.
- Raven, Michael J. 2019. “(Re)discovering Ground.” In Cambridge History of Philosophy, 1945 to 2015, edited by K. M. Becker and I. Thomson. Cambridge: Cambridge University Press.
- Raven, Michael J., ed. 2020. The Routledge Handbook of Metaphysical Grounding. New York: Routledge.
- Spinoza, Baruch. 1677. Ethics, Demonstrated in Geometrical Order.
- Stalnaker, Robert. 1968. “A Theory of Conditionals.” In Studies in Logical Theory, edited by N. Rescher. Oxford: Blackwell.
- Williamson, Timothy. 2013b. Modal Logic as Metaphysics. Oxford: Oxford University Press.
Author Information
Mike Raven
Email: mike@mikeraven.net
University of Victoria
Canada









 Plato’s enormous impact on later philosophy, education, and culture can be traced to three interrelated aspects of his philosophical life: his written philosophical dialogues, the teaching and writings of his student Aristotle, and the educational organization he began, “the Academy.” Plato’s Academy took its name from the place where its members congregated, the Akadēmeia, an area outside of the Athens city walls that originally held a sacred grove and later contained a religious precinct and a public gymnasium.
Plato’s enormous impact on later philosophy, education, and culture can be traced to three interrelated aspects of his philosophical life: his written philosophical dialogues, the teaching and writings of his student Aristotle, and the educational organization he began, “the Academy.” Plato’s Academy took its name from the place where its members congregated, the Akadēmeia, an area outside of the Athens city walls that originally held a sacred grove and later contained a religious precinct and a public gymnasium.
 Eduard Hanslick was a Prague-born Austrian aesthetic theorist, music critic, and the first professor of aesthetics and history of music at the University of Vienna, who is commonly considered the founder of musical
Eduard Hanslick was a Prague-born Austrian aesthetic theorist, music critic, and the first professor of aesthetics and history of music at the University of Vienna, who is commonly considered the founder of musical