Mathematical Nominalism
Mathematical nominalism can be described as the view that mathematical entities—entities such as numbers, sets, functions, and groups—do not exist. However, stating the view requires some care. Though the opposing view (that mathematical objects do exist) may seem like a somewhat exotic metaphysical claim, it is usually motivated by the thought that mathematical objects are required to exist in order for mathematical claims to be true. If, for instance, it is true that there are infinitely many prime numbers, then prime numbers prima facie exist. Much contemporary work in mathematical nominalism divides into efforts to argue either that mathematical truths do not in fact require the existence of mathematical objects, or that we are entitled to regard mathematical claims, such as the one above, as false.
This article surveys contemporary attempts to defend mathematical nominalism. Firstly, it considers how to formulate mathematical nominalism, surveys the origins of the contemporary debate, and explains epistemic motivations for nominalism. Secondly, it examines a particularly prominent family of objections to mathematical nominalism, issuing from the applicability of mathematics. Thirdly, it looks at three kinds of response to that family of objections: reconstructive nominalism (aiming to show that, in principle, one can recreate the applications of mathematics without making mathematical claims), deflationary nominalism (aiming to show that the truth of mathematical claims does not require the existence of mathematical objects), and instrumentalist nominalism (aiming to show that one can make sense of standard mathematical practices without incurring a commitment to the truth of mathematical claims). Finally, it surveys the claims of some leading thinkers about the relationship between mathematical nominalism and naturalism.
Table of Contents
- Formulating Mathematical Nominalism
- The Origins of the Contemporary Debate
- Motivations for Nominalism
- Nominalism and the Application of Mathematics
- Reconstructive Nominalism
- Deflationary Nominalism
- Instrumentalism
- Mathematical Nominalism and Naturalism
- References and Further Reading
1. Formulating Mathematical Nominalism
At a first pass, one can describe mathematical nominalism as the view that mathematical entities do not exist. Some clarifications and caveats, however, should be kept in mind. Firstly, some theorists have held that mathematical entities are, in some sense, mental objects. (The Dutch mathematician and philosopher L.E.J. Brouwer is sometimes interpreted as having endorsed this view.) Nominalists, however, deny the existence of mathematical objects understood as abstract objects whose existence does not depend on any mental or linguistic activity. To understand this claim, one must appreciate the thought that all that there is, or that there might be, can be divided into two exclusive and exhaustive categories: the concrete and the abstract. Nominalists hold that abstract objects do not exist. Examples of concrete objects are tables, chairs, stars, human beings, molecules, microbes, as well as more exotic theoretical entities such as electrons, bosons, dark matter and so on. Paradigmatically, concrete objects are spatiotemporal, contingent, have causal powers and can themselves be affected, participate in events, and can be interacted with, even if only indirectly. There are two different senses in which entities can be abstract. On one sense, to be abstract means to be non-particular. It is in this sense that universals are said to be abstract. Universals are properties which can be instantiated by particular objects. The property of being negatively charged would be instantiated by particular electrons, for example. Some theorists have understood mathematical objects as universals (Bigelow 1988, Shapiro 1997). However, mathematical objects are typically conceived as being abstract in a different way: they are particular, but non-concrete. Paradigmatically, objects that are abstract in this sense are particular, but non-spatial, necessary, unchanging, acausal, and cannot be interacted with, even indirectly. (The distinction between concrete and abstract entities is, however, difficult to analyze. Rosen (2020) provides a detailed discussion. See also Lewis (1986, 81–86) and Fitzgerald (2003).) Mathematical nominalism then can be more specifically described as the view that abstract mathematical entities do not exist, in either sense of “abstract”.
Secondly, some theorists hold that the term “exist” and its cognates are not univocal (see, for instance, Russell 1903; Brandom 1994; Miller 2002; Vallicella 2002; Putnam 2004; Hirsch 2011; Hofweber 2016; McDaniel 2017; Kimhi 2018). For example, the meaning of “exist(s)” in “Electrons exist” may not be the same as in “Giants exist in both Mesopotamian and Shinto mythology” or “A special bond exists between all philosophers of mathematics”. Further, some theorists hold that some usages of “exist(s)” are not ontologically committing—that is, one can talk of some things existing without thereby committing to those things being part of the furniture of reality—and, additionally, that this is true of existence claims about mathematical objects (Azzouni 2010b, 2017). On this view, mathematical objects can be said to exist in a way that is not ontologically significant, such that the existence of mathematical objects makes no demand on the world. Put differently, mathematical objects could be said to exist regardless of what the world is like. Mathematical nominalism, then, can be more specifically described as the view that abstract mathematical entities do not exist independently of mental or linguistic activity and in an ontologically significant sense of “exist”. However, to avoid being unnecessarily involute, going forward, these caveats will mostly be left implicit.
The terminology used is not uniform across the literature. Those who hold that abstract mathematical objects exist independently of mental or linguistic activity, in an ontologically significant sense, are usually called mathematical platonists. However, small-“p” platonists in this sense are not necessarily followers of Plato, and some reserve the term “Platonist” for views that have more in common with Plato’s own platonism, distinguishing platonism from the more generic object realism (Linnebo 2017) or the apophatic anti-nominalism (Burgess and Rosen 1997). At least one theorist, Rayo (2016), refers to the view that mathematical objects exist in an ontologically insignificant sense of “exist” as trivialist platonism or subtle platonism.
2. The Origins of the Contemporary Debate
Understanding contemporary defenses of nominalism requires understanding the motivations underlying anti-nominalism. Perhaps primary among these is a broadly representationalist view of language, according to which declarative claims (at the very least, simple declarative claims of subject-predicate form) purport to represent or describe the world as being a certain way. Declarative claims (again, at the very least, simple declarative claims of subject-predicate form) are true just in those cases where the world is the way they represent it as being, and to take a claim of this sort to be true is to take the world to be the way the claim represents it as being. For example, “The Forth Rail Bridge is red” says of the Forth Rail Bridge (the subject) that it is red (the predicate). So, a claim of this sort purports to denote something (the Forth Rail Bridge) and attributes a property to that thing (redness). The claim is true just in case the thing it purports to denote exists and has the property it ascribes to it. If the Forth Rail Bridge was turquoise, or did not exist, the claim would not be an accurate representation or description.
Mathematics similarly contains simple declarative claims of subject-predicate form, such as “Seven is prime”. This says of the number seven that it is prime. So, according to this broadly representationalist view, the claim purports to denote something (the number seven) and attributes a property to that thing (primeness). Since simple declarative claims are true just in those cases in which they accurately describe that of which they speak, “Seven is prime” is true just in case the thing it purports to denote exists and has the property it ascribes to it. If seven was not prime, or did not exist, the claim would not be an accurate representation or description.
A major influence here is Gottlob Frege’s pathbreaking work in the foundations of mathematics. In his Grundlagen der Arithmetik (1884), Frege defended the view that numerical expressions function as singular terms, and that singular terms are the parts of language which purport to pick out or refer to exactly one object. For Frege, singular terms are those that can correctly flank an identity sign “=”, or “is” when used to express identity, for instance: “The shortest serving prime minister of the twentieth century is Bonar Law” or “The smallest number expressible as the sum of two cubes in two different ways = 1729”. The terms “The shortest serving prime minister of the twentieth century”, “Bonar Law”, “the smallest number expressible as the sum of two cubes in two different ways”, and “1729” all purport to refer to exactly one object. For Frege, the truth of claims such as these not only requires that they purport to refer to exactly one object, but also that they succeed in doing so; that is, there must be such an object. The claim “The smallest number expressible as the sum of two cubes in two different ways is 1729” is true because there is a number, 1729, that is the smallest number expressible as the sum of two cubes. On the other hand, no claim about the largest prime number can be true, because there is no largest prime. These semantic considerations lay the groundwork for a simple but influential argument for mathematical platonism: some mathematical claims are true; therefore, there are mathematical objects. Since, it is widely supposed, these claims are true regardless of what anyone thinks or says, the existence of mathematical objects is mind- and language-independent.
The Polish logician Alfred Tarski’s (also pathbreaking) work on truth helped to ensconce this broadly representationalist picture. Tarski’s own interests were not in defending a philosophical account of language, but in showing how to define a notion true-in-L for some formal language L in a way that avoids the Liar Paradox (Tarski 1935, 1944). What emerged is known as a semantic theory of truth, so-called not because it has to do with meaning per se, but because, in line with contemporaneous usage of the word “semantic”, it has to do with relations between words and things. Tarski’s approach depends in part on stipulating what each singular term in L denotes, and which things or sequences of things “satisfy” the predicates of L. For example: “x is red” is satisfied by the Forth Rail Bridge if and only if the Forth Rail Bridge is red, and “x admires y” is satisfied by the ordered pair <Thom, Jonny> if and only if Thom admires Jonny.
Tarski’s work formed the basis of a new branch of mathematics, model theory, and, subsequently, of the model-theoretic accounts of language, which became mainstream in formal semantics by the end of the twentieth century. This is the approach to semantics familiar from logic textbooks. There, an interpretation of a language is understood as a function from the set of elements of the language itself—variables, constants, predicates, sentences—to the domain of that language—the set of things that language is about (given the interpretation).
Like Frege’s analysis of singular terms, the formal semantics that stems from Tarski’s semantic account of truth appears to entail platonism, so long as one holds that there are true mathematical sentences. This point was made by Paul Benacerraf in a canonical and widely cited 1973 paper “Mathematical Truth”. Benacerraf holds that Tarski’s is “the only viable systematic general account we have of truth” (Benacerraf 1973, 670) and that a uniform semantics or theory of truth should be given to both non-mathematical parts of natural language (for example, “There are at least three large cities older than New York”) and to mathematese (for example, “There are at least three perfect numbers greater than 17”). One reason is that:
The semantical apparatus of mathematics [should] be seen as part and parcel of that of the natural language in which it is done, and thus that whatever semantical account we are inclined to give of names or, more generally, of singular terms, predicates, and quantifiers in the mother tongue include those parts of the mother tongue which we classify as mathematese. (Benacerraf 1973, 666)
A distinct, but closely related, reason is that logical consequence is standardly defined in terms of truth (Tarski 1936). Roughly speaking: a set of sentences Σ logically entails a sentence ϕ just in case there is no interpretation function according to which Σ is true but ϕ is false. If mathematical truth is not understood along Tarskian (and therefore apparently platonist) lines, we would require a new account not just of mathematical truth but also of logical consequence, but no such accounts are forthcoming (Benacerraf 1973, 670).
Similarly influential was the Harvard logician W.V.O. Quine. Quine’s (also canonical and widely cited) 1948 paper “On What There Is” did much to establish as orthodox the view that the existential quantifier is ontologically committing. In Quine’s own words:
The variables of quantification, ‘something’, ‘nothing’, ‘everything’, range over our whole ontology, whatever it may be; and we are convicted of a particular ontological presupposition if, and only if, the alleged presuppositum has to be reckoned among the entities over which our variables range in order to render one of our affirmations true. (Quine 1948, 32)
Despite the paper’s influence, what the argument for that conclusion is, or whether it offers an argument at all, is disputed. Elsewhere, however, Quine defends the claim that the existential quantifier expresses existence on the grounds that its meaning is given by the English phrase “there is an object x such that…” and that this expresses existence (Quine 1986, 89).
3. Motivations for Nominalism
Although mathematical nominalism is the metaphysical claim that no mathematical objects exist, the chief argument for nominalism centers around the epistemological concern that we cannot have knowledge of mind-independent and language-independent mathematical objects even if they do exist, or, more weakly, that it is a mystery how we could have knowledge of mathematical objects so conceived. (See the article on The Benacerraf Problem of Mathematical Truth and Knowledge.) The upshot of these arguments is not the de facto claim that mathematical objects do not exist, but the de jure claim that we ought not to believe in mathematical objects. The epistemological problem with mathematical objects arises from the difficulty in squaring what abstract objects are like, if they exist, with what we know about ourselves as enquirers with particular capacities, abilities, and faculties for gaining knowledge of what the world is like. Mathematical objects as abstract objects are not only the sort of things that cannot be touched or seen, but they also cannot be interacted with or manipulated in any way. They have no effects, nor do they participate in events that could, even in principle, impinge on one’s experience. Facts about abstract objects, as the platonist understands them, cannot make a difference to any data one might have or come to acquire, or to any beliefs one might come to hold.
The canonical articulation of the epistemological problem is due to Benacerraf (in the same paper in which he advocates a Tarskian account of mathematical truth). Our account of mathematical knowledge, Benacerraf claimed, “must fit into an over-all account of knowledge in a way that makes it intelligible how we have the mathematical knowledge that we have” (Benacerraf 1973, 667), in particular:
A causal account of knowledge on which for [some person] X to know that [some sentence] S is true requires some causal relation to obtain between X and the referents of the names, predicates, and quantifiers of S. (Benacerraf 1973, 671)
A causal criterion for knowledge immediately rules out knowledge of abstract objects since they are acausal.
As the causal theory of knowledge waned in popularity so did Benacerraf’s particular formulation of the epistemological problem. However, it is too quick to conclude from the failure of causal analyses of knowledge that there is no sound causal-epistemological argument against the possibility of knowledge of abstract objects. This depends on whether the analysis fails because an appropriate causal connection between an agent and the object of belief is not sufficient for knowledge, or because such a connection is not necessary for knowledge. If it is the latter, then showing that there are no causal connections between an agent who holds mathematical beliefs and mathematical objects would not show that something required for knowledge is lacking. On the other hand, if appropriate causal connections are insufficient but necessary for knowledge, then the causal objection would go through. The most influential objections to causal theories are of the former sort: appropriate causal connections, it is argued, are necessary but not sufficient for knowledge, as an appropriate causal connection can exist between a person’s belief and the object of this belief, while the belief is true only by luck, and hence not known (Goldman 1976). Others however have claimed that causal connections cannot be necessary for knowledge, as this would rule out knowledge of the future (Burgess and Rosen 1997; Potter 2007).
Some have argued for more modest, restricted versions of a causal criterion, which are not committed to the claim that all knowledge requires an appropriate causal connection between the knower and the object of her knowledge. Colin Cheyne (1998, 2001) claims that the causal criterion applies to existential knowledge, arguing that this is supported by examples from empirical science. However, subsequently Nutting (2016) has argued that a Benacerraf-like argument can be made that does not rely on a general causal criterion, but on the more defensible claim that direct knowledge (that is, knowledge of a claim that is not gained via an inference from another claim) requires some kind of appropriate causal connection. This, along with the premise that the objects of mathematical knowledge are acausal mathematical objects, and the premise that if we have any mathematical knowledge, some of it must be direct, entails that mathematical knowledge is impossible.
Others have characterized the epistemological objection in different terms. W.D. Hart claims that the epistemological problem does not concern causal theories of knowledge in particular, but empiricism more generally. Empiricism, as Hart understands it, is “the doctrine that all knowledge is a posteriori” (Hart 1977, 125). A posteriori knowledge is “justified ultimately by experience” (ibid.). Experience, in turn, “requires causal interaction with the objects experienced” (ibid.). Yet, causal interaction with mathematical objects is impossible. Though there is not a strict incompatibility between these tenets—unless one reads them as making the more specific claim that, for all x, knowledge of x requires experience of x—it is enough to set up a prima facie tension between empiricism and platonism.
Hartry Field (1989) reformulated the epistemic problem as a challenge to explain how our beliefs about abstract, mathematical objects could be reliable. Realists about mathematical objects think that their beliefs about mathematical objects are largely true. If so, those beliefs are highly correlated with the mathematical facts. The platonist, however, “must not only accept the reliability, but must commit himself or herself to the possibility of explaining it” (Field 1989, 26). However, there appears to be serious difficulties in doing so. On the one hand, the platonist conception of mathematical objects as acausal and mind-independent:
means that we cannot explain the mathematicians’ beliefs and utterances on the basis of those mathematical facts being causally involved in the production of those beliefs and utterances; or on the basis of the beliefs and utterances causally producing the mathematical facts; or on the basis of some common cause producing both. (Field 1989, 231)
On the other hand, “it is very hard to see what [a] supposed non-causal explanation could be” (Field 1989, 231). If the reliability of mathematical beliefs—as understood by the Platonist, that is, as beliefs about mind-independent abstract objects—appears impossible to explain, this would “undermine the belief in mathematical entities, despite whatever reason we might have for believing in them” (Field 1989, 26).
A prominent attempt to explain the reliability of mathematical beliefs, given platonism, is due to Balaguer (1998). Balaguer responds to Field’s challenge by invoking a “full-blooded platonist” view (often referred to as “set-theoretic pluralism” or as a “set-theoretic multiverse” view) according to which, roughly, every coherently describable universe of mathematical objects exists. So long, then, as our mathematical belief-forming methods result in consistent mathematical beliefs, they will accurately describe some mathematical objects. This, Balaguer argues, offers a platonistic explanation of the reliability of mathematical beliefs.
Two issues should be noted. Firstly, for the explanation to succeed, there must be something about our linguistic practices that makes it the case that our mathematical claims are always about the mathematical objects of which they would be true (Clarke-Doane 2020). For example, Zermelo-Fraenkel set theory with the axiom of choice (ZFC) is consistent both with the hypothesis CH that there is no set with cardinality larger than the integers but smaller than the real numbers, and with the negation of CH. On a universe view, there is one set-theoretic universe (characterizable, say, by ZFC), and it is the case that CH either accurately or inaccurately characterizes that universe. On a multiverse view, there is a plurality of set-theoretic universes characterizable by ZFC (as well as yet further universes characterizable by different consistent sets of axioms), some of which are accurately characterizable by CH (ZFC + CH universes) and other are accurately characterizable by the negation of CH (ZFC + ¬CH universes). To secure reliability, it must be the case that when one makes claims that are true of for instance ZFC + CH universes, one is in fact talking about ZFC + CH universes and not, rather, making false claims about ZFC + ¬CH universes. There are some difficulties in pinning down what it is about our language that would make this the case. (See Putnam (1980). Button (2013) gives a book-length treatment and Button and Walsh (2018, chapter 2) provides an introduction to these issues concerning reference.)
Secondly, meeting Field’s challenge removes one epistemological objection to platonism, but does not show that knowledge of mathematical objects, as understood by the platonist, is possible. This is because reliability is a necessary, but not a sufficient, condition for knowledge. It is possible for a belief-forming process to be serendipitously reliable in a way that is not sufficient for knowledge. For instance if someone has a brain lesion that causes them to believe that they have a brain lesion (Plantinga 1993), that person’s belief-forming process reliably leads, in the case of this belief (that they have a brain lesion), to a true belief, but still involves a kind of epistemic luck that is antithetical to knowledge. Standard accounts of epistemic luck appeal to safety or sensitivity conditions to secure knowledge, which in turn are analyzed in terms of what the agent would have believed in metaphysically possible worlds suitably related to the actual world. For this reason, they are often taken to be inapplicable to mathematical platonism. If platonism is true, it is true in all metaphysically possible worlds. The upshot is that standard safety and sensitivity conditions are trivially met in cases of necessary truths, so that every belief whose object is a necessary truth would count as knowledge even if it is gained by luck. Collin (2018) argues that it is possible to formulate an epistemological argument against platonism in terms of epistemic luck: by analyzing safety and sensitivity conditions in terms of epistemically possible scenarios, rather than metaphysically possible worlds, one can apply safety and sensitivity conditions to necessary truths.
No formulation of the epistemological objection is uncontroversial, but a felt sense that something is epistemically worrying about abstract objects is common in the philosophical literature. Pinning down exactly what the epistemological problem with mathematical objects is remains an open task for nominalists.
4. Nominalism and the Application of Mathematics
The semantic argument for mathematical platonism presented above suggests two genera of nominalist responses. The first is to deny the mainstream semantic assumptions that undergird the inference from the truth of simple declarative mathematical claims to the existence of mathematical objects. In broad terms, this could mean either dropping representationalism—and holding that simple declarative mathematical claims do not purport to represent a domain of mathematical objects in any substantive sense of “represent”—or retaining representationalism but holding that the mathematical objects being represented are non-existent objects. The second is to accept mainstream semantic assumptions, but to hold that simple declarative mathematical claims are false because there are no mathematical objects. On this second kind of view, the standards of correctness or incorrectness for mathematical claims are not, strictly speaking, standards of truth and falsehood.
Both sorts of response are complicated by the applicability of mathematics. There exists a large literature on the applicability of mathematics (see, for example, Frege 1884; Suppes 1960; Carnap 1967; Putnam 1971; Krantz and others 1971; Field 1980; Resnik 1997; Shapiro 1997; Steiner 1998; Azzouni 2004; Chang 2004; Chihara 2004; van Fraassen 2008; Bueno and Colyvan 2011; Bangu 2012; Pincock 2012; Weisberg 2013; Morrison 2015; Bueno and French 2018; Ketland 2021; Leng 2021; the article on The Applicability of Mathematics). However, a brief overview is enough to reveal its relevance to mathematical nominalism. At a high level of generality, mathematics is applied within the sciences in the following way. Scientists devise equations which can be used to model or represent concrete systems. Measurement procedures are used to assign mathematical values to aspects of the target concrete system and these values are “plugged in” to the equations. When mathematics is not merely a predictive tool, different values within the equations correspond to different magnitudes of properties of the concrete system. By manipulating the equations, one can then make predictions about the concrete system. These predictions are (directly or indirectly) testable when the mathematical results are (directly or indirectly) associated with measurement procedures.
Consider, for example, a closed vessel of volume V (in m3) containing a gas. The pressure P (in Pascals) of the gas can be measured using a manometer, and the temperature T (in Kelvin) can be measured using a thermometer. Letting n be the number of moles of gas (where 1 mole = 6.02 x 1023 molecules), and R be the ideal gas constant (~ 8.314), the ideal gas law (in molar form) tells us:
PV = nRT
Though only approximately accurate, the ideal gas law allows one to calculate physical quantities and make predictions about the behavior of gasses in a range of circumstances. It not only tells us, for instance, that increasing the temperature of the gas while holding fixed the volume of the vessel will increase the pressure but allows us to calculate precisely (idealization notwithstanding) to what extent this is the case. It also allows us, for instance, to calculate the number of moles of gas, so long as we are able to measure the pressure, volume, and temperature of the system, by rearranging the equation:
n = PV/RT
In other cases, the mathematics and the measurement procedures are far more complex. There are also enduring questions in areas such as the philosophy of quantum mechanics about what physical quantities mathematical objects such as wavefunctions correspond to, or whether they are merely predictive tools. However, the general contours of the picture remain the same: representing properties of physical systems using numbers allows algebraic reasoning to be used to describe, make predictions about, and explain features of the concrete world.
One, then, can think of the language of mathematical science as being two-sorted, that is, ranging over two kinds of thing:
-
- concrete entities, using primary variables: x1, x2,…,xn.
- abstract entities, using secondary variables: y1, y2,…,yn.
and, therefore, containing three kinds of predicate:
-
- concrete predicates, expressing relations between concreta: C1, C2,…
- abstract predicates, expressing relations between abstracta: A1, A2,…
- mixed predicates, expressing relations between concrete and abstract objects: M1, M2,…
Measurement is one clear example of (iii). Measurements describe physical quantities by associating them with numerical magnitudes. Take the claim “The mass of d1 is 5 kilogrammes”, where d1 is a concrete object, or “The temperature of d2 is 30 Kelvin”, where d2 is a concrete system. The first is expressed more formally as “Mkg(d1) = 5”—which describes a function from a concrete object, d1, to an abstract object, the number 5—and the second as “Tk(d2) = 30”—which describes a function from a concrete system, d2, to an abstract object, the number 30. Although these are, in one sense, about the concrete world, they refer to both physical objects and abstract mathematical objects. Scientific theories, then, when regimented, involve a combination of claims about concrete entities, claims about mathematical entities, and claims about both concrete and mathematical entities.
a. The Indispensability Argument
This puts pressure on the two genera of nominalist views mentioned above. Regarding the first, if nominalists deny that mathematical sentences have the same semantics as sentences about concrete objects, then a puzzle arises about mixed sentences, roughly: what is the semantics for mathematical sentences and how does it combine with ordinary semantics to produce meaningful mixed sentences? Regarding the second, if nominalists deny that mathematical sentences are (strictly speaking) true, then they must also deny that many of the best scientific theories are true, for the best scientific theories are replete with mathematical claims. Moreover, we appear to have at least some justification for believing that the best scientific theories are true, as they receive empirical confirmation as a result of making testable predictions.
Considerations like these have brought about a very important and influential challenge to nominalism: the indispensability argument. In fact, to talk of the indispensability argument is misleading since there are a number of distinct arguments that fall under that rubric (see, for instance, Quine 1948, 1951, 1976, 1981; Putnam 1971; Maddy 1992; Resnik 1995; Colyvan 2001; Leng 2010; the article on the Indispensability Argument). Something like a core indispensability argument can however be isolated, and, because many forms that nominalism might take have come about largely in response to the premises of this core argument, describing it allows us to produce a useful taxonomy of nominalisms. At its heart, the indispensability argument is designed to show that nominalism is incompatible with the claims of science. Science—or at least the science of the twentieth and beginning of the twenty-first centuries—asserts the existence of abstract objects, so if its claims are true, nominalism is false; if we are justified in believing its claims, we are not justified in believing nominalism. This core indispensability argument has three premises:
(Realism) The best current scientific theories are true (or at least approximately true).
(Indispensability) The best current scientific theories indispensably quantify over abstract objects.
(Quine’s Criterion) The existential quantifier ∃x expresses existence.
Something should be said about each of the premises. (Realism) is not as straightforward as it looks, since the denial of realism, instrumentalism, can be characterized in a number of different ways. The anti-nominalists John Burgess and Gideon Rosen have characterized a rejection of (Realism) as amounting to the claim that “standard science and mathematics are no reliable guides to what there is” (Burgess and Rosen 1997, 60–61). However, the most fully developed instrumentalist nominalism, that of Mary Leng, seeks to provide an account of how a denial of realism is compatible with substantive scientific knowledge of the concrete world. (Quine’s Criterion) is motivated by broadly the sort of semantic considerations discussed earlier. Finally, (Indispensability) is also not wholly straightforward. For one thing, technical results show that, strictly speaking, (Indispensability) is false. The method of Craigian elimination can transform a two-sorted theory Γ, quantifying over two kinds of things, into a theory Γ° with infinitely many primitives and axioms that quantifies over only one of those kinds of things. So, there is a known mechanism by which quantification over mathematical entities can be dispensed with. Recommending Craigian elimination as a response to (Indispensability) appears however not to be sufficient for the nominalist, partly because the process is not thought to explain the success of mathematical theories (see Burgess and Rosen 1997, I.B.4.b for details). For another thing, the indispensability of quantification over mathematical objects may appear idle with respect to the argument. If the best scientific theories are true and assert the existence of mathematical objects, then nominalism is false regardless of whether it is possible to formulate other theories that dispense with quantification over mathematical objects. However, as it is expounded below, some have taken programs of dispensing with quantification over mathematical objects in physical theories as a means of explaining the predictive success of theories that do quantify over mathematical objects, without assuming the truth of what they say about mathematical objects, thereby undercutting the main motivation for (Realism). Alternatively, or in addition, nominalists who take it to be possible to dispense with quantification over mathematical objects may argue that the resulting theories are superior, perhaps on the grounds of ontological parsimony, or on the grounds that they avoid the epistemological problems associated with abstract objects, or on the grounds that they provide more perspicuous intrinsic descriptions and explanations of physical systems and their behavior—descriptions and explanations that appeal to intrinsic facts about those systems rather than their relations to mathematical objects. In that case, the best scientific theories will not quantify over mathematical objects.
A fourth premise, confirmation holism, is also often thought to be crucial to the indispensability argument, both by those who defend and those who resist the argument (see, for instance, Colyvan 2001; Maddy 1997; Sober 1993; Leng 2010; Resnik 1997). Confirmation holism is the claim that confirmation accrues to theories as a whole rather than accruing only to proper parts of those theories. (Realism), (Indispensability) and (Quine’s Criterion) mutually entail the falsity of nominalism, so confirmation holism is not required to make the argument logically valid. However, confirmation holism is sometimes taken to support (Realism). If empirical confirmation could accrue only to proper parts of theories, nominalists might be able to argue that it only accrues to those claims that quantified only over concrete objects. If confirmation holism is true, however, then the empirical confirmation the best scientific theories enjoy also applies to the claims they make about mathematical objects.
The three premises of the core indispensability argument are reflected in a trifurcation of approaches to nominalism. Some nominalists reject (Indispensability) and attempt to show that we can (in certain important contexts) get by without talking about abstract objects. This is reconstructive nominalism. Others reject (Quine’s criterion): one can make true claims “about” abstract objects without abstract objects existing. “There are infinitely many primes” really can be true without any primes existing (in an ontologically significant sense). This is hermeneutic or deflationary nominalism. Still others reject (Realism). They take mathematical claims, even those that appear in the best scientific theories, to be strictly false, and do not attempt to show that we can get by without them but offer an account of why we speak this way and why it is useful to do so that is not committed to the existence of mathematical objects. This is instrumentalist nominalism.
5. Reconstructive Nominalism
The first of the premises to be concertedly challenged by nominalists was (Indispensability), and there have been many attempts to discharge or partially discharge this aim (a useful overview can be found in Burgess and Rosen 1997, III.B.I.a). Hartry Field’s efforts, and responses to them, have been dominant in the philosophical literature on indispensability, to the extent that some discussion of indispensability carries on as though the failure of Field’s project would amount to the failure of reconstructive nominalism. Here we examine two important and representative strategies of dispensing with reference to and quantification over mathematical objects in some detail: Charles Chihara’s modal strategy, and Field’s geometrical strategy.
a. Chihara
Originally, Chihara responded to (Indispensability) by developing a predicative system of mathematics which avoided quantification over mathematical objects by using constructibility quantifiers instead of the standard quantifiers (Chihara 1973). Concerned that not all of the mathematics needed for contemporary science could be reconstructed in a predicative system, he has since retained the use of constructibility quantifiers but developed a different system without these restrictions (Chihara 1990, 2004, 2005). It is Chihara’s developed view that is discussed here.
In standard mathematics, the “official claims”, as it were, come in an apparently existential form: they appear to be claims about what mathematical objects exist and what relations they bear to each other. Things were not always so. In Euclid’s Elements we find the following axioms of geometry:
A straight line can be drawn joining any two points;
Any finite straight line can be extended continuously in a straight line;
For any line a circle can be drawn with the line as radius and an endpoint of the line as center.
These axioms concern not what exists or is “out there”, but what it is possible to construct. The claims of Euclidean geometry are modal rather than existential and, as a result, do not have any obvious ontological commitments to abstract (or, for that matter, concrete) objects. Geometry was principally carried out in this modal language for thousands of years, though by the twentieth century it had become common to make geometrical claims in existential language. Hilbert in his 1899 Grundlagen der Geometrie (Foundations of Geometry) gives the following as his first three axioms of geometry:
For every two points A, B there exists a line L that contains each of the points A, B;
For every two points A, B there exists no more than one line that contains each of the points A, B;
There exist at least two points on a line. There exist at least three points that do not lie on a line.
Hibert’s axioms, in contrast to Euclid’s, appear existential, describing which points and lines exist. For the nominalist, this may be philosophically significant. It shows that it is possible to practice mathematics—at least one part of mathematics—without making any claims about the existence of abstract mathematical objects. Chihara’s nominalism takes its cue from Euclid’s modal geometry; it aims to do all mathematics—or all the mathematics we need—in the modal, rather than the existential, mode. His goal is to:
Develop a mathematical system in which the existential theorems of traditional mathematics have been replaced by constructibility theorems: where, in traditional mathematics, it is asserted that such and such exists, in this system it will be asserted that such and such can be constructed. (Chihara 1990, 25)
Although Chihara works out this project in a good deal of technical detail, the fundamental idea behind it is straightforward enough. Where Field, as it is explained below, attempts to replace mathematized physics with nominalistic physics, Chihara attempts to replace standard pure mathematics with a system of mathematics that makes no claims about the existence of mathematical objects. This nominalistic surrogate for standard mathematics, then, could be true without mathematical objects existing.
i. Constructibility theory
Chihara works out a modal version of simple type theory (henceforth STT) called “constructibility theory” (henceforth Ct). The language of STT contains the standard quantifiers “∃x” (meaning “there is an object x such that…”) and “∀x” (meaning “every object is such that…”) and the set-theoretic membership relation “∈” which is used to express which entities are in a set. “Thom ∈ {Thom, Jonny, Phil, Colin, Ed}” means that Thom is in the set containing Thom, Jonny, Phil, Colin and Ed, “√2∈ℝ” means that the number √2 is in the set of real numbers, and so on. As the language of STT contains “∃x”, “∀x” and “∈”, STT is used (at least apparently) to make assertions about which sets exist. Sets can contain ordinary objects, both concrete and abstract, and they can also contain other sets. The claims that can be made in STT about which sets exist are not wholly unrestricted; if they were, one could claim that there is a set which contains all and only those sets that do not contain themselves: ∃x∀y(y∈x↔y∉y). Consider the set just described: does it contain itself? If it does not contain itself, then it follows that it does contain itself, as it is the set that contains all sets that do not contain themselves. On the other hand, if it does contain itself, then it follows that it does not contain itself because it is the set that contains only those sets that do not contain themselves. This is Russell’s paradox. To avoid this incoherence, sets in STT are on levels: a set can only contain objects or sets on a lower level than itself. On level-0 there are ordinary objects; on level-1, sets containing ordinary objects; on level-2, sets containing sets that contain ordinary objects; and so on.
In Chihara’s system, the existential quantifier “∃x” and universal quantifier “∀x” are supplemented with modal constructibility quantifiers “Cx” and “Ax”, which, instead of making assertions about what exists, make assertions about which sentences are constructible. Corresponding to the existential quantifier “∃x” is “Cx”. Claims of the form “(Cϕ)ψϕ” mean:
It is possible to construct an open sentence ϕ such that ϕ satisfies ψ
Corresponding to the universal quantifier “∀x” is “Ax”. Claims of the form “(Aϕ)ψϕ” mean:
Every open sentence ϕ that it is possible to construct is such that ϕ satisfies ψ
To understand the constructibility quantifiers “Cx” and “Ax”, one must understand what it is for an open sentence to be satisfied or to satisfy other open sentences. Take the open sentence “x is the writer of Gormenghast”. This sentence is satisfied by Mervyn Peake—that is, the person who wrote Gormenghast. So, open sentences can be satisfied by ordinary objects. But they can also be satisfied by other open sentences. Consider the sentence “There is at least one object that satisfies F”. This is satisfied by the open sentence “x is the writer of Gormenghast”. Open sentences, like the sets of STT, are on levels: at level-0, there are ordinary objects; at level-1, open sentences that are satisfied by ordinary objects; at level-2, open sentences that are satisfied by open sentences that are satisfied by ordinary objects, and so on.
For a sentence to be constructible is just for it to be possible to construct. The sort of possibility at play here is not practical possibility; no particular person need be capable of constructing the relevant sentences. What Chihara has in mind is metaphysical possibility, which is sometimes (somewhat misleadingly) called “broadly logical possibility”. This is absolute possibility concerning how the world could have been. (Chihara sometimes also talks in terms of “conceptual possibility”, although conceptual and metaphysical possibility are not generally thought by philosophers to be equivalent.) Notice that the constructibility quantifiers are not epistemic in any way. That an open sentence ϕ is constructible does not mean that we know how to construct it, or even that it is possible in principle to know how it can be constructed. Similarly, it need not be the case that it is in principle knowable which objects or open sentences would satisfy ϕ.
After this sketch of STT and Ct, it is quite easy to see, in a general way, how Chihara’s strategy works. For every claim in STT about the existence of particular sets there corresponds a claim in Ct about the satisfiability of open sentences. Where STT says, for example, “There is a level-1 set x such that no level-0 object is in x”, Ct can say “It is possible to construct a level-1 open sentence x such that no level-0 object would satisfy x”. The set-theoretic inclusion relation “∈” is replaced by the satisfaction relation between objects and open sentences (or open sentences and other open sentences), and assertions about sets are replaced by assertions about the constructibility of open sentences. In this way, Chihara creates a branch of mathematics that does not require reference to or quantification over abstract objects. Everything one can do with STT one can do with Ct. STT is a foundational branch of mathematics, which is to say that other branches of mathematics can be reconstructed in it. Plausibly, then, STT is sufficient for any applications of mathematics that might arise in the sciences. Since Ct is a modalized version of STT, Ct, plausibly, is itself sufficient for any application of mathematics that might arise in the sciences. According to Chihara, (Indispensability) is therefore false.
ii. Constructibility Theory and Standard Type Theory
Chihara thinks of Ct as a modal version of STT, but Stewart Shapiro (1993, 1997) has claimed that Ct is in fact equivalent to STT and so could have no epistemological (or other) advantage over STT. In defense of this, Shapiro provides a recipe for transforming sentences of Ct into sentences of STT: first, replace all the variables of Ct that range over level-n open sentences with variables of STT that range over level-n sets; second, replace the symbol for satisfaction with the “∈” symbol for set membership; third, replace the constructibility quantifiers “Cx” and “Ax” with the quantifiers of predicate logic “∃x” and “∀x”. Call a sentence of STT “ϕ” and its Ct counterpart “tr(ϕ)”. Shapiro shows that ϕ is a theorem of, that is provable in, STT if and only if tr(ϕ) is a theorem of Ct, and that ϕ is true according to STT if and only if tr(ϕ) is true according to Ct. That sentences of Ct can be transformed this way into sentences of STT and that these transformations preserve theoremhood and truth show, Shapiro claims, that the two systems are definitionally equivalent—that Ct is a mere “notational variant” of STT.
Chihara (2004) responds by noting that the ability to translate sentences of STT into Ct does not show that they are equivalent in a way that undermines his project. Though the ability to translate between the two theories would show that the sentences of STT and Ct share certain mathematically significant relationships, it would not show that these sentences have the same meaning, are true under the same circumstances, or are knowable or justifiably believed under the same circumstances. Sentences of STT entail the existence of sets and are true only if sets exist, whereas sentences of Ct do not and are not. Additionally, the two theories are confirmed in different ways. The Ct sentence “It is possible to construct an open sentence of level-1 that is not satisfied by any object” is supported by laws of modal logic, considerations about what is possible, coherent, and so on. The STT counterpart sentence “There exists a set of level-1 of which nothing is a member” is not supported by those considerations.
iii. The Role of Possible World Semantics
Another objection arises from the fact that Chihara (1990) uses possible world semantics to spell out, in a precise way, the logic of “Cx” and “Ax”. Possible world semantics is an extension of the model-theoretic semantics sketched earlier. Roughly speaking, instead of a single domain containing objects and sets of objects, possible world semantics makes use of possible worlds each with their own domain (at least in variable domain semantics). The basic, extensional model-theoretic semantics sketched before has an interpretation function mapping non-logical terms of the language to their extension: names are mapped to individuals of the (single) domain and predicates to sets of individuals in the (single) domain. Possible world semantics has an interpretation function mapping names and predicates to intensions. For names, intensions are functions mapping worlds to individuals in that world’s domain. For predicates, intensions are functions mapping worlds to sets in that world’s domain. Intuitively, an intension tells us what individual (if any) a name picks out at any given possible world, and what set of objects a predicate applies to at any given possible world. For example, the intension associated with “… is red” would map each world to the (possibly empty) set of red things in that world’s domain. Part of the philosophical interest of possible world semantics is that it allows one to characterize a logic (in fact a range of logics) for possibility and necessity operators. Intuitively, for some claim “ϕ”, the claim “Possibly ϕ” is true if and only if “ϕ” is true in at least one possible world, and the claim “Necessarily ϕ” is true if and only if “ϕ” is true in all possible worlds.
Possible world semantics itself, then, is a mathematical theory, quantifying over sets and functions. (Instead of modelling physical systems, it models meanings.) It might therefore be asked whether it is legitimate to engage in such possible worlds talk without believing in the mathematical objects it quantifies over, or whether this would be an instance of intellectual doublethink. Shapiro (1997) claims that possible world semantics is not available to the nominalist since it not only quantifies over abstract objects but is used in explanations. If possible world semantics is just a myth, then its falsehood precludes it from explaining anything, just as a story about Zeus (assuming his non-existence) cannot explain facts about the weather. Chihara (2004) responds by drawing a distinction between scientific explanations of natural phenomena and explications of ideas and concepts. The role of possible world semantics in Ct is not akin to a scientific explanation of an event, but to an explication of a concept. Possible world semantics is used to spell out how to make inferences using constructibility quantifiers. Put more picturesquely, it shows one how to reason with the constructibility quantifiers in broadly the same way that an allegorical tale, such as Animal Farm, shows one how to reason about totalitarian government (though the latter does so in a less rigorous but more open-ended way than the former). Just as a novel is capable of doing this without the things depicted in it really existing, so, too, possible world semantics is capable of doing this without possible worlds really existing.
None of the prominent objections to Chihara’s brand of reconstructive nominalism are decisive. Although the view has received comparatively little attention in the literature, it remains a live option for the nominalist who denies indispensability.
b. Field
Field’s reconstructive project has been utterly dominant in the literature on reconstructive nominalism since the publication of Field’s short but remarkable monograph Science Without Numbers in 1980, even if Field himself has said little about his project in print since the early nineteen nineties. Field takes there to be no mathematical objects, but also holds that the truth of mathematical sentences requires the existence of mathematical objects. As such, for Field, standard mathematical theories are (strictly speaking) false (see the introduction to Field (1989)). Mathematized science, however, uses mathematical models, equations, and so on to represent concrete systems. As a reconstructive nominalist, Field aims to show firstly that the best scientific theories can be restated in a way that avoids using mathematics. Here is a point of contrast with Chihara. Whereas Chihara claims not that mathematics per se is dispensable to science, but only the sort of mathematics that quantifies over abstract objects, Field’s project is to formulate scientific theories that do not make use of mathematics of any sort. Field also wants to establish that mathematical language is dispensable in principle: there is no context in which science would require mathematics to do something which it could not do without mathematics. To this end, the second goal of his project is to show that adding mathematical claims to claims about the concrete world does not allow us to infer anything about the concrete world that claims about the concrete world would not allow us to infer on their own.
i. Field’s Program
Field calls the process of removing reference to and quantification over mathematical objects “nominalization”. Field does not nominalize all of contemporary science—the task would be colossal—but one important theory: Newtonian Gravitational Theory (NGT). His hope is that, in doing so, he would show that a complete nominalization of science is, at least in principle, accomplishable.
Some mixed claims, expressing relationships between concrete and abstract objects, are easy to reformulate in a purely nominalistic way. “There are exactly two remaining Beatles” can be parsed:
∃x∃y(Bx∧By∧x≠y)∧∀x∀y∀z(Bx∧By∧Bz→x=y∨y=z∨x=z)
Where “Bx” means “x is a remaining Beatle”. The best scientific theories, however, go far beyond claims about how many of a particular kind of object there are, so the means of nominalizing these theories will be more complex. As a result, the details of Field’s project are highly technical. A non-technical overview of its general contours, however, can be given.
NGT describes the world by numerically assigning properties such as mass, distance, and so on, to points in space-time. Space-time itself is represented with a mathematical coordinate system, and quantity claims such as “The mass of b is 5kg” are understood as meaning that there exists a mass-in-kilograms function f from a domain of concrete objects C to the real numbers ℝ such that f(b)=5. Instead of describing the concrete world by assigning it numerical values, Field’s theory (henceforth FGT) describes the concrete domain directly, using comparative language. In particular, distance claims are made using a betweenness relation “y Bet xz”, a simultaneity relation “x Simul y”, and a congruence relation “xy Cong zw”. These are primitives of the theory, but intuitively “y Bet xz” means that y is between x and z, “x Simul y” that x and y are simultaneous, and “xy Cong zw” that the distance from x to y is the same as the distance from z to w. In the same way, mass claims are expressed using mass-betweenness and mass-congruence relations. From these building blocks, Field develops a scientific theory capable of describing space-time and many of its properties without quantifying over mathematical objects.
ii. Representation Theorems
The next step is to show that FGT really is a (nominalistic) counterpart to NGT. To this end, Field proves a representation theorem. Intuitively, what Field’s representation theorem shows is that the domain of concrete things represented by FGT using comparative predicates (a space-time with mass-density and gravitational properties) has the same structural features as the abstract mathematical model of space-time with mass-density and gravitational properties given by NGT. NGT is a mathematical mirror image of FGT. In more detail, Field proves that:
there is a structure-preserving mapping ϕ from the sort of space described by FGT onto ordered quadruples of real numbers;
there is a structure-preserving mapping ρ from the mass-density properties that FGT ascribes to space-time onto an interval of non-negative real numbers;
there is a structure-preserving mapping from ψ from the gravitational properties that FGT ascribes to space-time onto an interval of real numbers.
Where ϕ is unique up to a generalized Galilean transformation, ρ is unique up to a positive multiplicative transformation, and ψ is unique up to a positive linear transformation. (What this means, in essence, is that choice of measurement scales is conventional. Different measurement scales can be used, so long as they preserve the structural features of the measurement scales they replace. Saying that something is 95.6 kilograms or saying that it is 15.2 stones are two different ways of representing the same concrete fact about mass; no unique significance attaches to the numbers 95.6 or 15.2.)
The representation theorem explains the utility of false mathematical theories: if the abstract mathematical model they describe has the same structure as the concrete world (described by true nominalistic theories), then reasoning about the abstract mathematical model will not lead us astray when making inferences about the concrete world. The following picture of nominalistic physics and its relation to scientific practice emerges: Nominalistic claims N1 … Nn have abstract counterparts N*1 … N*n which use mathematical methods to describe the same physical world described by N1 … Nn. One can ascend from N1 … Nn to N*1 … N*n, carry out derivations within the mathematical theory to arrive at some mathematized conclusion A*, and then descend to its nominalistic counterpart A. Mathematics facilitates inferences about the physical world, but these inferences could, according to Field, be made without mathematics, albeit more laboriously.
iii. Conservativeness
Having developed a nominalistic physics and proved a representation theorem, Field also needs to show that mathematics is truly dispensable to physics, at least in principle. This involves showing that there are not claims about the physical world that follow from nominalistic theories plus mathematics but that would not follow from nominalistic theories alone. In the jargon, that mathematics is conservative over purely nominalistic theories. Conservativeness is important to Field’s kind of reconstructive nominalism. Firstly, because if the mathematics we apply is not conservative, then there are things that can be said about the physical world with mathematics that could not be said without mathematics, showing that it is not dispensable after all. Secondly, because it provides part of the explanation of why we manage to use (false) platonistic theories so successfully: they have the same consequences about the concrete world as the true, nominalistic theories underlying them. Field informally describes conservativeness in the following way:
A mathematical theory S is conservative [if and only if] for any nominalistic assertion A, and any body N of such assertions, A isn’t a consequence of N + S unless A is a consequence of N alone. (Field 2016, 16)
Some clarifications are in order. The first is that Field does not have in mind pure mathematical theories, that is, mathematical theories whose vocabulary only ranges over mathematical objects. These theories are more or less trivially conservative: as they do not say anything about the physical world, they do not entail anything about the physical world (unless they are inconsistent, since, in classical logic, a contradiction entails all sentences). The second is that Field does not have in mind physical theories that use mathematics. These are more or less trivially nonconservative: it is their job to say substantive things about the physical world. If for instance N is some meagre body of nominalistic assertions, and S is Newtonian physics, then N + S will clearly enough have consequences that N does not. Instead, Field has in mind impure mathematical theories. Impure set theory, for instance, posits the existence not only of sets, but also conditionally posits the existence of sets of physical objects. Roughly speaking, for any physical object or objects, there exists a set containing that object or objects. More specifically, consider ZFC (Zermelo-Fraenkel set theory with the axiom of choice)—a theory of pure mathematics within which all core mathematics can be modelled. ZFC can be made into an applied, impure theory by adding supplementary axioms. In particular:
- a comprehension scheme, allowing definable kinds of concrete objects to form sets;
- a replacement scheme, saying that if a function from a set of concrete objects to other objects can be defined, then those latter objects also form a set. (Note that this allows one to formulate the kinds of quantity claims mentioned earlier.)
Call the theory obtained from ZFC by adding these supplementary axioms ZFCV(N). Field argues that good mathematics should be conservative; mathematics, on its own, ought not to impose constraints on the way the concrete world is. Were it to be discovered that it did, that would be a reason to consider it in need of revision:
[I]f it were to be discovered that standard mathematics implied that there are at least 106 non-mathematical objects in the universe, or that the Paris Commune was defeated […] all but the most unregenerate rationalists would take this as showing that standard mathematics needed revision. Good mathematics is conservative; a discovery that accepted mathematics isn’t conservative would be a discovery that it isn’t good. (Field 1980, 13)
In addition to this, Field proves an important conservativeness result. An equivalent way of describing conservativeness is to say that a mathematical theory S is conservative if and only if for any consistent body N of nominalistic assertions, N + S is also consistent (Field 2016, 17). Field’s proof, in essence, gives a procedure that, beginning with a nominalistic theory N assumed to be consistent (that is, satisfied by a domain D of non-sets), shows one how to construct a domain that satisfies both N and ZFCV(N) (that is, shows that N and ZFCV(N) are jointly consistent). If one is able to construct a nominalistic counterpart theory such as FGT, conservativeness ensures that adding ZFCV(N) to that nominalistic theory will not entail any purely nominalistic claims that are not entailed by the nominalistic theory alone.
iv. The Prospects of Field’s Project
Field provides a nominalistic reconstruction of one important theory of physics, but some philosophers have questioned whether his project could be devloped with nominalistic reconstructions of other theories such as General Relativity and quantum mechanics (QM). NGT uses mathematics to represent facts about concrete objects which FGT represents more directly. QM works differently. The mathematical formalism of QM is sometimes used to represent probabilities of measurement events, and a probability is not a concrete object. Even if QM could be reformulated to avoid reference to mathematical objects, it would remain a theory about probabilities, which is to say, a theory that talks about entities the nominalist does not take to exist. Balaguer (1996, 1998) has suggested that the Fieldian nominalist could take these probabilities to represent the propensities of the concrete systems they model. However, Balaguer admits that even if the details of any such nominalization were worked out, this would not provide a means of nominalizing phase space theories. Phase space theories use vectors to represent possible states of a concrete system. A Fieldian reconstruction of a phase space theory which avoids quantification over vectors would still quantify over possible states of concrete systems (Malament 1982), and these abstract objects could not be taken to represent propensities of concrete systems in the way that, plausibly, probabilities do.
A number of commentators have taken these considerations to license pessimism about the prospects of nominalizing the best contemporary scientific theories, but the Fieldian nominalist could contest this conclusion. In the first place, one can question the inference from the fact that mathematical language has not, at some point in time, yet been dispensed from the best scientific theories to the modal conclusion that mathematical language is indispensable from the best scientific theories. One would not similarly conclude that because Goldbach’s conjecture has not, at some point in time, yet been proven, it is unprovable. In the second place, progress has been made since Science Without Numbers was first published in 1980. For instance, Arntzenius and Dorr (2012) take on the task of nominalizing general relativity, which uses differential equations to describe the behavior of fields and particles in curved space-time and vector bundles. They express confidence that, given an interpretation of what concrete facts the mathematical formalism of QM represents, nominalizing strategies could be extended to apply in these cases.
v. Conservativeness Again
Field’s conservativeness claim has been criticized on a number of grounds. One is that semantic accounts of logical consequence quantify over sets. According to these, a theory is logically possible just in case it has a model in the set-theoretic sense sketched above. A claim ϕ is a consequence of a theory Γ if and only if there is no model of Γ & ¬ϕ. Logical consequence, it is sometimes argued, can only be understood if one posits the existence of sets. Field (1989, chapter 3; 1991) has a response: he takes logical possibility to be a primitive notion, not ultimately to be explained in terms of the existence of certain sets. There are considerations in favor of this. Explaining modal facts in terms of set-theoretic ones may get things backwards. As Leng (2007) argues, one ought to explain the fact that there exists no set of all sets on the grounds that there could not exist a set of all sets, rather than to explain why there could not exist a set of all sets on the grounds that there is no set of all sets.
Another objection concerns the scope of Field’s conservativeness proof. Jospeh Melia (2006) points out that although Field provides a proof of the conservativeness of ZFCV(N), he does not provide an argument that all useful applied mathematics can be carried out in ZFCV(N). Unless the Fieldian nominalist provides reasons to believe that this is the case, it is hard to assess the significance of Field’s proof, as it is hard to assess whether future applications of mathematics will be carried out in ZFCV(N).
vi. The Best Theory?
Mark Colyvan argues that talking of mathematical objects is not dispensable to the best scientific theories because nominalistic versions of those theories will be worse than their mathematical counterparts. Good theories must be both internally consistent and consistent with observations, but there are additional theoretical virtues that must be taken into consideration. Colyvan (2001) lists the following:
- Simplicity / Parsimony: Given two theories with the same empirical consequences, we should prefer the theory that is simpler to state, and which has simpler ontological commitments;
- Unificatory / Explanatory Power: We should prefer theories that predict the maximum number of observable consequences with the minimum number of theoretical devises;
- Boldness / Fruitfulness: We should prefer theories that make bold predictions of novel phenomena over those that only account for familiar phenomena;
- Formal Elegance: We should prefer theories that are, in a hard-to-define way, more beautiful than other theories.
Colyvan contends that mathematical theories are often more virtuous than nominalistic ones. (See the section Unification, Explanation and Confirmation in the article on The Applicability of Mathematics and the section The Explanatory Indispensability Argument in the article on The Indispensability Argument for examples of the unificatory and explanatory power of mathematics.)
Field, however, takes nominalistic theories to have greater explanatory power in some respects. They provide intrinsic explanations of physical phenomena, rather than appealing to extrinsic mathematical facts, and they eliminate the arbitrariness in the choice of units of measurement that accompany mathematical theories (Field 1980, 1989 chapter 6). It is open to the Fieldian nominalist to argue that her theoretical virtues are somehow better or more fundamental than those enjoyed by mathematical theories. Since there is no agreed-upon metric for measuring theoretical virtues, nor agreement over their epistemic significance (are they really indicators of truth or mere pragmatic expediencies?), reaching a resolution in this area might not be easy.
6. Deflationary Nominalism
At the beginning of the twentieth century, attempts at reconstructive nominalism ebbed and many nominalists came to accept (Indispensability) or to see it as somehow orthogonal to ontological questions. As the indispensability argument is valid, this requires rejecting either (Realism) or (Quine’s Criterion). This section explores the latter option.
A number of philosophers have questioned the semantic assumptions driving (Quine’s Criterion). Many natural language sentences employ apparent reference or quantification even when commitment to the existence of the things apparently referred to or quantified over would be, for various reasons, implausible:
- There is a better way than this.
- His lack of insight was astounding.
- There are many similarities between Sellars and Brandom.
- There is a chance we will make it in time.
- I have a beef with the current administration.
- The view from my office is wonderful.
- She did it for your sake.
If one takes the semantic argument discussed earlier seriously, then, in holding these sentences to be true, one would be committed to the existence of ways, lacks, similarities, chances, beefs, views and sakes. Many, however, take it that positing the existence of objects such as these is bizarre, since they do not seem to be part of the “furniture of the universe”. One response, then, is to deny that “there is” always expresses existence, in an ontologically significant sense.
a. Azzouni
Jody Azzouni has been the most prominent defender of this approach to nominalism. Azzouni’s view (2004, 2007, 2010a, 2010b, 2017) is that both quantifiers and the term “exists” are neutral between ontologically committing and non-ontologically committing uses. Context decides whether they are being used in ontological or non-ontological ways. “God exists” uttered in a discussion between an atheist and a theist would (usually) express ontological commitment, but “Important similarities between Sellars and Brandom really do exist” would not (usually) be intended to express ontological commitment to similarities.
i. Quantifier Commitments and Ontological Commitments
Azzouni, then, draws a distinction between mere quantifier commitments and existential commitments (here understood in an ontologically significant sense); not all quantifier commitments are existential commitments. He replaces Quine’s semantic criterion for what a discourse is committed to with a metaphysical criterion for what exists. Something exists, according to Azzouni, if and only if it is mind- and language-independent. This requires both rejecting the Quinian criterion and motivating the metaphysical one. With respect to the latter, Azzouni does not give a metaphysical argument for the criterion but appeals instead to the de facto practices of people in general. One should adopt mind- and language-independence as a criterion for what exists because of the sociological fact that the community of speakers takes ontologically dependent items not to exist.
Given this criterion for existence, the heart of Azzouni’s account consists in spelling out the implications of mind- and language-independence for our knowledge-gathering behavior. For instance, language- and mind-independent objects cannot be stipulated into existence. Inventing a fictional character on the other hand involves nothing more than thinking of her. Fictional entities are paradigmatically mind-dependent and hence non-existent. This is to be contrasted with the way we form beliefs about mind-independent objects. In particular, our epistemic access to mind-independent posits possesses the following salient features: robustness, refinement, monitoring and grounding:
- Robustness: Epistemic access to a posit is robust if results about that posit are independent of our expectations about it. For example, Newtonian mechanics (in conjunction with some auxiliary assumptions) predicted that the planet Uranus would have a particular perihelion which observation revealed it not to have.
- Refinement: Epistemic access to a posit exhibits refinement when there are means by which to adjust or refine access to that posit. For example, more powerful telescopes allow improved access to distant parts of the observable universe.
- Monitoring: Epistemic access to a posit involves monitoring when what the posit does through time can be tracked or when different aspects of the posit can be explored. For example, C.T.R. Wilson’s experiments appeared to reveal the trajectory of atoms by their observable effects on water vapor.
- Grounding: Epistemic access to a posit exhibits grounding when properties of the posit itself explain why we can discover what properties the posit has. That stars emit light explains why they are visible to the naked eye at night.
If the way in which we establish truths about a posit does not fit with the way we establish truths about mind- and language-independent posits, then we are treating, in practice, this posit as mind- and language-dependent. Given Azzouni’s criterion for existence, this amounts to treating this posit as non-existent. The leading idea here is that an examination of scientific practice shows that we treat concrete posits—observables, but also theoretical posits such as subatomic particles—as mind- and language-independent but treat mathematical objects as mind- and language-dependent.
When robustness, refinement, monitoring, and grounding are active in deciding whether a posit exists and what features it has, one has what Azzouni calls “thick epistemic access” to it. Not all scientific posits which Azzouni takes to exist enjoy thick epistemic access, however. To take an example: because the expansion of the universe is accelerating, there are parts of the universe which are sufficiently distant from the Earth so that no information from them will ever reach observers on Earth—these regions are outside our past light cone. Accepted cosmology posits the existence of galaxies, stars, nebulae, and suchlike outside our past light cone, yet concrete entities in these regions of the universe clearly fail to exhibit, at the very least, monitoring and grounding. Azzouni calls the sort of access we have to entities such as these “thin epistemic access”. In Azzouni’s developed view, thin posits are “the items we commit ourselves to on the basis of our theories about what the things we thickly access are like” (Azzouni 2012, 963). Moreover, thin posits require “excuse clauses”: explanations, stemming from the scientific theories that describe them, of why we fail to have thick access to them. In the case of galaxies outside our past light cone, we have thick access to things inside our past light cone; widely accepted cosmological theories about the features of the posits in the early universe which, in conjunction with natural laws, entail the existence of galaxies outside our light cone. Hence, theories about the things we thickly access commit us to the existence of galaxies which we cannot thickly access. They also provide the needed excuse clause: special relativity does not allow entities to travel through space faster than the speed of light.
ii. The Coherence of Denying Quine’s Criterion
Some have objected that denying Quine’s criterion is incoherent: how can sense be made of the view that it is both true that there are infinitely many primes and that no primes exist (see, for instance, Burgess, 2004) ? However, it is open to the deflationary nominalist to claim that “There are infinitely many primes” and “Primes do not exist” can both be true, so long as the quantifier “there are” does not express existence. Further, it is open to the deflationary nominalist to claim that “There are primes” and “There are no primes” can both be true, so long as the first occurrence of “there are” is not being used in a sense that expresses ontological commitment and the second occurrence of “there are” is being used in a sense that expresses ontological commitment. Azzouni (2004, 2007, 2010, 2017) argues that both “there is” and “there exists” are ontologically neutral, on the basis of examples such as those listed above. According to Azzouni, it is implausible to suppose that one expresses ontological commitment to, for instance, ways, on the basis of uttering phrases such as “There is more than one way to skin a cat”. One quantifies over all sorts of things but undertakes ontological commitments only to those things one treats as mind- and language-independent.
There are other ways to motivate similar claims. Hofweber (2016) defends a view according to which some singular terms function syntactically like names but do not purport to refer to objects. Drawing on work in linguistics and developmental psychology, Hofweber argues that arithmetical singular terms are of this kind, and so do not come with ontological commitments. This is expanded to cover a similarly non-representational account of quantification in arithmetic. This view, Hofweber argues further, solves a number of puzzles in the philosophy of arithmetic.
Others have drawn a distinction between quantifier commitments and ontological commitments by defending versions of Meinongianism—named after Alexius Meinong, an Austrian philosopher whose interest in our ability to think about that which does not exist led him to theorize about nonexistent objects. Parsons (1980), Routley (1980), and Zalta (1988) have all defended views according to which some objects are non-existent. More recently, Priest (2016) develops a possible world semantics according to which all worlds share a domain of objects, though different objects exist at different worlds. Here the “particular quantifier”—Priest avoids using the term “existential quantifier”, which he takes to bias the issue—ranges over all objects in the domain (existent and non-existent), and an existence predicate is used to make claims about what exists at a given world. According to Priest, only concrete objects exist at possible worlds, so mathematical objects do not exist at any possible world. On Priest’s view, then, mathematical objects do not exist, but (nonexistent) mathematical objects are included in the domain of discourse. When one talks about mathematical objects, what one says is true or false depending on how things stand with those non-existent objects.
Rayo (2013) rejects what he calls “metaphysicalism”: the view that there is a metaphysically privileged way of carving reality into its fundamental constituents, and that for a simple sentence of subject-predicate form to be true, there must be a correspondence between the logical form of the sentence and the metaphysical structure of reality. Once one has dropped the requirement that the structure of a true sentence must be mirrored in the metaphysical structure of the world, one is free to specify truth conditions for sentences according to which this is not the case. In particular, one can give truth conditions for mathematical sentences that are trivialist, that is, that make no requirements on the world (Rayo 2013, 2015, 2016). Claims such as “Infinitely many prime numbers exist” are, on this view, both true and ontologically insignificant. (Rayo, it should be noted, refers to the view as an ontologically weightless “trivialist subtle Platonism”, and presents it as a rival to nominalism.) A number of positions, then, provide frameworks within which it is prima facie coherent to deny Quine’s criterion.
iii. Excuse Clauses
Mark Colyvan has taken issue with Azzouni’s account of excuse clauses. On Azzouni’s view, posits can fail to exhibit robustness, refinement, monitoring, and grounding but still be included in our ontology so long as there is an excuse clause explaining why they fail to exhibit these features. Colyvan (2010) objects that abstract objects do have an excuse clause: namely they are acausal. Azzouni (2012) responds by noting that Colyvan’s excuse is a philosophical gloss, rather than stemming from actual scientific and mathematical practices. The force of this objection, and of the response, will depend on criteria for what counts as a legitimate excuse clause.
Bangu (2012, 28–30) has objected to Azzouni’s claim that the community of speakers treats ontological independence as the criterion for existence. Bangu points out that this is an empirical, statistical claim, but that Azzouni presents no empirical, statistical evidence for it. Were a study to be carried out, it may turn out that opinion on the matter is not uniform (and this much seems true in the philosophical community at least).
7. Instrumentalism
Until the beginning of the twenty-first century, instrumentalism—the rejection of (Realism)—was not a popular nominalist response to indispensability arguments. This may have been motivated by the thought that a rejection of (Realism) constituted a rejection of the ability of science to informatively represent the world. Indeed Burgess (1983, 93) characterizes instrumentalism as the view that “science is just a useful mythology, and no sort of approximation to or idealization of the truth”. However, some instrumentalist nominalist views that aim to avoid this result whilst maintaining that the theories of mathematical science are not strictly true have been proposed.
a. Leng
A detailed and sophisticated view of this sort is developed by Mary Leng (2002, 2007, 2010, 2005). Leng draws on earlier work by Mark Balaguer and Steven Yablo—both of whom, ultimately, defend the view that there is no fact of the matter over whether mathematical objects exist (see Balaguer 1998; Yablo 2009)—to defend a distinctive instrumentalist nominalism.
Instrumentalist nominalism stands apart from all other forms of nominalism by rejecting the claim that the best scientific theories are, strictly speaking, true or approximately true. One does not need to find replacement theories that do not quantify over abstract objects, nor to show that the theories that do quantify over abstract objects are in fact true, in order to vindicate nominalism. Leng aims to explain the usefulness of mathematics directly by studying mathematical practices and seeing if those practices can be understood without assuming the existence of mathematical objects. If one can make sense of mathematical-scientific practices—how they are used to describe, make predictions about, and explain features of the concrete domain—without positing mathematical objects, then positing the existence of mathematical objects is unnecessary. (An important and closely related program, though one that does not reject (Realism), is developed by Otávio Bueno (2005, 2009, 2012, 2016). Like Leng, Bueno looks to account for mathematical practices in a way that does not presuppose the existence of mathematical objects, but without challenging (Indispensability). Bueno’s program, however, is agnostic about the existence of mathematical objects.)
i. Mathematics and Make-Believe
Leng’s account is fictionalist. Mathematical objects can rationally be treated as fictional; doing so does not jar with mathematical practices. Leng adopts the account of fiction as make-believe developed by the aesthetician Kendal Walton’s (1990, 1993) to spell out the details. According to this account, in articulating a fiction, one generates a prescription to imagine that things are thus and so. When Dorothy Sayers writes that Lord Peter Wimsey earned a first at Oxford, we are invited to imagine that there is a person, Wimsey, who has this particular property. This prescription to imagine and the subsequent imagining do not require the existence of Wimsey. A text is a kind of “prop” which, in conjunction with the usual conventions and practices involving fiction, generates the content of the fiction. Other principles are involved in what one is prescribed to imagine: logical consequences, facts about the (real) world, the laws of nature, and so on also come into play. This is what prevents us from imagining, or being prescribed to imagine, that Wimsey both gained a first and did not gain a first at Oxford, or that he can fly by flapping his arms.
According to Walton’s account of fictionality, a claim S is fictional if we are prescribed to imagine S is true. While sentences such as “Lord Peter Wimsey plays cricket” are strictly false (since no such person exists), there is something correct about it. This is what Walton’s notion of fictionality is supposed to capture. The sentence’s correctness is due to its fictionality—that is, to the fact that we are prescribed to imagine it as true; the writings of Sayers, along with our conventions regarding what we do with fictions—that is, how we use fictions in practice—prescribe us to imagine that Lord Peter Wimsey plays cricket.
Just as there can be mixed mathematical-concrete sentences, such as measurement claims, that describe relations between concrete and abstract entities, so, too, there can be mixed fictional-real sentences describing relations between fictions and the real world (Walton 1990, 410):
- Oscar Wilde killed off Dorian Gray by putting a knife through his heart.
- Most children like E.T. better than Mickey Mouse.
- Sherlock Holmes is more famous than any other detective.
- Vanquished by reality, by Spain, Don Quixote died in his native village in the year 1614. He was survived for a short time by Miguel de Cervantes.
Again, Walton rejects the strict truth of these sentences, but grants that their correctness is related to their fictionality, although not in as straightforward a sense as for the pure sentences of fiction. These sentences are not fictional within their respective fictions. The novel The Picture of Dorian Gray does not depict Oscar Wilde committing an act of murder and Mickey Mouse is not in E.T. (and vice versa). Instead, in making utterances like these we are engaged in “unofficial” games of fiction-making. In these contexts, we are invited to imagine that there are worlds created by their authors, allowing us to imagine relations between those worlds and between them and the real world. The correctness or incorrectness of these claims depends on their being partly fictional: they are correct if they are in accordance with what we are prescribed to imagine. Here, however, the fictionality of the sentences does not only depend on what the author’s writings prescribe one to imagine, they also depend on how things stand with the real world. The fictionality of “Sherlock Holmes is more intelligent than any detective I’ve met” depends both on real world “props” (in this case, the detectives that the utterer has met) and what the prop of Doyle’s writings prescribes one to image of Holmes.
One value of this intermingling of fiction and reality—what Walton calls “prop-oriented make-believe”—is that it allows one to represent the real world indirectly. Saying “Sherlock Holmes is more intelligent than any detective I’ve met” allows one to indirectly express something about the intelligence of real detectives that might not otherwise be easy to express. Talk of fictional objects can be used to place restrictions on real objects. That sentences describing things that do not exist are strictly false does not disqualify them from being used to express or grasp facts about the real world.
Leng appropriates Walton’s account of prop-oriented make-believe to make sense of mathematized science. Mathematical make-believe can be used to place restrictions on non-mathematical objects, and hence to describe, indirectly, the concrete world. If one imagines that the set of real numbers, ℝ exists, one can imagine that there are functions that map concreta onto different real numbers depending on their properties, and which would allow one to represent those properties quantitatively. Imagining that there is a mass function, one could say of a concrete object, d1, that Mass kg(d1)=5, and in doing so place restrictions on d1 thus representing it indirectly. When this goes right, the measurement ascription will be fictionally or nominalistically adequate: that is, correct with respect to the facts about the concrete world. (Rosen (2001) calls a theory Γ nominalistically adequate so long as the “concrete core” or largest wholly concrete part of a world W at which Γ is true is an exact intrinsic duplicate of the concrete core of the actual world.)
The falsity of “Sherlock Holmes is more intelligent than any detective I’ve met” does not prevent it from being capable of accurately representing the real world. According to Leng, in grasping sentences like these we grasp their nominalistic content: what they “say” about the real world. In an analogous way, when we grasp mixed mathematical-physical claims, we grasp their nominalistic content. Scientific instrumentalism, on this account, does not debar science from being an accurate guide to what the world is like. Treating mathematics as a form of make-believe is consistent with treating scientific theories as having the power to accurately represent the world.
ii. Explaining the success of mathematics
This however is not the end of the story. One reason many philosophers accept (Realism) is that they take it to be the only way to explain the predictive success of science. If mathematized scientific theories are false, it would then be a hugely improbable coincidence that the very precise predictions they make are correct. J.J.C. Smart (1963, 36) gave a well-known formulation of this thought:
Is it not off that the phenomena of the world should be such as to make a purely instrumental theory true? On the other hand, if we interpret a theory in a realist way, then we have no need of such a cosmic coincidence: it is not surprising that galvanometers and cloud chambers behave in the sort of way they do, for if there really are electrons, etc., this is just what we should expect. A lot of surprising facts no longer seem surprising.
Smart had in mind instrumentalism regarding (concrete) theoretical entities such as subatomic particles, but many have endorsed the idea that the same problem carries over to instrumentalism about mathematical entities (Putnam 1971). Leng claims that the success of mathematized scientific theories is best explained in terms of their nominalistic adequacy, as opposed to their truth. Mathematized scientific theories describe non-causal relations between mathematical and concrete objects, but the behavior of concrete systems—the behavior that results in the observable events the theory predicts—cannot be in virtue of these relationships, since mathematical objects are abstract and cannot affect the behavior of concrete systems in any way. The explanation for the predictive success of mathematized theories must be that they respect the underlying concrete facts: the fundamental regularities that hold between concrete objects. Predictive success, in other words, is explained by nominalistic adequacy. Similar reasoning leads Leng to claim that what is tested empirically is the nominalistic adequacy of scientific theories, as opposed to their truth. This undercuts both (Realism) and confirmation holism. Regarding (Realism), what gets confirmed empirically is not the truth of these scientific theories, but their nominalistic adequacy. Regarding confirmation holism, the truth of the wholly nominalistic parts of these scientific theories does enjoy empirical confirmation—since truth and nominalistic adequacy are equivalent for wholly nominalistic claims—but the truth of the mathematical and mixed mathematical-concrete parts of them is not empirically confirmed. Leng notes that this line of reasoning applies to the platonist as well as the nominalist; even platonists should deny that the concrete objects described by scientific theories are the way they are because of abstract mathematical objects.
While it follows from the truth of a theory that it will be predictively successful, the explanation for why it is successful must be in terms of its nominalistic adequacy. Recall that Field explained the success of a (false) mathematized theory M by showing that it respects the non-mathematical relations that hold between concreta. He does this by creating a nominalistic theory N which describes the concrete world directly and proving a representation theorem which shows that N and M both place the same sorts of restrictions on the concrete world. If Leng’s reasoning is correct, Field’s project is superfluous, at least with regards to defending nominalism. One does not have to go to the trouble of spelling out a nominalistic counterpart theory, since it is the nominalistic adequacy of mathematized theories which explains their success regardless of whether a nominalistic counterpart theory is available.
iii. Mathematical Explanations
Some have argued that the ability to provide mathematical explanations of physical phenomena provides a reason to believe in the existence of mathematical objects over and above the reason provided by traditional indispensability arguments (see, for example, Bangu 2008, 2013; Baker 2005, 2009, 2012, 2017; Colyvan 2002; Lyon and Colyvan 2008; Lyon 2012). So, in addition to addressing the predictive success of mathematical science, Leng looks to account for the explanatory success of mathematical science. For many mathematical explanations, this is straightforward: mathematical models can be explanatory as a result of their representational role. The nominalistic adequacy of a theory explains why the concrete phenomenon in need of explanation occurs. Sometimes, though, the explanatory work done by mathematics is not exhausted by the nominalistic content of those theories, as there are cases in which, if one were able to represent the nominalistic content directly, explanatory power would actually be lost. Here is an example: the Honeycomb Conjecture—the claim that a hexagonal grid divides a surface into regions of equal area in a way that minimizes the total perimeter of cells—was proven in 1999 by Thomas Hales (this example is discussed in Lyon and Colyvan 2008 and Colyvan 2012). This proof, in conjunction with the premise that bees have evolved to minimize the amount of wax they must use while maximizing the amount of honey they can store, can be used to explain why bees build hexagonal honeycombs. It is not clear that any nominalistic explanation could do the same explanatory work as this abstract one. An explanation which quantified over particular concrete honeycombs would lack the scope of the abstract explanation, which allows us to see that any hives that respond to these evolutionary pressures will have a hexagonal structure.
Leng (2012, 2021) claims that structural explanations of this sort can also be accommodated by her form of nominalism. Structural explanations explain phenomena by showing that they will result if certain structural features are in place. The Honeycomb Conjecture is about abstract structures, but theories about abstract hexagonal structures can be (re)interpreted as being about concrete approximately hexagonal objects. Roughly speaking, what goes for ideal abstract hexagonal structures goes approximately for imperfect, concrete hexagonal structures. Axioms Γ characterizing abstract hexagonal structures will be approximately true of imperfect concrete hexagonal structures. If some claim ϕ (such as that hexagonal grids minimise the total perimeter of cells) is entailed by Γ, then ϕ will also hold in concrete systems approximately characterizable by Γ. More generally, a model of a theory Γ is a domain of objects that satisfies the axioms of Γ. If Γ entails some claim ϕ, then any model of Γ must also be a model of ϕ. Γ characterizes an abstract structure, which means that mathematical methods can be used to determine whether any model of Γ is a model of ϕ. However, the axioms of Γ can also be interpreted as being about a concrete system (the terms of Γ will be taken to denote concrete objects), in which case Γ will characterize the structural features of that concrete system. A mathematical proof that any model of Γ is a model of ϕ will, then, explain why any concrete system characterizable by Γ will exhibit ϕ (with ϕ now also interpreted as being about a concrete system).
According to Leng, then, using mathematical explanations does not commit one to the existence of mathematical objects, but only to the fact that the concrete system being modelled has the structural features which mathematical methods allow one to describe. The applicability of the explanation is accounted for not in terms of the existence of mathematical objects, but in terms of our ability to interpret the axioms of Γ as being approximately true of concrete systems. Again, Leng’s take on nominalism is not to rid ourselves of abstract talk, or to show how abstract talk could be true without abstract objects, but to explain why engaging in abstract talk can achieve certain ends despite its literal falsehood.
iv. Nominalistic Content
Leng claims that although the best scientific theories are not true, they allow us to grasp what the physical world is like. The best scientific theories are nominalistically adequate: they, in some sense, express a true nominalistic content given by what those theories require of the concrete domain. There are difficulties in explicating what this amounts to. One way to give the nominalistic content of a mixed mathematical-concrete sentence ϕ is to provide a nominalistic paraphrase ϕN of ϕ in the manner of Field’s reconstructive project. ϕ would describe the way the physical world would have to be for ϕ to be true. However, if one renounces the project of providing Field-style nominalizations, it is not clear how to articulate the nominalistic content of mathematical descriptions of the physical world (Field 1989, chapter 7).
Melia (2000) suggests that it is possible for the nominalist to “communicate or express his picture of what the world is really like” by asserting a mixed mathematical-concrete sentence ϕ and then denying some of its consequences. One might say for example “Everyone who Fs also Gs. Except Harry—he’s the one exception”. In doing so, it is possible to successfully communicate a picture of what the world is like. Similarly, one might say “ϕ—but there are no mathematical objects”. Colyvan (2010) objects to strategies of this kind on the grounds that what is communicated or expressed is ill-defined. Colyvan compares the strategy to Tolkien retracting the (fictional) existence of hobbits late on the Lord of the Rings. We have no real grip on what is left of the story once hobbits have been extracted.
A number of theorists, however, have given accounts of nominalistic content—or the closely related notion of nominalistic adequacy—that may allow nominalistic content to be more clearly picked out without providing Field-style nominalistic paraphrases of mixed mathematical-physical sentences. Rosen (2001), Dorr (2007), and Yablo (2012) explore ways of cashing out nominalistic adequacy and nominalistic content by appealing to physically indiscernible worlds. Ketland (2011) defines nominalistic adequacy model-theoretically. Rayo (2015) defends a way of specifying nominalistic contents by “outscoping” mathematical vocabulary. Roughly speaking, instead of characterizing a world w as containing both mathematical and concrete objects and describing the relations that obtain between them, one characterizes w as containing only concrete objects and uses mathematical language to characterize the concrete objects at w. Since doing this still involves making mathematical assertions, there are interesting questions about whether the strategy is available to instrumentalist nominalists.
8. Mathematical Nominalism and Naturalism
Though the term “naturalism” is used in many different, sometimes conflicting ways, there are broadly two kinds of naturalism: metaphysical naturalism and methodological naturalism. Metaphysical naturalism is the claim that only natural things exist—there are no supernatural beings that, in some way, transcend the natural order. In many reasonable senses of “transcend the natural order”, platonism apparently violates metaphysical naturalism: mathematical objects are nonmaterial, eternal, immutable, acausal, not in space-time or subject to natural laws. For instance, Weir (2005, 473) says that “the ontological naturalist holds that we have a reasonably determinate conception of what it is to be physical and avers that everything is physical”. Mathematical objects would not usually be regarded as physical objects, even by those who regard them as postulates of physics.
Methodological naturalism involves a deferential attitude towards scientific practice. This cannot be quite as strong as the claim that one can only come to know (or be justified in believing) any given claim by scientific means, since the claim that one can only come to know (or be justified in believing) any given claim by scientific means is not something that one can come to know (or be justified in believing) by scientific means. It is not, after all, part of any empirically testable scientific hypothesis: no researcher could devise an experimental setup to empirically confirm this claim. That version of naturalism is not thereby shown to be strictly inconsistent, but it would entail its own unknowability (or inability to be justified under any circumstances). Instead, methodological naturalism can be parsed as something like the following: in scientific domains of inquiry, we should defer to the epistemic standards employed by working scientists, since there is no higher or better perspective from which to inquire into the nature of the world or from which to assess the claims of science (see, for instance, Quine 1975). If, for example, working scientists take themselves to be justified in holding that the universe is approximately 13 billion years old, we should not take ourselves to be in possession of philosophical reasons to reject this claim.
a. Quine’s Naturalism
Quine is probably the most famous advocate of methodological naturalism, particularly as it pertains to nominalism. According to Quine, natural science is:
An inquiry into reality, fallible and corrigible but not answerable to any supra-scientific tribunal, and not in need of any justification beyond observation and the hypothetico-deductive method. (Quine 1981, 72)
As such, ontology should be decided by looking to the content of the best contemporary scientific theories. If the overall body of scientific theory, suitably regimented into the language of first-order logic, states that something exists—which, for Quine, is equivalent to quantifying over that thing—then we are sufficiently justified in taking that thing to exist. (See the article on the Indispensability Argument for details of how this goes.) Quine takes empirical science to be the arbiter of what exists. Although he understands science broadly, including disciplines like psychology, economics, sociology and history, pure mathematics does not fall under this rubric. For Quine, we ought to believe the claims of mathematics, but only because they find application in empirical science. Quine changes his mind over what to make of mathematics that is not applied; at one point he claims the higher reaches of set theory are on a par with uninterpreted languages (Quine 1984), but later that we regard them as meaningful because they are “couched in the same grammar and vocabulary” as mathematics, which does get applied (Quine 1990, 94).
b. Maddy’s Naturalism
Penelope Maddy (1997) claims that the Quinian ignores some nuances of scientific practice that have a bearing on what the naturalist should take to be the real scientific standards of evidence. Maddy points out that a historical study of scientific practice reveals that, though atomic theory was entrenched to the point that quantification over atoms was indispensable to the best science by 1860, scientists did not believe in the existence of atoms until atoms themselves were detected directly by Jean Baptiste Perrin, who was able to experimentally verify the predictions made by Einstein’s 1905 account of Brownian motion in terms of atoms. Similarly, general relativity treats space-time as dense—for any two space-time points, there exists another point between them, meaning space-time is “smooth” rather than quantized—but scientists who model space-time this way do not assume that space-time itself really has this property. The choice of model is based on pragmatic factors such as convenience, effectiveness, and computational tractability. There are, then, things that the best scientific theories indispensably quantify over but which working scientists do not take themselves to be justified in believing in. As such, scientific practice appears at odds with confirmation holism: there are things affirmed by the best scientific theories that scientists do not treat as being empirically confirmed. With regards to nominalism, Maddy notes that, since mathematical objects could not be directly detectable in the manner of theoretical posits like atoms, the evidence for the existence of mathematical objects cannot be of the same sort as the evidence for the existence of some other theoretical posits. As with some concrete posits of theories, scientists include the mathematical posits they do because of pragmatic factors like convenience, effectiveness, and computational tractability. Maddy takes this to undermine the claim that the mere presence of reference to or quantification over mathematical objects in the best scientific theories provides justification for taking those objects to exist.
c. Burgess and Rosen’s Naturalism
John Burgess and Gideon Rosen (1997, 2005) have given an influential naturalistic argument against nominalism and in response to epistemological objections to belief in mathematical objects. The Burgess-Rosen-style naturalist makes no attempt to reconcile the picture of ourselves—given to us by biology, neuroscience, empirical psychology and so on—as embodied creatures availed of particular information-gathering abilities, with the claim that we have knowledge of a domain of abstract objects. Instead, he appeals to mathematical practices and the manner in which mathematicians come to accept mathematical claims. If one asks a working scientist why she believes in protons, she will cite the usual scientific evidence for the existence of protons. For the naturalist, this standard of evidence should be sufficient for belief in protons. In the same way, argue Burgess and Rosen, one should look to the usual means by which mathematicians provide evidence for mathematical claims—for the naturalist, the usual mathematical standards of evidence should be enough for us to accept the mathematical claims they aim to establish. Burgess and Rosen argue that nominalism requires rejecting the standards of justification at play in the mathematical community. They look to the circumstances under which mathematicians come to accept mathematical claims. Consider the claim:
There are numbers greater than 101010 that are prime.
Mathematicians accept this claim on the basis of mathematical proofs. There are many such proofs, but we can consider just one to form a sense of what is involved in mathematical standards of justification:
Assume that there are finitely many primes. These can be represented in a list: p1, p2, p3, p4, …, pn. Consider the number N = p1 x p2 x p3 x p4 x … pn + 1. Either N is a prime number, or it is not. If N is prime, this contradicts the assumption that the list p1, p2, p3, p4, …, pn includes all the primes, so N cannot be prime. If N is not prime, then it must have prime divisors (all natural numbers are either prime or are the products of primes). But this divisor cannot be on the list p1, p2, p3, p4, …, pn since dividing N by numbers on the list would leave a remainder of 1. This also contradicts the assumption that the list includes all the primes, so N cannot not be prime. The assumption that there are finitely many primes entails that N cannot be prime and cannot be not prime, which is absurd. So, there are infinitely many primes. QED
That there are infinitely many prime numbers entails that there are numbers and, so, is incompatible with nominalism (given the kind of mainstream semantic presuppositions discussed earlier). Moreover, it is a claim that mathematicians take to be established by the reasoning above. If nominalists reject that claim, they must be using standards of justification different than the standards of mathematicians. Philosophers though have no higher or better vantage point from which to assess mathematical claims than mathematicians, so one should defer to the justificatory standards of mathematicians and accept that there is (decisive) justification for believing in abstract objects. Burgess and Rosen (2005) parse the argument the following way:
- The claims of standard mathematics appear to assert the existence of mathematical objects;
- Experts—mathematicians and scientists—accept these claims, using them in practical and theoretical reasoning;
- These claims are acceptable by mathematical standards. The claims that are not taken as axioms are supplied with proofs;
- The claims of standard mathematics not only appear to assert the existence of mathematical objects, they do assert the existence of mathematical objects;
- Accepting a claim—assenting to it verbally without reservations, using it in practical and theoretical reasoning and so on—just is believing the claim to be true;
- The claims of standard mathematics are not only acceptable by mathematical standards but are acceptable by scientific standards: empirical scientists defer to mathematicians on mathematical matters and there are no empirical scientific arguments against the claims of standard mathematics;
- There are no philosophical considerations that can override mathematical and scientific standards of acceptability;
- From (1), (2), (4) and (5): competent mathematicians and scientists believe in the existence of mathematical objects;
- From (3), (6), (7), (8): we are justified in believing in mathematical objects.
An interesting feature of the argument is that, if successful, it shows that nominalism is implausible whether or not mathematics is, in principle, dispensable to science: the de facto endorsement of mathematical claims by mathematicians is enough to undermine nominalism. Parts of the argument, however, can be contested by nominalists. For example, it might be answered that the seemingly formidable mathematicians who have denied the existence of mathematical objects—such as Alfred Tarski (see Frost-Arnold 2008), Timothy Gowers (2011), Solomon Feferman (1998), Abraham Robinson (1979), and so on—are not incompetent, contrary to what premise 8 would entail.
There have been different responses from nominalists to the considerations that motivate the argument. Leng’s pragmatic nominalism aims at showing why strictly false mathematical claims can reasonably be asserted and relied on in practical and theoretical reasoning. If her project is successful, then (5) is undercut, since accepting a claim, in the relevant sense of being nominalistically adequate, is very different from believing it to be true. Chihara (2006) has questioned (4). The claims of standard mathematics may not be genuine claims about the world, but they may, for instance, express what would be true in a structure, or may be only partially meaningful and lack complete truth conditions. Azzouni could also be understood as rejecting (1) and (4).
9. References and Further Reading
- Arntzenius, Frank, and Cian Dorr. 2012. “Calculus as Geometry”. In Arntzenius, Frank, Space, Time, and Stuff. Oxford University Press.
- Azzouni, Jody. 2004. “Theory, Observation and Scientific Realism”. Philosophy of Science 55: 371–92.
- Azzouni, Jody. 2007. “A Cause for Concern: Standard Abstracta and Causation”. Philosophia Mathematica 16(3): 397–401.
- Azzouni, Jody. 2010a. Talking about Nothing: Numbers, Hallucinations, and Fictions. Oxford University Press.
- Azzouni, Jody 2010b. “Ontology and the Word ‘Exist’: Uneasy Relations”. Philosophia Mathematica 18(1): 74–101.
- Azzouni, Jody. 2012. “Taking the Easy Road Out of Dodge”. Mind 121(484): 951–65.
- Azzouni, Jody 2017. Ontology Without Borders. Oxford University Press.
- Baker, Alan. 2005. “Are There Genuine Mathematical Explanations of Physical Phenomena?” Mind 114(454): 223–38.
- Baker, Alan. 2009. “Mathematical Accidents and the End of Explanation”. In New Waves in Philosophy of Mathematics, edited by Otávio Bueno and Øysten Linnebo. Palgrave Macmillan: 137-159.
- Baker, Alan. 2012. “Science-Driven Mathematical Explanation”. Mind 121(482): 243–67.
- Baker, Alan. 2017. “Mathematical Spandrels”. Australasian Journal of Philosophy 95(4): 243–67.
- Balaguer, Mark. 1996. “A Fictionalist Account of the Indispensable Applications of Mathematics”. Philosophical Studies 83(3): 291–314.
- Balaguer, Mark. 1998. Platonism and Anti-Platonism in Mathematics. Oxford University Press.
- Bangu, Sorin. 2008. “Inference to the Best Explanation and Mathematical Realism”. Synthese 160(1): 13–20.
- Bangu, Sorin. 2012. The Applicability of Mathematics in Science: Indispensability and Ontology. Palgrave Macmillan.
- Bangu, Sorin. 2013. “Indispensability and Explanation”. British Journal for the Philosophy of Science 64(2): 225–77.
- Benacerraf, Paul. 1973. “Mathematical Truth”. The Journal of Philosophy 70(19): 661–79.
- Bigelow, John. 1988. The Reality of Numbers: A Physicalist’s Philosophy of Mathematics. Clarendon Press.
- Brandom, Robert. 1994. Making It Explicit: Reasoning, Representing, and Discursive Commitment. Harvard University Press.
- Bueno, Otávio. 2005. “Dirac and the Dispensability of Mathematics”. Studies in History and Philosophy of Modern Physics 36: 465–90.
- Bueno, Otávio. 2009. “Mathematical Fictionalism”. In New Waves in Philosophy of Mathematics, edited by Otávio Bueno and Øysten Linnebo. Palgrave Macmillan: 59-79.
- Bueno, Otávio. 2012. “An Easy Road to Nominalism”. Mind 121(484): 967–82.
- Bueno, Otávio. 2016. “An Anti-Realist Account of the Application of Mathematics”. Philosophical Studies 173: 2591–2604.
- Bueno, Otávio, and Mark Colyvan. 2011. “An Inferential Conception of the Application of Mathematics”. Noûs 45(2): 345–74.
- Bueno, Otávio, and Steven French. 2018. Applying Mathematics: Immersion, Inference, Interpretation. Oxford University Press.
- Burgess, John. 1983. “Why I Am Not a Nominalist”. Notre Dame Journal of Formal Logic 24(1): 93–105.
- Burgess, John. 2004. “Review of Deflating Existential Consequence: A Case for Nominalism”. The Bulletin of Symbolic Logic 10: 573–77.
- Burgess, John, and Gideon Rosen. 1997. A Subject with No Object: Strategies for Nominalistic Interpretation of Mathematics. Oxford University Press.
- Button, Tim. 2013. The Limits of Realism. Oxford University Press.
- Button, Tim, and Sean Walsh. 2018. Philosophy and Model Theory. Oxford University Press.
- Carnap, Rudolf. 1967. The Logical Structure of the World. University of California Press.
- Chang, Hasok. 2004. Inventing Temperature: Measurement and Scientific Progress. Oxford University Press.
- Cheyne, Colin. 1998. “Existence Claims and Causality”. Australasian Journal of Philosophy 76(1): 34–47.
- Cheyne, Colin. 2001. Knowledge, Cause, and Abstract Objects: Causal Objections to Platonism. Kluwer Academic Publishers.
- Chihara, Charles. 1973. Ontology and the Vicious Circle Principle. Cornell University Press.
- Chihara, Charles. 1990. Constructibility and Mathematical Existence. Clarendon Press.
- Chihara, Charles. 2004. A Structural Account of Mathematics. Oxford University Press.
- Chihara, Charles. 2005. “Nominalism”. In The Oxford Handbook of Philosophy of Mathematics and Logic, edited by Stewart Shapiro. Oxford University Press: 483–514.
- Chihara, Charles. 2006. “Burgess’s ‘Scientific’ Arguments for the Existence of Mathematical Objects”. Philosophia Mathematica 14: 318–37.
- Clarke-Doane, Justin. 2020. Morality and Mathematics. Oxford University Press.
- Collin, James Henry. 2018. “Towards an Account of Epistemic Luck for Necessary Truths”. Acta Analytica 33: 483–504.
- Colyvan, Mark. 2001. The Indispensability of Mathematics. Oxford University Press.
- Colyvan, Mark. 2002. “Mathematics and Aesthetic Considerations in Science”. Mind 111(411): 69–74.
- Colyvan, Mark. 2010. “There Is No Easy Road to Nominalism”. Mind 119(474): 285–306.
- Colyvan, Mark. 2012. An Introduction to the Philosophy of Mathematics. Cambridge University Press.
- Dorr, Cian. 2008. “There Are No Abstract Objects”. In Contemporary Debates in Metaphysics, edited by John Hawthorne, Theodore Sider, and Dean Zimmerman. Blackwell: 32-63.
- Feferman, Solomon. 1998. In the Light of Logic. New York: Oxford University Press.
- Field, Hartry. 1980. Science Without Numbers. Princeton University Press.
- Field, Hartry. 1989. “Realism and Anti-Realism about Mathematics”. In Hartry, Field, Realism, Mathematics and Modality. Blackwell: 53-78
- Field, Hartry. 1991. “Metalogic and Modality”. Philosophical Studies 62(1): 1–22.
- Field, Hartry. 2016. Science Without Numbers. 2nd ed. Oxford University Press.
- Fitzgerald, Henry. 2003. “Nominalist Things”. Analysis 63(2): 170–71.
- Frege, Gottlob. 1884. Die Grundlagen Der Arithmetik: Eine Logisch-Mathematische Untersuchung Über Den Begriff Der Zahl. Breslau: Verlage Wilhelm Koebner.
- Frost-Arnold, Greg. 2008. “Tarski’s Nominalism”. In New Essays on Tarski and Philosophy, edited by Douglas Patterson. Oxford University Press: 225-246.
- Goldman, Alvin. 1976. “Discrimination and Perceptual Knowledge”. The Journal of Philosophy 73 (20): 771–91.
- Gowers, Timothy. 2011. “Comment on Gideon Rosen’s ‘The Reality of Mathematical Objects’”. In Meaning in Mathematics, edited by John Polkinghorne. Oxford University Press: 132-133.
- Hart, W.D. 1977. “Review of Steiner, Mathematical Knowledge”. Journal of Philosophy 74: 118–29.
- Hirsch, Eli. 2011. Quantifier Variance and Realism: Essays in Metaontology. Oxford University Press.
- Hofweber, Thomas. 2016. Ontology and the Ambitions of Metaphysics. Oxford University Press.
- Ketland, Jeffrey. 2011. “Nominalistic Adequacy”. Proceedings of the Aristotelian Society 111(2): 201–17.
- Ketland, Jeffrey. 2021. “Foundations of Applied Mathematics I”. Synthese 199(1-2): 4151-4193.
- Kimhi, Irad. 2018. Thinking and Being. Harvard University Press.
- Krantz, David, R., Duncan Luce, Patrick Suppes, and Amos Tversky. 1971. Foundations of Measurement. Vol. 1. Academic Press.
- Leng, M. 2005. “Revolutionary Fictionalism: A Call to Arms”. Philosophia Mathematica 13(3): 277–93.
- Leng, Mary. 2002. “What’s Wrong with Indispensability? (Or, the Case for Recreational Mathematics)”. Synthese 131(03): 395–417.
- Leng, Mary. 2007. “What’s There to Know? A Fictionalist Account of Mathematical Knowledge”. In Mathematical Knowledge, edited by Alexander Paseau, Mary Leng and Michael Potter. Oxford University Press: 84-108.
- Leng, Mary. 2010. Mathematics and Reality. Oxford University Press.
- Leng, Mary. 2012. “Taking It Easy: A Response to Colyvan”. Mind 121(484): 983–95.
- Leng, Mary. 2021. “Models, Structures, and the Explanatory Role of Mathematics in Empirical Science”. Synthese 199(3): 10415–40.
- Lewis, David. 1986. On the Plurality of Worlds. John Wiley & Sons.
- Linnebo, Øysten. 2017. Philosophy of Mathematics. Princeton University Press.
- Lyon, Aidan. 2012. “Mathematical Explanations of Empirical Facts, and Mathematical Realism”. Australasian Journal of Philosophy 90(3): 559–78.
- Lyon, Aidan, and Mark Colyvan. 2008. “The Explanatory Power of Phase Spaces”. Philosophia Mathematica 16(2): 227–43.
- Maddy, Penelope. 1992. “Indispensability and Practice”. Journal of Philosophy 89(6): 275–89.
- Maddy, Penelope. 1997. Naturalism in Mathematics. Oxford University Press.
- Malament, David. 1982. “Review of Field’s Science Without Numbers”. Journal of Philosophy 79: 523–34.
- McDaniel, Kris. 2017. The Fragmentation of Being. Oxford University Press.
- Melia, Joseph. 2000. “Weaseling Away the Indispensability Argument”. Mind 109(435): 455–79.
- Melia, Joseph. 2006. “The Conservativeness of Mathematics”. Analysis 66 (291): 202–8.
- Miller, Barry. 2002. The Fullness of Being: A New Paradigm for Existence. University of Notre Dame Press.
- Morrison, Margaret. 2015. Reconstructing Reality: Models, Mathematics, and Simulations. Oxford University Press.
- Nutting, Eileen S. 2016. “To Bridge Gödel’s Gap”. Philosophical Studies 173: 2133–50.
- Parsons, Terence. 1980. Nonexistent Objects. Yale University Press.
- Pincock, Christopher. 2012. Mathematics and Scientific Representation. Oxford University Press.
- Plantinga, Alvin. 1993. Warrant: The Current Debate. Oxford University Press.
- Potter, Michael. 2007. “What Is the Problem of Mathematical Knowledge?”. In Mathematical Knowledge, edited by Mary Leng, Alexander Paseau, and Michael Potter. Oxford University Press: 16-32.
- Priest, Graham. 2016. Towards Non-Being: The Logic and Metaphysics of Intentionality. 2nd ed. Oxford University Press.
- Putnam, Hilary. 1971. Philosophy of Logic. Harper & Row.
- Putnam, Hilary. 1980. “Models and Reality”. The Journal of Symbolic Logic 45(3): 464–82.
- Putnam, Hilary. 2004. Ethics Without Ontology. Harvard University Press.
- Quine, W.V.O.. 1948. “On What There Is”. Review of Metaphysics 2(5): 21–36.
- Quine, W.V.O.. 1951. “Two Dogmas of Empiricism”. The Philosophical Review 60(1): 20–43.
- Quine, W.V.O.. 1975. “Five Milestones of Empiricism”. Reprinted in Theories and Things. Harvard University Press: 67-72.
- Quine, W.V.O.. 1976. “Whither Physical Objects?”. Studies in the Philosophy of Science 39: 303–10.
- Quine, W.V.O.. 1981. Theories and Things. Harvard University Press.
- Quine, W.V.O.. 1984. “Review of Charles Parsons’ Mathematics in Philosophy”. Journal of Philosophy.
- Quine, W.V.O.. 1986. Philosophy of Logic. 2nd ed. Harvard University Press.
- Quine, W.V.O.. 1990. Pursuit of Truth. Harvard University Press.
- Rayo, Agustín . 2013. The Construction of Logical Space. Oxford University Press.
- Rayo, Agustín . 2015. “Nominalism, Trivialism, Logicism”. Philosophia Mathematica 23(1): 65–86.
- Rayo, Agustín . 2016. “Neo-Fregeanism Reconsidered”. In Abstractionism: Essays in Philosophy of Mathematics, edited by Philip Ebert and Marcus Rossberg. Oxford University Press: 203-221.
- Resnik, Michael. 1995. “Scientific vs. Mathematical Realism: The Indispensability Argument”. Philosophia Mathematica 3(2): 166–74.
- Resnik, Michael. 1997. Mathematics as a Science of Patterns. Clarendon Press.
- Robinson, Abraham. 1979. “Formalism”. In Selected Papers of Abraham Robinson, edited by W.A.J. Luxemburg and S. Körner. North-Holland Publishing Company.
- Rosen, Gideon. 2001. “Nominalism, Naturalism, Epistemic Relativism”. Philosophical Perspectives 15: 69–91.
- Rosen, Gideon. 2020. “Abstract Objects.” In The Stanford Encyclopedia of Philosophy, edited by Edward N. Zalta.
- Rosen, Gideon, and John Burgess. 2005. “Nominalism Reconsidered”. In The Oxford Handbook of Philosophy of Mathematics and Logic, edited by Stewart Shapiro. Oxford University Press: 515-535.
- Routley, Richard. 1980. Exploring Meinong’s Jungle and Beyond. Canberra: Philosophy Department, Research School of the Social Sciences.
- Russell, Bertrand. 1903. Principles of Mathematics. Cambridge University Press.
- Shapiro, Stewart. 1993. “Modality and Ontology”. Mind 102(407): 455–81.
- Shapiro, Stewart . 1997. Philosophy of Mathematics: Structure and Ontology. Oxford University Press.
- Sober, Eliot. 1993. “Mathematics and Indispensability”. The Philosophical Review 102 (1): 35–57.
- Steiner, Mark. 1998. The Applicability of Mathematics as a Philosophical Problem. Harvard University Press.
- Suppes, Patrick. 1960. “A Comparison of the Meaning and Use of Models in Mathematics and the Empirical Sciences”. Synthese 12(2-3): 287–301.
- Tarski, Alfred. 1935. “Der Wahrheitsbegriff in der formalisierten Sprachen”. Studia Philosophica 1: 261–405.
- Tarski, Alfred . 1936. “Über den Begriff der logischen Folgerung”. Actes du Congrès international de philosophie scientifique: Logique, Volume 7: 1–11.
- Tarski, Alfred . 1944. “The Semantic Conception of Truth”. Philosophy and Phenomenological Research 3: 341–76.
- Vallicella, William F. 2002. A Paradigm Theory of Existence: Onto-Theology Vindicated. Kluwer Academic Publishers.
- van Fraassen, Bas. 2008. Scientific Representation: Paradoxes of Perspective. Oxford University Press.
- Walton, Kendall. 1990. Mimesis as Make-Believe. Harvard University Press.
- Walton, Kendall. 1993. “Metaphor and Prop Oriented Make-Believe”. European Journal of Philosophy 1: 39-57.
- Weir, Alan. 2005. “Naturalism Reconsidered”. In The Oxford Handbook of Philosophy of Mathematics and Logic, edited by Stewart Shapiro. Oxford University Press: 460–82
- Weisberg, Michael. 2013. Simulation and Similarity: Using Models to Understand the World. Oxford University Press.
- Yablo, Stephen. 2009. “Must Existence-Questions Have Answers?”. In Metametaphysics: New Essays on the Foundations of Ontology, edited by David Manley, David Chalmers and Ryan Wasserman. Oxford University Press: 507-525.
- Yablo, Stephen. 2012. “Explanation, Extrapolation, and Existence”. Mind 121: 1007–29.
- Zalta, Edward N. 1988. Intensional Logic and the Metaphysics of Intensionality. MIT Press.
Author Information
James Henry Collin
Email: James.Collin@glasgow.ac.uk
University of Glasgow
Scotland


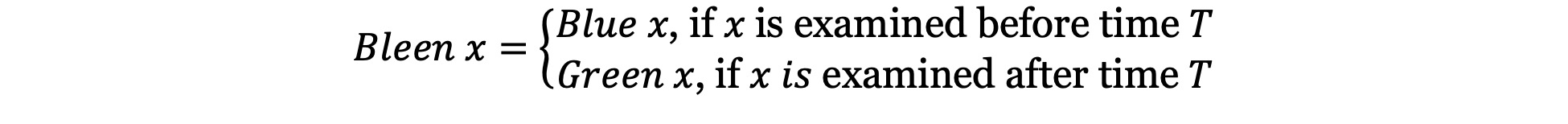
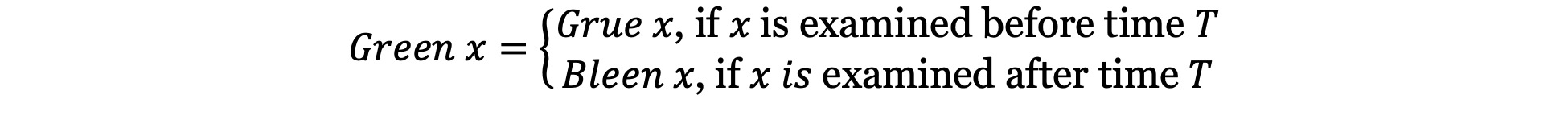
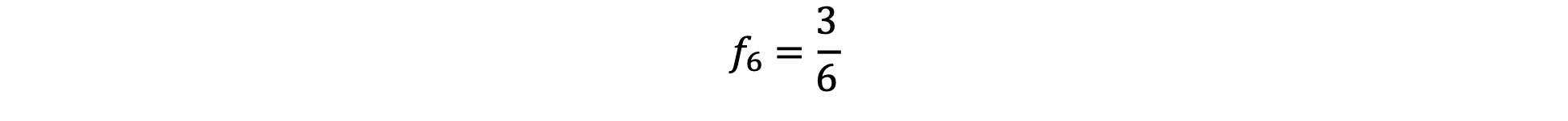
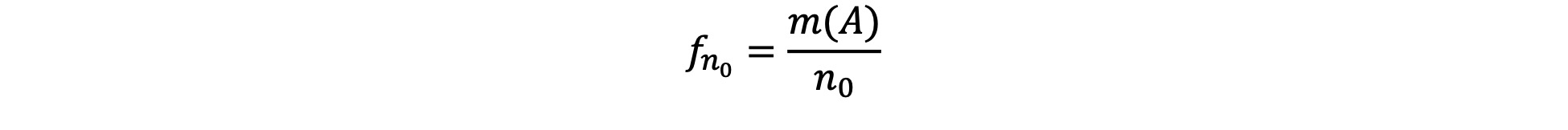

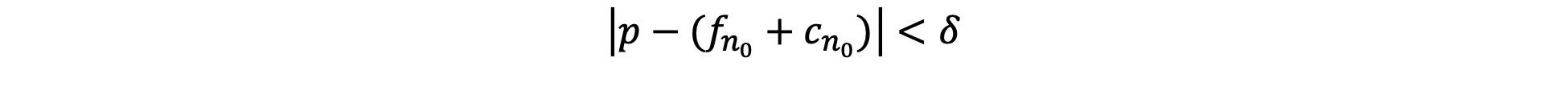
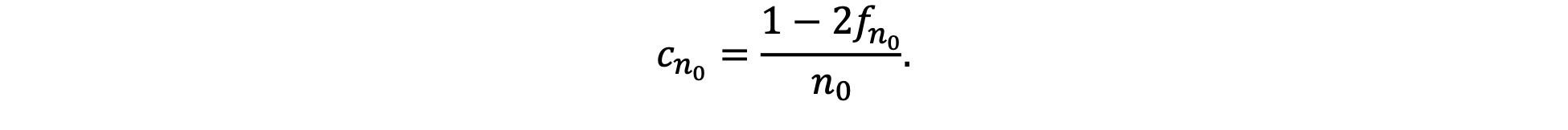
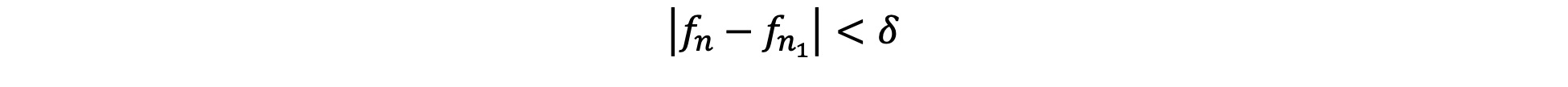
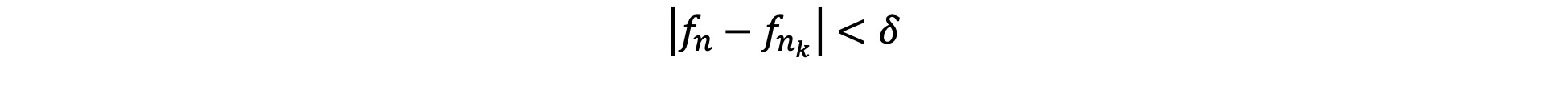
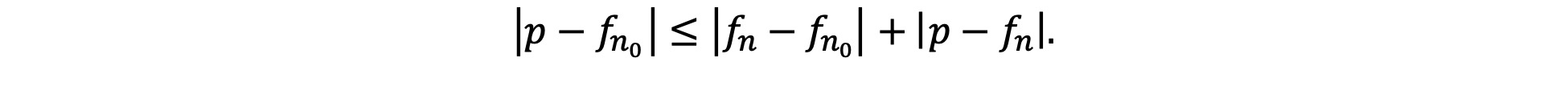






 In the fifth century B.C.E., Zeno offered arguments that led to conclusions contradicting what we all know from our physical experience—that runners run, that arrows fly, and that there are many different things in the world. The arguments were paradoxes for the ancient Greek philosophers. Because many of Zeno’s arguments turn crucially on the notion that space and time are infinitely divisible, he was the first person to show that the concept of
In the fifth century B.C.E., Zeno offered arguments that led to conclusions contradicting what we all know from our physical experience—that runners run, that arrows fly, and that there are many different things in the world. The arguments were paradoxes for the ancient Greek philosophers. Because many of Zeno’s arguments turn crucially on the notion that space and time are infinitely divisible, he was the first person to show that the concept of