Pseudoscience and the Demarcation Problem
The demarcation problem in philosophy of science refers to the question of how to meaningfully and reliably separate science from pseudoscience. Both the terms “science” and “pseudoscience” are notoriously difficult to define precisely, except in terms of family resemblance. The demarcation problem has a long history, tracing back at the least to a speech given by Socrates in Plato’s Charmides, as well as to Cicero’s critique of Stoic ideas on divination. Karl Popper was the most influential modern philosopher to write on demarcation, proposing his criterion of falsifiability to sharply distinguish science from pseudoscience. Most contemporary practitioners, however, agree that Popper’s suggestion does not work. In fact, Larry Laudan suggested that the demarcation problem is insoluble and that philosophers would be better off focusing their efforts on something else. This led to a series of responses to Laudan and new proposals on how to move forward, collected in a landmark edited volume on the philosophy of pseudoscience. After the publication of this volume, the field saw a renaissance characterized by a number of innovative approaches. Two such approaches are particularly highlighted in this article: treating pseudoscience and pseudophilosophy as BS, that is, “bullshit” in Harry Frankfurt’s sense of the term, and applying virtue epistemology to the demarcation problem. This article also looks at the grassroots movement often referred to as scientific skepticism and to its philosophical bases.
Table of Contents
- An Ancient Problem with a Long History
- The Demise of Demarcation: The Laudan Paper
- The Return of Demarcation: The University of Chicago Press Volume
- The Renaissance of the Demarcation Problem
- Pseudoscience as BS
- Virtue Epistemology and Demarcation
- The Scientific Skepticism Movement
- References and Further Readings
1. An Ancient Problem with a Long History
In the Charmides (West and West translation, 1986), Plato has Socrates tackle what contemporary philosophers of science refer to as the demarcation problem, the separation between science and pseudoscience. In that dialogue, Socrates is referring to a specific but very practical demarcation issue: how to tell the difference between medicine and quackery. Here is the most relevant excerpt:
SOCRATES: Let us consider the matter in this way. If the wise man or any other man wants to distinguish the true physician from the false, how will he proceed? . . . He who would inquire into the nature of medicine must test it in health and disease, which are the sphere of medicine, and not in what is extraneous and is not its sphere?
CRITIAS: True.
SOCRATES: And he who wishes to make a fair test of the physician as a physician will test him in what relates to these?
CRITIAS: He will.
SOCRATES: He will consider whether what he says is true, and whether what he does is right, in relation to health and disease?
CRITIAS: He will.
SOCRATES: But can anyone pursue the inquiry into either, unless he has a knowledge of medicine?
CRITIAS: He cannot.
SOCRATES: No one at all, it would seem, except the physician can have this knowledge—and therefore not the wise man. He would have to be a physician as well as a wise man.
CRITIAS: Very true. (170e-171c)
The conclusion at which Socrates arrives, therefore, is that the wise person would have to develop expertise in medicine, as that is the only way to distinguish an actual doctor from a quack. Setting aside that such a solution is not practical for most people in most settings, the underlying question remains: how do we decide whom to pick as our instructor? What if we mistake a school of quackery for a medical one? Do quacks not also claim to be experts? Is this not a hopelessly circular conundrum?
A few centuries later, the Roman orator, statesman, and philosopher Marcus Tullius Cicero published a comprehensive attack on the notion of divination, essentially treating it as what we would today call a pseudoscience, and anticipating a number of arguments that have been developed by philosophers of science in modern times. As Fernandez-Beanato (2020a) points out, Cicero uses the Latin word “scientia” to refer to a broader set of disciplines than the English “science.” His meaning is closer to the German word “Wissenschaft,” which means that his treatment of demarcation potentially extends to what we would today call the humanities, such as history and philosophy.
Being a member of the New Academy, and therefore a moderate epistemic skeptic, Cicero writes: “As I fear to hastily give my assent to something false or insufficiently substantiated, it seems that I should make a careful comparison of arguments […]. For to hasten to give assent to something erroneous is shameful in all things” (De Divinatione, I.7 / Falconer translation, 2014). He thus frames the debate on unsubstantiated claims, and divination in particular, as a moral one.
Fernandez-Beanato identifies five modern criteria that often come up in discussions of demarcation and that are either explicitly or implicitly advocated by Cicero: internal logical consistency of whatever notion is under scrutiny; degree of empirical confirmation of the predictions made by a given hypothesis; degree of specificity of the proposed mechanisms underlying a certain phenomenon; degree of arbitrariness in the application of an idea; and degree of selectivity of the data presented by the practitioners of a particular approach. Divination fails, according to Cicero, because it is logically inconsistent, it lacks empirical confirmation, its practitioners have not proposed a suitable mechanism, said practitioners apply the notion arbitrarily, and they are highly selective in what they consider to be successes of their practice.
Jumping ahead to more recent times, arguably the first modern instance of a scientific investigation into allegedly pseudoscientific claims is the case of the famous Royal Commissions on Animal Magnetism appointed by King Louis XVI in 1784. One of them, the so-called Society Commission, was composed of five physicians from the Royal Society of Medicine; the other, the so-called Franklin Commission, comprised four physicians from the Paris Faculty of Medicine, as well as Benjamin Franklin. The goal of both commissions was to investigate claims of “mesmerism,” or animal magnetism, being made by Franz Mesmer and some of his students (Salas and Salas 1996; Armando and Belhoste 2018).
Mesmer was a medical doctor who began his career with a questionable study entitled “A Physico-Medical Dissertation on the Influence of the Planets.” Later, he developed a theory according to which all living organisms are permeated by a vital force that can, with particular techniques, be harnessed for therapeutic purposes. While mesmerism became popular and influential for decades between the end of the 18th century and the full span of the 19th century, it is now considered a pseudoscience, in large part because of the failure to empirically replicate its claims and because vitalism in general has been abandoned as a theoretical notion in the biological sciences. Interestingly, though, Mesmer clearly thought he was doing good science within a physicalist paradigm and distanced himself from the more obviously supernatural practices of some of his contemporaries, such as the exorcist Johann Joseph Gassner.
For the purposes of this article, we need to stress the importance of the Franklin Commission in particular, since it represented arguably the first attempt in history to carry out controlled experiments. These were largely designed by Antoine Lavoisier, complete with a double-blind protocol in which both subjects and investigators did not know which treatment they were dealing with at any particular time, the allegedly genuine one or a sham control. As Stephen Jay Gould (1989) put it:
The report of the Royal Commission of 1784 is a masterpiece of the genre, an enduring testimony to the power and beauty of reason. … The Report is a key document in the history of human reason. It should be rescued from its current obscurity, translated into all languages, and reprinted by organizations dedicated to the unmasking of quackery and the defense of rational thought.
Not surprisingly, neither Commission found any evidence supporting Mesmer’s claims. The Franklin report was printed in 20,000 copies and widely circulated in France and abroad, but this did not stop mesmerism from becoming widespread, with hundreds of books published on the subject in the period 1766-1925.
Arriving now to modern times, the philosopher who started the discussion on demarcation is Karl Popper (1959), who thought he had formulated a neat solution: falsifiability (Shea no date). He reckoned that—contra popular understanding—science does not make progress by proving its theories correct, since it is far too easy to selectively accumulate data that are favorable to one’s pre-established views. Rather, for Popper, science progresses by eliminating one bad theory after another, because once a notion has been proven to be false, it will stay that way. He concluded that what distinguishes science from pseudoscience is the (potential) falsifiability of scientific hypotheses, and the inability of pseudoscientific notions to be subjected to the falsifiability test.
For instance, Einstein’s theory of general relativity survived a crucial test in 1919, when one of its most extraordinary predictions—that light is bent by the presence of gravitational masses—was spectacularly confirmed during a total eclipse of the sun (Kennefick 2019). This did not prove that the theory is true, but it showed that it was falsifiable and, therefore, good science. Moreover, Einstein’s prediction was unusual and very specific, and hence very risky for the theory. This, for Popper, is a good feature of a scientific theory, as it is too easy to survive attempts at falsification when predictions based on the theory are mundane or common to multiple theories.
In contrast with the example of the 1919 eclipse, Popper thought that Freudian and Adlerian psychoanalysis, as well as Marxist theories of history, are unfalsifiable in principle; they are so vague that no empirical test could ever show them to be incorrect, if they are incorrect. The point is subtle but crucial. Popper did not argue that those theories are, in fact, wrong, only that one could not possibly know if they were, and they should not, therefore, be classed as good science.
Popper became interested in demarcation because he wanted to free science from a serious issue raised by David Hume (1748), the so-called problem of induction. Scientific reasoning is based on induction, a process by which we generalize from a set of observed events to all observable events. For instance, we “know” that the sun will rise again tomorrow because we have observed the sun rising countless times in the past. More importantly, we attribute causation to phenomena on the basis of inductive reasoning: since event X is always followed by event Y, we infer that X causes Y.
The problem as identified by Hume is twofold. First, unlike deduction (as used in logic and mathematics), induction does not guarantee a given conclusion, it only makes that conclusion probable as a function of the available empirical evidence. Second, there is no way to logically justify the inference of a causal connection. The human mind does so automatically, says Hume, as a leap of imagination.
Popper was not satisfied with the notion that science is, ultimately, based on a logically unsubstantiated step. He reckoned that if we were able to reframe scientific progress in terms of deductive, not inductive logic, Hume’s problem would be circumvented. Hence falsificationism, which is, essentially, an application of modus tollens (Hausman et al. 2021) to scientific hypotheses:
If P, then Q
Not Q
Therefore, not P
For instance, if General Relativity is true then we should observe a certain deviation of light coming from the stars when their rays pass near the sun (during a total eclipse or under similarly favorable circumstances). We do observe the predicted deviation. Therefore, we have (currently) no reason to reject General Relativity. However, had the observations carried out during the 1919 eclipse not aligned with the prediction then there would have been sufficient reason, according to Popper, to reject General Relativity based on the above syllogism.
Science, on this view, does not make progress one induction, or confirmation, after the other, but one discarded theory after the other. And as a bonus, thought Popper, this looks like a neat criterion to demarcate science from pseudoscience.
In fact, it is a bit too neat, unfortunately. Plenty of philosophers after Popper (for example, Laudan 1983) have pointed out that a number of pseudoscientific notions are eminently falsifiable and have been shown to be false—astrology, for instance (Carlson 1985). Conversely, some notions that are even currently considered to be scientific, are also—at least temporarily—unfalsifiable (for example, string theory in physics: Hossenfelder 2018).
A related issue with falsificationism is presented by the so-called Duhem-Quine theses (Curd and Cover 2012), two allied propositions about the nature of knowledge, scientific or otherwise, advanced independently by physicist Pierre Duhem and philosopher Willard Van Orman Quine.
Duhem pointed out that when scientists think they are testing a given hypothesis, as in the case of the 1919 eclipse test of General Relativity, they are, in reality, testing a broad set of propositions constituted by the central hypothesis plus a number of ancillary assumptions. For instance, while the attention of astronomers in 1919 was on Einstein’s theory and its implications for the laws of optics, they also simultaneously “tested” the reliability of their telescopes and camera, among a number of more or less implicit additional hypotheses. Had something gone wrong, their likely first instinct, rightly, would have been to check that their equipment was functioning properly before taking the bold step of declaring General Relativity dead.
Quine, later on, articulated a broader account of human knowledge conceived as a web of beliefs. Part of this account is the notion that scientific theories are always underdetermined by the empirical evidence (Bonk 2008), meaning that different theories will be compatible with the same evidence at any given point in time. Indeed, for Quine it is not just that we test specific theories and their ancillary hypotheses. We literally test the entire web of human understanding. Certainly, if a test does not yield the predicted results we will first look at localized assumptions. But occasionally we may be forced to revise our notions at larger scales, up to and including mathematics and logic themselves.
The history of science does present good examples of how the Duhem-Quine theses undermine falsificationism. The twin tales of the spectacular discovery of a new planet and the equally spectacular failure to discover an additional one during the 19th century are classic examples.
Astronomers had uncovered anomalies in the orbit of Uranus, at that time the outermost known planet in the solar system. These anomalies did not appear, at first, to be explainable by standard Newtonian mechanics, and yet nobody thought even for a moment to reject that theory on the basis of the newly available empirical evidence. Instead, mathematician Urbain Le Verrier postulated that the anomalies were the result of the gravitational interference of an as yet unknown planet, situated outside of Uranus’ orbit. The new planet, Neptune, was in fact discovered on the night of 23-24 September 1846, thanks to the precise calculations of Le Verrier (Grosser 1962).
The situation repeated itself shortly thereafter, this time with anomalies discovered in the orbit of the innermost planet of our system, Mercury. Again, Le Verrier hypothesized the existence of a hitherto undiscovered planet, which he named Vulcan. But Vulcan never materialized. Eventually astronomers really did have to jettison Newtonian mechanics and deploy the more sophisticated tools provided by General Relativity, which accounted for the distortion of Mercury’s orbit in terms of gravitational effects originating with the Sun (Baum and Sheehan 1997).
What prompted astronomers to react so differently to two seemingly identical situations? Popper would have recognized the two similar hypotheses put forth by Le Verrier as being ad hoc and yet somewhat justified given the alternative, the rejection of Newtonian mechanics. But falsificationism has no tools capable of explaining why it is that sometimes ad hoc hypotheses are acceptable and at other times they are not. Nor, therefore, is it in a position to provide us with sure guidance in cases like those faced by Le Verrier and colleagues. This failure, together with wider criticism of Popper’s philosophy of science by the likes of Thomas Kuhn (1962), Imre Lakatos (1978), and Paul Feyerabend (1975) paved the way for a crisis of sorts for the whole project of demarcation in philosophy of science.
2. The Demise of Demarcation: The Laudan Paper
A landmark paper in the philosophy of demarcation was published by Larry Laudan in 1983. Provocatively entitled “The Demise of the Demarcation Problem,” it sought to dispatch the whole field of inquiry in one fell swoop. As the next section shows, the outcome was quite the opposite, as a number of philosophers responded to Laudan and reinvigorated the whole debate on demarcation. Nevertheless, it is instructive to look at Laudan’s paper and to some of his motivations to write it.
Laudan was disturbed by the events that transpired during one of the classic legal cases concerning pseudoscience, specifically the teaching of so-called creation science in American classrooms. The case, McLean v. Arkansas Board of Education, was debated in 1982. Some of the fundamental questions that the presiding judge, William R. Overton, asked expert witnesses to address were whether Darwinian evolution is a science, whether creationism is also a science, and what criteria are typically used by the pertinent epistemic communities (that is, scientists and philosophers) to arrive at such assessments (LaFollette 1983).
One of the key witnesses on the evolution side was philosopher Michael Ruse, who presented Overton with a number of demarcation criteria, one of which was Popper’s falsificationism. According to Ruse’s testimony, creationism is not a science because, among other reasons, its claims cannot be falsified. In a famous and very public exchange with Ruse, Laudan (1988) objected to the use of falsificationism during the trial, on the grounds that Ruse must have known that that particular criterion had by then been rejected, or at least seriously questioned, by the majority of philosophers of science.
It was this episode that prompted Laudan to publish his landmark paper aimed at getting rid of the entire demarcation debate once and for all. One argument advanced by Laudan is that philosophers have been unable to agree on demarcation criteria since Aristotle and that it is therefore time to give up this particular quixotic quest. This is a rather questionable conclusion. Arguably, philosophy does not make progress by resolving debates, but by discovering and exploring alternative positions in the conceptual spaces defined by a particular philosophical question (Pigliucci 2017). Seen this way, falsificationism and modern debates on demarcation are a standard example of progress in philosophy of science, and there is no reason to abandon a fruitful line of inquiry so long as it keeps being fruitful.
Laudan then argues that the advent of fallibilism in epistemology (Feldman 1981) during the nineteenth century spelled the end of the demarcation problem, as epistemologists now recognize no meaningful distinction between opinion and knowledge. Setting aside that the notion of fallibilism far predates the 19th century and goes back at the least to the New Academy of ancient Greece, it may be the case, as Laudan maintains, that many modern epistemologists do not endorse the notion of an absolute and universal truth, but such notion is not needed for any serious project of science-pseudoscience demarcation. All one needs is that some “opinions” are far better established, by way of argument and evidence, than others and that scientific opinions tend to be dramatically better established than pseudoscientific ones.
It is certainly true, as Laudan maintains, that modern philosophers of science see science as a set of methods and procedures, not as a particular body of knowledge. But the two are tightly linked: the process of science yields reliable (if tentative) knowledge of the world. Conversely, the processes of pseudoscience, such as they are, do not yield any knowledge of the world. The distinction between science as a body of knowledge and science as a set of methods and procedures, therefore, does nothing to undermine the need for demarcation.
After a by now de rigueur criticism of the failure of positivism, Laudan attempts to undermine Popper’s falsificationism. But even Laudan himself seems to realize that the limits of falsificationism do not deal a death blow to the notion that there are recognizable sciences and pseudosciences: “One might respond to such criticisms [of falsificationism] by saying that scientific status is a matter of degree rather than kind” (Laudan 1983, 121). Indeed, that seems to be the currently dominant position of philosophers who are active in the area of demarcation.
The rest of Laudan’s critique boils down to the argument that no demarcation criterion proposed so far can provide a set of necessary and sufficient conditions to define an activity as scientific, and that the “epistemic heterogeneity of the activities and beliefs customarily regarded as scientific” (1983, 124) means that demarcation is a futile quest. This article now briefly examines each of these two claims.
Ever since Wittgenstein (1958), philosophers have recognized that any sufficiently complex concept will not likely be definable in terms of a small number of necessary and jointly sufficient conditions. That approach may work in basic math, geometry, and logic (for example, definitions of triangles and other geometric figures), but not for anything as complex as “science” or “pseudoscience.” This implies that single-criterion attempts like Popper’s are indeed to finally be set aside, but it does not imply that multi-criterial or “fuzzy” approaches will not be useful. Again, rather than a failure, this shift should be regarded as evidence of progress in this particular philosophical debate.
Regarding Laudan’s second claim from above, that science is a fundamentally heterogeneous activity, this may or may not be the case, the jury is still very much out. Some philosophers of science have indeed suggested that there is a fundamental disunity to the sciences (Dupré 1993), but this is far from being a consensus position. Even if true, a heterogeneity of “science” does not preclude thinking of the sciences as a family resemblance set, perhaps with distinctly identifiable sub-sets, similar to the Wittgensteinian description of “games” and their subdivision into fuzzy sets including board games, ball games, and so forth. Indeed, some of the authors discussed later in this article have made this very same proposal regarding pseudoscience: there may be no fundamental unity grouping, say, astrology, creationism, and anti-vaccination conspiracy theories, but they nevertheless share enough Wittgensteinian threads to make it useful for us to talk of all three as examples of broadly defined pseudosciences.
3. The Return of Demarcation: The University of Chicago Press Volume
Laudan’s 1983 paper had the desired effect of convincing a number of philosophers of science that it was not worth engaging with demarcation issues. Yet, in the meantime pseudoscience kept being a noticeable social phenomenon, one that was having increasingly pernicious effects, for instance in the case of HIV, vaccine, and climate change denialism (Smith and Novella, 2007; Navin 2013; Brulle 2020). It was probably inevitable, therefore, that philosophers of science who felt that their discipline ought to make positive contributions to society would, sooner or later, go back to the problem of demarcation.
The turning point was an edited volume entitled The Philosophy of Pseudoscience: Reconsidering the Demarcation Problem, published in 2013 by the University of Chicago Press (Pigliucci and Boudry 2013). The editors and contributors consciously and explicitly set out to respond to Laudan and to begin the work necessary to make progress (in something like the sense highlighted above) on the issue.
The first five chapters of The Philosophy of Pseudoscience take the form of various responses to Laudan, several of which hinge on the rejection of the strict requirement for a small set of necessary and jointly sufficient conditions to define science or pseudoscience. Contemporary philosophers of science, it seems, have no trouble with inherently fuzzy concepts. As for Laudan’s contention that the term “pseudoscience” does only negative, potentially inflammatory work, this is true and yet no different from, say, the use of “unethical” in moral philosophy, which few if any have thought of challenging.
The contributors to The Philosophy of Pseudoscience also readily admit that science is best considered as a family of related activities, with no fundamental essence to define it. Indeed, the same goes for pseudoscience as, for instance, vaccine denialism is very different from astrology, and both differ markedly from creationism. Nevertheless, there are common threads in both cases, and the existence of such threads justifies, in part, philosophical interest in demarcation. The same authors argue that we should focus on the borderline cases, precisely because there it is not easy to neatly separate activities into scientific and pseudoscientific. There is no controversy, for instance, in classifying fundamental physics and evolutionary biology as sciences, and there is no serious doubt that astrology and homeopathy are pseudosciences. But what are we to make of some research into the paranormal carried out by academic psychologists (Jeffers 2007)? Or of the epistemically questionable claims often, but not always, made by evolutionary psychologists (Kaplan 2006)?
The 2013 volume sought a consciously multidisciplinary approach to demarcation. Contributors include philosophers of science, but also sociologists, historians, and professional skeptics (meaning people who directly work on the examination of extraordinary claims). The group saw two fundamental reasons to continue scholarship on demarcation. On the one hand, science has acquired a high social status and commands large amounts of resources in modern society. This means that we ought to examine and understand its nature in order to make sound decisions about just how much trust to put into scientific institutions and proceedings, as well as how much money to pump into the social structure that is modern science. On the other hand, as noted above, pseudoscience is not a harmless pastime. It has negative effects on both individuals and societies. This means that an understanding of its nature, and of how it differs from science, has very practical consequences.
The Philosophy of Pseudoscience also tackles issues of history and sociology of the field. It contains a comprehensive history of the demarcation problem followed by a historical analysis of pseudoscience, which tracks down the coinage and currency of the term and explains its shifting meaning in tandem with the emerging historical identity of science. A contribution by a sociologist then provides an analysis of paranormalism as a “deviant discipline” violating the consensus of established science, and one chapter draws attention to the characteristic social organization of pseudosciences as a means of highlighting the corresponding sociological dimension of the scientific endeavor.
The volume explores the borderlands between science and pseudoscience, for instance by deploying the idea of causal asymmetries in evidential reasoning to differentiate between what are sometime referred to as “hard” and “soft” sciences, arguing that misconceptions about this difference explain the higher incidence of pseudoscience and anti-science connected to the non-experimental sciences. One contribution looks at the demographics of pseudoscientific belief and examines how the demarcation problem is treated in legal cases. One chapter recounts the story of how at one time the pre-Darwinian concept of evolution was treated as pseudoscience in the same guise as mesmerism, before eventually becoming the professional science we are familiar with, thus challenging a conception of demarcation in terms of timeless and purely formal principles.
A discussion focusing on science and the supernatural includes the provocative suggestion that, contrary to recent philosophical trends, the appeal to the supernatural should not be ruled out from science on methodological grounds, as it is often done, but rather because the very notion of supernatural intervention suffers from fatal flaws. Meanwhile, David Hume is enlisted to help navigate the treacherous territory between science and religious pseudoscience and to assess the epistemic credentials of supernaturalism.
The Philosophy of Pseudoscience includes an analysis of the tactics deployed by “true believers” in pseudoscience, beginning with a discussion of the ethics of argumentation about pseudoscience, followed by the suggestion that alternative medicine can be evaluated scientifically despite the immunizing strategies deployed by some of its most vocal supporters. One entry summarizes misgivings about Freudian psychoanalysis, arguing that we should move beyond assessments of the testability and other logical properties of a theory, shifting our attention instead to the spurious claims of validation and other recurrent misdemeanors on the part of pseudoscientists. It also includes a description of the different strategies used by climate change “skeptics” and other denialists, outlining the links between new and “traditional” pseudosciences.
The volume includes a section examining the complex cognitive roots of pseudoscience. Some of the contributors ask whether we actually evolved to be irrational, describing a number of heuristics that are rational in domains ecologically relevant to ancient Homo sapiens, but that lead us astray in modern contexts. One of the chapters explores the non-cognitive functions of super-empirical beliefs, analyzing the different attitudes of science and pseudoscience toward intuition. An additional entry distinguishes between two mindsets about science and explores the cognitive styles relating to authority and tradition in both science and pseudoscience. This is followed by an essay proposing that belief in pseudoscience may be partly explained by theories about the ethics of belief. There is also a chapter on pseudo-hermeneutics and the illusion of understanding, drawing inspiration from the cognitive psychology and philosophy of intentional thinking.
A simple search of online databases of philosophical peer reviewed papers clearly shows that the 2013 volume has succeeded in countering Laudan’s 1983 paper, yielding a flourishing of new entries in the demarcation literature in particular, and in the newly established subfield of the philosophy of pseudoscience more generally. This article now turns to a brief survey of some of the prominent themes that have so far characterized this Renaissance of the field of demarcation.
4. The Renaissance of the Demarcation Problem
After the publication of The Philosophy of Pseudoscience collection, an increasing number of papers has been published on the demarcation problem and related issues in philosophy of science and epistemology. It is not possible to discuss all the major contributions in detail, so what follows is intended as a representative set of highlights and a brief guide to the primary literature.
Sven Ove Hansson (2017) proposed that science denialism, often considered a different issue from pseudoscience, is actually one form of the latter, the other form being what he terms pseudotheory promotion. Hansson examines in detail three case studies: relativity theory denialism, evolution denialism, and climate change denialism. The analysis is couched in terms of three criteria for the identification of pseudoscientific statements, previously laid out by Hansson (2013). A statement is pseudoscientific if it satisfies the following:
- It pertains to an issue within the domains of science in the broad sense (the criterion of scientific domain).
- It suffers from such a severe lack of reliability that it cannot at all be trusted (the criterion of unreliability).
- It is part of a doctrine whose major proponents try to create the impression that it represents the most reliable knowledge on its subject matter (the criterion of deviant doctrine).
On these bases, Hansson concludes that, for example, “The misrepresentations of history presented by Holocaust deniers and other pseudo-historians are very similar in nature to the misrepresentations of natural science promoted by creationists and homeopaths” (2017, 40). In general, Hansson proposes that there is a continuum between science denialism at one end (for example, regarding climate change, the holocaust, the general theory of relativity, etc.) and pseudotheory promotion at the other end (for example, astrology, homeopathy, iridology). He identifies four epistemological characteristics that account for the failure of science denialism to provide genuine knowledge:
- Cherry picking. One example is Conservapedia’s entry listing alleged counterexamples to the general theory of relativity. Never mind that, of course, an even cursory inspection of such “anomalies” turns up only mistakes or misunderstandings.
- Neglect of refuting information. Again concerning general relativity denialism, the proponents of the idea point to a theory advanced by the Swiss physicist Georges-Louis Le Sage that gravitational forces result from pressure exerted on physical bodies by a large number of small invisible particles. That idea might have been reasonably entertained when it was proposed, in the 18th century, but not after the devastating criticism it received in the 19th century—let alone the 21st.
- Fabrication of fake controversies. Perhaps the most obvious example here is the “teach both theories” mantra so often repeated by creationists, which was adopted by Ronald Reagan during his 1980 presidential campaign. The fact is, there is no controversy about evolution within the pertinent epistemic community.
- Deviant criteria of assent. For instance, in the 1920s and ‘30s, special relativity was accused of not being sufficiently transpicuous, and its opponents went so far as to attempt to create a new “German physics” that would not use difficult mathematics and would, therefore, be accessible by everyone. Both Einstein and Planck ridiculed the whole notion that science ought to be transpicuous in the first place. The point is that part of the denialist’s strategy is to ask for impossible standards in science and then use the fact that such demands are not met (because they cannot be) as “evidence” against a given scientific notion. This is known as the unobtainable perfection fallacy (Gauch, 2012).
Hansson lists ten sociological characteristics of denialism: that the focal theory (say, evolution) threatens the denialist’s worldview (for instance, a fundamentalist understanding of Christianity); complaints that the focal theory is too difficult to understand; a lack of expertise among denialists; a strong predominance of men among the denialists (that is, lack of diversity); an inability to publish in peer-reviewed journals; a tendency to embrace conspiracy theories; appeals directly to the public; the pretense of having support among scientists; a pattern of attacks against legitimate scientists; and strong political overtones.
Dawes (2018) acknowledges, with Laudan (1983), that there is a general consensus that no single criterion (or even small set of necessary and jointly sufficient criteria) is capable of discerning science from pseudoscience. However, he correctly maintains that this does not imply that there is no multifactorial account of demarcation, situating different kinds of science and pseudoscience along a continuum. One such criterion is that science is a social process, which entails that a theory is considered scientific because it is part of a research tradition that is pursued by the scientific community.
Dawes is careful in rejecting the sort of social constructionism endorsed by some sociologists of science (Bloor 1976) on the grounds that the sociological component is just one of the criteria that separate science from pseudoscience. Two additional criteria have been studied by philosophers of science for a long time: the evidential and the structural. The first refers to the connection between a given scientific theory and the empirical evidence that provides epistemic warrant for that theory. The second is concerned with the internal structure and coherence of a scientific theory.
Science, according to Dawes, is a cluster concept grouping a set of related, yet somewhat differentiated, kinds of activities. In this sense, his paper reinforces an increasingly widespread understanding of science in the philosophical community (see also Dupré 1993; Pigliucci 2013). Pseudoscience, then, is also a cluster concept, similarly grouping a number of related, yet varied, activities that attempt to mimic science but do so within the confines of an epistemically inert community.
The question, therefore, becomes, in part, one of distinguishing scientific from pseudoscientific communities, especially when the latter closely mimic the first ones. Take, for instance, homeopathy. While it is clearly a pseudoscience, the relevant community is made of self-professed “experts” who even publish a “peer-reviewed” journal, Homeopathy, put out by a major academic publisher, Elsevier. Here, Dawes builds on an account of scientific communities advanced by Robert Merton (1973). According to Merton, scientific communities are characterized by four norms, all of which are lacking in pseudoscientific communities: universalism, the notion that class, gender, ethnicity, and so forth are (ideally, at least) treated as irrelevant in the context of scientific discussions; communality, in the sense that the results of scientific inquiry belong (again, ideally) to everyone; disinterestedness, not because individual scientists are unbiased, but because community-level mechanisms counter individual biases; and organized skepticism, whereby no idea is exempt from critical scrutiny.
In the end, Dawes’s suggestion is that “We will have a pro tanto reason to regard a theory as pseudoscientific when it has been either refused admission to, or excluded from, a scientific research tradition that addresses the relevant problems” (2018, 293). Crucially, however, what is or is not recognized as a viable research tradition by the scientific community changes over time, so that the demarcation between science and pseudoscience is itself liable to shift as time passes.
One author who departs significantly from what otherwise seems to be an emerging consensus on demarcation is Angelo Fasce (2019). He rejects the notion that there is any meaningful continuum between science and pseudoscience, or that either concept can fruitfully be understood in terms of family resemblance, going so far as accusing some of his colleagues of “still engag[ing] in time-consuming, unproductive discussions on already discarded demarcation criteria, such as falsifiability” (2019, 155).
Fasce’s criticism hinges, in part, on the notion that gradualist criteria may create problems in policy decision making: just how much does one activity have to be close to the pseudoscientific end of the spectrum in order for, say, a granting agency to raise issues? The answer is that there is no sharp demarcation because there cannot be, regardless of how much we would wish otherwise. In many cases, said granting agency should have no trouble classifying good science (for example, fundamental physics or evolutionary biology) as well as obvious pseudoscience (for example, astrology or homeopathy). But there will be some borderline cases (for instance, parapsychology? SETI?) where one will just have to exercise one’s best judgment based on what is known at the moment and deal with the possibility that one might make a mistake.
Fasce also argues that “Contradictory conceptions and decisions can be consistently and justifiably derived from [a given demarcation criterion]—i.e. mutually contradictory propositions could be legitimately derived from the same criterion because that criterion allows, or is based on, ‘subjective’ assessment” (2019, 159). Again, this is probably true, but it is also likely an inevitable feature of the nature of the problem, not a reflection of the failure of philosophers to adequately tackle it.
Fasce (2019, 62) states that there is no historical case of a pseudoscience turning into a legitimate science, which he takes as evidence that there is no meaningful continuum between the two classes of activities. But this does not take into account the case of pre-Darwinian evolutionary theories mentioned earlier, nor the many instances of the reverse transition, in which an activity initially considered scientific has, in fact, gradually turned into a pseudoscience, including alchemy (although its relationship with chemistry is actually historically complicated), astrology, phrenology, and, more recently, cold fusion—with the caveat that whether the latter notion ever reached scientific status is still being debated by historians and philosophers of science. These occurrences would seem to point to the existence of a continuum between the two categories of science and pseudoscience.
One interesting objection raised by Fasce is that philosophers who favor a cluster concept approach do not seem to be bothered by the fact that such a Wittgensteinian take has led some authors, like Richard Rorty, all the way down the path of radical relativism, a position that many philosophers of science reject. Then again, Fasce himself acknowledges that “Perhaps the authors who seek to carry out the demarcation of pseudoscience by means of family resemblance definitions do not follow Wittgenstein in all his philosophical commitments” (2019, 64).
Because of his dissatisfaction with gradualist interpretations of the science-pseudoscience landscape, Fasce (2019, 67) proposes what he calls a “metacriterion” to aid in the demarcation project. This is actually a set of four criteria, two of which he labels “procedural requirements” and two “criterion requirements.” The latter two are mandatory for demarcation, while the first two are not necessary, although they provide conditions of plausibility. The procedural requirements are: (i) that demarcation criteria should entail a minimum number of philosophical commitments; and (ii) that demarcation criteria should explain current consensus about what counts as science or pseudoscience. The criterion requirements are: (iii) that mimicry of science is a necessary condition for something to count as pseudoscience; and (iv) that all items of demarcation criteria be discriminant with respect to science.
Fasce (2018) has used his metacriterion to develop a demarcation criterion according to which pseudoscience: (1) refers to entities and/or processes outside the domain of science; (2) makes use of a deficient methodology; (3) is not supported by evidence; and (4) is presented as scientific knowledge. This turns out to be similar to a previous proposal by Hansson (2009). Fasce and Picó (2019) have also developed a scale of pseudoscientific belief based on the work discussed above.
Another author pushing a multicriterial approach to demarcation is Damian Fernandez‐Beanato (2020b), whom this article already mentioned when discussing Cicero’s early debunking of divination. He provides a useful summary of previous mono-criterial proposals, as well as of two multicriterial ones advanced by Hempel (1951) and Kuhn (1962). The failure of these attempts is what in part led to the above-mentioned rejection of the entire demarcation project by Laudan (1983).
Fernandez‐Beanato suggests improvements on a multicriterial approach originally put forth by Mahner (2007), consisting of a broad list of accepted characteristics or properties of science. The project, however, runs into significant difficulties for a number of reasons. First, like Fasce (2019), Fernandez-Beanato wishes for more precision than is likely possible, in his case aiming at a quantitative “cut value” on a multicriterial scale that would make it possible to distinguish science from non-science or pseudoscience in a way that is compatible with classical logic. It is hard to imagine how such quantitative estimates of “scientificity” may be obtained and operationalized. Second, the approach assumes a unity of science that is at odds with the above-mentioned emerging consensus in philosophy of science that “science” (and, similarly, “pseudoscience”) actually picks a family of related activities, not a single epistemic practice. Third, Fernandez-Beanato rejects Hansson’s (and other authors’) notion that any demarcation criterion is, by necessity, temporally limited because what constitutes science or pseudoscience changes with our understanding of phenomena. But it seems hard to justify Fernandez-Beanato’s assumption that “Science … is currently, in general, mature enough for properties related to method to be included into a general and timeless definition of science” (Fernandez-Beanato 2020b, 384).
Kåre Letrud (2019), like Fasce (2019), seeks to improve on Hansson’s (2009) approach to demarcation, but from a very different perspective. He points out that Hansson’s original answer to the demarcation problem focuses on pseudoscientific statements, not disciplines. The problem with this, according to Letrud, is that Hansson’s approach does not take into sufficient account the sociological aspect of the science-pseudoscience divide. Moreover, following Hansson—again according to Letrud—one would get trapped into a never-ending debunking of individual (as distinct from systemic) pseudoscientific claims. Here Letrud invokes the “Bullshit Asymmetry Principle,” also known as “Brandolini’s Law” (named after the Italian programmer Alberto Brandolini, to which it is attributed): “The amount of energy needed to refute BS is an order of magnitude bigger than to produce it.” Going pseudoscientific statement by pseudoscientific statement, then, is a losing proposition.
Letrud notes that Hansson (2009) adopts a broad definition of “science,” along the lines of the German Wissenschaft, which includes the social sciences and the humanities. While Fasce (2019) thinks this is problematically too broad, Letrud (2019) points out that a broader view of science implies a broader view of pseudoscience, which allows Hansson to include in the latter not just standard examples like astrology and homeopathy, but also Holocaust denialism, Bible “codes,” and so forth.
According to Letrud, however, Hansson’s original proposal does not do a good job differentiating between bad science and pseudoscience, which is important because we do not want to equate the two. Letrud suggests that bad science is characterized by discrete episodes of epistemic failure, which can occur even within established sciences. Pseudoscience, by contrast, features systemic epistemic failure. Bad science can even give rise to what Letrud calls “scientific myth propagation,” as in the case of the long-discredited notion that there are such things as learning styles in pedagogy. It can take time, even decades, to correct examples of bad science, but that does not ipso facto make them instances of pseudoscience.
Letrud applies Lakatos’s (1978) distinction of core vs. auxiliary statements for research programs to core vs. auxiliary statements typical of pseudosciences like astrology or homeopathy, thus bridging the gap between Hansson’s focus on individual statements and Letrud’s preferred focus on disciplines. For instance: “One can be an astrologist while believing that Virgos are loud, outgoing people (apparently, they are not). But one cannot hold that the positions of the stars and the character and behavior of people are unrelated” (Letrud 2019, 8). The first statement is auxiliary, the second, core.
To take homeopathy as an example, a skeptic could decide to spend an inordinate amount of time (according to Brandolini’s Law) debunking individual statements made by homeopaths. Or, more efficiently, the skeptic could target the two core principles of the discipline, namely potentization theory (that is, the notion that more diluted solutions are more effective) and the hypothesis that water holds a “memory” of substances once present in it. Letrud’s approach, then, retains the power of Hansson’s, but zeros in on the more foundational weakness of pseudoscience—its core claims—while at the same time satisfactorily separating pseudoscience from regular bad science. The debate, however, is not over, as more recently Hansson (2020) has replied to Letrud emphasizing that pseudosciences are doctrines, and that the reason they are so pernicious is precisely their doctrinal resistance to correction.
5. Pseudoscience as BS
One of the most intriguing papers on demarcation to appear in the course of what this article calls the Renaissance of scholarship on the issue of pseudoscience is entitled “Bullshit, Pseudoscience and Pseudophilosophy,” authored by Victor Moberger (2020). Moberger has found a neat (and somewhat provocative) way to describe the profound similarity between pseudoscience and pseudophilosophy: in a technical philosophical sense, it is all BS.
Moberger takes his inspiration from the famous essay by Harry Frankfurt (2005), On Bullshit. As Frankfurt puts it: “One of the most salient features of our culture is that there is so much bullshit.” (2005, 1) Crucially, Frankfurt goes on to differentiate the BSer from the liar:
It is impossible for someone to lie unless he thinks he knows the truth. … A person who lies is thereby responding to the truth, and he is to that extent respectful of it. When an honest man speaks, he says only what he believes to be true; and for the liar, it is correspondingly indispensable that he consider his statements to be false. For the bullshitter, however, all these bets are off: he is neither on the side of the true nor on the side of the false. His eye is not on the facts at all, as the eyes of the honest man and of the liar are. … He does not care whether the things he says describe reality correctly. (2005, 55-56)
So, while both the honest person and the liar are concerned with the truth—though in opposite manners—the BSer is defined by his lack of concern for it. This lack of concern is of the culpable variety, so that it can be distinguished from other activities that involve not telling the truth, like acting. This means two important things: (i) BS is a normative concept, meaning that it is about how one ought to behave or not to behave; and (ii) the specific type of culpability that can be attributed to the BSer is epistemic culpability. As Moberger puts it, “the bullshitter is assumed to be capable of responding to reasons and argument, but fails to do so” (2020, 598) because he does not care enough.
Moberger does not make the connection in his paper, but since he focuses on BSing as an activity carried out by particular agents, and not as a body of statements that may be true or false, his treatment falls squarely into the realm of virtue epistemology (see below). We can all arrive at the wrong conclusion on a specific subject matter, or unwittingly defend incorrect notions. And indeed, to some extent we may all, more or less, be culpable of some degree of epistemic misconduct, because few if any people are the epistemological equivalent of sages, ideally virtuous individuals. But the BSer is pathologically epistemically culpable. He incurs epistemic vices and he does not care about it, so long as he gets whatever he wants out of the deal, be that to be “right” in a discussion, or to further his favorite a priori ideological position no matter what.
Accordingly, the charge of BSing—in the technical sense—has to be substantiated by serious philosophical analysis. The term cannot simply be thrown out there as an insult or an easy dismissal. For instance, when Kant famously disagreed with Hume on the role of reason (primary for Kant, subordinate to emotions for Hume) he could not just have labelled Hume’s position as BS and move on, because Hume had articulated cogent arguments in defense of his take on the subject.
On the basis of Frankfurt’s notion of BSing, Moberger carries out a general analysis of pseudoscience and even pseudophilosophy. He uses the term pseudoscience to refer to well-known examples of epistemic malpractice, like astrology, creationism, homeopathy, ufology, and so on. According to Moberger, the term pseudophilosophy, by contrast, picks out two distinct classes of behaviors. The first is what he refers to as “a seemingly profound type of academic discourse that is pursued primarily within the humanities and social sciences” (2020, 600), which he calls obscurantist pseudophilosophy. The second, a “less familiar kind of pseudophilosophy is usually found in popular scientific contexts, where writers, typically with a background in the natural sciences, tend to wander into philosophical territory without realizing it, and again without awareness of relevant distinctions and arguments” (2020, 601). He calls this scientistic (Boudry and Pigliucci 2017) pseudophilosophy.
The bottom line is that pseudoscience is BS with scientific pretensions, while pseudophilosophy is BS with philosophical pretensions. What pseudoscience and pseudophilosophy have in common, then, is BS. While both pseudoscience and pseudophilosophy suffer from a lack of epistemic conscientiousness, this lack manifests itself differently, according to Moberger. In the case of pseudoscience, we tend to see a number of classical logical fallacies and other reasoning errors at play. In the case of pseudophilosophy, instead, we see “equivocation due to conceptual impressionism, whereby plausible but trivial propositions lend apparent credibility to interesting but implausible ones.”
Moberger’s analysis provides a unified explanatory framework for otherwise seemingly disparate phenomena, such as pseudoscience and pseudophilosophy. And it does so in terms of a single, more fundamental, epistemic problem: BSing. He then proceeds by fleshing out the concept—for instance, differentiating pseudoscience from scientific fraud—and by responding to a range of possible objections to his thesis, for example that the demarcation of concepts like pseudoscience, pseudophilosophy, and even BS is vague and imprecise. It is so by nature, Moberger responds, adopting the already encountered Wittgensteinian view that complex concepts are inherently fuzzy.
Importantly, Moberger reiterates a point made by other authors before, and yet very much worth reiterating: any demarcation in terms of content between science and pseudoscience (or philosophy and pseudophilosophy), cannot be timeless. Alchemy was once a science, but it is now a pseudoscience. What is timeless is the activity underlying both pseudoscience and pseudophilosophy: BSing.
There are several consequences of Moberger’s analysis. First, that it is a mistake to focus exclusively, sometimes obsessively, on the specific claims made by proponents of pseudoscience as so many skeptics do. That is because sometimes even pseudoscientific practitioners get things right, and because there simply are too many such claims to be successfully challenged (again, Brandolini’s Law). The focus should instead be on pseudoscientific practitioners’ epistemic malpractice: content vs. activity.
Second, what is bad about pseudoscience and pseudophilosophy is not that they are unscientific, because plenty of human activities are not scientific and yet are not objectionable (literature, for instance). Science is not the ultimate arbiter of what has or does not have value. While this point is hardly controversial, it is worth reiterating, considering that a number of prominent science popularizers have engaged in this mistake.
Third, pseudoscience does not lack empirical content. Astrology, for one, has plenty of it. But that content does not stand up to critical scrutiny. Astrology is a pseudoscience because its practitioners do not seem to be bothered by the fact that their statements about the world do not appear to be true.
One thing that is missing from Moberger’s paper, perhaps, is a warning that even practitioners of legitimate science and philosophy may be guilty of gross epistemic malpractice when they criticize their pseudo counterparts. Too often so-called skeptics reject unusual or unorthodox claims a priori, without critical analysis or investigation, for example in the notorious case of the so-called Campeche UFOs (Pigliucci, 2018, 97-98). From a virtue epistemological perspective, it comes down to the character of the agents. We all need to push ourselves to do the right thing, which includes mounting criticisms of others only when we have done our due diligence to actually understand what is going on. Therefore, a small digression into how virtue epistemology is relevant to the demarcation problem now seems to be in order.
6. Virtue Epistemology and Demarcation
Just like there are different ways to approach virtue ethics (for example, Aristotle, the Stoics), so there are different ways to approach virtue epistemology. What these various approaches have in common is the assumption that epistemology is a normative (that is, not merely descriptive) discipline, and that intellectual agents (and their communities) are the sources of epistemic evaluation.
The assumption of normativity very much sets virtue epistemology as a field at odds with W.V.O. Quine’s famous suggestion that epistemology should become a branch of psychology (see Naturalistic Epistemology): that is, a descriptive, not prescriptive discipline. That said, however, virtue epistemologists are sensitive to input from the empirical sciences, first and foremost psychology, as any sensible philosophical position ought to be.
A virtue epistemological approach—just like its counterpart in ethics—shifts the focus away from a “point of view from nowhere” and onto specific individuals (and their communities), who are treated as epistemic agents. In virtue ethics, the actions of a given agent are explained in terms of the moral virtues (or vices) of that agent, like courage or cowardice. Analogously, in virtue epistemology the judgments of a given agent are explained in terms of the epistemic virtues of that agent, such as conscientiousness, or gullibility.
Just like virtue ethics has its roots in ancient Greece and Rome, so too can virtue epistemologists claim a long philosophical pedigree, including but not limited to Plato, Aristotle, the Stoics, Thomas Aquinas, Descartes, Hume, and Bertrand Russell.
But what exactly is a virtue, in this context? Again, the analogy with ethics is illuminating. In virtue ethics, a virtue is a character trait that makes the agent an excellent, meaning ethical, human being. Similarly, in virtue epistemology a virtue is a character trait that makes the agent an excellent cognizer. Here is a partial list of epistemological virtues and vices to keep handy:
| Epistemic virtues | Epistemic vices |
| Attentiveness | Close-mindedness |
| Benevolence (that is, principle of charity) | Dishonesty |
| Conscentiousness | Dogmatism |
| Creativity | Gullibility |
| Curiosity | Naïveté |
| Discernment | Obtuseness |
| Honesty | Self-deception |
| Humility | Superficiality |
| Objectivity | Wishful thinking |
| Parsimony | |
| Studiousness | |
| Understanding | |
| Warrant | |
| Wisdom |
Linda Zagzebski (1996) has proposed a unified account of epistemic and moral virtues that would cast the entire science-pseudoscience debate in more than just epistemic terms. The idea is to explicitly bring to epistemology the same inverse approach that virtue ethics brings to moral philosophy: analyzing right actions (or right beliefs) in terms of virtuous character, instead of the other way around.
For Zagzebski, intellectual virtues are actually to be thought of as a subset of moral virtues, which would make epistemology a branch of ethics. The notion is certainly intriguing: consider a standard moral virtue, like courage. It is typically understood as being rooted in the agent’s motivation to do good despite the risk of personal danger. Analogously, the virtuous epistemic agent is motivated by wanting to acquire knowledge, in pursuit of which goal she cultivates the appropriate virtues, like open-mindedness.
In the real world, sometimes virtues come in conflict with each other, for instance in cases where the intellectually bold course of action is also not the most humble, thus pitting courage and humility against each other. The virtuous moral or epistemic agent navigates a complex moral or epistemic problem by adopting an all-things-considered approach with as much wisdom as she can muster. Knowledge itself is then recast as a state of belief generated by acts of intellectual virtue.
Reconnecting all of this more explicitly with the issue of science-pseudoscience demarcation, it should now be clearer why Moberger’s focus on BS is essentially based on a virtue ethical framework. The BSer is obviously not acting virtuously from an epistemic perspective, and indeed, if Zagzebski is right, also from a moral perspective. This is particularly obvious in the cases of pseudoscientific claims made by, among others, anti-vaxxers and climate change denialists. It is not just the case that these people are not being epistemically conscientious. They are also acting unethically because their ideological stances are likely to hurt others.
A virtue epistemological approach to the demarcation problem is explicitly adopted in a paper by Sindhuja Bhakthavatsalam and Weimin Sun (2021), who both provide a general outline of how virtue epistemology may be helpful concerning science-pseudoscience demarcation. The authors also explore in detail the specific example of the Chinese practice of Feng Shui, a type of pseudoscience employed in some parts of the world to direct architects to build in ways that maximize positive “qi” energy.
Bhakthavatsalam and Sun argue that discussions of demarcation do not aim solely at separating the usually epistemically reliable products of science from the typically epistemically unreliable ones that come out of pseudoscience. What we want is also to teach people, particularly the general public, to improve their epistemic judgments so that they do not fall prey to pseudoscientific claims. That is precisely where virtue epistemology comes in.
Bhakthavatsalam and Sun build on work by Anthony Derksen (1993) who arrived at what he called an epistemic-social-psychological profile of a pseudoscientist, which in turn led him to a list of epistemic “sins” that pseudoscientists regularly engage in: lack of reliable evidence for their claims; arbitrary “immunization” from empirically based criticism (Boudry and Braeckman 2011); assigning outsized significance to coincidences; adopting magical thinking; contending to have special insight into the truth; tendency to produce all-encompassing theories; and uncritical pretension in the claims put forth.
Conversely, one can arrive at a virtue epistemological understanding of science and other truth-conducive epistemic activities. As Bhakthavatsalam and Sun (2021, 6) remind us: “Virtue epistemologists contend that knowledge is non‐accidentally true belief. Specifically, it consists in belief of truth stemming from epistemic virtues rather than by luck. This idea is captured well by Wayne Riggs (2009): knowledge is an ‘achievement for which the knower deserves credit.’”
Bhakthavatsalam and Sun discuss two distinct yet, in their mind, complementary (especially with regard to demarcation) approaches to virtue ethics: virtue reliabilism and virtue responsibilism. Briefly, virtue reliabilism (Sosa 1980, 2011) considers epistemic virtues to be stable behavioral dispositions, or competences, of epistemic agents. In the case of science, for instance, such virtues might include basic logical thinking skills, the ability to properly collect data, the ability to properly analyze data, and even the practical know-how necessary to use laboratory or field equipment. Clearly, these are precisely the sort of competences that are not found among practitioners of pseudoscience. But why not? This is where the other approach to virtue epistemology, virtue responsibilism, comes into play.
Responsibilism is about identifying and practicing epistemic virtues, as well as identifying and staying away from epistemic vices. The virtues and vices in question are along the lines of those listed in the table above. Of course, we all (including scientists and philosophers) engage in occasionally vicious, or simply sloppy, epistemological practices. But what distinguishes pseudoscientists is that they systematically tend toward the vicious end of the epistemic spectrum, while what characterizes the scientific community is a tendency to hone epistemic virtues, both by way of expressly designed training and by peer pressure internal to the community. Part of the advantage of thinking in terms of epistemic vices and virtues is that one then puts the responsibility squarely on the shoulders of the epistemic agent, who becomes praiseworthy or blameworthy, as the case may be.
Moreover, a virtue epistemological approach immediately provides at least a first-level explanation for why the scientific community is conducive to the truth while the pseudoscientific one is not. In the latter case, comments Cassam:
The fact that this is how [the pseudoscientist] goes about his business is a reflection of his intellectual character. He ignores critical evidence because he is grossly negligent, he relies on untrustworthy sources because he is gullible, he jumps to conclusions because he is lazy and careless. He is neither a responsible nor an effective inquirer, and it is the influence of his intellectual character traits which is responsible for this. (2016, 165)
In the end, Bhakthavatsalam and Sun arrive, by way of their virtue epistemological approach, to the same conclusion that we have seen other authors reach: both science and pseudoscience are Wittgensteinian-type cluster concepts. But virtue epistemology provides more than just a different point of view on demarcation. First, it identifies specific behavioral tendencies (virtues and vices) the cultivation (or elimination) of which yield epistemically reliable outcomes. Second, it shifts the responsibility to the agents as well as to the communal practices within which such agents operate. Third, it makes it possible to understand cases of bad science as being the result of scientists who have not sufficiently cultivated or sufficiently regarded their virtues, which in turn explains why we find the occasional legitimate scientist who endorses pseudoscientific notions.
How do we put all this into practice, involving philosophers and scientists in the sort of educational efforts that may help curb the problem of pseudoscience? Bhakthavatsalam and Sun articulate a call for action at both the personal and the systemic levels. At the personal level, we can virtuously engage with both purveyors of pseudoscience and, likely more effectively, with quasi-neutral bystanders who may be attracted to, but have not yet bought into, pseudoscientific notions. At the systemic level, we need to create the sort of educational and social environment that is conducive to the cultivation of epistemic virtues and the eradication of epistemic vices.
Bhakthavatsalam and Sun are aware of the perils of engaging defenders of pseudoscience directly, especially from the point of view of virtue epistemology. It is far too tempting to label them as “vicious,” lacking in critical thinking, gullible, and so forth and be done with it. But basic psychology tells us that this sort of direct character attack is not only unlikely to work, but near guaranteed to backfire. Bhakthavatsalam and Sun claim that we can “charge without blame” since our goal is “amelioration rather than blame” (2021, 15). But it is difficult to imagine how someone could be charged with the epistemic vice of dogmatism and not take that personally.
Far more promising are two different avenues: the systemic one, briefly discussed by Bhakthavatsalam and Sun, and the personal not in the sense of blaming others, but rather in the sense of modeling virtuous behavior ourselves.
In terms of systemic approaches, Bhakthavatsalam and Sun are correct that we need to reform both social and educational structures so that we reduce the chances of generating epistemically vicious agents and maximize the chances of producing epistemically virtuous ones. School reforms certainly come to mind, but also regulation of epistemically toxic environments like social media.
As for modeling good behavior, we can take a hint from the ancient Stoics, who focused not on blaming others, but on ethical self-improvement:
If a man is mistaken, instruct him kindly and show him his error. But if you are not able, blame yourself, or not even yourself. (Marcus Aurelius, Meditations, X.4)
A good starting point may be offered by the following checklist, which—in agreement with the notion that good epistemology begins with ourselves—is aimed at our own potential vices. The next time you engage someone, in person or especially on social media, ask yourself the following questions:
- Did I carefully consider the other person’s arguments without dismissing them out of hand?
- Did I interpret what they said in a charitable way before mounting a response?
- Did I seriously entertain the possibility that I may be wrong? Or am I too blinded by my own preconceptions?
- Am I an expert on this matter? If not, did I consult experts, or did I just conjure my own unfounded opinion?
- Did I check the reliability of my sources, or just google whatever was convenient to throw at my interlocutor?
- After having done my research, do I actually know what I’m talking about, or am I simply repeating someone else’s opinion?
After all, as Aristotle said: “Piety requires us to honor truth above our friends” (Nicomachean Ethics, book I), though some scholars suggested that this was a rather unvirtuous comment aimed at his former mentor, Plato.
7. The Scientific Skepticism Movement
One of the interesting characteristics of the debate about science-pseudoscience demarcation is that it is an obvious example where philosophy of science and epistemology become directly useful in terms of public welfare. This, in other words, is not just an exercise in armchair philosophizing; it has the potential to affect lives and make society better. This is why we need to take a brief look at what is sometimes referred to as the skeptic movement—people and organizations who have devoted time and energy to debunking and fighting pseudoscience. Such efforts could benefit from a more sophisticated philosophical grounding, and in turn philosophers interested in demarcation would find their work to be immediately practically useful if they participated in organized skepticism.
That said, it was in fact a philosopher, Paul Kurtz, who played a major role in the development of the skeptical movement in the United States. Kurtz, together with Marcello Truzzi, founded the Committee for the Scientific Investigation of Claims of the Paranormal (CSICOP), in Amherst, New York in 1976. The organization changed its name to the Committee for Skeptical Inquiry (CSI) in November 2006 and has long been publishing the premier world magazine on scientific skepticism, Skeptical Inquirer. These groups, however, were preceded by a long history of skeptic organizations outside the US. The oldest skeptic organization on record is the Dutch Vereniging tegen de Kwakzalverij (VtdK), established in 1881. This was followed by the Belgian Comité Para in 1949, started in response to a large predatory industry of psychics exploiting the grief of people who had lost relatives during World War II.
In the United States, Michael Shermer, founder and editor of Skeptic Magazine, traced the origin of anti-pseudoscience skepticism to the publication of Martin Gardner’s Fads and Fallacies in the Name of Science in 1952. The French Association for Scientific Information (AFIS) was founded in 1968, and a series of groups got started worldwide between 1980 and 1990, including Australian Skeptics, Stichting Skepsis in the Netherlands, and CICAP in Italy. In 1996, the magician James Randi founded the James Randi Educational Foundation, which established a one-million-dollar prize to be given to anyone who could reproduce a paranormal phenomenon under controlled conditions. The prize was never claimed.
After the fall of the Berlin Wall, a series of groups began operating in Russia and its former satellites in response to yet another wave of pseudoscientific claims. This led to skeptic organizations in the Czech Republic, Hungary, and Poland, among others. The European Skeptic Congress was founded in 1989, and a number of World Skeptic Congresses have been held in the United States, Australia, and Europe.
Kurtz (1992) characterized scientific skepticism in the following manner: “Briefly stated, a skeptic is one who is willing to question any claim to truth, asking for clarity in definition, consistency in logic, and adequacy of evidence.” This differentiates scientific skepticism from ancient Pyrrhonian Skepticism, which famously made no claim to any opinion at all, but it makes it the intellectual descendant of the Skepticism of the New Academy as embodied especially by Carneades and Cicero (Machuca and Reed 2018).
One of the most famous slogans of scientific skepticism “Extraordinary claims require extraordinary evidence” was first introduced by Truzzi. It can easily be seen as a modernized version of David Hume’s (1748, Section X: Of Miracles; Part I. 87.) dictum that a wise person proportions his beliefs to the evidence and has been interpreted as an example of Bayesian thinking (McGrayne 2011).
According to another major, early exponent of scientific skepticism, astronomer Carl Sagan: “The question is not whether we like the conclusion that emerges out of a train of reasoning, but whether the conclusion follows from the premises or starting point and whether that premise is true” (1995).
Modern scientific skeptics take full advantage of the new electronic tools of communication. Two examples in particular are the Skeptics’ Guide to the Universe podcast published by Steve Novella and collaborators, which regularly reaches a large audience and features interviews with scientists, philosophers, and skeptic activists; and the “Guerrilla Skepticism” initiative coordinated by Susan Gerbic, which is devoted to the systematic improvement of skeptic-related content on Wikipedia.
Despite having deep philosophical roots, and despite that some of its major exponents have been philosophers, scientific skepticism has an unfortunate tendency to find itself far more comfortable with science than with philosophy. Indeed, some major skeptics, such as author Sam Harris and scientific popularizers Richard Dawkins and Neil deGrasse Tyson, have been openly contemptuous of philosophy, thus giving the movement a bit of a scientistic bent. This is somewhat balanced by the interest in scientific skepticism of a number of philosophers (for instance, Maarten Boudry, Lee McIntyre) as well as by scientists who recognize the relevance of philosophy (for instance, Carl Sagan, Steve Novella).
Given the intertwining of not just scientific skepticism and philosophy of science, but also of social and natural science, the theoretical and practical study of the science-pseudoscience demarcation problem should be regarded as an extremely fruitful area of interdisciplinary endeavor—an endeavor in which philosophers can make significant contributions that go well beyond relatively narrow academic interests and actually have an impact on people’s quality of life and understanding of the world.
8. References and Further Readings
- Armando, D. and Belhoste, B. (2018) Mesmerism Between the End of the Old Regime and the Revolution: Social Dynamics and Political Issues. Annales historiques de la Révolution française 391(1):3-26
- Baum, R. and Sheehan, W. (1997) In Search of Planet Vulcan: The Ghost in Newton’s Clockwork Universe. Plenum.
- Bhakthavatsalam, S. and Sun, W. (2021) A Virtue Epistemological Approach to the Demarcation Problem: Implications for Teaching About Feng Shui in Science Education. Science & Education 30:1421-1452. https://doi.org/10.1007/s11191-021-00256-5.
- Bloor, D. (1976) Knowledge and Social Imagery. Routledge & Kegan Paul.
- Bonk, T. (2008) Underdetermination: An Essay on Evidence and the Limits of Natural Knowledge. Springer.
- Boudry, M. and Braeckman, J. (2011) Immunizing Strategies and Epistemic Defense Mechanisms. Philosophia 39(1):145-161.
- Boudry, M. and Pigliucci, M. (2017) Science Unlimited? The Challenges of Scientism. University of Chicago Press.
- Brulle, R.J. (2020) Denialism: Organized Opposition to Climate Change Action in the United States, in: D.M. Konisky (ed.) Handbook of U.S. Environmental Policy, Edward Elgar, chapter 24.
- Carlson, S. (1985) A Double-Blind Test of Astrology. Nature 318:419-25.
- Cassam, Q. (2016) Vice Epistemology. The Monist 99(2):159-180.
- Cicero (2014) On Divination, in: Cicero—Complete Works, translated by W.A. Falconer, Delphi.
- Curd, M. and Cover, J.A. (eds.) (2012) The Duhem-Quine Thesis and Underdetermination, in: Philosophy of Science: The Central Issues. Norton, pp. 225-333.
- Dawes, G.W. (2018) Identifying Pseudoscience: A Social Process Criterion. Journal of General Philosophy of Science 49:283-298.
- Derksen, A.A. (1993) The Seven Sins of Demarcation. Journal for General Philosophy of Science 24:17-42.
- Dupré, J. (1993) The Disorder of Things: Metaphysical Foundations of the Disunity of Science. Harvard University Press.
- Fasce, A. (2018) What Do We Mean When We Speak of Pseudoscience? The Development of a Demarcation Criterion Based on the Analysis of Twenty-One Previous Attempts. Disputatio 6(7):459-488.
- Fasce, A. (2019) Are Pseudosciences Like Seagulls? A Discriminant Metacriterion Facilitates the Solution of the Demarcation Problem. International Studies in the Philosophy of Science 32(3-4):155-175.
- Fasce, A. and Picó, A. (2019) Conceptual Foundations and Aalidation of the Pseudoscientific Belief Scale. Applied Cognitive Psychology 33(4):617-628.
- Feldman, R. (1981) Fallibilism and Knowing that One Knows, The Philosophical Review 90:266-282.
- Fernandez-Beanato, D. (2020a) Cicero’s Demarcation of Science: A Report of Shared Criteria. Studies in History and Philosophy of Science Part A 83:97-102.
- Fernandez-Beanato, D. (2020b) The Multicriterial Approach to the Problem of Demarcation. Journal for General Philosophy of Science 51:375-390.
- Feyerabend, P. (1975) Against Method: Outline of an Anarchistic Theory of Knowledge. New Left Books.
- Frankfurt, H. (2005) On Bullshit. Princeton University Press.
- Gardner, M. (1952) Fads and Fallacies in the Name of Science. Dover.
- Gauch, H.G. (2012) Scientific Method in Brief. Cambridge University Press.
- Gould, S.J. (1989) The Chain of Reason vs. The Chain of Thumbs, Natural History, 89(7):16.
- Grosser, M. (1962) The Discovery of Neptune. Harvard University Press.
- Hansson, S.O. (2009) Cutting the Gordian Knot of Demarcation. International Studies in the Philosophy of Science 23(3):237-243.
- Hansson, S.O. (2013) Defining Pseudoscience—and Science, in: M. Pigliucci and M. Boudry (eds.), The Philosophy of Pseudoscience. University of Chicago University Press, pp. 61-77.
- Hansson, S.O. (2017) Science Denial as a Form of Pseudoscience. Studies in History and Philosophy of Science 63:39-47.
- Hansson, S.O. (2020) Disciplines, Doctrines, and Deviant Science. International Studies in the Philosophy of Science 33(1):43-52.
- Hausman, A., Boardman, F., and Kahane, H. (2021) Logic and Philosophy: A Modern Introduction. Hackett.
- Hempel, C.G. (1951) The Concept of Cognitive Significance: A Reconsideration. Proceedings of the American Academy of Arts and Sciences 80:61–77.
- Hossenfelder, S. (2018) Lost in Math: How Beauty Leads Physics Astray. Basic Books.
- Hume, D. (1748) An Enquiry Concerning Human Understanding, online at https://davidhume.org/texts/e/.
- Jeffers, S. (2007) PEAR Lab Closes, Ending Decades of Psychic Research. Skeptical Inquirer 31(3), online at https://skepticalinquirer.org/2007/05/pear-lab-closes-ending-decades-of-psychic-research/.
- Kaplan, J.M. (2006) More Misuses of Evolutionary Psychology. Metascience 15(1):177-181.
- Kennefick, D. (2019) No Shadow of a Doubt: The 1919 Eclipse That Confirmed Einstein’s Theory of Relativity. Princeton University Press.
- Kuhn, T. (1962) The Structure of Scientific Revolutions. University of Chicago Press.
- Kurtz, P. (1992) The New Skepticism. Prometheus.
- LaFollette, M. (1983) Creationism, Science and the Law. MIT Press.
- Lakatos, I. (1978) The Methodology of Scientific Research Programmes. Cambridge University Press.
- Laudan, L. (1983) The Demise of the Demarcation Problem, in: R.S. Cohen and L. Laudan (eds.), Physics, Philosophy and Psychoanalysis. D. Reidel, pp. 111–127.
- Laudan, L. (1988) Science at the Bar—Causes for Concern. In M. Ruse (ed.), But Is It Science? Prometheus.
- Letrud, K. (2019) The Gordian Knot of Demarcation: Tying Up Some Loose Ends. International Studies in the Philosophy of Science 32(1):3-11.
- Machuca, D.E. and Reed, B. (2018) Skepticism: From Antiquity to the Present. Bloomsbury Academic.
- Mahner, M. (2007) Demarcating Science from Non-Science, in: T. Kuipers (ed.), Handbook of the Philosophy of Science: General Philosophy of Science—Focal Issues. Elsevier, pp. 515-575.
- McGrayne, S.B. (2011) The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines, and Emerged Triumphant from Two Centuries of Controversy. Yale University Press.
- Merton, R.K. (1973) The Normative Structure of Science, in: N.W. Storer (ed.), The Sociology of Science: Theoretical and Empirical Investigations. University of Chicago Press, pp. 267-278.
- Moberger, V. (2020) Bullshit, Pseudoscience and Pseudophilosophy. Theoria 86(5):595-611.
- Navin, M. (2013) Competing Epistemic Spaces. How Social Epistemology Helps Explain and Evaluate Vaccine Denialism. Social Theory and Practice 39(2):241-264.
- Pigliucci, M. (2013) The Demarcation Problem: A (Belated) Response to Laudan, in: M. Pigliucci and M. Boudry (eds.), The Philosophy of Pseudoscience. University of Chicago Press, pp. 9-28.
- Pigliucci, M. (2017) Philosophy as the Evocation of Conceptual Landscapes, in: R. Blackford and D. Broderick (eds.), Philosophy’s Future: The Problem of Philosophical Progress. John Wiley & Sons, pp. 75-90.
- Pigliucci, M. (2018) Nonsense on Stilts, 2nd edition. University of Chicago Press, pp. 97-98.
- Pigliucci, M. and Boudry, M. (eds.) (2013) The Philosophy of Pseudoscience: Reconsidering the Demarcation Problem. University of Chicago Press.
- Plato (1986) Charmides. Translated by T.G. West and G.S. West, Hackett Classics.
- Popper, K. (1959) The Logic of Scientific Discovery. Hutchinson.
- Riggs, W. (2009) Two Problems of Easy Credit. Synthese 169(1):201-216.
- Sagan, C. (1995) The Demon Haunted World. Ballantine.
- Salas D. and Salas, D. (translators) (1996) The First Scientific Investigation of the Paranormal Ever Conducted, Commissioned by King Louis XVI. Designed, conducted, & written by Benjamin Franklin, Antoine Lavoisier, & Others. Skeptic (Fall), pp.68-83.
- Shea, B. (no date) Karl Popper: Philosophy of Science. Internet Encyclopedia of Philosophy. https://iep.utm.edu/pop-sci/
- Smith, T.C. and Novella, S.P. (2007) HIV Denial in the Internet Era. PLOS Medicine, https://doi.org/10.1371/journal.pmed.0040256.
- Sosa, E. (1980) The Raft and the Pyramid: Coherence versus Foundations in the Theory of Knowledge. Midwest Studies in Philosophy 5(1):3-26.
- Sosa, E. (2011) Knowing Full Well. Princeton University Press.
- Wittgenstein, L. (1958) Philosophical Investigations. Blackwell.
- Zagzebski, L.T. (1996) Virtues of the Mind: An Inquiry into the Nature of Virtue and the Ethical Foundations of Knowledge. Cambridge University Press.
Author Information
Massimo Pigliucci
Email: mpigliucci@ccny.cuny.edu
The City College of New York
U. S. A.




 All B is either o or i.
All B is either o or i.

 Darii
Darii Ferio
Ferio 2nd Figure
2nd Figure Camestres
Camestres Festino
Festino Baroco
Baroco 3rd Figure
3rd Figure Felapton
Felapton Disamis
Disamis Datisi
Datisi Bocardo
Bocardo Ferison
Ferison
 Dimatis
Dimatis
 Bamalip
Bamalip Fresison
Fresison




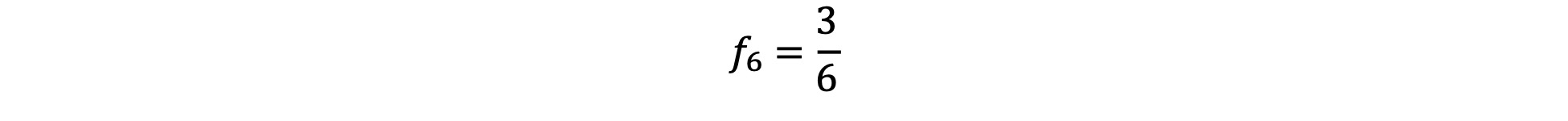
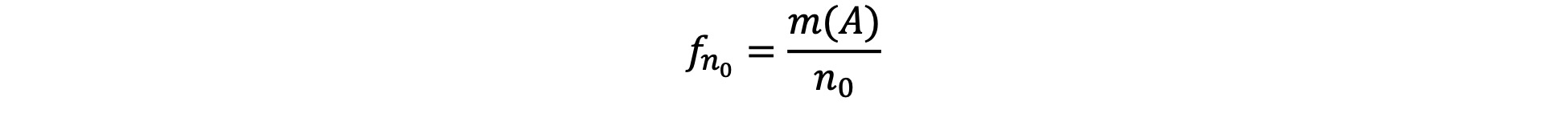
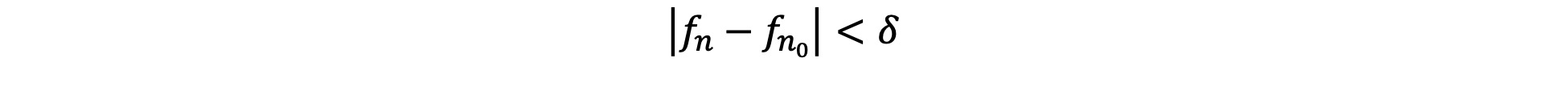
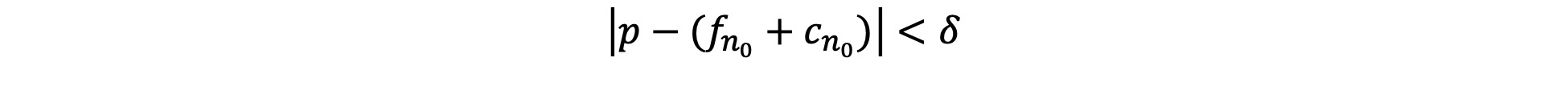
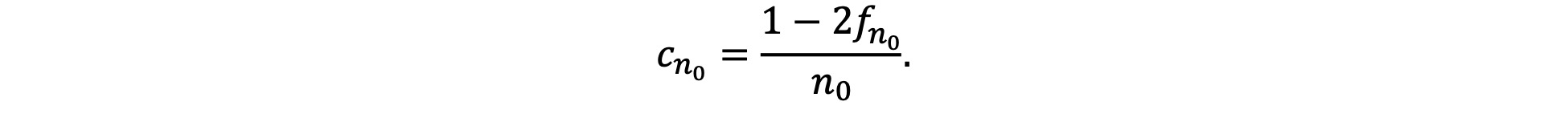





 In the fifth century B.C.E., Zeno offered arguments that led to conclusions contradicting what we all know from our physical experience—that runners run, that arrows fly, and that there are many different things in the world. The arguments were paradoxes for the ancient Greek philosophers. Because many of Zeno’s arguments turn crucially on the notion that space and time are infinitely divisible, he was the first person to show that the concept of
In the fifth century B.C.E., Zeno offered arguments that led to conclusions contradicting what we all know from our physical experience—that runners run, that arrows fly, and that there are many different things in the world. The arguments were paradoxes for the ancient Greek philosophers. Because many of Zeno’s arguments turn crucially on the notion that space and time are infinitely divisible, he was the first person to show that the concept of