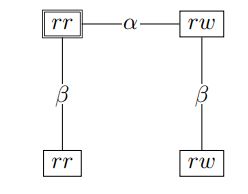
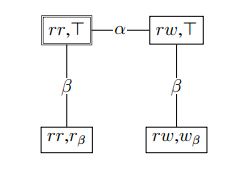
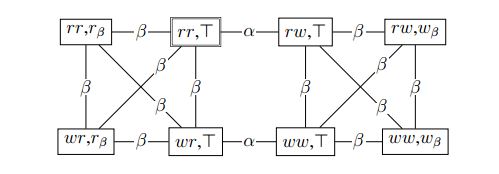
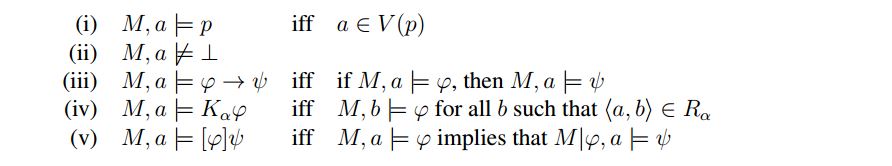Thick Concepts
A term expresses a thick concept if it expresses a specific evaluative concept that is also substantially descriptive. It is a matter of debate how this rough account should be unpacked, but examples can help to convey the basic idea. Thick concepts are often illustrated with virtue concepts like courageous and generous, action concepts like murder and betray, epistemic concepts like dogmatic and wise, and aesthetic concepts like gaudy and brilliant. These concepts seem to be evaluative, unlike purely descriptive concepts such as red and water. But they also seem different from general evaluative concepts. In particular, thick concepts are typically contrasted with thin concepts like good, wrong, permissible, and ought, which are general evaluative concepts that do not seem substantially descriptive. When Jane says that Max is good, she appears to be evaluating him without providing much description, if any. Thick concepts, on the other hand, are evaluative and substantially descriptive at the same time. For instance, when Max says that Jane is courageous, he seems to be doing two things: evaluating her positively and describing her as willing to face risk. Because of their descriptiveness, thick concepts are especially good candidates for evaluative concepts that pick out properties in the world. Thus they provide an avenue for thinking about ethical claims as being about the world in the same way as descriptive claims.
Thick concepts became a focal point in ethics during the second half of the twentieth century. At that time, discussions of thick concepts began to emerge in response to certain disagreements about thin concepts. For example, in twentieth-century ethics, consequentialists and deontologists hotly debated various accounts of good and right. It was also claimed by non-cognitivists and error-theorists that these thin concepts do not correspond to any properties in the world. Dissatisfaction with these viewpoints prompted many ethicists to consider the implications of thick concepts. The notion of a thick concept was thought to provide insight into meta-ethical questions such as whether there is a fact-value distinction, whether there are ethical truths, and, if there are such truths, whether these truths are objective. Some ethicists also theorized about the role that thick concepts can play in normative ethics, such as in virtue theory. By the beginning of the twenty-first century, the interest in thick concepts had spread to other philosophical disciplines such as epistemology, aesthetics, metaphysics, moral psychology, and the philosophy of law.
Nevertheless, the emerging interest in thick concepts has sparked debates over many questions: How exactly are thick concepts evaluative? How do they combine evaluation and description? How are thick concepts related to thin concepts? And do thick concepts have the sort of significance commonly attributed to them? This article surveys various attempts at answering these questions.
Table of Contents
- Background and Preliminaries
- Significance of Thick Concepts
- How Do Thick Concepts Combine Evaluation and Description?
- How Do Thick and Thin Differ?
- Are Thick Terms Truth-Conditionally Evaluative?
- Broader Applications
- References and Further Reading
1. Background and Preliminaries
Bernard Williams first introduced the phrase ‘thick concept’ in his 1985 book, Ethics and the Limits of Philosophy. Williams used this phrase to classify a number of ethical concepts that are plausibly controlled by the facts, such as treachery, brutality, and courage. But his use of the phrase was assimilated from Clifford Geertz’ notion of a thick description—an anthropologist’s tool for describing “a multiplicity of complex conceptual structures, many of them superimposed upon or knotted into one another” (1973:). Incidentally, Geertz borrowed the phrase ‘thick description’ from Gilbert Ryle, who took thick description to be a way of categorizing actions and personality traits by reference to intentions, desires, and beliefs (1971). Although Geertz’ and Ryle’s notions of thick description influenced Williams’ terminology, their notions did not necessarily involve evaluation. By contrast, Williams’ notion of a thick concept is bound up with both evaluation and description. Or, in Williams’ terms, thick concepts are both “action-guiding” and “guided by the world”. They are action-guiding in that they typically indicate the presence of reasons for action, and they are world-guided in that their correct application depends on how the world is (1985: 128, 140-41).
Although the phrase ‘thick concept’ first appeared in Williams’ Ethics and the Limits of Philosophy, there was a distinction between thick and thin that predated Williams’ 1985 book. In R.M. Hare’s The Language of Morals, published in 1952, Hare distinguished between primarily evaluative words and secondarily evaluative words (121-2). Hare later identified the former with thin terms, and the latter with thick terms (1997:54). So, the idea of a thick term was present in ethics well before Williams’ terminology.
Hare’s distinction between thick and thin is explicitly about words, and it makes no mention of concepts. But, in general, the literature on the thick speaks about both thick concepts and thick terms. Very roughly, concepts are on the level of propositions and meanings (broadly construed), whereas terms are the linguistic entities used to express these items. In this entry, expressions with single-quotes, for example ‘chaste’, will be used to designate terms. Italicized expressions, for example chaste, will be used to designate concepts. Thick concepts, then, can approximately be seen as the meanings of thick terms.
Thick and thin terms are two distinct subclasses of the evaluative. However, readers should exercise caution when encountering the phrase ‘thin term’, since some theorists allow wholly descriptive terms like ‘red’, ‘grass’, and ‘green’ to count as thin (for example, Elgin 2008: 372). Their usage of ‘thin’ diverges from prevailing philosophical jargon, where the thin is seen as a subclass of the evaluative. This article uses the prevailing jargon: on this way of speaking, there are no wholly descriptive thin terms.
It is typically claimed that thick terms are in some sense evaluative and descriptive, but what do these notions mean? The evaluative and the descriptive are normally meant to distinguish between two classes of terms. Descriptive terms can be illustrated with words like ‘red’, ‘solid’, ‘small’, ‘tall’, ‘water’, ‘cat’, and ‘hydrogen’. Paradigmatic evaluative terms include thin terms like ‘good’, ‘bad’, and ‘best’, as well as normative words like ‘ought’, ‘should’, ‘right’, and ‘wrong’. Although some theorists deny that there is any substantive difference between the descriptive and the evaluative (for example, Jackson 1998:120), on the face of it there is a difference. Various attempts have been made to account for this putative difference. Two general approaches are relevant for our purposes.
One approach stems from traditional non-cognitivism. On this view, descriptive terms express beliefs and are capable of picking out properties and facts. But paradigmatic evaluative terms, such as ‘good’ and ‘right’, have neither of these features. These terms do not express beliefs and are incapable of picking out properties and facts. Instead, the function of an evaluative term is to express and induce attitudes, or to commend, condemn, and instruct. Basically, for traditional non-cognitivism, descriptive expressions are capable of representing properties and facts, whereas evaluative one’s express attitudes or imperatives that cannot represent properties or facts. Since this version of the distinction denies that evaluations can be factual, we can call it the strong distinction.
The strong distinction is also known as the fact/value distinction. Thick terms are often seen as a problem for this distinction because they seem both descriptive and evaluative. Indeed, Williams holds that the world-guidedness of thick concepts “is enough to refute the simplest oppositions of fact and value” (1985:150).
There is also a weak distinction between description and evaluation, which is neutral on the question of whether evaluations can be factual. Proponents of this weak distinction may agree with the strong distinction regarding the primary function of evaluative terms. For example, they might agree that evaluative terms function to express and induce attitudes, or to commend, condemn, and instruct. However, they do not rule out the possibility that evaluations are also factual. What then distinguishes the evaluative from the descriptive? Simply put, descriptive terms are all the other predicates within a language—that is, descriptive terms just are non-evaluative. Since this distinction allows that evaluations can be factual, we can call it the weak distinction.
Thick terms are seen as significant because they straddle the above distinctions—they have something in common with both the evaluative and the descriptive. Consequently, thick terms raise interesting questions about whether there is value in the world and whether value claims can be inferred from factual ones. The main arguments and views in this vicinity are from Philippa Foot, John McDowell, and Bernard Williams, which are discussed next.
2. Significance of Thick Concepts
a. Foot’s Argument against the Is-Ought Gap
David Hume is often interpreted as holding that one cannot derive an ‘ought’ from an ‘is’, or more generally, that one cannot derive an evaluative statement from a purely descriptive statement. This view has some intuitive appeal. The basic thought is that evaluative statements can condemn, commend and instruct, whereas descriptive statements can do none of these things. So any inference from purely descriptive premises to an evaluative conclusion would involve a conclusion with content nowhere expressed in its premises. Hence, the inference as a result must be invalid. If we do have a valid inference to an evaluative conclusion, then the premises must somehow involve evaluative content, perhaps covertly. This claim that there are no conceptually valid inferences from purely descriptive premises to evaluative conclusions is known as the “is-ought gap”.
The is-ought gap may seem plausible when the evaluative conclusion employs thin terms like ‘right’ and ‘wrong’. Philippa Foot rejects the is-ought gap by focusing instead on an evaluative conclusion that employs a thick term: ‘rude.’ She points out that ‘rude’ should count as evaluative, because it seems to express an attitude, or to condemn, much like ‘bad’ and ‘wrong’. But, according to Foot, this evaluation can be derived from a description. Consider the description D1: that x causes offence by indicating a lack of respect. Can one accept D1 as true, but deny that x is rude? Foot thinks this denial would be inconsistent. If she is right, then a thick evaluative claim—that x is rude—can be derived from a descriptive claim (Foot 1958).
Foot’s argument is primarily aimed at non-cognitivists, like Hare. But Hare replies by considering an analogous inference involving a racial slur. To demonstrate Hare’s point, consider a racial slur like ‘gringo’, ‘kraut’, or ‘honky’. Most of us disagree with the attitude of contempt that is expressed by the slur ‘kraut’. But, according to Hare, an analogous inference would logically require us to accept that attitude—that is, to despise Germans. And this is absurd. Consider the descriptive claim D1*: that x is a native of Germany. Is it logically consistent for one to accept D1* as true but deny that x is a kraut? If the denial in Foot’s example is inconsistent, then, according to Hare’s thinking, it should also be inconsistent in this example. So, by Foot’s reasoning, D1* should entail ‘x is a kraut’. Moreover, ‘kraut’ is a term of contempt, which means that this conclusion entails that one must despise x. By the transitivity of entailment, it follows that an acceptance of D1* requires one to despise x, which is an unintuitive result. According to Hare, the two inferences are “identical in form.” So, there must be something wrong with both inferences (1963:188).
Where do the above inferences go wrong? Hare holds that people who reject the attitude associated with ‘kraut’ will substitute it with an evaluatively-neutral expression, such as ‘German’, which does not commit them to the attitude of contempt. So, people who accept D1* are not required to use the evaluative word ‘kraut’ in expressing the conclusion of the inference. Analogous points hold for ‘rude’. Hare concedes that we rarely have evaluatively-neutral expressions corresponding to paradigmatic thick terms, but he thinks such expressions are at least possible. After all, we could use ‘rude’ with a certain tone of voice or with scare-quotes around it, thereby indicating that we mean it in a purely descriptive sense (1963:188-89).
Hare’s response to Foot assumes that slurs are evaluative in the same way as thick terms. This, however, has been taken by some to be unintuitive. But Hare could modify his reply: instead of employing slurs he could use thick terms like ‘chaste’, ‘blasphemous’, ‘perverse’, and ‘lewd’, which are often called “objectionable thick terms”. Objectionable thick terms are terms that embody values that ought to be rejected. It is, of course, a matter of debate whether these thick terms really are objectionable. But Hare could run his argument by using thick terms that are commonly regarded as objectionable. Such terms seem to be evaluative in much the same way as ‘rude’. And, much like slurs, there are many people who reject the values embodied by such terms; these people are consequently reluctant to use the term in question. Notice that arguments like Foot’s would require such people to accept the values embodied by the thick terms they regard as objectionable, and this seems equally implausible. So, Hare’s basic reply need not assume any fundamental similarity between thick terms and slurs.
However, it is unclear that Hare has shown what he needs to show—that the relevant is-ought inferences are invalid. In particular, he has not shown that it’s possible for D1 to be true while ‘x is rude’ is false, or for D1* to be true while ‘x is a kraut’ is false. The mere fact that reluctant speakers will substitute the evaluative conclusions with neutral ones does not show that the evaluative conclusions are false. For instance, you may hate the word ‘prune’ and prefer to substitute it with ‘dried plum’, but that doesn’t mean it’s false that the thing in question is a prune (Foot 1958:509).
Hare could claim that the is-ought gap only exists on the level of concepts or propositions, not on the level of terms or sentences. This makes a difference because Hare holds that the evaluations of thick terms are detachable in the sense that there could be evaluatively-neutral expressions that are propositionally equivalent to sentences involving thick terms. Detachability is the upshot of Hare’s view that ‘German’ can be substituted for ‘kraut’. If the evaluations of thick terms are detachable, then they only attach to the terms, but are not entailed by the propositions expressed by such terms. So, there is no breach of the is-ought gap on the level of propositions. From D1, one can infer the proposition that x is German. And this proposition can also be expressed by using the term ‘kraut’. But one cannot infer a negative evaluation from this proposition; the negative evaluation is only inferable from uses the term ‘kraut’, not from the proposition expressed by such uses.
Hare’s view that the evaluations of thick terms are detachable has led to debates over how exactly thick terms are evaluative. For example, is the evaluation merely pragmatically associated with the term in a way that would make it detachable? Or are these evaluations part of its truth-conditions? These debates are discussed in section 5.
b. McDowell’s Disentangling Argument
Even if Foot is right that there are descriptions that are sufficient for the correct application of thick terms, it need not be the case that these descriptions are necessary. John McDowell’s Disentangling Argument is believed to show that there could not be a description that is both necessary and sufficient for the correct application of a thick term. In this argument McDowell is primarily arguing against non-cognitivists, such as Hare, who accept the strong distinction between description and evaluation.
Before diving into the argument, recall that thick terms seem to straddle the strong distinction. For example, the claim that OJ committed murder seems to aim at stating a fact, which is a feature of descriptive claims (on the strong distinction). But this claim also seems evaluative; by calling it murder, rather than killing, we seem to be evaluating OJ’s action negatively. Thus, thick terms such as ‘murder’ call into doubt the strong distinction because they seem to be both descriptive and evaluative. This issue does not present any obvious challenge to those who accept only the weak distinction, since a term’s being evaluative on the weak-distinction does not preclude it from being fact-stating. How do proponents of the strong distinction meet this challenge?
A.J. Ayer is one non-cognitivist who holds that thick terms like ‘hideous’, ‘beautiful’, and ‘virtue’ are solely on the evaluative side of the strong distinction—they are purely non-factual, evaluative concepts (1946:108-13). Ayer’s view is counterintuitive, and, if generalized, would oddly entail that there is no fact as to whether OJ committed murder.
Most non-cognitivists disagree with Ayer, and claim that thick terms have hybrid meanings that contain two different kinds of content: a descriptive content and an evaluative content. This kind of view is called a Reductive View because it reduces the meaning of a thick term to a descriptive content along with a more basic evaluative content (for example, a thin concept).
McDowell’s Disentangling Argument targets a specific kind of Reductive View, one that is coupled with the strong distinction between description and evaluation. We may thus call his target “the Strong Reductive View”. McDowell assumes that Strong Reductive Views must hold that the thick concept’s descriptive content completely determines the thick concept’s extension. It does so by identifying a property that completely determines what does and does not fall within the thick concept’s extension. The evaluative content plays no role in determining what property the thick concept picks out, but is instead an attitudinal or prescriptive tag that explains the concept’s evaluative perspective.
McDowell’s argument against Strong Reductive Views invites us to consider the epistemic position of an outsider who does not share the evaluative perspective associated with a given thick term. Consider, for example, someone who fails to understand the sexual mores associated with ‘chaste’. Will this person be able to anticipate what this term applies to in new cases? Initially, one might think this is possible: is this not what anthropologists are trained to do? Williams, a proponent of McDowell’s argument, says that anthropologists must at least “grasp imaginatively” the evaluative point of ‘chaste’ (1985:142). She must imagine that she accepts the evaluative point of this term, at least for the purposes of anticipating its usage. Even this might be a problem for Strong Reductive Views. If a Strong Reductive View is correct, then there would be no need for an outsider to grasp the evaluative content of ‘chaste’, even imaginatively. After all, the descriptive content is supposedly what drives the extension of ‘chaste’, which means that an unsympathetic outsider could master its extension just by grasping the descriptive content and observing that it applies to all and only the features that the insiders call ‘chaste’. So, the Strong Reductive View seems to predict that an unsympathetic outsider could anticipate the insider’s usage of ‘chaste’. Many find this implausible.
McDowell’s argument has two premises: (1) If a Strong Reductive View is true of ‘chaste’, then an unsympathetic outsider could master the extension of ‘chaste’ (that is, she could know what things ‘chaste’ would apply to in new cases) without having any grasp of its evaluative content. But, (2) an unsympathetic outsider surely could not achieve this—she could not anticipate its usage if she stands completely outside the evaluative perspective of those who employ the concept. Therefore, the Strong Reductive View is not true of ‘chaste’ (1981:201-3). This sort of argument could be advanced with respect to any thick term and perhaps even thin ones.
The Disentangling Argument is sometimes thought to be a distinctive problem for all Reductive Views, not just Strong Reductive Views. But this is a mistake. Consider Reductive Views that accept only a weak distinction between description and evaluation: call such views “Weak Reductive Views”. Weak Reductive Views can allow that the evaluative content of ‘chaste’ picks out a property, and can therefore allow that this evaluative content plays a role in determining the extension of ‘chaste’. For example, if morally good is the evaluative content associated with ‘chaste’, and morally good picks out a property, then morally good can also play a role in determining the extension of ‘chaste’. This means that its extension need not be completely determined by its descriptive content. In this case, an unsympathetic outsider would be a very strange person—that is, someone who does not accept the evaluative point of morally good, even imaginatively. But such a person does not seem impossible.
To be sure, Weak Reductive Views could be vulnerable to the Disentangling Argument if they accept an additional claim, namely, that chaste is coextensive with a descriptive concept that is perhaps not encoded within the content of chaste. Consider an analogy: it is plausible that water and H2O are coextensive, even though neither concept is encoded within the other. If Weak Reductive Views hold that this situation is true of chaste and some descriptive concept D, which is not encoded in the content of chaste, then the Disentangling Argument could be run against these views. This type of Weak Reductive View predicts that an outsider could master the extension of ‘chaste’ just by grasping D and observing that insiders apply ‘chaste’ to all and only things that are D. Thus, the Disentangling Argument could be run against Weak Reductive Views if they accept the additional claim that chaste is coextensive with a descriptive concept.
However, the same problem also arises for Non-Reductive Views that accept this additional claim. Non-Reductive Views hold that thick concepts cannot be divided into distinct contents (more on this in section 3). And, strictly speaking, Non-Reductive Views are compatible with the additional claim just mentioned—that chaste is coextensive with a descriptive concept. If Non-Reductivists accept this additional claim—which would be uncharacteristic, though not inconsistent— then the combined view would also be vulnerable to the Disentangling Argument.
So, the Disentangling Argument can be used to target any view, Reductive or Non-Reductive, that holds thick concepts to be coextensive with descriptive concepts. It is thus a mistake to think the Disentangling Argument is a problem for all and only Reductive Views. The reason McDowell’s argument targets Strong Reductive Views is that these views appear fit to accept the problematic claim—that thick concepts are coextensive with descriptive concepts.
Most opponents of the Disentangling Argument reject premise (1), by showing that Strong Reductive Views can allow that an unsympathetic outsider could not master the extension of thick terms. This approach is discussed in section 3a. But Hare takes a different approach. He accepts the Strong Reductive View but rejects premise (2). Recall Hare’s way of arguing that there could be a descriptive concept that is extensionally equivalent to a thick concept. One can express this descriptive concept by muting the thick term’s evaluative content in one of two ways: either by using the thick term with a certain tone of voice or by placing scare-quotes around the term. Suppose that these methods successfully show that there is a purely descriptive concept—call it des-chaste—which is coextensive with chaste. In this case, an outsider could employ des-chaste to track the insider’s usage of ‘chaste’.
One might object that Hare’s two methods of uncovering des-chaste reveal that this concept cannot be grasped without already grasping chaste. So, the interpreter in question would not be a genuine outsider. However, although Hare’s methods of uncovering des-chaste require a grasp of chaste, there is no automatic reason to assume that there could not be another method of uncovering des-chaste without grasping chaste—for example, by learning des-chaste independently of any encounter with insiders or their value system.
Would the outsider’s grasp of des-chaste help her anticipate the insider’s use of ‘chaste’ in new cases? Hare thinks so. According to Hare, the outsider could anticipate their use in new cases because she could observe similarities between the old cases and the new cases, and infer based on those similarities that ‘chaste’ would or would not apply in new cases (1997: 61). Of course, McDowell and followers would not be convinced by this claim, since they hold that the similarities between such cases are evaluative. In other words, they accept what is known as “the shapelessness hypothesis”—that the extensions of thick terms are only unified by evaluative similarity relations.
The fundamental disagreement between Hare and McDowell concerns whether the shapelessness hypothesis is true. Is there any reason to accept shapelessness? This hypothesis is sometimes supported by the fact that it can explain why premise (2) of the Disentangling Argument is plausible—that is, it can explain why an unsympathetic outsider could not master the extension of ‘chaste’ (Roberts 2013: 680). Of course, this idea won’t convince someone like Hare who rejects premise (2). Something more should be said. In section 5b, further support for shapelessness is discussed.
It is worth noting that there is a common thread running through Hare’s replies to both Foot and McDowell. In both replies Hare claims that there could be a descriptive expression that is extensionally equivalent to a thick term. Without this claim he could not hold that des-chaste is coextensive with chaste. He also could not escape Foot’s objection to the is-ought gap by claiming that the evaluations of thick terms are detachable.
c. Williams on Ethical Truth
If successful, McDowell’s argument would show that there could not be a wholly descriptive expression coextensive with a thick term. Furthermore, if we assume that utterances involving thick terms are sometimes true, McDowell’s argument might show that there are evaluative facts—facts that can only be characterized in evaluative terms. But this is too quick. After all, sentences involving thick terms might only be true in a minimalist sense. On the minimalist theory of truth, to say that ‘lying is dishonest’ is true is equivalent to saying simply that lying is dishonest. This is all that can be significantly said about the truth of this sentence. Since nothing more can be said, its mere truth does not entail the existence of a fact to which the sentence corresponds. So, even if McDowell’s argument succeeds, the truth of sentences involving thick terms does not guarantee that there are facts that can only be characterized in evaluative terms.
To get a fuller picture of how the truth of such sentences might support the existence of evaluative facts, we must turn to Bernard Williams. According to Williams, utterances involving thick terms show promise of being more than just minimally true, whereas utterances involving thin terms do not. The main difference, according to Williams, is that thick terms bear a close connection to the concept of knowledge and to the notion of a helpful advisor.
Consider the connection between knowledge and thick concepts. There is a precedent for thinking that certain epistemic difficulties arise for thin concepts but not thick ones. For example, how exactly can one come to know that lying is sometimes wrong? This plausible truth, which involves a thin concept, seems to be neither analytic nor a posteriori. Some ethicists have thus held that it is synthetic a priori and is knowable by a special faculty of the mind, such as moral intuition. But many ethicists find this view implausible and have instead turned to thick concepts for an account of ethical knowledge. It may seem more plausible that we can know a posteriori that a thick concept applies, for example, that a certain action is cowardly. According to Mark Platts, we can know such truths “by looking and seeing,” without any special faculty, such as moral intuition (1988: 285).
Williams agrees that thick ethical knowledge is more feasible than thin ethical knowledge. His reasons, however, are different from Platts’. Williams holds that the concept of knowledge is associated with the notion of a helpful informant or advisor, and that there are only such advisors with regard to the application of thick concepts, not thin ones. According to Williams, a helpful advisor is someone who is better than others at seeing that a certain outcome, policy, or action falls under a concept. And Williams holds that there are helpful advisors with regard to thick concepts. For example, the advice that a certain action would be cowardly “can offer the person who is being advised a genuine discovery” (1993: 217). Are there helpful advisors with regard to thin concepts? Not according to Williams—“not many people are going to say ‘Well, I didn’t understand the professor’s argument for his conclusion that abortion is wrong, but since he is qualified in the subject, abortion probably is wrong’” (1995: 235). Thus, according to Williams, utterances involving thick terms show promise of being more than minimally true, given that thick terms have this association with knowledge and helpful informants.
Even though Williams holds that utterances involving thick terms can be more than minimally true, he does not think these utterances can be objectively true—that is, true independently of particular perspectives. To illustrate this, Williams asks us to compare ethics with science. Although there are disagreements in science, there is at least some chance of scientists converging on a perspective-free account of the world, and this convergence would be best explained by the correctness of that account. But Williams thinks our ethical opinions stand no chance of converging on an account of how the world really is independently of particular perspectives—at any rate, if they do converge, this will not be because these opinions have tracked how the world is independently of perspective (1985: 135-6). So, on Williams’ view, the truth of ethical opinions is dependent upon perspective, and hence, not objectively true.
How exactly is the truth of utterances involving thick terms dependent upon perspective? Williams illustrates his view by asking us to envision a hyper-traditional society which is maximally homogenous and minimally reflective. Williams holds that ethical reflection primarily employs thin concepts, and that this hyper-traditional society is unreflective because it only employs thick concepts. According to Williams, their utterances involving thick terms can be true in their language L, which is distinct from our language since L does not express thin concepts whereas our language does. Williams thinks it is undeniable that the thick concepts expressed in L need not be expressible with our language, which means that we may be unable to use our language to assert or deny what insiders say with their thick terms. Of course, it is possible for a sympathetic outsider, such as an anthropologist, to understand and speak L. But, according to Williams, the outsider cannot formulate an equivalent utterance in his own language because “the expressive powers of his own language are different from those of the native language precisely in the respect that the native language contains an ethical concept which his doesn’t” (1995: 239).
To explain Williams’ view further, we can borrow an example from Allan Gibbard (1992). Imagine that gopa is a positive thick concept expressible in L but not expressible in our language. Although a reflective outsider cannot assert that x is gopa in her own language, she can likely reject the proposition that x is good, which involves a thin concept. And if the local’s thick concept gopa entails good, then the outsider could reject the insider’s statement as false by denying that x is good. So, it looks like the insider’s statement can be assessed as false from an outside perspective. However, Williams does not accept that the insider’s concept gopa entails good. A judgment involving a thin concept, such as good, “is essentially the product of reflection” which comes about “when someone stands back from the practices of the society and its use of the concepts and asks… whether these are good ways in which to assess actions…” (1985:146). But this hyper-traditional society is unreflective, which means they do not employ the thin concept good. So, according to Williams, there’s no reason to assume that their concept gopa entails good, which means the outsider’s denial that x is good poses no clear threat to the truth of ‘x is gopa’.
On Williams’ view, if a person from the hyper-traditional society has knowledge that x is gopa, but later reflects and draws the conclusion that x is good, this reflection may unseat his previous knowledge by making it so that this person no longer possesses the traditional concept gopa (1995: 238). In this way, “rejection can destroy knowledge,” because the one who reflects may thereby cease to possess their traditional thick concepts (1985, 148).
Williams has here outlined a possibility in which utterances involving thick terms could be true in a way that is dependent upon perspective—in particular, the perspective of a person who speaks a certain ethical language, such as L. Opposition to Williams comes from at least two fronts.
First, McDowell (1998) and Hilary Putnam (1990) have both objected to Williams’ conception of science as providing a perspective-free account of the world. They hold that science is perspective-dependent. Although this objection would destroy Williams’ contrast between science and ethics, it would not mean that ethical truth is perspective-free, but only that science and ethics are both perspective-dependent, which leaves ethics in good company.
A second source of opposition is known as Thin Centralism—the view that thin concepts are conceptually prior to, and independent of, thick concepts. If good is conceptually prior to gopa, then the locals cannot grasp gopa without also grasping good. This would mean that Williams is wrong to claim that the locals may lose the concept gopa when they draw the reflective inference from x is gopa to x is good. Furthermore, the outsider who denies that x is good is required, by way of this inference, to deny that x is gopa. So, the truth or falsity of ‘x is gopa’ would not depend on what is knowable solely from the local’s perspective, contrary to Williams’ view. It may depend partly on whether x is good, which may be discernible from the outsider’s perspective.
Williams rejects Thin Centralism, though he does not give any arguments against it (1995: 234). He is plausibly a Thick Centralist, holding that thick concepts are conceptually prior to, and independent of, thin concepts. That is, one cannot grasp a thin concept without grasping some thick concept or other, but not vice versa. This view can be understood by way of a color analogy. The concept color is a very general concept that, according to Susan Hurley, cannot be understood independently of specific color concepts, such as red, green, etc. (1989: 16). And according to Thick Centralism, thin concepts like good cannot be grasped independently of specific thick concepts like courageous, kind, and so on.
It might be true that the grasp of color requires the grasp of some specific color concept (for example, red), but is the opposite also true? Does the grasp of red require a grasp of color? If so, then the color analogy would actually support what is known as the No-Priority View—thick and thin concepts are conceptually interdependent with neither one being prior to the other (Dancy 2013). It is worth noting that the No-Priority View is not available to Williams, since this view would mean that the local’s grasp of gopa requires the grasp of a thin concept, and this presents the same problem that Thin Centralism presents for Williams’ view.
d. Thick Concepts in Normative Ethics
It is often urged that ethicists should stop focusing as much on thin concepts and should expand or shift attention towards the thick (Anscombe 1958; Williams 1985). As a result, there has been much attention paid to thick concepts within meta-ethics, primarily regarding the issues discussed above. Have thick concepts also played a substantive role in normative ethics? They have to some extent. Normative ethics is partly concerned with the question of what kind of person one should be. And the virtue and vice concepts, which are paradigmatic thick concepts, have played a significant role in these discussions.
However, normative ethics is also concerned with the question of how one should act, and in this context it is common to focus on thin concepts, like right, wrong, and good. Of course, there are some thick concepts, such as just and equitable that figure into these discussions, but it is not immediately clear why it would matter whether these concepts are thick, rather than thin or purely descriptive. There is at least one attempt at giving thick concepts a substantive role in a theory of how to act. This comes from Rosalind Hursthouse’s virtue theory of right action.
Virtue theory is sometimes criticized for being unable to provide a theory of right action. The mere fact that virtues are character traits of persons does not mean that virtue concepts cannot be applied to actions. Actions can also be honest, courageous, patient, and so on. The problem is that these characterizations of action do not clearly tell us anything about rightness, which would be a major flaw of a normative ethical theory.
Hursthouse meets this criticism by providing a theory of right action in terms of virtue. She holds that an action is right just in case it is what a virtuous agent would characteristically do in the circumstances (1999: 28). The virtuous agent is one who has the virtuous character traits and exercises them. And a virtue is a character trait that a human being needs to flourish or live well. These particular virtues must be enumerated, but the list typically includes paradigmatic thick terms, such as ‘courage’, ‘honesty’, ‘patience’, ‘generosity’, and so on. Hursthouse explicitly claims that the virtue terms are thick (1996: 27). Does it matter for her view whether the virtue terms are thick? Hursthouse’s theory faces an objection, and it is in response to this objection that it might matter.
The objection alleges that the virtue theory of right action cannot provide clear action-guidance, whereas rival normative theories, such as deontology and utilitarianism, can provide clear action-guidance by generating rules, such as “Don’t lie” or “Maximize happiness.” According to this objection, the virtue theory of right action can only generate a very unhelpful rule: “Do what a virtuous person would do.” This rule is not likely to provide action-guidance. If you are a fully virtuous person, you will already know what to do and so would not require the rule. If you are less than fully virtuous, you may have no idea what a virtuous person would do in the circumstances, especially if you don’t know of anyone who is fully virtuous (indeed, such a person might be purely hypothetical). So, according to this objection, the virtue theory of right action cannot provide action-guidance.
In response, Hursthouse points out that every virtue generates positive instruction on how to act—do what is honest, charitable, generous, and so on. And every vice generates a prohibition—do not do what is dishonest, uncharitable, mean, and so on (1999: 36). So, one can get action-guidance without reflecting on what a hypothetical virtuous agent would do in the circumstances. According to Hursthouse, “the agent may employ her concepts of the virtues and vices directly, rather than imagining what some hypothetical exemplar would do” (1991: 227). For example, the agent may reason “I must not tell this lie, since it would be dishonest.” And since dishonesty is a vice, which no virtuous person would have, this agent will be directed towards right action.
Thus, it’s important for Hursthouse’s view that the virtue concepts are at least action-guiding. After all, imagine that the virtue concepts were wholly descriptive concepts of character traits, like slow, calm, or quiet. These descriptive concepts would not generate any prohibitions or positive instruction.
Does it matter whether the virtue concepts are thick rather than thin concepts? Hursthouse does not speak directly to this question, though she does claim that, if we are unclear on what to do in a circumstance, we can seek advice from people who are morally better than ourselves (1999: 35). And, here, Williams’ point about helpful advisors might be useful. If the virtue concepts were thin, then on Williams’ view there would be no helpful advisor with regard to whether the virtue concepts apply. But such advice is possible if the virtue concepts are thick. In short, it is important for Hursthouse that the virtue concepts are action-guiding. And, if Williams is right, it may also matter whether the virtue concepts are thick.
One potential challenge to Hursthouse’s reply might contest the traditional list of virtues, and claim that there is no reason to think this list, when properly enumerated, will contain thick action-guiding concepts. For example, why should we think that courageous will be on the list of virtues rather than a similar concept that rarely generates positive instruction (for example, gutsy)? In considering this objection, readers are advised to consult Hursthouse’s approach to enumerating the virtues (1999: Ch. 8).
Another potential challenge may come from Thin Centralism. Suppose that right is conceptually prior to, and independent of, courageous. In this case, it might be argued that the positive instruction generated by courage (for example, “Do what is courageous”) is wholly due to the action-guidingness of right. The latter is precisely what we wanted to explain, which means that Hursthouse’s reply might be uninformative. However, Hursthouse does not account for particular virtue concepts in terms of right. Furthermore, even if Thin Centralism is true, it could still be claimed that some other thin concept, such as good, is conceptually prior to thick virtue concepts. So, Hursthouse’s account cannot be deemed uninformative merely on the basis of Thin Centralism.
3. How Do Thick Concepts Combine Evaluation and Description?
Thin Centralists typically accept Reductive Views of the thick, which aim to analyze the meanings of thick terms by citing more fundamental concepts (for example, thin concepts and descriptive concepts). Proponents of these Reductive Views often aim at escaping the Disentangling Argument. In particular, they aim to reject premise (1) of that argument by showing that Reductive Views can consistently claim that an outsider could not grasp the extension of a thick term. This strategy proceeds by providing different versions of the Reductive View, which shall be discussed below.
It is worth noting that Reductive Views are typically neutral on whether the weak or strong distinction ought to be accepted. They also tend to be neutral on whether cognitivism or non-cognitivism is true. To be sure, Reductivism is often associated with non-cognitivists, like Hare, but there are some traditional cognitivists, like Henry Sidgwick and G.E. Moore, who hold Reductive Views of the thick (Hurka 2011: 7).
Those who reject Thin Centralism and accept the Disentangling Argument normally accept Non-Reductive Views, holding that the meanings of thick terms are evaluative and descriptive in some sense, though cannot be divided into distinct contents. The basic disagreement between Reductive and Non-Reductive views is on whether thick concepts are fundamental evaluative concepts or are complexes built up from more fundamental concepts (for example, thin concepts). These two approaches are compared in the following sections.
a. Reductive Views
In general, Reductive Views understand the meaning of a thick term as the combination of a descriptive content with an evaluative content. Different Reductive Views can be distinguished based on how they specify this general account. There are three main types of Reductive Views: (i) some views specify the sort of descriptive content within the analysis; (ii) some views specify the relation between evaluative and descriptive contents; and (iii) other views specify what the evaluative content is. There are also various ways of combining (i)-(iii).
Consider type (i) first. Daniel Elstein and Thomas Hurka provide two patterns of analysis that explain the descriptive content of a thick term in two different ways. On their first pattern of analysis, the descriptive content of a thick term is not fully specified within the meaning of the thick term. The meaning of the thick term may only specify that there are some good-making descriptive properties of a general type, without specifying exactly what these good-making properties are. For example, on their view, ‘x is just’ means ‘x is good, and there are properties XYZ (not specified) that distributions have as distributions, such that x has XYZ and XYZ make any distribution that has them good’. Elstein and Hurka hold that this kind of Reductive View is not a Strong Reductive View, because the thick concept does not have a fully specified descriptive content that determines the thick concept’s extension. Still, their view is available to non-cognitivists who accept the strong distinction. Most importantly, Elstein and Hurka believe their view allows non-cognitivists to claim that an outsider could not grasp the extension of ‘just’. Grasping that extension requires determining which properties of the general type are the good-making ones, and doing this requires evaluative judgments that the outsider is not equipped to make (2009: 521-2).
Elstein and Hurka’s second pattern of analysis involves an additional evaluation, which is embedded within the descriptive content. Many virtue and vice concepts are supposed to fit into this second pattern of analysis. For example, on their view, ‘an act x is courageous’ means roughly ‘x is good, and x involves an agent’s accepting risk of harm for himself for the sake of goods greater than the evil of that harm, where this property makes any act that has it good’ (2009: 527). The reference to goods is an embedded evaluation, and it is impossible to determine the extension of ‘courageous’ without determining what can count as goods—but determining this requires an evaluation which the outsider is not equipped to make (2009: 526).
Stephen Burton offers an account of type (ii) by clarifying the relationship between descriptive and evaluative contents of a thick concept. A simple way of expressing the relationship between a thick term’s evaluative and descriptive contents is as follows: ‘x is D and therefore x is E’, where D is a description and E is an evaluation that follows from that description. The trouble is that this simple formula entails that D is coextensive with the thick term itself, and this makes the simple formula vulnerable to the Disentangling Argument. So, Burton modifies the account so that the thick term is not coextensive with D. Burton proposes that a thick term’s meaning can be analyzed as follows: ‘x is E in virtue of some particular instance of D’. For example, ‘courageous’ means ‘(pro tanto) good in virtue of some particular instance of sticking to one’s guns despite great personal risk’. Here, the thick term only groups together those cases in which a thing is E in virtue of some particular instance of D. But D does not entail E, and so is not coextensive with the thick term. Thus, an outsider’s ability to track D will not be enough for her to track the insider’s use of the thick term. But what does it mean for E to depend upon a particular instance of D? For Burton, this means that E “depends on the various different characteristics and contexts” of D, and so D alone is not sufficient for E. Various different characteristics and contexts, which are not encoded in the meaning of the thick term, also need to obtain (1992: 31).
Now consider a view of type (iii). Most Reductive Views hold that thick concepts inherit their evaluative-ness from a constituent thin concept. However, Christine Tappolet proposes that they are instead evaluative on account of specific affective concepts, like admirable, pleasant, desirable, and amusing. These concepts are not thin concepts, but Tappolet holds that they are the basic evaluative constituents of thick concepts, like courageous and generous. For example, Tappolet’s analysis of courageous goes like this: ‘x is courageous’ means ‘x is D and x is admirable in virtue of this particular instance of D’, where D is a description. Essentially, Tappolet accepts Burton’s account of the relation between descriptive and evaluative contents, but modifies the account so that it incorporates affective concepts instead of thin concepts. In doing so, she parts company with other Reductivists by rejecting Thin Centralism. She rejects Thin Centralism because she holds that understanding a thin concept, such as good, requires an understanding of certain specific concepts such as pleasant and admirable (2004: 216).
An objection may arise: affective concepts are also thick concepts, but they do not fit into Tappolet’s analyses of thick concepts. This is because one affective concept, such as admirable, cannot be defined in terms of another, such as pleasant. How then should we account for these affective concepts? Tappolet’s answer is that affective concepts are to be treated differently from other thick concepts, like courageous. In particular, she treats positive affective concepts as determinates of the determinable good, and she holds that determinates cannot be analyzed in terms of their determinables. Roughly, the determinable/determinate relation is a relation of general concepts to more specific ones, where the general determinables are common to each specific determinate, but there is nothing distinguishing the determinates from each other except for the determinates themselves—for example, the only thing that distinguishes red from other colors is redness itself.
Edward Harcourt and Alan Thomas (2013) have pointed to a tension between Tappolet’s treatment of affective concepts and her treatment of other thick concepts. What reason is there to think courageous is analyzable but not admirable? Tappolet holds that admirable is unanalyzable because there is no way of stating the relevant descriptive content associated with admirable (2004: 217). In response, Harcourt and Thomas claim that this is just as much a problem for her analyses of other thick concepts. For example, it is far from clear what should be substituted for ‘D’ within Tappolet’s analysis of courageous. This objection leads Harcourt and Thomas to a Non-Reductive View, according to which all thick concepts are treated as determinates of thin concepts like good and bad (2013: 25-9).
One problem is that there is reason to think that both parties to this dispute are mistaken in claiming that affective concepts cannot be analyzed. There is a simple Reductive account of the meaning of ‘admirable’, which is not represented by any of the above views—‘admirable’ just means ‘worthy of admiration’. Similar accounts can be given for other affective concepts. If this simple analysis is correct, then Tappolet and Harcourt and Thomas are mistaken about the unanalyzability of thick affective concepts.
Some of the analyses provided above may not withstand potential counterexamples. But it is worth pointing out that our inability to state an adequate analysis for a given thick term does not show that its meaning is unanalyzable. Analyses can only be attempted by using a language, and it is possible that our language’s vocabulary does not contain the expressions needed for providing an adequate analysis of the thick term’s meaning. Reductive Views are only committed to the view that the meanings of thick terms involve appropriately related evaluative and descriptive contents; they are not committed to there being any actual language that can express these contents in a way that counts as a satisfactory analysis.
What then is the point in providing these patterns of analysis? The point is to illustrate the general ways in which descriptive and evaluative contents can be combined within the meanings of thick terms. Typically, Reductive Views only commit to the possibility of there being a certain general type of analysis and do not commit to the particular details of their sample analyses (for example, Elstein and Hurka, 2009: 531).
Are there any advantages to Reductivism about the thick? According to Hurka, Reductivism allows cognitivists to explain the difference between virtues and their cognate vices (2011: 7). For example, both courage and foolhardiness involve a willingness to face risk for a cause. What then differentiates courage from foolhardiness? It is plausible that courage requires that the cause be good enough to justify the risk, whereas foolhardiness does not require this. This explanation appeals to a thin concept—good—that many Reductivists are perfectly willing to cite as a constituent of courage. However, there is nothing forbidding Non-Reductivists from also claiming that courage requires a good enough cause, provided they do not take this content to be a constituent of courage. So, this may be no clear advantage for Reductivism.
Another potential advantage is that Reductivism allows us to explain a wide variety of evaluative concepts by recognizing only a few basic ones, such as ought or good. Moreover, if a successful analysis can be achieved, then Non-Reductivists are committed to positing two meanings where Reductivists can posit only one. For example, if the meaning of ‘admirable’ can be analyzed with ‘worthy of admiration’, then Reductivists can claim that the meanings of these two expressions are identical, whereas Non-Reductivists must hold that these meanings are distinct. Lastly, Reductive Views can explain how a thick term is both evaluative and descriptive, since the evaluative-ness of a thick term’s meaning is inherited from a constituent content that is paradigmatically evaluative (for example, a thin concept); and the descriptiveness of its meaning is inherited from a constituent descriptive content. In the next section, we shall examine whether Non-Reductivists can provide a comparable explanation.
b. Non-Reductive Views
Non-Reductive Views hold that the meanings of thick terms are both descriptive and evaluative, although these features are not due to constituent contents within the meanings of thick terms. In slogan form, thick concepts are irreducibly thick. For example, the thick term ‘brutal’ expresses a sui generis evaluative concept, which is not a combination of bad or wrong along with some descriptive content. The challenge is for Non-Reductive Views to explain how these meanings are both evaluative and descriptive. As noted, Reductive Views explain this in terms of constituent contents. The challenge is for Non-Reductive Views to explain how the meanings of thick terms are both descriptive and evaluative without appealing to constituent contents.
This challenge should be weakened in light of the fact that our notions of the descriptive and the evaluative are theoretically-loaded. Non-Reductive theorists do not accept the strong distinction between description and evaluation, because they hold that thick terms are both evaluative and capable of picking out properties. The strong distinction precludes this possibility, unless the content of the thick term is built up from constituents, which Non-Reductivists reject. Non-Reductivists typically accept some version of the weak distinction, but the present challenge cannot be framed in terms of this distinction. On the weak distinction, the descriptive is identical to the non-evaluative. This means that Non-Reductivists are being asked to explain how the meanings of thick terms are both evaluative and not evaluative, which is plainly contradictory. How then are we to understand the challenge faced by Non-Reductive Views?
The challenge can be framed in a two-fold way: (I) Non-Reductive Views need to explain what the meanings of thick terms have in common with the meanings of thin terms—this would explain the evaluative-ness of the thick term’s meaning. And (II) they also need to explain what the meanings of thick terms have in common with the meanings of paradigmatic descriptive terms—this would explain the descriptiveness of the thick term’s meaning.
Starting with (I), Jonathan Dancy holds that both thick and thin terms express concepts that have “practical relevance,” a feature that is lacked by descriptive concepts. To see what he means, consider how thick and thin concepts differ from descriptive concepts like water. The latter can make a practical difference in some circumstances: water may be something to seek when stranded in a desert. But in this case, we must explain the practical relevance of water by citing other properties in the particular situation, such as being thirsty, in a desert, and so forth. By contrast, there is nothing to be explained when a thick or thin concept makes a practical difference, since their practical relevance “is to be expected.” For example, it is expected that courage is something to aspire for and admire, and this does not require explanation by citing other concepts. Dancy expands upon this by claiming that competence with a thick concept requires not only an ability to determine when the concept applies, but also an ability to determine what practical relevance its application has in the circumstances. Competence with a descriptive concept requires only the former, not the latter (2013: 56).
At this point, Reductive theorists may emphasize a potential benefit of their view—they have a simple explanation for why competence with a thick concept requires an ability to determine its practical relevance. In particular, competence with a thick concept requires an ability to determine its practical relevance because its constituent thin concept is practically relevant. But Dancy and other Non-Reductivists cannot appeal to this explanation. How then can they explain the practical relevance of thick concepts?
Conceptual competence can surely be explained without appealing to constituent concepts, otherwise competence with a simple concept would be inexplicable. One potential explanation, which does not appeal to constituent concepts, comes from Harcourt and Thomas (2013: 24-7). Harcourt and Thomas hold that thick concepts are related to good and bad analogously to how red is related to colored. On their view, colored is not a constituent of red, since there are no other concepts that can be combined with colored to yield red. Instead, red is a determinate of the determinable color. Similarly, the thin concept bad is not a constituent of the thick concept brutal—according to Harcourt and Thomas, there is no other concept that can be combined with bad to yield brutal. Instead, brutal is a determinate of the determinable bad. Moreover, given that brutal is a determinate of bad, it can be claimed that the practical relevance of brutal is inherited from the practical relevance of bad, even though the latter is not a constituent of the former.
Debbie Roberts provides another explanation of what the meanings of thick terms have in common with thin terms. Many ethicists claim that thick and thin terms express and induce attitudes, or condemn, commend, and instruct. Roberts takes a different approach. On her view, a concept is evaluative in virtue of ascribing an evaluative property. A concept ascribes a property if and only if the real definition of the property it refers to is given by the content of that concept. What then is an evaluative property? According to Roberts, a property P is evaluative if (i) P is intrinsically linked to human concerns and purposes; (ii) there are various lower-level properties that can each make it the case that P is instantiated (that is, P is multiply-realizable); but (iii) these lower-level properties do not necessitate that P is instantiated (that is, other features must also obtain). Roberts holds that both thick and thin concepts ascribe properties that satisfy (i)-(iii) (2013).
One potential problem is that there might be some paradigmatically descriptive properties that satisfy (i)-(iii). Consider a particular mental state with moral content, such as the belief that lying is wrong. The property of being in this state is intrinsically linked to human concerns and purposes, since it is a moral belief. And if belief-states are multiply realizable, then this property will satisfy (ii) as well. And finally, if there are lower-level brain states that make it the case that someone has this belief, without necessitating it, then (iii) will be satisfied as well. Thus, certain mental properties may satisfy (i)-(iii), even though they seem descriptive. Roberts could reply by holding that the above-mentioned moral belief is not linked to human concerns and purposes in the right sort of way.
Turning to (II): What do the meanings of thick terms have in common with paradigmatic descriptive terms? Recall that a key point about paradigmatic descriptive terms is that these terms are capable of representing properties. Non-Reductive theorists can point out that thick terms also seem capable of representing properties. This, in fact, was the fundamental motivation for focusing on thick terms to begin with. And nearly all ethicists (except for Ayer) would agree that this is true. It plainly seems true that ‘courage’ is capable of picking out a property, and in this way ‘courage’ shares something in common with paradigmatic descriptive terms like ‘red’ and ‘water’.
Another key point about descriptive terms is that they are intuitively different from thin terms like ‘wrong’ and ‘good’. Indeed, a central motivation for classifying terms as descriptive is to exclude thin terms like ‘good’ and ‘wrong’ from paradigmatically descriptive expressions. How then do thick terms share this feature with the descriptive—that of being different from thin terms? There are two general answers that Non-Reductivists provide. On one approach, thick and thin differ in kind. On the other, thick and thin differ only in degree but not in kind. These general approaches are discussed in the next section. Reductivist theories are also discussed under each approach.
4. How Do Thick and Thin Differ?
a. In Kind: Williams’ View
Williams is a Non-Reductive theorist who holds that thick and thin differ in kind. On his view, thick terms are both world-guided and action-guiding. For Williams, a world-guided term is one whose usage is “controlled by the facts”—that is, there are conditions for its correct application and competent users can largely agree that it does or does not apply in new situations. An action-guiding term is one that is “characteristically related to reasons for action” (1985: 140-1). For Williams, thick terms are both world-guided and action-guiding, whereas thin terms are action-guiding but “do not display world-guidedness” (1985: 152).
There are some potential problems for Williams’ distinction. First, Williams’ claim that thin terms “do not display world-guidedness” seems to commit him to something controversial—namely, that non-cognitivism is true of thin terms. Other Non-Reductivists accept Williams’ characterization of thick terms, but hold that thin terms are also world-guided and action-guiding (Dancy 2013: 56). If they are right, then Williams’ distinction between thick and thin is compromised.
Nevertheless, there is a straightforward way of distinguishing between thick and thin, which does not assume non-cognitivism about thin terms. On this view, thin terms express wholly evaluative concepts, whereas thick terms express concepts that are partly evaluative and partly descriptive. This straightforward distinction gives us a difference in kind between thick and thin. The trouble is that it too appears to be theoretically loaded (much like Williams’ distinction). This straightforward distinction presupposes a Reductive View, since it holds that thick concepts are built up from evaluative and descriptive components. Another potential problem is that it is not clear whether thin concepts are wholly evaluative. For example, it looks as though the thin concept ought implies the descriptive concept can, assuming the ought-implies-can principle (Väyrynen 2013: 7). Of course, as Dancy points out, the mere fact that one concept entails another does not mean that the latter is a constituent of the former—cow entails not-a-horse, but neither is a constituent of the other (2013: 49).
A second potential problem for Williams’ view, and the straightforward view just mentioned, comes from Samuel Scheffler. Scheffler points out that there are many evaluative terms that are hard to classify as either thick or thin. Consider ‘just’, ‘fair’, ‘impartial’, ‘rights’, ‘autonomy’, and ‘consent’. Upon reflecting on such concepts, Scheffler suggests that world-guidedness is a matter of degree and that a division of ethical concepts into thick and thin is a “considerable oversimplification” (1987: 417-8).
In a later essay, Williams replies to Scheffler by agreeing that thickness comes in degrees, and that “there is an important class of concepts that lie between the thick and the thin” (1995: 234). This reply, however, does not entail that Williams must reject his earlier view. Assume that thickness and thinness each come in degrees, and that thick and thin do not exhaust all evaluative concepts. These two claims do not entail that the difference between thick and thin is merely a matter of degree. This can be seen via analogy: belief that P and disbelief that P are exclusive categories that each come in degree, and which do not exhaust all doxastic states since suspension of judgment is also possible. But the difference between belief that P and disbelief that P is not merely a matter of degree. These states are different in kind, assuming the former is about the affirmative proposition P while the latter is about the negation ¬P. Similarly, thick and thin could also differ in kind, even if they are exclusive degree categories that do not exhaust all evaluative concepts. Thus, Scheffler’s considerations and Williams’ concessions do not entail that Williams’ earlier view is false.
b. Only in Degree: The Continuum View
Still, many theorists have seized upon Scheffler’s point and have claimed that thick and thin differ only in degree, not in kind. Some consider this to be the standard view (Väyrynen 2008: 391). On this view, thin and thick lie on opposite ends of a continuum of evaluative concepts, with no sharp dividing line between them. For example, good and bad might lie on one end of the continuum, with kind, compassionate, and cruel on the other end. There are at least two gradable notions that can serve to distinguish the ends of this continuum—degrees of specificity or amounts of descriptive content. Greater specificity, or greater amounts of descriptive content, provides a thicker concept with a narrower range of application. Non-Reductive theorists typically focus on the greater specificity of thick terms. Reductive theorists can choose either path; indeed, they can explain the greater specificity of a thick concept in terms of how much descriptive content it has as a constituent. In general, a concept must have enough specificity, or enough descriptive content, for it to reside on the thicker end of the continuum.
Support for the continuum view may come from several considerations. First, consider that some thin concepts have narrower ranges of application than other thin concepts. For example, good can apply to actions, people, food, cars, and so on, whereas right cannot apply to all these things. This may suggest that there are degrees of thinness. Second, as already noted, some thin concepts have descriptive entailments—for instance, the thin concept ought entails the descriptive concept can. Even if can is not a constituent of ought, this entailment at least narrows down the range of application for ought, which could bring it closer to the thick end of the spectrum, even if it is still fairly thin. Thirdly, there seems to be a vague area between thick and thin—for example, it is not clear whether just has enough specificity or enough descriptive content for it to count as thick, but it is also hard to classify this concept as thin. So, perhaps just is a borderline case between thick and thin.
Given these considerations, one may be tempted to hold that thick and thin do not differ in kind. But the above considerations do not strictly entail this. Again, analogous considerations hold for both belief and disbelief—some beliefs have narrower ranges of application than other beliefs (for example, rabbits cannot have complex mathematical beliefs though they can have perceptual beliefs). There is also a vague area between belief and disbelief, yet these two doxastic states differ in kind. So, these considerations only seem to support the Continuum View if there is no way of drawing a distinction in kind. But Hare has provided a distinction in kind that has largely escaped notice.
c. In Kind: Hare’s View
Hare is a Reductivist who holds that thick and thin are distinct in kind, not merely in degree. He holds that thick terms have both descriptive and evaluative meanings associated with them. Interestingly, Hare holds that this is also true of thin terms. Thus, for Hare, thin terms are not wholly evaluative, contrary to the straightforward view mentioned in 4a.
What then is the difference between thick and thin? The difference has to do with the relationship that the two meanings bear to the term in question. A thin term is one whose evaluative meaning is “more firmly attached” to it than its descriptive meaning. And a thick term is one whose descriptive meaning is “more firmly attached” than its evaluative meaning (1963: 24-5). Although Hare agrees that being firmly attached is “only a matter of probability and degree” (1989: 125), this does not mean that the distinction between thick and thin is only a matter of degree. Indeed, Hare’s phrase “more firmly attached” actually marks out a difference in kind. Consider an analogy: a child who is more firmly attached to her mother than to her father is different in kind from a child who is more firmly attached to her father than to her mother. Both are different in kind from a child who is equally attached to both parents. So, the language that Hare uses actually suggests three possible categories of evaluative terms—thick, thin, and neither. Although Hare never mentions the third category, it is at least a potential category for Scheffler’s examples of the neither thick nor thin.
What does Hare mean by “more firmly attached”? For Hare, the more firmly attached meaning is the one that is less likely to change when language users alter their usage of the term. For example, it is less likely that ‘right’ will eventually be used to evaluate actions negatively (or neutrally) than that it will be used to describe lying, promise-breaking, killing, torture, and so forth. The reason is that, if we start using ‘right’ to evaluate actions negatively (or neutrally), there is a great chance that we will be misunderstood or accused of misusing the word. In this sense, the evaluative meaning of ‘right’ is more firmly attached than its descriptive meaning. But just the opposite is the case for thick terms like ‘generous’. If we start using ‘generous’ to evaluate actions negatively, we will not be misunderstood (for example, Ebenezer Scrooge could use ‘generous’ negatively and we would still understand him). Yet, if we started using ‘generous’ to describe selfish acts, for example, then we will be misunderstood or accused of misusing the term. In this sense, the descriptive meaning of ‘generous’ is more firmly attached than its evaluative meaning (1989: 125).
Hare frames his distinction in terms of descriptive and evaluative meanings, which assumes a Reductive View. But his distinction and thought experiment can be formulated without assuming a Reductive View. Rather than talking about descriptive and evaluative meanings, we could instead speak of two different speech acts—describing and evaluating—that are commonly performed through ordinary uses of the terms. Hare’s thought experiment can be formulated by changing the speech acts that we typically perform with the term. For example, although we ordinarily use ‘generous’ to perform a speech act of positive evaluation, a speaker who uses it to evaluate negatively would still be understood.
At the outset it was said that thick concepts are evaluative concepts that are substantially descriptive. Thin concepts, by contrast, are not substantially descriptive. Exactly what ‘substantially descriptive’ means can now be clarified, depending on which of the above three views is accepted. On Williams’ view, being substantially descriptive is matter of being world-guided. On the Continuum View, being substantially descriptive is a matter of having enough specificity or enough descriptive content. On Hare’s view, being substantially descriptive is a matter of having a descriptive meaning that is more firmly attached than its evaluative meaning.
5. Are Thick Terms Truth-Conditionally Evaluative?
The putative significance of the thick depends upon a crucial assumption about how thick terms are evaluative. Several of the arguments and hypotheses discussed in 2.a-c assume that thick terms are evaluative as a matter of truth-conditions—that is, the conditions that must obtain for utterances involving thick terms to express true propositions.
To see how this assumption is made, first recall Foot’s argument. If ‘x is rude’ were not evaluative as a matter of truth-conditions, then its truth would not require anything evaluative, and there would not be anything evaluative following from the purely descriptive claim that x causes offense by indicating lack of respect. Hare’s response, that the evaluation of ‘rude’ is detachable, is a denial of the assumption that ‘rude’ is evaluative in its truth-conditions. Consider McDowell’s premise (2) of the Disentangling Argument. It’s often assumed that the only reason an outsider could not master the extension of ‘chaste’ must be that the truth-conditions associated with ‘chaste’ incorporate something evaluative, which the outsider cannot track. Moreover, the shapelessness hypothesis states that the extensions of thick terms are only unified by evaluative similarity relations. This suggests that something evaluative must obtain for utterances involving thick terms to express true propositions.
Nevertheless, it is controversial that thick terms are evaluative as a matter of truth-conditions. Generally, ethicists agree that thick terms are somehow associated with evaluative contents, but not all agree that these contents are part of the truth-conditions of utterances involving thick terms. How else can a thick term be associated with evaluative content, if not by way of truth-conditions?
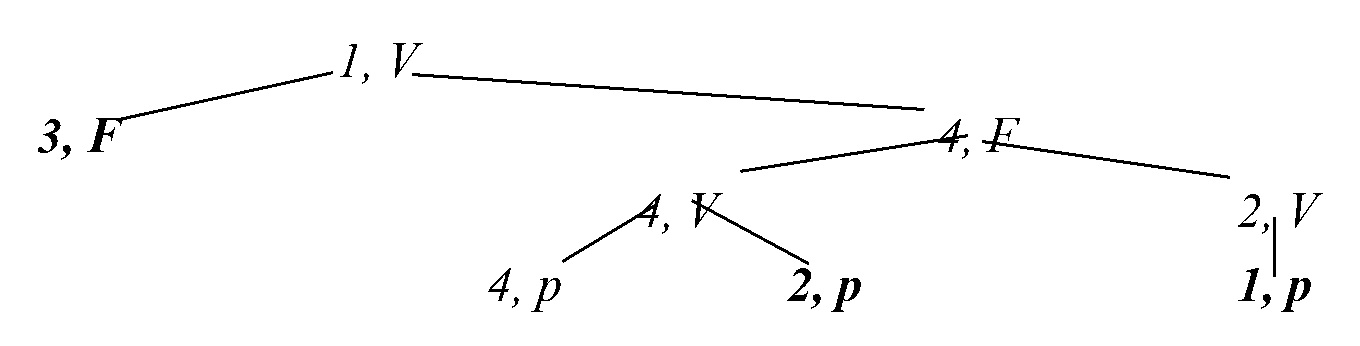
Our use of language can communicate lots of information that is not part of the truth-conditions of what we say. In each of the following cases, a speaker B communicates a proposition that is not part of the truth-conditions of B’s utterance. In this first example, the proposition is communicated by way of presupposition:
B: “I don’t regret going to the party.”
Presupposition: that B went to the party.
Plausibly, B’s utterance could express a true proposition even if its presupposition is false—one way to have no regrets about going to a party is by simply not going. This presupposition can plausibly be apart of the background of the conversation at hand, but not part of the truth-conditions of B’s utterance.
Now consider a slightly different example, involving a phone conversation between A and B. In this case, B communicates a proposition by way of conversational implicature:
A: “Is Bob there?”
B: “He’s in the shower.”
Conversational Implicature: that Bob cannot talk on the phone right now.
This proposition is not part of the truth-conditions of B’s utterance—it is obviously possible that Bob can talk on the phone while in the shower. Instead, this proposition is inferred from B’s utterance by relying on conversational maxims and observations from context (for example, that A and B are having a phone conversation, and that B would not provide irrelevant information about Bob’s showering unless he is trying to convey that Bob cannot talk).
Now consider a third example, where B communicates a proposition by way of conventional implicature:
B: “Sue is British but brave.”
Conventional Implicature: that Sue’s bravery is unexpected given that she is British.
The proposition communicated in this example is not part of the truth-conditions of B’s utterance. One way to see this is by comparing B’s utterance with “Sue is British and brave.” These two utterances would seem to be true in all the same circumstances. But the latter does not communicate the implicature in question. This implicature is detachable, in the sense that a truth-conditionally equivalent statement need not have the implicature in question. Although Hare does not mention conventional implicature, his view about the detachability of a thick term’s evaluation could be explained in terms of conventional implicature.
In short, there are many ways to communicate information without it being part of the truth-conditions of the utterance. There are three widely-discussed pragmatic mechanisms—presupposition, conversational implicature, and conventional implicature—and there are others as well. Some hold that utterances involving thick terms do not convey evaluations that are part of their truth-conditions, but instead convey them via some pragmatic mechanism. This view is known as the Pragmatic View. It should be noted that some proponents of the Pragmatic View write as though their view entails that there are no thick concepts (Blackburn 1992). In other words, if the only evaluation associated with courage is pragmatically associated with it, then these philosophers will say that courage is not really a thick concept. Still, others who accept the Pragmatic View are happy to talk of these concepts as thick (Väyrynen 2013). This article does so as well.
The traditional view, however, is that thick terms are evaluative as a matter of their truth-conditions—this view is known as the Semantic View. The follow two sections discuss the Pragmatic and Semantic View, respectively.
a. Pragmatic View
Sometimes the Pragmatic View is supported by the idea that thick terms are variable in what evaluations they express. Typically, a given thick term conveys a particular evaluation that is either positive or negative, but not both. It is natural to assume that the term conveys this evaluation (whichever it is) in all assertive contexts. But it turns out that many paradigmatic thick terms can be used to evaluate something negatively in some contexts while positively in others. There are two ways of illustrating this variability.
The first involves combining a thick term with comparative constructions, such as ‘too’ or ‘not…enough’. For example, ‘lewd’ is typically negative, but it appears to convey something positive in the following quote: “this year’s carnival was not lewd enough” (Blackburn 1992: 296). Similarly, ‘tidy’ is typically positive, but can be used to convey something negative if one is criticized as “too tidy” (Hare 1952: 121). These considerations may be taken to show that thick terms are not evaluative as a matter of truth-conditions—if these thick terms have an evaluation as part of their truth-conditions, one might think ‘not lewd enough’ and ‘too tidy’ should be semantically awkward, but they are not.
Opponents to this argument may claim that the atypical evaluation in each case can be explained solely by reference to ‘too’ and ‘not… enough’, without claiming that ‘lewd’ and ‘tidy’ express an atypical evaluation. Consider that ‘too F’ and ‘not F enough’ are evaluative even when F is a wholly non-evaluative expression—for example, one might say that a color sample is too red, which seems to characterize the sample negatively. Here, the negative evaluation is solely because of ‘too’, and so it should be no surprise if this word generates a negative evaluation when combined with ‘tidy’. Furthermore, there are contexts where F is clearly seen as a positive quality even when it is combined with ‘too’. Borrowing an example from Väyrynen, a military commander could count a soldier as too courageous to waste on a simple mission, and instead select him for a more formidable mission where his courage would be needed (2011: 7). Thus, it appears the atypical evaluation can be attributed to the modifiers ‘too’ and ‘not…enough’ rather than the thick term itself.
The second sort of example pertains to utterances that convey an atypical evaluation without employing a comparative construction. For example, even though ‘cruel’ typically conveys a negative evaluation, it might be that the cruelty of an action was “just what made it such fun” (Hare 1981: 73). Or, even though ‘frugal’ typically conveys a positive evaluation, a person could be condemned as frugal if his “main job is dispensing hospitality” (Blackburn 1992: 286).
A worry associated with examples of this second sort is that the atypical evaluation can be explained in ways that are consistent with the Semantic View. For instance, it might be claimed that the examples involve non-literal uses of the thick term, or that they only convey the alternative evaluation by way of speaker meaning, and not word meaning. Alternatively, one could hold that thick terms are context sensitive, and that there are several different evaluations conveyed by the thick term depending on the context of utterance. In this case, the thick term would be evaluative as a matter of truth-conditions —it is just that those truth-conditions incorporate different evaluations in different contexts (Väyrynen 2011: 8-14).
Another argument for the Pragmatic View comes from Pekka Väyrynen (2013), who focuses on objectionable thick terms. Recall that objectionable thick terms embody values that ought to be rejected. Potential examples include ‘lewd’, ‘perverse’, and ‘blasphemous’, and ‘chaste’. The last of these terms seems to embody the view that a certain kind of sexual restraint is praiseworthy. Those that reject this view regard ‘chaste’ as objectionable—one can refer to such individuals as chastity-objectors. Chastity-objectors tend to exhibit interesting linguistic behavior. They would obviously be reluctant to assert that, say, John is chaste; but they are also reluctant to utter non-affirmative sentences like the following:
(a) John is not chaste.
(b) Is John chaste?
(c) Possibly, John is chaste.
(d) If John is chaste, then so is Mary.
None of these utterances imply that the truth-conditions of ‘chaste’ are satisfied. So, if chastity-objectors are reluctant to utter (a-d), this leads us to expect that the evaluation projects outside of the truth-conditions of ‘chaste’. It is worth noting that this argument is not restricted to examples like ‘chaste’, ‘perverse’, ‘lewd’, and ‘blasphemous’. According to Väyrynen, virtually any thick term could be regarded as objectionable, at least in principle, which means that his argument should extend even to examples like ‘courageous’ and ‘murder’.
In addition to arguing against the Semantic View, proponents of the Pragmatic View need to explain what pragmatic mechanism is responsible for the evaluations of thick terms. The three pragmatic mechanisms cited above can provide potential explanations, but Väyrynen rejects these explanations in favor of an alternative view. He proposes that the evaluative implications of paradigmatic thick terms are “not-at-issue” in normal contexts. Roughly, an implication is at-issue if it is part of the main point of the conversation at hand, and it is not-at-issue if it is part of the background (2013: ch. 5). Väyrynen takes this pragmatic view to be “superior to its rivals by standard methodological principles” from the philosophy of language and linguistics (2013: 10).
Proponents of the Semantic View can provide at least two lines of response to Väyrynen’s argument involving objectionable thick terms. For the first, it is important to note that Väyrynen explains the objector’s reluctance by holding that (a-d) all project the same evaluation beyond the truth-conditions of ‘chaste’. But one might hold that there is no single evaluation projected by all of (a-d)—instead, there are at least two different claims implied throughout (a-d). For example, just as ‘not happy’ conversationally implicates ‘unhappy’, it is equally plausible that ‘not chaste’ conversationally implicates ‘unchaste’. Since chastity-objectors clearly do not want to imply that John is unchaste, they are reluctant to assert (a). Moreover, (b-d) conversationally imply (or assert) that John might be chaste. If chastity-objectors believe it is impossible for anyone to be chaste, then they will be reluctant to assert (b-d). This piecemeal approach calls into doubt Väyrynen’s claim that a single evaluation projects beyond the truth-conditions of ‘chaste’. Moreover, these ways of explaining the reluctance of chastity-objectors are perfectly consistent with the Semantic View (Kyle 2013a: 13-19).
For a second response, it can be pointed out that even Väyrynen’s preferred explanation is consistent with the Semantic View (Kyle 2015). The mere fact that an evaluation projects outside of the truth-conditions of ‘chaste’ does not entail that there is no evaluation within those truth-conditions. For example, it is possible that ‘John is chaste’ conveys two evaluations, one that is part of its truth-conditions, and another that projects outside of them. This possibility can be illustrated with the affirmative sentence ‘It is good that Sue is moral’, which has an evaluative content within its truth-conditions and also projects one outside those truth-conditions. Consider the corresponding non-affirmative sentences:
(a′) It is not good that Sue is moral.
(b′) Is it good that Sue is moral?
(c′) Possibly, it’s good that Sue is moral.
(d′) If it is good that Sue is moral, then we should applaud her.
An evaluative content—that Sue is moral—is implied by each of (a′-d′), as well as the affirmative sentence. So this evaluation projects much like the evaluation that Väyrynen thinks is projected by ‘chaste’. But none of this precludes the affirmative statement from having a different evaluation as part of its truth-conditions, namely the evaluation associated with ‘good’. Of course, this doubling of evaluation will have no purchase unless there is reason to think there is an evaluation within the truth-conditions of ‘chaste.’
b. Semantic View
What reason is there to think the evaluations of thick terms might be part of their truth-conditions? One potential reason stems from considering additional linguistic data. Notice that the following claim seems highly awkward:
(e) Sue is generous and not good in any way.
Similar statements can be provided using negative thick terms and ‘not bad in any way’. The Semantic View provides a straightforward explanation of the awkwardness of (e). This view can claim that (e) is a contradiction, assuming goodness-in-a-way is a part of the truth-conditions associated with ‘generous’ (Kyle 2013a). This, of course, is only one potential explanation—there may be other ways of explaining the awkwardness of (e), for example, by claiming that ‘generous’ presupposes or conventionally implicates an evaluation that incorporates goodness-in-a-way. Just as before, the issue must be decided by figuring out which view is the best explanation of this and other linguistic data. The matter is up for debate.
Still, one might object that the Semantic View is ill-suited to explain the oddity of (e), since this view mistakenly predicts that (e) would sound odd in every context, yet there are some unusual contexts in which (e) would not sound odd. For example, imagine Ebenezer Scrooge uttering (e) in a context where generosity is seen as a bad thing. (e) might not seem awkward in this context. However, it is a mistake to think that the Semantic View predicts that (e) is awkward in all contexts. Consider that its second conjunct involves a quantifier expression—‘any’—and quantifiers are notoriously context-sensitive. In one context, it might be true to say ‘O.J. Simpson is not good in any way’; but in other contexts, where being a good athlete is relevant to discussion, an utterance of the same sentence could be false. Similarly, the second conjunct in (e) is true or false relative to context. And it is only in contexts where generosity is a relevant way of being good that (e) should sound contradictory. In contexts where generosity is not a relevant way of being good—such as Scrooge’s context—(e) should not sound contradictory. In those contexts, the first part of (e) could be true while the second part is false (Kyle 2013a).
It’s worth emphasizing that the linguistic data about thick terms does not strictly entail the Semantic View, or the Pragmatic View. Rather, the proponents of such views only claim that their respective view is part of the best explanation of a wide-body of linguistic data involving thick terms. This matter has only been explored in recent years, with proponents on each side (Kyle 2013a; Väyrynen 2013).
Another way of supporting the Semantic View stems from the shapelessness hypothesis, that the extensions of thick terms are only unified by evaluative similarity relations. If the shapelessness hypothesis is true, then the truth-conditions associated with thick terms must be at least partly evaluative. But what reason is there to accept the shapelessness hypothesis?
The main support for shapelessness comes from the idea that thick terms seem to “outrun” any descriptive characterizations we can give to the items in their extensions (Kirchin 2010). Consider the various types of action that can be considered kind—shoveling snow for a neighbor, giving chocolate to a child, adopting a stray cat, standing up to someone’s bully, paying a complement to a friend, and so on. Furthermore, there are some actions that would be considered kind in some circumstances even though the opposite action would be considered kind in other circumstances—for example, telling the truth is sometimes kind but so is telling a white lie. Can these various actions be descriptively classified in a way that allows us to correctly characterize kind actions in new cases? The descriptive classification might be a long disjunction of unrelated features, a shapeless classification that would be unhelpful in confronting new cases.
One way of opposing this argument is to show that the various actions mentioned above can be unified under a shapely descriptive classification. For example, each of the above actions seems to benefit others by treating them as ends in themselves. This shapely classification helps us classify at least some new cases of kind action (for example, giving food to a homeless person). And benefit can be understood in purely descriptive terms—for example, as the increasing of happiness. So, it is not obvious that shapelessness is actually supported by the outrunning data given above, although other data could perhaps be provided.
Suppose that thick terms do outrun our ability to provide wholly descriptive characterizations of their extensions. Väyrynen argues that this does not support the Semantic View, because our inability to give a descriptive classification for a thick term can be explained even if the Semantic View is false. Consider that, for some terms T, the extension of T cannot be unified under relations that are expressible in independently intelligible T-free terms (that is, terms that can be understood independently of T). For example, it might be that the extension of ‘pain’ across all sentient animals cannot be unified without employing the word ‘pain’ itself. Now return to the question of what explains our inability to give a wholly descriptive characterization of the extension of ‘kind’. It might be that the only way to characterize its extension is by employing the word ‘kind’ itself. But this would not be a descriptive classification, if the Pragmatic View were true of ‘kind’. It is just that the evaluative-ness of ‘kind’ would be explained by a pragmatic mechanism, rather than its truth-conditions. So, if ‘kind’ is a term like T, then one could not give a wholly descriptive classification of the extension of ‘kind’, even if the Semantic View is false (2013 193-201).
6. Broader Applications
Thick concepts have been an interest primarily among ethicists, although these concepts have made an entrance into discussions in other areas, such as aesthetics, metaphysics, philosophy of law, moral psychology, and epistemology. This section focuses mainly on epistemology’s recent discussions on thick concepts, since these discussions have been the most extensive (outside of ethics). But the discussions from the first four areas shall be briefly summarized.
In aesthetics, there is much discussion about thick aesthetic concepts, like gaudy, elegant, delicate, and brilliant. However, many of these discussions are centered on the question of whether there are any thick aesthetic concepts at all. In this context, it is often assumed that an aesthetic concept is not thick if it is only pragmatically associated with evaluative content (recall that this assumption is sometimes made in ethics as well). So, the discussions over whether there are any thick aesthetic concepts often mirrors the discussions in ethics on whether thick concepts are only pragmatically evaluative, or whether they are evaluative as a matter of truth-conditions (Bronzon 2009; Zangwill 2001). It is worth noting that Burton’s Reductive View (discussed in 3a) is explicitly aimed at accounting for thick aesthetic concepts, as well as ethical ones.
In metaphysics, Gideon Yaffe criticizes two competing views on the nature of freedom of will—one that equates freedom of will with self-expression and one that equates it with self-transcendence. Yaffe then holds that the debates between these approaches have proceeded from the (at least implicit) assumption that freedom of will is a descriptive concept. He argues that there are facts about freedom of will that are best explained if freedom of will is instead assumed to be thick. According to Yaffe, the descriptive content of this concept would correspond to the features that make the agent either self-expressive or self-transcendent. But, according to Yaffe, this is not enough to account for freedom of will. We must also determine whether “the agent has choices that come about through worthwhile processes, processes possessing a certain kind of value” (2000: 219-20). And it is this kind of value that corresponds to the evaluative content of freedom of will.
In the philosophy of law David Enoch and Kevin Toh (2013) point out that legal statements often straddle the divide between the descriptive and the evaluative. They put forth the hypothesis that many legal statements express thick concepts. Potential examples of such thick concepts may include crime, constitutional, inheritance, and infringement, though Enoch and Toh focus primarily on the concept legal, which they argue is a thick concept. The descriptive content of legal consists in its representation of certain social facts, and its evaluative content is a kind of endorsement. They do not assert that the thickness of legal can by itself settle debates over the nature of law. But they hold that its classification as thick can situate these debates within a broader philosophical context analogous to that of ethics, and can introduce new options for thinking about the nature of law.
Thick concepts also play a role in Gabriel Abend’s critique of current moral psychology and neuroscience. Abend argues that moral psychologists and neuroscientists unwarrantedly restrict their research to thin ethical concepts, but ignore thick ones. In particular, these scientists attempt to understand the psychological or neural bases for moral judgments, and they do so by testing various subjects’ judgments involving thin concepts like right and permissible. But judgments involving thick ethical concepts, like cruel and courageous, have scarcely been featured in these experiments. This is no small oversight, given “that thick concepts appear in some or much of people’s moral lives” (2011: 150). Abend also argues that this problem cannot be fixed merely by expanding out psychological and neurological research to include thick ethical judgments, because thick concepts “challenge the conception of a hardwired and universal moral capacity in a way that thin concepts do not” (2011: 145-6). In advancing this last point, Abend relies on the Disentangling Argument and the shapelessness hypothesis, as well as the claim that thick concepts presuppose institutional and cultural facts that do not hold universally.
Outside of ethics, the most extensive discussions on thick concepts occur in epistemology. In 2008, a special issue of the journal Philosophical Papers (vol. 37 no. 3) was devoted to thick concepts in epistemology. Examples of thick epistemic concepts include concepts like intellectual curiosity, truthfulness, open-mindedness, and dogmatic; these are contrasted with thin epistemic concepts, which are typically illustrated with concepts like justification, rationality, and knowledge. The editors of this issue hold that “traditional epistemology has tended towards using the thin concepts in theorizing,” but “these thin epistemic concepts are far less prevalent in everyday discourse than the thick epistemic” (2008: 342). The overarching question of this collection is whether epistemology would benefit from substantive investigations of thick epistemic concepts.
One way of addressing this question is simply to do a substantive investigation of a particular thick epistemic concept, and to show that epistemological theories are enhanced by the investigation. Two contributors to the Philosophical Papers collection take this approach. Catherine Elgin focuses on the concept trustworthy. She argues that trustworthiness does not reduce to justified or reliable true belief, but can help to explain why justified or reliable true beliefs are valuable (2008: 371-87). Harvey Siegel considers whether education is an epistemic virtue concept, and whether it makes sense to classify it as thick. Siegel is skeptical about the helpfulness of the thin/thin distinction, but, to the extent that this distinction is viable, he maintains that education is “more thick than thin.” He also seeks to clarify the relationship between education and virtue epistemology (2008: 467).
The other contributors focus on general issues concerning thick epistemic concepts. Heather Battaly’s contribution seeks to address an objection advanced by Simon Blackburn against Non-Reductive Views. According to Blackburn, Non-Reductive Views mistakenly imply that the differences in how we respond to, say, lewdness would not count as genuine disagreements, because the disputants would be employing different concepts and therefore talking past one another. For example, a person who thinks the carnival was not lewd enough might be employing a different concept from someone who disvalues lewdness, because there would be “no detachable description, no ‘semantic anchor,’ that they can share” (1992: 297-99). (This is an expanded version of the variability objection discussed in section 5a). Battaly responds by arguing that certain thick epistemic concepts, such as open-minded, are subject to combinatorial vagueness—these concepts have several independent conditions of application, but there is no sharp distinction between the conditions that are necessary or sufficient and those conditions that are neither. Battaly holds that disputants can share the same vague concept, while disagreeing over which conditions are necessary and/or sufficient. Battaly maintains that this allows them to have genuine disagreements about whether the concept refers to an epistemic virtue. According to Battaly, this at least shows that virtue epistemologists can disagree about the epistemic virtues without talking past one another (2008: 435-54).
Väyrynen’s contribution focuses on whether thick and thin epistemic concepts can be distinguished in ways comparable to thick and thin ethical concepts, and on whether a focus on thick epistemic concepts can lead to a preferable epistemology. Regarding the first issue, he argues that the way thick and thin concepts are typically distinguished in ethics provides no straightforward distinction between thick and thin epistemic concepts (2008: 390-95). Regarding the second, he argues that neither semantics nor substantive epistemological theory provides a basis for assigning thick epistemic concepts theoretical priority over thin epistemic concepts (2008: 395-408). Väyrynen concludes by claiming that we so far lack good reasons for taking a theoretical turn to a thick epistemology.
Despite Väyrynen’s final conclusion, the Philosophical Papers collection contains an explicit defense of the view that epistemology should expand its focus to thick epistemic concepts. Bernard Williams pushed for a similar expansion in the ethical sphere. And the comparison here brings up an important question, which is the main question of Alan Thomas’ contribution: Can Williams’ treatment of thick ethical concepts be applied analogously in the epistemic sphere? Recall that Williams holds that utterances involving thick ethical concepts cannot be objectively true. Thus, if epistemologists want to model their theory of thick epistemic concepts after Williams’ view in ethics, it appears they will not be able to claim that there are objectively true claims involving thick epistemic concepts. Thomas, however, points out that Williams’ non-objectivism in ethics “is based on the assumption that there are a variety of social worlds, structured by plural sets of thick ethical concepts.” But Williams’ view of thick epistemic concepts, such as truthfulness, allows for the possibility of “only one epistemic world.” According to Thomas, truthfulness is “such a central need of human life that it can be abstractly modeled in a way that… [is] culturally invariant” (2008: 368).
Guy Axtell and J. Adam Carter focus on outlining a positive account for how thick epistemic concepts could play a central role in epistemological theory. The account begins by claiming that epistemic value should be a central focus in epistemology, and that not all epistemic values can be reduced to the value of truth (or to some other single epistemic good). Other values, such as open-mindedness, “can be useful in articulating our epistemic aims,” even if they cannot be thusly reduced (2008: 418). Axtell and Carter also reject Thin Centralism in the epistemic sphere—the view that “general concepts like ‘justified’ and ‘ought’ are logically prior to and independent of specific reason-giving thick epistemic concepts of virtue and vice” (2008: 418). In the epistemic sphere, ‘justified’ and ‘ought’ are primarily used to evaluate beliefs, but the rejection of Thin Centralism allows that there could be fundamental ways of evaluating agents with virtue and vice concepts, and that these evaluations may not be reducible to belief evaluations. The above tenets open up the possibility of, what Axtell and Carter call, a “second-wave of virtue epistemology.” This contrasts with the “first-wave” which takes thick epistemic concepts to be theoretically important primarily because they play a role in analyzing knowledge. On the second wave of virtue epistemology, thick epistemic concepts are “a subject for research in their own right, apart from whatever role they might have in explaining knowledge” (2008: 427).
Many authors in the Philosophical Papers collection take knowledge to be a paradigmatic example of a thin epistemic concept (Battaly 2008: 435; Axtell and Carter 2008: 427; Thomas 2008: 363; Väyrynen 2008: 392; Kotzee and Wanderer 2008: 339). It is not immediately clear whether their arguments rely substantively on this assumption, but the assumption has been contested in a separate context. Brent Kyle argues that knowledge is actually a thick concept. According to Kyle, knowledge is best accounted for as a close relation between a descriptive content—true belief—and an evaluative content—justification. If successful, this argument would establish that traditional epistemology has already focused on at least one thick concept—namely knowledge. But Kyle’s main goal is not to defend the traditional focus of epistemological theories. Instead, he aims to argue that the thickness of knowledge can explain why the Gettier Problem arises. He does so by arguing that the Gettier Problem is a specific instance of a general problem about analyzing thick concepts. It is worth noting that his argument takes no stand on whether thick concepts can be analyzed, or on whether the Gettier Problem is resolvable (Kyle 2013b).
Generally speaking, thick concepts have become a source of optimism for many philosophers who find traditional research within normative disciplines to be myopic, stagnant, or misdirected. Nevertheless, it is still a matter of debate whether a plausible theory of thick concepts actually has the implications typically hoped for. In particular, the literature on thick concepts still contains lively debates regarding fundamental issues such as the Disentangling Argument, the shapelessness hypothesis, non-reductivism, and the Semantic View. And if proponents of the significance of thick concepts make assumptions regarding these controversial issues, then their views will be met with significant opposition, at least until these issues are resolved. But, on the flip side, if opposing theorists account for all normativity with thin concepts, and take these concepts to be non-factual, they too will meet significant opposition. The recent debates about thick concepts are largely responsible for this. Ultimately, whatever approach one takes to these fundamental issues, it is clear that theories of value and normativity cannot be complete unless they give some attention to the thick.
7. References and Further Reading
- Abend, G. 2011, “Thick Concepts and the Moral Brain,” European Journal of Sociology 52, 143-72.
- Anscombe, E. 1958, “Modern Moral Philosophy,” Philosophy 33, 1-19.
- Axtell, G. and A. Carter, 2008, “Just the Right Thickness: A Defense of Second-Wave Virtue Epistemology,” Philosophical Papers 37, 413–434.
- Ayer, A.J. 1946, Language, Truth, and Logic, Dover, New York.
- Battaly, H. 2008, “Metaethics Meets Virtue Epistemology: Salvaging Disagreement about the Epistemically Thick,” Philosophical Papers 37, 435–454.
- Blackburn, S. 1992, “Through Thick and Thin,” Proceedings of the Aristotelian Society, suppl. vol. 66, 285-99.
- Bronzon, R. 2009, “Thick Aesthetic Concepts,” The Journal of Aesthetics and Art Criticism 67:2, 191-99.
- Burton, S. 1992, “‘Thick’ Concepts Revisited,” Analysis 52, 28-32.
- Dancy, J. 2013, “Practical Concepts,” in S. Kirchin (ed.) Thick Concepts, Oxford University Press, Oxford.
- Dancy, J. 1995, “In Defense of Thick Concepts,” Midwest Studies in Philosophy 20, 263-79.
- Elgin, C. 2008, “Trustworthiness,” Philosophical Papers 37, 371-87.
- Elstein, D. and T. Hurka, 2009, “From Thick to Thin: Two Moral Reduction Plans,” The Canadian Journal of Philosophy 39, 551-36.
- Enoch, D. and K. Toh 2013, “Legal as a Thick Concept,” in W.J. Waluchow and S. Sciaraffa (eds.), Philosophical Foundations of the Nature of Law, Oxford University Press, Oxford.
- Foot, P. 1958, “Moral Arguments,” Mind 67, 502-13.
- Geertz, C. 1973, “Thick Description: Toward and Interpretive Theory of Culture,” The Interpretation of Cultures: Selected Essays, Basic Books, New York, 3-30.
- Gibbard, A. 1992, “Thick Concepts and Warrant for Feelings,” Proceedings of the Aristotelian Society, suppl. vol. 66, 285-99.
- Harcourt E. and A. Thomas, 2013, “Thick Concepts, Analysis, and Reductionism,” in S. Kirchin (ed.) Thick Concepts, Oxford University Press, Oxford.
- Hare, R.M. 1952, The Language of Morals, Oxford University Press, Oxford.
- Hare, R.M. 1963, Freedom and Reason, Oxford University Press, Oxford.
- Hare, R.M. 1989, Essays in Ethical Theory, Oxford University Press, Oxford.
- Hare, R.M. 1997, Sorting Out Ethics, Clarendon Press, Oxford.
- Hurka, T. 2011, “Common Themes from Sidgwick to Ewing,” in T. Hurka (ed.) Underivative Duty, Oxford University Press, Oxford, 6-25.
- Hurley, S. 1989, Natural Reasons, Oxford: Oxford University Press.
- Hursthouse, R. 1991, “Virtue Theory and Abortion,” Philosophy and Public Affairs 20, 223-46.
- Hursthouse, R. 1996, “Normative Virtue Ethics,” in Roger Crisp (ed.) How Should One Live? Oxford University Press, Oxford, 19-36.
- Hursthouse, R. 1999, On Virtue Ethics, Oxford University Press, Oxford.
- Jackson, F. 1998, From Metaphysics to Ethics: A Defence of Conceptual Analysis, Oxford University Press, Oxford.
- Kirchin, S. 2010, “The Shapelessness Hypothesis,” Philosophers Imprint 10, 1-28.
- Kotzee, B. and J. Wanderer, 2008, “Introduction: A Thicker Epistemology?” Philosophical Papers 37, 337-343.
- Kyle, B. 2013a, “How Are Thick Terms Evaluative?” Philosophers’ Imprint 13, 1-20.
- Kyle, B. 2013b, “Knowledge as a Thick Concept: Explaining Why the Gettier Problem Arises,” Philosophical Studies 165, 1-27.
- Kyle, B. 2015, “Review of ‘The Lewd, the Rude, and the Nasty: A Study of Thick Concepts in Ethics’ by Pekka Väyrynen,” The Philosophical Quarterly 65, 576-82.
- McDowell, J. 1981, “Non-Cognitivism and Rule-Following,” in S. Holtzman and C. Leich (eds.) Wittgenstein: To Follow a Rule, Routledge, London.
- McDowell, J. 1998, “Aesthetic Value, Objectivity, and the Fabric of the World,” in Mind, Value, and Reality, Harvard University Press, Cambridge, Mass.
- Platts, M. 1988, “Moral Reality,” in G. Sayer-McCord (ed.) Essays on Moral Realism, Cornell University Press, Ithaca, NY.
- Putnam, H. 1990, “Objectivity and the Science/Ethics Distinction,” in J. Conant (ed.) Realism with a Human Face, Harvard University Press, Cambridge, Mass.
- Roberts, D. 2011, “Shapelessness and the Thick,” Ethics 121, 489-520.
- Roberts, D. 2013, “It’s Evaluation, Only Thicker,” in S. Kirchin (ed.) Thick Concepts, Oxford University Press, Oxford.
- Ryle, G. 1971, “The Thinking of Thoughts: What is ‘Le Penseur’ Doing?” in Collected Papers 2, Routledge, London, 480-83.
- Scheffler, S. 1987, “Morality through Thick and Thin: A Critical Notice of Ethics and the Limits of Philosophy,” Philosophical Review 96, 411-34.
- Siegel, H. 2008, “Is ‘Education’ a Thick Epistemic Concept?” Philosophical Papers 37, 455-469.
- Tappolet, C. 2004, “Through Thick and Thin: Good and Its Determinates,” Dialectica 58, 207-21.
- Thomas, A. 2008, “The Genealogy of Epistemic Virtue Concepts,” Philosophical Papers 37, 345–369.
- Väyrynen, P. 2008, “Slim Epistemology with a Thick Skin,” Philosophical Papers 37, 389–412.
- Väyrynen, P. 2011, “Thick Concepts and Variability,” Philosophers’ Imprint 11, 1-17.
- Väyrynen, P. 2013, The Rude, the Lewd, and the Nasty: A Study of Thick Concepts in Ethics, Oxford University Press, Oxford.
- Williams, B. 1985, Ethics and the Limits of Philosophy, Harvard University Press, Cambridge, Mass.
- Williams, B. 1993, “Who Needs Ethical Knowledge?” in A Griffiths, Royal Institute of Philosophy, suppl. vol. 35, 213-22.
- Williams, B. 1995, “Truth in Ethics,” Ratio 8(3), 227-42.
- Yaffe, G. 2000, “Free Will and Agency at Its Best,” Philosophical Perspectives 14, 203-29.
- Zangwill, N. 2001, “The Beautiful, the Dainty, and the Dumpy,” in Metaphysics of Beauty, Cornell University Press, Ithaca, NY.
Author Information
Brent G. Kyle
Email: brent.kyle@usafa.edu
United States Air Force Academy
U. S. A.


 Parmenides of Elea was a
Parmenides of Elea was a  From Thales, who is often considered the first Western philosopher, to the Stoics and Skeptics, ancient Greek philosophy opened the doors to a particular way of thinking that provided the roots for the Western intellectual tradition. Here, there is often an explicit preference for the life of reason and rational thought. We find proto-scientific explanations of the natural world in the Milesian thinkers, and we hear Democritus posit atoms—indivisible and invisible units—as the basic stuff of all matter. With Socrates comes a sustained inquiry into ethical matters—an orientation towards human living and the best life for human beings. With Plato comes one of the most creative and flexible ways of doing philosophy, which some have since attempted to imitate by writing philosophical dialogues covering topics still of interest today in ethics, political thought, metaphysics, and epistemology. Plato’s student, Aristotle, was one of the most prolific of ancient authors. He wrote treatises on each of these topics, as well as on the investigation of the natural world, including the composition of animals. The Hellenists—Epicurus, the Cynics, the Stoics, and the Skeptics—developed schools or movements devoted to distinct philosophical lifestyles, each with reason at its foundation.
From Thales, who is often considered the first Western philosopher, to the Stoics and Skeptics, ancient Greek philosophy opened the doors to a particular way of thinking that provided the roots for the Western intellectual tradition. Here, there is often an explicit preference for the life of reason and rational thought. We find proto-scientific explanations of the natural world in the Milesian thinkers, and we hear Democritus posit atoms—indivisible and invisible units—as the basic stuff of all matter. With Socrates comes a sustained inquiry into ethical matters—an orientation towards human living and the best life for human beings. With Plato comes one of the most creative and flexible ways of doing philosophy, which some have since attempted to imitate by writing philosophical dialogues covering topics still of interest today in ethics, political thought, metaphysics, and epistemology. Plato’s student, Aristotle, was one of the most prolific of ancient authors. He wrote treatises on each of these topics, as well as on the investigation of the natural world, including the composition of animals. The Hellenists—Epicurus, the Cynics, the Stoics, and the Skeptics—developed schools or movements devoted to distinct philosophical lifestyles, each with reason at its foundation. Thomas Reid (1710-1796) made important contributions to the fields of epistemology and
Thomas Reid (1710-1796) made important contributions to the fields of epistemology and 
 Richard Gale was an American philosopher known for defending the
Richard Gale was an American philosopher known for defending the  Although Ludwig
Although Ludwig 
 It could be argued that ‘ancient aesthetics’ is an anachronistic term, since
It could be argued that ‘ancient aesthetics’ is an anachronistic term, since